Multiscale Modeling of Glacial Loading by a 3D Thermo-Hydro-Mechanical Approach Including Erosion and Isostasy
Abstract
:1. Introduction
- (i)
- it combines the global deformation of the lithosphere with the local simulation of pressure and temperature fields;
- (ii)
- it is built on available geophysical and geological information on the whole sedimentary system and relying on information available at selected wells;
- (iii)
- it allows considering the effects of erosion induced by glaciation, which is often neglected in previous studies.
2. Isostatic Glacial Rebound Model
A Viscoelastic Model for the Earth
3. The Thermo-Hydro-Mechanical Model Including Erosion
3.1. The Geological Model of a Sedimentary Basin
3.2. Extraction of the Basin Tilting From the Isostasy Model
3.3. A Poromechanical Approach to Coupled Hydro-Mechanical Effects
3.4. Thermal Effects
4. Results and Discussion
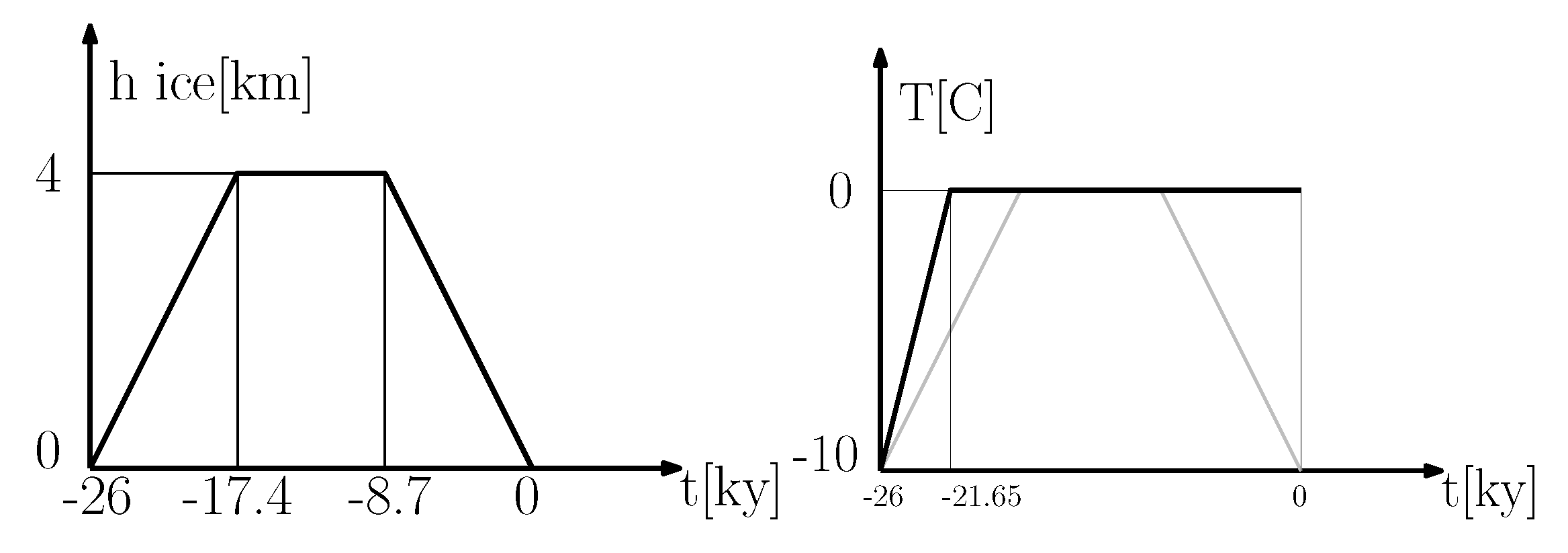
4.1. Results of the Glacial Rebound Model
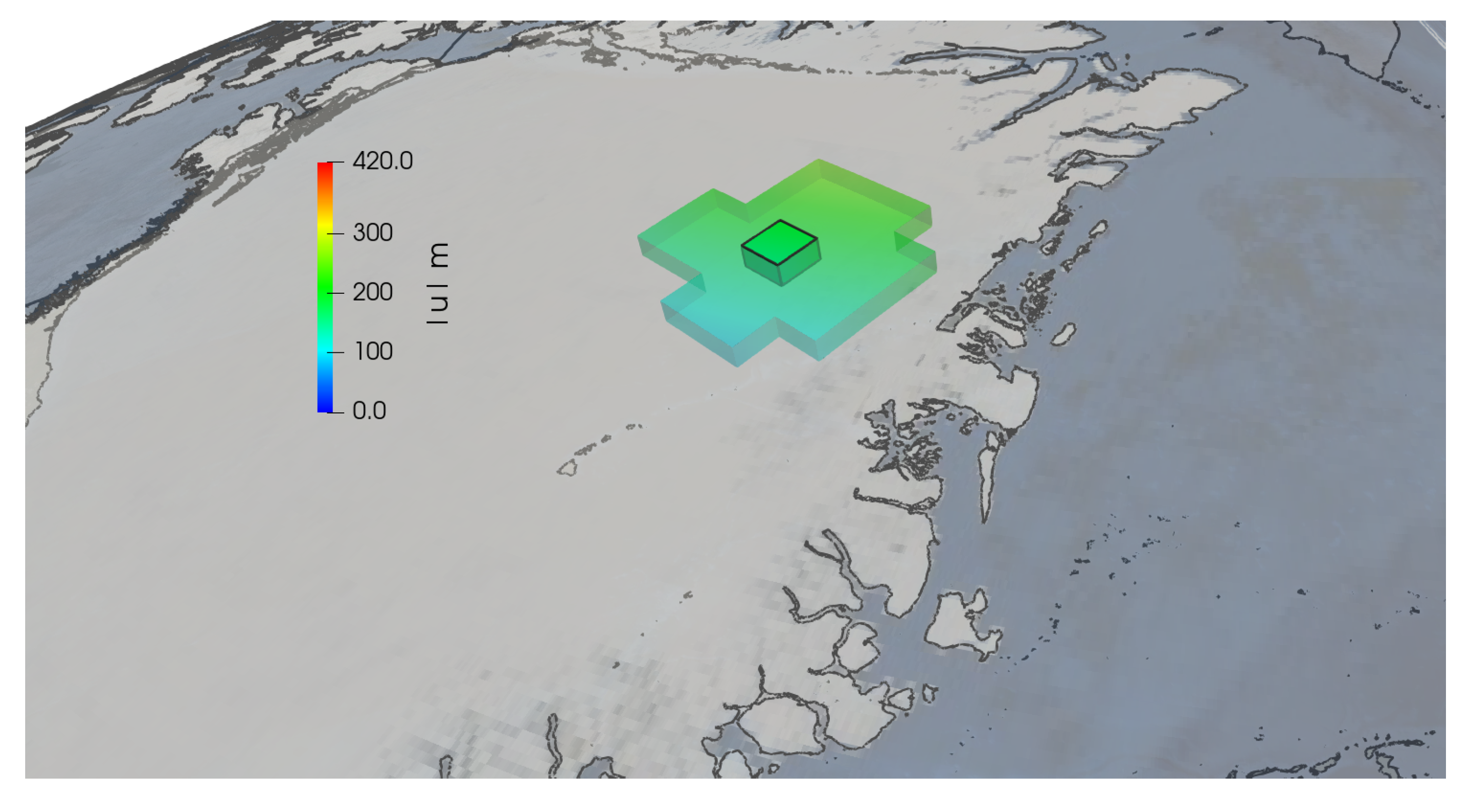
4.2. Results of the Kriging Algorithm for the Geological Basin Model Setup
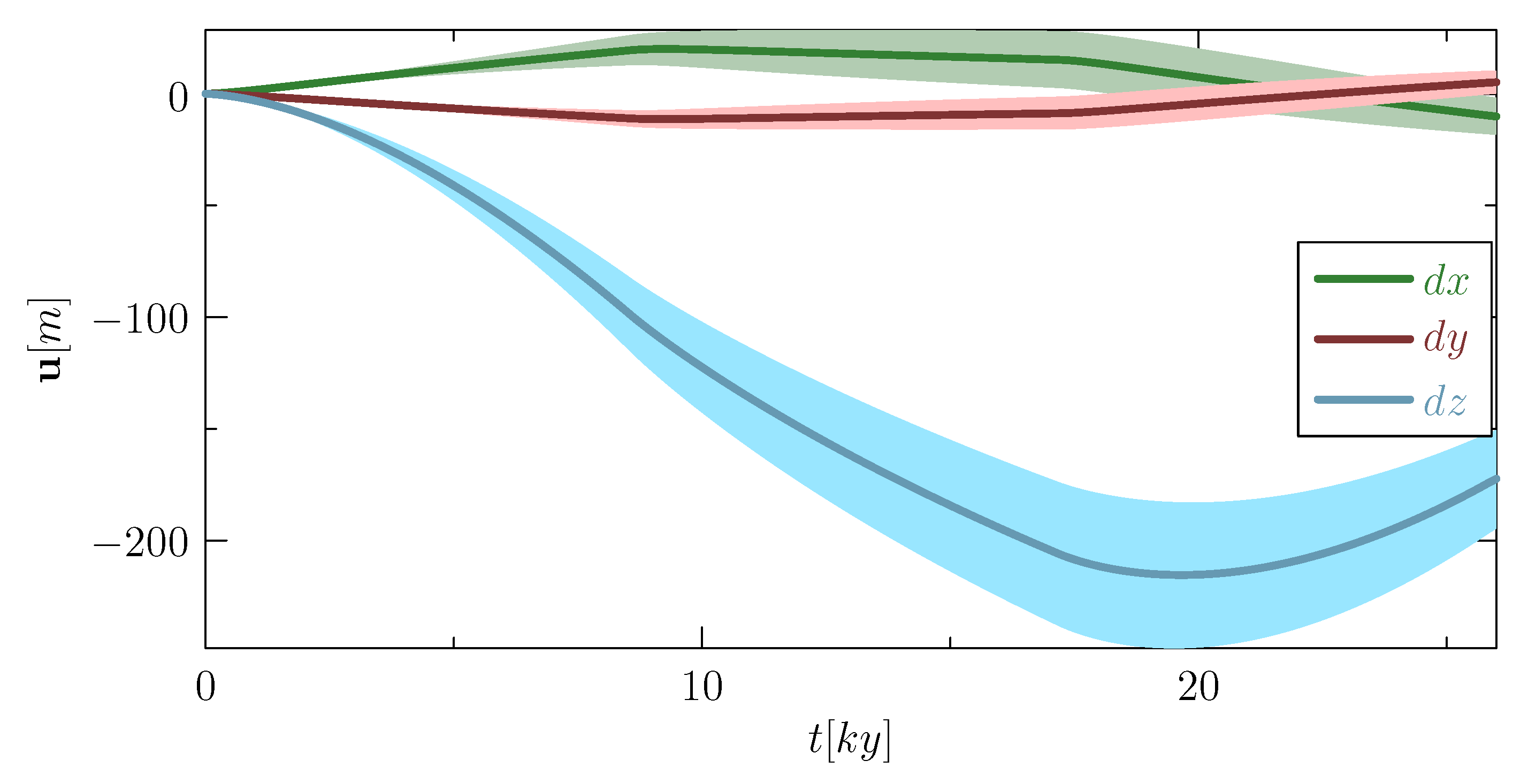
4.3. Results of the Thermo-Hydro-Mechanical Effects of Glaciation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| THM | Thermo-Hydro-Mechanical |
Appendix A. The Numerical Solver for the Isostatic Glacial Rebound Model
Appendix B. The Numerical Solver for the THM Model


References
- Tuncay, K.; Park, A.; Ortoleva, P. Sedimentary basin deformation: An incremental stress approach. Tectonophysics 2000, 323, 77–104. [Google Scholar] [CrossRef]
- Wangen, M. Physical Principles of Sedimentary Basin Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bethke, C. A numerical-model of compaction-driven groundwater-flow and heat-transfer and its application to the paleohydrology of intracratonic sedimentary basins. J. Geophys. Res. 1985, 90, 6817–6828. [Google Scholar] [CrossRef]
- Tuncay, K.; Ortoleva, P. Quantitative basin modeling: Present state and future developments towards predictability. Geofluids 2004, 4, 23–39. [Google Scholar] [CrossRef]
- Formaggia, L.; Guadagnini, A.; Imperiali, I.; Lever, V.; Porta, G.; Riva, M.; Scotti, A.; Tamellini, L. Global sensitivity analysis through polynomial chaos expansion of a basin-scale geochemical compaction model. Comput. Geosci. 2013, 17, 25–42. [Google Scholar] [CrossRef]
- Giovanardi, B.; Scotti, A.; Formaggia, L.; Ruffo, P. A general framework for the simulation of geochemical compaction. Comput. Geosci. 2015, 19, 1027–1046. [Google Scholar] [CrossRef]
- Colombo, I.; Porta, G.; Ruffo, P.; Guadagnini, A. Uncertainty quantification of overpressure buildup through inverse modeling of compaction processes in sedimentary basins. Hydrogeol. J. 2017, 25, 385–403. [Google Scholar] [CrossRef]
- Neuzil, C.E. Hydromechanical effects of continental glaciation on groundwater systems. Geofluids 2012, 12, 22–37. [Google Scholar] [CrossRef]
- Rayleigh, L. On the Dilatational Stability of the Earth. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; Royal Society: London, UK, 1906; Volume 77, pp. 486–499. [Google Scholar]
- Love, A.E.H. Some Problems of Geodynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Peltier, W.R.; Andrews, J.T. Glacial-Isostatic Adjustment—I. The Forward Problem. Geophys. J. Int. 1976, 46, 605–646. [Google Scholar] [CrossRef]
- Peltier, W.R.; Wu, P.; Yuen, D.A. The Viscosities of the Earth’s Mantle. In Anelasticity in the Earth; American Geophysical Union: Washington, DC, USA, 1981; pp. 59–77. [Google Scholar] [CrossRef]
- Wu, P.; Peltier, W.R. Viscous gravitational relaxation. Geophys. J. Int. 1982, 70, 435–485. [Google Scholar] [CrossRef] [Green Version]
- Biot, M.A. Mechanics of Incremental Deformations. Theory of Elasticity and Viscoelasticity of Initially Stressed Solids and Fluids, Including Thermodynamic Foundations and Applications to Finite Strain; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1965; p. xvii+504. [Google Scholar]
- Ogden, R.W. Incremental statics and dynamics of pre-stressed elastic materials. In Waves in Nonlinear Pre-Stressed Materials; Springer: Vienna, Austria, 2007; Volume 495, pp. 1–26. [Google Scholar] [CrossRef]
- Nasir, O.; Fall, M.; Nguyen, S.; Evgin, E. Modeling of the thermo-hydro-mechanical-chemical response of sedimentary rocks to past glaciations. Int. J. Rock Mech. Min. Sci. 2013, 64, 160–174. [Google Scholar] [CrossRef]
- Ruhaak, W.; Bense, V.; Sass, I. 3D hydro-mechanically coupled groundwater flow modelling of Pleistocene glaciation effects. Comput. Geosci. 2014, 67, 89–99. [Google Scholar] [CrossRef]
- Sterckx, A.; Lemieux, J.M.; Vaikmäe, R. Representing glaciations and subglacial processes in hydrogeological models: A numerical investigation. Geofluids 2017, 2017. [Google Scholar] [CrossRef]
- Turcotte, D.; Schubert, G. Geodynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Peltier, W. Impulse response of a Maxwell Earth. Rev. Geophys. 1974, 12, 649–669. [Google Scholar] [CrossRef]
- Whitehouse, P. Glacial Isostatic Adjustment and Sea-Level Change. State of the Art Report; Technical Report; Svensk Kärnbränslehantering AB Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2009. [Google Scholar]
- Whitehouse, P. Glacial isostatic adjustment modelling: Historical perspectives, recent advances and future directions. Earth Surf. Dynam. 2018, 6, 401–429. [Google Scholar] [CrossRef]
- Kjemperud, A.; Fjeldskaar, W. Pleistocene glacial isostasy—implications for petroleum geology. In Structural and Tectonic Modelling and its Application to Petroleum Geology; Elsevier: Amsterdam, The Netherlands, 1992; pp. 187–195. [Google Scholar]
- Zieba, K.; Grøver, A. Isostatic response to glacial erosion, deposition and ice loading. Impact on hydrocarbon traps of the southwestern Barents Sea. Mar. Pet. Geol. 2016, 78, 168–183. [Google Scholar] [CrossRef]
- Fjeldskaar, W.; Amantov, A. Effects of glaciations on sedimentary basins. J. Geodyn. 2018, 118, 66–81. [Google Scholar] [CrossRef]
- Simo, J.; Hughes, T. Computational Inelasticity. In Interdisciplinary Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Colombo, I.; Nobile, F.; Porta, G.; Scotti, A.; Tamellini, L. Uncertainty Quantification of geochemical and mechanical compaction in layered sedimentary basins. Comput. Methods Appl. Mech. Eng. 2018, 328, 122–146. [Google Scholar] [CrossRef] [Green Version]
- Remy, N. S-GeMS: The Stanford Geostatistical Modeling Software: A Tool for New Algorithms Development. Geostat. Banff 2004 2005, 865–871. [Google Scholar] [CrossRef]
- Gurtin, M. An Introduction to Continuum Mechanics; Elsevier Science: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Biot, M. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Both, J.; Borregales, M.; Nordbotten, J.; Kumar, K.; Radu, F. Robust fixed stress splitting for Biot’s equations in heterogeneous media. Appl. Math. Lett. 2017, 68, 101–108. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Cheng, A.D. Poroelasticity; Springer: Berlin/Heidelberg, Germany, 2016; Volume 27. [Google Scholar]
- Taylor, T.; Giles, M.; Hathon, L.; Diggs, T.; Braunsdorf, N.; Birbiglia, G.; Kittridge, M.; Macaulay, C.; Espejo, I. Sandstone diagenesis and reservoir quality prediction: Models, myths, and reality. AAPG Bull 2010, 94, 1093–1132. [Google Scholar] [CrossRef]
- Fowler, A.; Yang, X.S. Dissolution/precipitation mechanisms for diagenesis in sedimentary basins. J. Geophys. Res. Solid Earth 2003, 108, EPM 13-1–EPM 13-14. [Google Scholar] [CrossRef]
- Ruffo, P.; Porta, G.; Colombo, I.; Scotti, A.; Guadagnini, A. Global sensitivity analysis of geochemical compaction in a sedimentary Basin. In Proceedings of the 1st EAGE Basin and Petroleum Systems Modeling Workshop: Advances in Basin and Petroleum Systems Modeling in Risk and Resource Assessment, Dubai, UAE, 19–22 October 2014. [Google Scholar]
- Čermák, V.; Laštovičková, M. Temperature profiles in the Earth of importance to deep electrical conductivity models. In Electrical Properties of the Earth’s Mantle; Springer: Berlin/Heidelberg, Germany, 1987; pp. 255–284. [Google Scholar]
- Pellerin, J.; Botella, A.; Bonneau, F.; Mazuyer, A.; Chauvin, B.; Lévy, B.; Caumon, G. RINGMesh: A programming library for developing mesh-based geomodeling applications. Comput. Geosci. 2017, 104, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Gibert, B.; Seipold, U.; Tommasi, A.; Mainprice, D. Thermal diffusivity of upper mantle rocks: Influence of temperature, pressure, and the deformation fabric. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Alzetta, G.; Arndt, D.; Bangerth, W.; Boddu, V.; Brands, B.; Davydov, D.; Gassmoeller, R.; Heister, T.; Heltai, L.; Kormann, K.; et al. The deal.II Library, Version 9.0. J. Numer. Math. 2018, 26, 173–183. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal.II—A General Purpose Object Oriented Finite Element Library. ACM Trans. Math. Softw. 2007, 33, 1–27. [Google Scholar] [CrossRef]
- Arnold, D.N.; Brezzi, F.; Cockburn, B.; Marini, L.D. Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 2001, 39, 1749–1779. [Google Scholar] [CrossRef]
- Kanschat, G. Multilevel methods for discontinuous Galerkin FEM on locally refined meshes. Comput. Struct. 2004, 82, 2437–2445. [Google Scholar] [CrossRef]
- Rivière, B. Discontinuous Galerkin Methods for Solving Elliptic And Parabolic Equations; Frontiers in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008; Volume 35, p. xxii+190. [Google Scholar] [CrossRef]
- Carriero, S. Tidal Forces Influence on Earth’s Crust Deformation. A Massive Parallel Solver for the Solid Earth Tide Phenomenon. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018. [Google Scholar]
- Burman, E.; Hansbo, P. Fictitious domain finite element methods using cut elements: II. A stabilized Nitsche method. Appl. Numer. Math. 2012, 62, 328–341. [Google Scholar] [CrossRef] [Green Version]
- Bukač, M.; Yotov, I.; Zakerzadeh, R.; Zunino, P. Partitioning strategies for the interaction of a fluid with a poroelastic material based on a Nitsche’s coupling approach. Comput. Methods Appl. Mech. Eng. 2015, 292, 138–170. [Google Scholar] [CrossRef]
- Lehrenfeld, C.; Reusken, A. Optimal preconditioners for Nitsche-XFEM discretizations of interface problems. Numer. Math. 2017, 135, 313–332. [Google Scholar] [CrossRef]
- Hansbo, A.; Hansbo, P. An unfitted finite element method, based on Nitsche’s method, for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 5537–5552. [Google Scholar] [CrossRef]
- Hansbo, P.; Larson, M.; Zahedi, S. A cut finite element method for a Stokes interface problem. Appl. Numer. Math. 2014, 85, 90–114. [Google Scholar] [CrossRef] [Green Version]
- Mikelić, A.; Wheeler, M. Convergence of iterative coupling for coupled flow and geomechanics. Comput. Geosci. 2013, 17, 455–461. [Google Scholar] [CrossRef]
- Cerroni, D.; Radu, F.A.; Zunino, P. Numerical solvers for a poromechanic problem with a moving boundary. Math. Eng. 2019, 1, 824. [Google Scholar] [CrossRef]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerroni, D.; Penati, M.; Porta, G.; Miglio, E.; Zunino, P.; Ruffo, P. Multiscale Modeling of Glacial Loading by a 3D Thermo-Hydro-Mechanical Approach Including Erosion and Isostasy. Geosciences 2019, 9, 465. https://doi.org/10.3390/geosciences9110465
Cerroni D, Penati M, Porta G, Miglio E, Zunino P, Ruffo P. Multiscale Modeling of Glacial Loading by a 3D Thermo-Hydro-Mechanical Approach Including Erosion and Isostasy. Geosciences. 2019; 9(11):465. https://doi.org/10.3390/geosciences9110465
Chicago/Turabian StyleCerroni, Daniele, Mattia Penati, Giovanni Porta, Edie Miglio, Paolo Zunino, and Paolo Ruffo. 2019. "Multiscale Modeling of Glacial Loading by a 3D Thermo-Hydro-Mechanical Approach Including Erosion and Isostasy" Geosciences 9, no. 11: 465. https://doi.org/10.3390/geosciences9110465
APA StyleCerroni, D., Penati, M., Porta, G., Miglio, E., Zunino, P., & Ruffo, P. (2019). Multiscale Modeling of Glacial Loading by a 3D Thermo-Hydro-Mechanical Approach Including Erosion and Isostasy. Geosciences, 9(11), 465. https://doi.org/10.3390/geosciences9110465





