The Role of Shear Wave Velocity and Non-Linearity of Soil in the Seismic Response of a Coupled Tunnel-Soil-Above Ground Building System
Abstract
:1. Introduction
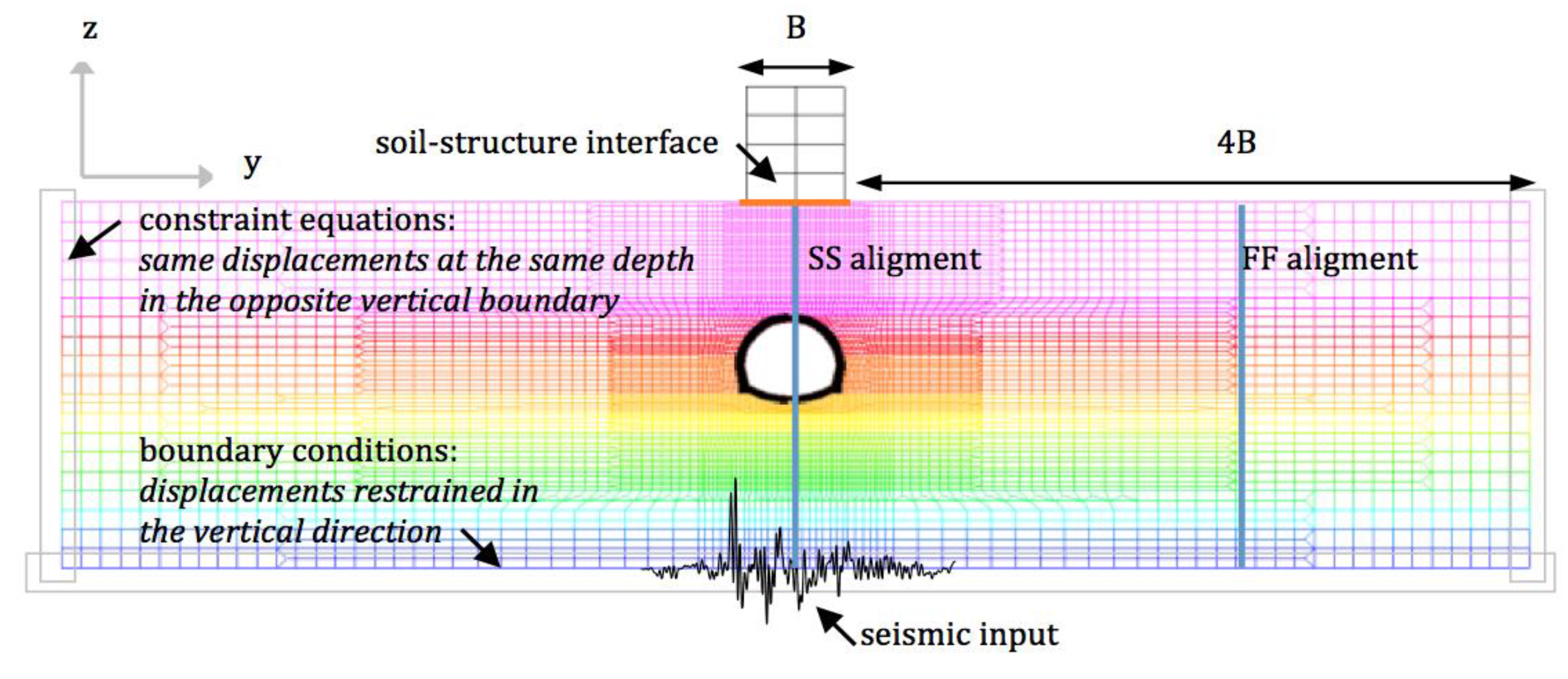
2. The TSS System Investigated
3. FEM Modeling
3.1. General Information
3.2. Equivalent Linear Visco-Elastic Modeling
3.3. Non-Linear Visco-Elastic Modeling
4. Results of the Equivalent Visco-Linear Elastic Analyses
4.1. Response in the Time Domain
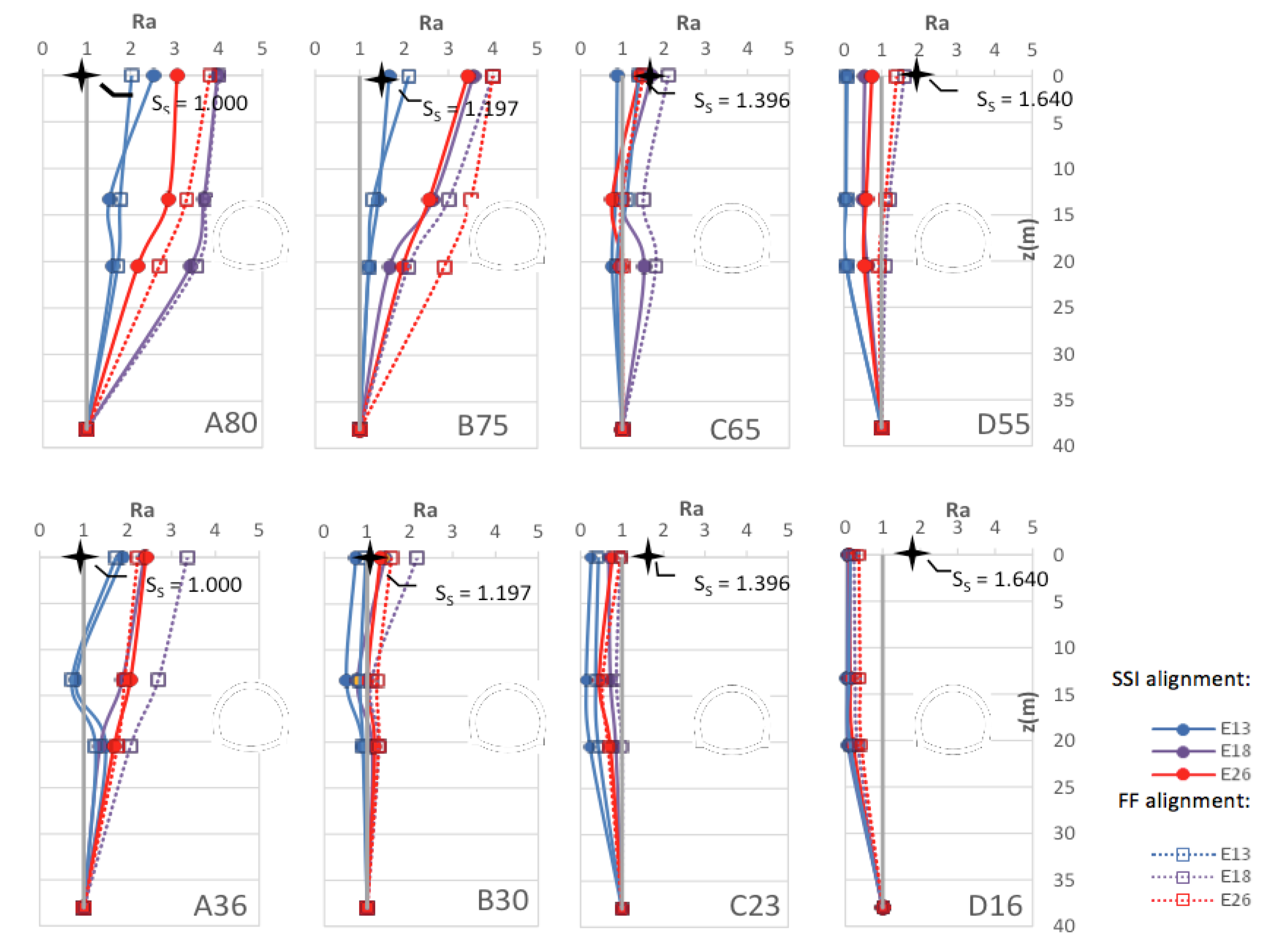
4.1.1. Amplification Ratio in the Soil
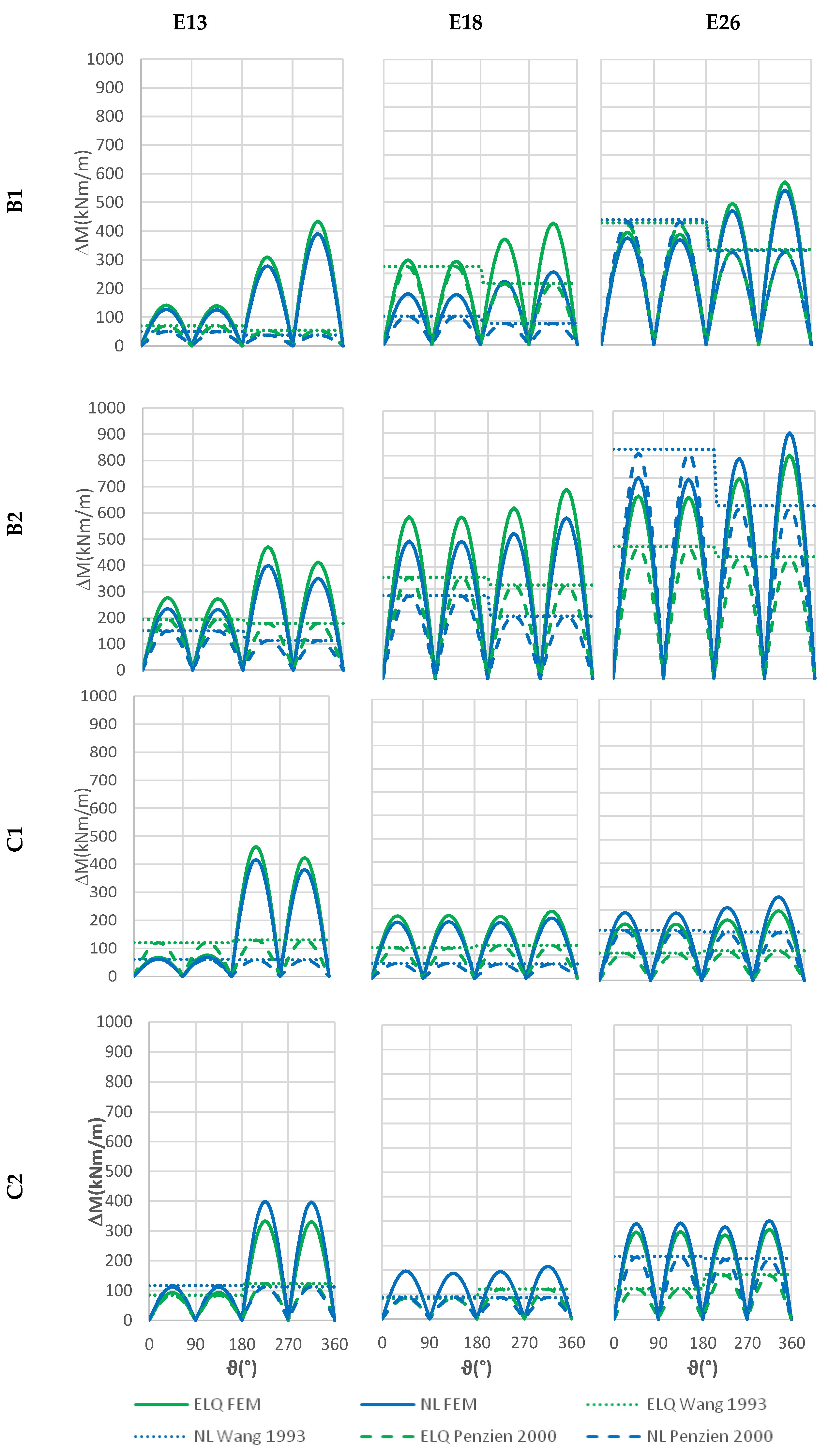
4.1.2. Bending Moments in The Tunnel
4.2. Response in the Frequency Domain
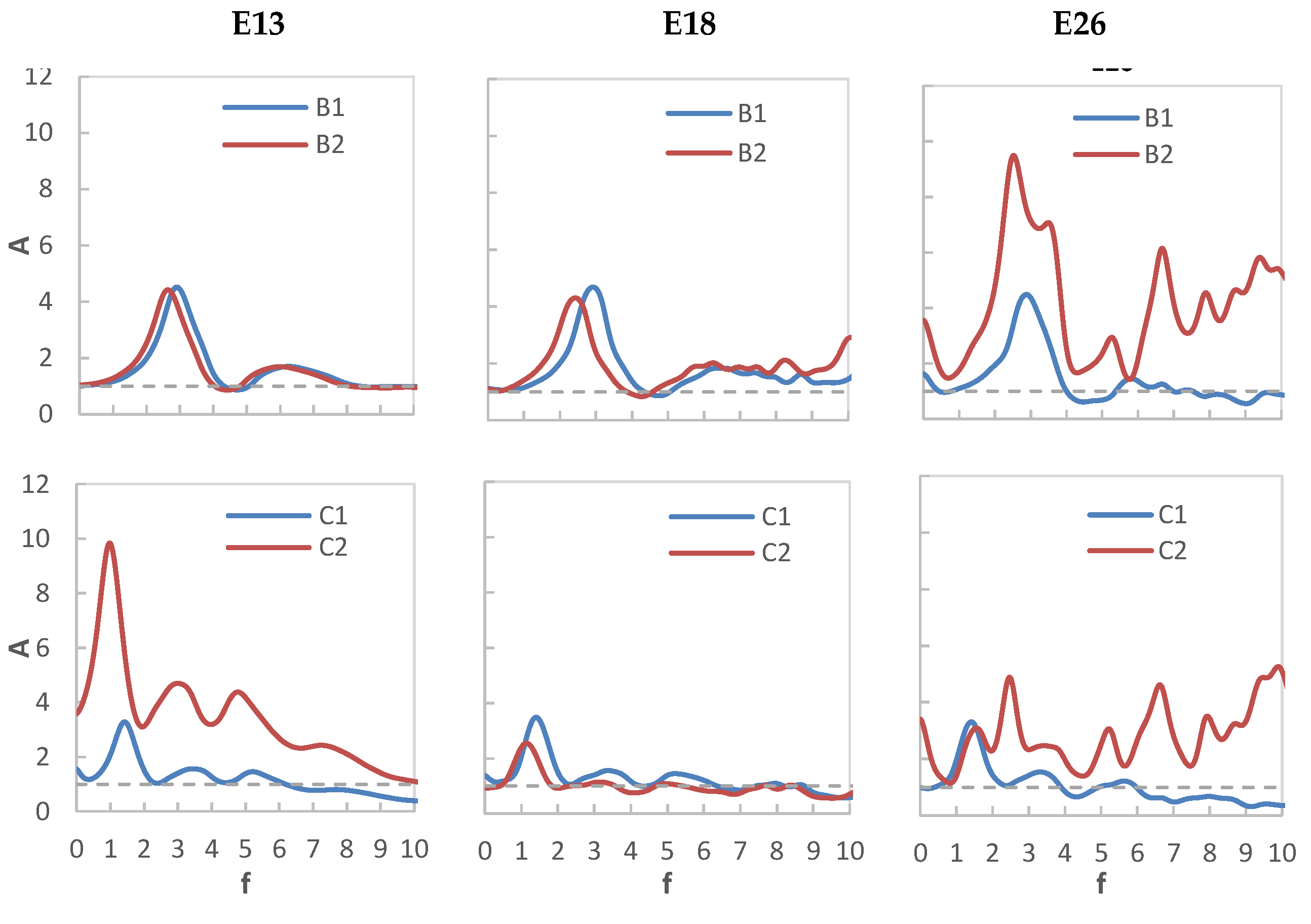
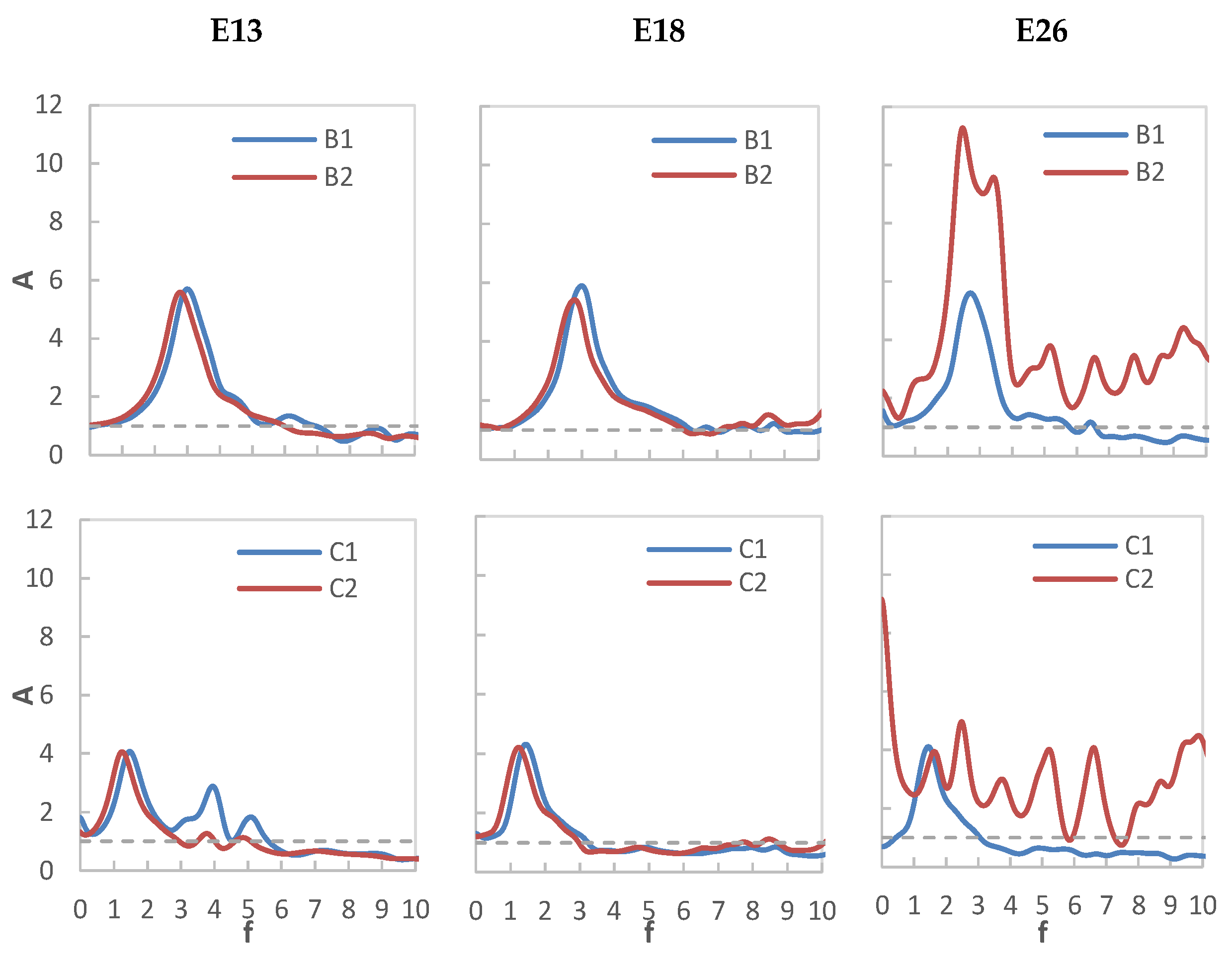
4.2.1. Amplification Function in the Soil
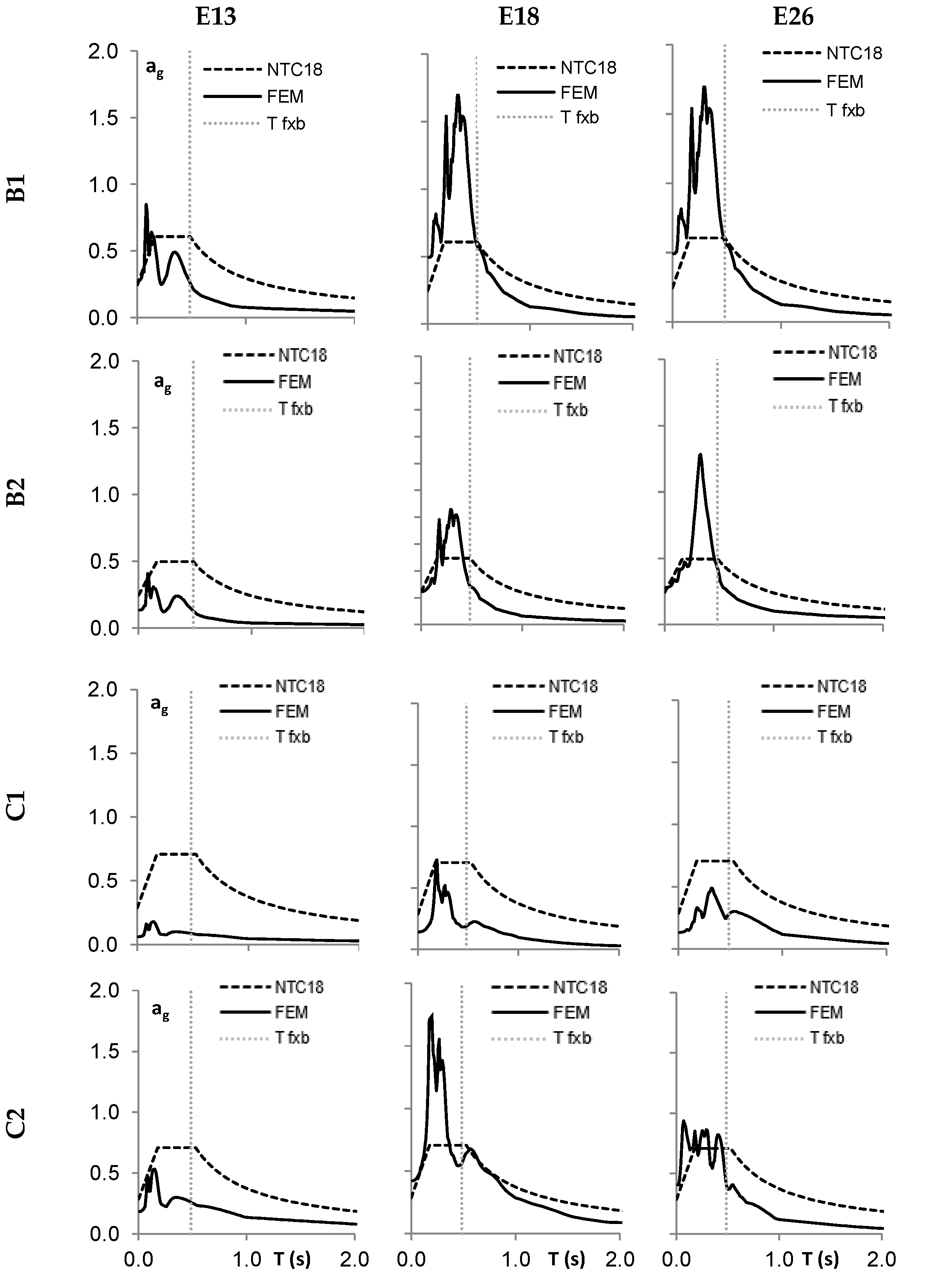
4.2.2. Response Spectra at the Base of the Building
5. Results of the Visco-Nonlinear Analyses
5.1. Response in the Time Domain
5.1.1. Amplification Ratio of the Soil
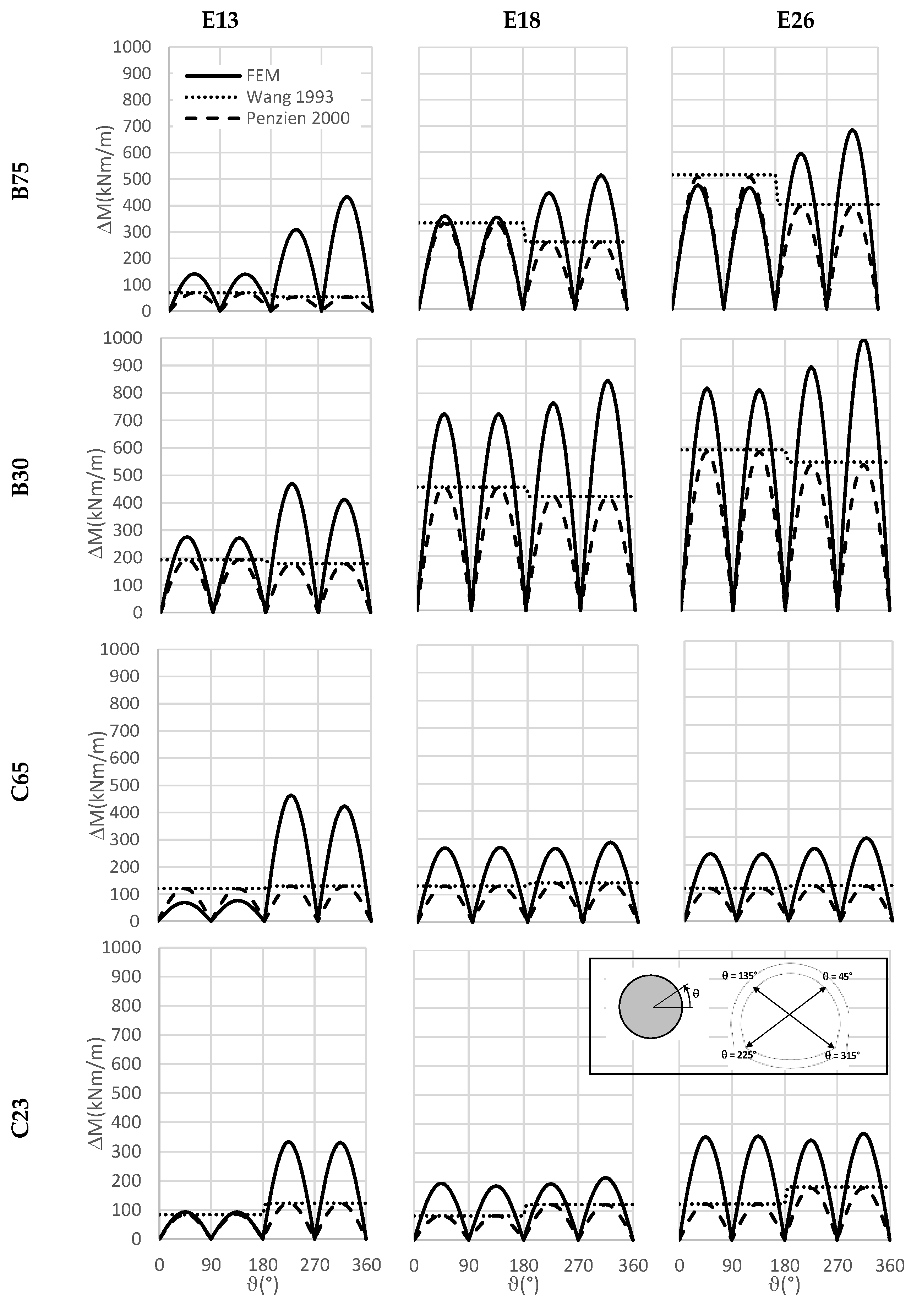
5.1.2. Bending Moments in the Tunnel
5.2. Response in the Frequency Domain
5.2.1. Amplification Function of the Soil
5.2.2. Response Spectra at the base of the building
6. Comparison between the Results of the Two Different Linear and Non-Linear Analyses
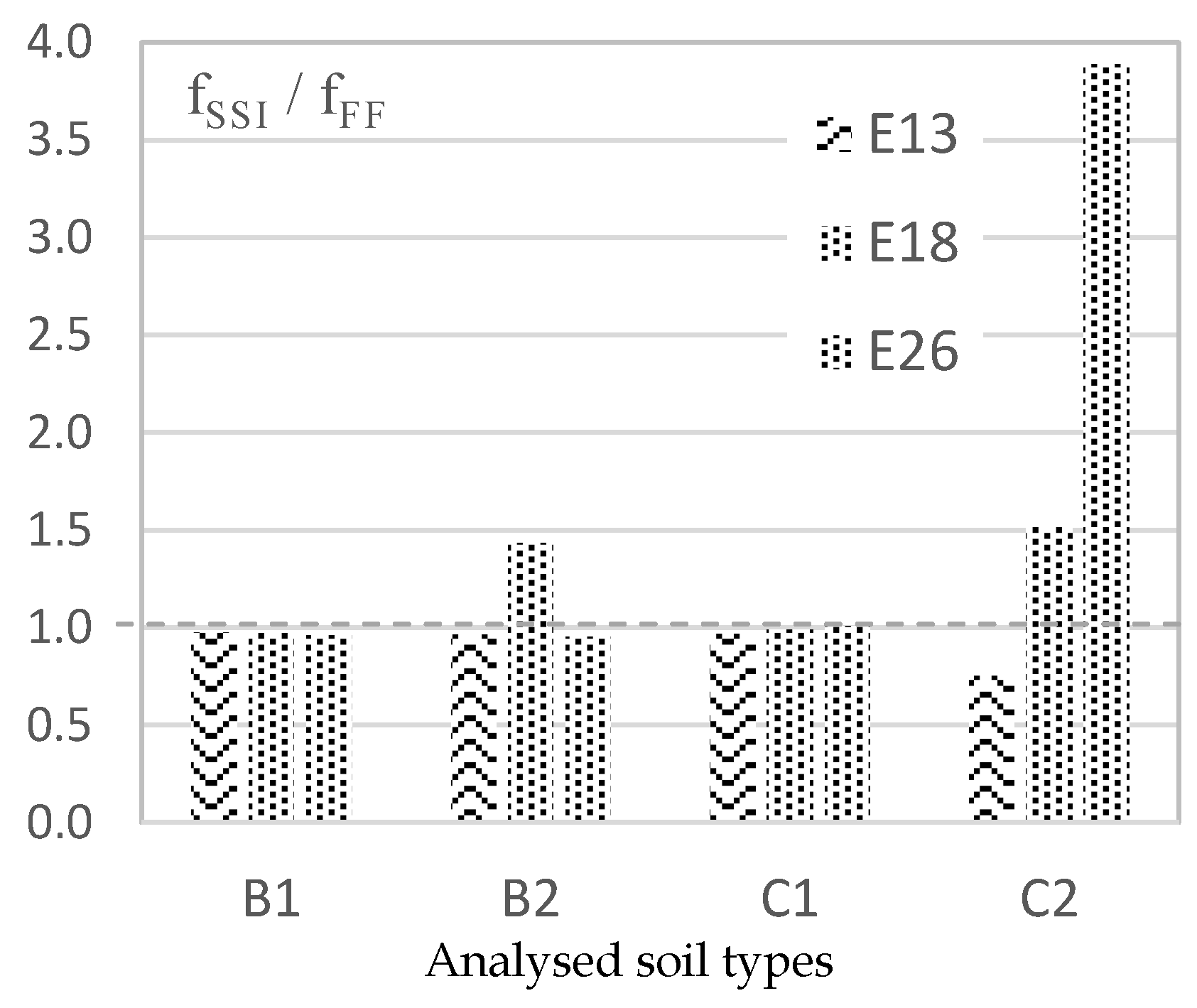
6.1. Amplification Ratios and Amplification Functions
6.2. Response Spectra at the Base of the Building
6.3. Bending Moments in the Tunnel
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kawashima, K. Seismic design of underground structures in soft ground: A review. In Geotechnical Aspects of Underground Construction in Soft Ground; Fujita, M., Ed.; Balkema: Rotterdam, The Netherlands, 2000. [Google Scholar]
- Hashash, Y.M.; Hook, J.J.; Schmidt, B.; Yao, J.I.-C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Wang, W.; Wang, T.; Su, J.; Lin, C.; Seng, C.; Huang, T. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Menkiti, C.O.; Kontoe, S.; Zdravkovic, L.; Potts, D.M. Case study on seismic tunnel response. Can. Geotech. J. 2008, 45, 1743–1764. [Google Scholar] [Green Version]
- Wang, Z.; Gao, B.; Jiang, Y.; Yuan, S. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan earthquake. Sci. China Ser. E Technol. Sci. 2009, 52, 546–558. [Google Scholar] [CrossRef]
- Gazetas, G. Case histories of tunnel failures during earthquakes and during construction. In Proceedings of the half-day conference a tunnel/underground station failure conference, by the Israeli Geotechnical Society, Herzelia, Israe, 19 January 2014. [Google Scholar]
- Lee, V.; Karl, J. Diffraction of SV waves by underground, circular, cylindrical cavities. Soil Dyn. Earthq. Eng. 1992, 11, 445–456. [Google Scholar] [CrossRef]
- Luco, J.; De Barros, F. Diffraction of obliquely incident waves by a cylindrical cavity embedded in a layered viscoelastic half-space. Soil Dyn. Earthq. Eng. 1993, 12, 159–171. [Google Scholar]
- Hashash, Y.M.; Park, D.; Yao, J.I.-C. Ovaling deformations of circular tunnels under seismic loading, an update on seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gerolymos, N.; Drosos, V.; Kourkoulis, R.; Georgarakos, T.; Gazetas, G. Nonlinear Response of Deep Immersed Tunnel to Strong Seismic Shaking. J. Geotech. Geoenvironmental Eng. 2007, 133, 1067–1090. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gerolymos, N.; Drosos, V.; Georgarakos, T.; Kourkoulis, R.; Gazetas, G. Behaviour of deep immersed tunnel under combined normal fault rupture deformation and subsequent seismic shaking. Bull. Earthq. Eng. 2008, 6, 213–239. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gazetas, G. Analysis of cut-and-cover tunnels against large tectonic deformation. Bull. Earthq. Eng. 2010, 8, 283–307. [Google Scholar] [CrossRef]
- Hung, C.J.; Monsees, J.; Munfah, N.; Wisniewski, J. Technical manual for design and construction of road tunnels—Civil elements; Parsons Brinckerhoff, Inc.: New York, NY, USA, December 2009. [Google Scholar]
- Lanzano, G.; Bilotta, E.; Russo, G.; Silvestri, F.; Madabhushi, S.P.G.; Madabhushi, S.P.G. Centrifuge Modeling of Seismic Loading on Tunnels in Sand. Geotech. Test. J. 2012, 35, 104348. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, M.R.; Maugeri, M. Numerical modelling of centrifuge tests on tunnel-soil systems. Bull. Earthq. Eng. 2015, 13, 1927–1951. [Google Scholar] [CrossRef]
- Luco, J.E.; De Barros, F.C.P. Dynamic displacements and stresses in the vicinity of a cylindrical cavity embedded in a half-space. Earthq. Eng. Struct. Dyn. 1994, 23, 321–340. [Google Scholar] [CrossRef]
- Kouretzis, G.; Bouckovalas, G.; Sofianos, A.; YioutaMitra, P. Detrimental effects of urban tunnels on design seismic ground motions. In Proceedings of the 2nd Japan-Greece Workshop on Seismic Design, Observation, and Retrofit of Foundations, Tokyo, Japan, 3–4 April 2007. [Google Scholar]
- Smerzini, C.; Avilés, J.; Paolucci, R.; Sánchez-Sesma, F.J. Effect of underground cavities on surface earthquake ground motion under SH wave propagation. Earthq. Eng. Struct. Dyn. 2009, 38, 1441–1460. [Google Scholar] [CrossRef]
- Wang, H.-F.; Lou, M.-L.; Chen, X.; Zhai, Y.-M. Structure–soil–structure interaction between underground structure and ground structure. Soil Dyn. Earthq. Eng. 2013, 54, 31–38. [Google Scholar] [CrossRef]
- Abate, G.; Corsico, S.; Massimino, M.R. FEM modeling of the seismic behavior of a tunnel-soil-aboveground building system: A case history in Catania (Italy). Procedia Eng. 2016, 158, 380–385. [Google Scholar] [CrossRef]
- Caruso, S.; Ferraro, A.; Grasso, S.; Massimino, M.R. Site response analysis in eastern sicily based on direct and indirect Vs measurements. In Proceedings of the 1st IMEKO TC4 international workshop on metrology for geotechnics, metrogeotechnics 2016, Benevento, Italy, 17–18 March 2016; pp. 115–120. [Google Scholar]
- Ferraro, A.; Grasso, S.; Massimino, M.R.; Maugeri, M. Influence of geotechnical parameters and numerical modelling on local seismic response analysis. In Proceedings of the 16th European conference on soil mechanics and geotechnical engineering, ECSMGE 2015, Edinburgh International Conference Center, Edinburgh, UK, 13–17 September 2015; Volume 4, pp. 2183–2188. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V.; Massimino, M.R. Static and dynamic properties of soils in Catania (Italy). Ann. Geophys-Italy 2018, 61. [Google Scholar] [CrossRef]
- NTC - D.M. 17/01/18 - Update technical standards for buildings, Official Journal of the Italian Republic, 17th January 2018 (in Italian). Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 27 September 2019).
- Pitilakis, K.; Tsinidis, G.; Leanza, A.; Maugeri, M. Seismic behaviour of circular tunnels accounting for above ground structures interaction effects. Soil Dyn. Earthq. Eng. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- EC8 - Design of structures for earthquake resistance. European Pre-standard. ENV 1998. Europ. Com. for Standard. Bruxelles. 2003. Available online: https://www.phd.eng.br/wp-content/uploads/2015/02/en.1998.1.2004.pdf (accessed on 27 September 2019).
- Gajo, A.; Wood, D.M. A kinematic hardening constitutive model for sands: The multiaxial formulation. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 925–965. [Google Scholar] [CrossRef]
- Abate, G.; Caruso, C.; Massimino, M.R.; Maugeri, M. Validation of a New Soil Constitutive Model for Cyclic Loading by FEM Analysis. Contact Mech. 2007, 146, 759–768. [Google Scholar]
- Wang, J.N. Seismic Design of Tunnels: A Simple State of the Art Design Approach; Parsons Brinckerhoff Inc.: New York, NY, USA, 1993. [Google Scholar]
- Penzien, J. Seismically induced racking of tunnel linings. Earthq. Eng. Struct. Dyn. 2000, 29, 683–691. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: New Jersey, NJ, USA, 1996. [Google Scholar]
- ADINA. Automatic dynamic incremental nonlinear analysis. In Theory and Modelling Guide; ADINA R&D: Watertown, MA, USA, 2008. [Google Scholar]
- Grassi, F.; Massimino, M.R. Evaluation of kinematic bending moments in a pile foundation using the finite element approach. WIT Trans. Built Environ. 2009, 104, 479–488. [Google Scholar]
- Abate, G.; Massimino, M.R. Dynamic soil-structure interaction analysis by experimental and numerical modelling. Riv. Ital. Geotec. 2016, 50, 44–70. [Google Scholar]
- Abate, G.; Massimino, M.R.; Romano, S. Finite Element analysis of DSSI effects for a building of strategic importance in Catania (Italy). Procedia Eng. 2016, 158, 374–379. [Google Scholar] [CrossRef]
- Maugeri, M.; Abate, G.; Massimino, M.R. Soil-Structure interaction for seismic improvement of noto Cathedral (Italy). Geotech. Geol. Eng. 2012, 16, 217–239. [Google Scholar]
- Massimino, M.R.; Abate, G.; Corsico, S.; Louarn, R. Comparison between two approaches for non-linear FEM modelling of the seismic behaviour of a coupled soil–structure system. Geotech. Geol. Eng. 2019, 37, 1957–1975. [Google Scholar] [CrossRef]
- Gajo, A.; Muir Wood, D. Numerical Analysis of Behaviour of Shear Stacks under Dynamic Loading; Report of ECOEST Project, EERC laboratory; Bristol University: Bristol, UK, 1997. [Google Scholar]
- Abate, G.; Massimino, M.R.; Maugeri, M. Finite element modeling of a shaking table test to evaluate the dynamic behaviour of a soil-foundation system. In Proceedings of the AIP Conference, Reggio Calabria, Italy, 8–11 July 2008; Volume 1020, pp. 569–576. [Google Scholar]
- Abate, G.; Massimino, M.R.; Maugeri, M.; Muir Wood, D. Numerical modelling of a shaking table test for soil-foundation-superstructure interaction by means of a soil constitutive model implemented in a FEM code. Geotech. Geol. Eng. 2010, 28, 37–59. [Google Scholar] [CrossRef]
- Lanzo, G.; Silvestri, F. Risposta Sismica Locale: Teorie ed Esperienze; Helvius: Napoli, Italy, 1999. [Google Scholar]
- Bonaccorso, R.; Grasso, S.; Giudice, E.L. Cavities and hypogeal structures of the historical part of the City of Catania. WIT Trans. State-of-the-art Sci. Eng. 2005, 1, 197–223. [Google Scholar]
- Cavallaro, A.; Grasso, S.; Maugeri, M. Volcanic soil characterisation and site response analysis in the city of Catania. In Proceedings of the 8th national conference on earthquake engineering, San Francisco, CA, USA, , 18–22 April 2006; pp. 835–844. [Google Scholar]
- Cavallaro, A.; Ferraro, A.; Grasso, S.; Maugeri, M.; Santini, A.; Moraci, N. Site Response Analysis of the Monte Po Hill in the City of Catania. AIP Conf. Pro. 2008, 1020, 240–251. [Google Scholar]
- Cavallaro, A.; Ferraro, A.; Grasso, S.; Maugeri, M. Topographic Effects of the Monte Po Hill in Catania. Soil Dyn. Earthq. Eng. 2012, 43, 97–113. [Google Scholar] [CrossRef]
- NTC - D.M. 14/01/08 - New technical standards for buildings, Official Journal of the Italian Republic, 14th January 2008 (in Italian). Available online: https://www.gazzettaufficiale.it/eli/id/2008/02/04/08A00368/sg (accessed on 27 September 2019).
- Idriss, I.M.; Seed, H.B. Seismic response of horizontal soil layers. Soil Mech Found Eng ASCE 1968, 94, 1003–1031. [Google Scholar]
- Grasso, S.; Maugeri, M. Seismic microzonation studies for the city of Ragusa (Italy). Soil Dyn. Earthq. Eng. 2014, 56, 86–97. [Google Scholar] [CrossRef]
- Ferraro, A.; Grasso, S.; Maugeri, M.; Totani, F. Seismic response analysis in the southern part of the historic centre of the City of L’Aquila (Italy). Soil Dyn. Earthq. Eng. 2016, 88, 256–264. [Google Scholar] [CrossRef]
- Castelli, F.; Cavallaro, A.; Grasso, S.; Lentini, V. Seismic microzoning from synthetic ground motion earthquake scenarios parameters: The case study of the city of Catania (Italy). Soil Dyn. Earthq. Eng. 2016, 88, 307–327. [Google Scholar] [CrossRef]














| Soil types | Vs (m/s) | Vs * (m/s) | Ss |
|---|---|---|---|
| A | >800 | 1000 | 1.000 |
| B | 360 ÷ 800 | 500 | 1.197 |
| C | 180 ÷ 360 | 250 | 1.396 |
| D | <180 | 100 | 1.640 |
| Inputs | Original ag (m/s2) | f1 (Hz) | f2 (Hz) | f3 (Hz) | Time History |
|---|---|---|---|---|---|
| E13 (Timfristos, Greece 1986) | 3.02 | 12.70 | 6.86 | 8.26 |  |
| E18 (Friuli, Italy 1976) | 1.59 | 5.53 | 4.54 | 4.24 | 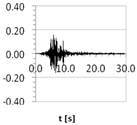 |
| E26 (Friuli, Italy 1976) | 1.83 | 2.95 | 3.26 | 2.12 | 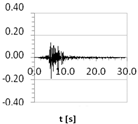 |
| Expected Surface Acceleration, SS∙ag | D | Vs/Vs,max | G/Gmax |
|---|---|---|---|
| 0.10 | 0.03 | 0.9 ± 0.07 | 0.80 ± 0.10 |
| 0.20 | 0.06 | 0.7 ± 0.15 | 0.50 ± 0.20 |
| 0.30 | 0.10 | 0.6 ± 0.15 | 0.36 ± 0.20 |
| Model | SS∙ag (g) | G/Gmax | Doperative | Goperative (MPa) |
|---|---|---|---|---|
| A80 | 0.10 | 0.80 | 0.03 | 1600 |
| B75 | 0.12 | 0.75 | 0.03 | 375 |
| C65 | 0.14 | 0.65 | 0.03 | 81.25 |
| D55 | 0.16 | 0.55 | 0.03 | 11 |
| A36 | 0.30 | 0.36 | 0.10 | 720 |
| B30 | 0.36 | 0.30 | 0.10 | 150 |
| C23 | 0.42 | 0.23 | 0.10 | 28.75 |
| D16 | 0.49 | 0.16 | 0.10 | 3.2 |
| Soil Parameter | Soil Type B: | Soil Type C: | ||
|---|---|---|---|---|
| B1 (ag = 0.1 g) | B2 (ag = 0.3 g) | C1 (ag = 0.1 g) | C2 (ag = 0.3 g) | |
| E (MPa) | 1300 | 325 | ||
| ν | 0.3 | 0.3 | ||
| φcv (°) | 24 | 24 | ||
| λ | 0.06 | 0.06 | ||
| vλ | 1.712 | 1.712 | ||
| R | 0.01 | 0.01 | ||
| A | 0.9 | 0.9 | ||
| kd | 1 | 1 | ||
| B | 0.01 | 0.01 | ||
| k | 2 | 2 | ||
| D | 0.03 | 0.10 | 0.03 | 0.10 |
| B1 | B2 | C1 | C2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fSSI,ELQ (Hz) | fSSI,NL (Hz) | fSSI,ELQ/fSSI,NL | fSSI,ELQ (Hz) | fSSI,NL (Hz) | fSSI,ELQ/fSSI,NL | fSSI,ELQ (Hz) | fSSI,NL (Hz) | fSSI,ELQ/fSSI,NL | fSSI,ELQ (Hz) | fSSI,NL (Hz) | fSSI,ELQ/fSSI,NL | |
| E13 | 2.54 | 2.97 | 0.86 | 1.58 | 2.74 | 0.58 | 4.30 | 1.46 | 2.95 | 0.65 | 0.97 | 0.67 |
| E18 | 2.56 | 2.98 | 0.86 | 2.08 | 2.41 | 0.86 | 1.10 | 1.44 | 0.76 | 0.73 | 1.15 | 0.63 |
| E26 | 2.56 | 2.90 | 0.88 | 1.22 | 2.53 | 0.48 | 1.15 | 1.46 | 0.79 | 1.97 | 2.10 | 0.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abate, G.; Grasso, S.; Massimino, M.R. The Role of Shear Wave Velocity and Non-Linearity of Soil in the Seismic Response of a Coupled Tunnel-Soil-Above Ground Building System. Geosciences 2019, 9, 473. https://doi.org/10.3390/geosciences9110473
Abate G, Grasso S, Massimino MR. The Role of Shear Wave Velocity and Non-Linearity of Soil in the Seismic Response of a Coupled Tunnel-Soil-Above Ground Building System. Geosciences. 2019; 9(11):473. https://doi.org/10.3390/geosciences9110473
Chicago/Turabian StyleAbate, Glenda, Salvatore Grasso, and Maria Rossella Massimino. 2019. "The Role of Shear Wave Velocity and Non-Linearity of Soil in the Seismic Response of a Coupled Tunnel-Soil-Above Ground Building System" Geosciences 9, no. 11: 473. https://doi.org/10.3390/geosciences9110473
APA StyleAbate, G., Grasso, S., & Massimino, M. R. (2019). The Role of Shear Wave Velocity and Non-Linearity of Soil in the Seismic Response of a Coupled Tunnel-Soil-Above Ground Building System. Geosciences, 9(11), 473. https://doi.org/10.3390/geosciences9110473







