Next Article in Journal
Archaeometric Characterisation of Decorated Pottery from the Archaeological Site of Villa dei Quintili (Rome, Italy): Preliminary Study
Next Article in Special Issue
Toward Core-Free Pavement Compaction Evaluation: An Innovative Method Relating Asphalt Permittivity to Density
Previous Article in Journal
A Detailed Reconstruction of the Roman Landscape and the Submerged Archaeological Structure at “Castel dell’Ovo islet” (Naples, Southern Italy)
Previous Article in Special Issue
GPR Imaging for Deeply Buried Objects: A Comparative Study Based on Compositing of Scanning Frequencies and a Chirp Excitation Function
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 9
Issue 4
10.3390/geosciences9040171
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Data Acquisition Methodologies Utilizing Ground Penetrating Radar for Cassava (Manihot esculenta Crantz) Root Architecture

by
Alfredo Delgado
1,*,
Alexandre Novo
1 and
Dirk B. Hays
2
1
IDS GeoRadar North America, Golden, CO 80401, USA
2
Soil and Crop Sciences, Texas A&M University, College Station, TX 77843-2474, USA
*
Author to whom correspondence should be addressed.
Geosciences 2019, 9(4), 171; https://doi.org/10.3390/geosciences9040171
Submission received: 5 March 2019 / Revised: 8 April 2019 / Accepted: 10 April 2019 / Published: 15 April 2019
(This article belongs to the Special Issue Advances in Ground Penetrating Radar Research)
Browse Figures
Versions Notes

Abstract

:
Cassava (Manihot esculenta Crantz), a root crop utilized as food and industrial starch product, develops and maintains its marketable product sub-surface. Often, however, it is difficult to determine the potentially marketable goods available at any given time due to the sub-surface nature of the product and the inability to non-destructively sample. This dilemma has provided an avenue for application of ground penetrating radar. Relatively available designs of this technology, however, are cumbersome and do not provide the efficiencies for field applications. The objective of this research was to determine the functionality of a two Gigahertz frequency IDS GeoRadar C-Thrue antenna for the detection and parameterization of root architecture to be utilized for estimating marketable product. Cassava roots were buried across three horizontal and two vertical orientations to simulate the multi-directional nature of cassava roots. The antenna has dual polarization which also allowed to testing efficacy of polarization for detecting the varying root orientations. This study found that the C-Thrue system, more specifically, the Vertical transmit and Vertical receive polarization, was the most effective at accurately estimating cassava root length and widths at varying angles that simulate root development in true fields.

1. Introduction

Cassava (Manihot esculenta Crantz) is a tropical root crop originally from South America and serves as a staple food source for an estimated 800 million people [1]. More than a tenth of the world’s population relies on this food source, and in tropical countries, it follows only maize and rice in caloric intake [2]. Worldwide, cassava is the second most important source of starch after maize [3]. Between 1991–1993 and 2011–2013, the global harvested area of cassava expanded by 25%, from 16.5 million to 20.7 million hectares, which was the biggest percentage increase among the world’s five major food crops. Most of this cultivated increase occurred in Africa (with an increase of 39.2%), which alone produces nearly 145 million metric tons of cassava per year while South East (SE) Asia’s (particularly, Thailand, Cambodia, and Vietnam) average fresh root yields have almost doubled in the last 20 years [4]. In SE Asia, cassava is mostly an industrial crop used for the production of starch and dried chips which allow the breeders to concentrate basically on high fresh root yield, high dry matter content, and adequate plant architecture [3,5]. Strong markets in SE Asia encourage the adoption of new technologies (e.g., highly productive varieties and appropriate cultivation practices).
This improvement would be expected to occur if new traits for root architecture can be incorporated into breeding programs and tools for early selection of marketable material are available. However, limited information on growth patterns in cassava roots as compared to aboveground biomass exists [6]. This is a serious constraint considering that root is the main commercial product. This limitation and the need to perform destructive samplings restrict the farmers’ ability to screen root development through the growing season. As such, cassava researchers and farmers need new rapid, non-destructive procedures to capture root traits [7].
Many technologies currently exist and are utilized for non-destructive root characterization. Some can include minirhizotrons, computed tomography, and magnetic resonance imaging [8,9,10]. However, these technologies are currently limited by time requirements and costs for implementing these tools. Ground penetrating radar (GPR) is an existing, affordable, and rapidly evolving technology. GPR has often been utilized as a small cross-section near-surface object detection tool [11,12,13,14]. GPR has been utilized to non-destructively image coarse root biomass and architecture in various tree and shrub species [15,16,17,18,19,20,21,22,23,24,25,26,27,28]. More recently, GPR has demonstrated that it can be used as a high throughput (HT), non-destructive, three-dimensional imaging method for quantifying cassava root mass [29]. Most GPR systems work in a time domain function by emitting electromagnetic pulses into the ground in which part of the energy is reflected, transmitted, or scattered at boundaries of contrasting materials [30,31]. The reflected strength of the return is recorded as a function of two-way travel time [31]. Many thousands of measurements are acquired across a planned grid network by moving the antenna along a ground transect at fixed intervals. These returns can be quantified and rendered into a 3D field allowing for visualization and mapping of near-surface root biomass.
We hypothesize that current technology can detect and measure root features and root orientation parameters. By utilizing a controlled in-vitro environment, we can reduce the unexplained variance in data capture and enhance the sampling protocol to more accurately detect rooting parameters that are necessary for estimating cassava size and shape necessary for decision support in breeding programs and to identify marketable materials near real-time.

2. Materials and Methods

The unit utilized for this study was the IDS GeoRadar C-Thrue system [32]. This unit is of compact design that is fully integrated into one handheld unit (antenna, computer, control unit, and battery). This system design is considered optimal for maneuverability and access to closed canopy rows often found in cassava fields. The C-Thrue design was originally developed for concrete scanning in civil applications. The system utilizes a dual polarization for multi-level detection, which is optimal for root architecture in that some roots may overlap and root orientations can vary. The specific polarizations are horizontal transmit and horizontal receive (HH) and vertical transmit and vertical receive (VV). The system is ground coupled and allows for minimized signal dispersion at the surface. Acquisition parameters for the sensor were set at 1 scan per 0.2 cm and a time window of 12 ns and 512 samples per scan.
To reduce the error incurred in gridded data acquisition by human interaction, a computer numerical control (CNC) machine was utilized. This would allow for precision in instrument alignment and movement when defining sampling protocols. The CNC machine utilized is accurate to within 0.01 cm over this area and moves at speed ranging from 0.1 cm/s to 10 cm/s (Figure 1). A controlled test site was utilized for this experiment to maintain a high level of uniformity in data acquisition. For this study, it was necessary to control environmental variables, such as soil variability and soil moisture, so that optimization of system sampling protocol can occur for only root variability. The test site was in the form of a rectangular sandbox that measures 400 cm long by 300 cm wide by 110 cm deep. Base and walls are constructed of untreated plywood and assembled together with stainless steel screws and high weight capacity straps. To secure high fidelity of repeated trials for replication, the test area was covered in a carbon-based microwave absorber (PPG Aerospace—Cuming Microwave). This material reduces electromagnetic interference and repetitive backscatter from sandbox bounds. This component is a flexible carbon loaded microwave and radar absorbing material specifically designed to better absorb the range of frequencies that were utilized in this study.
Full-resolution GPR data acquisition has demonstrated a high level of near-surface object visualization [33,34]. For this reason, the minimum allowable cross-line spacing was utilized. This cross-line spacing was set to 2.5 cm. Full-resolution for this system as determined utilizing the Nyquist Theorem exceeds this value. The theoretical full-resolution was derived by estimating wavelength (λ) which is defined by Equation (1):
λ = ( c ε r ) / f ,
where the media utilized had a relative dielectric permittivity (εr) of 4.5, frequency (f) of our system was 2 GHz, and c is the speed of light (30 cm/ns). Therefore, a quarter of the wavelength for this host material was 1.8 cm when velocity is calculated at 14 cm/ns. However, the cross-line spacing that was set at 2.5 cm was due to a structural limitation in the system in which the wheel spacing of the unit is 18 cm. Since the wheels require enough contact for encoder functionality, a gridded platform was constructed with notches (Figure 2) to minimize encoder slippage that would occur by solely having contact with the sand. This adjustment, therefore, limited the minimum spacing between scans to 2.5 cm to allow for equal interval passes without encoder slippage.
Roots were chosen based on three size classes (Small, Medium, Large) with three roots per class. This would allow for estimating accuracy at each class and sensitivity to size characteristics. These characteristics can be found in Table 1. Measurements were taken for total root length, and three root diameters were taken at equal intervals across the root to account for root tapering. Figure 3 provides an illustration of the measurement procedure.
Root orientation in true fields is omnidirectional and, for this reason, efforts were taken to determine the sensor efficacy with multiple root orientations. Each of the nine roots was buried in two vertical positions relative to the surface (0-degrees & 45-degrees) as well as three horizontal directions relative to the scan direction (parallel to scan, perpendicular to scan, and a 45-degree angle to scan). Roots were buried in the sandbox at a depth similar to that of an actively growing root in the field. More specifically, if the root was buried parallel to the surface, it was buried at 15 cm from the surface, and when roots were at a 45-degree angle to the surface, they were buried at 0 cm from the surface and continued downwards to a maximum depth relative to the root length. Visual representation of the root orientation parameters and burying conditions can be found in Figure 4.
The data pre-processing procedure was performed using GPR-Slice software [35]. The data was processed in GPR-Slice, which allows for three-dimensional rendering and volume extraction utilizing an OpenGL interface. Before the export of root volumes, a pre-processing procedure was performed to create the isosurfaces. This process required a signal gain correction, which was followed by filtering of the raw radargrams for noise removal using a bandpass filter (Low: 500 MHz / High: 5000 MHz) followed by a median background filter. Median background filters provide better filtering than standard average scan—background filtering—as the peak responses from cassava reflections would not overweight a median scan used in this subtraction filter. Kirchhoff migrations were then performed on the background filtered data to migrate hyperbolic responses and to collapse diffractions. The previously calculated 14 cm/ns propagation velocity generated satisfactory results and was also used for time-to-depth conversion of the data. The migrated image was then converted using a Hilbert transform to rectify the pulse data into the pulse envelope. The sinusoidal pulses were converted to positive domain envelopes. This was accomplished by conducting a Fourier Transform to convert the radargrams to the frequency domain and shifting the imaginary frequencies by 90-degrees followed by an inverse Fourier Transform. This is useful to define regions of just strong or weak reflections as the signal is completely rectified in the positive domain. We then began a depth- slice process utilizing the Slice XYZ function in GPR-Slice. Data were sampled at 12 ns per scan; however, relative data to the root zone was only found between 1.07 ns and 6.07 ns. Therefore, 5 ns was sliced into 15-time slices at 25% overlap between slice for an estimate time slice depth of 0.54 ns. The data then underwent a gridding process to create 2D horizontal images of the slices at different depths in which data are interpolated to fill gaps between radargrams utilizing an inverse distance weighting function. Volume renderings were developed from the 2D depth-slices which were interpolated vertically to enhance 3D visualization creating more images between depth levels (Figure 5a).
These interpolation methods may have some effect on the X, Y dimension of the root feature. Finally, the isosurface renderings were generated to extract a volumetric body, which represents the shapes and dimensions of the targets. An amplitude threshold value defines a maximum number of possible surfaces within the three-dimensional volume, which are automatically calculated. Then, any surface with a value equal to or greater than 70% of the maximum amplitude value (threshold) was displayed. Therefore, isosurface functions may affect the dimensions of the root feature (Figure 5b). These isosurface volumes were measured for accuracy assessment relative to true root dimensions. This procedure was done by exporting the isosurfaces as graphical tins that could be rendered and characterized in AutoCAD 2012 [36]. The logic block diagram in Figure 6 provides context on the processing flow discussed here.

3. Results

The following results are presented as an analysis of accuracy by size class as established in the methods. This was done since the objective of the article was to establish what are the capabilities of a current sensor for detecting root size and orientation. Size class large references data were obtained from roots 1, 2, and 3. Size class medium reference data were obtained from roots 4, 5, and 6. Size class small references data were obtained from roots 7, 8, and 9. The accuracy analysis was conducted utilizing standard root mean squared error (Equation (2)). Where Pi is the predicted value, Oi is the observed value, and n is the number of samples.
R M S E   =   ∑ ( P i − O i ) 2 n
Also utilized was a standard deviation value to understand the precision of the measurement. This would allow for greater confidence in defining parameters. The standard deviation was calculated using Equation (3), where Pi is the predicted sample value, P i ¯ is the mean predicted sample value, and n is the number of samples.
S D =   ∑ ( P i − P i ¯ ) 2 n
The results are broken down into three categories. These were Cross-line spacing, Polarization, and Depth. Depth analysis was accomplished by analyzing the differences between Width 1, Width 2, and Width 3 as each measurement would be located at different depths since the root was buried at a 45-degree angle to surface.

3.1. Cross-Line Spacing

It is defined as the spatial distance between two radargrams. From the original dense (2.5 cm cross-line spacing) data set, a decimation study was conducted. The purpose of this study was to identify the maximum spacing allowable for accurate analysis. This information could be utilized to modify future antenna array designs to minimize the expense and size of future units. Three data sets with three different cross-line spacing values were compared: 2.5 cm, 5 cm, and 10 cm. As 2 GHz dual polarization antenna arrays with a 10 cm cross-line spacing are already commercially available [37], we did not continue decimating further than that. In-line spacing was kept constant at 0.2 cm as set by the antenna acquisition software configuration.
When analyzing this data across all variables, it was found that the cross-line spacing decimation until 10 cm did not create a significant difference in accuracy for both root length and root width for small, medium, or large root classes. However, in most instances, the standard deviation increased with cross-line spacing. These results can be found in Table 2.

3.2. Polarization

Since cross-line spacing decimation up to 10 cm was not found to create significant differences in accuracy, the analysis for Polarization was performed utilizing solely the 2.5 cm cross-line spacing. For this section, the results are constructed based on the fact that polarization, in theory, would be affected by root orientation. Each root across the three size classes was buried in all orientations to include vertical and horizontal to surface and parallel, perpendicular, and angled to scan direction. This would allow for sampling like that of real field root orientation. The results of the analysis can be found in Table 3.
The results in Table 3 would suggest that the VV polarization is the most effective at accurately characterizing root shape across multiple root orientations. Though VV was the most accurate at detecting across root orientations, it did, however, demonstrate inaccuracies and, in some instances, was not capable of discerning root features. This was evident for (1) Root features that are parallel to the scan direction of the antenna, however, as expected, VV clearly outperformed HH and (2) For features that are vertically oriented to the surface and parallel to scan direction.

3.3. Depth

In the polarization results, it was evident that the vertical to surface orientation influenced the accuracy of the data. Previous literature [22] has suggested that depth would have a negative effect on root characterization. To validate this, the analysis was done for roots buried vertical to the surface. Each root had three width measures taken. Each width would be positioned at varying depths based on the downward angle of the buried root feature. Based on the findings of cross-line spacing and polarization, the optimal data set was utilized for this analysis. Specifically, data acquired at 2.5 cm cross-line spacing with the VV polarization antenna was utilized. Also, only data acquired in which the root ran perpendicular to the scan direction was utilized. This was because the overall precision for this data was best. This would allow for the optimal estimation effect by the depth to be achieved. The results for the depth analysis can be found in Table 4.
The results from Table 4 would suggest that depth does have a significant effect on characterizing root shape. However, this was only evident for medium to large roots as small roots did not exhibit the same trend of accuracy degradation with depth.

4. Discussion

The objective of this research was to determine the functionality of currently available antenna design for the detection and parameterization of root architecture to be utilized for estimating marketable product, more specifically, root shape. The system was to be tested across multiple root orientations and dimensions to define the limitations and capabilities of the system with modified acquisition methodologies. The long-term objective of the study is the optimization of currently available sensor platforms for the use in root architecture mapping, which can be transferable to breeding programs for developing new cultivars that have more marketable root traits and a decision support platform for large scale farming in delivering marketable goods at an earlier delivery point.
The results demonstrated highly accurate capabilities of the sensor when roots ran at a perpendicular or 45-degree angle to the scan line. This result was also confirmed by Cui et al., [21] in which they found an average R2 value of 0.86 with an average root mean squared error (RMSE) of 0.36 cm for root width at two locations. Though the method utilized in this study was not the same, the results of each method would provide validity to the ability of GPR to detect root architecture. This is only evident for certain root orientations, however. Roots ran parallel to the scan direction created inaccurate results. We attribute this issue to two-dimensional migration. Since the migration functions performed on the data were only performed in two dimensions, the function would not collapse the signal from the opposite direction. This migration is done solely on the radargram in the scan direction. Since the root feature would cover multiple radargrams across scan lines, it is expected that the feature would appear in scan lines beyond the root dimension limits due to the emitted radiation pattern that would capture responses from further than the root feature. This creates a false feature at greater distances perpendicular to the root feature since the signal was not migrated in that cross direction and, therefore, increases the dimension of the root. The expected solution to this issue would be utilizing a more computationally intensive three-dimensional migration function.
When characterizing root features for roots with an inclination of 45-degrees from the surface, there were discrepancies in the accuracy of the measures. Root features were not evident at all when utilizing a root orientation parallel to the scan direction which could be attributed again to the migration issue. However, in this case, the widebody reconstruction of the root features began to merge into one another after interpolation which did not allow for estimation of dimensions. This issue is clearly evident in Figure 7. Though migration is expected to be a factor in this scenario, it can also be inferred that interpolation would have created distortions in the images. When conducting interpolation, an inverse distance weighted function is utilized. Based on spatial autocorrelation, it would be expected that the interpolation would over enhance these larger features in the parallel direction while reducing the overlap when the spacing between features is increased. A factor that can also be contributing to these merged features would be depth. As found in Depth Analysis shown in Table 4, the greater the depth, the less accurate the measure becomes. This could suggest that the deeper root features are characterized to a larger dimension creating overlap and, therefore, loss of clarity when creating isosurfaces.
The VV polarization suggested optimal detection capabilities as found in the polarization results in Table 3. However, theoretical knowledge would suggest that for root detection perpendicular to scan line direction, an HH antenna would have the best results. This is validated in Simi et al. [37]. In this study, the same sensor concept of dual polarization and frequency was utilized, and results suggested that the HH polarization had the best detection capabilities of rebar running perpendicular to the scan line direction. However, a dense array of VV sensors have already been proven at producing outstanding results in mapping underground utilities running perpendicular to the scan direction [38,39]. These are particularly encouraging results as VV polarization permits building denser arrays, which may be necessary for characterizing small roots features.
A statistic that was also of interest and would be introduced for discussion in this article is the accuracy of the sensor in relation to root features that run at a 45-degree angle to the scan direction. Theoretically, a cross polarization antenna would be the best approach for acquisition of this type of feature; however, both the VV and HH polarizations exhibited high accuracy and, in some cases, better accuracy than that of a feature most expected to exhibit greater detection. When collecting data with a horizontal polarization antenna on a feature that is moving perpendicular to the scan direction, the HH polarization would be expected to perform best on this feature. However, the HH polarization was found to be more accurate on the feature that runs at an angle to the scan line. This result is of interest and should be studied further to determine if the effect can be attributed to pre-processing methods or interpolation methods.
Though the results suggest positive findings, it should be communicated that limitations still exist for full field deployment. Current antenna designs are not suitable for rugged agricultural conditions creating a constraint in data capture. Field deployed systems must also consider the limitations of the environment. This could include soil variability and moisture [40,41,42,43]. The system utilized in this study allows for high spatial resolution; however, in the field conditions expected in true agricultural fields, the chance for increased energy dissipation would be expected.
In conclusion, based on these findings, it can be inferred that the currently available C-Thrue sensor by IDS GeoRadar and GPR-Slice software would allow for accurate estimation of root metrics. The combination of dual polarization is effective for the omnidirectional nature of roots. The findings in this study would provide context for future development and begin a dialogue for the future applications of GPR in agricultural applications in which the opportunity for root characterization is considered a new frontier for development.

Author Contributions

Conceptualization, A.D., A.N., and D.B.H.; Data curation, A.D.; Formal analysis, A.D. and A.N.; Funding acquisition, D.B.H.; Investigation, A.D. and A.N.; Methodology, A.D., A.N., and D.B.H.; Project administration, A.N. and D.B.H.; Resources, A.N. and D.B.H.; Software, A.D.; Supervision, A.N. and D.B.H.; Validation, A.D. and A.N.; Visualization, A.D.; Writing—original draft, A.D. and A.N.; Writing—review and editing, A.D., A.N., and D.B.H.

Funding

This research was funded by the National Science Foundation, grant number 1543957.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Allem, A.C. The Origins and Taxonomy of Cassava, in Cassava: Biology, Production and Utilization; Hillcocks, R.J., Thresh, J.M., Bellotti, A.C., Eds.; CABI Publishing: New York, NY, USA, 2002; pp. 1–16. [Google Scholar]
  2. Nassar, N.; Ortiz, R. Breeding cassava to feed the poor. Sci. Am. 2010, 302, 78–84. [Google Scholar] [CrossRef] [PubMed]
  3. Ceballos, H.; Ramirez, J.; Bellotti, A.C.; Jarvis, A.; Alvarez, E. Adaptation of cassava to changing climates. In Crop Adaptation to Climate Change; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2011; pp. 411–425. [Google Scholar]
  4. FAO. FAOSTAT—Country/Territorial Notes: Yield of Commodity. [Database] 2015; Group—Production, Domain—Crops, Area—Africa and South Eastern Asia, Item—Cassava, Element—Yield]. Available online: http://faostat3.fao.org/compare (accessed on 29 March 2016).
  5. Ceballos, H.; Hershey, C.; Becerra-López-Lavalle, L.A. New approaches to cassava breeding. Plant Breed. Rev. 2012, 36, 427–504. [Google Scholar]
  6. Okogbenin, E.; Setter, T.L.; Ferguson, M.; Mutegi, R.; Ceballos, H.; Olasanmi, B.; Fregene, M. Phenotypic approaches to drought in cassava: Review. Front. Physiol. 2013, 4, 93. [Google Scholar] [CrossRef] [PubMed]
  7. Ceballos, H.; Hershey, C.H. Cassava (Manihot esculenta Crantz). In Genetic Improvement of Tropical Crops; Springer: Cham, Switzerland, 2017; pp. 129–180. [Google Scholar]
  8. Majdi, H. Root sampling methods-applications and limitations of the minirhizotron technique. Plant Soil 1996, 185, 255–258. [Google Scholar] [CrossRef]
  9. Perret, J.S.; Al-Belushi, M.E.; Deadman, M. Non-destructive visualization and quantification of root using computed tomography. Soil Biol. Biochem. 2007, 39, 391–399. [Google Scholar] [CrossRef]
  10. Metzner, R.; Eggert, A.; van Dusschoten, D.; Pflugfelder, D.; Gerth, S.; Schurr, U.; Uhlmann, N.; Jahnke, S. Direct comparison of MRI and X-ray CT technologies for 3D maging of root systems in soil: Potential and challenges for root trait quantification. Plant Methods 2015, 11, 17. [Google Scholar] [CrossRef]
  11. Al-Nuaimy, W.; Huang, Y.; Nakhkash, M.; Fang, M.T.C.; Nguyen, V.T.; Eriksen, A. Automatic detection of buried utilities and solid objects with GPR using neural networks and pattern recognition. J. Appl. Geophys. 2000, 43, 157–165. [Google Scholar] [CrossRef]
  12. Frigui, H.; Gader, P. Detection and discrimination of land mines in ground-penetrating radar based on edge histogram descriptors and a possibilistic-nearest neighbor classifier. IEEE Trans. Fuzzy Syst. 2009, 17, 185–199. [Google Scholar] [CrossRef]
  13. Ho, K.; Carin, L.; Gader, P.D.; Wilson, J.N. An investigation of using the spectral characteristics from ground penetrating radar for landmine/clutter discrimination. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1177–1191. [Google Scholar] [CrossRef]
  14. Pasolli, E.; Melgani, F.; Donelli, M.; Attoui, R.; De Vos, M. Automatic detection and classification of buried objects in GPR images using genetic algorithms and support vector machines. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
  15. Andrén, O.; Rajkai, K.; Kätterer, T. A non-destructive technique for studies of root distribution in relation to soil moisture. Agric. Ecosyst. Environ. 1991, 34, 269–278. [Google Scholar] [CrossRef]
  16. Bassuk, N.; Grabosky, J.; Mucciardi, A.; Raffel, G. Ground-penetrating radar accurately locates tree roots in two soil media under pavement. Arboric. Urban For. 2011, 37, 160–166. [Google Scholar]
  17. Butnor, J.; Pruyn, M.L.; Shaw, D.C.; Harmon, M.E.; Mucciardi, A.N.; Ryan, M.G. Detecting defects in conifers with ground penetrating radar: Applications and challenges. For. Pathol. 2009, 39, 309–322. [Google Scholar] [CrossRef]
  18. Butnor, J.R.; Barton, C.; Day, F.P.; Johnsen, K.H.; Mucciardi, A.N.; Schroeder, R.; Stover, D.B. Using Ground Penetrating to Detect Tree Roots and Estimate Biomass. In Measuring Roots: An Updated Approach; Mancuso, S., Ed.; Springer: New York, NY, USA, 2011; pp. 213–246. [Google Scholar]
  19. Butnor, J.R.; Doolittle, J.A.; Johnsen, K.H.; Samuelson, L.; Stokes, T.; Kress, L. Utility of ground-penetrating radar as a root biomass survey tool in forest systems. Soil Sci. Soc. Am. J. 2003, 67, 1607–1615. [Google Scholar] [CrossRef]
  20. Butnor, J.R.; Doolittle, J.A.; Kress, L.; Cohen, S.; Johnsen, K.H. Use of ground-penetrating radar to study tree roots in the southeastern United States. Tree Physiol. 2001, 21, 1269–1278. [Google Scholar] [CrossRef] [Green Version]
  21. Cui, X.; Chen, J.; Shen, J.; Cao, X.; Chen, X.; Zhu, X. Modeling tree root diameter and biomass by ground-penetrating radar. Sci. China Earth Sci. 2011, 54, 711–719. [Google Scholar] [CrossRef]
  22. Cui, X.; Guo, L.; Chen, J.; Chen, X.; Zhu, X. Estimating tree-root biomass in different depths using ground-penetrating radar: Evidence from a controlled experiment. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3410–3423. [Google Scholar] [CrossRef]
  23. Guo, L.; Lin, H.; Fan, B.; Cui, X.; Chen, J. Forward simulation of root’s ground penetrating radar signal: Simulator development and validation. Plant Soil 2013, 372, 487–505. [Google Scholar] [CrossRef]
  24. Guo, L.; Lin, H.; Fan, B.; Cui, X.; Chen, J. Impact of root water content on root biomass estimation using ground penetrating radar: Evidence from forward simulations and field controlled experiments. Plant Soil 2013, 371, 503–520. [Google Scholar] [CrossRef]
  25. Hirano, Y.; Dannoura, M.; Aono, K.; Igarashi, T.; Ishii, M.; Yamase, K.; Makita, N.; Kanazawa, Y. Limiting factors in the detection of tree roots using ground-penetrating radar. Plant Soil 2009, 319, 15–24. [Google Scholar] [CrossRef]
  26. Molon, M.M. Quantitative, Non-Destructive Estimates of Forest Coarse Root Biomass Using 3-D Ground-Penetrating Radar (GPR). Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2012. [Google Scholar]
  27. Raz-Yaseef, N.; Koteen, L.; Baldocchi, D.D. Coarse root distribution of a semi-arid oak savanna estimated with ground penetrating radar. J. Geophys. Res. Biogeosci. 2013, 118, 135–147. [Google Scholar] [CrossRef] [Green Version]
  28. Zhu, S.; Huang, C.; Su, Y.; Sato, M. 3D Ground Penetrating Radar to Detect Tree Roots and Estimate Root Biomass in the Field. Remote Sens. 2014, 6, 5754–5773. [Google Scholar] [CrossRef] [Green Version]
  29. Delgado, A.; Hays, D.B.; Bruton, R.K.; Ceballos, H.; Novo, A.; Boi, E.; Selvaraj, M.G. Ground penetrating radar: A case study for estimating root bulking rate in cassava (Manihot esculenta Crantz). Plant Methods 2017, 13, 65. [Google Scholar] [CrossRef]
  30. Daniels, D.J. Ground penetrating radar. In Encyclopedia of RF and Microwave Engineering; IET: Hoboken, NJ, USA, 2004; Volume 1. [Google Scholar]
  31. Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
  32. Pasculli, D.; Natali, A.; Salvatore, W.; Morelli, F.; Morandi, D. Investigation of reinforced concrete bridges by using a dual-polarized high-frequency GPR. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018. [Google Scholar]
  33. Grasmueck, M.; Novo, A. 3D GPR imaging of shallow plastic pipes, tree roots, and small objects. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016. [Google Scholar]
  34. Grasmueck, M.; Weger, R.; Horstmeyer, H.J.G. Full-resolution 3D GPR imaging. Geophysics 2005, 70, K12–K19. [Google Scholar] [CrossRef]
  35. Goodman, D. GPR-SLICE Software; Geophysical Archaeometry Laboratory Inc.: Woodland Hills, CA, USA, 2016. [Google Scholar]
  36. Autodesk, Inc. AutoCAD 2012; Autodesk, Inc.: San Rafael, CA, USA, 2011. [Google Scholar]
  37. Simi, A.; Manacorda, A. Benedetto. Bridge deck survey with high resolution ground penetrating radar. In Proceedings of the 2012 14th International Conference on Ground Penetrating Radar (GPR), Shanghai, China, 4–8 June 2012. [Google Scholar]
  38. Pasculli, D.; Giannino, F.; Simi, A.; Manacorda, G. High-density dual polarized GPR array for underground asset mapping. In Proceedings of the 2017 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Edinburgh, UK, 28–30 June 2017. [Google Scholar]
  39. Simi, A.; Manacorda, G.; Miniati, M.; Bracciali, S.; Buonaccorsi, A. Underground asset mapping with dual-frequency dual-polarized GPR massive array. In Proceedings of the XIII International Conference on Ground Penetrating Radar (GPR), Lecce, Italy, 21–25 June 2012. [Google Scholar]
  40. Detsch, R.M.; Jenkins, T.F.; Arcone, S.A.; Koh, G.; O’Neill, K. Environmental effects on detection of buried mines and UXO. In Detection and Remediation Technologies for Mines and Minelike Targets III; Aerospace/Defense Sensing and Controls; Intermational Society for Optics and Photonics: Bellingham, WA, USA, 1998. [Google Scholar]
  41. Doolittle, J.A.; Collins, M.E. Use of soil information to determine application of ground penetrating radar. J. Appl. Geophys. 1995, 33, 101–108. [Google Scholar] [CrossRef]
  42. Igel, J. The small-scale variability of electrical soil properties-influence on GPR measurements. In Proceedings of the 12th International Conference on Ground Penetrating Radar, Birmingham, UK, 16–19 June 2008. [Google Scholar]
  43. Miller, T.W.; Borchers, B.; Hendrickx, J.M.; Hong, S.; Dekker, L.W.; Ritsema, C.J. Effects of soil physical properties on GPR for landmine detection. In Proceedings of the Fifth International Symposium on Thecnology and the Mine Problem, Monterey, CA, USA, 22–25 April 2002. [Google Scholar]
Geosciences 09 00171 g001 550
Figure 1. Image of Computer Numerical Control unit over test sandbox.
Figure 1. Image of Computer Numerical Control unit over test sandbox.
Geosciences 09 00171 g001
Geosciences 09 00171 g002 550
Figure 2. Illustration of C-Thrue sensor on the gridded platform to limit encoder slippage. The distance between the center of each wheel track is 2.5 cm. The sensor dimensions are 20 cm wide by 30 cm long.
Figure 2. Illustration of C-Thrue sensor on the gridded platform to limit encoder slippage. The distance between the center of each wheel track is 2.5 cm. The sensor dimensions are 20 cm wide by 30 cm long.
Geosciences 09 00171 g002
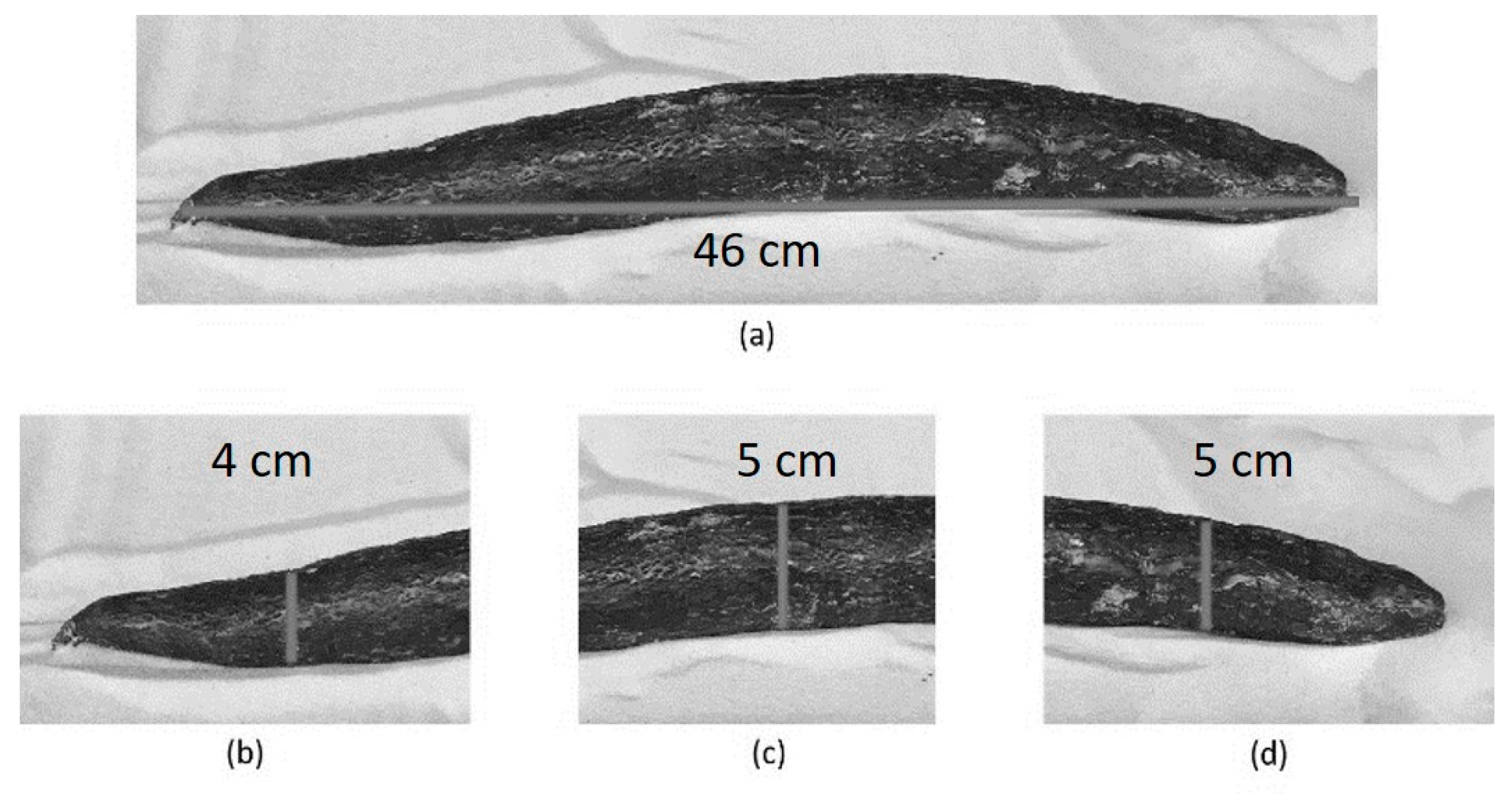
Geosciences 09 00171 g003 550
Figure 3. Illustration of root measurement procedure: (a) Root Length; (b) Root Width 1; (c) Root Width 2; (d) Root Width 3.
Figure 3. Illustration of root measurement procedure: (a) Root Length; (b) Root Width 1; (c) Root Width 2; (d) Root Width 3.
Geosciences 09 00171 g003
Geosciences 09 00171 g004 550
Figure 4. Illustration of root planting parameters: (a) 3D representation of the sandbox: Vertical position in relation to the surface (0-degree to surface and 45-degrees to surface). Roots at 0-degree to the surface were buried at 15 cm depth, while roots at 45-degrees to surface were buried starting at surface and continuing downward to the max depth dependent on root length. (b) Plan (Top) view of the sandbox: Horizontal position in relation to the scan direction. There were three root positions being perpendicular to the scan direction, parallel to the scan direction, and a 45-degree angle to the scan direction.
Figure 4. Illustration of root planting parameters: (a) 3D representation of the sandbox: Vertical position in relation to the surface (0-degree to surface and 45-degrees to surface). Roots at 0-degree to the surface were buried at 15 cm depth, while roots at 45-degrees to surface were buried starting at surface and continuing downward to the max depth dependent on root length. (b) Plan (Top) view of the sandbox: Horizontal position in relation to the scan direction. There were three root positions being perpendicular to the scan direction, parallel to the scan direction, and a 45-degree angle to the scan direction.
Geosciences 09 00171 g004
Geosciences 09 00171 g005 550
Figure 5. Illustration of: (a) time slice and associated filtered radargram; (b) isosurfaces derived utilizing Hilbert processed radargram data.
Figure 5. Illustration of: (a) time slice and associated filtered radargram; (b) isosurfaces derived utilizing Hilbert processed radargram data.
Geosciences 09 00171 g005
Geosciences 09 00171 g006 550
Figure 6. Flow diagram of pre-processing and processing steps for data extraction.
Figure 6. Flow diagram of pre-processing and processing steps for data extraction.
Geosciences 09 00171 g006
Geosciences 09 00171 g007 550
Figure 7. Illustration of isosurfaces in which no root features could be identified.
Figure 7. Illustration of isosurfaces in which no root features could be identified.
Geosciences 09 00171 g007
Table
Table 1. Dimensions of all roots utilized in the study. Measurements were derived by taking the full root length and segmenting into three sections; each section diameter was then measured to obtain width value.
Table 1. Dimensions of all roots utilized in the study. Measurements were derived by taking the full root length and segmenting into three sections; each section diameter was then measured to obtain width value.
Root NumberLengthWidth 1Width 2Width 3
Large Root Classification
Root 138 cm6 cm9 cm8 cm
Root 236 cm5 cm8 cm9 cm
Root 346 cm4 cm5 cm5 cm
Medium Root Classification
Root 437 m4 cm5 cm5 cm
Root 535 m4 cm5 cm5 cm
Root 630 m4 cm6 cm5 cm
Small Root Classification
Root 725 m4 cm4 cm4 cm
Root 820 m4 cm5 cm4 cm
Root 920 m3 cm6 cm5 cm
Table
Table 2. Cross-line spacing for root length measures. The root mean squared error (RMSE) and standard deviation (SD) for each root category are provided.
Table 2. Cross-line spacing for root length measures. The root mean squared error (RMSE) and standard deviation (SD) for each root category are provided.
Results of Cross-Line Spacing Decimation for three Root Size Classes
Root Length
SmallMediumLarge
Cross-line SpacingRMSE SDRMSE SDRMSE SD
2.5 cm9.0 cm ± 2.4 cm8.4 cm ± 4.8 cm6.3 cm ± 2.4 cm
5 cm7.1 cm ± 1.9 cm9.7 cm ± 6.5 cm6.4 cm ± 3.4 cm
10 cm7.5 cm ± 1.4 cm10.9 cm ± 7.9 cm4.8 cm ± 5.2 cm
Root Width
SmallMediumLarge
Cross-line SpacingRMSE SDRMSE SDRMSE SD
2.5 cm7.9 cm ± 2.3 cm5.6 cm ± 2.3 cm9.6 cm ± 2.5 cm
5 cm6.9 cm ± 2.7 cm6.5 cm ± 2.3 cm9.9 cm ± 2.2 cm
10 cm7.7 cm ± 3.3 cm6.9 cm ± 3.0 cm11.9 cm ± 3.2 cm
Table
Table 3. Results of accuracy analysis utilizing root mean squared error (RMSE) and standard deviation (SD) for identifying Polarization response to orientation across three root size classes. Asterisks signify no data available for that parameter due to the inability to segment root features from isosurfaces.
Table 3. Results of accuracy analysis utilizing root mean squared error (RMSE) and standard deviation (SD) for identifying Polarization response to orientation across three root size classes. Asterisks signify no data available for that parameter due to the inability to segment root features from isosurfaces.
Polarization Response to Orientation
VV Polarization
Root Length
Horizontal to SurfaceVertical to Surface
SmallMediumLargeSmallMediumLarge
RMSE SDRMSE SDRMSE SDRMSE SDRMSE SDRMSE SD
Angle4.7 cm ± 2.1 cm3.3 cm ± 2.7 cm2.3 cm ± 1.4 cm11.1 cm ± 3.8 cm8.4 cm ± 6.2 cm6.8 cm ± 4.7 cm
Parallel3.1 cm ± 2.5 cm4.6 cm ± 3.4 cm3.1 cm ± 2.8 cm***
Perpendicular5.8 cm ± 5.2 cm2.1 cm ± 2.6 cm4.2 cm ± 3.1 cm8.8 cm ± 1.5 cm9.1 cm ± 2.5 cm7.9 cm ± 2.5 cm
Root Width
Horizontal to SurfaceVertical to Surface
SmallMediumLargeSmallMediumLarge
RMSE SDRMSE SDRMSE SDRMSE SDRMSE SDRMSE SD
Angle1.2 cm ± 1.2 cm2.6 cm ± 1.5 cm1.8 cm ± 1.5 cm5.8 cm ± 1.5 cm9.7 cm ± 3.7 cm5.3 cm ± 2.1 cm
Parallel3.1 cm ± 2.5 cm6.0 cm ± 2.3 cm19.1 cm ± 2.6 cm***
Perpendicular1.4 cm ± 0.6 cm4.2 cm ± 3.2 cm3.9 cm ± 1.5 cm3.1 cm ± 1.0 cm4.8 cm ± 1.5 cm3.7 cm ± 2.6 cm
HH Polarization
Root Length
Horizontal to SurfaceVertical to Surface
SmallMediumLargeSmallMediumLarge
RMSE SDRMSE SDRMSE SDRMSE SDRMSE SDRMSE SD
Angle6.7 cm ± 1.2 cm5.2 cm ± 2.1 cm3.5 cm ±2.0 cm7.4 cm ± 4.0 cm9.3 cm ± 3.8 cm11.5 cm ± 7.6 cm
Parallel10.9 cm ± 8.1 cm8.7 cm ± 7.3 cm16.5 cm ± 9.6 cm***
Perpendicular12.3 cm ± 0.6 cm10.0 cm ± 1.9 cm9.2 cm ± 3.4 cm***
Root Width
Horizontal to SurfaceVertical to Surface
SmallMediumLargeSmallMediumLarge
RMSE SDRMSE SDRMSE SDRMSE SDRMSE SDRMSE SD
Angle4.0 cm ± 2.1 cm3.0 cm ± 3.5 cm7.4 cm ± 4.0 cm5.0 cm ± 3.1 cm6.2 cm ± 2.0 cm9.2 cm ± 2.0 cm
Parallel16.7 cm ± 7.0 cm20.9 cm ± 3.5 cm11.0 cm ± 4.7 cm***
Perpendicular7.4 cm ± 1.5 cm8.7 cm ± 0.6 cm7.9 cm ± 2.5 cm***
VV: vertical transmit and vertical receive; HH: horizontal transmit and horizontal receive.
Table
Table 4. Depth analysis in which data was captured at 2.5 cm cross-line spacing using a VV polarization for roots that were vertical to surface and perpendicular to scan direction. This was done for the three size classes of small, medium, and large.
Table 4. Depth analysis in which data was captured at 2.5 cm cross-line spacing using a VV polarization for roots that were vertical to surface and perpendicular to scan direction. This was done for the three size classes of small, medium, and large.
Depth Analysis
SmallMediumLarge
RMSE SDRMSE SDRMSE SD
Width 13.1 cm ± 1.0 cm5.0 cm ± 3.1 cm5.8 cm ± 1.5 cm
Width 24.8 cm ± 1.5 cm6.2 cm ± 2.0 cm13.1 cm ± 1.7 cm
Width 33.7 cm ± 2.6 cm9.1 cm ± 2.0 cm20.8 cm ± 3.1 cm
RMSE: root mean squared error; SD: standard deviation.

Share and Cite

MDPI and ACS Style

Delgado, A.; Novo, A.; Hays, D.B. Data Acquisition Methodologies Utilizing Ground Penetrating Radar for Cassava (Manihot esculenta Crantz) Root Architecture. Geosciences 2019, 9, 171. https://doi.org/10.3390/geosciences9040171

AMA Style

Delgado A, Novo A, Hays DB. Data Acquisition Methodologies Utilizing Ground Penetrating Radar for Cassava (Manihot esculenta Crantz) Root Architecture. Geosciences. 2019; 9(4):171. https://doi.org/10.3390/geosciences9040171

Chicago/Turabian Style

Delgado, Alfredo, Alexandre Novo, and Dirk B. Hays. 2019. "Data Acquisition Methodologies Utilizing Ground Penetrating Radar for Cassava (Manihot esculenta Crantz) Root Architecture" Geosciences 9, no. 4: 171. https://doi.org/10.3390/geosciences9040171

APA Style

Delgado, A., Novo, A., & Hays, D. B. (2019). Data Acquisition Methodologies Utilizing Ground Penetrating Radar for Cassava (Manihot esculenta Crantz) Root Architecture. Geosciences, 9(4), 171. https://doi.org/10.3390/geosciences9040171

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop