The Increased Release Kinetics of Quercetin from Superparamagnetic Nanocarriers in Dialysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Synthesis of Superparamagnetic Magnetite Nanoparticles
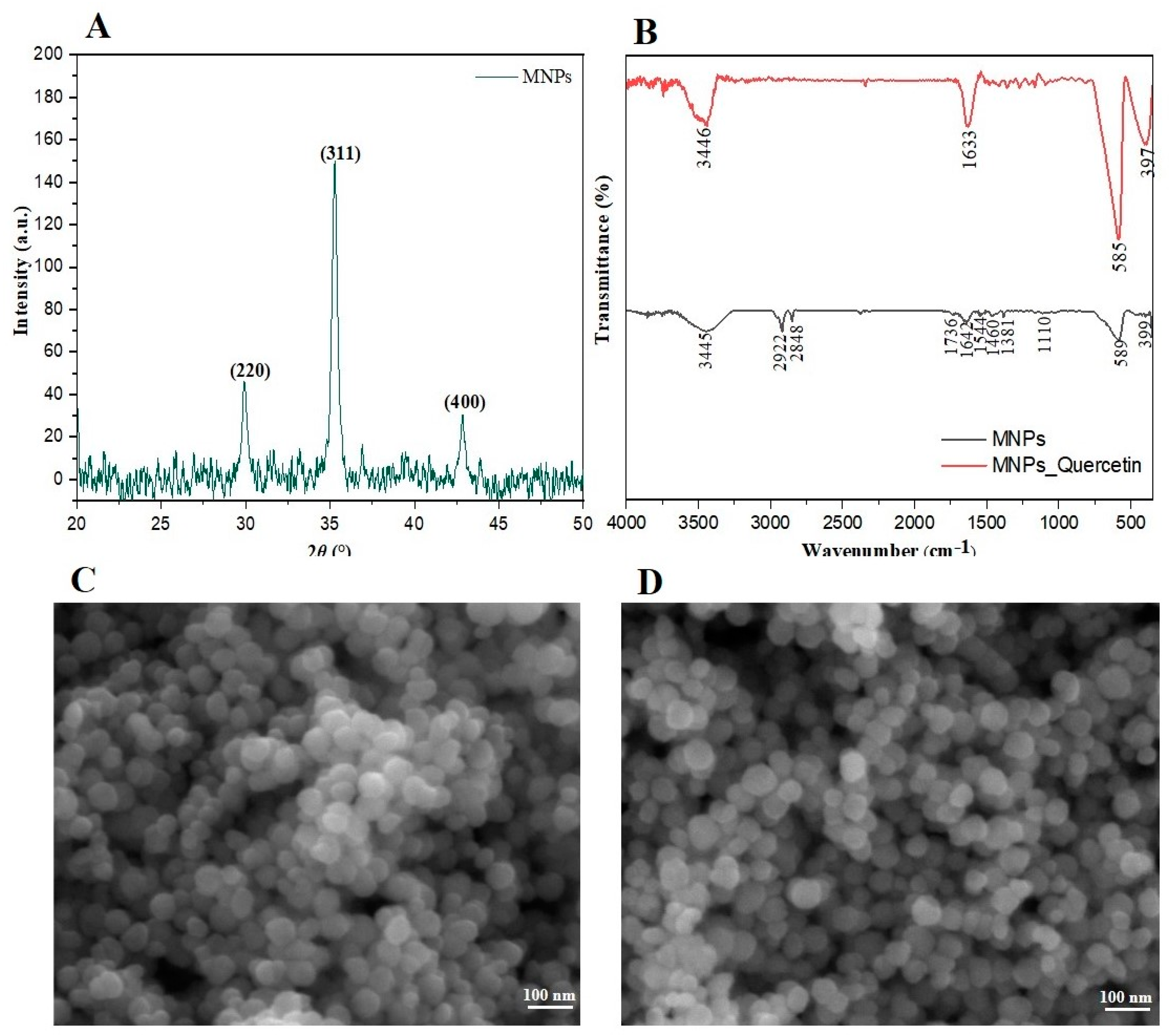
2.3. Instrumentation and Material Characterization
2.4. Loading of Quercetin into MNPs
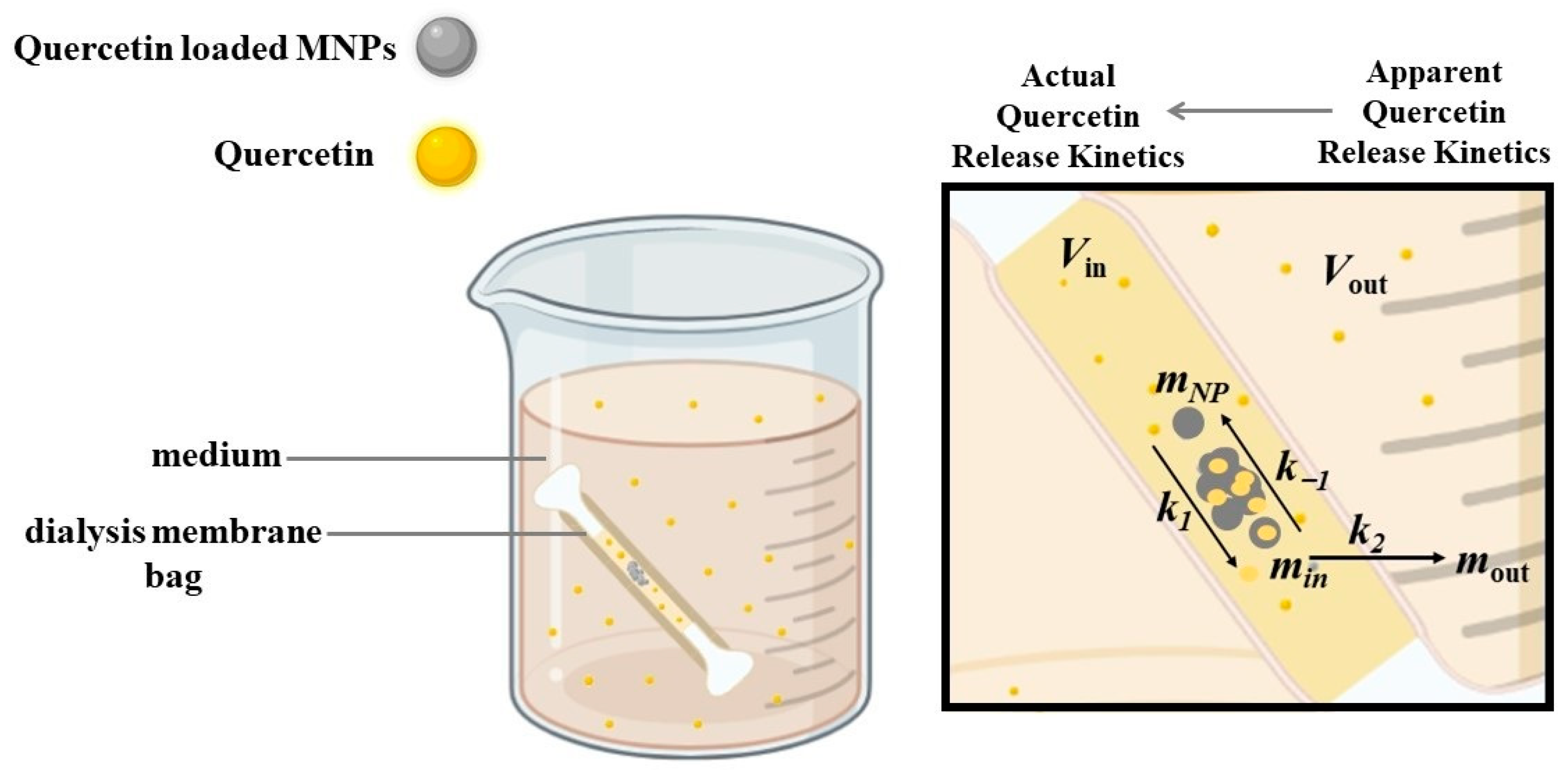
2.5. Release Study of Quercetin under Stationary and Alternating Magnetic Fields
2.6. Dynamic and Electrophoretic Light Scattering
2.7. Viscosity Measurements
2.8. Kinetics
2.9. Calculation of Standard Deviations
3. Results and Discussion
3.1. Characterization of Synthesized Magnetite MNPs
3.2. Viscosity Measurements
3.3. Dynamic and Electrophoretic Light Scattering Experiment
3.4. Kinetics
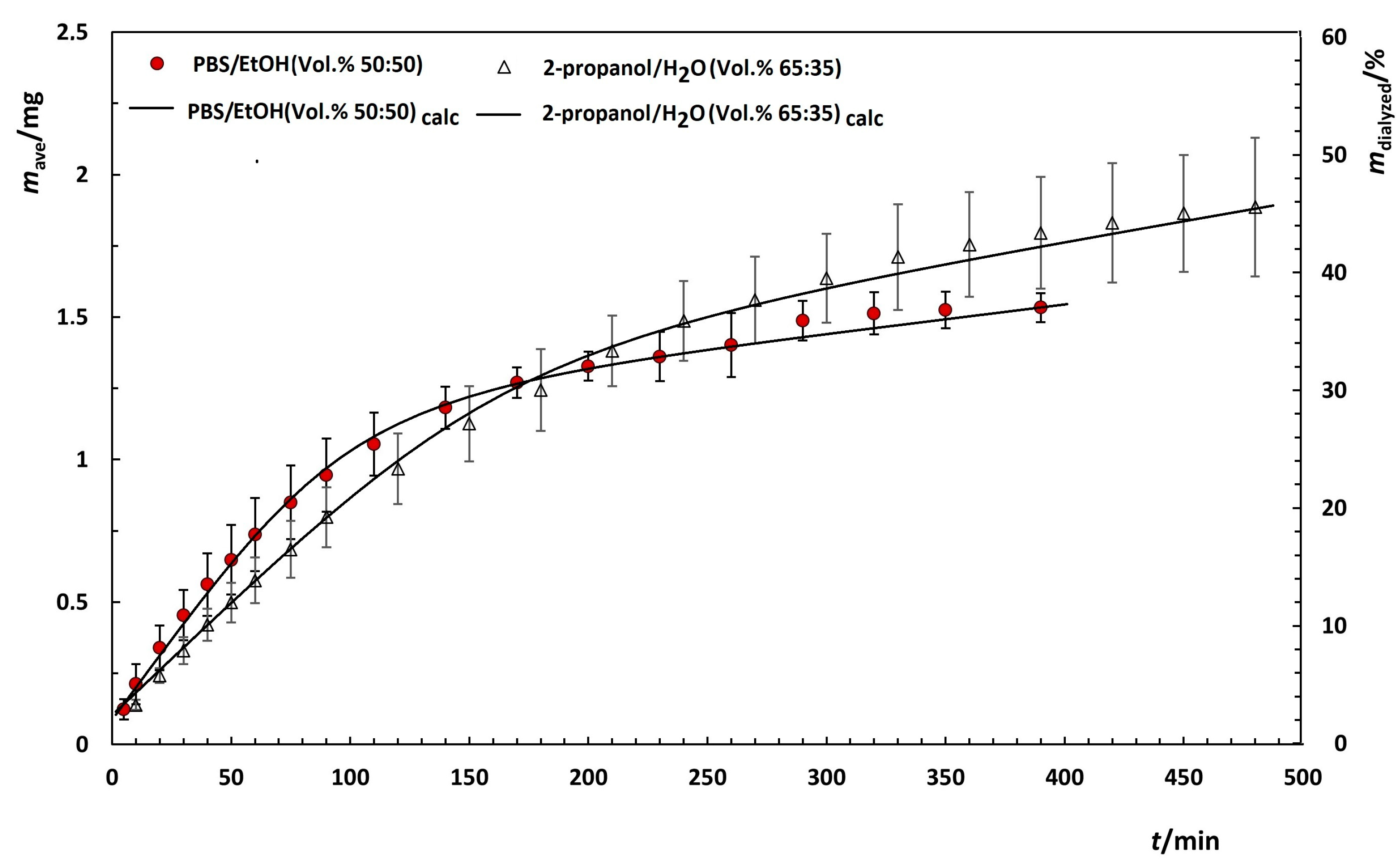
3.4.1. Influence of Membrane Molecular Weight on Dialysis Rate of Quercetin in PBS/EtOH
3.4.2. Influence of Media on the Dialysis
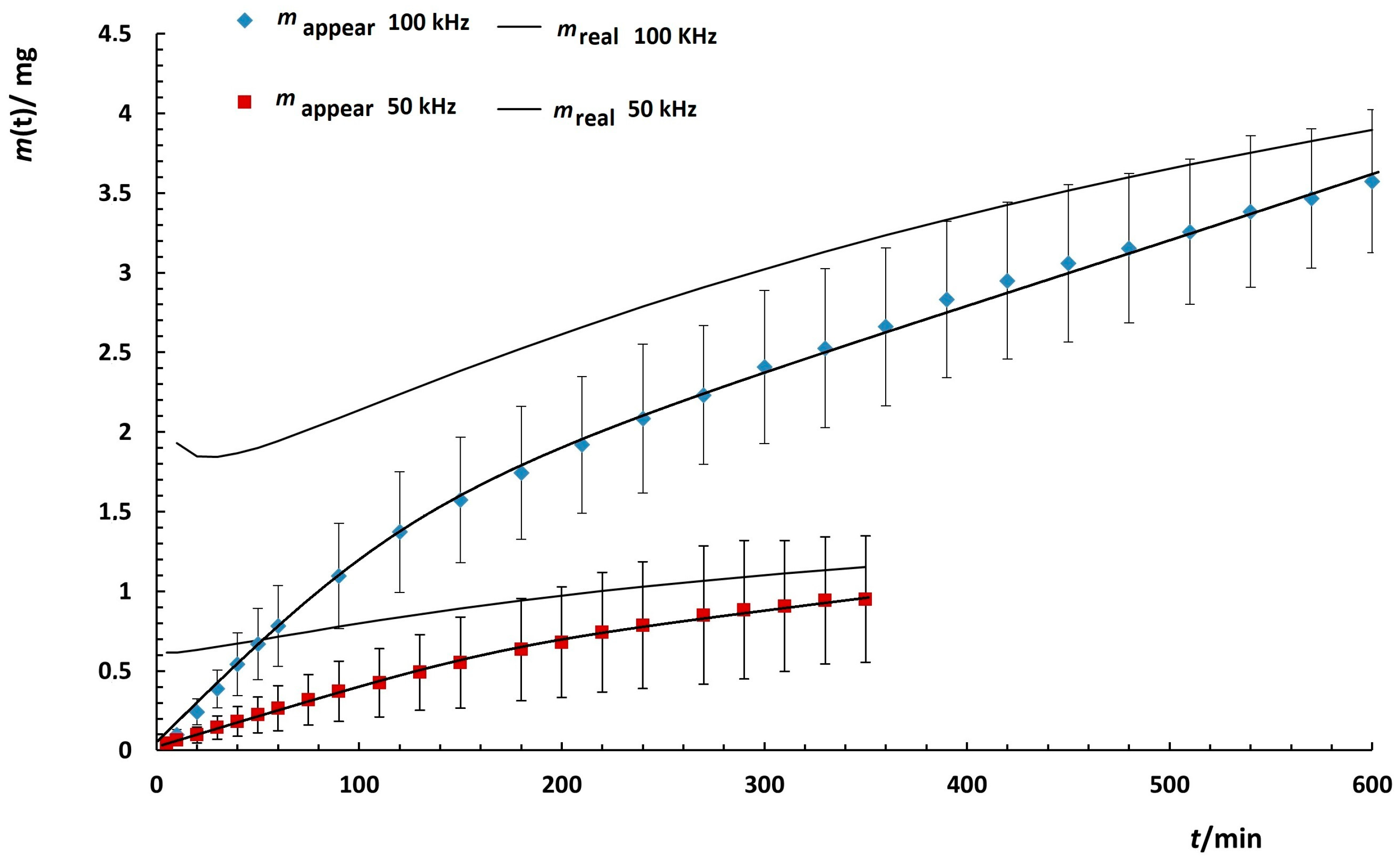
3.4.3. Kinetics of Quercetin Release from MNPs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huda, S.; Alam, M.A.; Sharma, P.K. Smart nanocarriers-based drug delivery for cancer therapy: An innovative and developing strategy. J. Drug Deliv. Sci. Technol. 2020, 60, 102018. [Google Scholar] [CrossRef]
- Koksharov, Y.A.; Gubin, S.P.; Taranov, I.V.; Khomutov, G.B.; Gulyaev, Y.V. Magnetic Nanoparticles in Medicine: Progress, Problems, and Advances. J. Commun. Technol. Electron. 2022, 67, 101–116. [Google Scholar] [CrossRef]
- Hossen, S.; Khalid Hossain, M.; Basher, M.K.; Mia, M.N.H.; Rahman, M.T.; Jalal Uddin, M. Smart nanocarrier-based drug delivery systems for cancer therapy and toxicity studies: Areview. J. Adv. Res. 2019, 15, 1–18. [Google Scholar] [CrossRef]
- Kumar, K.; Chawla, R. Nanocarriers-mediated therapeutics as a promising approach for treatment and diagnosis of lung cancer. J. Drug. Deliv. Sci. Technol. 2021, 65, 102677. [Google Scholar] [CrossRef]
- Hu, J.; Obayemi, J.; Malatesta, K.; Kosmrlj, A.; Soboyejo, W. Enhanced cellular uptake of LHRH-conjugated PEG-coated magnetite nanoparticles for specifific targeting of triple negative breast cancer cells. Mater. Sci. Eng. C 2018, 88, 32–45. [Google Scholar] [CrossRef]
- Krukemeyer, M.G.; Krenn, V.; Huebner, F.; Wagner, W.; Resch, R. History and Possible Uses of Nanomedicine Based on Nanoparticles and Nanotechnological Progress. J. Nanomed. Nanotechnol. 2015, 6, 336. [Google Scholar] [CrossRef] [Green Version]
- Etemadi, H.; Plieger, P.G. Magnetic Fluid Hyperthermia Based on Magnetic Nanoparticles: Physical Characteristics, Historical Perspective, Clinical Trials, Technological Challenges, and Recent Advances. Adv. Ther. 2020, 3, 2000061. [Google Scholar] [CrossRef]
- Wu, W.; Wu, Z.; Yu, T.; Jiang, J.; Kim, W.S. Recent progress on magnetic iron oxide nanoparticles: Synthesis, surface functional strategies and biomedical applications. Sci. Technol. Adv. Mater. 2015, 16, 023501. [Google Scholar] [CrossRef] [PubMed]
- Barreto, A.C.H.; Santiago, V.R.; Mazzetto, S.E.; DeNardin, J.C.; Lavín, R.; Mele, G.; Ribeiro, M.E.N.P.; Vieira, I.G.P.; Gonçalves, T.; Ricardo, N.M.P.S. Magnetic nanoparticles for a new drug delivery system to control quercetin releasing for cancer chemotherapy. J. Nanopart. Res. 2011, 13, 6545–6553. [Google Scholar] [CrossRef]
- García-Jimeno, S.; Estelrich, J. Ferroflfluid based on polyethylene glycol-coated iron oxide nanoparticles: Characterization and properties. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 420, 74–81. [Google Scholar] [CrossRef]
- Wahajuddin, S.A. Superparamagnetic iron oxide nanoparticles: Magnetic nanoplatforms as drug carriers. Int. J. Nanomed. 2012, 7, 3445–3471. [Google Scholar] [CrossRef] [Green Version]
- Assa, F.; Jafarizadeh-Malmiri, H.; Ajamein, H.; Anarjan, N.; Vaghari, H.; Sayyar, Z.; Berenjian, A. A biotechnological perspective on the application of iron oxide nanoparticles. Nano Res. 2016, 9, 2203–2225. [Google Scholar] [CrossRef]
- Kurczewska, J.; Cegłowski, M.; Schroeder, G. Preparation of multifunctional cascade iron oxide nanoparticles for drug delivery. Mater. Chem. Phys. 2018, 211, 34–41. [Google Scholar] [CrossRef]
- Tietze, R.; Zaloga, J.; Unterweger, H.; Lyer, S.; Friedrich, R.P.; Janko, C.; Pöttler, M.; Dürr, S.; Alexiou, C. Magnetic Nanoparticlebased drug delivery for cancer therapy. Biochem. Biophys. Res. Commun. 2015, 468, 463–470. [Google Scholar] [CrossRef] [PubMed]
- Akbarzadeh, A.; Samiei, M.; Davaran, S. Magnetic nanoparticles: Preparation, physical properties, and applications in biomedicine. Nanoscale Res. Lett. 2012, 7, 144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tansık, G.; Yakar, A.; Gündüz, U. Tailoring magnetic PLGA nanoparticles suitable for doxorubicin delivery. J. Nanopart. Res. 2013, 16, 2171. [Google Scholar] [CrossRef]
- Podaru, G.; Chikan, V. Magnetism in Nanomaterials: Heat and Force from Colloidal Magnetic Particles. In Magnetic Nanomaterials: Applications in Catalysis and Life Sciences; Bossmann, H.S., Wang, H., Eds.; The Royal Society of Chemistry: Croydon, UK, 2017; pp. 1–24. [Google Scholar] [CrossRef]
- Gupta, A.K.; Wells, S. Surface-modified superparamagnetic nanoparticles for drug delivery: Preparation, characterization, and cytotoxicity studies. IEEE Trans. Nanobiosci. 2004, 3, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, W.; Wang, M.; Liao, Z. Magnetic nanoparticles for cancer theranostics: Advances and prospects. J. Control. Release 2021, 335, 437–448. [Google Scholar] [CrossRef]
- Li, H.; Zhao, X.; Ma, Y.; Zhai, G.; Li, L.; Lou, H. Enhancement of gastrointestinal absorption of quercetin by solid lipid nanoparticles. J. Control. Release 2009, 133, 238–244. [Google Scholar] [CrossRef]
- Pawlikowska-Pawlinega, B.; Dziubinska, H.; Król, E.; Trebacz, K.; Jarosz-Wilkolazka, A.; Paduch, R.; Gawron, A.; Gruszecki, W. Characteristics of quercetin interactions with liposomal and vacuolar membranes. Biochim. Biophys. Acta 2014, 1838, 254–265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandić, L.; Sadžak, A.; Strasser, V.; Baranović, G.; Jurašin, D.D.; Sikirić, M.D.; Šegota, S. Enhanced Protection of Biological Membranes during Lipid Peroxidation: Study of the Interactions between Flavonoid Loaded Mesoporous Silica Nanoparticles and Model Cell Membranes. Int. J. Mol. Sci. 2019, 20, 2709. [Google Scholar] [CrossRef] [Green Version]
- Mandić, L.; Sadžak, A.; Erceg, I.; Baranović, G.; Šegota, S. The Fine-Tuned Release of Antioxidant from Superparamagnetic Nanocarriers under the Combination of Stationary and Alternating Magnetic Fields. Antioxidants 2021, 10, 1212. [Google Scholar] [CrossRef]
- Khursheed, R.; Singh, S.K.; Wadhwa, S.; Gulati, M.; Awasthi, A. Enhancing the potential preclinical and clinical benefits of quercetin through novel drug delivery systems. Drug Discov. 2020, 25, 209–222. [Google Scholar] [CrossRef]
- Sathishkumar, P.; Li, Z.; Govindan, R.; Jayakumar, R.; Wang, C.; Long Gu, F. Zinc oxide-quercetin nanocomposite as a smart nano-drug delivery system: Molecular-level interaction studies. Appl. Surf. Sci. 2020, 536, 147741. [Google Scholar] [CrossRef]
- Washington, C. Evaluation of non-sink dialysis methods for the measurement of drug release from colloids: Effects of drug partition. Int. J. Pharm. 1989, 56, 71–74. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Han, L.; Li, J.; Liu, C.; Sun, C. Role of Flavonoids in the Treatment of Iron Overload. Front. Cell Dev. Biol. 2021, 9, 685364. [Google Scholar] [CrossRef]
- Kim, G.N.; Jang, H.D. Protective mechanism of quercetin and rutin using glutathione metabolism on HO-induced oxidative stress in HepG2 cells. Ann. N. Y. Acad. Sci. 2009, 1171, 530–537. [Google Scholar] [CrossRef]
- Koskenkorva-Frank, T.S.; Weiss, G.; Koppenol, W.H.; Burckhardt, S. The complex interplay of iron metabolism, reactive oxygen species, and reactive nitrogen species: Insights into the potential of various iron therapies to induce oxidative and nitrosative stress. Free Radic. Biol. Med. 2013, 65, 1174–1194. [Google Scholar] [CrossRef] [PubMed]
- Mertz, D.; Sandre, O.; Bégin-Colin, S. Drug releasing nanoplatforms activated by alternating magnetic fields. Biochim. Biophys. Acta Gen. Subj. 2017, 1861, 1617–1641. [Google Scholar] [CrossRef]
- Available online: http://murov.info/orgsolvents.htm (accessed on 22 January 2021).
- Yu, M.; Yuan, W.; Li, D.; Schwendeman, A.; Schwendeman, S. Predicting Drug Release Kinetics from Nanocarriers inside Dialysis Bags. J. Control. Release 2019, 315, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Langenbucher, F. Letters to the Editor: Linearization of dissolution rate curves by the Weibull distribution. J. Pharm. Pharmacol. 1972, 24, 979–981. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2013. Available online: http://www.R-project.org/ (accessed on 22 January 2021).
- Li, S.; Zhang, T.; Tang, R.; Qiu, H.; Wang, C.; Zhou, Z. Solvothermal synthesis and characterization of monodisperse superparamagnetic iron oxide nanoparticles. J. Magn. Magn. Mater. 2015, 379, 226–231. [Google Scholar] [CrossRef]
- Wang, W.; Li, Q.; Zheng, A.; Li, X.; Pan, Z.; Jiang, J.; Zhuang, L. Superparamagnetic iron oxide nanoparticles for full-color photonic materials with tunable properties. Results Phys. 2019, 14, 102366. [Google Scholar] [CrossRef]
- González, B.; Domínguez, A.; Tojo, J. Dynamic Viscosities, Densities, and Speed of Sound and Derived Properties of the Binary Systems Acetic Acid with Water, Methanol, Ethanol, Ethyl Acetate and Methyl Acetate at T = (293.15, 298.15, and 303.15) K at Atmospheric Pressure. J. Chem. Eng. Data 2004, 49, 1590–1596. [Google Scholar] [CrossRef]
- Khattab, I.S.; Bandarkar, F.; Fakhree, M.A.A.; Jouyban, A. Density, viscosity, and surface tension of water+ethanol mixtures from 293 to 323 K. Korean J. Chem. Eng. 2012, 29, 812–817. [Google Scholar] [CrossRef]
- Pires, R.M.; Costa, H.F.; Ferreira, A.G.M.; Fonseca, I.M.A. Viscosity and Density of Water + Ethyl Acetate + Ethanol Mixtures at 298.15 and 318.15 K and Atmospheric Pressure. J. Chem. Eng. Data. 2004, 52, 1240–1245. [Google Scholar] [CrossRef] [Green Version]
- Pang, F.M.; Seng, C.E.; Teng, T.T.; Ibrahim, M.H. Densities and viscosities of aqueous solutions of 1-propanol and 2-propanol at temperatures from 293.15 K to 333.15 K. J. Mol. Liq. 2007, 136, 71–78. [Google Scholar] [CrossRef]
- Avedian, N.; Zaaeri, F.; Daryasari, M.P.; Javar, H.A.; Khoobi, M. pH-sensitive biocompatible mesoporous magnetic nanoparticles labeled with folic acid as an efficient carrier for controlled anticancer drug delivery. J. Drug Deliv. Sci. Technol. 2018, 44, 323–332. [Google Scholar] [CrossRef]
- Naseerali, C.P.; Hari, P.R.; Sreenivasan, K. The release kinetics of drug eluting stents containing sirolimus as coated drug: Role of release media. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci. 2010, 878, 709–712. [Google Scholar] [CrossRef]
- Zambito, Y.; PedreschI, E.; Di Colo, G. Is dialysis a reliable method for studying drug release from nanoparticulate systems?-A case study. Int. J. Pharm. 2012, 434, 28–34. [Google Scholar] [CrossRef] [PubMed]
- D’Souza, S. A Review of In Vitro Drug Release Test Methods for Nano-Sized Dosage Forms. Adv. Pharm. J. 2014, 2014, 304757. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Bautista, G.; Tam, K.C. Evaluation of dialysis membrane process for quantifying the in vitro drug-release from colloidal drug carriers. Colloids Surf. A Physicochem. Eng. Asp. 2011, 389, 299–303. [Google Scholar] [CrossRef]
- Schwarzl, R.; Du, F.; Haag, R.; Netz, R.R. General method for the quantification of drug loading and release kinetics of nanocarriers. Eur. J. Pharm. Biopharm. 2016, 116, 131–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maderuelo, C.; Zarzuelo, A.; Lanao, J.M. Critical factors in the release of drugs from sustained release hydrophilic matrices. J. Control. Release 2011, 154, 2–19. [Google Scholar] [CrossRef] [PubMed]
- Aguda, R.; Chen, C.C. Solubility of Nutraceutical Compounds in Generally Recognized as Safe Solvents at 298 K. Int. J. Chem. Eng. Appl. 2016, 7, 289–294. [Google Scholar] [CrossRef] [Green Version]
- Razmara, R.S.; Daneshfar, A.; Sahraei, R. Solubility of Quercetin in Water + Methanol and Water + Ethanol from (292.8 to 333.8) K. J. Chem. Eng. Data 2010, 55, 3934–3936. [Google Scholar] [CrossRef]


| Sample | Dynamic Viscosity/mPa s | ||
|---|---|---|---|
| Temperature/°C | |||
| 25 | 30 | 37 | |
| H2O | 0.902 ± 0.007 | 0.812 ± 0.006 | 0.705 ± 0.006 |
| PBS/EtOH (Vol.% 50:50) | 2.38 ± 0.02 | 2.01 ± 0.02 | 1.61 ± 0.01 |
| 2-Propanol/H2O (Vol.% 65:35) | 3.08 ± 0.03 | 2.57 ± 0.03 | 2.03 ± 0.02 |
| MNPs | dHave/nm | PDI | ξ/mV |
|---|---|---|---|
| bare MNPs | 1602 ± 103 | 0.38 ± 0.05 | −6.1 ± 0.3 |
| Q-MNPs | 953 ± 366 | 0.2 ± 0.10 | −3.1 ± 0.3 |
| Medium | Membrane/kDa | 103 × kcal/min−1 |
|---|---|---|
| PBS/EtOH (Vol.% 50:50) | 8 | 1.1 ± 0.3 |
| PBS/EtOH (Vol.% 50:50) | 25 | 9.2 ± 0.8 |
| 2-Propanol/H2O (Vol.% 65:35) | 25 | 5.47 ± 0.08 |
| Medium | Frequency/ kHz | MWCO/ kDa | a/min−1 | b | a mapp/mg | b m0/mg |
|---|---|---|---|---|---|---|
| 2-Propanol/H2O (Vol.% 65:35) | 100 | 25 | 0.017 ± 0.001 | 0.80 ± 0.01 | 2.1 ± 0.1 | 2.34 ± 0.03 |
| PBS/EtOH (Vol.% 50:50) | 0 | 8 | 0.0021 ± 0.0003 | 1.06 ± 0.05 | 0.70 ± 0.08 | 0.91 ± 0.07 |
| 50 | 0.0038 ± 0.002 | 1.10 ± 0.03 | 1.0 ± 0.2 | 1.5 ± 0.1 | ||
| 100 | 0.0049 ± 0.0003 | 0.84 ± 0.02 | 3.54 ± 0.3 | 5.4 ± 0.4 | ||
| 50 | 25 | 0.011 ± 0.002 | 0.93 ± 0.05 | 0.83 ± 0.03 | 0.87 ± 0.03 | |
| 100 | 0.010 ± 0.002 | 1.07 ± 0.04 | 0.706 ± 0.002 | 0.707 ± 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandić, L.; Matković, M.; Baranović, G.; Šegota, S. The Increased Release Kinetics of Quercetin from Superparamagnetic Nanocarriers in Dialysis. Antioxidants 2023, 12, 732. https://doi.org/10.3390/antiox12030732
Mandić L, Matković M, Baranović G, Šegota S. The Increased Release Kinetics of Quercetin from Superparamagnetic Nanocarriers in Dialysis. Antioxidants. 2023; 12(3):732. https://doi.org/10.3390/antiox12030732
Chicago/Turabian StyleMandić, Lucija, Marija Matković, Goran Baranović, and Suzana Šegota. 2023. "The Increased Release Kinetics of Quercetin from Superparamagnetic Nanocarriers in Dialysis" Antioxidants 12, no. 3: 732. https://doi.org/10.3390/antiox12030732
APA StyleMandić, L., Matković, M., Baranović, G., & Šegota, S. (2023). The Increased Release Kinetics of Quercetin from Superparamagnetic Nanocarriers in Dialysis. Antioxidants, 12(3), 732. https://doi.org/10.3390/antiox12030732







