Efficiency of δ-Tocopherol in Inhibiting Lipid Oxidation in Emulsions: Effects of Surfactant Charge and of Surfactant Concentration
Abstract
:1. Introduction
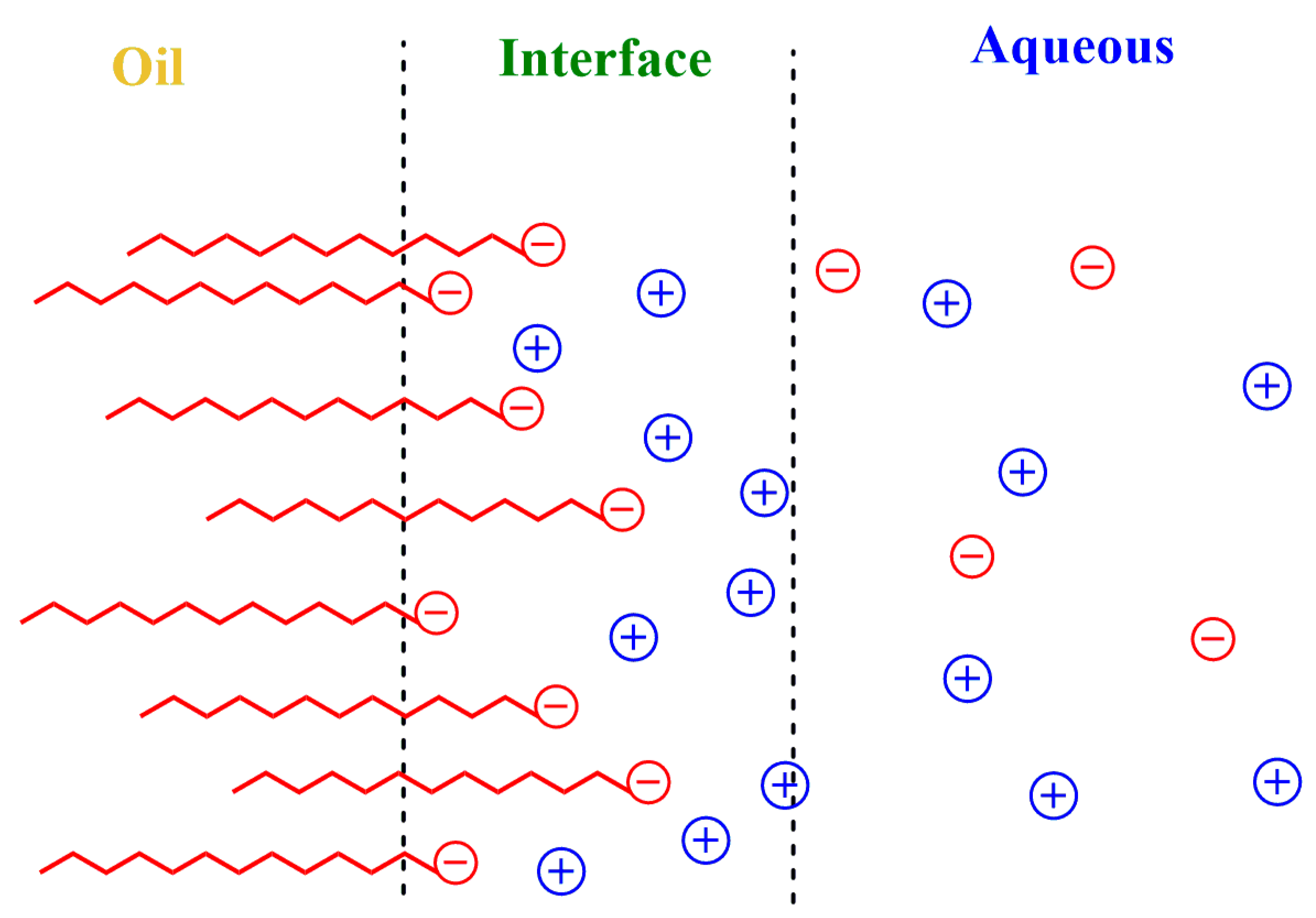
An Overview of the General Effects of Charged Interfaces on Chemical Reactivity
2. Materials and Methods
2.1. Materials
2.2. Emulsion Preparation
2.3. Interfacial Charge of Emulsions: ξ Potential
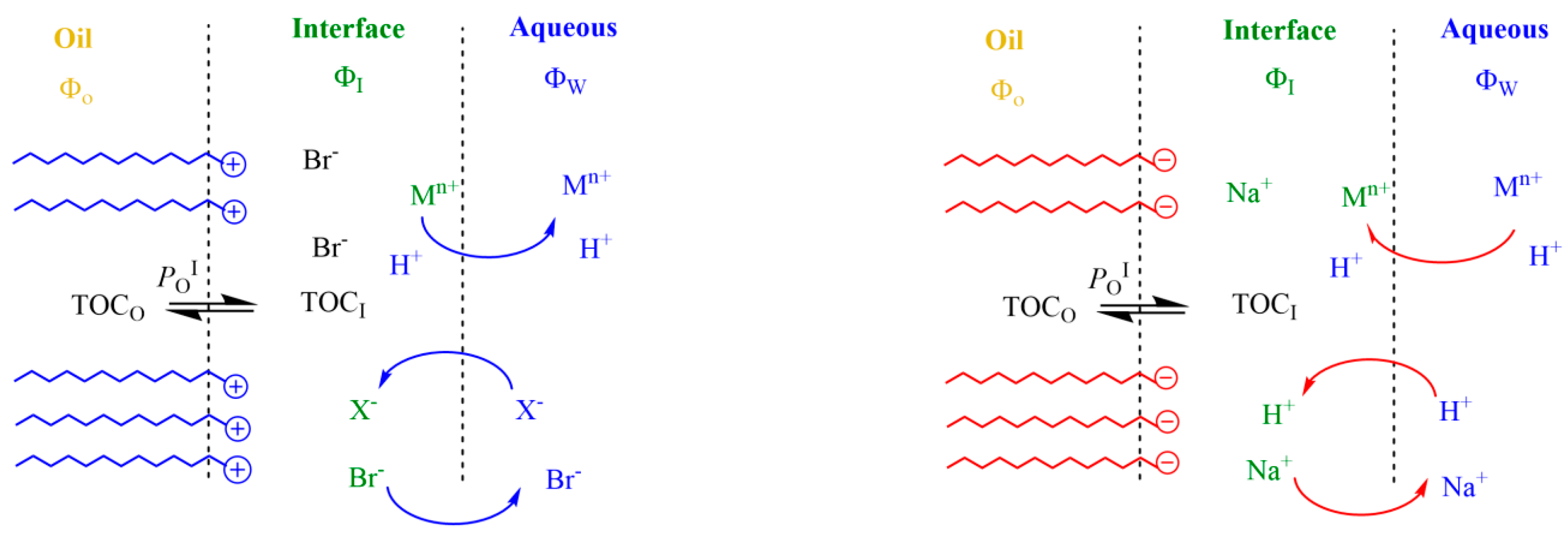
2.4. Application of the Pseudophase Kinetic Model
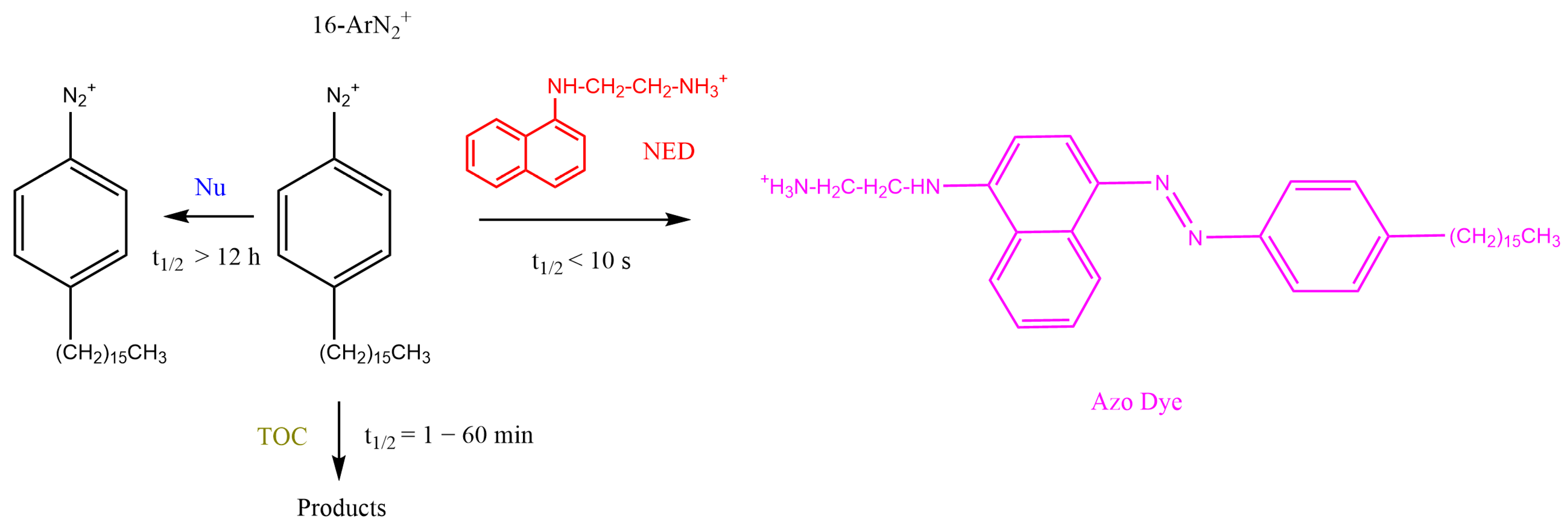
2.5. Determining kobs Values for the Reaction between 16-ArN2+ and δ-TOC in Intact Emulsions
2.6. Determining Antioxidant Distributions and Effective Concentrations
2.7. Oxidative Stability of Emulsions: Schaal Method
3. Results and Discussion
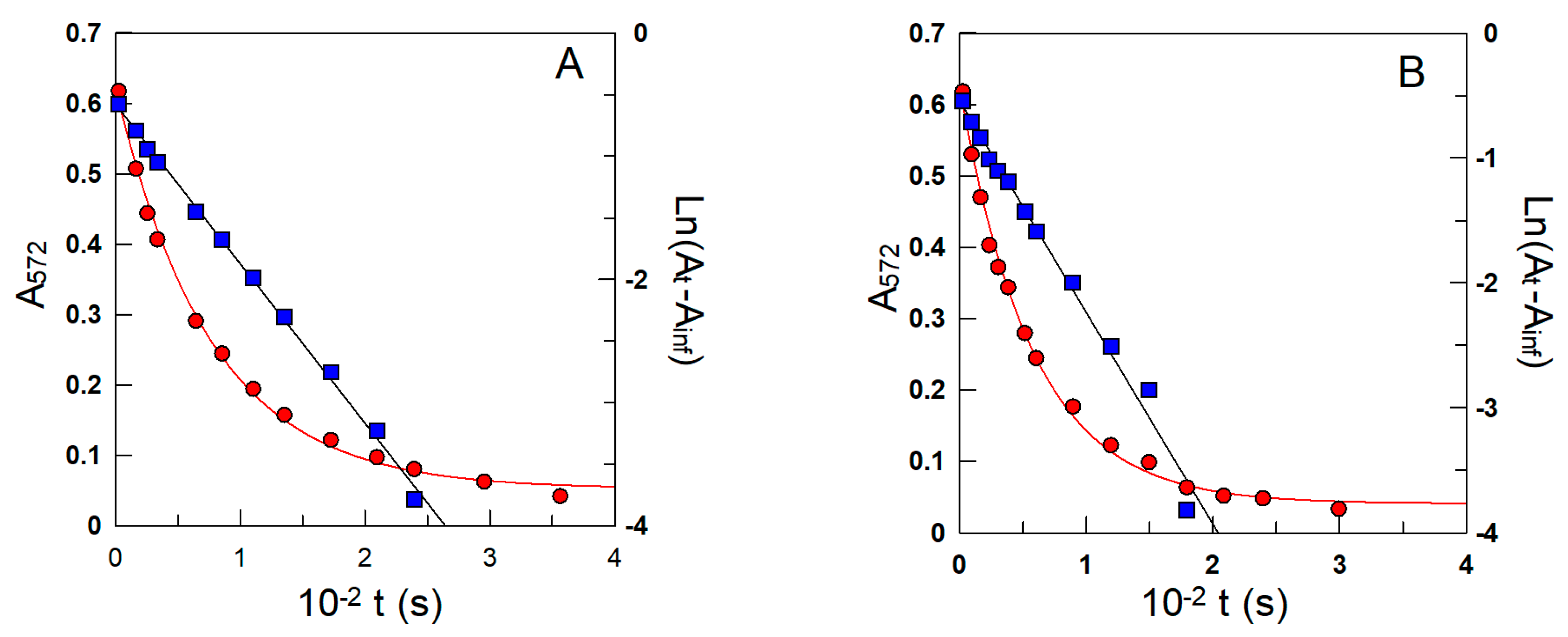
3.1. Determining the Partition Constants of δ-TOC in the Oil–Interfacial, POI, Region in Intact Soybean Oil Emulsions
3.2. Distribution and Interfacial Concentrations of δ-TOC
3.3. Oxidative Stability of Emulsions: Effects of the Interfacial Charge
- (1)
- The acidity of the interfacial region does not affect the oxidative stability or the distribution of δ-TOC;
- (2)
- The effective interfacial concentration is a crucial parameter that controls the oxidative stability of emulsions;
- (3)
- There exists a direct relationship between the effective concentration of the antioxidant in the interfacial region and the oxidative stability.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Tadros, T.F. Emulsions: Formation, Stability, Industrial Applications; De Gruyter: Berlin, Germany, 2016. [Google Scholar]
- Sjöblom, J. Emulsions: A Fundamental and Practical Approach; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Jacobsen, C. Chapter 8—Oxidative Stability and Shelf Life of Food Emulsions. In Oxidative Stability and Shelf Life of Foods Containing Oils and Fats; Hu, M., Jacobsen, C., Eds.; AOCS Press: Urbana, IL, USA, 2016; pp. 287–312. [Google Scholar] [CrossRef]
- McClements, D.J. Food Emulsions, Principles, Practices and Techniques; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Ozturk, B.; McClements, D.J. Progress in natural emulsifiers for utilization in food emulsions. Curr. Opin. Food Sci. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Engineers, N.B.C. The Complete Book on Emulsifiers with Uses, Formulae and Processes: How to Start an Emulsifier Production Business, How to Start Emulsifier Processing Industry in India, Industrial Applications of Emulsion Technology, Industrial Uses of Emulsifier, Leather and Paper Treatment Emulsions Manufacturing Process, Manufacturing Process of Emulsifier, Most Profitable Emulsifier Processing Business Ideas, Nature and Use of Emulsifiers in Foods, New Small Scale Ideas in Emulsifier Processing Industry, 2nd ed.; NIIR Project Consultancy Services: Delhi, India, 2014. [Google Scholar]
- Hasenhuettl, G.L.; Hartel, R.W. Food Emulsifiers and Their Applications; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Yi, B.; Kim, M.J.; Lee, J. Effects of emulsifier charges on the oxidative stability in oil-in-water emulsions under riboflavin photosensitization. Food Sci. Biotechnol. 2016, 25, 1003–1009. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Wei, Y.; Shi, A.; Zhong, J.; Rao, P.; Wang, Q.; Zhang, H. Correlation between interfacial layer properties and physical stability of food emulsions: Current trends, challenges, strategies, and further perspectives. Adv. Colloid Interface Sci. 2023, 313, 102863. [Google Scholar] [CrossRef] [PubMed]
- Maldonado-Valderrama, J.; del Castillo-Santaella, T.; Gálvez-Ruiz, M.J.; Holgado-Terriza, J.A.; Cabrerizo-Vílchez, M.Á. Chapter 1—Structure and functionality of interfacial layers in food emulsions. In Food Structure and Functionality; Galanakis, C.M., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 1–22. [Google Scholar] [CrossRef]
- Romsted, L.S. Introduction to Surfactant Self-Assembly. In Supramolecular Chemistry: From Molecules to Nanomaterials; Gale, P.A., Steed, J.W., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2012; pp. 181–203. [Google Scholar]
- Bunton, C.A.; Nome, F.; Quina, F.H.; Romsted, L.S. Ion Binding and Reactivity at Charged Aqueous Interfaces. Acc. Chem. Res. 1991, 24, 357–364. [Google Scholar] [CrossRef]
- Gao, X.; Bravo-Díaz, C.; Romsted, L.S. Interpreting ion-specific effects on the reduction of an arenediazonium Ion by t-butylhydroquinone (TBHQ) using the pseudophase kinetic model in emulsions prepared with a zwitterionic sulfobetaine surfactant. Langmuir 2013, 29, 4928–4933. [Google Scholar] [CrossRef]
- Losada-Barreiro, S.; Bravo-Díaz, C.; Romsted, L.S. Distributions of phenolic acid antioxidants between the interfacial and aqueous regions of corn oil emulsions: Effects of pH and emulsifier concentration. Eur. J. Lipid Sci. Technol. 2015, 117, 1801–1813. [Google Scholar] [CrossRef]
- Quina, F.H.; Chaimovich, H. Ion exchange in micellar solutions. 1. Conceptual framework for ion exchange in micellar solutions. J. Phys. Chem. 1979, 83, 1844–1850. [Google Scholar] [CrossRef]
- Mackay, R.A. Reactions in microemulsions. The ion-exchange model. J. Phys. Chem. 1982, 86, 4756–4758. [Google Scholar] [CrossRef]
- Vessela, D.K.; Olga, T.K. Lipid Oxidation in Homogeneous and Micro-Heterogeneous Media in Presence of Prooxidants, Antioxidants and Surfactants. In Lipid Peroxidation; Angel, C., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 2. [Google Scholar] [CrossRef]
- Osborn, H.; Akoh, C. Effects of Natural Antioxidants on Iron-Catalyzed Lipid Oxidation of Structured Lipid-Based Emulsions. J. Am. Oil Chem. Soc. 2003, 80, 847–852. [Google Scholar] [CrossRef]
- Mei, L.; McClements, D.J.; Wu, J.; Decker, E.A. Iron-catalyzed lipid oxidation in emulsion as affected by surfactant, pH and NaCl. Food Chem. 1998, 61, 307–312. [Google Scholar] [CrossRef]
- Mei, L.; McClements, D.J.; Decker, E.A. Lipid oxidation in emulsions as affected by charge status of antioxidants and emulsion droplets. J. Agric. Food Chem. 1999, 47, 2267–2273. [Google Scholar] [CrossRef]
- Bravo-Díaz, C. Advances in the control of lipid peroxidation in oil-in-water emulsions: Kinetic approaches. Crit. Rev. Food Sci. Nutr. 2022, 1–33. [Google Scholar] [CrossRef]
- Costa, M.; Freiría-Gándara, J.; Losada-Barreiro, S.; Paiva-Martins, F.; Aliaga, C.; Bravo-Díaz, C. Interfacial kinetics in olive oil-in-water nanoemulsions: Relationships between rates of initiation of lipid peroxidation, induction times and effective interfacial antioxidant concentrations. J. Colloid Interface Sci. 2021, 604, 248–259. [Google Scholar] [CrossRef]
- Berton-Carabin, C.C.; Sagis, L.; Schroën, K. Formation, Structure, and Functionality of Interfacial Layers in Food Emulsions. Annu. Rev. Food Sci. Technol. 2018, 9, 551–587. [Google Scholar] [CrossRef]
- Costa, M.; Paiva-Martins, F.; Bravo-Díaz, C.; Losada-Barreiro, S. Control of Lipid Oxidation in Oil-in Water Emulsions: Effects of Antioxidant Partitioning and Surfactant Concentration. In Lipid Oxidation in Food and Biological Systems: A Physical Chemistry Perspective; Bravo-Diaz, C., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 201–216. [Google Scholar] [CrossRef]
- Costa, M.; Losada-Barreiro, S.; Bravo-Díaz, C.; Paiva-Martins, F. Effects of Emulsion Droplet Size on the Distribution and Efficiency of Antioxidants. In Lipid Oxidation in Food and Biological Systems: A Physical Chemistry Perspective; Bravo-Diaz, C., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 217–235. [Google Scholar] [CrossRef]
- Aliaga, C.; Rezende, M.C. Location, Orientation and Buoyance Effects of Radical Probes as Studied by EPR. In Lipid Oxidation in Food and Biological Systems: A Physical Chemistry Perspective; Bravo-Diaz, C., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 133–150. [Google Scholar] [CrossRef]
- Costa, M.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Díaz, C. Physical evidence that the variations in the efficiency of homologous series of antioxidants in emulsions are a result of differences in their distribution. J. Sci. Food Agric. 2017, 97, 564–571. [Google Scholar] [CrossRef]
- Costa, M.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Diaz, C. Optimizing the efficiency of antioxidants in emulsions by lipophilization: Tuning interfacial concentrations. RSC Adv. 2016, 6, 91483–91493. [Google Scholar] [CrossRef]
- Stöckman, H.; Schwarz, K.; Huynh-Ba, T. The Influence of Various Emulsifiers on the Partitioning and Antioxidant Activity of Hydrobenzoic acids and Their Derivatives in Oil-in-Water Emulsions. J.Am. Oil Chem. Soc. 2000, 77, 535–542. [Google Scholar] [CrossRef]
- Losada-Barreiro, S.; Sánchez Paz, V.; Bravo-Díaz, C. Effects of emulsifier hydrophile–lipophile balance and emulsifier concentration the distributions of gallic acid, propyl gallate, and a-tocopherol in corn oil emulsions. J. Colloid. Interface Sci. 2013, 389, 1–9. [Google Scholar] [CrossRef]
- Costa, M.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Díaz, C.; Romsted, L.S. A direct correlation between the antioxidant efficiencies of caffeic acid and its alkyl esters and their concentrations in the interfacial region of olive oil emulsions. The pseudophase model interpretation of the “cut-off” effect. Food Chem. 2015, 175, 233–242. [Google Scholar] [CrossRef]
- Kiralan, S.S.; Doğu-Baykut, E.; Kittipongpittaya, K.; McClements, D.J.; Decker, E.A. Increased Antioxidant Efficacy of Tocopherols by Surfactant Solubilization in Oil-in-Water Emulsions. J. Agric. Food Chem. 2014, 62, 10561–10566. [Google Scholar] [CrossRef]
- Tan, B.; Watson, R.R.; Preedy, V.R. Tocotrienols: Vitamin E Beyond Tocopherols, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Huang, S.-W.; Frankel, E.N.; German, J.B. Antioxidant activity of .alpha.- and .gamma.-tocopherols in bulk oils and in oil-in-water emulsions. J. Agric. Food Chem. 1994, 42, 2108–2114. [Google Scholar] [CrossRef]
- Stipanuk, M.H.; Caudill, M.A. Biochemical, Physiological, and Molecular Aspects of Human Nutrition-E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Chaiyasit, W.; McClements, D.; Decker, E.A. The Relationship between the Physicochemical Properties of Antioxidants and Their Ability to Inhibit Lipid Oxidation in Bulk Oil and Oil-in-Water Emulsions. J. Agric. Food Chem. 2005, 53, 4982–4988. [Google Scholar] [CrossRef] [PubMed]
- Dar, A.A.; Romsted, L.S.; Nazir, N.; Zhang, Y.; Gao, X.; Gu, Q.; Liu, C. A novel combined chemical kinetic and trapping method for probing the relationships between chemical reactivity and interfacial H2O, Br− and H+ ion molarities in CTAB/C12E6 mixed micelles. Phys. Chem. Chem. Phys. 2017, 19, 23747–23761. [Google Scholar] [CrossRef] [PubMed]
- Afzal, S.; Lone, M.S.; Nazir, N.; Dar, A.A. pH Changes in the Micelle–Water Interface of Surface-Active Ionic Liquids Dictate the Stability of Encapsulated Curcumin: An Insight Through a Unique Interfacial Reaction between Arenediazonium Ions and t-Butyl Hydroquinone. ACS Omega 2021, 6, 14985–15000. [Google Scholar] [CrossRef]
- Gu, Q.; Bravo-Díaz, C.; Romsted, L.S. Using the pseudophase kinetic model to interpret chemical reactivity in ionic emulsions: Determining antioxidant partition constants and interfacial rate constants. J. Colloid Interface Sci. 2012, 400, 41–48. [Google Scholar] [CrossRef]
- García-Río, L.; Hervella, P. Application of the pseudophase ion-exchange model to reactivity in quaternary water in oil microemulsions. New J. Chem. 2007, 31, 860–870. [Google Scholar] [CrossRef]
- Ferreira, L.C.M.; Zucco, C.; Zanette, D.; Nome, F. Pseudophase ion-exchange model applied to kinetics in aqueous micelles under extreme conditions: A simple modification. J. Phys. Chem. 1992, 96, 9058–9061. [Google Scholar] [CrossRef]
- Antonio, C.; Aangel, A.; Manuel, A.-F.; Gonzalo, A.; Luis, G.-R.; Jesus, S.-G.; Juan, C.M. Pseudophase Model in Microemulsions. In Microemulsion; Juan, C.M., Ed.; IntechOpen: Rijeka, Croatia, 2019; Chapter 1. [Google Scholar] [CrossRef]
- Lissi, E.A.; Abuin, E.B.; Sepulveda, L.; Quina, F.H. Ion exchange between monovalent and divalent counterions in cationic micellar solution. J. Phys. Chem. 1984, 88, 81–85. [Google Scholar] [CrossRef]
- Bravo-Díaz, C.; Romsted, L.S.; Liu, C.; Losada-Barreiro, S.; Pastoriza-Gallego, M.J.; Gao, X.; Gu, Q.; Krishnan, G.; Sánchez-Paz, V.; Zhang, Y.; et al. To Model Chemical Reactivity in Heterogeneous Emulsions, Think Homogeneous Microemulsions. Langmuir 2015, 31, 8961–8979. [Google Scholar] [CrossRef]
- Romsted, L.S.; Bravo-Díaz, C. Modelling chemical reactivity in emulsions. Curr. Opin. Colloid Interface Sci. 2013, 18, 3–14. [Google Scholar] [CrossRef]
- Gunaseelan, K.; Romsted, L.S.; Pastoriza-Gallego, M.J.; González-Romero, E.; Bravo-Díaz, C. Determining a-tocopherol distributions betweeen the Oil, Water and Interfacial Regions of Macroemulsions: Novel Applications of Electrocanalytical Chemistry and a Pseudophase Kinetic Model. Adv. Colloid Interface Sci. 2006, 123–126, 303–311. [Google Scholar] [CrossRef]
- Romsted, L.S. Micellar Effects on Reaction Rates and Equilibria, in “Surfactants in Solution”; Mittal, K.L., Lindman, J., Eds.; Plenum Press: New York, NY, USA, 1984. [Google Scholar]
- Bravo-Díaz, C. Estudio Cinético de la Influencia de Agregados Micelares Sobre Reacciones de Descomposición de Nitrosocompluestos. Ph.D. Thesis, Universidad de Santiago de Compostela (Spain), Santiago de Compostela, Spain, 1991. [Google Scholar]
- Martinez-Aranda, N.; Losada-Barreiro, N.; Bravo-Díaz, C.; Romsted, L.S. Influence of Temperature on the Distribution of Catechin in Corn oil-in-water Emulsions and some Relevant Thermodynamic Parameters. Food Biophys. 2014, 9, 380–388. [Google Scholar] [CrossRef]
- Losada-Barreiro, S.; Bravo-Díaz, C.; Costa, M.; Paiva-Martins, F. Distribution of catechol in emulsions. J. Phys. Org. Chem. 2013, 27, 290–296. [Google Scholar] [CrossRef]
- Losada-Barreiro, S.; Bravo Díaz, C.; Paiva Martins, F.; Romsted, L.S. Maxima in antioxidant distributions and efficiencies with increasing hydrophobicity of gallic acid and its alkyl esters. The pseudophase model interpretation of the “Cut-off effect”. J. Agric. Food Chem. 2013, 61, 6533–6543. [Google Scholar] [CrossRef]
- Pastoriza-Gallego, M.J.; Sánchez-Paz, V.; Losada-Barreiro, S.; Bravo-Diaz, C.; Gunaseelan, K.; Romsted, L.S. Effects of Temperature and Emulsifier Concentration on a-Tocopherol Distribution in a Stirred, Fluid, Emulsion. Thermodynamics of a-Tocopherol transfer between the Oil and Interfacial Regions. Langmuir 2009, 25, 2646–2653. [Google Scholar] [CrossRef]
- Pastoriza-Gallego, M.J.; Losada-Barreiro, S.; Bravo Díaz, C. Effects of acidity and emulsifier concentration on the distribution of Vitamin C in a model food emulsion. J. Phys. Org. Chem. 2012, 25, 908–915. [Google Scholar] [CrossRef]
- Losada-Barreiro, S.; Sánchez Paz, V.; Bravo Díaz, C.; Paiva Martins, F.; Romsted, L.S. Temperature and emulsifier concentration effects on gallic acid distribution in a model food emulsion. J. Colloid Interface Sci. 2012, 370, 73–79. [Google Scholar] [CrossRef]
- Bravo Díaz, C. Diazohydroxides, diazoethers and related species. In The Chemistry of Hydroxylamines, Oximes and Hydroxamic Acids; Rappoport, Z., Liebman, J.F., Eds.; John Wiley & Sons: Chichester, UK, 2011; Volume 2, p. 853. [Google Scholar]
- Drummond, C.J.; Grieser, F. The ionization behaviour of DL-alpha-tocopherol (vitamin E) in model membranes: Micelles and vesicles. Biochim. Biophys. Acta 1985, 836, 275–278. [Google Scholar] [CrossRef]
- Fernández-Ventoso, L.; Toba-Pérez, A.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Díaz, C. Distributions of α- and δ-TOCopherol in Intact Olive and Soybean Oil-in-Water Emulsions at Various Acidities: A Test of the Sensitivity of the Pseudophase Kinetic Model. Antioxidants 2022, 11, 2477. [Google Scholar] [CrossRef]
- Sánchez-Paz, V.; Pastoriza-Gallego, M.J.; Losada-Barreiro, S.; Bravo-Diaz, C.; Gunaseelan, K.; Romsted, L.S. Quantitative determination of a-tocopherol distribution in a tributyrin/Brij 30/water model food emulsion. J. Colloid Interface Sci. 2008, 320, 1–8. [Google Scholar] [CrossRef]
- Gunaseelan, K.; Romsted, L.S.; González-Romero, E.; Bravo-Díaz, C. Determining Partition Constants of Polar Organic Molecules between the Oil/Interfacial and Water/ Interfacial Regions in Emulsions: A Combined Electrochemical and Spectrometric Method. Langmuir 2004, 20, 3047–3055. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Díaz, C. Polyphenolic Antioxidants in Lipid Emulsions: Partitioning Effects and Interfacial Phenomena. Foods 2021, 10, 539. [Google Scholar] [CrossRef] [PubMed]
- Meireles, M.; Losada-Barreiro, S.; Costa, M.; Paiva-Martins, F.; Bravo-Díaz, C.; Monteiro, L.S. Control of antioxidant efficiency of chlorogenates in emulsions: Modulation of antioxidant interfacial concentrations. J. Sci. Food Agric. 2019, 99, 3917–3925. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Losada-Barreiro, S.; Bravo-Díaz, C.; Vicente, A.A.; Monteiro, L.S.; Paiva-Martins, F. Influence of AO chain length, droplet size and oil to water ratio on the distribution and on the activity of gallates in fish oil-in-water emulsified systems: Emulsion and nanoemulsion comparison. Food Chem. 2020, 310, 125716. [Google Scholar] [CrossRef]
- Costa, M.; Freiría-Gándara, J.; Losada-Barreiro, S.; Paiva-Martins, F.; Bravo-Díaz, C. Effects of droplet size on the interfacial concentrations of antioxidants in fish and olive oil-in-water emulsions and nanoemulsions and on their oxidative stability. J. Colloid Interface Sci. 2020, 562, 352–362. [Google Scholar] [CrossRef]
- Raimúndez-Rodríguez, E.A.; Losada-Barreiro, S.; Bravo-Díaz, C. Enhancing the fraction of antioxidants at the interfaces of oil-in-water emulsions: A kinetic and thermodynamic analysis of their partitioning. J. Colloid Interface Sci. 2019, 555, 224–233. [Google Scholar] [CrossRef]
- Mitrus, O.; Żuraw, M.; Losada-Barreiro, S.; Bravo-Díaz, C.; Paiva-Martins, F. Targeting Antioxidants to Interfaces: Control of the Oxidative Stability of Lipid-Based Emulsions. J. Agric. Food Chem. 2019, 67, 3266–3274. [Google Scholar] [CrossRef]
- Inchingolo, R.; Bayram, I.; Uluata, S.; Kiralan, S.S.; Rodriguez-Estrada, M.T.; McClements, D.J. Ability of Sodium Dodecyl Sulfate (SDS) Micelles to Increase the Antioxidant Activity of α-Tocopherol. J. Agric. Food Chem. 2021, 69, 5702–5708. [Google Scholar] [CrossRef]
- McClements, D.J.; Dungan, S.R. Factors That Affect the Rate of Oil Exchange between Oil-in-Water Emulsion Droplets Stabilized by a Nonionic Surfactant: Droplet Size, Surfactant Concentration, and Ionic Strength. J. Phys. Chem. 1993, 97, 7304–7308. [Google Scholar] [CrossRef]
- Costa, M.; Losada-Barreiro, S. Unexpected Antioxidant Efficiency of Chlorogenic Acid Phenolipids in Fish Oil-in-Water Nanoemulsions: An Example of How Relatively Low Interfacial Concentrations Can Make Antioxidants to Be Inefficient. Molecules 2022, 27, 861. [Google Scholar] [CrossRef]
- Lee, J.; Choi, S.J. Influence of Blending of Nonionic Emulsifiers Having Various Hydrophilic Head Sizes on Lipid Oxidation: Investigation of Antioxidant Polarity Interfacial Characteristics Relationship. Antioxidants 2021, 10, 886. [Google Scholar] [CrossRef]
- Kasaikina, O.T.; Kartasheva, Z.S.; Pisarenko, L.M. Effect of surfactants on liquid-phase oxidation of hydrocarbons and lipids. Russ. J. Gen. Chem. 2008, 78, 1533–1544. [Google Scholar] [CrossRef]

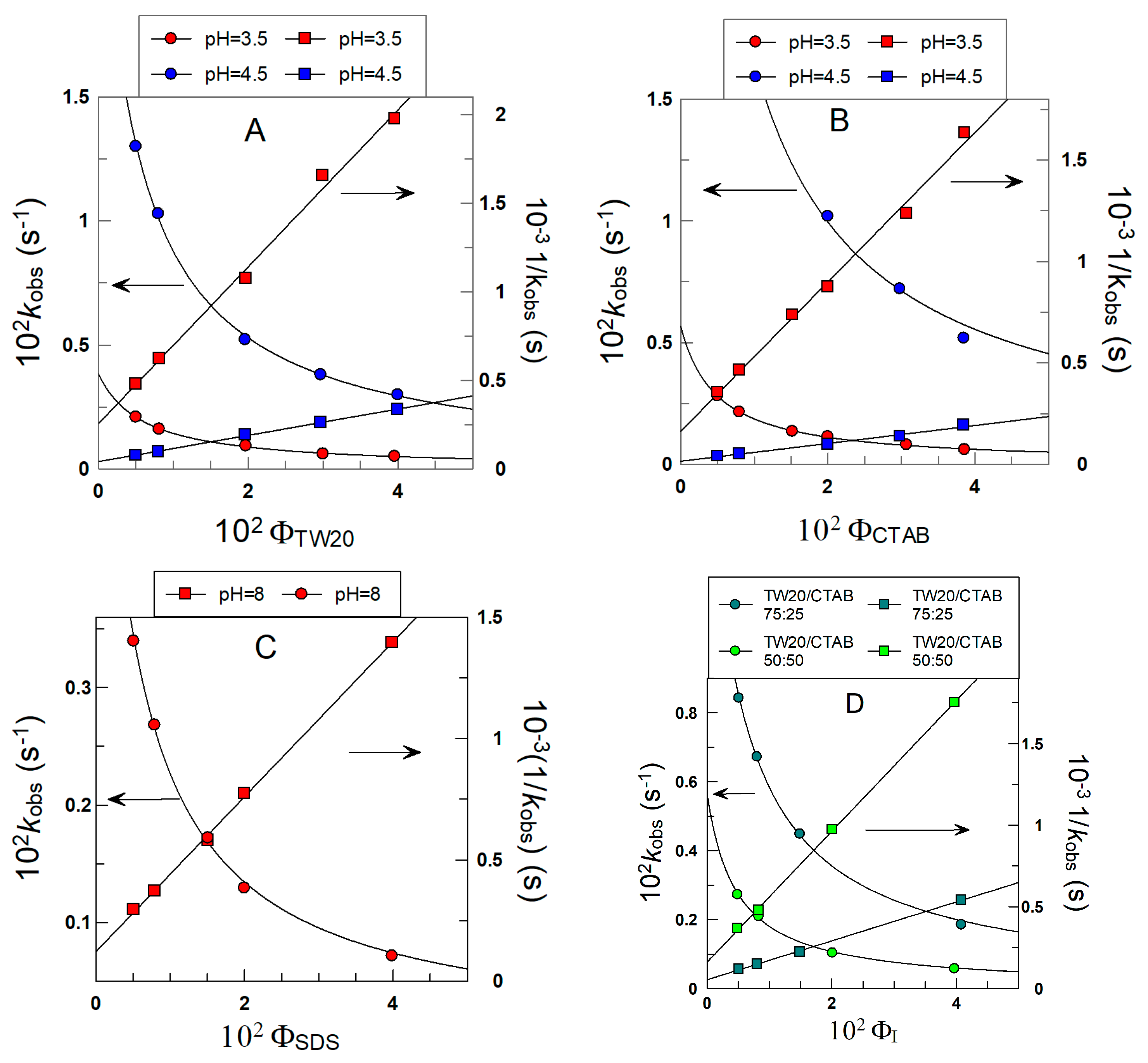


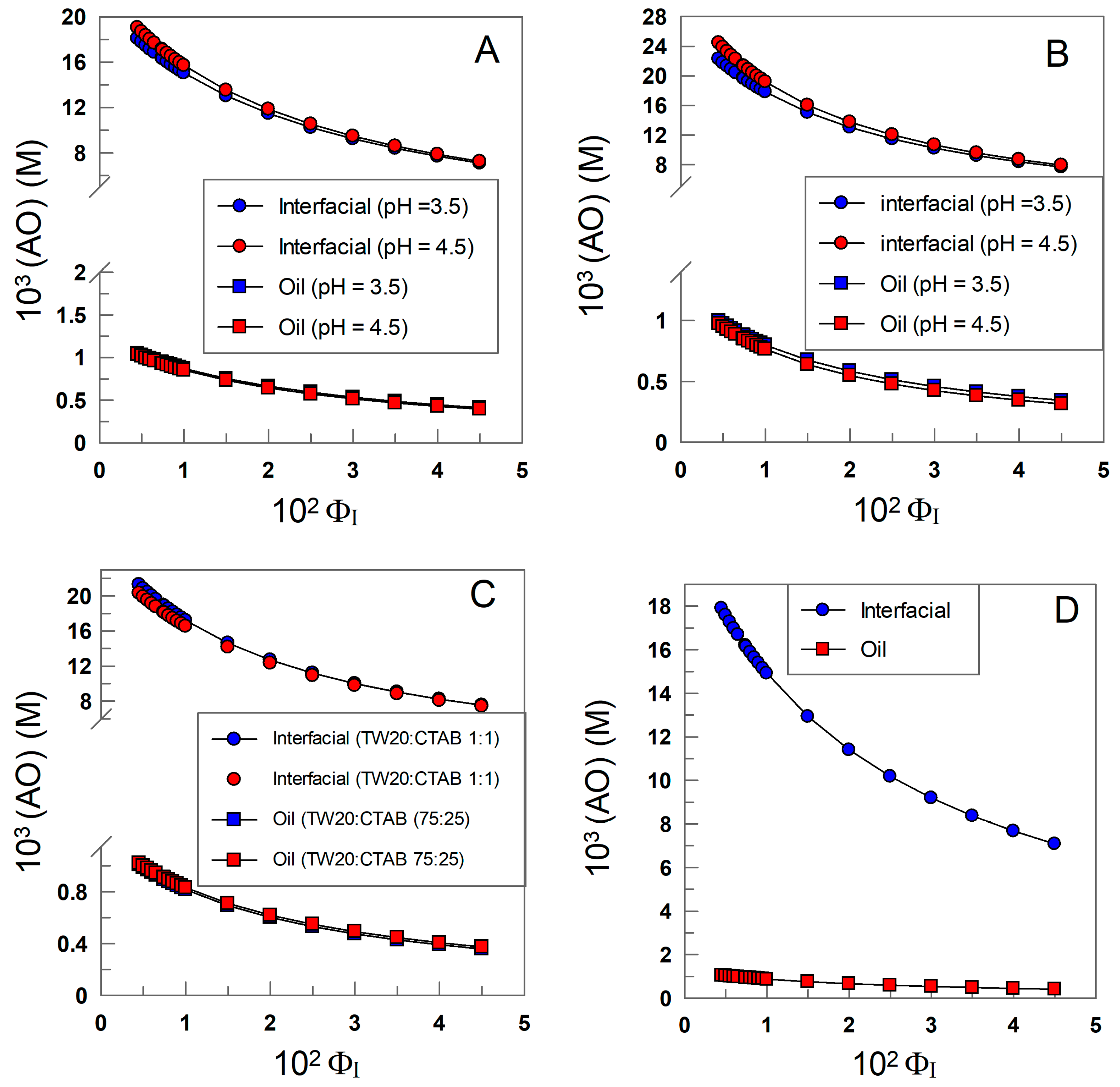
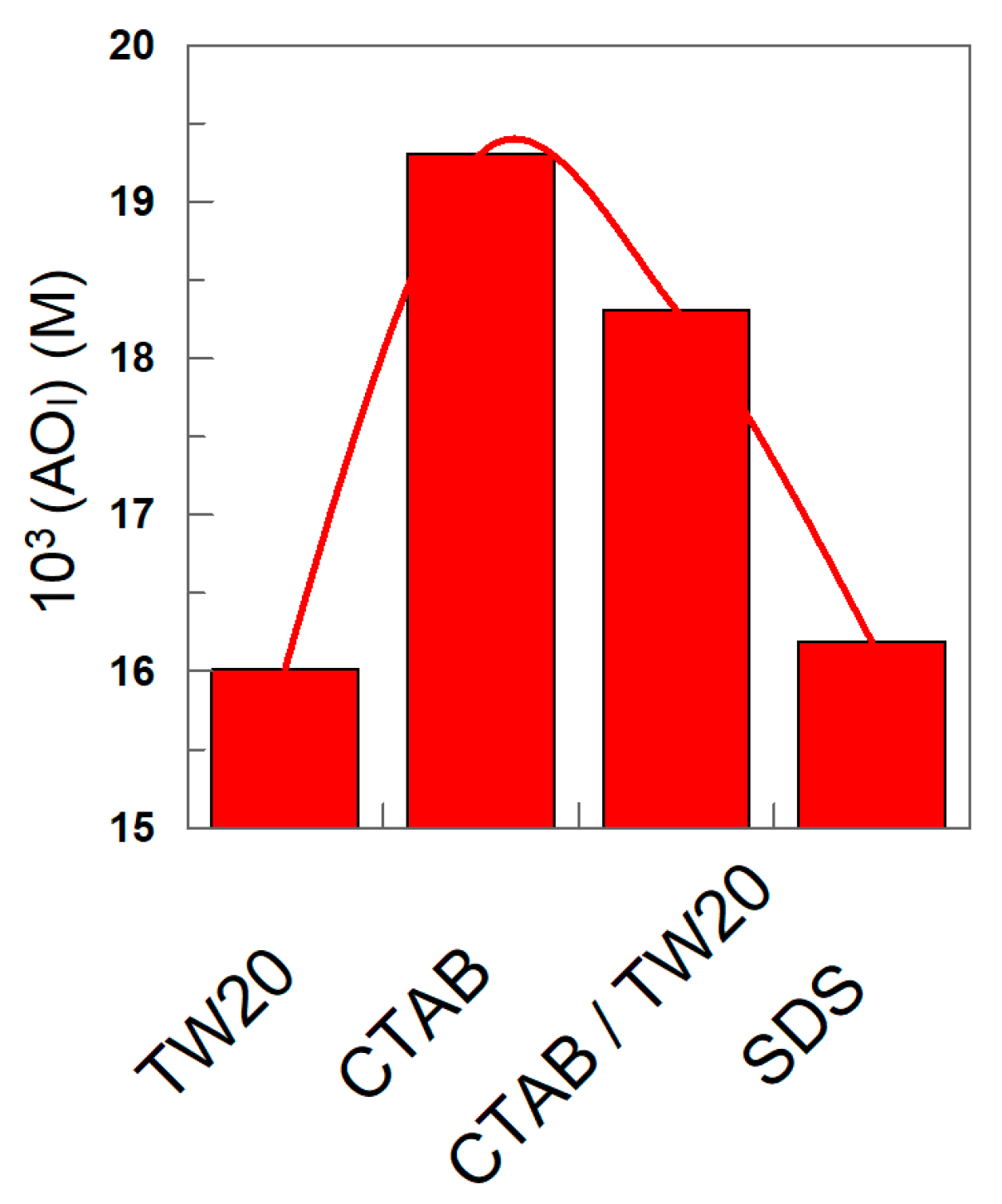


| Surfactant | HLB | pH | ξ (mV) | POI | 102 kI (M−1 s−1) |
|---|---|---|---|---|---|
| TW20 | 16.7 | 3.5 | −2.0 | 17.3 ± 4.0 | 0.57 ± 0.03 |
| 4.5 | --- | 18.4 ± 1.3 | 3.37 ± 0.07 | ||
| CTAB | 15.8 | 3.5 | 58.7 | 22.3 ± 6.7 | 0.68 ± 0.03 |
| 4.5 | --- | 25.1 ± 7.6 | 5.67 ± 0.34 | ||
| SDS | 40.0 | 8 | −74.5 | 17.1 ± 3.3 | 0.78 ± 0.02 |
| TW20/CTAB (50:50) | 16.3 | 3.5 | 31.8 | 21.1 ± 2.2 | 0.62 ± 0.01 |
| TW20/CTAB (75:25) | 16.5 | 3.5 | 44.5 | 19.9 ± 2.3 | 0.59 ± 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Senra, T.; Losada-Barreiro, S.; Bravo-Díaz, C. Efficiency of δ-Tocopherol in Inhibiting Lipid Oxidation in Emulsions: Effects of Surfactant Charge and of Surfactant Concentration. Antioxidants 2023, 12, 1158. https://doi.org/10.3390/antiox12061158
Martínez-Senra T, Losada-Barreiro S, Bravo-Díaz C. Efficiency of δ-Tocopherol in Inhibiting Lipid Oxidation in Emulsions: Effects of Surfactant Charge and of Surfactant Concentration. Antioxidants. 2023; 12(6):1158. https://doi.org/10.3390/antiox12061158
Chicago/Turabian StyleMartínez-Senra, Tamara, Sonia Losada-Barreiro, and Carlos Bravo-Díaz. 2023. "Efficiency of δ-Tocopherol in Inhibiting Lipid Oxidation in Emulsions: Effects of Surfactant Charge and of Surfactant Concentration" Antioxidants 12, no. 6: 1158. https://doi.org/10.3390/antiox12061158






