Analysis of CO2 Facilitation Transport Effect through a Hybrid Poly(Allyl Amine) Membrane: Pathways for Further Improvement
Abstract
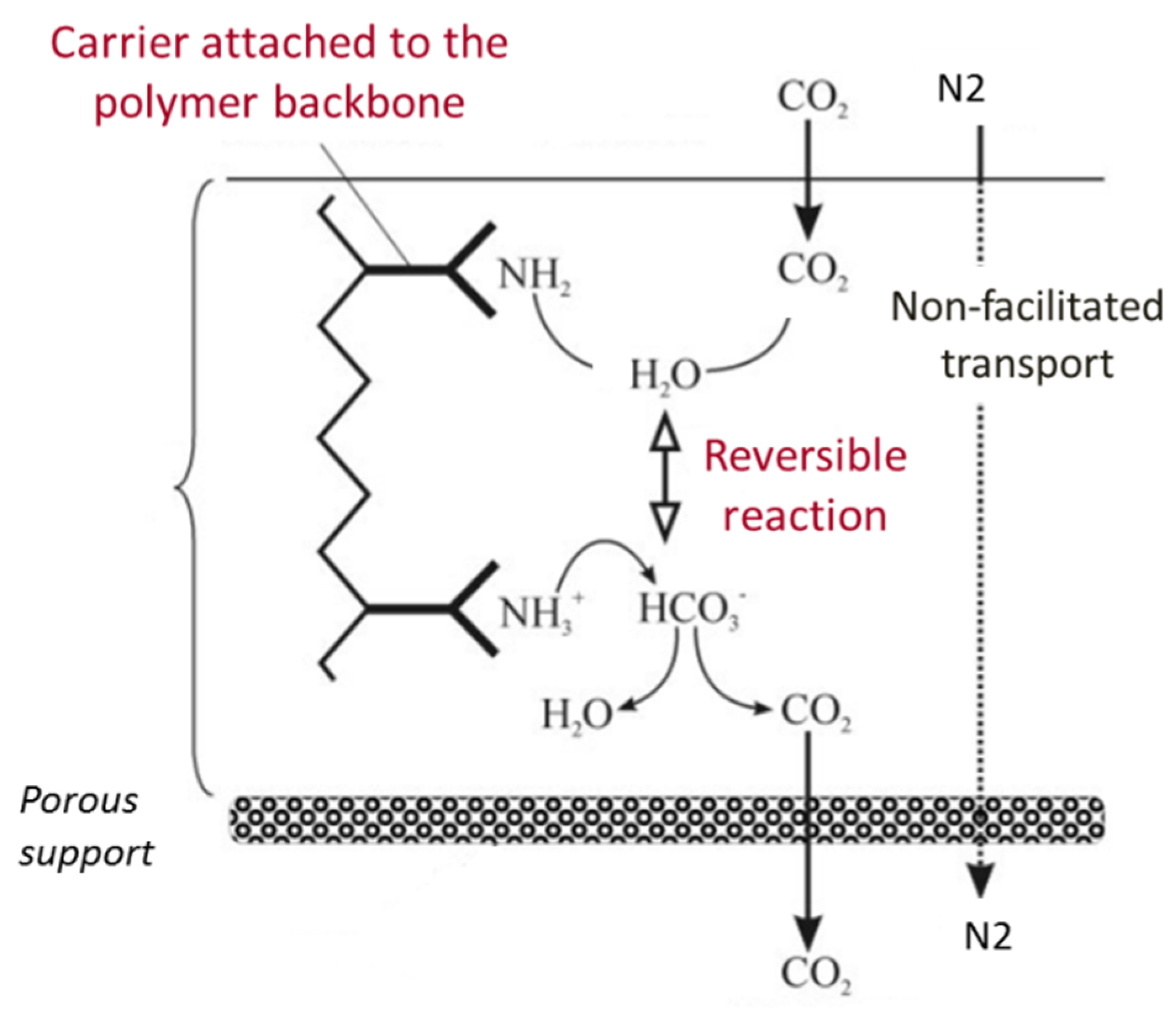
:1. Introduction
2. Modelling Background
3. Membrane Fabrication
4. Experiments: Results and Discussion
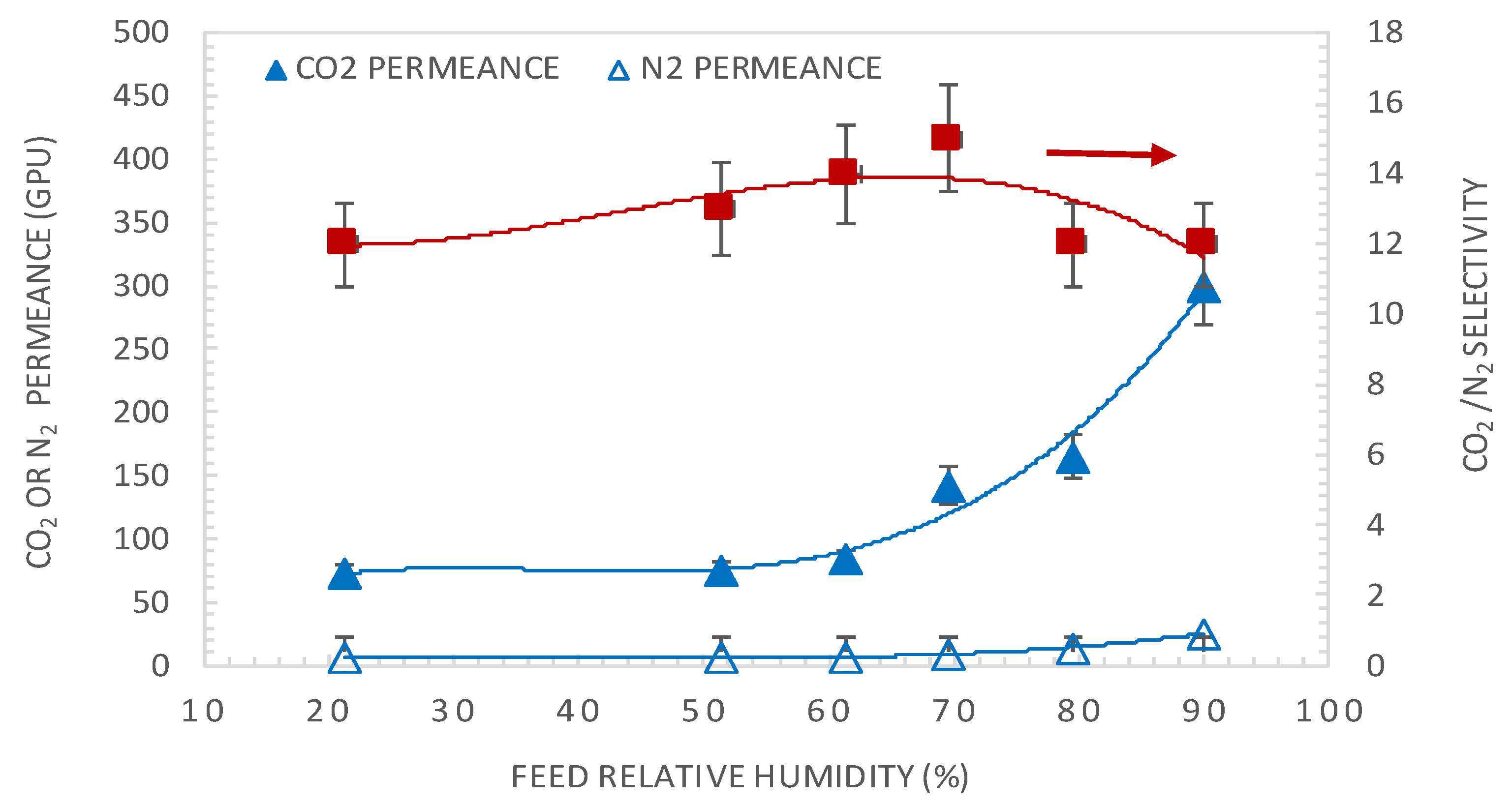
4.1. Effect of Feed Relative Humidity
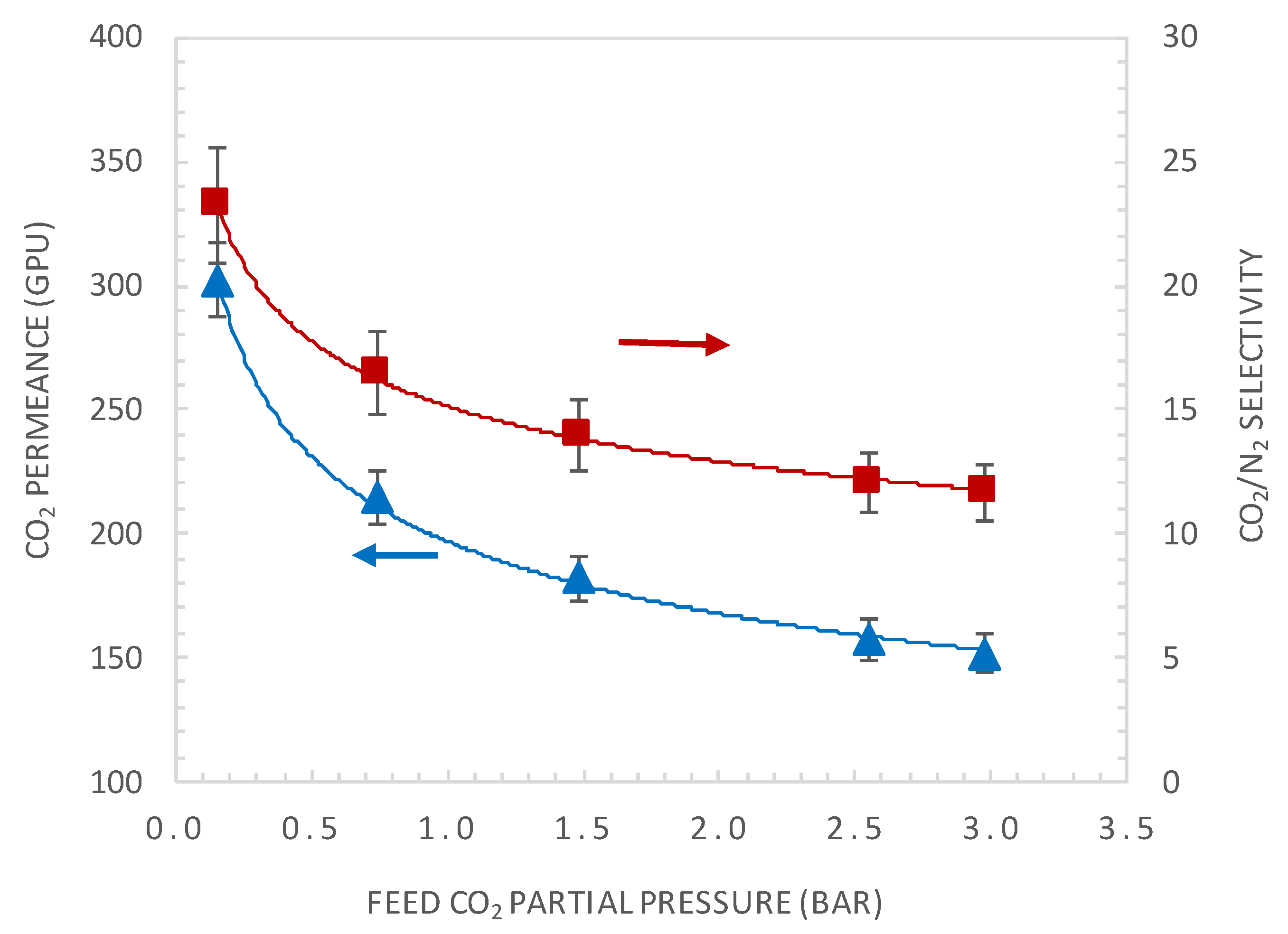
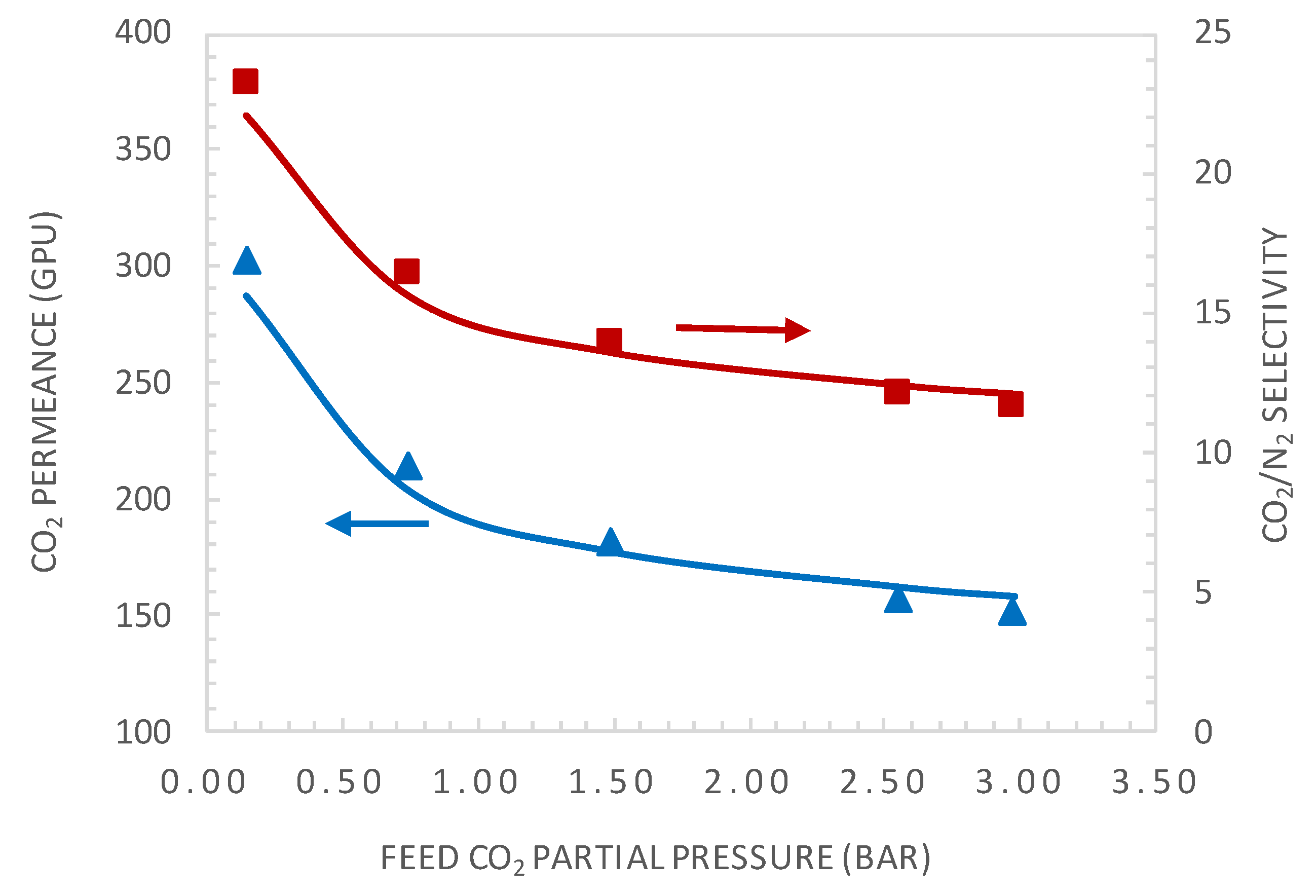
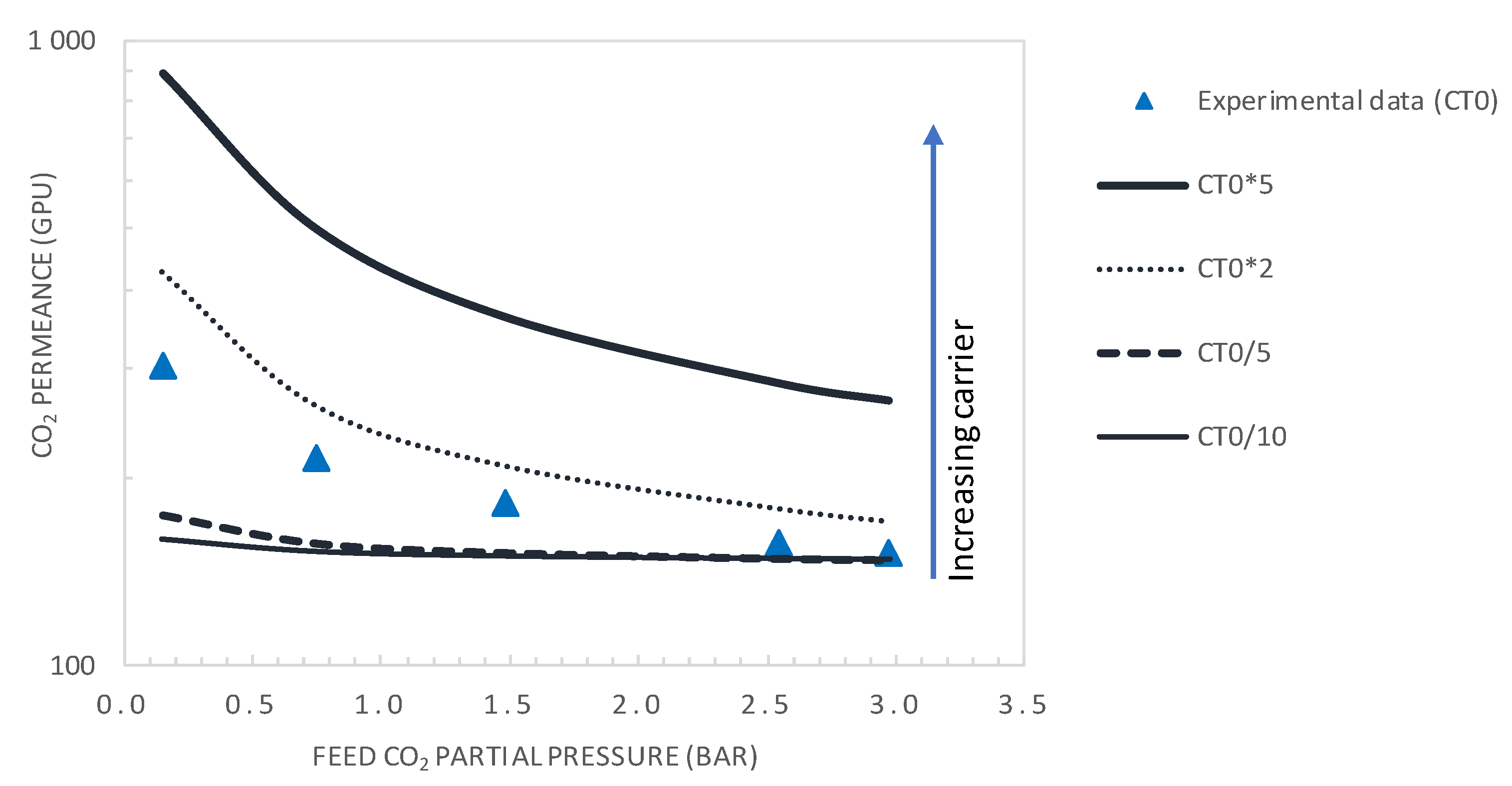
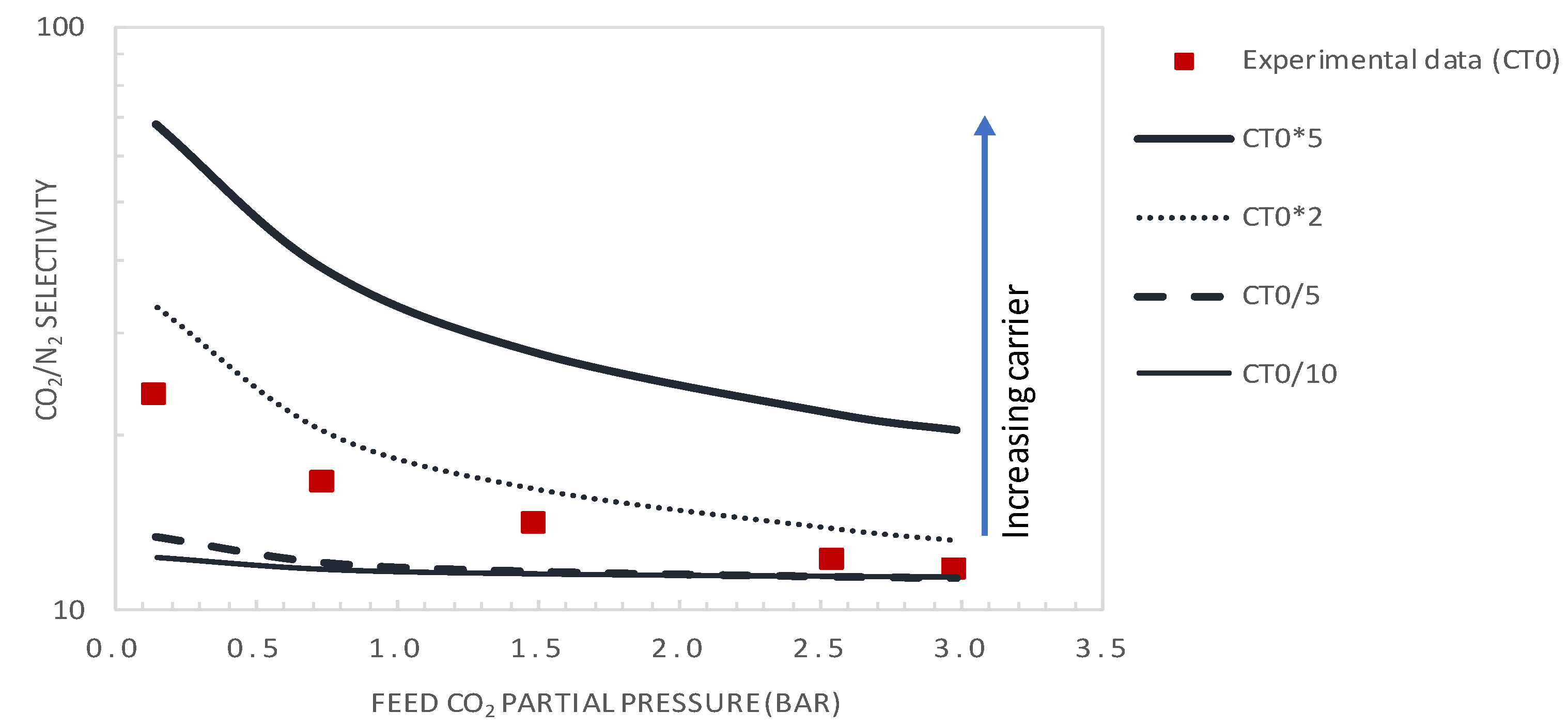
4.2. Effect of CO2 Partial Pressure
5. Simulations: Results and Discussion
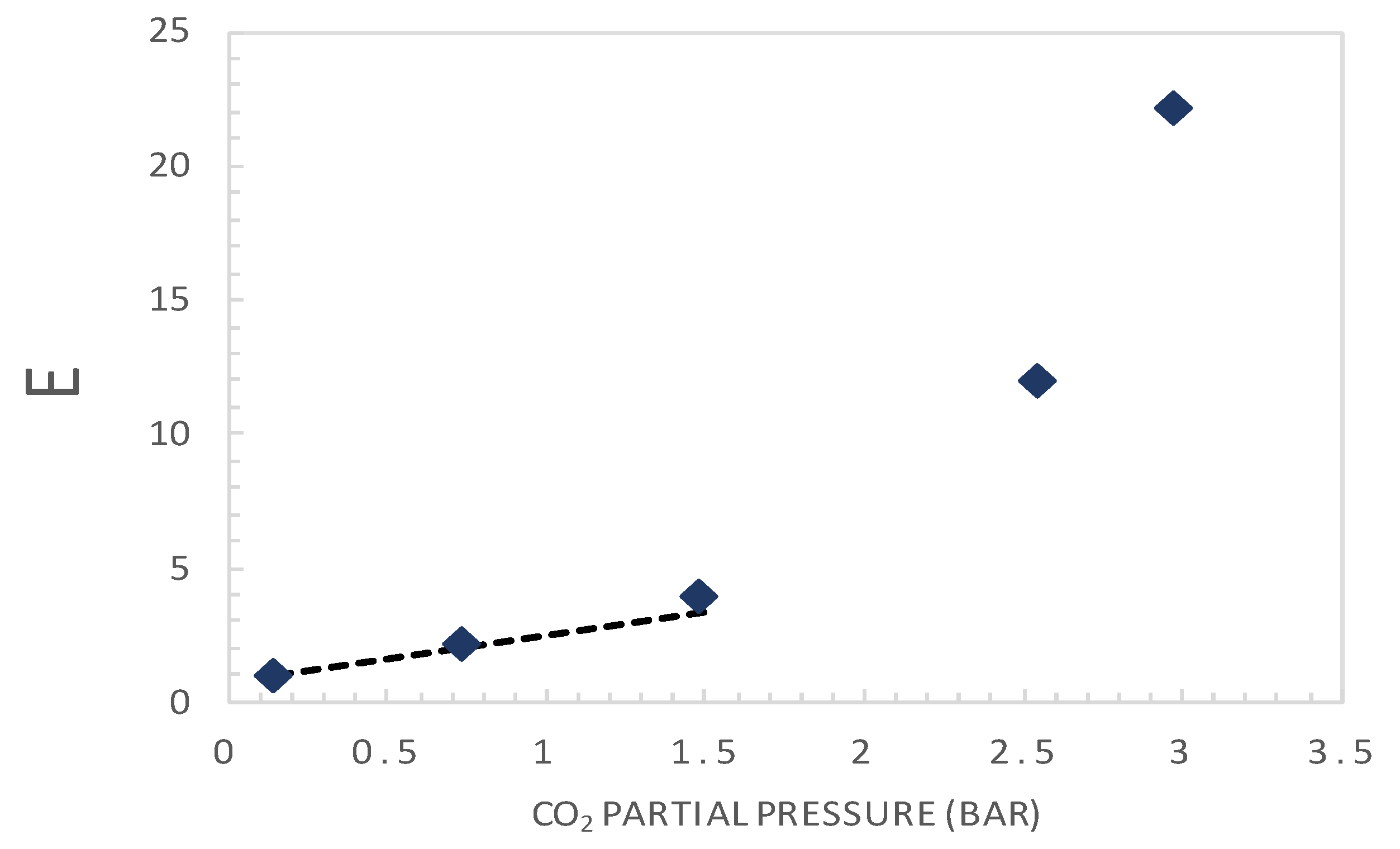
5.1. Retrieval of Key Facilitation Parameters
5.2. Comparison of Experimental and Simulation Results
5.3. Parametric Analysis
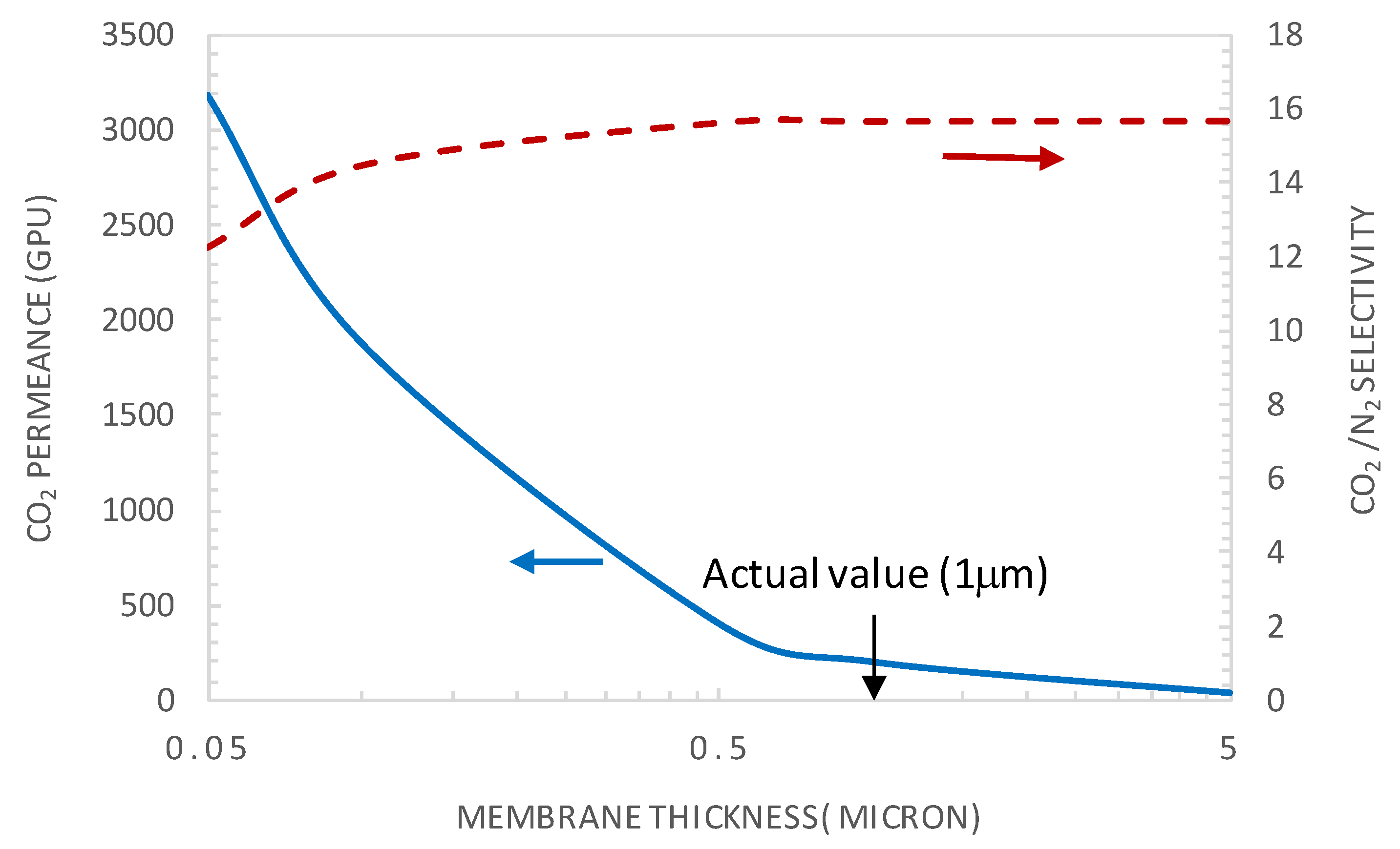
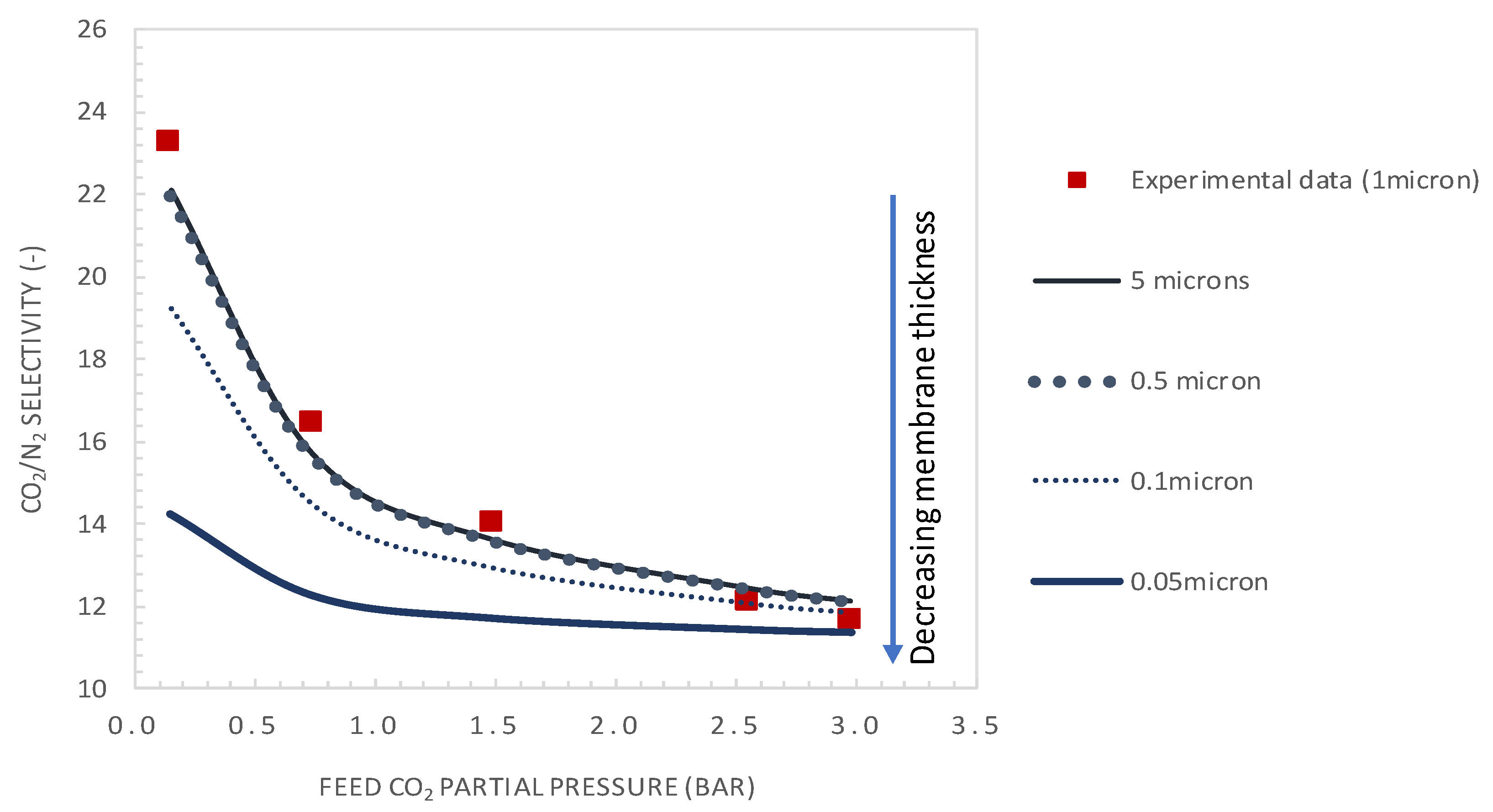
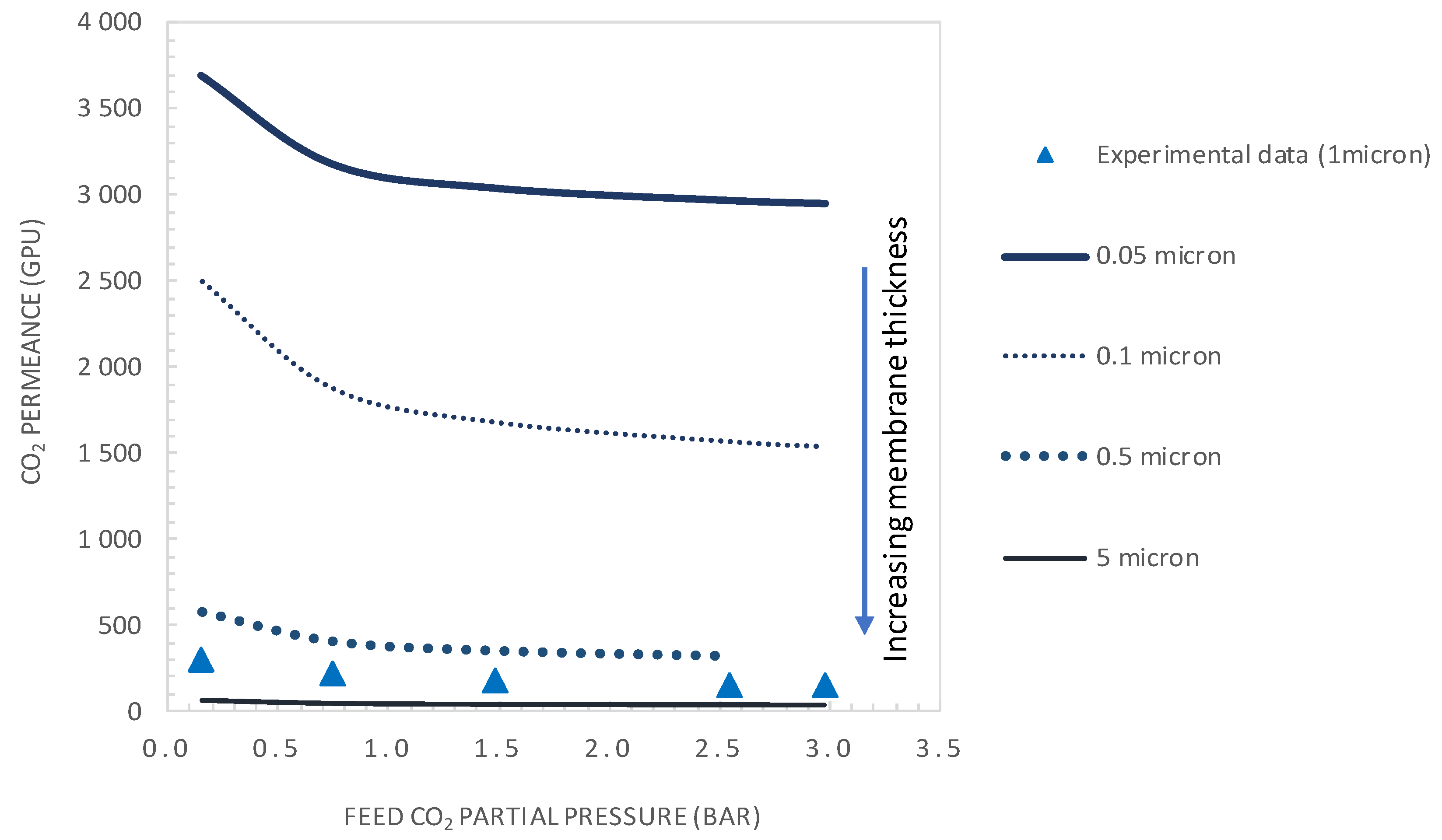
5.3.1. Effect of Membrane Thickness
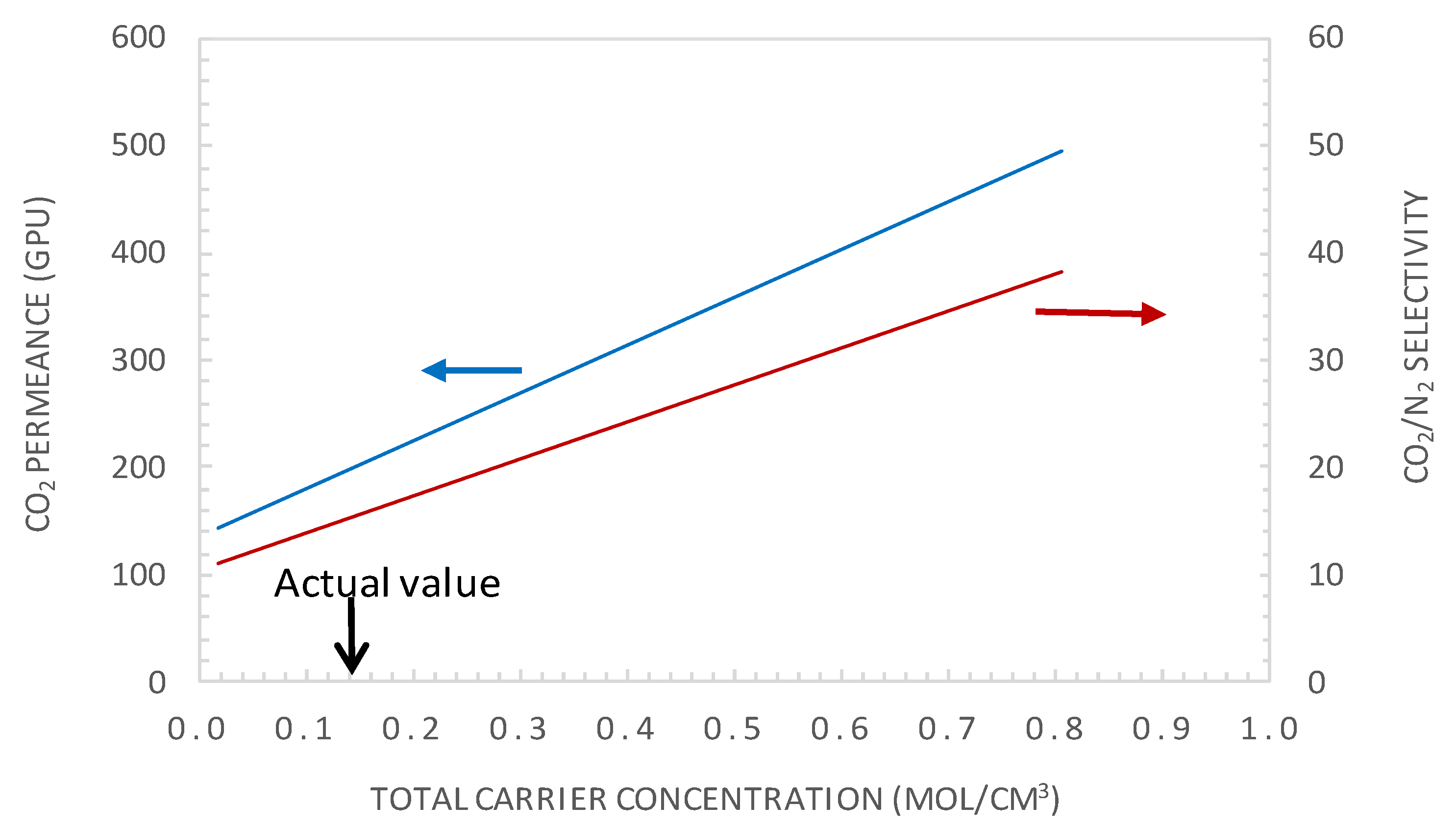
5.3.2. Effect of Carrier Concentration
6. Conclusions
- It was demonstrated that the current system operated near the reaction equilibrium regime (i.e., diffusion limitation), maximizing the facilitated transport of CO2. This indicated that, under the investigated operating conditions, the membrane thickness was already at its optimal value maximizing the facilitation factor.
- Increasing the membrane selectivity of the actual membrane by increasing the mobility ratio through increasing the carrier concentration and amine-CO2 complex diffusivity is key to improving the membrane performances.
- It was shown that after decreasing the membrane selective layer thickness below the actual value of 1 µm to a value of 0.1 µm and CO2 upstream partial pressure of 0.15 bar, a CO2 permeance as high as 2500 GPU can be attained while maintaining the selectivity at a value of about 19.
- Moreover, increasing the carrier solubility by a factor of two permitted the attainment of a CO2 permeance of 429 GPU and CO2/N2 selectivity of 33, performances that are above the Robeson upper bound of the CO2/N2 pair.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Diffusion coefficient (cm−2∙s−1) |
| e | Membrane selective layer thickness (cm) |
| F | Facilitation factor (dimensionless) |
| RH | Relative humidity (dimensionless) |
| Keq | Reaction equilibrium constant (cm3·moL−1) |
| ℘i | Permeability of gas i (Barrer) |
| p | Partial pressure (bar) |
| PM | Permeance (GPU) |
| K | Dimensionless equilibrium constant |
| k | Reaction rate constant (s−1) |
| Ji | Permeate flowrate of gas i (cm3 (STP)·s−1) |
| DAC | Diffusion coefficient of the carrier-permeant complex (cm−2∙s−1) |
| p′ | upstream or feed partial pressure (bar) |
| p″ | downstream partial pressure (bar) |
| S | Effective membrane surface area (cm2) |
| CT | Total carrier concentration (mol·cm−3) |
| kd,,CO2 | Sorption coefficient of CO2 in the membranes (mol·cm−3∙bar−1) |
| C | Molar concentration (moL·cm−3) |
| z | distance from the upstream side of the membrane (m) |
| Greek symbols | |
| αm | Mobility ratio (dimensionless) |
| α | Membrane selectivity (dimensionless) |
| ε | Inverse Damkhöler number (dimensionless) |
| K | Reaction equilibrium number (dimensionless) |
| αi/j | CO2/N2 ideal selectivity between tow gas species i and j (dimensionless) |
| λ | A measure of the facilitation factor (dimensionless) |
| ℘i | Permeability of gas i (Barrer) |
| Subscripts | |
| f | Feed |
| A | Solute |
| AC | Carrier-solute complex |
| r | Reverse |
| f | Forward |
| i | Compound |
| 0 | Upstream side (z = 0) |
| Superscripts | |
| SD | Relative to solution-diffusion |
| * | Relative to dimensionless |
References
- Davidson, O.; Metz, B. Special Report on Carbon Dioxide Capture and Storage; International Panel on Climate Change: Geneva, Switzerland, 2005. [Google Scholar]
- Belaissaoui, B.; Favre, E. Membrane Separation Processes for Post-Combustion Carbon Dioxide Capture: State of the Art and Critical Overview. Oil Gas Sci. Technol. Rev. 2013, 69, 1005–1020. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A. State-of-the-art Adsorption and Membrane Separation Processes for Carbon Dioxide Production from Carbon Dioxide Emitting Industries. Sep. Sci. Technol. 2009, 44, 1273–1421. [Google Scholar] [CrossRef]
- Luis, P.; Van Gerven, T.; Van Der Bruggen, B. Recent developments in membrane-based technologies for CO2 capture. Prog. Energy Combust. Sci. 2012, 38, 419–448. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of Permeability/Selectivity Tradeoff Relations in Polymeric Gas Separation Membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Steeneveldt, R.; Berger, B.; Torp, T. CO2 Capture and Storage. Chem. Eng. Res. Des. 2006, 84, 739–763. [Google Scholar] [CrossRef]
- Belaissaoui, B.; Willson, D.; Favre, E. Membrane gas separations and post-combustion carbon dioxide capture: Parametric sensitivity and process integration strategies. Chem. Eng. J. 2012, 122–132. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Ho, W.S.W. Recent developments on membranes for post-combustion carbon capture. Curr. Opin. Chem. Eng. 2011, 1, 47–54. [Google Scholar] [CrossRef]
- Matsuyama, H.; Terada, A.; Nakagawara, T.; Kitamura, Y.; Teramoto, M. Facilitated transport of CO2 through polyethylenimine/poly(vinyl alcohol) blend membrane. J. Membr. Sci. 1999, 163, 221–227. [Google Scholar] [CrossRef]
- Zou, J.; Ho, W.W. CO2-selective polymeric membranes containing amines in crosslinked poly(vinyl alcohol). J. Membr. Sci. 2006, 286, 310–321. [Google Scholar] [CrossRef]
- Huang, J.; Zou, J.; Ho, W.S.W. Carbon Dioxide Capture Using a CO2-Selective Facilitated Transport Membrane. Ind. Eng. Chem. Res. 2008, 47, 1261–1267. [Google Scholar] [CrossRef]
- Kim, T.-J.; Li, B.; Hagg, M.-B. Novel fixed-site-carrier polyvinylamine membrane for carbon dioxide capture. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 4326–4336. [Google Scholar] [CrossRef]
- Sandru, M.; Haukebø, S.H.; Hagg, M.-B. Composite hollow fiber membranes for CO2 capture. J. Membr. Sci. 2010, 346, 172–186. [Google Scholar] [CrossRef]
- Cussler, E.; Aris, R.; Bhown, A. On the limits of facilitated diffusion. J. Membr. Sci. 1989, 43, 149–164. [Google Scholar] [CrossRef]
- Noble, R.D. Generalized microscopic mechanism of facilitated transport in fixed site carrier membranes. J. Membr. Sci. 1992, 75, 121–129. [Google Scholar] [CrossRef]
- Rea, R.; De Angelis, M.G.; Baschetti, M.G. Models for Facilitated Transport Membranes: A Review. Membranes 2019, 9, 26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, U.R.; Quinn, J.A. The prediction of facilitation factors for reaction augmented membrane transport. AIChE J. 1979, 25, 197–200. [Google Scholar] [CrossRef]
- Noble, R.D.; Way, J.D.; Powers, L.A. Effect of external mass-transfer resistance on facilitated transport. Ind. Eng. Chem. Fundam. 1986, 25, 450–452. [Google Scholar] [CrossRef]
- Jemaa, N.; Noble, R.; Koval, C. Combined mass and energy balance analysis of an electrochemically modulated equilibrium stage process. Chem. Eng. Sci. 1992, 47, 1469–1479. [Google Scholar] [CrossRef]
- Paul, D.R.; Koros, W.J. Effect of partially immobilizing sorption on permeability and the diffusion time lag. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 675–685. [Google Scholar] [CrossRef]
- Noble, R.D. Relationship of system properties to performance in facilitated transport systems. Gas Sep. Purif. 1988, 2, 16–19. [Google Scholar] [CrossRef]
- Koval, C.A.; Reyes, Z.E. Chemical aspects of facilitated transport through liquid membranes. In Liquid Membranes: Theory and Applications; ACS Symposium Series No. 347; American Chemical Society: Washington, DC, USA, 1987; pp. 27–38. [Google Scholar]
- Kemena, L.; Noble, R.; Kemp, N. Optimal regimes of facilitated transport. J. Membr. Sci. 1983, 15, 259–274. [Google Scholar] [CrossRef]
- Noble, R.D. Analysis of facilitated transport with fixed site carrier membranes. J. Membr. Sci. 1990, 50, 207–214. [Google Scholar] [CrossRef]
- Rafiq, S.; Deng, L.; Hägg, M.-B. Role of Facilitated Transport Membranes and Composite Membranes for Efficient CO2 Capture—A Review. ChemBioEng Rev. 2016, 3, 68–85. [Google Scholar] [CrossRef]
- Ansaloni, L.; Zhao, Y.; Jung, B.T.; Ramasubramanian, K.; Baschetti, M.G.; Ho, W.W. Facilitated transport membranes containing amino-functionalized multi-walled carbon nanotubes for high-pressure CO2 separations. J. Membr. Sci. 2015, 490, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Gottschlich, D.; Roberts, D.; Way, J. A theoretical comparison of facilitated transport and solution-diffusion membrane modules for gas separation. Gas Sep. Purif. 1988, 2, 65–71. [Google Scholar] [CrossRef]
- Janakiram, S.; Espejo, J.L.M.; Yu, X.; Ansaloni, L.; Deng, L. Facilitated transport membranes containing graphene oxide-based nanoplatelets for CO2 separation: Effect of 2D filler properties. J. Membr. Sci. 2020, 616, 118626. [Google Scholar] [CrossRef]
- Janakiram, S.; Espejo, J.L.M.; Høisæter, K.K.; Lindbråthen, A.; Ansaloni, L.; Deng, L. Three-phase hybrid facilitated transport hollow fiber membranes for enhanced CO2 separation. Appl. Mater. Today 2020, 21, 100801. [Google Scholar] [CrossRef]
- Janakiram, S.; Santinelli, F.; Costi, R.; Lindbråthen, A.; Nardelli, G.M.; Milkowski, K.; Ansaloni, L.; Deng, L. Field trial of hollow fiber modules of hybrid facilitated transport membranes for flue gas CO2 capture in cement industry. Chem. Eng. J. 2020, 2020, 127405. [Google Scholar] [CrossRef]
- Janakiram, S.; Yu, X.; Ansaloni, L.; Dai, Z.; Deng, L. Manipulation of Fibril Surfaces in Nanocellulose-Based Facilitated Transport Membranes for Enhanced CO2 Capture. ACS Appl. Mater. Interfaces 2019, 11, 33302–33313. [Google Scholar] [CrossRef]
- Dhuiège, B.; Lasseuguette, E.; Brochier-Salon, M.-C.; Ferrari, M.-C.; Missoum, K. Crosslinked Facilitated Transport Membranes Based on Carboxymethylated NFC and Amine-Based Fixed Carriers for Carbon Capture, Utilization, and Storage Applications. Appl. Sci. 2020, 10, 414. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Hagg, M.-B. Swelling Behavior and Gas Permeation Performance of PVAm/PVA Blend FSC Membrane. J. Membr. Sci. 2010, 363, 295–301. [Google Scholar] [CrossRef]
- Chen, G.Q.; Scholes, C.A.; Doherty, C.M.; Hill, A.J.; Qiao, G.G.; Kentish, S.E. The thickness dependence of Matrimid films in water vapor permeation. Chem. Eng. J. 2012, 209, 301–312. [Google Scholar] [CrossRef]
- Pfister, M.; Belaissaoui, B.; Favre, E. Membrane Gas Separation Processes from Wet Postcombustion Flue Gases for Carbon Capture and Use: A Critical Reassessment. Ind. Eng. Chem. Res. 2017, 56, 591–602. [Google Scholar] [CrossRef]
- Lasseuguette, E.; Carta, M.; Brandani, S.; Ferrari, M.-C. Effect of humidity and flue gas impurities on CO2 permeation of a polymer of intrinsic microporosity for post-combustion capture. Int. J. Greenh. Gas Control. 2016, 50, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Schultz, J.S.; Goddard, J.D.; Suchdeo, S.R. Facilitated Transport via Carrier-Mediated Diffusion in Membranes Part 1. Mechanistic Aspects, Regimes. AlChE J. 1974, 20, 417–445. [Google Scholar] [CrossRef]
- Han, Y.; Wu, D.; Ho, W.S.W. Simultaneous effects of temperature and vacuum and feed pressures on facilitated transport membrane for CO2/N2 separation. J. Membr. Sci. 2019, 573, 476–484. [Google Scholar] [CrossRef]
- Zhao, Y.; Ho, W.W. Steric hindrance effect on amine demonstrated in solid polymer membranes for CO2 transport. J. Membr. Sci. 2012, 132–138. [Google Scholar] [CrossRef]
- Way, J.D.; Noble, R.D.; Reed, D.L.; Ginley, G.M.; Jarr, L.A. Facilitated transport of CO2 in ion exchange membranes. AIChE J. 1987, 33, 480–487. [Google Scholar] [CrossRef]
- Way, J.; Noble, R.D. Competitive facilitated transport of acid gases in perfluorosulfonic acid membranes. J. Membr. Sci. 1989, 46, 309–324. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Boetje, L.M.; Koval, C.A.; Noble, R.D.; Bowman, C.N. Transport Properties of Carbon Dioxide through Amine Functionalized Carrier Membranes. Ind. Eng. Chem. Res. 1995, 34, 4071–4077. [Google Scholar] [CrossRef]
- Sharifzadeh, M.M.M.; Amooghin, A.E.; Pedram, M.Z.; Omidkhah, M. Time-dependent mathematical modeling of binary gas mixture in facilitated transport membranes (FTMs): A real condition for single-reaction mechanism. J. Ind. Eng. Chem. 2016, 39, 48–65. [Google Scholar] [CrossRef]
- Lin, H.; Freeman, B.D. Gas solubility, diffusivity and permeability in poly(ethylene oxide). J. Membr. Sci. 2004, 239, 105–117. [Google Scholar] [CrossRef]
- Jensen, A.; Christensen, R.; Bonnichsen, R.; Virtanen, A.I. Studies on Carbamates. XI. The Carbamate of Ethylenediamine. Acta Chem. Scand. 1955, 9, 486–492. [Google Scholar] [CrossRef]
- Wang, X.; Conway, W.; Fernandes, D.; Lawrance, G.; Burns, R.; Puxty, G.; Maeder, M. Kinetics of the Reversible Reaction of CO2(aq) with Ammonia in Aqueous Solution. J. Phys. Chem. A 2011, 115, 6405–6412. [Google Scholar] [CrossRef]
- Versteeg, G.; Swaaij, W. On the kinetics between CO2 and alkanolamines both in aqueous and non-aqueous solutions—I. Primary and secondary amines. Chem. Eng. Sci. 1988, 43, 573–585. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, M.; Shudo, S.; Sanui, K.; Ogata, N. Active transport of organic acids through poly(4-vinylpyridine-co-acrylonitrile) membranes. J. Membr. Sci. 1986, 26, 51–61. [Google Scholar] [CrossRef]
- Ogata, N.; Sanui, K.; Fujimura, H. Active transport membrane for chlorine ion. J. Appl. Polym. Sci. 1980, 25, 1419–1425. [Google Scholar] [CrossRef]
- Tsuchida, E.; Nishide, H.; Ohyanagi, M.; Kawakami, H. Facilitated transport of molecular oxygen in the membranes of polymer-coordinated cobalt Schiff base complexes. Macromolecules 1987, 20, 1907–1912. [Google Scholar] [CrossRef]
- Francisco, G.J.; Chakma, A.; Feng, X. Membranes comprising of alkanolamines incorporated into poly(vinyl alcohol) matrix for CO2/N2 separation. J. Membr. Sci. 2007, 303, 54–63. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, Z.; Yi, C.; Bai, Y.; Wang, J.; Wang, S. Gas transport property of polyallylamine–poly(vinyl alcohol)/polysulfone composite membranes. J. Membr. Sci. 2008, 310, 184–196. [Google Scholar] [CrossRef]



| Dimensionless Numbers | Definition | Expression |
|---|---|---|
| ε | Inverse Damkohler number, ratio of the characteristic reverse reaction to diffusion time | |
| αm | Mobility ratio of mobility of carrier to mobility of solute | , with |
| K | Dimensionless reaction equilibrium constant | |
| λ | Measure of the facilitation factor |
| Model Hypothesis | Model Name | Model Equation (F Expression) | |
|---|---|---|---|
| Chemical equilibrium (tanhλ/λ ~ 0) | Zero downstream CO2 concentration ( = 0) (very dilute CO2 gas) | Simplified equilibrium model | Equation (14) |
| Non-zero downstream CO2 concentration | Equilibrium model | Equation (16) | |
| Non-chemical equilibrium (reaction limitation) | Zero downstream CO2 concentration | General model | Equation (13) |
| Operating Conditions | Value |
|---|---|
| Temperature °C | 40 and 50 |
| Feed composition | 10−100% CO2/N2 |
| Sweep gas composition | Pure He |
| Feed pressure (bar) | 1–3 |
| CO2 partial pressure, PCO2 (bar) | 0.15–3 |
| Sweep pressure (bar) | 1 |
| Feed Relative humidity, RHf (%) | 20–90 |
| Sweep Relative humidity, RHs (%) | 50 |
| Feed flow rate, QF (Ncm3/min) | 150 |
| Sweep flow rate, Qs (Ncm3/min) | 10 |
| DCO2 (cm2·s−1) | kd,CO2 (mol·cm−3·bar−1) | DAC (cm2·s−1) | Keq (cm3·mol−1) | Kr (s−1) | SDCO2 Permeability (Barrer) | SDCO2 Permeance (GPU), * e = 1 µm | N2 Permeability (Barrer) | N2 Permeance (GPU) * e = 1 µm |
|---|---|---|---|---|---|---|---|---|
| 1 × 10−6 | 4.84 × 10−5 | 1.7 × 10−9 | 5.20 × 104 | 110 | 145 | 145 | 13 | 13 |
| PCO2 (bar) | αm | ε | K | tanhλ/λ |
|---|---|---|---|---|
| 0.15 | 3.78 | 1.54 × 10−3 | 0.377 | 1.52 × 10−3 |
| 3 | 0.91 | 1.54 × 10−3 | 7.49 | 2.64 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belaissaoui, B.; Lasseuguette, E.; Janakiram, S.; Deng, L.; Ferrari, M.-C. Analysis of CO2 Facilitation Transport Effect through a Hybrid Poly(Allyl Amine) Membrane: Pathways for Further Improvement. Membranes 2020, 10, 367. https://doi.org/10.3390/membranes10120367
Belaissaoui B, Lasseuguette E, Janakiram S, Deng L, Ferrari M-C. Analysis of CO2 Facilitation Transport Effect through a Hybrid Poly(Allyl Amine) Membrane: Pathways for Further Improvement. Membranes. 2020; 10(12):367. https://doi.org/10.3390/membranes10120367
Chicago/Turabian StyleBelaissaoui, Bouchra, Elsa Lasseuguette, Saravanan Janakiram, Liyuan Deng, and Maria-Chiara Ferrari. 2020. "Analysis of CO2 Facilitation Transport Effect through a Hybrid Poly(Allyl Amine) Membrane: Pathways for Further Improvement" Membranes 10, no. 12: 367. https://doi.org/10.3390/membranes10120367
APA StyleBelaissaoui, B., Lasseuguette, E., Janakiram, S., Deng, L., & Ferrari, M.-C. (2020). Analysis of CO2 Facilitation Transport Effect through a Hybrid Poly(Allyl Amine) Membrane: Pathways for Further Improvement. Membranes, 10(12), 367. https://doi.org/10.3390/membranes10120367







