Improvement of Component Flux Estimating Model for Pervaporation Processes
Abstract
:1. Introduction
2. Materials and Methods
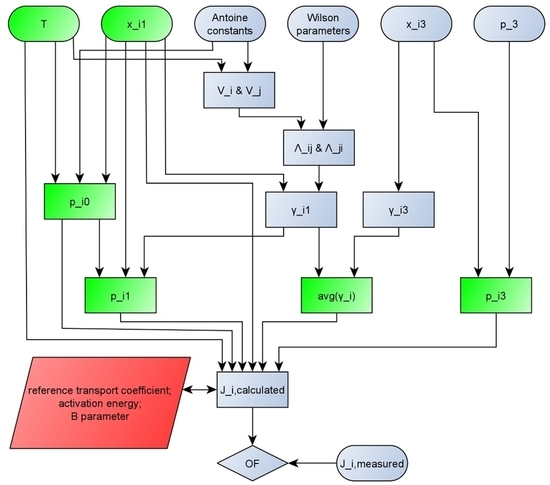
2.1. Pervaporation Modelling
- absorption of components in the membrane;
- selective diffusion of components through the length of the membrane;
- desorption and consequential evaporation to vapour phase on the permeate side.
2.2. Model Improvement
- mole fraction of the feed (xi1) [mole/mole];
- mole fraction of the permeate (xi3) [mole/mole];
- coefficients of the Wilson equation (Aij, Aji) [cal/moleK];
- input temperature (T) [°C. K];
- constants of the Antoine equation for both components (A, B, C, D and E) [-];
- pressure on the permeate side (p3) [bar. kPa];
- partial fluxes of both components (Ji) [kg/m2h].
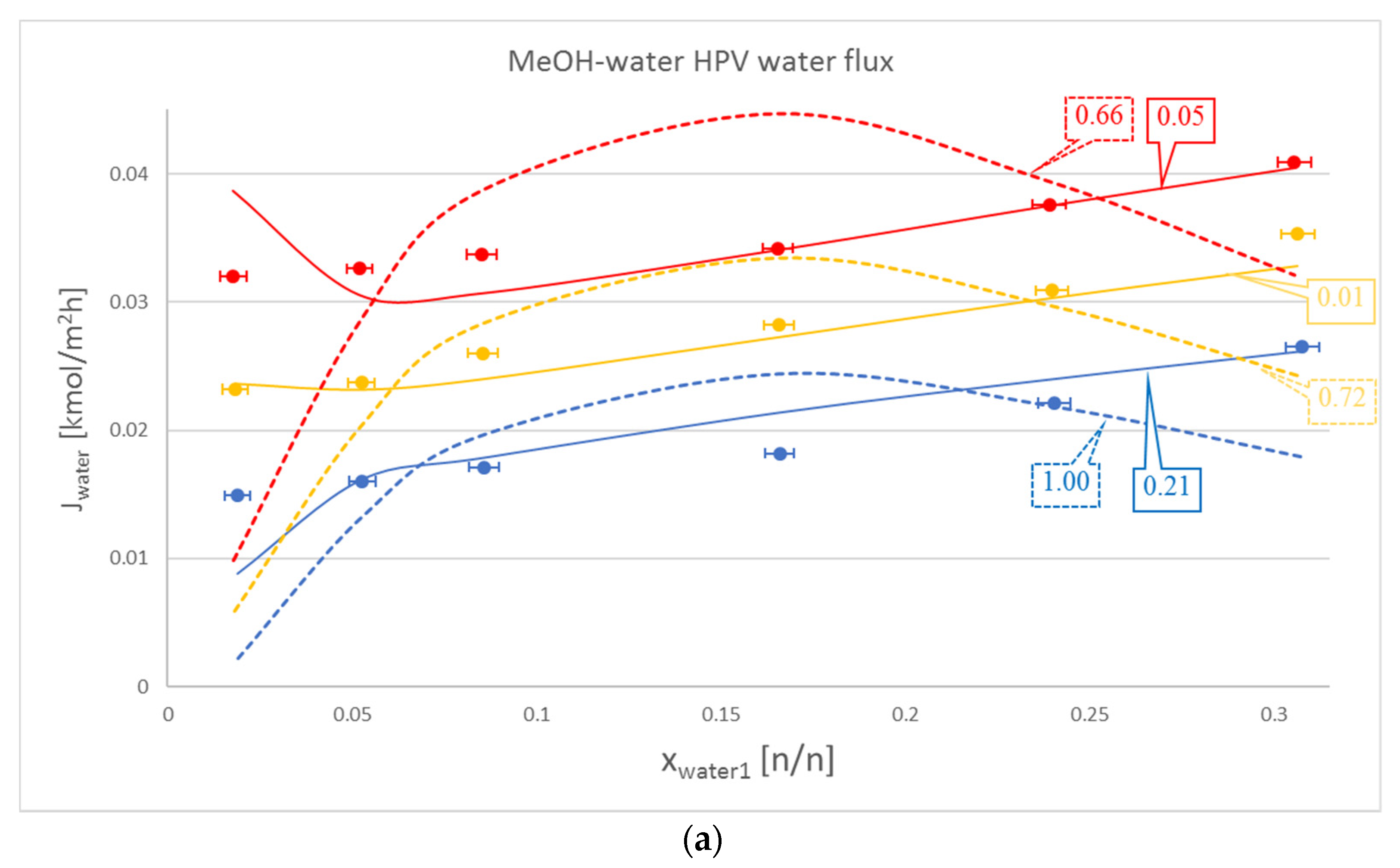
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | membrane area [m2] |
| B | constant in Model I, II and III |
| c | total molar concentration [mol/mol] |
| ci | concentration of component i [mol/m3] |
| Di | diffusion coefficient [m2/h] |
| Di0 | diffusion coefficient of component i [ kmol/m2 h] |
| transport coefficient of component i [kmol/m2 h] | |
| modified transport coefficient of component i in Model I, II and III [kmol/m2 h] | |
| relative transport coefficient of component i [kmol/m2 h] | |
| Ei | activation energy of component i [kJ/mol] |
| fi0 | fugacity of pure i component [mbar, kPa] |
| fi1 | fugacity of component i in the feed side [mbar, kPa] |
| fi3 | fugacity of component i in the permeate side [mbar, kPa] |
| J | total flux [kg/m2h] |
| Ji | partial flux [kg/m2h] |
| L | distance of diffusion [m] |
| ni | weight of component i [mol] |
| pi0 | vapour pressure of pure i component [bar, kPa] |
| pi1 | partial pressure of component i in the feed side [bar, kPa] |
| pi2 | partial pressure of component i between the two layers of the membrane [bar, kPa] |
| pi3 | partial pressure of component i in the permeate side [bar, kPa] |
| p3 | pressure on the permeate side [bar, kPa] |
| Q0 | permeability of the porous supporting layer of the membrane [kmol/m2 h bar] |
| R | gas constant [kJ/kmol K] |
| t | time [s, h] |
| T | temperature [K, °C] |
| T* | reference temperature: 273 K = 20 °C |
| wF | feed concentration of component i [wt%] |
| xi1 | mol fraction of component i in the feed [mol/mol] |
| yi | mol fraction of component i in the permeate [mol/mol] |
| Greek letters: | |
| βij | selectivity for component i and j |
| δ | thickness of the membrane [m] |
| γi1 | activity coefficient of component i in the feed |
| γi3 | activity coefficient of component i in the permeate |
| average activity coefficient of component i |
References
- Figoli, A.; Santoro, S.; Galiano, F.; Basile, A. Pervaporation membranes: Preparation characterization and application. In Pervaporation, Vapour Permeation and Membrane Distillation; Basile, A., Figoli, A., Khayet, M., Eds.; Woodhead Publishing: Cambridge, UK, 2015; Volume 1, pp. 19–63. [Google Scholar]
- Heintz, A.; Stephan, W. A generalized solution—Diffusion model of the pervaporation process through composite membranes Part I. Prediction of mixture solubilities in the dense active layer using the UNIQUAC model. J. Membr. Sci. 1994, 89, 143–151. [Google Scholar] [CrossRef]
- Penkova, A.V.; Pientka, Z.; Polotskaya, G.A. MWCNT/poly(phenylene isophtalamide) Nanocomposite Membranes for Pervaporation of Organic Mixtures. Fuller. Nanotub. Carbon Nanostruct. 2010, 19, 137–140. [Google Scholar] [CrossRef]
- Smitha, B.; Suhanya, D.; Sridhar, S.; Ramakrishna, M. Separation of organic-organic mixtures by pervaporation—a review. J. Membr. Sci. 2004, 241, 1–21. [Google Scholar] [CrossRef]
- Tang, J.; Sirkar, K.K.; Majumdar, S. Permeation and sorption of organic solvents and separation of their mixtures through an amorphous perfluoropolymer membrane in pervaporation. J. Membr. Sci. 2013, 447, 345–354. [Google Scholar] [CrossRef]
- Zhang, Q.G.; Han, G.L.; Hu, W.W.; Zhu, A.M.; Liu, Q.L. Pervaporation of Methanol–Ethylene Glycol Mixture over Organic–Inorganic Hybrid Membranes. Ind. Eng. Chem. Res. 2013, 52, 7541–7549. [Google Scholar] [CrossRef]
- Ling, W.S.; Thian, T.C.; Bhatia, S. Process optimization studies for the dehydration of alcohol–water system by inorganic membrane based pervaporation separation using design of experiments (DOE). Sep. Purif. Technol. 2010, 71, 192–199. [Google Scholar] [CrossRef]
- Liu, P.; Chen, M.; Ma, Y.; Hu, C.; Zhang, Q.; Zhu, A.; Liu, Q. A hydrophobic pervaporation membrane with hierarchical microporosity for high-efficient dehydration of alcohols. Chem. Eng. Sci. 2019, 206, 489–498. [Google Scholar] [CrossRef]
- Schiffmann, P.; Repke, J.-U. Design of pervaporation modules based on computational process modelling. Comput. Aided Chem. Eng. 2011, 29, 397–401. [Google Scholar] [CrossRef]
- Toth, A.J.; Andre, A.; Haaz, E.; Mizsey, P. New horizon for the membrane separation: Combination of organophilic and hydrophilic pervaporations. Sep. Purif. Technol. 2015, 156, 432–443. [Google Scholar] [CrossRef]
- Lipnizki, F.; Trägårdh, G. Modeling of pervaporation: Models to analyze and predict the mass transport in pervaporation. Sep. Purif. Rev. 2007, 30, 49–125. [Google Scholar] [CrossRef]
- Schaetzel, P.; Vauclair, C.; Nguyen, Q.T.; Bouzerar, R. A simplified solution–diffusion theory in pervaporation: The total solvent volume fraction model. J. Membr. Sci. 2004, 244, 117–127. [Google Scholar] [CrossRef]
- Sukitpaneenit, P.; Chung, T.-S.; Jiang, L.Y. Modified pore-flow model for pervaporation mass transport in PVDF hollow fiber membranes for ethanol–water separation. J. Membr. Sci. 2010, 362, 393–406. [Google Scholar] [CrossRef]
- Haaz, E.; Valentinyi, N.; Tarjani, A.J.; Fozer, D.; Andre, A.; Asmaa, S.; Rahimli, F.; Nagy, T.; Mizsey, P.; Deak, C.; et al. Platform molecule removal from aqueous mixture with organophilic pervaporation: Experiments and modelling. Period. Polytech. Chem. Eng. 2019, 63, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Virag, B. Investigation of Ethanol-Water Mixture with Organophilic Pervaporation. Master’s Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2007. [Google Scholar]
- Toth, A.J.; Andre, A.; Haaz, E.; Nagy, T.; Valentinyi, N.; Fozer, D.; Mizsey, P. Application of pervaporation and distillation for utilization process wastewaters. In Proceedings of the Hungarian Water- and Wastewater Association Dr. Dulovics Dezső Junior Symposium, Budapest, Hungary, 22 March 2018. [Google Scholar]
- Poraczki, A. Investigation of Separation of Ethyl Acetate–Water Mixture with Pervaporation. Master’s Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2016. [Google Scholar]
- Vatani, M.; Raisi, A.; Pazuki, G. Mixed matrix membrane of ZSM-5/poly (ether-block-amide)/polyethersulfone for pervaporation separation of ethyl acetate from aqueous solution. Microporous Mesoporous Mater. 2018, 263, 257–267. [Google Scholar] [CrossRef]
- Haaz, E.; Toth, A.J. Methanol dehydration with pervaporation: Experiments and modelling. Sep. Purif. Technol. 2018, 205, 121–129. [Google Scholar] [CrossRef]
- Wesselingh, J.A. Non-Equilibrium Modelling of Distillation. Chem. Eng. Res. Des. 1997, 75, 529–538. [Google Scholar] [CrossRef]
- Tränkle, F.; Gerstlauer, A.; Zeitz, M.; Gilles, E.D. Application of the modeling and simulation environment ProMoT/Diva to the modeling of distillation processes. Comput. Chem. Eng. 1997, 21, S841–S846. [Google Scholar] [CrossRef]
- Heintz, A.; Stephan, W. A generalized solution–diffusion model of the pervaporation process through composite membranes Part II. Concentration polarization, coupled diffusion and the influence of the porous support layer. J. Membr. Sci. 1994, 89, 153–169. [Google Scholar] [CrossRef]
- Marriott, J.; Sørensen, E. A general approach to modelling membrane modules. Chem. Eng. Sci. 2003, 58, 4975–4990. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Rautenbach, R.; Herion, C. Meyer-Blumentoth, U. Pervaporation membrane separation processes. Membr. Sci. Technol. Ser. 1990, 1, 181–191. [Google Scholar]
- Mizsey, P.; Koczka, K.; Deák, A.; Fonyó, Z. Simulation of pervaporation using the “solution–diffusion” model. Hung. Chem. J. 2005, 7, 239–242. [Google Scholar]
- Valentínyi, N.; Cséfalvay, E.; Mizsey, P. Modelling of pervaporation: Parameter estimation and model development. Chem. Eng. Res. Des. 2013, 91, 174–183. [Google Scholar] [CrossRef]
- Himics, M. Examination of Pervaporation Modeling Determination of Model Parameters in the Case of Butanol–Water Mixture. Bachelor’s Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2009. [Google Scholar]
- Koczka, K. Environmental Conscious Design and Industrial Application of Separation Processes. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2009. [Google Scholar]
- Ortiz, I.; Gorri, D.; Casado, C.; Urtiaga, A. Modelling of the pervaporative flux through hydrophilic membranes. J. Chem. Technol. Biotechnol. 2005, 80, 397–405. [Google Scholar] [CrossRef]
- Gonzalez, B.; Ortiz, I. Mathematical Modeling of the Pervaporative Separation of Methanol–Methylterbutyl Ether Mixtures. Ind. Eng. Chem. Res. 2001, 40, 1720–1731. [Google Scholar] [CrossRef]
- Matsui, S.; Paul, D.R. A simple model for pervaporative transport of binary mixtures through rubbery polymeric membranes. J. Membr. Sci. 2004, 235, 25–30. [Google Scholar] [CrossRef]
- Ebneyamini, A.; Azimi, H.; Tezel, F.H.; Thibault, J. Modelling of mixed matrix membranes: Validation of the resistance-based model. J. Membr. Sci. 2017, 543, 361–369. [Google Scholar] [CrossRef]


| Mixture | Type | Examined Temperatures [°C] | Water Content of Feed [wt%] | Membrane | Ref. |
|---|---|---|---|---|---|
| OPV | |||||
| EtOH-water | azeotropic | 40, 50, 60, 70, 80 | 91.57–99.63 | Sulzer PERVAP 4060 | [14,15] |
| iBuOH-water | azeotropic | 50, 60, 70 | 98.16–99.89 | Sulzer PERVAP 4060 | [10,16] |
| EtAc-water | azeotropic | 50, 60, 70 | 98.86–99.82 | Sulzer PERVAP 4060 | [17] |
| 30, 40, 45, 50 | 98.93–99.80 | ZSM-5 filled PEBA | [18] | ||
| HPV | |||||
| MeOH-water | zeotropic | 50, 60, 70 | 1.78–3.075 | Sulzer PERVAP 1510 | [16,19] |
| iBuOH-water | azeotropic | 70, 80, 90 | 4.57–36.39 | Sulzer PERVAP 1510 | [10,16] |
| Component | Model I | Model II | Model III |
|---|---|---|---|
| OPV | |||
| water | 6.0 × 10−4 | 0.003 | 5.7 × 10−4 * |
| EtOH | 0.783 * | 0.800 | 0.987 |
| water | 0.028 | 0.508 | 0.027 * |
| iBuOH | 2.139 * | 2.142 | 2.140 |
| water | 0.658 | 0.719 | 0.095 * |
| EtAc | 0.084 * | 0.087 | 0.086 |
| water | 1.942 | 5.327 | 1.688 * |
| EtAc | n/a 1 | n/a 1 | n/a 1 |
| HPV | |||
| water | 2.385 | 6.022 | 0.274 * |
| MeOH | 0.074 | 1.714 | 0.070 * |
| water | 3.321 * | 6.507 | 6.493 |
| iBuOH | 4.873 * | 8.077 | 4.359 2 |
| Components | Ei [kJ/mol] | B [-] | Model | |
|---|---|---|---|---|
| OPV | ||||
| water | 31.28 | 4.94 | −0.49 | III |
| EtOH | 33.09 | 77.78 | −0.04 | I |
| water | 42.20 | 3.45 | −22.58 | III |
| iBuOH | −18.28 | 14,879.52 | −1.83 | I |
| water | 30.96 | 6.99 | −52.22 | III |
| EtAc | 8.96 | 8373.44 | −4.48 | I |
| water | 3.69 | 5468.59 | −0.64 | III |
| EtAc | n/a 1 | n/a 1 | n/a 1 | n/a 1 |
| HPV | ||||
| water | 23.50 | 167.30 | −6.52 | III |
| MeOH | 30.77 | 0.01 | −1.49 | III |
| water | 58.25 | 0.535 | 8.12 | I |
| iBuOH | 52.25 | 2.63 | −8.06 | I |
| Mixture | Temperature [°C] | Model I | Model III | ||
|---|---|---|---|---|---|
| Water | Organic | Water | Organic | ||
| OPV | |||||
| Water-EtOH | 40 | 2.57 × 10−4 | n/a 1 | 0.290 | n/a 1 |
| 60 | 1.54 × 10−4 | n/a 1 | 0.262 | n/a 1 | |
| 80 | 1.91 × 10−4 | n/a 1 | 0.231 | n/a 1 | |
| Water-iBuOH | 50 | 0.011 | 0.011 | 1.973 | 1.995 |
| 60 | 0.010 | 0.010 | 0.091 | 0.082 | |
| 70 | 0.006 | 0.006 | 0.075 | 0.063 | |
| Water-EtAc | 50 | 0.159 | 0.007 | 0.052 | 0.056 |
| 60 | 0.366 | 0.077 | 0.021 | 0.022 | |
| 70 | 0.133 | 0.010 | 0.011 | 0.008 | |
| Water-EtAc | 30 | 0.302 | 0.121 | n/a 1 | n/a 1 |
| 40 | 0.243 | 0.125 | n/a 1 | n/a 1 | |
| 45 | 0.719 | 0.634 | n/a 1 | n/a 1 | |
| 50 | 0.678 | 0.808 | n/a 1 | n/a 1 | |
| HPV | |||||
| MeOH-water | 50 | 1.003 | 0.206 | 0.032 | 0.027 |
| 60 | 0.720 | 0.013 | 0.017 | 0.020 | |
| 70 | 0.662 | 0.056 | 0.028 | 0.025 | |
| iBuOH-Water | 70 | 1.147 | 2.489 | 1.937 | n/a 2 |
| 80 | 1.169 | 2.484 | 1.708 | n/a 2 | |
| 90 | 1.004 | 1.490 | 1.203 | n/a 2 | |
| Mixture | Recommended Model for | |
|---|---|---|
| Aqueous Component | Organic Component | |
| OPV | ||
| EtOH-water | III (I) | I |
| iBuOH-water | III | I (III) |
| EtAc-water | III (I) | I (III) |
| HPV | ||
| MeOH-water | III (I) | I (III) |
| iBuOH-water | I (III) | I |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szilagyi, B.; Toth, A.J. Improvement of Component Flux Estimating Model for Pervaporation Processes. Membranes 2020, 10, 418. https://doi.org/10.3390/membranes10120418
Szilagyi B, Toth AJ. Improvement of Component Flux Estimating Model for Pervaporation Processes. Membranes. 2020; 10(12):418. https://doi.org/10.3390/membranes10120418
Chicago/Turabian StyleSzilagyi, Botond, and Andras Jozsef Toth. 2020. "Improvement of Component Flux Estimating Model for Pervaporation Processes" Membranes 10, no. 12: 418. https://doi.org/10.3390/membranes10120418
APA StyleSzilagyi, B., & Toth, A. J. (2020). Improvement of Component Flux Estimating Model for Pervaporation Processes. Membranes, 10(12), 418. https://doi.org/10.3390/membranes10120418