Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model
Abstract
1. Introduction
2. Methodology
2.1. Electrochemical Model
2.2. Conservation Equation
2.3. Boundary and Initial Conditions
2.4. Experimental Setup
3. Results and Discussion
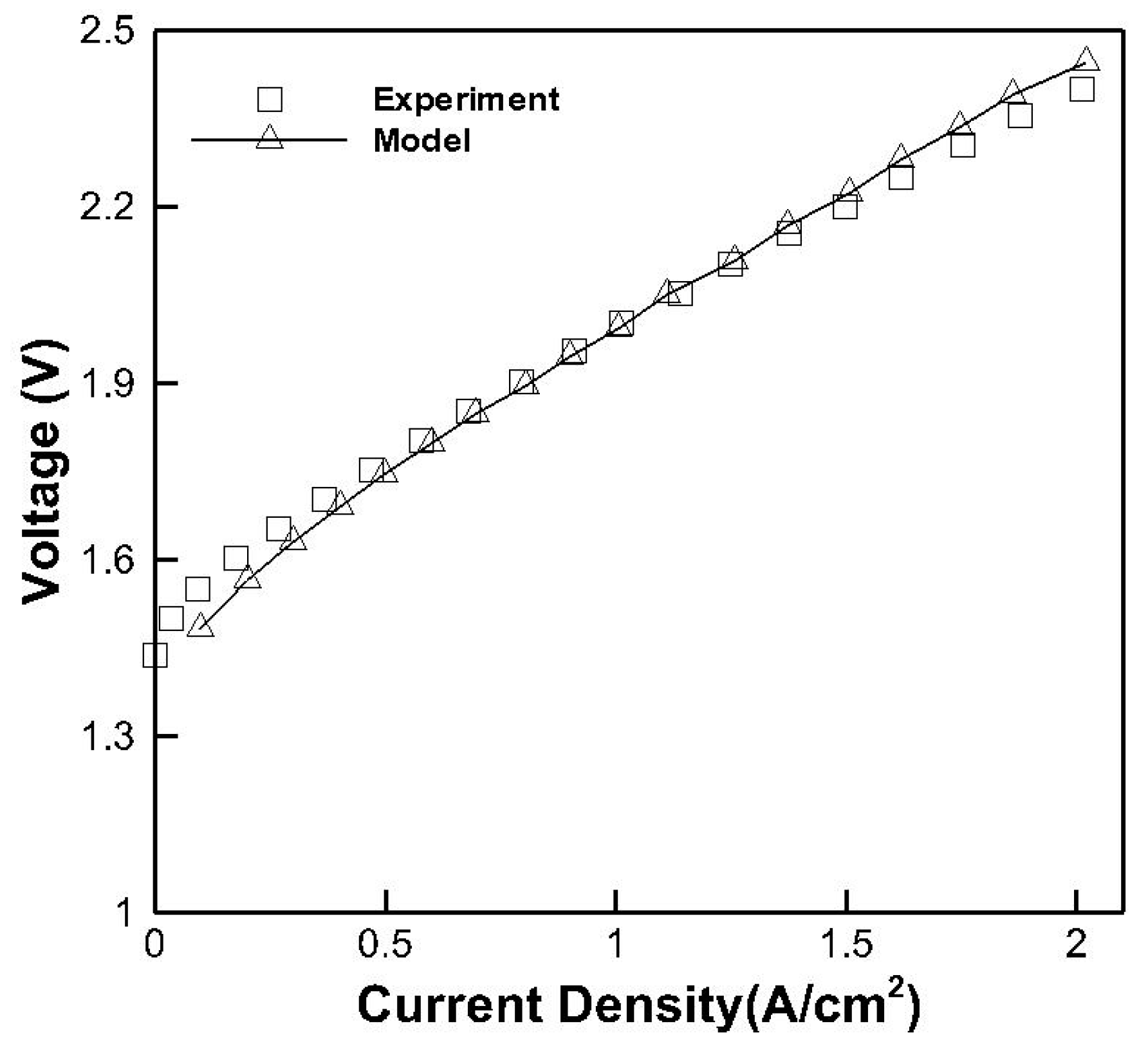
3.1. Model Validation
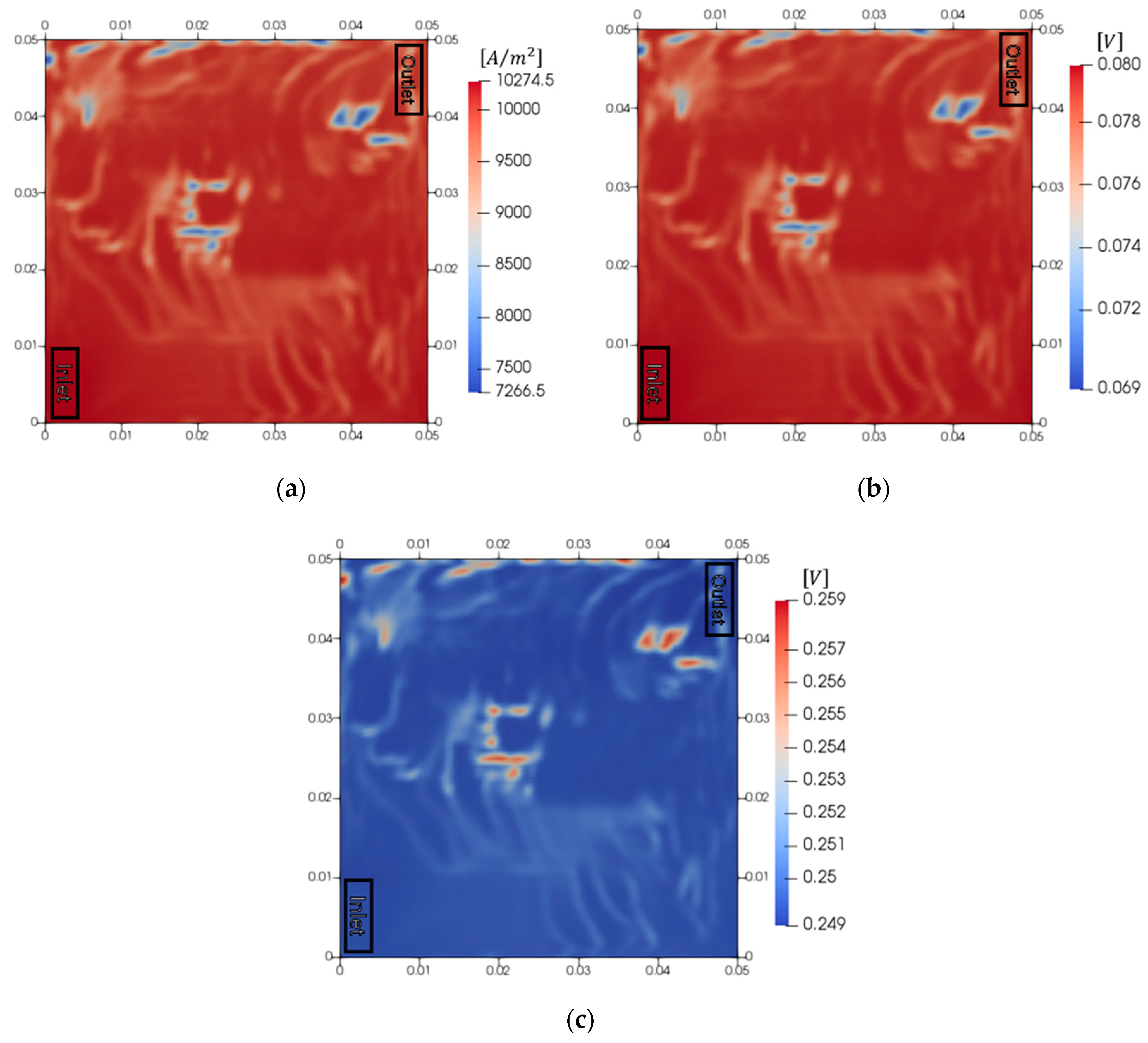
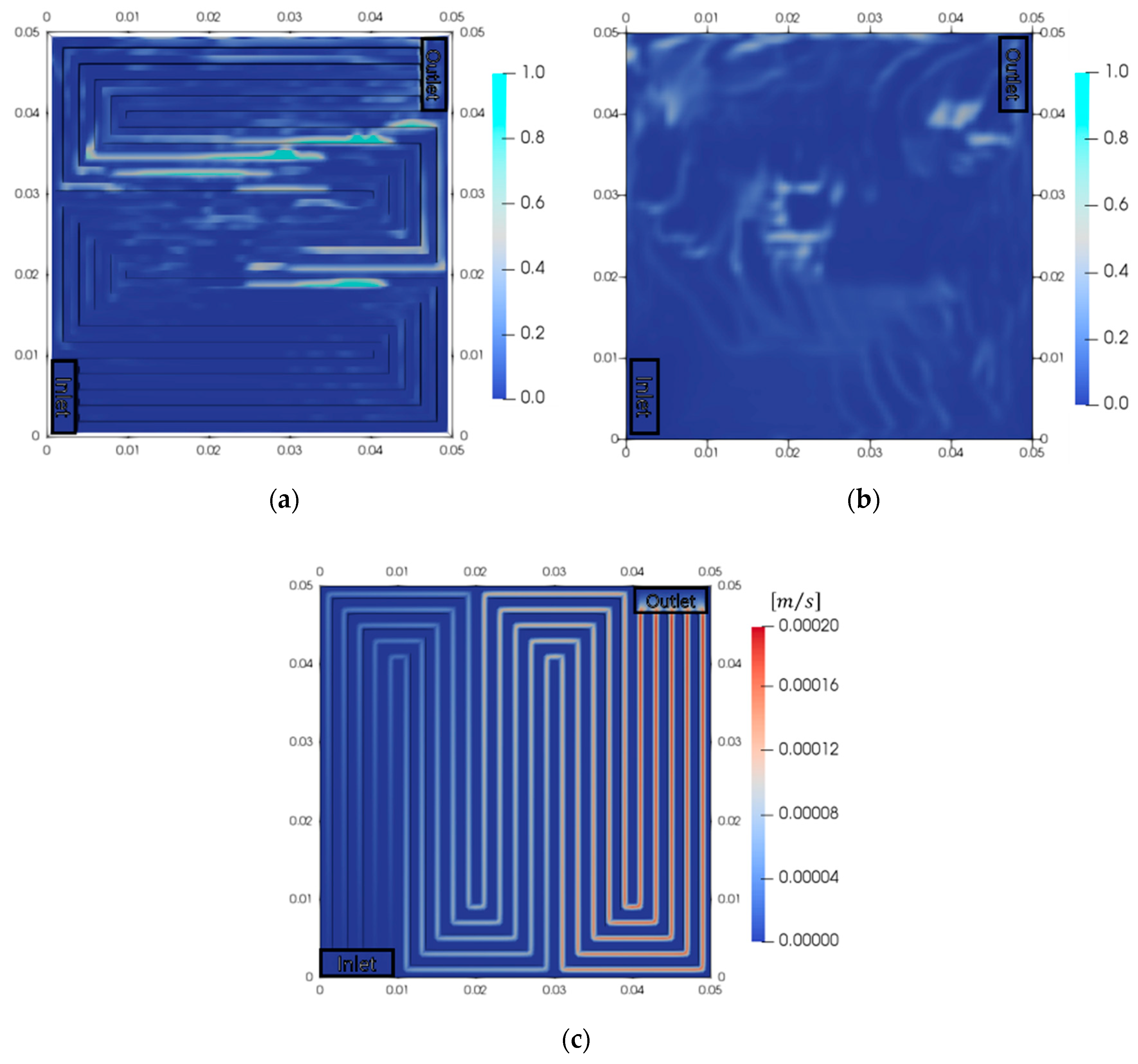
3.2. Analysis of Electrochemical Reaction of PEMWE
3.3. Analysis of Electrochemical Reaction According to the Current Density
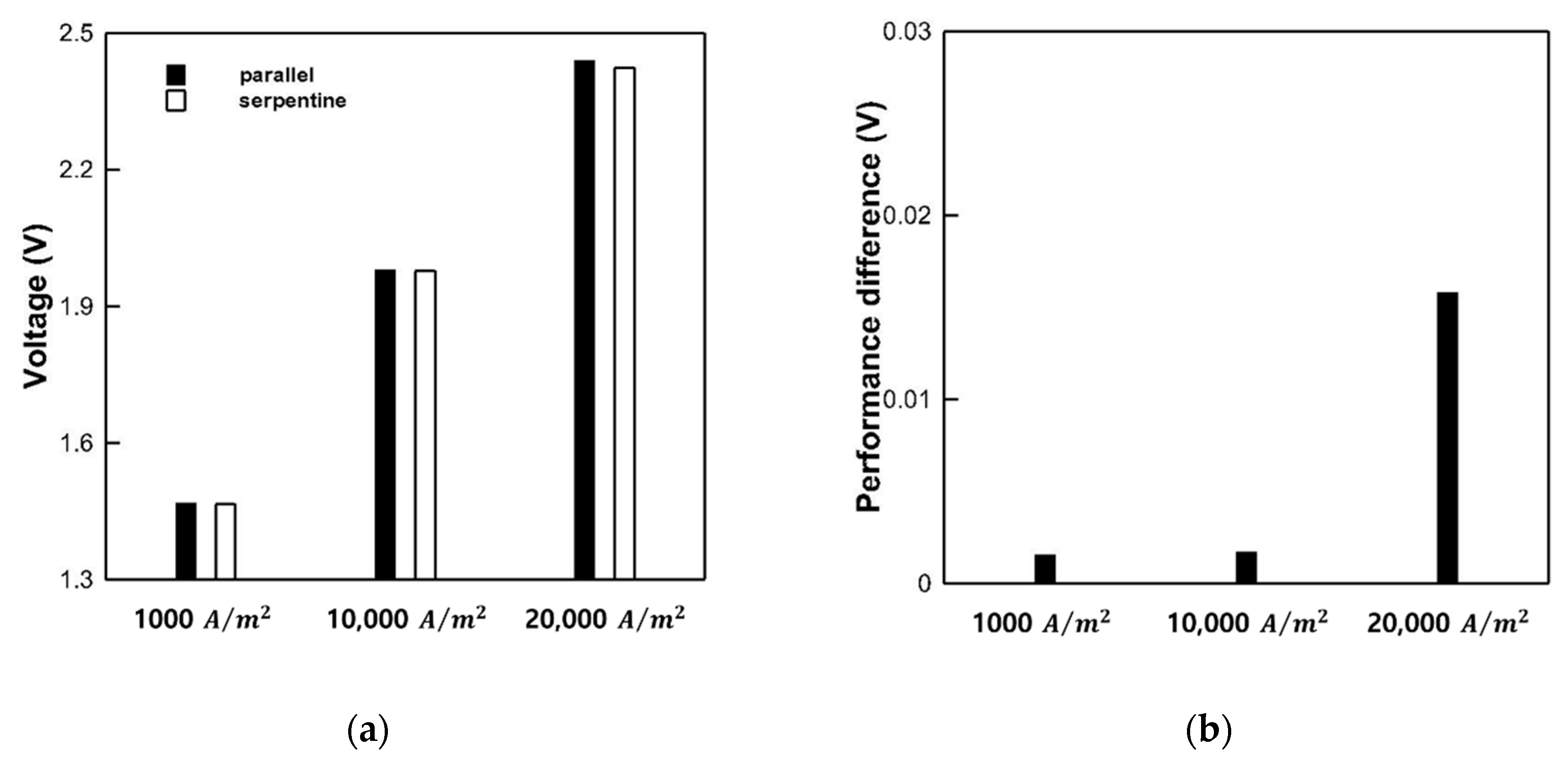
3.4. Performance Analysis of Serpentine and Parallel Channel for PEMWE
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Area of inlet, outlet of electrolyzer (m2) |
| ASR | Area specific resistance (Ω m2) |
| E | Voltage (V), activation energy (J/mol) |
| F | Faraday’s constant (C/mol) |
| H | Height of channel (m) |
| i | Current density (A/m2) |
| i0 | Exchange current density (A/m2) |
| L | Thickness of membrane and PTL (m) |
| P | Pressure (Pa) |
| Q | Flow rate (cm3/min) |
| R | Gas constant (J/mol K) |
| U | Velocity of fluid (m/s) |
| T | Temperature (K) |
| Volume flux of oxygen and water (m3/s) | |
| W | Width of channel and lib (m) |
| α | Transfer coefficient, volume fraction of fluid |
| η | Overpotential (V) |
| µ | Viscosity of fluid (kg/m s) |
| ρ | Density of fluid (kg/m3) |
| σ | Conductivity of membrane (S/m) |
| γ | Roughness factor of electrode |
| Subscripts | |
| A | Anode |
| C | Cathode |
| H | Hydrogen |
| i | Pertaining to species i |
| mem | Membrane |
| O | Oxygen |
| ohm | Ohmic loss |
| W | Water |
| Acronyms | |
| PEMWE | Polymer electrolyte membrane water electrolyzer |
| MEA | Membrane electrode assembly |
| PTL | Porous transport layer |
| OCV | Open circuit voltage |
| ORR | Oxygen reduction reaction |
| OOR | Oxygen oxidation reaction |
| HRR | Hydrogen reduction reaction |
| HOR | Hydrogen oxidation reaction |
References
- Kim, M.S.; Song, J.H.; Kim, D.K. Development of Optimal Conditioning Method to Improve Economic Efficiency of Polymer Electrolyte Membrane (PEM) Fuel Cells. Energies 2020, 13, 2831. [Google Scholar] [CrossRef]
- Bodner, M.; Cermenek, B.; Rami, M.; Hacker, V. The Effect of Platinum Electrocatalyst on Membrane Degradation in Polymer Electrolyte Fuel Cells. Membranes 2015, 5, 888–902. [Google Scholar] [CrossRef] [PubMed]
- Felix, C.; Bladergroen, B.; Linkov, V.; Pollet, B.; Pasupathi, S. Ex-Situ Electrochemical Characterization of IrO2 Synthesized by a Modified Adams Fusion Method for the Oxygen Evolusion Reactin. Catalysts 2019, 9, 318. [Google Scholar] [CrossRef]
- Jung, G.-B.; Chan, S.-H.; Lai, C.-J.; Yeh, C.-C.; Yu, J.-W. Innovative Membrane Electrode Assembly (MEA) Fabrication for Proton Exchange Membrane Water Electrolysis. Energies 2019, 12, 4218. [Google Scholar] [CrossRef]
- Lee, C.; Hinebaugh, J.; Banerjee, R.K.; Chevalier, S.; Abouatallah, R.; Wang, R.; Bazylak, A. Influence of limiting throat and flow regime on oxygen bubble saturation of polymer electrolyte membrane electrolyzer porous transport layers. Int. J. Hydrog. Energy 2017, 42, 2724–2735. [Google Scholar] [CrossRef]
- Siracusano, S.; Trocino, S.; Briguglio, N.; Baglio, V.; Aricò, A.S. Electrochemical Impedance Spectroscopy as a Diagnostic Tool in Polymer Electrolyte Membrane Electrolysis. Materials 2018, 11, 1368. [Google Scholar] [CrossRef]
- Lee, C.; Lee, J.; Zhao, B.; Fahy, K.; Lamanna, J.; Baltic, E.; Hussey, D.; Jacobson, D.; Schulz, V.; Bazylak, A. Temperature-dependent gas accumulation in polymer electrolyte membrane electrolyzer porous transport layers. J. Power Sources 2020, 446, 227312. [Google Scholar] [CrossRef]
- Arbabi, F.; Montazeri, H.; Abouatallah, R.; Wang, R.; Bazylak, A. Three-Dimensional Computational Fluid Dynamics Modelling of Oxygen Bubble Transport in Polymer Electrolyte Membrane Electrolyzer Porous Transport Layers. J. Electrochem. Soc. 2016, 163, F3062–F3069. [Google Scholar] [CrossRef]
- Marković, N.M.; Grgur, A.B.N.; Ross, P.N. Temperature-Dependent Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Acid Solutions. J. Phys. Chem. B 1997, 101, 5405–5413. [Google Scholar] [CrossRef]
- Thampan, T.; Malhotra, S.; Zhang, J.; Datta, R. PEM fuel cell as a membrane reactor. Catal. Today 2001, 67, 15–32. [Google Scholar] [CrossRef]
- Beattie, P.D.; Basura, V.I.; Holdcroft, S. Temperature and pressure dependence of O2 reduction at Pt|Nafion 117 and Pt|BAM 407 interfaces. J. Electroanal. Chem. 1999, 468, 180–192. [Google Scholar] [CrossRef]
- Damjanovic, A.; Dey, A.; Bockris, J.O. Electrode Kinetics of Oxygen Evolution and Dissolution on Rh, Ir, and Pt-Rh Alloy Electrodes. J. Electrochem. Soc. 1966, 113, 739. [Google Scholar] [CrossRef]
- Mishima, K.; Hibiki, T. Some characteristics of air-water two-phase flow in small diameter vertical tubes. Int. J. Multiph. Flow 1996, 22, 703–712. [Google Scholar] [CrossRef]
- Ito, H.; Maeda, T.; Nakano, A.; Hwang, C.M.; Ishida, M.; Kato, A.; Yoshida, T. Experimental study on porous current collectors of PEM electrolyzers. Int. J. Hydrog. Energy 2012, 37, 7418–7428. [Google Scholar] [CrossRef]
- Dedigama, I.; Angeli, P.; Ayers, K.; Robinson, J.; Shearing, P.; Tsaoulidis, D.; Brett, D.J.L. In situ diagnostic techniques for characterisation of polymer electrolyte membrane water electrolysers—Flow visualisation and electrochemical impedance spectroscopy. Int. J. Hydrog. Energy 2014, 39, 4468–4482. [Google Scholar] [CrossRef]
- Nie, J.; Chen, Y. Numerical modeling of three-dimensional two-phase gas-liquid flow in the flow field plate of a PEM electrolysis cell. Int. J. Hydrog. Energy 2010, 35, 3183–3197. [Google Scholar] [CrossRef]
- Olesen, A.C.; Frensch, S.H.; Kær, S.K. Towards uniformly distributed heat, mass and charge: A flow field design study for high pressure and high current density operation of PEM electrolysis cells. Electrochim. Acta 2019, 293, 476–495. [Google Scholar] [CrossRef]
- Olesen, A.C.; Rømer, C.; Kær, S.K. A numerical study of the gas-liquid, two-phase flow maldistribution in the anode of a high pressure PEM water electrolysis cell. Int. J. Hydrog. Energy 2016, 41, 52–68. [Google Scholar] [CrossRef]
- Sazali, N.; Salleh, W.N.W.; Jamaludin, A.S.; Razali, M.N.M. New Perspectives on Fuel Cell Technology: A Brief Review. Membranes 2020, 10, 99. [Google Scholar] [CrossRef]
- Nishida, R.; Beale, S.B.; Pharoah, J.G. Comprehensive computational fluid dynamics model of solid oxide fuel cell stacks. Int. J. Hydrog. Energy 2016, 41, 20592–20605. [Google Scholar] [CrossRef]
- Choi, P.; Bessarabov, D.; Datta, R. A simple model for solid polymer electrolyte (SPE) water electrolysis. Solid State Ion. 2004, 175, 535–539. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, D.K. Parametric study on dynamic heat and mass transfer response in polymer electrolyte membrane fuel cell for automotive applications. Appl. Therm. Eng. 2020, 167, 114729. [Google Scholar] [CrossRef]
- Kucernak, A. Analysis of the electrical and mechanical time response of solid polymer-platinum composite membranes. Electrochim. Acta 2001, 46, 1313–1322. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Scale-adaptive analysis of Euler-Euler large eddy simulation for laboratory scale dispersed bubbly flows. Chem. Eng. J. 2018, 338, 465–477. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical Simulation of Gas and Liquid Two-Phase Flow in Gas-Stirred Systems Based on Euler-Euler Approach. Met. Mater. Trans. A 2013, 44, 1251–1263. [Google Scholar] [CrossRef]
- Beale, S.B.; Choi, H.-W.; Pharoah, J.G.; Roth, H.K.; Jasak, H.; Jeon, D.H. Open-source computational model of a solid oxide fuel cell. Comput. Phys. Commun. 2016, 200, 15–26. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A three-dimensional model for negative half cell of the vanadium redox flow battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
- Pollet, B.G. The Use of Power Ultrasound for the Production of PEMFC and PEMWE Catalysts and Low-Pt Loading and High-Performing Electrodes. Catalysts 2019, 9, 246. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value |
|---|---|---|
| Area of electrolyzer | Acell | 25 cm2 |
| Area of inlet and outlet | Ain, Aout | 27 mm2 |
| Membrane thickness | Lm | 0.13 mm |
| PTL thickness at anode | LA | 0.36 mm |
| PTL thickness at cathode | LC | 0.20 mm |
| Channel height | HC | 1 mm |
| Channel width | WC | 1 mm |
| Lib width | WL | 1 mm |
| Parameter | Symbol | Value |
|---|---|---|
| Reference exchange current density for ORR | iA0ref | 1 × 10−3 A/m2 [12] |
| Reference exchange current density for HOR | iC0ref | 1 A/m2 [9] |
| Effective activation energy for anode reaction | EA | 18 × 103 J/mol [10] |
| Effective activation energy for cathode reaction | EC | 76 × 103 J/mol [10] |
| Transfer coefficient for anode reaction | αA | 0.5 |
| Transfer coefficient for cathode reaction | αC | 0.5 |
| Conductivity of membrane | σ | 10 S/cm |
| Roughness factor of electrode | γm | 100 [23] |
| Equilibrium constant of reaction | KA,C | 6.2 [10] |
| Parameter | Symbol | Value |
|---|---|---|
| Density of liquid water | ρW | 971.60 kg/m3 |
| Density of oxygen | ρO | 1.089 kg/m3 |
| Density of hydrogen | ρH | 0.0686 kg/m3 |
| Viscosity of liquid water | µW | 0.355 kg/ms |
| Viscosity of oxygen | µO | 2.341 × 10−5 kg/ms |
| Viscosity of hydrogen | µH | 9.932 × 10−6 kg/ms |
| Parameter | Symbol | Value |
|---|---|---|
| Flow rate of water | QA | 20 cm3/min |
| Inlet temperature | Tin | 80 °C |
| Outlet pressure | PO | 101,325 Pa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rho, K.H.; Na, Y.; Ha, T.; Kim, D.K. Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model. Membranes 2020, 10, 441. https://doi.org/10.3390/membranes10120441
Rho KH, Na Y, Ha T, Kim DK. Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model. Membranes. 2020; 10(12):441. https://doi.org/10.3390/membranes10120441
Chicago/Turabian StyleRho, Kyu Heon, Youngseung Na, Taewook Ha, and Dong Kyu Kim. 2020. "Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model" Membranes 10, no. 12: 441. https://doi.org/10.3390/membranes10120441
APA StyleRho, K. H., Na, Y., Ha, T., & Kim, D. K. (2020). Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model. Membranes, 10(12), 441. https://doi.org/10.3390/membranes10120441





