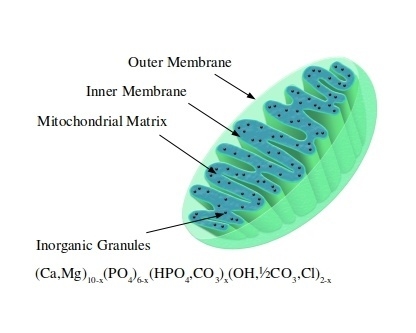
Precipitation of Inorganic Salts in Mitochondrial Matrix
Abstract
1. Introduction
2. Calculations and Data
2.1. Mitochondrial pH, Ionic Concentrations and Activities
| Value | Measuring Technique | Type of Cell | Ref. | |
|---|---|---|---|---|
| pH | 7.14 | SNARF | pig heart | [32] |
| 7.8 | BCECF | beef heart | [43] | |
| 7.65–8.1 | SNARF | beef heart | [33] | |
| 8.0–8.9 | DMO distribution | rat heart | [39] | |
| 7.40–7.51 | DMO distribution | beef heart | [44] | |
| 7.74–7.95 | ratiometric pericam | motor nerve of Drosophila fly larvae | [40] | |
| 7.7 | SNARF | canine kidney (MDCK) | [34] | |
| 7.64 | YFP (SypHer) | HeLa | [38] | |
| 7.6–8.2 | GFP (mtAlpHi) | HeLa | [36] | |
| 7.8 | enhanced YFP | human bladder carcinoma | [45] | |
| 7.7–8.2 | pH-sensitive GFP | (Jurkat) T lymphocyte and HEK-293 | [37] | |
| 7.98 | enhanced YFP | HeLa | [46] | |
| 7.91 | enhanced YFP | rat cardiomyocytes | [46] | |
| 7.2–7.7 | isotope distribution ‡ | rat liver | [47] | |
| 7.2–8.4 | [U-14C]glutamate efflux | rat kidney | [48] | |
| Na+ | 50–113 mM | CoroNa Red | canine kidney (MDCK) | [49] |
| 5 mM | SBFI | pig heart | [50] | |
| 5.1 mM | SBFI | rat ventricular myocytes | [51] | |
| 5 mM | assumed physiol. value | --------- | [52] | |
| K+ | 15 mM | PBFI | isolated rat hepatocytes | [53] |
| 10–20 mM | PBFI | rat heart | [54] | |
| 20–60 mM † | Potentiometric ISE | rat liver | [55] | |
| 150 mM | assumed physiol. value | --------- | [52] | |
| Mg2+ | 0.35 mM | Mg2+ efflux null-point | rat hepatocytes | [56] |
| 0.9 mM | Mg2+ efflux null-point | beef heart | [57] | |
| 2.4 mM | 31P-NMR spectroscopy | heterotrophic sycamore | [58] | |
| 0.5 mM | Fura-2 | beef heart | [59] | |
| 0.8–1.5 mM | Indo-1 and Fura-2 | rat heart | [60] | |
| Ca2+ | 0.22 µM | mito-TN-XXL | motor nerve of Drosophila fly larvae | [40] |
| 24 µM * | Rhod-FF/Rhod-5N | motor nerve of Drosophila fly larvae | [40] | |
| 0.19–3.34 µM | YC2 | HEK-293 and HeLa | [61] | |
| 0.41 µM | aequorin luminescence | bovine adrenal glomerulosa cells | [62] | |
| 183 nM | Indo-1 | rat heart | [63] | |
| 0.1–0.6 µM | Indo-1/AM | rat cardiac myocytes | [64] | |
| 0.2–1.1 µM | Indo-1 | rat heart | [65] | |
| 0.17–0.92 µM | Fura-2/AM | rat heart | [66] | |
| 0.2–1.8 µM | Fura-2 | rat heart | [67] | |
| 0.4–2.1 µM | Fura-2 | rat heart myocytes | [68] | |
| 1–5 µM | Fura-2/AM | rat brain | [29] | |
| Cl- | 4.2 mM | liquid chromatography | human liver | [69] |
| 0.9–22.2 mM | liquid chromatography | human liver | [69] |
2.2. Precipitation of Carbonates
2.2.1. Calcium Carbonates
- (1)
- calcite, anhydrous CaCO3 with trigonal structure
- (2)
- aragonite, anhydrous CaCO3 with orthorhombic structure
- (3)
- vaterite, anhydrous CaCO3 with hexagonal structure
- (4)
- monohydrocalcite, CaCO3·H2O with trigonal structure
- (5)
- hexahydrate known as ikaite, CaCO3·6H2O with monoclinic structure
- (6)
- amorphous calcium carbonate (ACC), colloidal hydrate containing less than one molecule of water per molecule of CaCO3.
2.2.2. Magnesium Carbonates
- (1)
- magnesite, anhydrous MgCO3 with trigonal crystal structure
- (2)
- barringtonite, dihydrate MgCO3·2H2O with triclinic structure
- (3)
- nesquehonite, trihydrate MgCO3·3H2O with monoclinic structure
- (4)
- lansfordite, pentahydrate MgCO3·5H2O with monoclinic structure
- (5)
- pokrovskite, basic carbonate Mg2CO3(OH)2 with monoclinic structure
- (6)
- artinite, hydrated basic carbonate Mg2CO3(OH)2·3H2O with monoclinic structure
- (7)
- hydromagnesite, hydrated basic carbonate Mg5(CO3)4(OH)2·4H2O with monoclinic structure
- (8)
- dypingite, hydrated basic carbonate Mg5(CO3)4(OH)2·5H2O with monoclinic structure
- (9)
- giorgiosite, hydrated basic carbonate Mg5(CO3)4(OH)2·6H2O
- (10)
- octahydrate (UM1973-06-CO:MgH) with the formula Mg5(CO3)4(OH)2·8H2O, possibly identical to dypingite, but differs in optical properties
- (11)
- protomagnesite, hydrated basic carbonate Mg5(CO3)4(OH)2·11H2O
- (12)
- shelkovite, hydrated basic carbonate Mg7(CO3)5(OH)4·24H2O
2.3. Precipitation of Orthophosphates
2.3.1. Calcium Orthophosphates
- (1)
- monocalcium phosphate monohydrate (MCPM), Ca(H2PO4)2∙H2O with Ca/P ratio = 0.5
- (2)
- anhydrous monocalcium phosphate (AMCP), Ca(H2PO4)2 with Ca/P ratio = 0.5
- (3)
- dicalcium phosphate dihydrate, CaHPO4∙H2O, known as brushite (BRU), Ca/P ratio = 1.0
- (4)
- anhydrous dicalcium phosphate, CaHPO4, known as monetite, Ca/P ratio = 1.0
- (5)
- octacalcium phosphate (OCP) with the formula Ca8(HPO4)2(PO4)4∙5H2O, Ca/P ratio = 1.33
- (6)
- α-tricalcium phosphate (α-TCP), Ca3(PO4)2 with monoclinic crystallographic structure and Ca/P ratio = 1.5
- (7)
- β-tricalcium phosphate (β-TCP), Ca3(PO4)2 with rhombohedral crystallographic structure and Ca/P ratio = 1.5
- (8)
- amorphous calcium phosphates (ACP), CaxHy(PO4)z·nH2O, n = 3 to 4.5, Ca/P ratio = 1.2 to 2.2
- (9)
- calcium-deficient hydroxyapatite (CDHA), Ca10−x(HPO4)x(PO4)6−x(OH)2−x (0 < x ≤ 2) with Ca/P ratio = 1.5 to 1.67
- (10)
- hydroxyapatite (HA) with the formula Ca10(PO4)6(OH)2, Ca/P ratio = 1.67
- (11)
- chloroapatite (ClA) with the formula Ca10(PO4)6(Cl)2, Ca/P ratio = 1.67
- (12)
- carbonated apatite (CO3A), Ca10(PO4)6CO3, known as dahllite, Ca/P ratio = 1.67
- (13)
- fluoroapatite (FA), with the formula Ca10(PO4)6F2 and Ca/P ratio = 1.67
- (14)
- oxyapatite (OA), with the formula Ca10(PO4)6O and Ca/P ratio = 1.67
- (15)
- tetracalcium phosphate (TetCP), Ca4(PO4)2O, known as hilgenstockite, Ca/P ratio = 2.0
2.3.2. Magnesium Orthophosphates
- (1)
- anhydrous trimagnesium phosphate, Mg3(PO4)2 with monoclinic crystal structure, occurs as the natural mineral farringtonite
- (2)
- trimagnesium phosphate octahydrate, Mg3(PO4)2·8H2O with monoclinic structure, occurs as the natural mineral babierrite
- (3)
- trimagnesium phosphate docosahydrate, Mg3(PO4)2·22H2O with triclinic structure, occurs as the natural mineral cattiite
- (4)
- anhydrous dimagnesium phosphate, Mg(HPO4)
- (5)
- dimagnesium phosphate monohydrate, Mg(HPO4)·H2O
- (6)
- dimagnesium phosphate trihydrate, Mg(HPO4)·3H2O with orthorhombic structure, occurs as the natural mineral newberyite
- (7)
- dimagnesium phosphate heptahydrate, Mg(HPO4)·7H2O with monoclinic structure, occurs as the natural mineral phosphorrösslerite
- (8)
- anhydrous monomagnesium phosphate, Mg(H2PO4)2
- (9)
- monomagnesium phosphate dihydrate, Mg(H2PO4)2·2H2O
- (10)
- monomagnesium phosphate tetrahydrate, Mg(H2PO4)2 ·4H2O
- (11)
- magnesium hydroxyphosphate, Mg2(PO4)(OH) with trigonal structure, occurs as the natural mineral holtedahlite
- (12)
- magnesium ammonium phosphate, NH4MgPO4·6H2O with orthorhombic structure, occurs as the natural mineral struvite
- (13)
- magnesium potassium phosphate, KMgPO4·6H2O
2.4. Precipitation of Polyphosphates
3. Results
3.1. Precipitation of Calcium Carbonates
3.2. Precipitation of Magnesium Carbonates
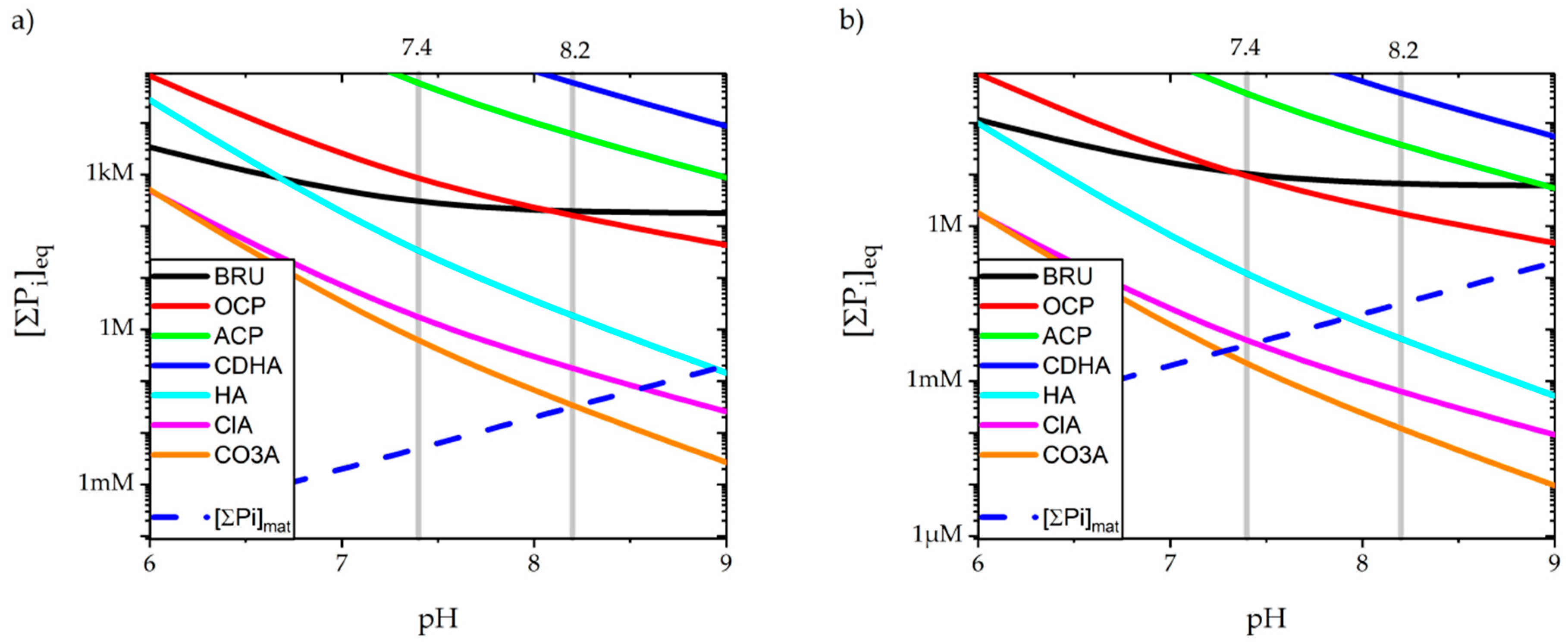
3.3. Precipitation of Calcium Orthophospates
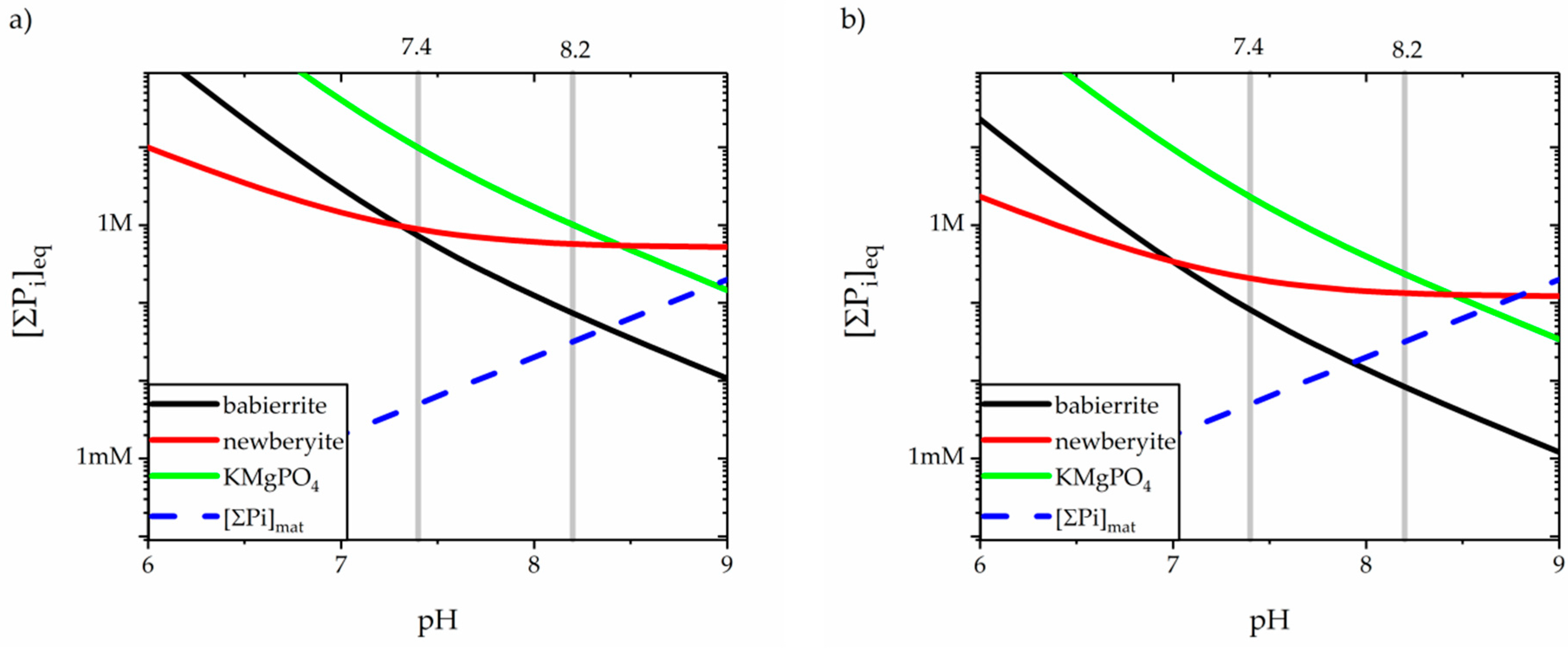
3.4. Precipitation of Magnesium Orthophospates
4. Discussion
4.1. Carbonates in the Ca/Mg System
4.2. Carbonated Apatite in Physiological Solutions
5. Summary and Conclusions
(10 − x)Ca2+ + xHCO3− + (6 − x)HPO42− + (2 − x)H2O ↔ Ca10−x(PO4)6−x(CO3)x(OH)2−x + (8 − x)H+
Ca10−x(PO4)6−x(CO3)x(OH)2−x + 6H2O → (10 − x)Ca2+↑ + xCO2↑ + (6 − x)HPO42− + 8OH−
Author Contributions
Funding
Conflicts of Interest
References
- Santo-Domingo, J.; Demaurex, N. The renaissance of mitochondrial pH. J. Gen. Physiol. 2012, 139, 415–423. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, T.; Evans, M.C.; Meldrum, B.S. Intracellular sites of early calcium accumulation in the rat hippocampus during status epilepticus. Neurosci. Lett. 1982, 30, 329–334. [Google Scholar] [CrossRef]
- Erecińska, M.; Silver, I.A. Relationships between ions and energy metabolism: Celebral calcium movements during ischemia and subsequent recovery. Can. J. Physiol. Pharmacol. 1992, 70, S190–S193. [Google Scholar] [CrossRef] [PubMed]
- Zaidan, E.; Sims, N.R. The calcium content of mitochondria from brain subregions following short-term forebrain ischemia and recirculation in the rat. J. Neurochem. 1994, 63, 1812–1819. [Google Scholar] [CrossRef] [PubMed]
- Fineman, I.; Hovda, D.A.; Smith, M.; Yoshino, A.; Becker, D.P. Concussive brain injury is associated with a prolonged accumulation of calcium: A 45Ca autoradiographic study. Brain Res. 1993, 624, 94–102. [Google Scholar] [CrossRef]
- Nelson, D.L; Cox, M.M. Lehninger Principles of Biochemistry, 6th ed.; Freeman/Worth: New York, USA, 2012; pp. 690–748. [Google Scholar]
- Lehninger, A.L.; Rossi, C.S.; Greenawalt, J.W. Respiration-dependent accumulation of inorganic phosphate and Ca ions by rat liver mitochondria. Biochem. Biophys. Res. Commun. 1963, 10, 444–448. [Google Scholar] [CrossRef]
- Lehninger, A.L. Mitochondria and calcium ion transport. Biochem. J. 1970, 119, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Rossi, C.S.; Lehninger, A.L. Stoichiometric relationships between accumulation of ions by mitochondria and the energy-coupling sites in the respiratory chain. Biochem. Z. 1963, 338, 698–713. [Google Scholar]
- Rossi, C.S.; Lehninger, A.L. Stoichiometry of respiratory stimulation, accumulation of Ca2+ and phosphate and oxidative phosphorylation in rat liver mitochondria. J. Biol. Chem. 1964, 239, 3971–3980. [Google Scholar]
- Lehninger, A.L.; Carafoli, E.; Rossi, C.S. Energy-linked ion movements in mitochondrial systems. Adv. Enzymol. Relat. Areas Mol. Biol. 1967, 29, 259–320. [Google Scholar]
- Brookes, P.S.; Yoon, Y.; Robotham, J.L.; Anders, M.W.; Sheu, S. Calcium, ATP, and ROS: A mitochondrial love-hate triangle. Am. J. Physiol. 2004, 287, 817–833. [Google Scholar] [CrossRef] [PubMed]
- Clapham, D.E. Calcium signaling. Cell 2007, 131, 1047–1058. [Google Scholar] [CrossRef] [PubMed]
- McCormack, J.G.; Denton, R.M. The role of mitochondrial Ca2+ transport and matrix Ca2+ in signal transduction in mammalian tissues. Biochim. Biophys. Acta 1990, 1018, 287–291. [Google Scholar] [CrossRef]
- Gonzales, F.; Karnovsky, M.J. Electron microscopy of osteoblasts in healing fractures of rat bone. J. Biophys. Biochem. Cytol. 1961, 9, 299–316. [Google Scholar] [CrossRef] [PubMed]
- Sutfin, L.V.; Holtrop, M.E.; Ogilvie, R.E. Microanalysis of individual mitochondrial granules with diameters less than 1000 angstroms. Science 1971, 174, 947–949. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.H.; Matthews, J.L. Mitochondrial granules in chondrocytes. Calcif. Tissue Res. 1969, 3, 184–193. [Google Scholar] [CrossRef]
- Landis, W.J.; Paine, M.C.; Glimcher, M.J. Use of acrolein vapors for the anhydrous preparation of bone tissue for electron microscopy. J. Ultrastruct. Res. 1980, 70, 171–180. [Google Scholar] [CrossRef]
- Matthews, J.L. Ultrastructure of calcifying tissues. Am. J. Anat. 1970, 129, 450–457. [Google Scholar] [CrossRef]
- Martin, J.H.; Matthews, J.L. Mitochondrial granules in chondrocytes, osteoblasts and osteocytes: An ultrastructural and microincineration study. Clin. Orthop. Relat. Res. 1970, 68, 273–278. [Google Scholar] [CrossRef]
- Matthews, J.L.; Martin, J.H.; Sampson, H.W.; Kunin, A.S.; Roan, J.H. Mitochondrial granules in the normal and rachitic rat epiphysis. Calcif. Tissue Res. 1970, 5, 91–99. [Google Scholar] [CrossRef]
- Landis, W.J.; Glimcher, M.J. Electron optical and analytical observations of rat growth plate cartilage prepared by ultracryomicrotomy: The failure to detect a mineral phase in matrix vesicles and the identification of heterodispersed particles as the initial solid phase of calcium phosphate deposited in the extracellular matrix. J. Ultrastruct. Res. 1982, 78, 227–268. [Google Scholar] [PubMed]
- Gay, C.; Schraer, H. Frozen thin-sections of rapidly forming bone: Bone cell ultrastructure. Calcif. Tissue Res. 1975, 19, 39–49. [Google Scholar] [CrossRef]
- Landis, W.J.; Glimcher, M.J. Electron diffraction and electron probe microanalysis of the mineral phase of bone tissue prepared by anhydrous techniques. J. Ultrastruct. Res. 1978, 63, 188–223. [Google Scholar] [CrossRef]
- Landis, W.J.; Hauschka, B.T.; Rogerson, C.A.; Glimcher, M.J. Electron microscopic observations of bone tissue prepared by ultracryomicrotomy. J. Ultrastruct. Res. 1977, 59, 185–206. [Google Scholar] [CrossRef]
- Nicholls, D.G.; Chalmers, S. The integration of mitochondrial calcium transport and storage. J. Bioenerg. Biomembr. 2004, 36, 277–281. [Google Scholar] [CrossRef]
- Kristian, T.; Pivovarova, N.B.; Fiskum, G.; Andrews, S.B. Calcium-induced precipitate formation in brain mitochondria: Composition, calcium capacity, and retention. J. Neurochem. 2007, 102, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.S.; Greenawalt, J.W. Microincineration, electron microscopy, and electron diffraction of calcium phosphateloaded mitochondria. J. Cell Biol. 1968, 39, 55–76. [Google Scholar] [CrossRef]
- Chalmers, S.; Nichols, D.G. The relationship between free and total calcium concentration in the matrix of liver and brain mitochondria. J. Biol. Chem. 2003, 278, 19062–19070. [Google Scholar] [CrossRef] [PubMed]
- Dołowy, K. Calcium phosphate buffer formed in the mitochondrial matrix during preconditioning supports ΔpH formation and ischemic ATP production and prolongs cell survival—A hypothesis. Mitochondrion 2019, 47, 210–217. [Google Scholar] [CrossRef]
- Bal, W.; Kurowska, E.; Maret, W. The Final Frontier of pH and the Undiscovered Country Beyond. PLoS ONE 2012, 7, e45832. [Google Scholar] [CrossRef]
- Bose, S.; French, S.; Evans, F.J.; Joubert, F.; Balaban, R.S. Metabolic network control of oxidative phosphorylation. Multiple roles of inorganic phosphate. J. Biol. Chem. 2003, 278, 39155–39165. [Google Scholar] [CrossRef] [PubMed]
- Baysal, K.; Brierley, G.P.; Novgorodov, S.; Jung, D.W. Regulation of the mitochondrial Na+/Ca2+ antiport by matrix pH. Arch. Biochem. Biophys. 1991, 291, 383–389. [Google Scholar] [CrossRef]
- Balut, C.; vandeVen, M.; Despa, S.; Lambrichts, I.; Ameloot, M.; Steels, P.; Smets, I. Measurement of cytosolic and mitochondrial pH in living cells during reversible metabolic inhibition. Kidney Int. 2008, 73, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, A.; Zhang, Y.; Centonze, V.E.; Herman, B. Measurement of Mitochondrial pH In Situ. BioTechniques 2001, 30, 804–815. [Google Scholar] [CrossRef]
- Abad, M.F.C.; Di Benedetto, G.; Magalhães, P.J.; Filippin, L.; Pozzan, T. Mitochondrial pH monitored by a new engineered green fluorescent protein mutant. J. Biol. Chem. 2003, 279, 11521–11529. [Google Scholar] [CrossRef]
- Matsuyama, S.; Llopis, J.; Deveraux, Q.L.; Tsien, R.Y.; Reed, J.C. Changes in intramitochondrial and cytosolic pH: Early events that modulate caspase activation during apoptosis. Nature Cell Biol. 2000, 2, 318–325. [Google Scholar] [CrossRef]
- Poburko, D.; Santo-Domingo, J.; Demaurex, N. Dynamic regulation of the mitochondrial proton gradient during cytosolic calcium elevations. J. Biol. Chem. 2011, 286, 11672–11684. [Google Scholar] [CrossRef]
- Hutson, S. M. pH regulation of mitochondrial branched chain α-keto acid transport and oxidation in rat heart mitochondria. J. Biol. Chem. 1987, 262, 9629–9635. [Google Scholar]
- Ivannikov, M.V.; Macleod, G.T. Mitochondrial free Ca2+ levels and their effects on energy metabolism in Drosophila motor nerve terminals. Biophys. J. 2013, 104, 2353–2361. [Google Scholar] [CrossRef]
- Al-Nassar, I.; Crompton, M. The entrapment of the Ca2+ indicator arsenazo III in the matrix space of rat liver mitochondria by permeabilization and resealing. Na+-dependent and -independent effluxes of Ca2+ in arsenazo III-loaded mitochondria. Biochem. J. 1986, 239, 31–40. [Google Scholar] [CrossRef]
- Samson, E.; Lemaire, G.; Marchand, J.; Beaudoin, J.J. Modeling chemical activity effects in strong ionic solutions. Comp. Mat. Sci. 1999, 15, 285–294. [Google Scholar] [CrossRef]
- Jung, D.W.; Davis, M.H.; Brierley, G.P. Estimation of matrix pH in isolated heart mitochondria using a fluorescent probe. Anal. Biochem. 1989, 178, 348–354. [Google Scholar] [CrossRef]
- Addanki, S.; Cahill, F.D.; Sotos, J.F. Determination of intramitochondrial pH and intramitochondrial- extramitochondrial pH gradient of isolated heart mitochondria by the use of 5,5-dimethyl-,4- oxazolidinedione. J. Biol. Chem. 1968, 243, 2337–2348. [Google Scholar] [PubMed]
- Porcelli, A.M.; Ghelli, A.; Zanna, C.; Pinton, P.; Rizzuto, R.; Rugolo, M. pH difference across the outer mitochondrial membrane measured with a green fluorescent protein mutant. Biochem. Biophys. Res. Commun. 2005, 326, 799–804. [Google Scholar] [CrossRef] [PubMed]
- Llopis, J.; McCaffery, J.M.; Miyawaki, A.; Farquhar, M.G.; Tsien, R.Y. Measurement of cytosolic, mitochondrial, and Golgi pH in single living cells with green fluorescent proteins. Proc. Natl. Acad. Sci. 1998, 95, 6803–6808. [Google Scholar] [CrossRef] [PubMed]
- Greenbaum, N.L.; Wilson, D.F. Role of intramitochondrial pH in the energetics and regulation of mitochondrial oxidative phosphorylation. Biochim. Biophys. Acta Bioenerg. 1991, 1058, 113–120. [Google Scholar] [CrossRef]
- Schoolwerth, A.C.; LaNoue, K.F.; Hoover, W.J. Effect of pH on glutamate efflux from rat kidney mitochondria. Am. J. Physiol. Renal Physiol. 1984, 246, F266–F271. [Google Scholar] [CrossRef]
- Baron, S. Role of mitochondrial Na+ concentration, measured by CoroNa Red, in the protection of metabolically inhibited MDCK cells. J. Am. Soc. Nephrol. 2005, 16, 3490–3497. [Google Scholar] [CrossRef]
- Jung, D.W.; Apel, L.M.; Brierley, G.P. Transmembrane gradients of free Na+ in isolated heart mitochondria estimated using a fluorescent probe. Am. J. Physiol. 1992, 262, C1047–C1055. [Google Scholar] [CrossRef]
- Donoso, P.; Mill, J.G.; O’Neill, S.C.; Eisner, D.A. Fluorescence measurements of cytoplasmic and mitochondrial sodium concentration in rat ventricular myocytes. J. Physiol. 1992, 448, 493–509. [Google Scholar] [CrossRef]
- Augustynek, B.; Wrzosek, A.; Koprowski, P.; Kiełbasa, A.; Bednarczyk, P.; Łukasiak, A.; Dołowy, K.; Szewczyk, A. What we don’t know about mitochondrial potassium channels? Postępy Biochemii 2016, 62, 189–198. [Google Scholar] [PubMed]
- Zoeteweij, J.P.; van de Water, B.; de Bont, H.J.; Nagelkerke, J.F. Mitochondrial K+ as modulator of Ca2+-dependent cytotoxicity in hepatocytes. Novel application of the K+-sensitive dye PBFI (K+-binding benzofuran isophthalate) to assess free mitochondrial K+ concentrations. Biochem. J. 1994, 299, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Costa, A.D.T.; Quinlan, C.L.; Andrukhiv, A.; West, I.C.; Jabůrek, M.; Garlid, K.D. The direct physiological effects of mitoKATP opening on heart mitochondria. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H406–H415. [Google Scholar] [CrossRef] [PubMed]
- Dordick, R.S.; Brierley, G.P.; Garlid, K.D. On the mechanism of A23187-induced potassium efflux in rat liver mitochondria. J. Biol. Chem. 1980, 255, 10299–10305. [Google Scholar] [PubMed]
- Corkey, B.E.; Duszynski, J.; Rich, T.L.; Matschinsky, B.; Williamson, J.R. Regulation of free and bound magnesium in rat hepatocyte and isolated mitochondria. J. Biol. Chem. 1986, 261, 2567–2574. [Google Scholar] [PubMed]
- Jung, D.W.; Brierley, G.P. Matrix magnesium and the permeability of heart mitochondria to potassium ion. J. Biol. Chem. 1986, 261, 6408–6415. [Google Scholar] [PubMed]
- Gout, E.; Rebeille, F.; Douce, R.; Bligny, R. Interplay of Mg2+, ADP, and ATP in the cytosol and mitochondria: Unravelling the role of Mg2+ in cell respiration. Proc. Natl. Acad. Sci. 2014, 111, E4560–E4567. [Google Scholar] [CrossRef]
- Jung, D.W.; Apel, L.; Brierley, G.P. Matrix free magnesium changes with metabolic state in isolated heart mitochondria. Biochemistry 1990, 29, 4121–4128. [Google Scholar] [CrossRef]
- Rutter, G.A.; Osbaldeston, N.J.; McCormack, J.G.; Denton, R.M. Measurement of matrix free Mg2+ concentration in rat heart mitochondria by using entrapped fluorescent probes. Biochem. J. 1990, 271, 627–634. [Google Scholar] [CrossRef]
- Arnaudeau, S.; Kelley, W.L.; Walsh, J.V.; Demaurex, N. Mitochondria recycle Ca2+ to the endoplasmic reticulum and prevent the depletion of neighboring endoplasmic reticulum regions. J. Biol. Chem. 2001, 276, 29430–29439. [Google Scholar] [CrossRef]
- Brandenburger, Y.; Kennedy, E.D.; Python, C.P.; Rossier, M.F.; Vallotton, M.B.; Wollheim, C.B.; Capponi, A.M. Possible role for mitochondrial calcium in angiotensin II- and potassium-stimulated steroidogenesis in bovine adrenal glomerulosa cells. Endocrinology 1996, 137, 5544–5551. [Google Scholar] [CrossRef] [PubMed]
- Schreur, J.H.; Figueredo, V.M.; Miyamae, M.; Shames, D.M.; Baker, A.J.; Camacho, S.A. Cytosolic and mitochondrial [Ca2+] in whole hearts using indo-1 acetoxymethyl ester: effects of high extracellular Ca2+. Biophys. J. 1996, 70, 2571–2580. [Google Scholar] [CrossRef]
- Miyata, H.; Silverman, H.S.; Sollott, S.J.; Lakatta, E.G.; Stern, M.D.; Hansford, R.G. Measurement of mitochondrial free Ca2+ concentration in living single rat cardiac myocytes. Am. J. Physiol. 1991, 261, H1123–H1134. [Google Scholar] [CrossRef]
- Moreno-Sanchez, R.; Hansford, R.G. Dependence of cardiac mitochondrial pyruvate dehydrogenase activity on intramitochondrial free Ca2+ concentration. Biochem. J. 1988, 256, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Allen, S.P.; Stone, D.; McCormack, J.G. The loading of fura-2 into mitochondria in the intact perfused rat heart and its use to estimate matrix Ca2+ under various conditions. J. Mol. Cell. Cardiol. 1992, 24, 765–773. [Google Scholar] [CrossRef]
- Lukács, G.L.; Kapus, A. Measurement of the matrix free Ca2+ concentration in heart mitochondria by entrapped fura-2 and quin2. Biochem. J. 1987, 248, 609–613. [Google Scholar] [CrossRef]
- Davis, M.H.; Altschuld, R.A.; Jung, D.W.; Brierley, G.P. Estimation of intramitochondrial pCa and pH by fura-2 and 2,7 biscarboxyethyl-5(6)-carboxyfluorescein (BCECF) fluorescence. Biochem. Biophys. Res. Commun. 1987, 149, 40–45. [Google Scholar] [CrossRef]
- Jahn, S.C.; Rowland-Faux, L.; Stacpoole, P.W.; James, M.O. Chloride concentrations in human hepatic cytosol and mitochondria are a function of age. Biochem. Biophys. Res. Commun. 2015, 459, 463–468. [Google Scholar] [CrossRef]
- Kielland, J. Individual Activity Coefficients of Ions in Aqueous Solutions. J. Am. Chem. Soc. 1937, 59, 1675–1678. [Google Scholar] [CrossRef]
- Arthurs, G.J.; Sudhakar, M. Carbon dioxide transport. Contin. Educ. Anaesth. Critical Care Pain 2005, 5, 207–210. [Google Scholar] [CrossRef]
- Sun, X.-G.; Hansen, J.E.; Stringer, W.W.; Ting, H.; Wasserman, K. Carbon dioxide pressure-concentration relationship in arterial and mixed venous blood during exercise. J. Appl. Physiol. 2001, 90, 1798–1810. [Google Scholar] [CrossRef] [PubMed]
- Henry, W. Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Phil. Trans. R. Soc. Lond. 1803, 93, 29–274. [Google Scholar]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Plummer, L.N.; Busenberg, E. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90 °C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O. Geochim. Cosmochim. Acta 1982, 46, 1011–1040. [Google Scholar] [CrossRef]
- Dąbrowska, S.; Migdalski, J.; Lewenstam, A. A Breakthrough Application of a Cross-Linked Polystyrene Anion-Exchange Membrane for a Hydrogencarbonate Ion-Selective Electrode. Sensors 2019, 19, 1268. [Google Scholar] [CrossRef]
- Harned, H.S.; Davis, R.D., Jr. The ionization constant of carbonic acid in water and the solubility of carbon dioxide in water and aqueous salt solutions from 0 to 50 °C. J. Am. Chem. Soc. 1943, 65, 2030–2037. [Google Scholar] [CrossRef]
- Harned, H.S.; Bonner, F.T. The first ionization constant of carbonic acid in aqueous solutions of sodium chloride. J. Am. Chem. Soc. 1945, 67, 1026–1031. [Google Scholar] [CrossRef]
- Harned, H.S.; Scholes, S.R. The ionization constant of HCO3- from 0 to 50 °C. J. Am. Chem. Soc. 1941, 63, 1706–1709. [Google Scholar] [CrossRef]
- Ryzhenko, B.N. Determination of dissociation constants of carbonic acid and the degree of hydrolysis of the CO:- and HCO; ions in solutions of alkali carbonates and bicarbonates at elevated temperatures. Geochemistry 1963, 2, 151–164. [Google Scholar]
- Millero, F.J. The thermodynamics of the carbonate system in seawater. Geochim. Cosmochim. Acta 1979, 43, 1651–1661. [Google Scholar] [CrossRef]
- Prieto, F.J.M.; Millero, F.J. The determination of pK1+pK2 in seawater as a function of temperature and salinity. Geochim. Cosmochim. Acta 2002, 66, 2529–2540. [Google Scholar]
- Millero, F. J.; Graham, T.B.; Huang, F.; Bustos-Serrano, H.; Pierrot, D. Dissociation constants of carbonic acid in seawater as a function of salinity and temperature. Marine Chem. 2006, 100, 80–94. [Google Scholar] [CrossRef]
- Flear, C.T.G.; Covington, A.K.; Stoddart, J.C. Bicarbonate or CO2? Arch. Int. Med. 1984, 144, 2285–2287. [Google Scholar] [CrossRef]
- Flear, C.T.G.; Roberts, S.W.; Hayes, S.; Stoddart, J.C.; Covington, A.K. pK1’ and bicarbonate concentration in plasma. Clin. Chem. 1987, 33, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Tibi, L.; Bhattacharya, S.S.; Flear, C.T.G. Variability of pK1’ of human plasma. Clin. Chim. Acta 1982, 121, 15–31. [Google Scholar] [CrossRef]
- Natelson, S.; Nobel, D. Effect of the variation of pK’ of the Henderson-Hasselbalch equation on values obtained for total CO2 calculated from pCO2 and pH values. Clin. Chem. 1977, 23, 767–769. [Google Scholar]
- Masters, P.; Blackburn, M.E.C.; Henderson, M.J.; Barrett, J.F.R.; Dear, P.R.F. Determination of plasma bicarbonate of neonates in intensive care. Clin. Chem. 1988, 34, 1483–1485. [Google Scholar] [CrossRef]
- Rosan, R.; Enlander, D.; Ellis, S. Unpredictable error in calculated bicarbonate homeostasis during pediatric intensive care: The delusion of the fixed pK’. Clin. Chem. 1983, 29, 69–73. [Google Scholar] [CrossRef]
- Kost, G.J.; Trent, J.K.T.; Saeed, D. Indications for measurement of total carbon dioxide in arterial blood. Clin. Chem. 1988, 34, 1650–1652. [Google Scholar] [CrossRef]
- Fresenius, R. Ueber die Löslichkoitsverhältnisse voп einigen bei der quantitativen Analyse als Bestimmungsformen, etc., dienenden Niederschlägen. Ann. Chem. Pharm. 1846, 59, 117–128. [Google Scholar] [CrossRef]
- Lassaigne, J.L. Löslichkeit einiger kohlensauren Salze in kohlensaurem Wasser. Ann. Chem. Pharm. 1848, 68, 253–254. [Google Scholar]
- De Visscher, A.; Vanderdeelen, J. Estimation of the Solubility Constant of Calcite, Aragonite, and Vaterite at 25 °C Based on Primary Data Using the Pitzer Ion Interaction Approach. Monatshefte für Chemie 2003, 134, 769–775. [Google Scholar] [CrossRef]
- Clarkson, J.R.; Price, T.J.; Adams, C.J. Role of metastable phases in the spontaneous precipitation of calcium carbonate. J. Chem. Sot. Faraday Trans. 1992, 88, 243–249. [Google Scholar] [CrossRef]
- Brečević, L.; Nielsen, A.E. Solubility of Calcium Carbonate Hexahydrate. Acta Chim. Scandinav. 1993, 47, 668–673. [Google Scholar] [CrossRef][Green Version]
- Kralj, D.; Brečević, L. Dissolution kinetics and solubility of calcium carbonate monohydrate. Colloids Surf. A: Physicochem. Eng. Aspects 1995, 96, 287–293. [Google Scholar] [CrossRef]
- Hull, H.; Turnbull, A.G. A thermochemical study of monohydrocalcite. Geochim. Cosmochim. Acta 1973, 37, 685–694. [Google Scholar] [CrossRef]
- Brečević, L.; Nielsen, A.E. Solubility of amorphous calcium carbonate. J. Cryst. Growth 1989, 98, 504–510. [Google Scholar] [CrossRef]
- Canterford, J.H.; Tsambourakis, G.; Lambert, B. Some observations on the properties of dypingite, Mg5(CO3)4(OH)2·5H2O, and related minerals. Mineral. Mag. 1984, 48, 437–442. [Google Scholar] [CrossRef]
- Hänchen, M.; Prigiobbe, V.; Baciocchi, R.; Mazzotti, M. Precipitation in the Mg-carbonate system—Effects of temperature and CO2 pressure. Chem. Eng. Sci. 2008, 63, 1012–1028. [Google Scholar] [CrossRef]
- Ropp, R.C. Encyclopedia of the Alkaline Earth Compounds, 1st ed.; Elsevier Science Ltd.: Oxford, UK, 2013; pp. 360–362. [Google Scholar]
- Rheinheimer, V.; Unluer, C.; Liu, J.; Ruan, S.; Pan, J.; Monteiro, P. XPS Study on the Stability and Transformation of Hydrate and Carbonate Phases within MgO Systems. Materials 2017, 10, 75. [Google Scholar] [CrossRef]
- Mineralogy Database. Available online: https://www.mindat.org/ (accessed on 4 February 2020).
- Nashar, B. Barringtonite—A new hydrous magnesium carbonate from Barrington Tops, New South Wales, Australia. Mineral. Mag. J. Mineral. Soc. 1965, 34, 370–372. [Google Scholar] [CrossRef]
- Fitzpatrick, J.J. Pokrovskite: Its possible relationship to mcguinnessite and the problem of excess water. In Proceedings of the 14th Meeting International Mineralogical Association, Abstracts, Stanford, CA, USA, 13–18 July 1986; p. 101. [Google Scholar]
- Gunter, J.R.; Oswald, H.R. Crystal structure of Mg2(OH)2(CO3), deduced from the topotactic thermal decomposition of artinite. J. Solid State Chem. 1977, 21, 211–215. [Google Scholar] [CrossRef]
- Hopkinson, L.; Kristova, P.; Rutt, K.; Cressey, G. Phase transitions in the system MgO–CO2–H2O during CO2 degassing of Mg-bearing solutions. Geochim. Cosmochim. Acta 2012, 76, 1–13. [Google Scholar] [CrossRef]
- Di Tommaso, D.; De Leeuw, N.H. Structure and dynamics of the hydrated magnesium ion and of the solvated magnesium carbonates: Insights from first principles simulations. Phys. Chem. Chem. Phys. 2010, 12, 894–901. [Google Scholar] [CrossRef] [PubMed]
- Saldi, G.D.; Jordan, G.; Schott, J.; Oelkers, E.H. Magnesite growth rates as a function of temperature and saturation state. Geochim. Cosmochim. Acta 2009, 73, 56465657. [Google Scholar] [CrossRef]
- Saldi, G.D.; Schott, J.; Pokrovsky, O.S.; Gautier, Q.; Oelkers, E.H. An experimental study of magnesite precipitation rates at neutral to alkaline conditions and 100–200 °C as a function of pH, aqueous solution composition and chemical affinity. Geochim. Cosmochim. Acta 2012, 83, 93109. [Google Scholar] [CrossRef]
- Sayles, F.L.; Fyfe, W.S. The crystallization of magnesite from aqueous solution. Geochim. Cosmochim. Acta 1973, 37, 87–99. [Google Scholar] [CrossRef]
- Dell, R.; Weller, S.W. The thermal decomposition of nesquehonite MgCO3 ·H2O and magnesium ammonium carbonate MgCO3·(NH4)2CO3·4H2O. Trans. Faraday Soc. 1959, 55, 2203–2220. [Google Scholar] [CrossRef]
- Ming, D.W.; Franklin, W.T. Synthesis and Characterization of Lansfordite and Nesquehonite. Soil Sci. Soc. Am. J. 1985, 49, 1303–1308. [Google Scholar] [CrossRef]
- Davies, P.J.; Bubela, B. The transformation of nesquehonite into hydromagnesite. Chem. Geol. 1973, 12, 289–300. [Google Scholar] [CrossRef]
- Kloprogge, J.T.; Martens, W.N.; Nothdurft, L.; Duong, L.V.; Webb, G.E. Low temperature synthesis and characterization of nesquehonite. J. Mater. Sci. Lett. 2003, 22, 825–829. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Zheng, Y.J.; Ni, Y.W.; Liu, Z.M.; Chen, J.P.; Liang, X.M. Temperature- and pH-dependent morphology and FT-IR analysis of magnesium carbonate hydrates. J. Phys. Chem. B 2006, 110, 12969–12973. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, A.I.; Chimenos, J.M.; Segarra, M.; Fernandez, M.A.; Espiell, F. Procedure to obtain hydromagnesite from a MgO-containing residue. Kinetic study. Ind. Eng. Chem. Res. 2000, 39, 3653–3658. [Google Scholar] [CrossRef]
- Kline, W. D. The solubility of magnesium carbonate (nesquehonite) in water at 25 °C and pressures of carbon dioxide up to one atmosphere. Am. Chem. Soc. J. 1929, 51, 2093–2097. [Google Scholar] [CrossRef]
- Langmuir, D. Stability of Carbonates in the System MgO-CO2-H2O. J. Geol. 1965, 73, 730–754. [Google Scholar] [CrossRef]
- Harrison, A.L.; Mavromatis, V.; Oelkers, E.H.; Bénézeth, P. Solubility of the hydrated Mg-carbonates nesquehonite and dypingite from 5 to 35 °C: Implications for CO2 storage and the relative stability of Mg-carbonates. Chem. Geol. 2019, 504, 123–135. [Google Scholar] [CrossRef]
- Johnston, J. The solubility-product constant of calcium and magnesium carbonates. J. Am. Chem. Soc. 1915, 37, 2001–2020. [Google Scholar] [CrossRef]
- Hemingway, B.S.; Robie, R.A. A calorimetric determination of the standard enthalpies of formation of huntite, CaMg(CO3)4, and artinite, Mg2(OH)2CO3·3H2O, and their standard Gibbs free energies of formation. J. Res. U.S. Geol. Surv. 1972, 1, 535–541. [Google Scholar]
- Cheng, W.; Li, Z. Controlled Supersaturation Precipitation of Hydromagnesite for the MgCl2-Na2CO3 System at Elevated Temperatures: Chemical Modeling and Experiment. Ind. Eng. Chem. Res. 2010, 49, 1964–1974. [Google Scholar] [CrossRef]
- Gautier, Q.; Bénézeth, P.; Mavromatis, V.; Schott, J. Hydromagnesite solubility product and growth kinetics in aqueous solution from 25 to 75 °C. Geochim. Cosmochim. Acta 2014, 138, 1–20. [Google Scholar] [CrossRef]
- Raade, G. Dypingite, a new hydrous basic carbonate of magnesium, from Norway. Am. Mineral. 1970, 55, 1457–1465. [Google Scholar]
- Botha, A.; Strydom, C.A. Preparation of a magnesium hydroxy carbonate from magnesium hydroxide. Hydrometallurgy 2001, 62, 175–183. [Google Scholar] [CrossRef]
- Power, I.M.; Wilson, S.A.; Thom, J.M.; Dipple, G.M.; Southam, G. Biologically induced mineralization of dypingite by cyanobacteria from an alkaline wetland near Atlin, British Columbia, Canada. Geochem. Trans. 2007, 8, 13. [Google Scholar] [CrossRef] [PubMed]
- Larsen, M.J. An investigation of the theoretical background for the stability of the calcium-phosphate salts and their mutual conversion in aqueous solutions. Arch. Oral Biol. 1986, 31, 757–761. [Google Scholar] [CrossRef]
- Fernández, E.; Gil, F.J.; Ginebra, M.P.; Driessens, F.C.M.; Planell, J.A.; Best, S.M. Calcium phosphate bone cements for clinical applications Part I: Solution chemistry. J. Mat. Sci. Mater. Med. 1999, 10, 169–176. [Google Scholar] [CrossRef]
- Dorozhkin, S.V. Calcium orthophosphates. J. Mat. Sci. 2007, 42, 1061–1095. [Google Scholar] [CrossRef]
- Dorozhkin, S.V. Calcium orthophosphates. Biomatter 2011, 1, 121–164. [Google Scholar] [CrossRef]
- Sandberger, F. Ueber Isoklas und Kollophan, zwei neue Phosphate. J. Prakt. Chemie Neue Folge 1870, 2, 125–130. [Google Scholar] [CrossRef]
- Ondruš, P.; Veselovský, F.; Hloušek, J.; Skála, R.; Vavřín, I.; Frýda, J.; Čejka, J.; Gabašová, A. Secondary minerals of the Jáchymov (Joachimsthal) ore district. J. Czech Geol. Soc. 1997, 42, 3–76. [Google Scholar]
- Madsen, H.E.L. Ionic Concentration in Calcium Phosphate Solutions, I. Solutions Saturated with Respect to Brushite or Tetracalcium Monohydrogen Phosphate at 37 °C. Acta Chem. Scand. 1970, 24, 1671–1676. [Google Scholar] [CrossRef][Green Version]
- Sutter, J.R.; McDowell, H.; Brown, W.E. Solubility study of calcium hydrogen phosphate. Ion-pair formation. Inorg. Chem. 1971, 10, 1638–1643. [Google Scholar] [CrossRef]
- Tung, M.S.; Eidelman, N.; Sieck, B.; Brown, W.E. Octacalcium phosphate solubility product from 4 to 37 °C. J. Res. Nat. Bur. Stand. 1988, 93, 613–624. [Google Scholar] [CrossRef]
- Shyu, L.J.; Perrez, L.; Zawacky, S.J.; Heughebaert, J.C.; Nancollas, G.H. The Solubility of Octacalcium Phosphate at 37 °C in the System Ca(OH)2-H3PO4-KNO3-H2O. J. Dent. Res. 1983, 62, 398–400. [Google Scholar] [CrossRef]
- Christoffersen, M.R.; Christoffersen, J.; Kibalczyc, W. Apparent solubilities of two amorphous calcium phosphates and of octacalcium phosphate in the temperature range 30–42 °C. J. Cryst. Growth 1990, 106, 349–354. [Google Scholar] [CrossRef]
- Ito, A.; Maekawa, K.; Tsutsumi, S.; Ikazaki, F.; Tateishi, T. Solubility product of OH-carbonated hydroxyapatite. J. Biomed. Mater. Res. 1997, 36, 522–528. [Google Scholar] [CrossRef]
- Narasaraju, T.S.B.; Rao, K.K.; Rai, U.S. Determination of solubility products of hydroxylapatite, chlorapatite, and their solid solutions. Can. J. Chem. 1979, 57, 1919–1922. [Google Scholar] [CrossRef]
- Moreno, E.C.; Kresak, M.; Zahradnik, R.T. Physicochemical Aspects of Fluoride-Apatite Systems Relevant to the Study of Dental Caries. Caries Res. 1977, 11, 142–171. [Google Scholar] [CrossRef]
- Schrödter, K.; Bettermann, G.; Staffel, T.; Wahl, F.; Klein, T.; Hofmann, T. Phosphoric Acid and Phosphates. In Ullmann’s Encyclopedia of Industrial Chemistry, 7th ed.; Wiley-VCH: Weinheim, Germany, 2012; Volume 26, pp. 679–712. [Google Scholar]
- Dudenhoefer, R.; Messing, G.L.; Brown, P.W.; Johnson, G.G. Synthesis and characterization of monomagnesium phosphate tetrahydrate. J. Cryst. Growth 1992, 125, 121–126. [Google Scholar] [CrossRef]
- Taylor, A.W.; Frazier, A.W.; Gurney, E.L.; Smith, J.P. Solubility products of di- and trimagnesium phosphates and the dissociation of magnesium phosphate solutions. Trans. Faraday Soc. 1963, 59, 1585–1589. [Google Scholar] [CrossRef]
- Norenberg, M. Oxidative and nitrosative stress in ammonia neurotoxicity. Hepatology 2003, 37, 245–248. [Google Scholar] [CrossRef]
- Felipo, V.; Butterworth, R.F. Mitochondrial dysfunction in acute hyperammonemia. Neurochem. Int. 2002, 40, 487–491. [Google Scholar] [CrossRef]
- Niknahad, H.; Jamshidzadeh, A.; Heidari, R.; Zarei, M.; Ommati, M.M. Ammonia-induced mitochondrial dysfunction and energy metabolism disturbances in isolated brain and liver mitochondria, and the effect of taurine administration: Relevance to hepatic encephalopathy treatment. Clin. Exp. Hepatol. 2017, 3, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.C.K; Cooper, A.J.L. Neurotoxicity of ammonia and fatty acids: Differential inhibition of mitochondrial dehydrogenases by ammonia and fatty acyl coenzyme a derivatives. Neurochem. Res. 1991, 16, 795–803. [Google Scholar] [CrossRef] [PubMed]
- Hird, F.J.R.; Marginson, M.A. Formation of Ammonia from Glutamate by Mitochondria. Nature 1964, 201, 1224–1225. [Google Scholar] [CrossRef] [PubMed]
- Beavon, J.; Heatley, N.G. The occurrence of struvite (magnesium ammonium phosphate hexahydrate) in microbial cultures. J. Gen. Microbiol. 1962, 31, 167–169. [Google Scholar] [CrossRef] [PubMed]
- Rivadeneyra, M.A.; Ramos-Cormenzana, A.; García-Cervigón, A. Bacterial formation of struvite. Geomicrobiol. J. 1983, 3, 151–163. [Google Scholar] [CrossRef]
- Holt, L.E.; Pierce, J.A.; Kajdi, C.N. The solubility of the phosphates of strontium, barium, and magnesium and their relation to the problem of calcification. J. Colloid Sci. 1954, 9, 409–426. [Google Scholar] [CrossRef]
- Racz, G.J.; Soper, R.J. Solubility of dimagnesium phosphate trihydrate and dimagnesium phosphate. Can. J. Soil Sci. 1968, 48, 265–269. [Google Scholar] [CrossRef][Green Version]
- Tabor, H.; Hastings, A.B. The ionization constant of secondary magnesium phosphate. Biol. Chem. 1943, 148, 627–632. [Google Scholar]
- Verbeeck, R.M.H.; De Bruyne, P.A.M.; Driessens, F.C.M.; Verbeek, F. Solubility of magnesium hydrogen phosphate trihydrate and ion-pair formation in the system magnesium hydroxide-phosphoric acid-water at 25 °C. Inorg. Chem. 1984, 23, 1922–1926. [Google Scholar] [CrossRef]
- Taylor, A.W.; Frazier, A.W.; Gurney, E.L. Solubility products of magnesium ammonium and magnesium potassium phosphates. Trans. Faraday Soc. 1963, 59, 1580–1584. [Google Scholar] [CrossRef]
- Crosby, C.H.; Bailey, J. The role of microbes in the formation of modern and ancient phosphatic mineral deposits. Front. Microbiol. 2012, 3, e241–e247. [Google Scholar] [CrossRef] [PubMed]
- Van Wazer, J.R.; Campanella, D.A. Structure and properties of the condensed phosphates. IV. Complex ion formation in polyphosphate solutions. J. Am. Chem. Soc. 1950, 72, 655–663. [Google Scholar] [CrossRef]
- Kulakovskaya, T.V.; Lichko, L.P.; Vagabov, V.M.; Kulaev, I.S. Inorganic polyphosphates in mitochondria. Biochemistry (Moscow) 2010, 75, 825–831. [Google Scholar] [CrossRef] [PubMed]
- Kornberg, A.; Rao, N.N.; Ault-Riché, D. Inorganic Polyphosphate: A Molecule of Many Functions. Ann. Rev. Biochem. 1999, 68, 89–125. [Google Scholar] [CrossRef] [PubMed]
- Beauvoit, B.; Rigoulet, M.; Guerin, B.; Canioni, P. Polyphosphates as a source of high energy phosphates in yeast mitochondria: A31P NMR study. FEBS Lett. 1989, 252, 17–21. [Google Scholar] [CrossRef]
- Mansurova, S. E. Inorganic pyrophosphate in mitochondrial metabolism. Biochim. Biophys. Acta (BBA) Bioenerg. 1989, 977, 237–247. [Google Scholar] [CrossRef]
- Pavlov, E.; Aschar-Sobbi, R.; Campanella, M.; Turner, R.J.; Gómez-García, M.R.; Abramov, A.Y. Inorganic Polyphosphate and Energy Metabolism in Mammalian Cells. J. Biol. Chem. 2010, 285, 9420–9428. [Google Scholar] [CrossRef]
- Bobtelsky, M.; Kertes, S. The polyphosphates of calcium, strontium, barium and magnesium: Their complex character, composition and behaviour. J. Appl. Chem. 1954, 4, 419–429. [Google Scholar] [CrossRef]
- Omelon, S.; Grynpas, M. Polyphosphates affect biological apatite nucleation. Cells Tissues Organs 2011, 194, 171–175. [Google Scholar] [CrossRef]
- Docampo, R.; de Souza, W.; Miranda, K.; Rohloff, P.; Moreno, S.N.J. Acidocalcisomes–conserved from bacteria to man. Nat. Rev. Microbiol. 2005, 3, 251–261. [Google Scholar] [CrossRef] [PubMed]
- Fleisch, H.; Neuman, W.F. Mechanisms of calcification: Role of collagen, polyphosphates, and phosphatase. Am. J. Physiol. 1961, 200, 1296–1300. [Google Scholar] [CrossRef] [PubMed]
- Francis, M. The inhibition of calcium hydroxyapatite crystal growth by polyphosphonates and polyphosphates. Calcif. Tissue Res. 1969, 3, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Bunker, B.C.; Arnold, G.W.; Wilder, J.A. Phosphate glass dissolution in aqueous solutions. J. Non-Cryst. Solids 1984, 64, 291–316. [Google Scholar] [CrossRef]
- Omelon, S.; Ariganello, M.; Bonucci, E.; Grynpas, M.; Nanci, A. A Review of Phosphate Mineral Nucleation in Biology and Geobiology. Calcif. Tissue Int. 2013, 93, 382–396. [Google Scholar] [CrossRef]
- Reusch, R. N. Poly- -hydroxybutyrate/Calcium Polyphosphate Complexes in Eukaryotic Membranes. Exp. Biol. Med. 1989, 191, 377–381. [Google Scholar] [CrossRef]
- Pavlov, E.; Zakharian, E.; Bladen, C.; Diao, C.T.M.; Grimbly, C.; Reusch, R.N.; French, R.J. A large, voltage-dependent channel, isolated from mitochondria by water-free chloroform extraction. Biophys. J. 2005, 88, 2614–2625. [Google Scholar] [CrossRef]
- Reusch, R. N. Transmembrane Ion Transport by Polyphosphate/Poly-(R)-3-hydroxybutyrate Complexes. Biochemistry (Moscow) 2000, 65, 280–295. [Google Scholar]
- Vagabov, V.M.; Trilisenko, L.V.; Kulaev, I.S. Dependence of inorganic polyphosphate chain length on the orthophosphate content in the culture medium of the yeast Saccharomyces cerevisae. Biochemistry 2000, 65, 349–354. [Google Scholar]
- Nancollas, G.H. The mechanism of precipitation of biological minerals. The phosphates, oxalates and carbonates of calcium. Croat. Chim. Acta 1983, 56, 741–752. [Google Scholar]
- Brečevič, L.; Füredi-Milhofer, H. Precipitation of calcium phosphates from electrolyte solutions. Calcif. Tissue Res. 1972, 10, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Söhnel, O.; Mullin, J.W. Precipitation of calcium carbonate. J. Crystal Growth 1982, 60, 239–250. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Bots, P.; Roncal-Herrero, T.; Benning, L.G. The role of Mg in the crystallization of monohydrocalcite. Geochim. Cosmochim. Acta 2014, 127, 204–220. [Google Scholar] [CrossRef]
- Kitamura, M. Crystallization and Transformation Mechanism of Calcium Carbonate Polymorphs and the Effect of Magnesium Ion. J. Colloid Interface Sci. 2001, 236, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Bots, P.; Benning, L.G.; Rodriguez-Blanco, J.D.; Roncal-Herrero, T.; Shaw, W. Mechanistic Insights into the Crystallization of Amorphous Calcium Carbonate (ACC). Cryst. Growth Des. 2012, 12, 3806–3814. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Bots, P.; Roncal-Herrero, T.; Benning, L.G. The role of pH and Mg on the stability and crystallization of amorphous calcium carbonate. J. Alloys Compd. 2012, 536, S477–S479. [Google Scholar] [CrossRef]
- Nishiyama, R.; Munemoto, T.; Fukushi, K. Formation condition of monohydrocalcite from CaCl2–MgCl2–Na2CO3 solutions. Geochim. Cosmochim. Acta 2013, 100, 217–231. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Benning, L.G. The realtime kinetics and mechanisms of nucleation and growth of dolomite from solution. Geochim. Cosmochim. Acta 2009, 73, A1111. [Google Scholar]
- Bischoff, J.L.; Fitzpatrick, J.A.; Rosenbauer, R.J. The solubility and stabilization of ikaite (CaCO3.6H2O) from 0° to 25 °C. J. Geol. 1992, 101, 21–33. [Google Scholar] [CrossRef]
- Njegić-Džakula, B.; Brečević, L.; Falini, G.; Kralj, D. Kinetic Approach to Biomineralization: Interactions of Synthetic Polypeptides with Calcium Carbonate Polymorphs. Croatica Chemica Acta 2011, 84, 301–314. [Google Scholar] [CrossRef]
- Cailleau, P.; Dragone, D.; Girou, A.; Humbert, L.; Jacquin, C.; Roques, H. Etude expérimentale de la précipitation des carbonates de calcium en présence de l’ion magnesium. Bull. Soc. Fran. Mineral. Crystallogr. 1977, 100, 81–88. [Google Scholar] [CrossRef]
- Rivadeneyra, M.A.; Delgado, R.; Quesada, E.; Ramos-Cormenzana, A. Precipitation of calcium carbonate by Deleya halophila in media containing NaCl as sole salt. Curr. Microbiol. 1991, 22, 185–190. [Google Scholar] [CrossRef]
- White, T.J.; Dong, Z.L. Structural derivation and crystal chemistry of apatite. Acta Cryst. B 2003, 59, 1–16. [Google Scholar] [CrossRef] [PubMed]
- McArthur, J.M. Francolite geochemistry—compositional controls during formation, diagenesis, metamorphism and weathering. Geochim. Cosmochim. Acta 1985, 49, 23–35. [Google Scholar] [CrossRef]
- Benmore, R.A.; Coleman, M.L.; McArthur, J.M. Origin of is sedimentary francolite from its sulphur and carbon isotope composition. Nature 1983, 302, 516–518. [Google Scholar] [CrossRef]
- Ferguson, J.F.; McCarty, P.L. Effects of carbonate and magnesium on calcium phosphate precipitation. Environ. Sci. Technol. 1971, 5, 534–540. [Google Scholar] [CrossRef]
- Van der Houwen, J.A.M.; Cressey, G.; Cressey, B.A.; Valsami-Jones, E. The effect of organic ligands on the crystallinity of calcium phosphate. J. Cryst. Growth 2003, 249, 572–583. [Google Scholar] [CrossRef]
- Suchanek, W.J.; Byrappa, K.; Shuk, P.; Riman, R.E.; Janas, V.F.; Tenhuisen, K.S. Mechanochemical-hydrothermal synthesis of calcium phosphate powders with coupled magnesium and carbonate substitution. J. Solid State Chem. 2004, 17, 793–799. [Google Scholar] [CrossRef]
- Fleet, M.E.; Liu, X. Coupled substitution of type A and B carbonate in sodium-bearing apatite. Biomaterials 2007, 28, 916–926. [Google Scholar] [CrossRef]
- LeGeros, R.Z.; Trautz, O.R.; Klein, E.; LeGeros, J.P. Two types of carbonate substitution in the apatite structure. Experientia 1969, 25, 5–7. [Google Scholar] [CrossRef]
- Rey, C.; Collins, B.; Goehl, T.; Dickson, R.I.; Glimcher, M.J. The carbonate environment in bone mineral: A resolution-enhanced fourier transform infrared spectroscopy study. Calcif. Tissue Int. 1989, 45, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Trautz, O.R. Crystallographic studies of calcium carbonate phosphate. Ann. N. Y. Acad. Sci. 1960, 85, 145–160. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Harris, W.G.; Josan, M.S.; Nair, V.D. Inhibition of calcium phosphate precipitation under environmentally-relevant conditions. Sci. Total Environ. 2007, 383, 205–215. [Google Scholar] [CrossRef]
- Legros, R.; Balmain, N.; Bonel, G. Age-related changes in mineral of rat and bovine cortical bone. Calcif. Tissue Int. 1987, 41, 137–144. [Google Scholar] [CrossRef]
- Wu, Y.; Glimcher, M.J.; Rey, C.; Ackerman, J.L. A unique protonated phosphate group in bone mineral not present in synthetic calcium phosphates. Identification by phosphorus-31 solid state NMR spectroscopy. J. Mol. Biol. 1994, 244, 423–435. [Google Scholar] [CrossRef]
- Rey, C.; Shimizu, M.; Collins, B.; Glimcher, M.J. Resolution-enhanced Fourier transform infrared spectroscopy study of the environment of phosphate ions in the early deposits of a solid phase of calcium phosphate in bone and enamel, and their evolution with age. I: Investigations in the ν4 PO4 domain. Calcif. Tissue Int. 1990, 46, 384–394. [Google Scholar] [CrossRef]
- Montel, G.; Bonel, G.; Heughebaert, J.C.; Trombe, J.C.; Rey, C. New concepts in the composition, crystallization and growth of the mineral component of calcified tissues. J. Cryst. Growth 1981, 53, 74–99. [Google Scholar] [CrossRef]
- Rey, C.; Combes, C.; Drouet, C.; Sfihi, H. Chemical Diversity of Apatites. Adv. Sci. Tech. 2006, 49, 27–36. [Google Scholar] [CrossRef]
- Combes, C.; Cazalbou, S.; Rey, C. Apatite Biominerals. Minerals 2016, 6, 34. [Google Scholar] [CrossRef]
- Cazalbou, S.; Eichert, D.; Ranz, X.; Drouet, C.; Combes, C.; Harmand, M.F.; Rey, C. Ion exchanges in apatites for biomedical application. J. Mater. Sci. Mater. Med. 2005, 16, 405–409. [Google Scholar] [CrossRef]
- Eichert, D.; Combes, C.; Drouet, C.; Rey, C. Formation and evolution of hydrated surface layers of apatites. Key Eng. Mater. 2005, 284–286, 3–6. [Google Scholar] [CrossRef]
- Busenberg, E.; Plummer, L.N. Thermodynamics of magnesian calcite solid-solutions at 25 °C and 1 atm total pressure. Geochim. Cosmochim. Acta 1989, 53, 1189–1208. [Google Scholar] [CrossRef]
- Bischoff, W.D.; Mackenzie, F.T.; Bishop, F.C. Stabilities of synthetic magnesian calcites in aqueous solution: Comparison with biogenic materials. Geochim. Cosmochim. Acta 1987, 51, 1413–1423. [Google Scholar] [CrossRef]
- Bertram, M.A.; Mackenzie, F.T.; Bishop, F.C.; Bischoff, W.D. Influence of temperature on the stability of magnesian calcite. Am. Mineral. 1991, 76, 1889–1896. [Google Scholar]
- Tribble, J.S.; Arvidson, R.S.; Lane, M.; Mackenzie, F.T. Crystal chemistry, and thermodynamic and kinetic properties of calcite, dolomite, apatite, and biogenic silica: Applications to petrologic problems. Sediment. Geol. 1995, 95, 11–37. [Google Scholar] [CrossRef]
- Michałowski, T.; Asuero, A.G. Thermodynamic Modelling of Dolomite Behavior in Aqueous Media. J. Thermodyn. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Moomaw, A.S.; Maguire, M.E. The unique nature of Mg2+ channels. Physiology (Bethesda) 2008, 23, 275–285. [Google Scholar] [CrossRef]
- Usdovski, E. Synthesis of dolomite and geochemical implications. In Dolomites: A Volume in Honour of Dolomieu; Purser, B.H., Tucker, M.E., Zenger, D.H., Eds.; Blackwell Sci. Publ.: Oxford, UK, 1994; pp. 345–360. [Google Scholar]
- Sherman, L.A.; Barak, P. Solubility and dissolution kinetics of dolomite in Ca-Mg-HCO3/CO3 solutions at 25 °C and 0.1 MPa carbon dioxide. Soil Sci. Soc. Am. J. 2000, 64, 1959–1968. [Google Scholar] [CrossRef]
- Pabst, A. The Crystallography Structure of Eitelite, Na2Mg(CO3)2. Am. Miner. 1973, 58, 211–217. [Google Scholar]
- Effenberger, H. Crystal-structure and infrared-absorption spectrum of synthetic monohydrocalcite, CaCO3.H2O. Monatsh. Chem. 1981, 112, 899–909. [Google Scholar] [CrossRef]
- Swainson, I. P. The structure of monohydrocalcite and the phase composition of the beachrock deposits of Lake Butler and Lake Fellmongery, South Australia. Am. Mineral. 2008, 93, 1014–1018. [Google Scholar] [CrossRef]
- Bachra, B.N.; Trautz, O.R.; Simon, S.L. Precipitation of calcium carbonates and phosphates. I. Spontaneous precipitation of calcium carbonates and phosphates under physiological conditions. Arch. Biochem. Biophys. 1963, 103, 124–138. [Google Scholar] [CrossRef]
- Ferguson, J.F.; McCarty, P.L. The Precipitation of PhosDhates from Fresh Waters and Waste Waters; Tech Report No. 120; Department of Civil Engineering, Stanford University: Stanford, CA, USA, 1969. [Google Scholar]
- Kibalczyc, W.; Christoffersen, J.; Christoffersen, M.R.; Zielenkiewicz, A.; Zielenkiewicz, W. The effect of magnesium-ions on the precipitation of calcium phosphates. J. Cryst. Growth 1990, 106, 355–366. [Google Scholar] [CrossRef]
- Bachra, B.N.; Trautz, O.R.; Simon, S.L. Precipitation of calcium carbonates and phosphates—III. Arch. Oral Biol. 1965, 10, 731–738. [Google Scholar] [CrossRef]
- Mekmene, O.; Quillard, S.; Rouillon, T.; Bouler, J.-M.; Piot, M.; Gaucheron, F. Effects of pH and Ca/P molar ratio on the quantity and crystalline structure of calcium phosphates obtained from aqueous solutions. Dairy Sci. Technol. EDP Sci./Springer 2009, 89, 301–316. [Google Scholar] [CrossRef]
- Terpstra, R.A.; Driessens, F.C.M. Magnesium in tooth enamel and synthetic apatites. Calcif. Tissue Int. 1986, 39, 348–354. [Google Scholar] [CrossRef]
- Martens, C.S.; Harriss, R.C. Inhibition of apatite precipitation in the marine environment by magnesium ions. Geochim. Cosmochim. Acta 1970, 34, 621–625. [Google Scholar] [CrossRef]
- Termine, J.D.; Conn, K.M. Inhibition of apatite formation by phosphorylated metabolites and macromolecules. Calcif. Tiss. Res. 1976, 22, 149–157. [Google Scholar] [CrossRef]
- Posner, A.S.; Betts, F.; Blumenthal, N.C. Role of ATP and Mg in the stabilization of biological and synthetic amorphous calcium phosphates. Calcif. Tissue Res. 1977, 22, 208–212. [Google Scholar] [CrossRef]
- Rey, C.; Trombe, J.C.; Montel, G. Some features of the incorporation of oxygen in different oxidation states in the apatitic lattice—III Synthesis and properties of some oxygenated apatites. J. Inorg. Nucl. Chem. 1978, 40, 27–30. [Google Scholar] [CrossRef]
- Pan, Y.; Fleet, M.E. Compositions of the Apatite-Group Minerals: Substitution Mechanisms and Controlling Factors. Rev. Mineral. Geochem. 2002, 48, 13–49. [Google Scholar] [CrossRef]
- Mason, A.Z.; Nott, J.A. The role of intracellular biomineralized granules in the regulation and detoxification of metals in gastropods with special reference to the marine prosobranch Littorina littorea. Aquat. Toxicol. 1981, 1, 239–256. [Google Scholar] [CrossRef]
- Nott, J.A.; Langston, W.J. Cadmium and the phosphate granules in Littorina littorea. J. Mar. Biol. Assoc. UK 1989, 69, 219–227. [Google Scholar] [CrossRef]
- Bonucci, E.; Derenzini, M.; Marinozzi, V. The organic-inorganic relationship in calcified mitochondria. J. Cell. Biol. 1973, 59, 185–211. [Google Scholar] [CrossRef]
- Baartscheer, A.; Schumacher, C.A.; Coronel, R.; Fiolet, J.W.T. The driving force of the Na+/Ca2+-exchanger during metabolic inhibition. Front. Physiol. 2011, 2, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, E. J.; Halestrap, A. P. Mitochondrial non-specific pores remain closed during cardiac ischaemia, but open upon reperfusion. Biochem. J. 1995, 307, 93–98. [Google Scholar] [CrossRef]
- Bernardi, P. Mitochondrial transport of cations: Channels, exchangers, and permeability transition. Physiol. Rev. 1999, 79, 1127–1155. [Google Scholar] [CrossRef]
- Meldrum, D.R.; Cleveland, J.C.J.; Mitchell, M.B.; Sheridan, B.C.; Gamboni-Robertson, F.; Harken, A.H.; Banerjee, A. Protein kinase C mediates Ca2+-induced cardioadaptation to ischemia-reperfusion injury. Am. J. Physiol. 1996, 271, R718–R726. [Google Scholar] [CrossRef]
- Miyawaki, H.; Zhou, X.; Ashraf, M. Calcium preconditioning elicits strong protection against ischemic injury via protein kinase C signaling pathway. Circ. Res. 1996, 79, 137–146. [Google Scholar] [CrossRef]




| Formula | Activity Product (Q) | Solubility Product, Ksp at 37 °C | Ref. | |
|---|---|---|---|---|
| Calcite | CaCO3 | {Ca2+} {CO32−} | 3.31 × 10−9 * | [75] |
| 3.27 × 10−9 to 4.02 × 10−9 | [93] | |||
| Aragonite | CaCO3 | {Ca2+} {CO32−} | 4.57 × 10−9 * | [75] |
| 4.67 × 10−9 to 5.41 × 10−9 | [93] | |||
| Varietite | CaCO3 | {Ca2+} {CO32−} | 1.23 × 10−8 * | [75] |
| 1.18 × 10−8 to 1.84 × 10−8 | [93] | |||
| Ikaite | CaCO3·6H2O | {Ca2+} {CO32−} | 2.40 × 10−7 * | [94] |
| 3.50 × 10−7 | [95] | |||
| Monohydro-calcite | CaCO3·H2O | {Ca2+} {CO32−} | 7.09 × 10−8 * | [96] |
| 2.51 × 10−8 | [97] | |||
| ACC | CaCO3·nH2O | {Ca2+} {CO32−} | 9.09 × 10−7 * | [94] |
| (n < 1) | 3.98 × 10−7 | [98] |
| Formula | Activity Product (Q) | Solubility Product, Ksp at 25 °C | Ref. | |
|---|---|---|---|---|
| Nesquehonite | MgCO3·3H2O | {Mg2+} {CO32−} | 2.38 × 10−6 | [99] |
| 1.10 × 10−5 | [118] | |||
| 2.57 × 10−6 | [119] | |||
| 5.37 × 10-6 | [120] | |||
| 4.57 × 10−6 *† | [120] | |||
| 5.90 × 10−5 | [121] | |||
| Artinite | Mg2CO3(OH)2·3H2O | {Mg2+}2 {CO32−} {OH−}2 | 6.31 × 10−18 | [119] |
| 7.76 × 10−18 * | [122] | |||
| Hydromagnesite | Mg5(CO3)4(OH)2·4H2O | {Mg2+}5 {CO32−}4 {OH−}2 | 6.31 × 10−31 | [119] |
| 1.25 × 10−32 | [123] | |||
| 3.16 × 10−33 *† | [123] | |||
| 8.32 × 10−38 | [124] | |||
| Dypingite | Mg5(CO3)4(OH)2·nH2O | {Mg2+}5 {CO32−}4 {OH−}2 | 1.12 × 10−35 | [120] |
| (n = 5 or 8) | 9.12 × 10−37 *† | [120] |
| Formula | Activity Product (Q) | Solubility Product, Ksp at 37 °C | Ref. | |
|---|---|---|---|---|
| BRU | CaHPO4 | {Ca2+} {HPO42−} | 2.34 × 10−7 * | [129] |
| 2.26 × 10−7 | [134] | |||
| 0.92 × 10−7 | [135] | |||
| OCP | Ca8(HPO4)2(PO4)4 | {Ca2+}8 {H+}2 {PO43−}6 | 1.25 × 10−96 * | [129] |
| 1.20 × 10−97 | [134] | |||
| 3.98 × 10−98 | [136] | |||
| 2.51 × 10−99 | [137] | |||
| ACP | CaxHy(PO4)z | {Ca2+}x {H+}y {PO43−}z | 2.0 × 10−26 *† | [130] |
| {Ca2+}3 {PO43−}2 | 2.0 × 10−33–1.6 × 10−25 | [29] | ||
| {Ca2+} {H+}0.22 {PO43−}0.74 | 2.3 × 10−11, 3.2 × 10−12 § | [138] | ||
| CDHA | Ca10-x(HPO4)x(PO4)6-x(OH)2-x | {Ca2+}10−x {H+}x {PO43−}6 {OH−}2−x | ~7.94 × 10−86 * | [130] |
| HA | Ca10(PO4)6(OH)2 | {Ca2+}10 {PO43−}6 {OH−}2 | 1.00 × 10−118 | [29] |
| 6.31 × 10−118 * | [129] | |||
| 2.00 × 10−119 ‡ | [139] | |||
| 2.51 × 10−111 | [140] | |||
| 5.42 × 10−119 | [141] | |||
| ClA | Ca10(PO4)6Cl2 | {Ca2+}10 {PO43−}6 {Cl−}2 | 3.98 × 10−116 * | [140] |
| CO3A | Ca10(PO4)6CO3 | {Ca2+}10 {PO43−}6 {CO32−} | 1.58 × 10−103 *‡ | [139] |
| Formula | Activity Product (Q) | Solubility Product, Ksp at 38 °C | Ref. | |
|---|---|---|---|---|
| Babierrite | Mg3(PO4)2·8H2O | {Mg2+}3 {PO43−}2 | 6.31 × 10−28 | [152] |
| 5.37 × 10−26 *†‡ | [144] | |||
| 2.00 × 10−26 § | [153] | |||
| Newberyite | Mg(HPO4)·3H2O | {Mg2+} {HPO42−} | 3.47 × 10−5 | [154] |
| 1.78 × 10−6 *† | [144] | |||
| 2.40 × 10−6 ‡ | [144] | |||
| 1.78 × 10−6 § | [155] | |||
| 1.48 × 10−6 § | [153] | |||
| Magnesium potassium phosphate | KMgPO4·6H2O | {K+} {Mg2+} {PO43−} | 2.4 × 10−11 § | [156] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasielec, J.J.; Filipek, R.; Dołowy, K.; Lewenstam, A. Precipitation of Inorganic Salts in Mitochondrial Matrix. Membranes 2020, 10, 81. https://doi.org/10.3390/membranes10050081
Jasielec JJ, Filipek R, Dołowy K, Lewenstam A. Precipitation of Inorganic Salts in Mitochondrial Matrix. Membranes. 2020; 10(5):81. https://doi.org/10.3390/membranes10050081
Chicago/Turabian StyleJasielec, Jerzy J., Robert Filipek, Krzysztof Dołowy, and Andrzej Lewenstam. 2020. "Precipitation of Inorganic Salts in Mitochondrial Matrix" Membranes 10, no. 5: 81. https://doi.org/10.3390/membranes10050081
APA StyleJasielec, J. J., Filipek, R., Dołowy, K., & Lewenstam, A. (2020). Precipitation of Inorganic Salts in Mitochondrial Matrix. Membranes, 10(5), 81. https://doi.org/10.3390/membranes10050081