3.1. Assessing Membrane–Electrode Interface Impedance
To measure the resistance associated with the electrode–membrane interface, area specific resistance was assessed for a series of N115 membranes. Flow cells with 9 cm
2 flow-through plates and as-received 39AA electrodes were used. A series of cells with one, two, three, and four layers of N115 ion-exchange membranes were assembled. In addition, area specific resistance was assessed for an identical cell architecture assembled with no membrane. This enabled quantification of the impedance associated with electrodes, electrolytes, flow plates, current collectors, and related contact resistances.
Figure 3 includes the area-specific resistance associated with the VRFBs assembled with various vanadium redox flow battery configurations.
The no-membrane architecture included as-received carbon paper electrodes (one layer, 39 AA) along with flow-through flow plates and current collectors. The solutions of aqueous sulfuric acid (3.3 M) and enriched vanadium solutions (1.5M V(IV), 3.3M sulfuric acid) were circulated through the cell and the area specific resistance was assessed for this case. Similar experiments were repeated for cell architectures including one, two, three, and four layers of N115. The ASR associated with each case has been summarized in
Table 1. In
Table 1, the ASR values for the cells with membranes have been listed correcting from the ASR associated with the no-membrane architecture.
To quantify the impedance associated with the electrode–membrane interface, as shown in
Figure 3, the ASR values have been plotted for different configuration of membranes with various flowing electrolytes. A linear trendline has been plotted for the data series and the
y-axis intercept has been evaluated for the impedance associated with the electrode–membrane interface. As shown in
Figure 3, for solution including aqueous sulfuric acid (3.3 M), the electrode–membrane impedance was ~0.008 ohm·cm
2 and for the electrolyte including the enriched-vanadium solution (i.e., 1.5 M V(IV) and 3.3 M sulfuric acid), the interface impedance was 0.067 ohm·cm
2. Therefore, the electrode–membrane interface resistance, accounting for the ionic sorption/desorption from both sides of the membrane–electrode interface, varies in the range of 0.008–0.067 ohm·cm
2 for an operando all-vanadium redox flow battery with concentrated electrolytes.
3.2. Determining MacMullin Number for Nafion® Membranes Used within VRFB Architecture
As illustrated in
Figure 3, the ASR values corresponding to stacked IEMs were greatly influenced by the concentration of the flowing electrolyte. Considering the porosity of the membranes, it is important to quantify the dependency of membrane conductivity to the conductivity of the flowing electrolyte. The MacMullin number is an important index to explore the interplay between the ionic conductivity of the electrolyte and membrane. The MacMullin number for a porous separator can be formulated using the following [
28]:
As formulated in Equation (6), the MacMullin number (
) relates the conductivity of the electrolyte (
) to the effective conductivity of the porous membrane (
). Therefore, to determine the MacMullin number, it is necessary to independently measure the conductivity of the electrolytes and membranes. In this work, conductivity cells (
Figure 2) were used to measure the ionic conductivities. Several samples of Nafion
® 115 were used to assess the in-plane ionic conductivity and to confirm the repeatability of the measurements. Various bathing solutions including deionized (DI) water, aqueous sulfuric acid, and enriched vanadium solution were prepared, and the membranes were soaked in these bathing solutions for more than a week. Subsequently, the in-plane conductivities were evaluated using Equation (5).
Figure 4 includes the in-plane conductivity of the Nafion
® 115 membranes soaked in different electrolytes. Similar analysis was conducted for assessing the in-plane ionic conductivity of NR211 membrane at similar testing conditions as shown in
Figure S1 within Supplementary Information (SI). According to
Figure 4, the in-plane conductivity of the Nafion
® membranes is a strong function of the bathing solution. The highest value of conductivity achieved for the membranes soaked in DI water (~0.09 S·cm
−1) followed by aqueous sulfuric acid (~0.076 S·cm
−1) and enriched vanadium solution (~0.032 S·cm
−1).
The in-plane conductivity of the membranes soaked in aqueous sulfuric acid is significantly higher compared to enriched vanadium solution. The conductivity trend observed in this case is consistent with the ASR values shown in
Figure 3 and
Table 1.
To further assess the influence of electrolyte composition on the in-plane conductivity of the membranes, the ionic conductivity of the electrolytes was also measured ex-situ. Electrolytes with various configurations were prepared; i.e., aqueous sulfuric acid (3.3 M and 4.8 M) and enriched vanadium solution (1.5M V(IV), 3.3M sulfuric acid). The conductivity cell shown in
Figure 2b was used to measure the ionic conductivity of the electrolytes. It is important to note that the conductivity measured for different electrolyte compositions was repeated across multiple cell configurations to confirm independent recording for the conductivities. Multiple configurations of conductivity cells with varied dimensions were designed and 3D printed in-house. Therefore, the ionic conductivities reported here were confirmed to be cell-independent.
Figure 5 includes the ionic conductivities measured for various electrolyte compositions.
According to
Figure 5, the ionic conductivity of the electrolytes varies significantly with the composition. The macroscopic description of the ionic conductivity can be formulated using the following equation [
6,
29].
In Equation (7),
represents the ionic conductivity (S·cm
−1),
the Faraday constant (C),
charge of species
i,
mobility of ion
i (cm
2.V
−1.s
−1), and
concentration of species
i (mol·cm
−3). Therefore, as formulated in Equation (7), the concentration of charge-carrying ions along with corresponding mobility are the major contributors to the ionic conductivity. As shown in
Figure 5, increased acid concentration within the electrolytes increases the ionic conductivity in this range. However, enriched vanadium solution demonstrates significantly lower ionic conductivity. This trend contributes to the decreased ionic mobility of the major charge carriers (protons) within concentrated electrolyte solutions [
30]. Decreased proton concentration upon adding VOSO
4 to the aqueous solution containing sulfuric acid also contributes to the reduced ionic conductivity since the sulfate anions react with H
+ ions to form bisulfate. Measuring ionic conductivity of the membranes along with the electrolytes enables quantifying the MacMullin number for Nafion
® perfluorinated membranes, as tabulated in
Table 2.
As tabulated in
Table 2, the MacMullin number for IEMs used within VRFB architectures with vanadium enriched and aqueous sulfuric acid solutions is in the range of 7.29–7.34. The error bars shown in
Table 2 have been assessed based on the variation in experimentally measured in-plane ionic conductivity of the Nafion
® membrane soaked in different electrolytes. Therefore, for both electrolyte compositions (i.e., aqueous sulfuric acid and concentrated vanadium solutions), the ionic conductivity of the ion-exchange membranes is more than seven times lower compared to the conductivity of the electrolyte. Thus, it can be deduced that for aqueous electrolytes, the ionic conductivity of the electrolytes, regardless of the concentration of electroactive species, is not a limiting factor. As a result, to enhance the performance of aqueous RFBs with vanadium ions as the electroactive compounds, efforts must be dedicated to improving the ionic conductivity of the membranes.
In addition, according to
Table 2, the variation in the MacMullin number as a function of electrolyte composition is inconsequential (~0.7%). Therefore, to further increase the ionic conductivity of the Nafion
® membranes, increasing the ionic conductivity of the electrolytes is an effective approach. A small increase in the MacMullin number for aqueous sulfuric acid solution (see
Table 2) reveals that the uptake of vanadium co-ions within the Nafion
® structure affects the mobility of the protons in the membrane phase and adversely affect the conductivity. It is important to note that a higher MacMullin number for enriched vanadium solution is expected since the mobility of the charge carrying ions is further constrained in the membrane phase [
20]. Although the influence of vanadium co-ion uptake is insignificant in the ionic conductivity, the transport of vanadium ions within the membrane phase is undesirable since it results in self-discharge, as discussed in the following section.
3.3. Formulating Vanadium Ion Crossover and ASR for a Stack of Ion-Exchange Membranes
As described in
Section 3.1, stacking multiple layers of ion-exchange membranes results in increased ASR due to increased overall thickness and interfacial regions. Increased ASR increases the ohmic overpotential associated with the cell according to the following equation [
6,
31,
32]:
where
is the ohmic overpotential (V),
is the area specific resistance (ohm·cm
2), and
is the current density (A·cm
−2). As formulated in Equation (8), increased ASR directly increases the ohmic overpotential and subsequently reduces the power generated by the battery. In
Section 3.2, it was shown that the conductivity of the Nafion
® membranes is directly correlated to the surrounding electrolyte. However, for the aqueous electrolytes with high concentration of sulfuric acid (2–5 M), the ionic conductivity of the electrolytes cannot be significantly altered. The other practical approach for reducing the ionic resistance imposed by the ion-exchange membrane is to reduce the membrane thickness. However, reduced membrane thickness results in increased crossover rate for a similar membrane microstructure. It has also been shown that via engineering membrane morphology, an optimum configuration can be achieved for reduced ionic crossover or reduced ASR without significantly altering the competing aspect [
16].
To investigate the influence of multiple ion-exchange membrane stacking on the ASR, the ASR for commercially available Nafion
® 115 (single layer) was initially measured.
Figure 6 includes the ASR value measured for a single layer of N115 as a function of membrane nominal thickness (marked with a triangular symbol on
Figure 6).
Within the acidic aqueous environment, the Nafion
® membrane is completely wetted by the electrolyte. Under this assumption, the ohmic resistance imposed by the membrane can be formulated using the following equation [
28].
Here,
is the ohmic resistance associated with the membrane (ohm),
is the tortuosity of the membrane,
is the thickness of the membrane swelled in the electrolyte (cm),
is the porosity of the membrane, and
is the conductivity of the membrane (S.cm
−1). In addition, for aqueous electrolytes, the dominant contributor to the ohmic overpotential is the ionic transport resistance imposed by the membrane; therefore, the area-specific resistance can be formulated as [
6]
Here,
is the projected area of the membrane (cm
2). Therefore, combining Equation (9) and Equation (10), we can write:
Therefore, as formulated in Equation (11), assuming the membrane properties remain unchanged; the ASR value is linearly dependent on the thickness of the membrane (for similar cell active areas). A similar trend has been shown in
Figure 6 (dashed line). Therefore, a linear trend is expected for ASR based on the ASR value measured for N115.
To explore the influence of multiple membrane stacking on the crossover of electroactive compounds, the concentration-gradient-induced vanadium crossover was assessed for a single layer of N115. The schematic of the setup, along with experimental details, was already provided in
Figure 1 and
Section 2. Circulating vanadium enriched electrolyte (1.5M V(IV) and 3.3M sulfuric acid) in one side and vanadium-deficient electrolyte (4.8M sulfuric acid) in the other side of the reactor assembled with as-received carbon paper electrodes and a single layer Nafion
® 115 membrane, the total concentration of vanadium ions (V(IV)) was measured at the end of experiments (~24 h) within the membrane deficient electrolyte. Further details on the experimental procedure are available in a recent publication [
20].
Figure 7 includes the concentration of vanadium within vanadium-deficient electrolyte at the end of experiment (highlighted in red). Assuming Fickian diffusion for concentration-gradient-induced crossover, the diffusive flux can be formulated in the form of Equation (12) [
6]:
The continuity equation in the membrane phase can be written in the form of Equation (13) assuming that the vanadium ions do not react in the membrane phase (zero source term in the continuity equation) [
15].
Assuming 1D transport through the membrane thickness is also justified considering the dimensions of the ion-exchange membrane (through-plane-diffusion-pathway/in-plane-diffusion-pathway = ~0.004). Therefore, assuming Fickian transport in the membrane phase, the continuity equation can be written in the form of:
Considering a steady state solution, Equation (14) can be written in the form of:
It is important to note that the diffusive model based on Fickian behavior only accounts for the interaction of species (i.e., vanadium ions) with the solvent. More rigorous modeling approaches based on concentrated solution theories can be used for modeling solute interactions within the flux formulation [
33]. However, the transport models based on concentrated solution theory require several transport parameters that have not yet been measured for all-vanadium redox flow batteries. Therefore, for an experimental assessment provided here, the Fickian-based transport model has been used since it does not significantly alter the major conclusions. Readers are encouraged to refer to other publications where more rigorous approaches have been implemented for modeling the flux of species [
21,
22,
30]. Adopting a steady-state and 1D framework, the continuity equation formulated in Equation (15) can be written in the form of Equation (16):
In Equation (16),
is the length of the membrane swelled in the concentrated electrolyte as formulated in Equation (9). In addition, for deriving Equation (16), we have assumed that the diffused vanadium ions immediately react in the opposite electrolyte (See Equations (1)–(4)). In Equation (16), the maximum concentration within the membrane phase has been assumed to happen at the membrane–electrode interface (
). To explore the influence of membrane thickness on the crossover of vanadium ions, a transient solution for the continuity equation (Equation (14)) must be considered. Several prior efforts have focused on analyzing the transient solution. In the
Supplementary Information (Equation (S1) through Equation (S27)), we have provided further details on deriving the characteristic time (
) as formulated in the following [
31].
As formulated in Equation (17), for a similar membrane structure and internal morphology, the variations of characteristic time with the membrane thickness is second-order. Such a second-order trend has been shown schematically in
Figure 7 as a function of membrane thickness. Consequently, the concentration-gradient-induced flux will approach zero (mathematically) as the membrane thickness approaches infinity.
The ionic transport formulation derived in Equation (15) strictly applies for the membrane phase. However, the concentration of vanadium ions measured with the setup illustrated in
Figure 1 was based on the analysis of the vanadium ion concentration within the external electrolytes. Therefore, permeability of the ion-exchange membrane towards a particular electroactive ionic species (e.g.,
) can be formulated as
In Equation (18),
is the permeability (mol·cm
−2·min
−1),
is the solubility, and
is diffusivity of species
within the membrane phase (cm
2·min
−1). Equation (7) formulates the correlation between ionic conductivity and mobility of ionic species within the electrolyte. The Nernst–Einstein equation describes the mobility (
) as a function of diffusivity for the ionic species [
6].
In Equation (19),
is the elementary charge (
),
is the Boltzmann constant, and
is the temperature [
17]. Therefore, plugging Equation (19) in Equation (18), we derive:
The membrane ionic uptake values for protons and vanadium ions (V(IV)) has already been measured for various concentrated bathing electrolytes [
34]. The concentration of protons in the membrane phase decreases as a function of decreased concentration in the bathing solution. The same trend has also been observed for the vanadium V(IV) ions. Therefore, according to Equation (20), the solubility plays a key role in influencing the permeability of ionic species through the membrane.
The solubility within the membrane phase, being a strong function of concentration of ionic species in the adjacent electrolyte phase, can be manipulated via stacking multiple IEMs and this is the core reasoning for adopting this approach for reducing ionic crossover without significantly altering the ASR. In the following section, more details are provided.
3.4. Multilayer IEM Membranes for Reduced Crossover
To explore the influence of stacking multiple IEMs on the crossover of vanadium ions, the system shown in
Figure 1 was utilized. Five layers of Nafion
® 211 were used along with flow-through flow plates and a single layer of as-received carbon paper electrodes (39AA, SGL, Germany). The concentration-gradient-induced crossover was explored based on the procedure explained in
Section 2.
The real-time UV/Vis spectra were recorded for vanadium-deficient electrolytes as shown in
Figure 8. The spectra were analyzed using the scripts written in-house to obtain the concentration of vanadium ions in the vanadium-deficient electrolyte in real-time based on the procedure outlined in our previous publications [
15,
20]. As illustrated in
Figure 8, the absorbance UV/Vis spectra at 760 nm was used to determine the concentration of vanadium ions within the vanadium-deficient electrolyte. Along with vanadium crossover measurement, electrochemical impedance spectroscopy was also utilized to assess the real-time influence of vanadium crossover on the area-specific resistance.
Figure 9 includes the real-time EIS spectra recorded during the vanadium crossover experiment.
As shown in
Figure 9a, the EIS spectra were obtained prior to the crossover test, where a similar aqueous sulfuric acid solution (3.3 M) was circulated in both sides of the redox flow battery. Subsequently, the vanadium deficient side was replaced with aqueous sulfuric acid with 4.8M acid concentration, and the vanadium-enriched side was set to 1.5M vanadium V(IV) and 3.3M sulfuric acid. The EIS spectra, as shown in
Figure 9b, were recorded at t = 0, 9, 18, and 25 h into the crossover measurement. Finally, both solutions were replaced with vanadium-enriched solution and the EIS spectra were recorded.
As shown in
Figure 9, the area-specific resistance for series of IEMs increases as a function of increased vanadium concentration in the vanadium-deficient electrolyte. This trend is consistent with the trend observed for single layer Nafion
® 115 (
Table 1).
The increased ASR as a function of increased vanadium concentration in the vanadium-deficient electrolyte can be explained via exploring the MacMullin number calculated for the Nafion
® membranes (
Table 2). As discussed in
Section 3.2, the MacMullin number correlates the ionic conductivity of the ionic electrolytes contacting the membrane to the effective ionic conductivity of the membrane itself. Increased vanadium ion concentration in the vanadium-deficient electrolyte increases the MacMullin number due to increased membrane impedance; thus, the conductivity of the membrane does not scale linearly with the changes in conductivity of electrolytes when the electrolytes include vanadium ions.
As demonstrated in
Figure 5, conductivity of electrolytes including vanadium ions (V(IV)) is significantly lower compared to aqueous vanadium solutions (3.3 M acid concentration). Therefore, increased ASR as a function of increased vanadium concentration in the vanadium-deficient electrolytes is expected. To explore the influence of IEM stacking on the ASR, a comparison has been provided between five layers of Nafion
® 211 and a single layer N115 in
Figure 10.
As shown in
Figure 10, the ASR associated with multilayers of NR211 is higher compared to a single layer N115 regardless of the contacting electrolyte. Similar to single-layer N115, for the NR211 multilayer stack, increased vanadium ion concentration within the electrolyte-deficient electrolyte, increases ASR. However, to provide a real-time comparison in the cell level, the ohmic overpotential (Equation (5)) associated with each membrane configuration was assessed (see
Table 3).
As tabulated in
Table 3, the application of five layers of NR211 instead of a single-layer N115 membrane increases the ohmic overpotential from 51 mV to 59 mV at 100 mA·cm
−2. For high performance VRFBs (i.e., high current density operation (e.g., 500 mA·cm
−2)) the ohmic overpotential increases from 255 mV to 294 mV when a stack of NR211 membranes is replaced with a single-layer N115. Therefore, implementation of multilayer NR211 membranes, in comparison to one layer of N115, increases the ohmic overpotential by ~15%. In the
Supplementary Information, we have also provided polarization curves along with voltage efficiency analysis for the VRFBs assembled with a single layer N115 versus NR211 membrane (see
Figure S2). To have a more comprehensive picture, it is also necessary to explore the influence of IEM stacking on the crossover. A comparison of concentration-gradient-induced crossover between five layers of NR211 and one layer of N115 is provided in
Figure 11.
According to
Figure 11, the concentration of vanadium ions in the vanadium-deficient side has been compared for both cases at various time frames (9, 18, and 25 h). As clearly illustrated in
Figure 11, the implementation of multiple membrane stacking (in this case, five layers of NR211 instead of N115) significantly reduces the crossover of ionic species. For instance, comparing the concentration of vanadium ions diffused through the membrane to the vanadium-deficient electrolyte at the end of experiment (after 25 h of continuous operation under concentration-gradient), the vanadium crossover is reduced by 37% when five layers of NR211 are replaced with one layer of N115. The operando vanadium ion crossover measurement is consistent with the long duration cycling analysis performed for VRFBs assembled with a single layer N115 versus NR211 membrane (see
Figure S3 within Supplementary Information). Therefore, the reduction in ionic species crossover compared to the increase in ASR is significantly higher when five layers of NR211 membranes are replaced with a single-layer N115 within the VRFB architecture.
Figure 12 schematically illustrates the mechanism of reduced ionic crossover for multilayers of IEMs at steady state operation (see Equation (15)).
As schematically illustrated in
Figure 12, imposing phase boundary within multilayers of IEMs results in reduced crossover since it results in ionic concentration discontinuity in the stack of membranes. It has already been shown that the ionic uptake from bathing solution reduces with reduced concentration of ions in the contacting electrolyte [
34]. The ratio of vanadium concentration in the membrane phase to the adjacent electrolyte phase increases with decreased concentration of vanadium ions in the contacting solution [
34]. Therefore, the concentration discontinuity in the membrane–membrane interface decreases as the concentration of vanadium ions in the adjacent membrane phase decreases. Such a discontinuity has been schematically illustrated in
Figure 12.
It is also important to note that increased ASR observed for multilayers of IEMs is primarily due to contact resistances imposed via stacking multiple IEMs. Under the compression and due to variations in the adjacent electrolyte composition, IEMs considerably deform. The conductivity of ion-exchange membranes also varies when the composition of contacting electrolyte is altered. However, for ion-exchange membranes, the ionic conductivity is a strong function of water content; therefore, as long as an aqueous electrolyte wets the entire membrane stack, the increased ASR due to contact interface between multilayers of the IEM stack is not as substantial compared to the significant reduction in vanadium ion crossover.
Finally, it is critical to compare the variations of ASR and vanadium ion crossover across different cell architectures from the cost perspective, since it enables comparing these two metrics using a similar criterion. It is already been shown that the RFB price (
) per unit discharge energy (
) can be formulated considering the contributions to the overall cost from the reactor (
), electrolyte (
), balance-of-plant (
), and some additional sources (
) [
35].
Further details regarding various terms shown in Equation (21) are available elsewhere [
35]. The variations in ASR and vanadium ion crossover directly affect the costs associated with the reactor and electrolyte shown in Equation (21).
Since all the other parameters affecting the reactor and electrolyte costs remain unchanged in Equation (21) when a single layer N115 is replaced with multilayer NR211, the reactor and electrolyte costs can be formulated as a function of ASR and ionic crossover [
35].
Here,
and
are variables that remain unchanged when various membranes are used. Therefore, we have treated these parameters as constants in our formulation. Details regarding these parameters are available elsewhere [
35]. In Equation (22),
resembles the resistance of all the sources of overpotentials including ohmic (
), kinetics (
), and mass transport (
) resistances. As a result, it can be re-written in the form of:
Replacing a single-layer N115 with multilayer NR211 directly influences the ohmic losses shown in Equation (24). Therefore, even if the most dominant overpotential within a cell architecture is the ohmic losses, the variation of reactor cost with ASR becomes linear (first-order). On the other hand, according to Equation (23), the round-trip coulombic efficiency () is a direct function of ionic crossover and shunt current in the cell stack. For a single cell configuration, the crossover of vanadium ions linearly influences the coulombic efficiency. Therefore, it can be concluded that the variations in ASR and vanadium crossover can be compared in terms of overall cost and both effects have a first-order influence on the cost, assuming the ohmic losses are the most dominant losses in a single-cell all-vanadium redox flow cell architecture. It is important to note that in our analysis, we assumed that the manufacturing costs associated with the membranes were not substantial and the overall material used for multilayer NR211 and single-layer N115 was comparable (similar thickness and identical polymer structure). Furthermore, in our cost analysis, we only focused on the reactor configuration and did not consider the costs associated with periodic re-balancing when the discharge capacity reaches a particular lower limit.
3.5. IEM Selection Criteria for Reducing Ionic Crossover in VRFBs
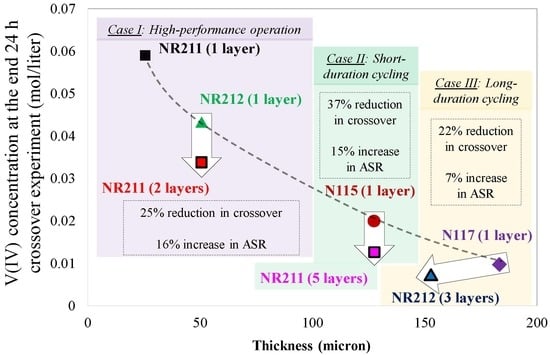
The comparison of multilayer NR211 with N115 in terms of ASR and concentration-gradient-induced crossover provided a promising approach for tacking crossover issues in VRFBs. Therefore, similar analysis was further expanded to cover other IEMs commonly used in the field. In this section (
Figure 13), more comprehensive analysis has been provided including commercially available IEMs (N117, N115, NR212, and NR211).
Figure 13 includes an IEM selection chart for reducing ionic crossover in VRFBs. Three cases are included in
Figure 13 which provide selection guidelines for designing the battery for a particular target. For high-performance VRFBs (Case I), it is necessary to minimize the ASR associated with the membrane. Therefore, among off-the-shelf IEMs, NR211 has the lowest ASR. However, the application of NR211 results in greater capacity decay due to crossover. Therefore, usually the second off-the-shelf choice is to utilize NR212. However, according to
Figure 13, utilizing two layers of NR211 instead of NR212 only increases the ASR by 16%, but reduces ionic crossover by 25% compared to single-layer NR212. Case II is for designing VRFBs for relatively short-term capacity retention. Implementation of five layers of NR211 instead of single-layer N115 is recommended according to
Figure 13 since the reduction in crossover (37%) is more pronounced compared to an increase in ASR (15%) when multilayer NR211s are utilized.
Designing VRFBs for extended and long-term duration is of special interest (Case III). Usually, Nafion® 117 is the primary off-the-shelf choice. However, using three layers of NR212 instead of a single layer N117 results in 22% higher capacity retention and an increase in ASR is small (only ~7%). It is also important to note that if the costs associated with the membrane within VRFB systems scales up linearly with the nominal thickness of the membrane, the implementation of multilayer IEM stacking does not significantly alter the overall cost. In some cases (e.g., Case III), it even reduces the total cost, since the thickness of the membrane is reduced.