1. Introduction
During the development of end-stage renal disease (ESRD), a considerable amount of toxins (ranging from small to large size molecules), naturally filtered by human kidneys, begins to accumulate in ESRD patient’s blood. When the patient is suffering from ESRD, hemodialysis is the most inexpensive and effective therapy to remove these solutes (toxins) from the blood. In this therapy, the blood flows from the patient’s body to an extracorporeal circuit that mimics the function of the human kidney with the help of a hollow fiber dialyzer. The hollow fibers are made of semi-permeable porous membranes with an active surface area of 0.8−2.5 m
2 and a diameter of nearly 200 nm [
1]. These fibers allow convective and diffusive transport of uremic solutes, but resist the transport of albumin and blood cells towards the dialysate compartment. Low molecular weight solute (i.e., urea, glucose) transport is governed by diffusion. The transfer of middle molecular weight solutes (i.e., endothelin, β2-Microglobulin, β2-microglobulin, complement factor D, albumin) requires convection (ultrafiltration). This transport phenomenon’s efficiency depends on hollow fiber geometry, membrane characteristics, and operating variables [
2,
3,
4].
In the past 30 years, numerous mathematical models have been proposed to mimic the transport phenomena occurring in vivo. Kunitomo et al. performed in-vitro and in-vivo experiments with polymethyl methacrylate (PMMA) hollow fiber units. He established that post-dilution of blood to compensate for the excessive removal of fluid is the most effective way to enhance the clearance of middle size molecules [
5]. Jaffrin et al. and Chang et al. developed a one-dimensional model for combine diffusive and convective transport of solutes through membranes. In-vitro verification of the model shows that values of urea clearance are closer to the experimental result [
6,
7]. Werynski et al. have reviewed the one-dimensional convection-diffusion model, typically used to explain mass transport in membrane equipped clinical devices [
8]. He concluded that the one-dimensional model is not applicable for studying the impact of module geometry and shape on clearance efficiency. Wüpper et al. theoretically analyzed the clinical data to determine density changes in radial direction and change in the concentration of large molecules in an axial direction [
9]. Annan et al. presented a two-dimensional axisymmetric model to analyze the effect of mismatch flow in the blood and dialysate compartment [
10].
The previous studies have presented a simplified description of solute transport across the membrane by assuming uniform convective flux that permits to solve the model equations analytically [
5,
6,
7]. However, the analytical solution provides the results only at the inlet and outlet of the hollow fibers. Therefore, in the current study, a CFD model is solved with the finite element method that provides solutions on a large number of points present in the computational domain. Some mathematical models established the solute transport from blood to the dialysate side and across the membrane with an overall mass transfer coefficient [
4,
5,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. The use of the overall mass transfer coefficient without considering the tortuosity and porosity of porous media introduces the difference between the in vitro and in silico clearance rates. To fill this void, TPDM is used in this study that incorporates the effect of membrane tortuosity and porosity to give better estimation of overall mass transfer coefficient [
17].
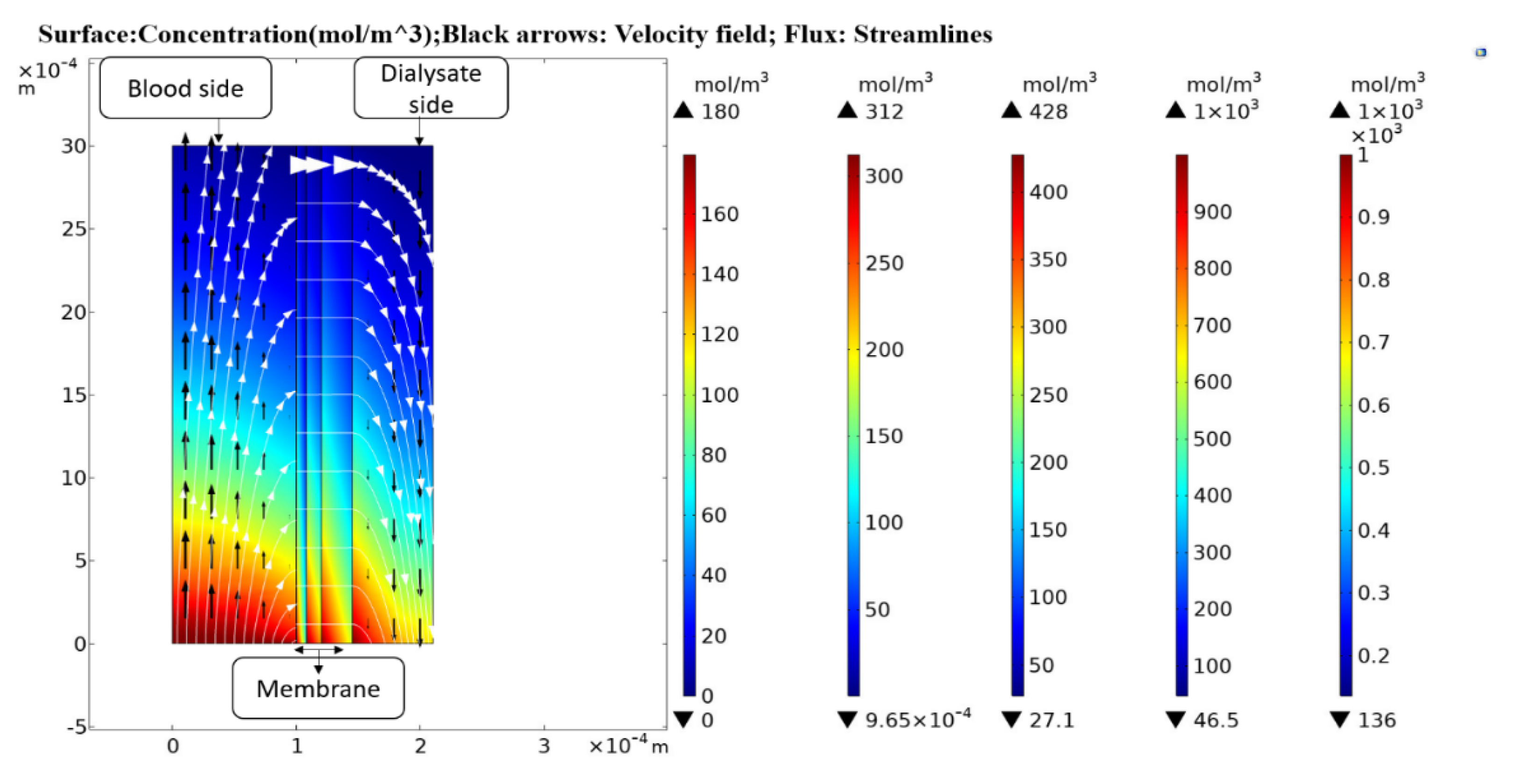
In this study, a two-dimensional axisymmetric mathematical model was developed to simulate the convective and diffusive transport of low molecular weight (LMW) solutes, i.e., urea and glucose and middle molecular weight (MMW) solutes, i.e., endothelin and β2-Microglobulin inside the dialyzer. Mass transfer in blood and dialysate compartment was modeled with convection diffusion equations. The blood and dialysate compartments were coupled with a multi-layer membrane by using TPDM. Computational analysis is performed with the finite element method to figure out those factors that play a vital role in enhancing the dialyzer clearance. Numerical results showed that the clearance efficiency of the dialyzer could be improved by increasing the blood and dialysate flow rate, and the fiber aspect ratio; but the clearance of large size molecules (i.e., endothelin, β2-Microglobulin, β2-microglobulin, complement factor D, albumin) does not increase much due to tortuosity τ of the porous medium. The enhanced clearance efficiency will ultimately reduce the dialysis cost and duration.
4. Conclusions
Tortuous pore diffusion model (TPDM) was used to describe mass transport through the dialyzer membrane. Porosity and tortuosity were incorporated in this model to achieve a better estimation of solute clearance across the membrane. The numerical results obtained from this model were found in good agreement with the experimental results. This observation suggests that this model can be used to optimize the design and process parameters of the dialyzer module. The proposed model gave an insight into the effect of porous medium tortuosity on the diffusion of different solutes. By increasing the blood flow, the model predicted values of urea and glucose clearance were found 1.28% and 3.26% more than the Islam et al. predicted values. Similarly, the percentage increase found in urea and glucose clearance rate by increasing the dialysate flow, fiber length, and fiber radius was 1.55% and 0.4%; 1.54 and 1.86%; 1.47 and 0.6%, respectively. The clearance rate of urea was increased by 37.71% of its initial value by increasing the fiber aspect ratio. Due to the high steric hindrance H and friction coefficient F(p) the diffusion of large size molecules (i.e., endothelin, β2-microglobulin, complement factor D and albumin) do not increase much. When the pore diameter increases from 10 to 20 nm, the clearance rate of urea and glucose rise by 2.09% and 7.93% of their initial values. The results suggest that the pore diameter cannot be increased beyond 20 nm as it leads to loss of albumin molecules, which cannot be tolerated.