Insight into Steam Permeation through Perovskite Membrane via Transient Modeling
Abstract
:1. Introduction
2. Experimental Section
2.1. Theory
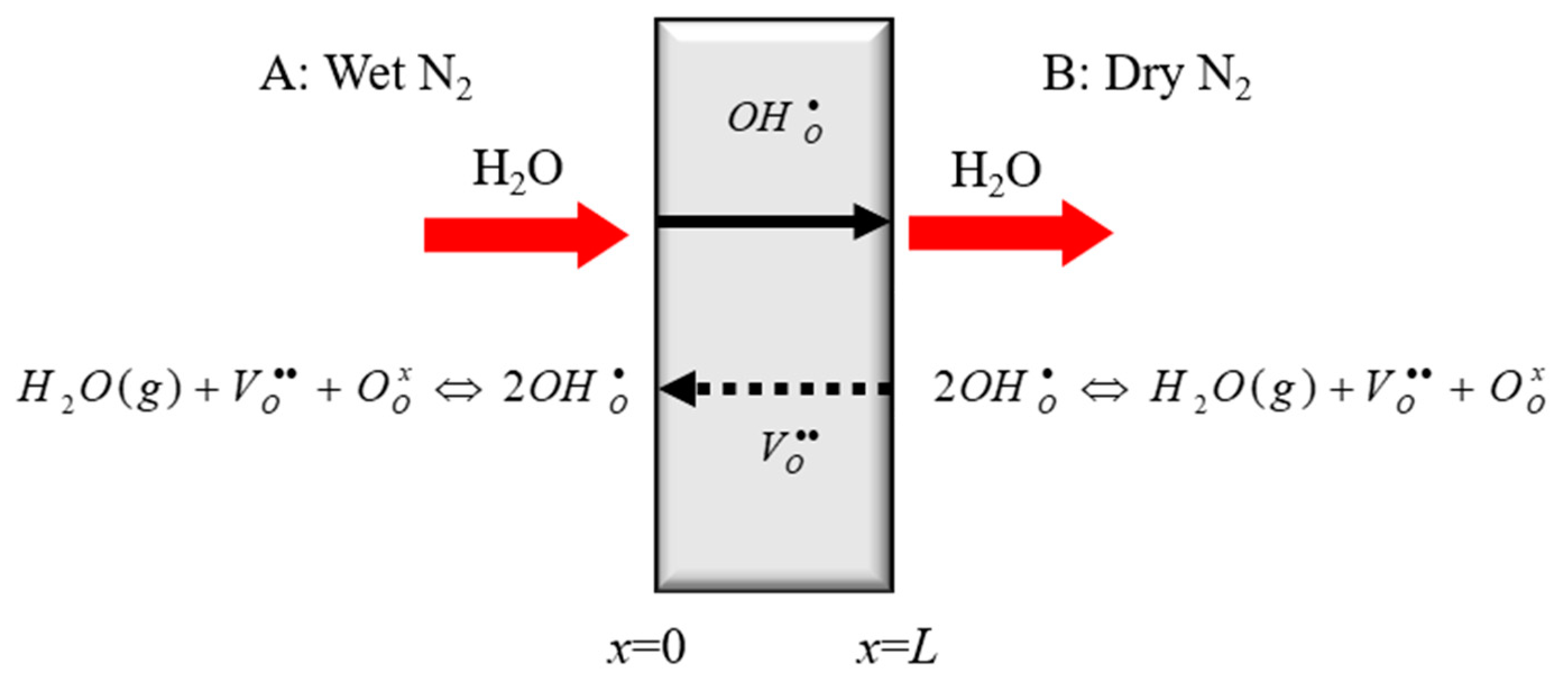
- Wet steam gas is pushed to the surface of the BCY10 membrane, generating a concentration gradient of steam between the gas block phase and the surface of membrane.
- The steam diffuses through the gas film, and then reacts with oxygen vacancies and oxygen ions, finally leading to the production of protons.
- On the surface of membrane, the vacancies react with water and the lattice oxygen with proton is produced. Thus, the produced protons diffuse into the membrane and the vacancies diffuse out of the membrane.
- When the protons permeate through the membrane, the steam is reproduced.
- The convection of steam with higher partial pressure in gas phase
- The steam diffusion in the gas boundary layer and Pt layer of Side A of the film
- The reaction of steam with BCY10 on Side A, and the generation of protons
- The migrations of proton and oxygen vacancy within the BCY10 membrane
- The reaction of proton, oxygen vacancy, and oxygen ion and the reproduction of steam on Side B of the membrane
- The steam diffusion on Side B of the membrane
- The convection of the steam with lower partial pressure in gas phase
2.2. Mathematical Model
- 1.
- The first process can be neglected, due to the negligible effect of gas mass transfer resistance in the bulk gas phase.
- 2.
- The film diffusion process can be represented with the linear driving force equation and the reaction rate as below:where kf is the film diffusion rate constant, m/s; represents the surface concentration of H2O, mol/m2; means surface reaction rate of H2O, mol/(m2.s); represents the concentration of steam equilibrium with the concentration of proton in the membrane, mol/m3; and Cout refers to the bulk concentration of H2O, mol/m3.
- 3.
- The third process represents the water splitting reaction shown below in Equations (3) to (6):where K is the reaction equilibrium constant of reaction 3, which is calculated with Equation (4); k1 is the forward reaction rate constant, m2/(mol·s); k2 is the reverse reaction rate constant, m2/(mol·s); Ra is the reaction rate of Equation (1), mol/(m2·s); and P0 is the atmospheric pressure, Pa.
- 4.
- The mass transfer of species, oxygen vacancy within the membrane can be calculated via the Poisson-Nernst-Planck equation (Equation (11)) [51].where i stands for the species permeating in the membrane, z stands for the charge number of species, F stands for Faraday constant, R stands for the ideal gas constant, T stands for Kelvin temperature, and E stands for the intensity of electric field in the membrane. By Equation (11), the distribution of species in the membrane with time and space can be calculated.
- 5.
- The steam is reproduced with oxygen vacancy and in the membrane of BCY10; the rate of reaction can be calculated with Equation (6).
- 6.
- The diffusion process of steam in the boundary of surface of BCY membrane and the mass transfer rate of steam can be calculated with Equation (2).
- 7.
- For the electro neutrality of the BCY10 membrane, one global constraint is used, as shown in Equation (13).
2.3. Solution Method
3. Result and Discussion
3.1. Validity of the Model
3.2. The Evolution of the Distribution of Charged Species and the Evolution of the Flux of Proton
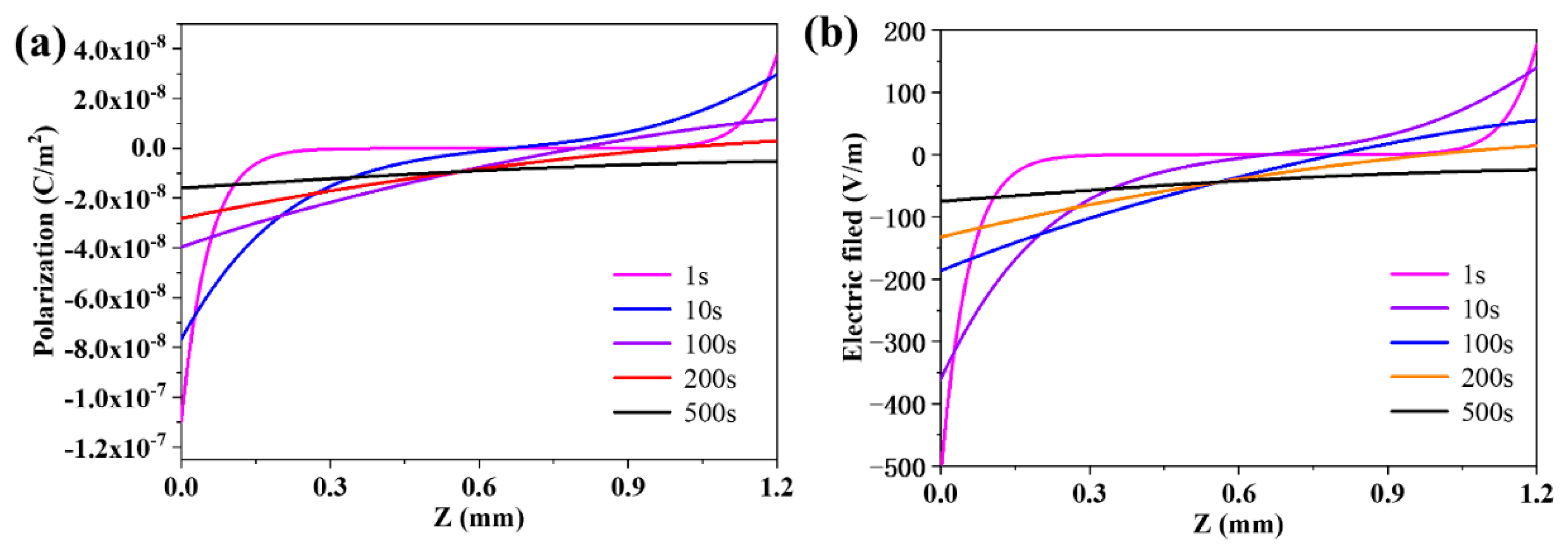
3.3. The Evolution of the Distribution of the Polarization and the Electric Field in the Membrane
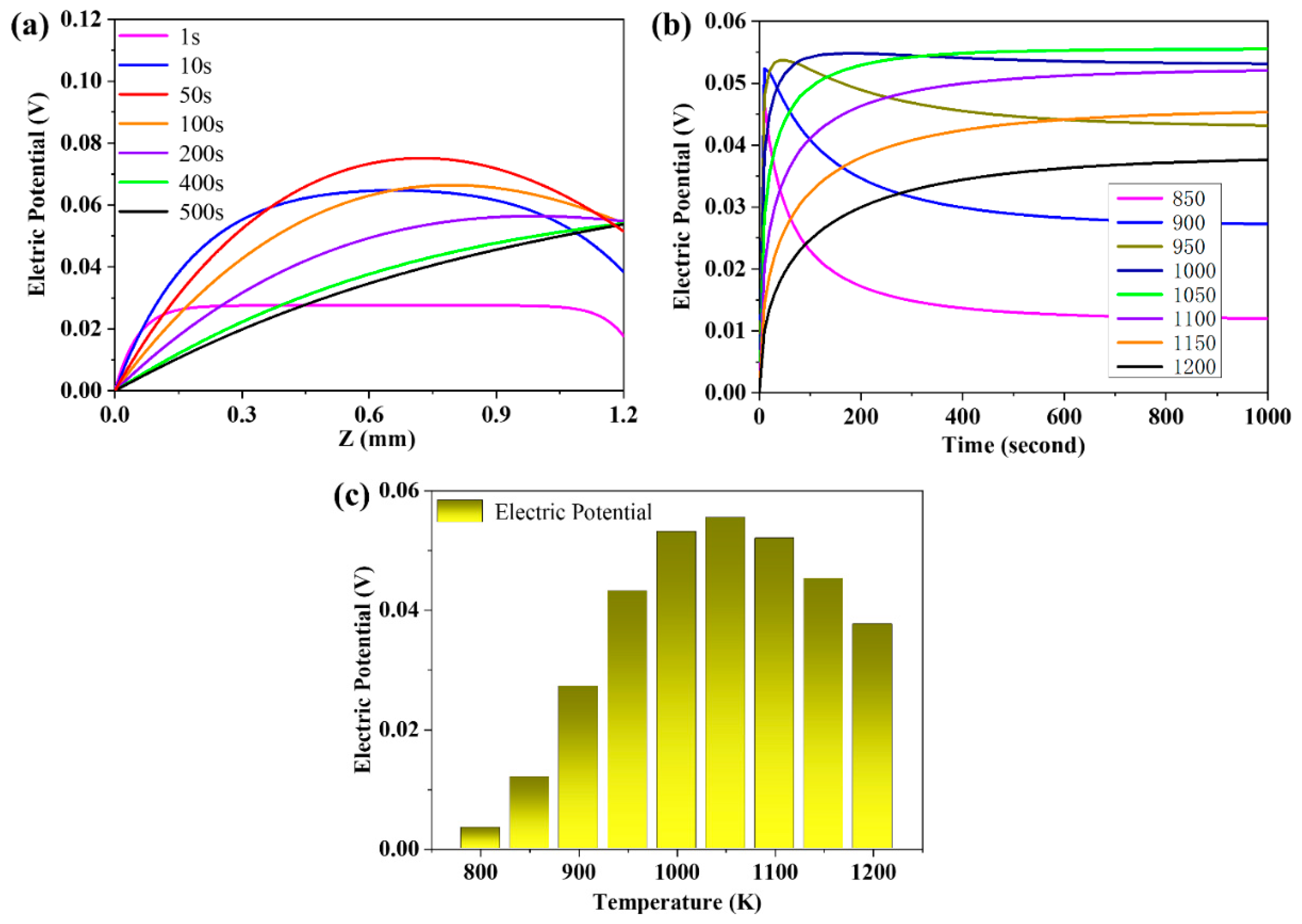
3.4. The Evolution of the Distribution of the Electric Potential
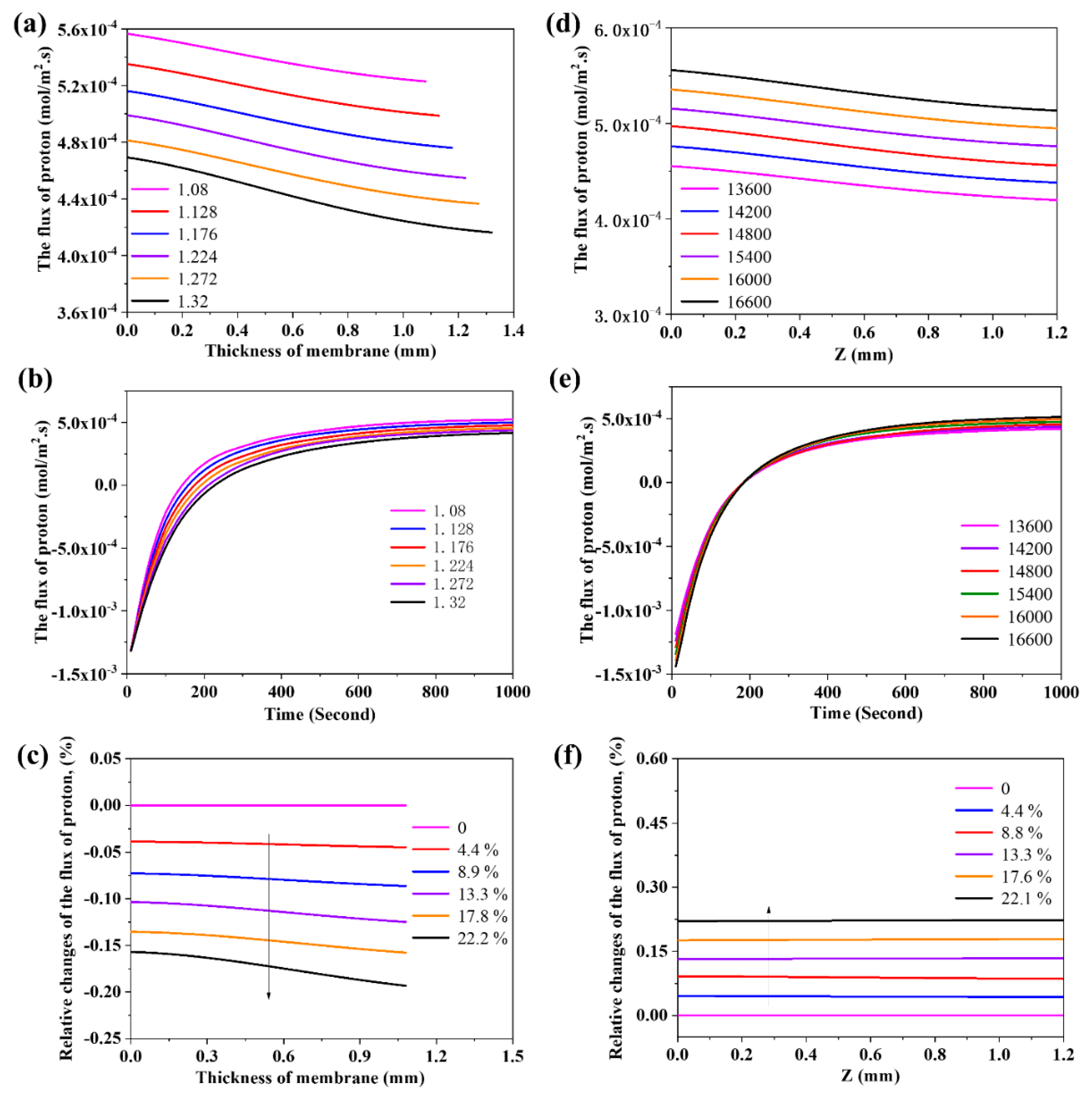
3.5. The Effects of Thickness and Density of the Membrane on the Flux of Proton
3.6. The Effects of Partial Pressure of Steam on the Flux of Proton
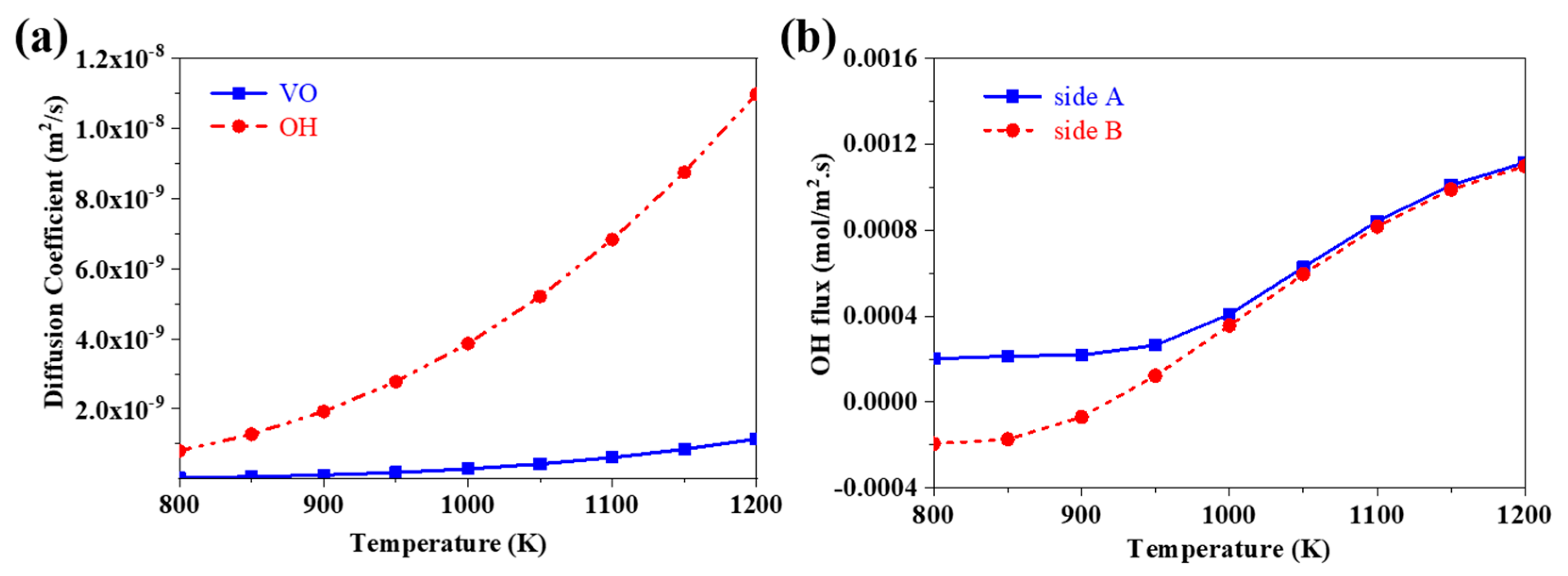
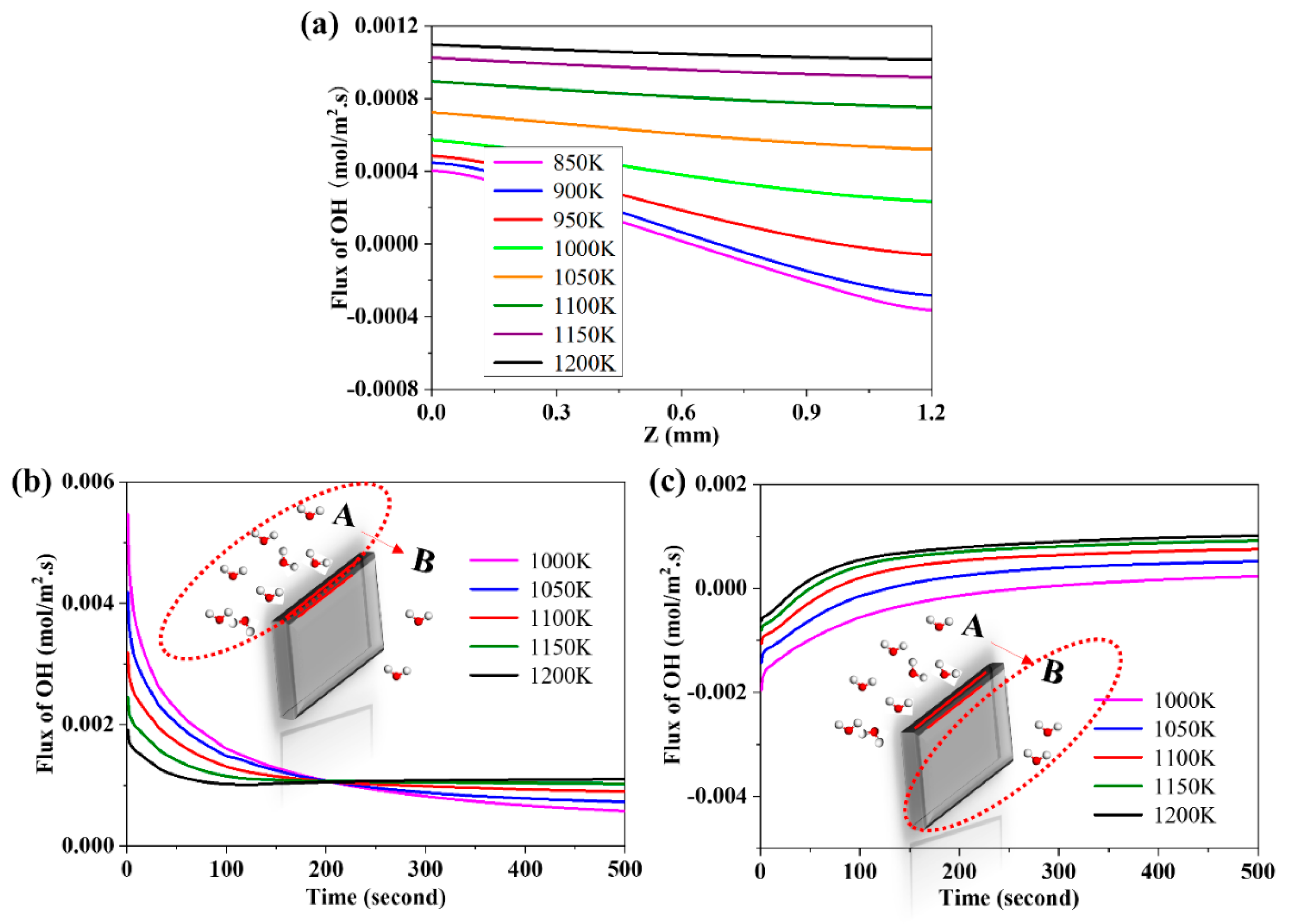
3.7. The Effects of Operating Temperature on the Flux of Proton
3.8. The Validity of the Simulation Resultant
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Z.; Oemar, U.; Ang, M.L.; Kawi, S. Oxidative steam reforming of biomass tar model compound via catalytic BaBi0.05Co0.8Nb0.15O3−δ hollow fiber membrane reactor. J. Membr. Sci. 2016, 510, 417–425. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Wei, Y.; Wang, H. Tantalum stabilized SrCoO3−δ perovskite membrane for oxygen separation. J. Membr. Sci. 2011, 368, 159–164. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, H.; Yang, W. Novel cobalt-free oxygen permeable membrane. Chem. Commun. 2004, 9, 1130–1131. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Efimov, K.; Jiang, H.; Feldhoff, A.; Wang, H.; Caro, J. CO2-Stable and Cobalt-Free Dual-Phase Membrane for Oxygen Separation. Angew. Chem. Int. Ed. 2011, 50, 759–763. [Google Scholar] [CrossRef]
- Zhu, X.; Li, M.; Liu, H.; Zhang, T.; Cong, Y.; Yang, W. Design and experimental investigation of oxide ceramic dual-phase membranes. J. Membr. Sci. 2012, 394–395, 120–130. [Google Scholar] [CrossRef]
- Han, N.; Zhang, C.; Tan, X.; Wang, Z.; Kawi, S.; Liu, S. Re-evaluation of La0.6Sr0.4Co0.2Fe0.8O3−δ hollow fiber membranes for oxygen separation after long-term storage of five and ten years. J. Membr. Sci. 2019, 587, 117180. [Google Scholar] [CrossRef]
- Song, J.; Feng, B.; Tan, X.; Han, N.; Sunarso, J.; Liu, S. Oxygen selective perovskite hollow fiber membrane bundles. J. Membr. Sci. 2019, 581, 393–400. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, X.; Zhang, J.; Chen, D.; Zeng, D.; Liu, S.; Zhou, W.; Shao, Z. Silver-doped strontium niobium cobaltite as a new perovskite-type ceramic membrane for oxygen separation. J. Membr. Sci. 2018, 563, 617–624. [Google Scholar] [CrossRef]
- Han, N.; Zhang, S.; Meng, X.; Yang, N.; Meng, B.; Tan, X.; Liu, S. Effect of enhanced oxygen reduction activity on oxygen permeation of La0.6Sr0.4Co0.2Fe0.8O3-δ membrane decorated by K2NiF4-type oxide. J. Alloy. Compd. 2016, 654, 280–289. [Google Scholar] [CrossRef]
- Li, W.; Cao, Z.; Zhu, X.; Yang, W. Effects of membrane thickness and structural type on the hydrogen separation performance of oxygen-permeable membrane reactors. J. Membr. Sci. 2019, 573, 370–376. [Google Scholar] [CrossRef]
- Han, N.; Wei, Q.; Tian, H.; Zhang, S.; Zhu, Z.; Liu, J.; Liu, S. Highly stable dual-phase membrane based on Ce0.9Gd0.1O2−δ-La2NiO4+δ for oxygen permeation under pure CO2 atmosphere. Energy Technol. 2019, 7, 1800701. [Google Scholar] [CrossRef]
- Xue, J.; Liao, Q.; Wei, Y.; Li, Z.; Wang, H. A CO2-tolerance oxygen permeable 60Ce0.9Gd0.1O2−δ–40Ba0.5Sr0.5Co0.8Fe0.2O3−δ dual phase membrane. J. Membr. Sci. 2013, 433, 124–130. [Google Scholar] [CrossRef]
- Zhuang, S.; Han, N.; Chen, R.; Yao, Z.; Zou, Q.; Song, F. Perovskite oxide based composite hollow fiber membrane for CO2 transport. Ceram. Int. 2020, 46, 2538–2544. [Google Scholar] [CrossRef]
- Gao, J.; Lun, Y.; Han, N.; Tan, X.; Fan, C.; Liu, S. Influence of nitric oxide on the oxygen permeation behavior of La0.6Sr0.4Co0.2Fe0.8O3−δ perovskite membranes. Sep. Purif. Technol. 2019, 210, 900–906. [Google Scholar] [CrossRef]
- Fang, W.; Steinbach, F.; Chen, C.; Feldhoff, A. An Approach to Enhance the CO2 Tolerance of Fluorite–Perovskite Dual-Phase Oxygen-Transporting Membrane. Chem. Mater. 2015, 27, 7820–7826. [Google Scholar] [CrossRef]
- Han, N.; Wei, Q.; Zhang, S.; Yang, N.; Liu, S. Rational design via tailoring Mo content in La2Ni1-xMoxO4+δ to improve oxygen permeation properties in CO2 atmosphere. J. Alloy Compd. 2019, 806, 153–162. [Google Scholar] [CrossRef]
- Partovi, K.; Liang, F.; Ravkina, O.; Caro, J. High-flux oxygen-transporting membrane Pr0.6Sr0.4Co0.5Fe0.5O3−δ: CO2 stability and microstructure. ACS Appl. Mater. Interfaces 2014, 6, 10274–10282. [Google Scholar] [CrossRef] [PubMed]
- Han, N.; Chen, R.; Chang, T.; Li, L.; Wang, H.; Zeng, L. A novel lanthanum strontium cobalt iron composite membrane synthesised through beneficial phase reaction for oxygen separation. Ceram. Int. 2019, 45, 18924–18930. [Google Scholar] [CrossRef]
- Ma, T.; Han, N.; Meng, B.; Yang, N.; Zhu, Z.; Liu, S. Enhancing Oxygen Permeation via the Incorporation of Silver Inside Perovskite Oxide Membranes. Processes 2019, 7, 199. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Han, N.; Han, D.; Meng, B.; Wang, G.; Liu, S. Novel SrCo0.9W0.1O3-δ hollow fiber ceramic membrane with enhanced oxygen delivery performance and CO2 resistance ability. ChemistrySelect 2018, 3, 13700–13704. [Google Scholar] [CrossRef]
- Han, N.; Cheng, J.; Han, D.; Chen, G.; Zhang, S.; Wang, G.; Yang, N.; Liu, S. Novel La0.7Sr0.3FeO3−δ/(La0.5Sr0.5)2CoO4+δ composite hollow fiber membrane for O2 separation with high CO2 resistance. Int. J. Energy Res. 2019, 43, 8890–8897. [Google Scholar]
- Song, Y.; Wang, W.; Ge, L.; Xu, X.; Zhang, Z.; Julião, P.S.B.; Zhou, W.; Shao, Z. Rational Design of a Water-Storable Hierarchical Architecture Decorated with Amorphous Barium Oxide and Nickel Nanoparticles as a Solid Oxide Fuel Cell Anode with Excellent Sulfur Tolerance. Adv. Sci. 2017, 4, 1700337. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhou, W.; Ding, D.; Liu, M.; Ciucci, F.; Tade, M.; Shao, Z. Advances in cathode materials for solid oxide fuel cells: Complex oxides without alkaline earth metal elements. Adv. Energy Mater. 2015, 5, 1500537. [Google Scholar] [CrossRef]
- Song, J.; Feng, B.; Chu, Y.; Tan, X.; Gao, J.; Han, N.; Liu, S. One-step thermal processing to prepare BaCo0.95-xBi0.05ZrxO3-δ membranes for oxygen separation. Ceram. Int. 2019, 45, 12579–12585. [Google Scholar] [CrossRef]
- Han, N.; Wang, S.; Yao, Z.; Zhang, W.; Zhang, X.; Zeng, L.; Chen, R. Superior three-dimensional perovskite catalyst for catalytic oxidation. EcoMat 2020. [Google Scholar] [CrossRef]
- Miao, J.; Sunarso, J.; Duan, X.; Zhou, W.; Wang, S.; Shao, Z. Nanostructured Co-Mn containing perovskites for degradation of pollutants: Insight into the activity and stability. J. Hazard. Mater. 2018, 349, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Han, N.; Yao, Z.; Ye, H.; Zhang, C.; Liang, P.; Sun, H.; Wang, S.; Liu, S. Efficient removal of organic pollutants by ceramic hollow fibre supported composite catalyst. Sustain. Mater. Technol. 2019, 20, e00108. [Google Scholar] [CrossRef]
- Chu, Y.; Tan, X.; Shen, Z.; Liu, P.; Han, N.; Kang, J.; Duan, X.; Wang, S.; Liu, L.; Liu, S. Efficient removal of organic and bacterial pollutants by Ag-La0.8Ca0.2Fe0.94O3-δ perovskite via catalytic peroxymonosulfate activation. J. Hazard. Mater. 2018, 356, 53–60. [Google Scholar] [CrossRef]
- Liu, L.; Gao, J.; Liu, P.; Duan, X.; Han, N.; Li, F.; Sofianos, M.V.; Wang, S.; Tan, X.; Liu, S. Novel applications of perovskite oxide via catalytic peroxymonosulfate advanced oxidation in aqueous systems for trace L-cysteine detection. J. Colloid Interface Sci. 2019, 545, 311–316. [Google Scholar] [CrossRef]
- Han, N.; Liu, P.; Jiang, J.; Ai, L.; Shao, Z.; Liu, S. Recent advances in nanostructured metal nitrides for water splitting. J. Mater. Chem. A 2018, 6, 19912. [Google Scholar] [CrossRef]
- Zhuang, S.; Han, N.; Wang, T.; Meng, X.; Meng, B.; Li, Y.; Sunarso, J.; Liu, S. Enhanced CO selectivity for reverse water-gas shift reaction using Ti4O7-doped SrCe0.9Y0.1O3−δ hollow fibre membrane reactor. Can. J. Chem. Eng. 2019, 97, 1619–1626. [Google Scholar] [CrossRef]
- Zhang, G.; Papaioannou, E.; Metcalfe, I. Selective, high-temperature permeation of nitrogen oxides using a supported molten salt membrane. Energy Environ. Sci. 2015, 8, 1220–1223. [Google Scholar] [CrossRef] [Green Version]
- Han, N.; Meng, B.; Yang, N.; Sunarso, J.; Zhu, Z.; Liu, S. Enhancement of oxygen permeation fluxes of La0.6Sr0.4CoO3−δ hollow fiber membrane via macrostructure modification and (La0.5Sr0.5)2CoO4+δ decoration. Chem. Eng. Res. Des. 2018, 134, 487–496. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Han, N.; Tan, X. Density functional theory calculations of atomic, electronic and thermodynamic properties of cubic LaCoO3 and La1−xSrxCoO3 surfaces. Rsc Adv. 2015, 5, 760. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, S.; Meng, B.; Han, N.; Zhu, Z.; Liu, S. Enhancing O2-permeability and CO2-tolerance of La2NiO4+δ membrane via internal ionic-path. Mater. Lett. 2018, 230, 161–165. [Google Scholar] [CrossRef]
- Cai, L.; Li, W.; Cao, Z.; Zhu, X.; Yang, W. Improving oxygen permeation of MIEC membrane reactor by enhancing the electronic conductivity under intermediate-low oxygen partial pressures. J. Membr. Sci. 2016, 520, 607–615. [Google Scholar] [CrossRef]
- Han, N.; Zhang, S.; Meng, B.; Tan, X. The effect of microstructure and surface decoration with K2NiF4-type oxide upon the oxygen permeability of perovskite-type La0.7Sr0.3FeO3-δ hollow fiber membranes. Rsc Adv. 2015, 5, 88602. [Google Scholar] [CrossRef]
- Zhuang, S.; Han, N.; Xing, M.; Meng, B.; Liu, S. Perovskite oxide and carbonate composite membrane for carbon dioxide transport. Mater. Lett. 2019, 236, 329–333. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, J.; Rykov, A.I.; Zhu, X.; Yang, W. Oxygen transport kinetics affected by grain size-A permeation model study. J. Membr. Sci. 2020, 630, 118038. [Google Scholar] [CrossRef]
- Li, C.; Li, W.; Chew, J.J.; Liu, S.; Zhu, X.; Sunarso, J. Rate determining step in SDC-SSAF dual-phase oxygen permeation membrane. J. Membr. Sci. 2019, 573, 628–638. [Google Scholar] [CrossRef]
- Han, N.; Wang, W.; Zhang, S.; Sunarso, J.; Zhu, Z.; Liu, S. A novel heterogeneous La0.8Sr0.2CoO3−δ/(La0.5Sr0.5)2CoO4+δ dual-phase membrane for oxygen separation. Asia-Pac. J. Chem. Eng. 2018, 13, e2239. [Google Scholar] [CrossRef]
- Kreuer, K.D. Aspects of the formation and mobility of protonic charge carriers and the stability of perovskite-type oxides. Solid State Ionics 1999, 125, 285–302. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Dippel, T.; Baikov, Y.M.; Maier, J. Water solubility, proton and oxygen diffusion in acceptor doped BaCeO3: A single crystal analysis. Solid State Ionics 1996, 86–88, 613–620. [Google Scholar] [CrossRef]
- Coors, W. Protonic ceramic steam-permeable membranes. Solid State Ionics 2007, 178, 481–485. [Google Scholar] [CrossRef]
- Coors, W. Steam Reforming and Water-Gas Shift by Steam Permeation in a Protonic Ceramic Fuel Cell. J. Electrochem. Soc. 2004, 151, A994. [Google Scholar] [CrossRef]
- Suksamai, W.; Metcalfe, I.S. Measurement of proton and oxide ion fluxes in a working Y-doped BaCeO3 SOFC. Solid State Ionics 2007, 178, 627–634. [Google Scholar] [CrossRef]
- Vollestad, E.; Zhu, H.; Kee, R.J. Interpretation of Defect and Gas-Phase Fluxes through Mixed-Conducting Ceramics Using Nernst-Planck-Poisson and Integral Formulations. J. Electrochem. Soc. 2014, 161, 114–124. [Google Scholar] [CrossRef]
- Kee, R.J.; Zhu, H.; Hildenbrand, B.W.; Vøllestad, E.; Sanders, M.D.; O’Hayre, R.P. Modeling the Steady-State and Transient Response of Polarized and Non-Polarized Proton-Conducting Doped-Perovskite Membranes. J. Electrochem. Soc. 2013, 160, 290–300. [Google Scholar] [CrossRef]
- Sanders, M.; O’Hayre, R. Development of a multi-species transport space theory and its application to permeation behavior in proton-conducting doped perovskites. J. Mater. Chem. 2010, 20, 6271. [Google Scholar] [CrossRef]
- Ricote, S.; Zhu, H.; Coors, W.; Chatzichristodoulou, C.; Kee, R.J. Equilibrium and transient conductivity for gadolinium-doped ceria under large perturbations: I. Experiments. Solid State Ionics 2014, 265, 22–28. [Google Scholar] [CrossRef]
- Britza, D.; Strutwolf, J. Several ways to simulate time dependent liquid junction potentials by finite difference. Electrochim. Acta 2014, 137, 328–335. [Google Scholar] [CrossRef] [Green Version]
- Kreuer, K.D. Proton-Conducting oxides. Annu. Rev. Mater. Res. 2003, 33, 333–359. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Feng, X.; Ren, G.K.; Wang, J.; Song, J. Effects of structural and concentration polarization on the efficiency of pd membrane permeator. Fusion Eng. Des. 2019, 148, 111279. [Google Scholar] [CrossRef]
- Song, F.; Zhuang, S.; Tan, X.; Liu, S. Modeling of Steam Permeation through the High Temperature Proton Conducting Ceramic Membranes. AIChE J. 2018, 65, 777–782. [Google Scholar] [CrossRef]



| Material | Investigator | ||
|---|---|---|---|
| BCY10 | −162.2 | −166.7 | Kreuer |
| BCY10 | −156.1 | −145.2 | Coors |
| Experimental Parameters | Values |
|---|---|
| Concentration of oxygen ions | 4.4633 × 104 mol/m3 |
| Concentration of Y doped Ce | 1.513 × 103 mol/m3 |
| Concentration of oxygen vacancy | 7.565 × 102 mol/m3 |
| Concentration of Proton | 0 |
| partial pressure of steam | Side A 0.14 atm; Side B 0.014 atm |
| V (the initial electric potential) | 0 |
| k1 (mass transfer coefficient of boundary layer) | 30 m/s |
| L (thickness of membrane) | 1.2 mm |
| pullet radius | 7 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, S.; Han, N.; Zou, Q.; Zhang, S.; Song, F. Insight into Steam Permeation through Perovskite Membrane via Transient Modeling. Membranes 2020, 10, 164. https://doi.org/10.3390/membranes10080164
Zhuang S, Han N, Zou Q, Zhang S, Song F. Insight into Steam Permeation through Perovskite Membrane via Transient Modeling. Membranes. 2020; 10(8):164. https://doi.org/10.3390/membranes10080164
Chicago/Turabian StyleZhuang, Shujuan, Ning Han, Qingchuan Zou, Shuguang Zhang, and Feng Song. 2020. "Insight into Steam Permeation through Perovskite Membrane via Transient Modeling" Membranes 10, no. 8: 164. https://doi.org/10.3390/membranes10080164
APA StyleZhuang, S., Han, N., Zou, Q., Zhang, S., & Song, F. (2020). Insight into Steam Permeation through Perovskite Membrane via Transient Modeling. Membranes, 10(8), 164. https://doi.org/10.3390/membranes10080164