A Molecular Dynamics Investigation of the Temperature Effect on the Mechanical Properties of Selected Thin Films for Hydrogen Separation
Abstract
:1. Introduction
2. Material and MD Simulation Methods
3. Results and Discussion
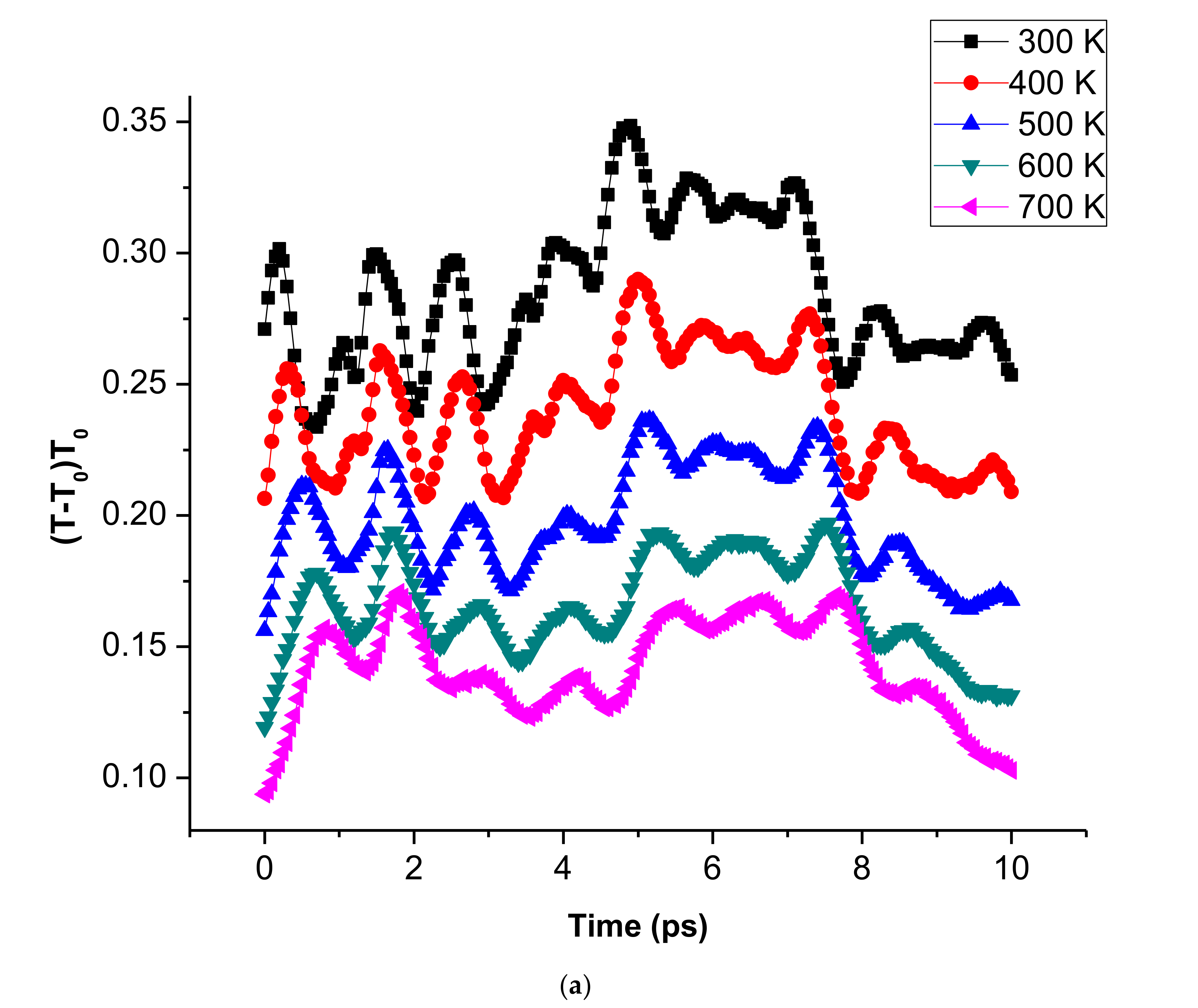
3.1. Effect of Temperature Distribution during Nanoindentation Test
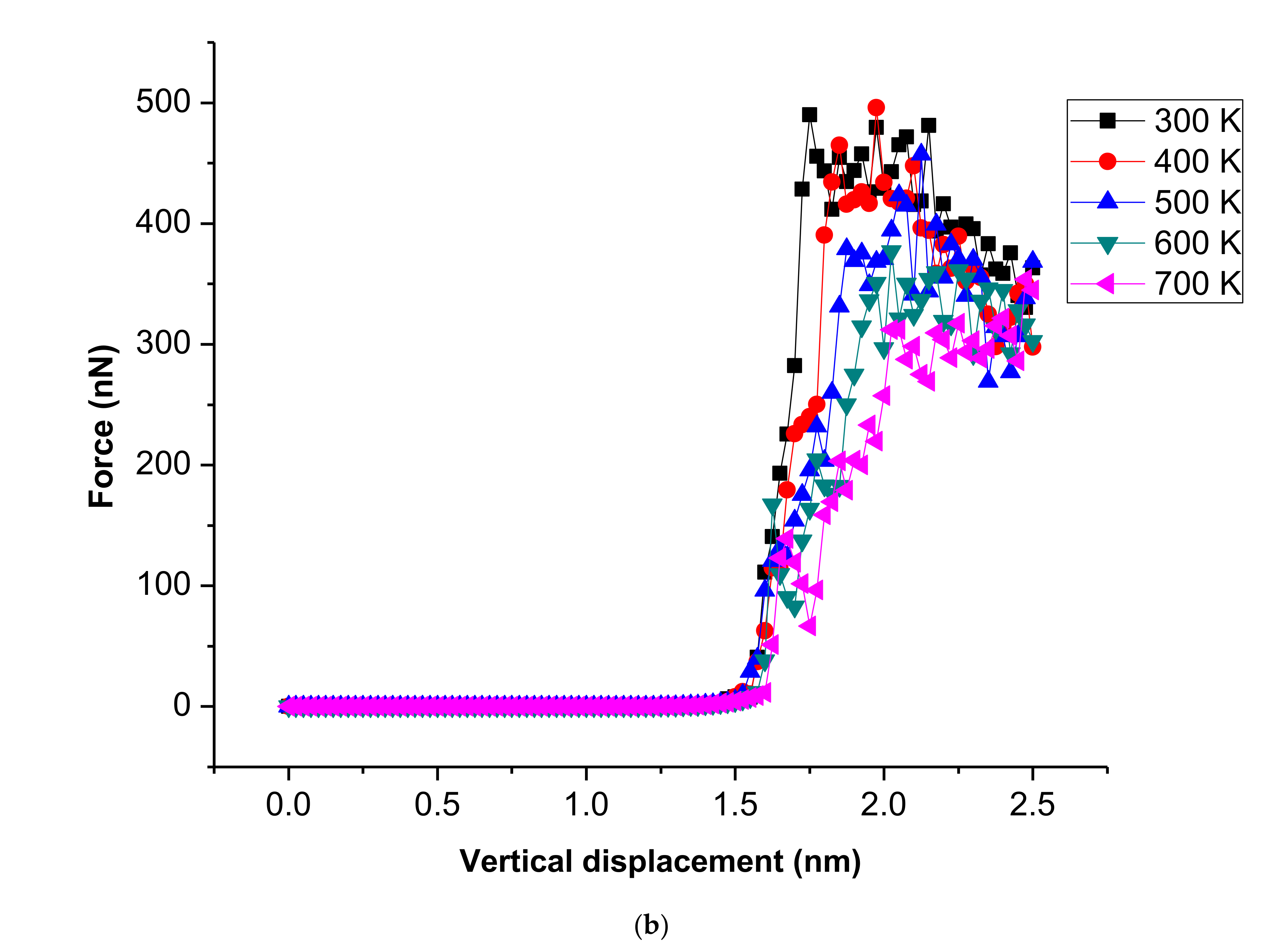
3.2. Effect of Indentation Loading Rate on the Thin Film Mechanical Properties
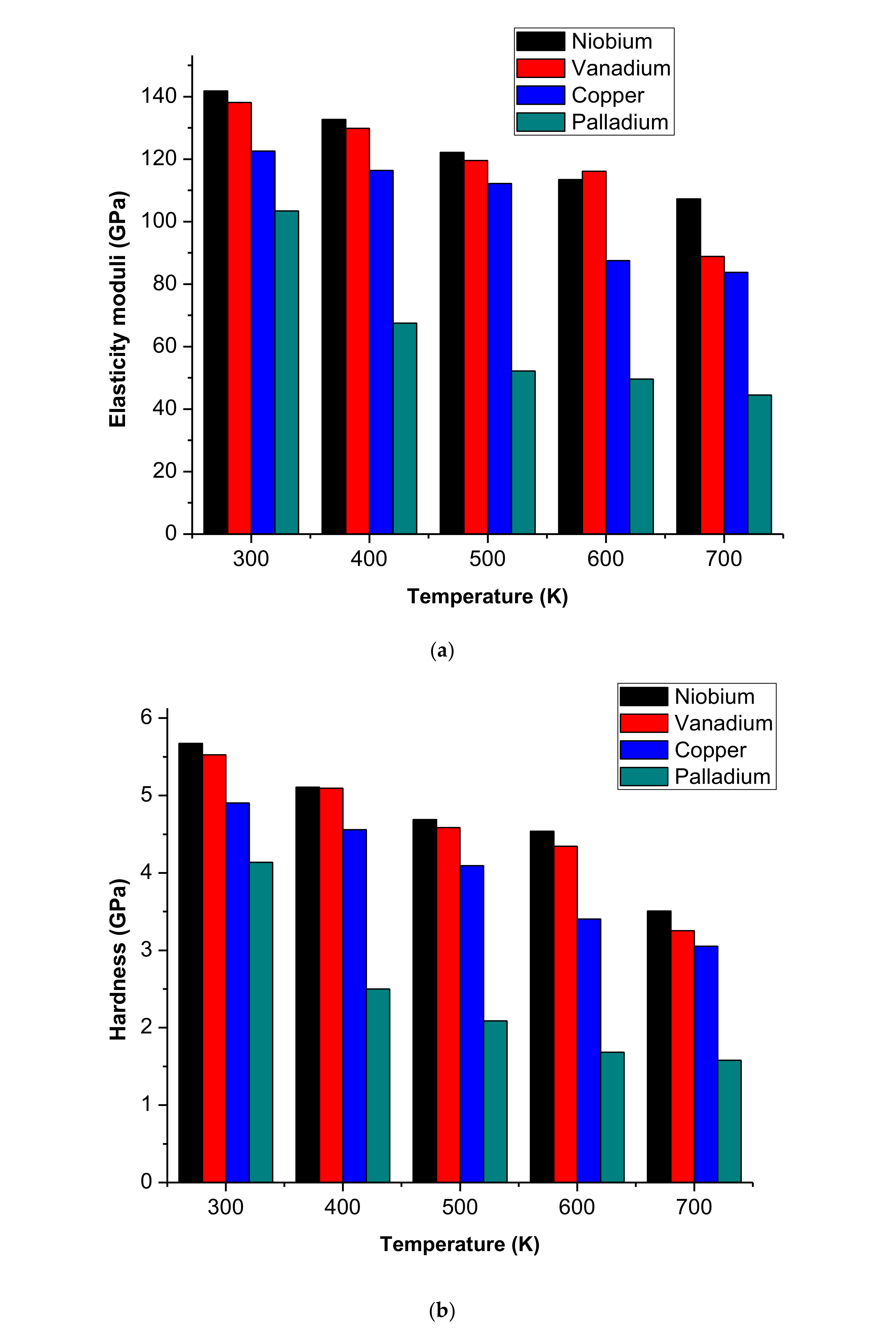
3.3. Comparison with Previous Experimental and Numerical Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cherne, I.J.; Deymier, P.A. Calculation of the transport properties of liquid aluminum with equilibrium and non-equilibrium molecular dynamics. Scr. Mater. 2001, 45, 985–991. [Google Scholar] [CrossRef]
- Cao, Y.; Allameh, S.; Nankivil, D.; Sathiaraj, T.S.; Otiti, T.; Soboyejo, W. Nanoindentation measurements of the mechanical properties of polycrystalline Au and Ag thin films on silicon substrates: Effects of grain size and film thickness. Mater. Sci. Eng. A 2008, 494, 466. [Google Scholar] [CrossRef]
- Oyinbo, S.T.; Jen, T.-C. A comparative review on cold gas dynamic spraying processes and technologies. Manuf. Rev. 2019, 11–13. [Google Scholar] [CrossRef] [Green Version]
- Ayatollahi, M.R.; Rahimi, A.S.; Karimzadeh, A. Atomic Simulation of Temperature Effect on the Mechanical Properties of Thin Films. Mech. Adv. Compos. Struct. 2015, 2, 31–38. [Google Scholar]
- Lee, D.H.; Choi, I.C.; Yang, G.; Lu, Z.; Kawasaki, M.; Ramamurty, U.; Schwaiger, R.; Jang, J.I. Activation energy for plastic flow in nanocrystalline CoCrFeMnNi high-entropy alloy: A high temperature nanoindentation study. Scr. Mater. 2018, 156, 129–133. [Google Scholar] [CrossRef]
- Sgambitterra, E.; Maletta, C.; Furgiuele, F. Temperature dependent local phase transformation in shape memory alloys by nanoindentation. Scr. Mater. 2015, 101, 64–67. [Google Scholar] [CrossRef]
- Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar]
- Liu, Y.; Ma, H.; Wei, Y.; Chen, P. Size effect investigation of indentation response of stiff film/compliant substrate composite structure. Int. J. Solids Struct. 2020, 193–194, 106–116. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Y. Effect of surface energy on the indentation response of hard nanofilm/soft substrate composite structure. Int. J. Mech. Sci. 2020, 185, 105759. [Google Scholar] [CrossRef]
- Saha, R.; Nix, W.D. Effects of the substrate on the determination of thin film mechanical properties by nanoindentation. Acta Mater. 2002, 50, 23–38. [Google Scholar] [CrossRef]
- Saha, R.; Xue, Z.; Huang, Y.; Nix, W.D. Indentation of a soft metal film on a hard substrate: Strain gradient hardening effects. J. Mech. Phys. Solids 2001, 49, 1997–2014. [Google Scholar] [CrossRef]
- Burik, P.; Pešek, L.; Voleský, L. Effect of pile-up on the mechanical characteristics of steel with different strain history by depth sensing indentation. In Proceedings of the 23rd International Conference on Metallurgy and Materials, Brno, Czech Republic, 21–23 May 2014. [Google Scholar]
- Li, Y.; Fang, X.; Xia, B.; Feng, X. In situ measurement of oxidation evolution at elevated temperature by nanoindentation. Scr. Mater. 2015, 103, 61–64. [Google Scholar] [CrossRef]
- Oyinbo, S.T.; Jen, T. Molecular dynamics investigation of temperature effect and surface configurations on multiple impacts plastic deformation in a palladiumcopper composite metal membrane (CMM): A cold gas dynamic spray (CGDS) process. Comput. Mater. Sci. 2020, 185, 109968. [Google Scholar] [CrossRef]
- Oyinbo, S.T.; Jen, T.-C.; Zhu, Y.; Abegunde, O.O.; Aasa, S. Development of Palladium Nanoparticles deposition on a Copper substrate using a Molecular Dynamic (MD) simulation: A Cold Gas Dynamic spray process. Manuf. Rev. 2020, 7, 1–15. [Google Scholar] [CrossRef]
- Shi, Y.; Falk, M.L. Structural transformation and localization during simulated nanoindentation of a noncrystalline metal film. Appl. Phys. Lett. 2005, 86. [Google Scholar] [CrossRef]
- Peng, P.; Liao, G.; Shi, T.; Tang, Z.; Gao, Y. Molecular dynamic simulations of nanoindentation in aluminum thin film on silicon substrate. Appl. Surf. Sci. 2010, 256, 6284–6290. [Google Scholar] [CrossRef]
- Hwang, S.F.; Li, Y.H.; Hong, Z.H. Molecular dynamic simulation for Cu cluster deposition on Si substrate. Comput. Mater. Sci. 2012, 56, 85–94. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short–Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Erkoç, Ş. Empirical Potential Energy Functions Used in the simulation of materials properties. Annu. Rev. Comput. Phys. 2001, 9, 1–103. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Cai, J.; Ye, Y.Y. Simple analytical embedded-atom-potential model including a long-range force for fcc metals and their alloys. Phys. Rev. B 1996, 54, 8398–8410. [Google Scholar] [CrossRef] [PubMed]
- Braga, C.; Travis, K.P. A configurational temperature Nosé-Hoover thermostat. J. Chem. Phys. 2005, 123, 134101. [Google Scholar] [CrossRef] [PubMed]
- Oyinbo, S.T.; Jen, T.C. Investigation of the process parameters and restitution coefficient of ductile materials during cold gas dynamic spray (CGDS) using finite element analysis. Addit. Manuf. 2020, 31, 100986. [Google Scholar] [CrossRef]
- Lebedev, A.B.; Burenkov, Y.A.; Romanov, A.E.; Kopylov, V.I.; Filonenko, V.P.; Gryaznov, V.G. Softening of the elastic modulus in submicrocrystalline copper. Mater. Sci. Eng. A 1995, 203, 165–170. [Google Scholar] [CrossRef]
- Huang, Z.; Gu, L.Y.; Weertman, J.R. Temperature dependence of hardness of nanocrystalline copper in low-temperature range. Scr. Mater. 1997, 37, 1071–1075. [Google Scholar] [CrossRef]
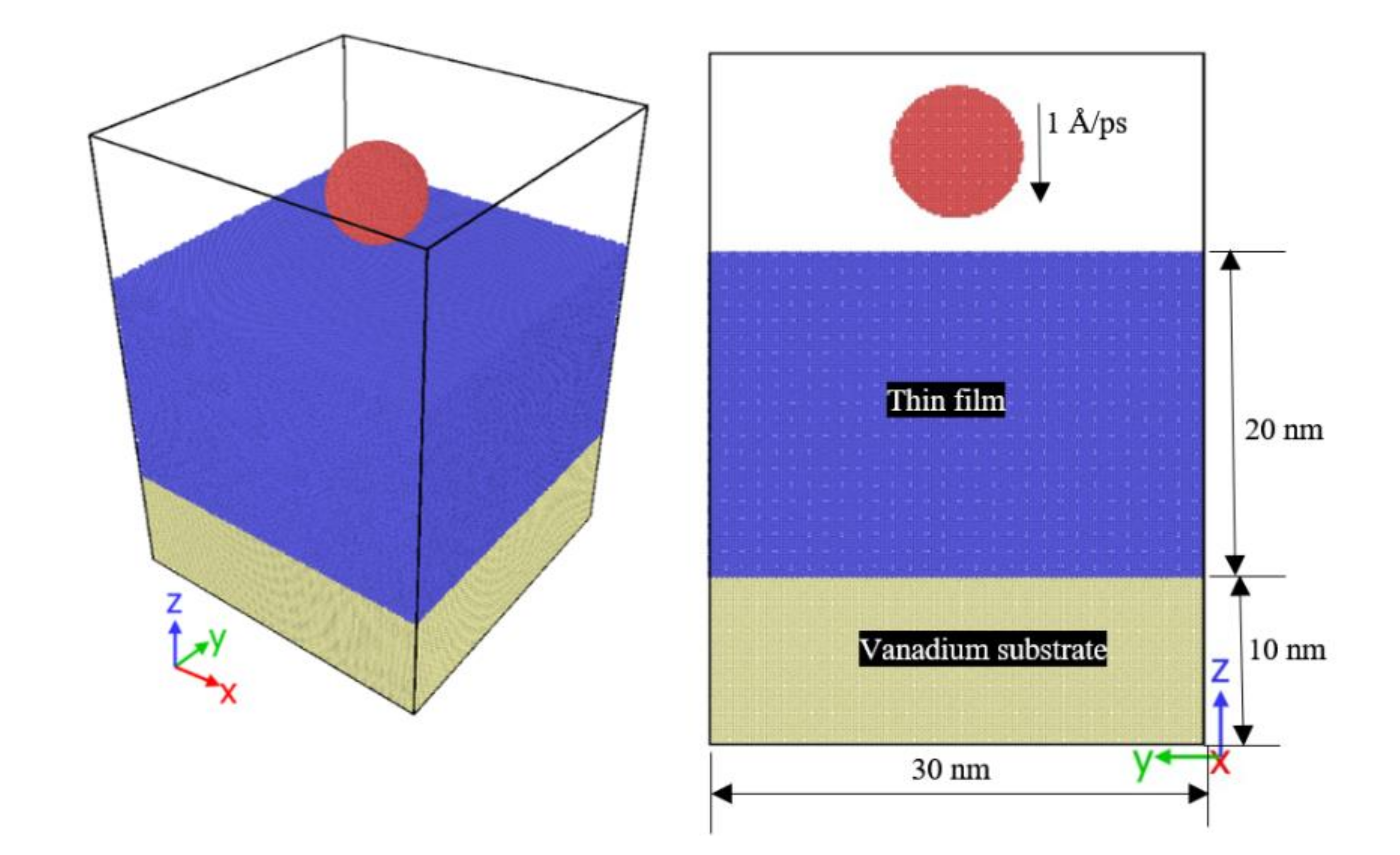



| Materials | Thin Films | Rectangular Block—30 nm × 30 nm × 20 nm Palladium (1,237,288 Atoms), Vanadium (1,306,866 atoms), Copper (1,515,580 Atoms) and (Niobium (1,002,001 Atoms) |
| Substrate | Rectangular block—30 nm × 30 nm × 10 nm Vanadium (663,433 atoms) | |
| Indenter | Spherical diamond indenter (diameter: 10 nm), 23,669 atoms | |
| Operating conditions | Duration of simulation | 10 ps (10,000 fs) |
| Timestep | 0.5 fs (0.0005 ps) | |
| Loading rate | 0.5 Å/ps | |
| Potential used | Lennard-Jones, Tersoff and EAM | |
| Preheating temperature | 300, 400, 500, 600 and 700 K | |
| Boundary condition | p p s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyinbo, S.T.; Jen, T.-C. A Molecular Dynamics Investigation of the Temperature Effect on the Mechanical Properties of Selected Thin Films for Hydrogen Separation. Membranes 2020, 10, 241. https://doi.org/10.3390/membranes10090241
Oyinbo ST, Jen T-C. A Molecular Dynamics Investigation of the Temperature Effect on the Mechanical Properties of Selected Thin Films for Hydrogen Separation. Membranes. 2020; 10(9):241. https://doi.org/10.3390/membranes10090241
Chicago/Turabian StyleOyinbo, Sunday Temitope, and Tien-Chien Jen. 2020. "A Molecular Dynamics Investigation of the Temperature Effect on the Mechanical Properties of Selected Thin Films for Hydrogen Separation" Membranes 10, no. 9: 241. https://doi.org/10.3390/membranes10090241
APA StyleOyinbo, S. T., & Jen, T.-C. (2020). A Molecular Dynamics Investigation of the Temperature Effect on the Mechanical Properties of Selected Thin Films for Hydrogen Separation. Membranes, 10(9), 241. https://doi.org/10.3390/membranes10090241







