Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel
Abstract
:1. Introduction
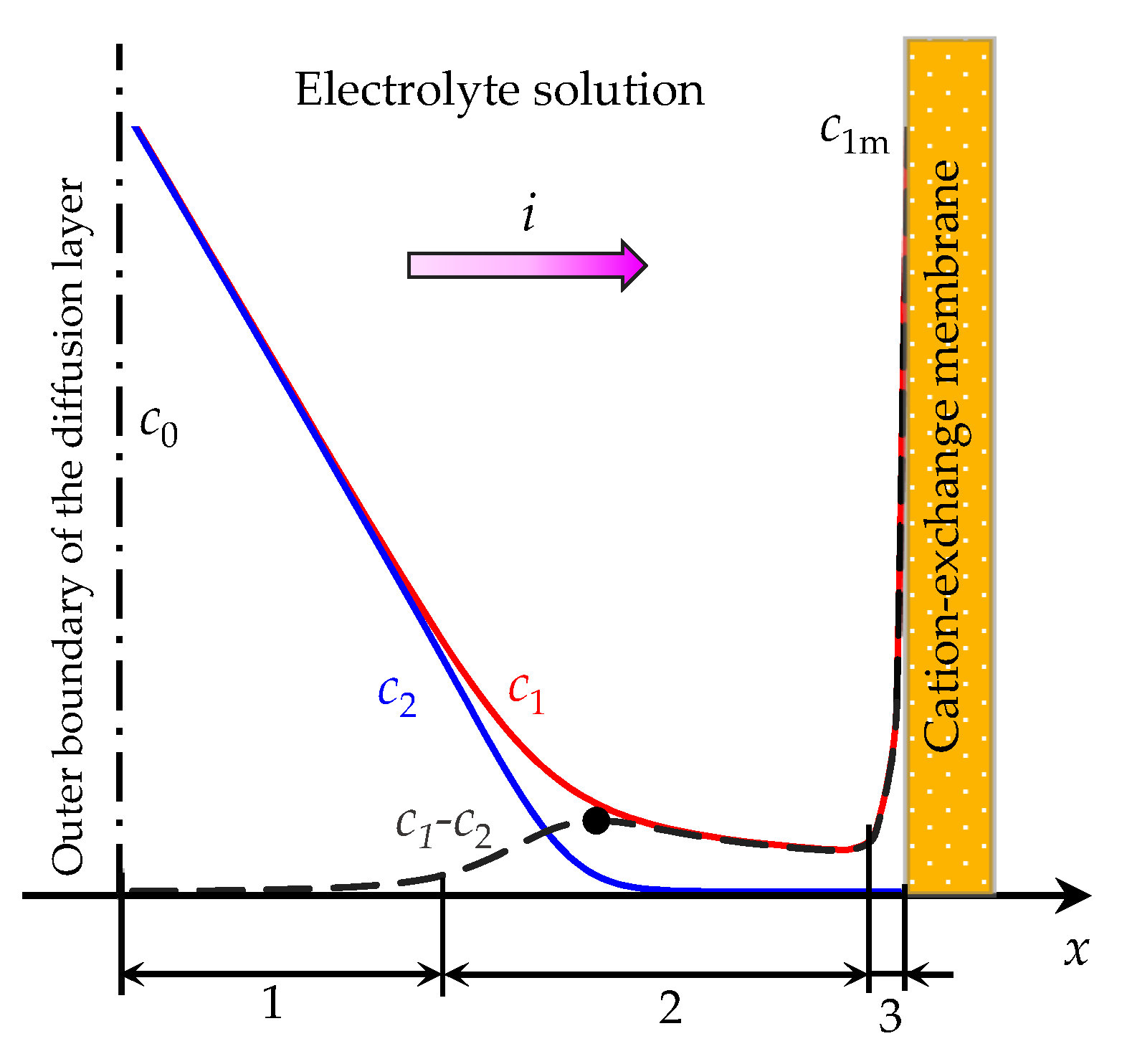
2. Mathematical Model
2.1. Governing Equations and Boundary Conditions
2.2. System Parameters
3. Results and Discussion
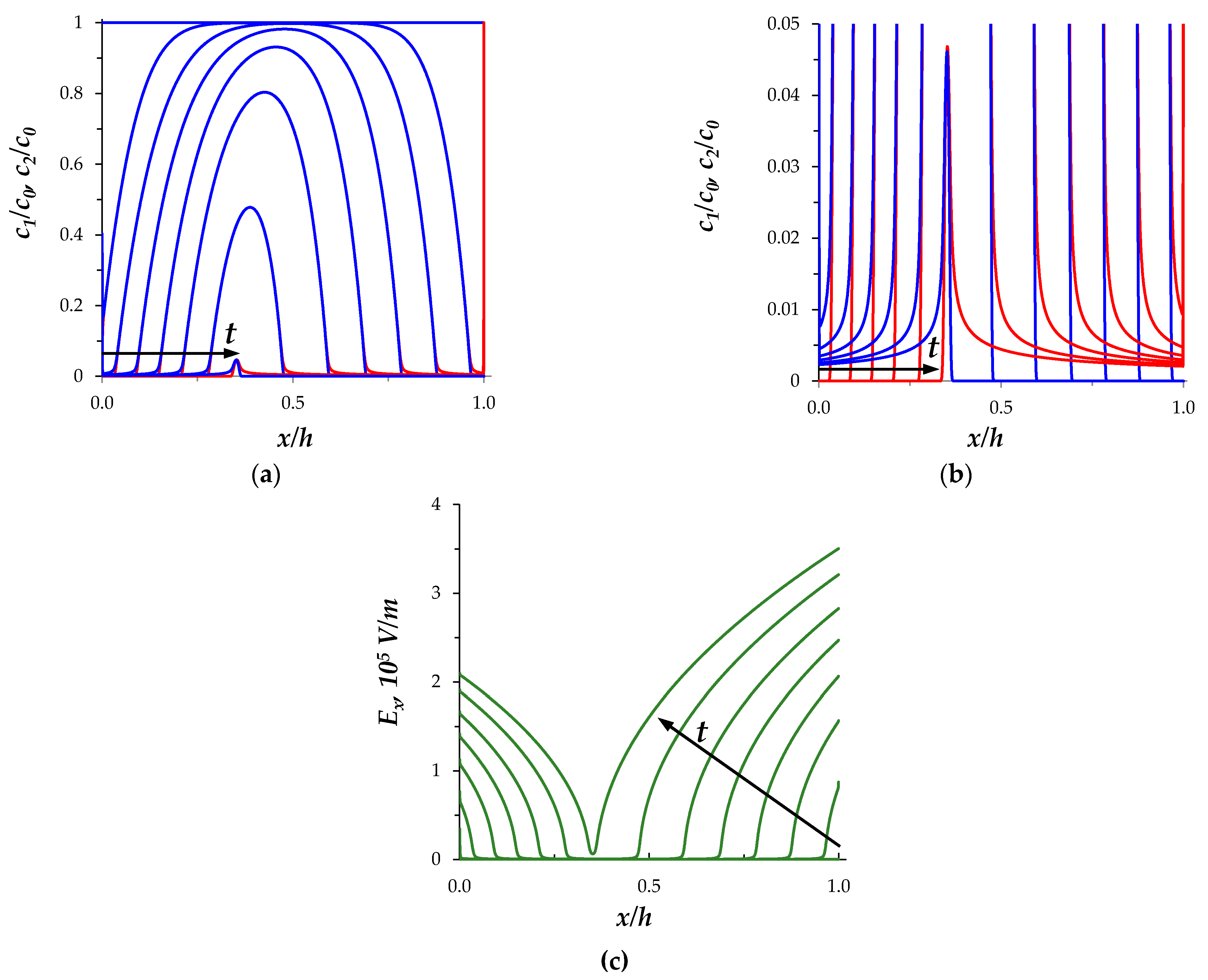
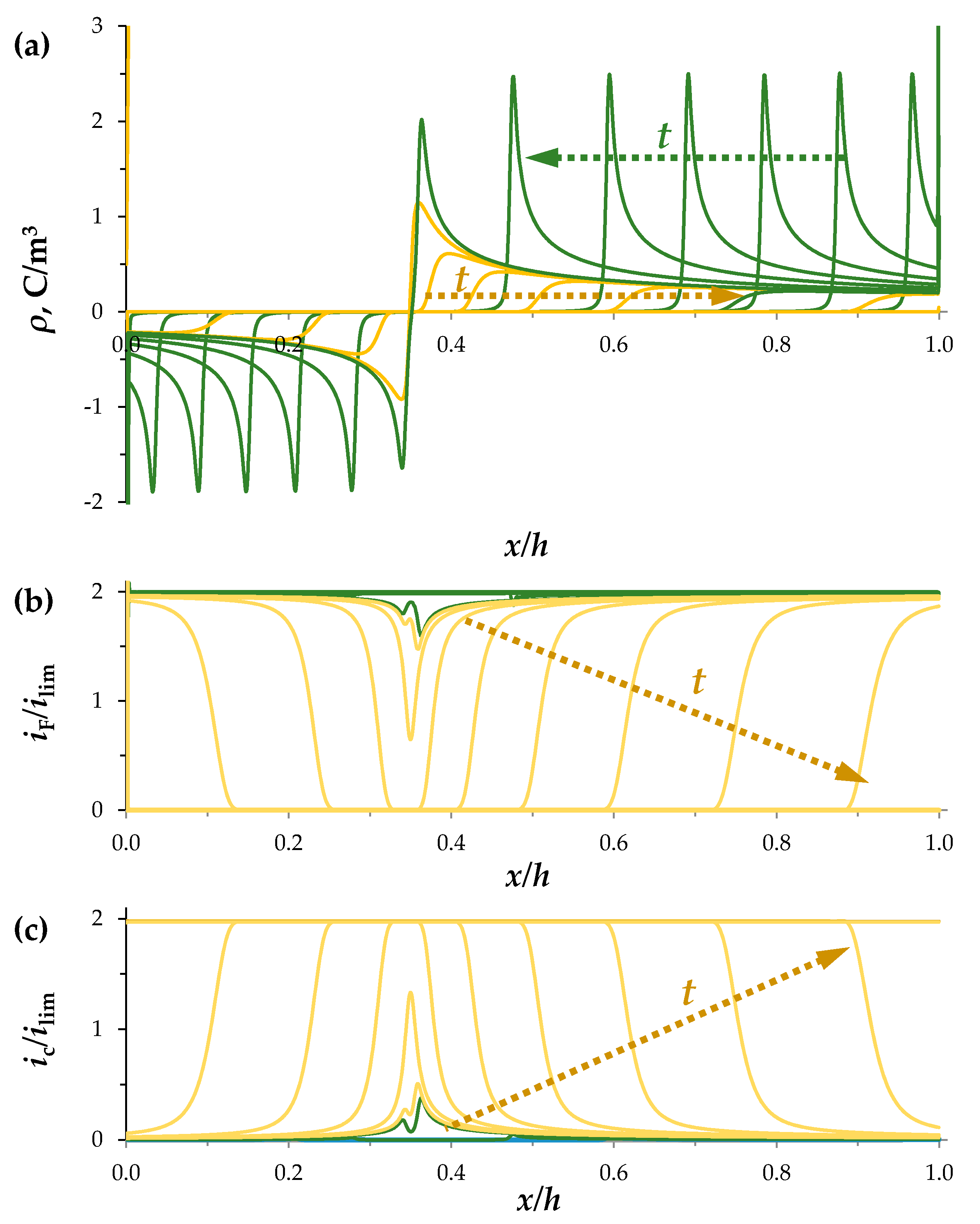
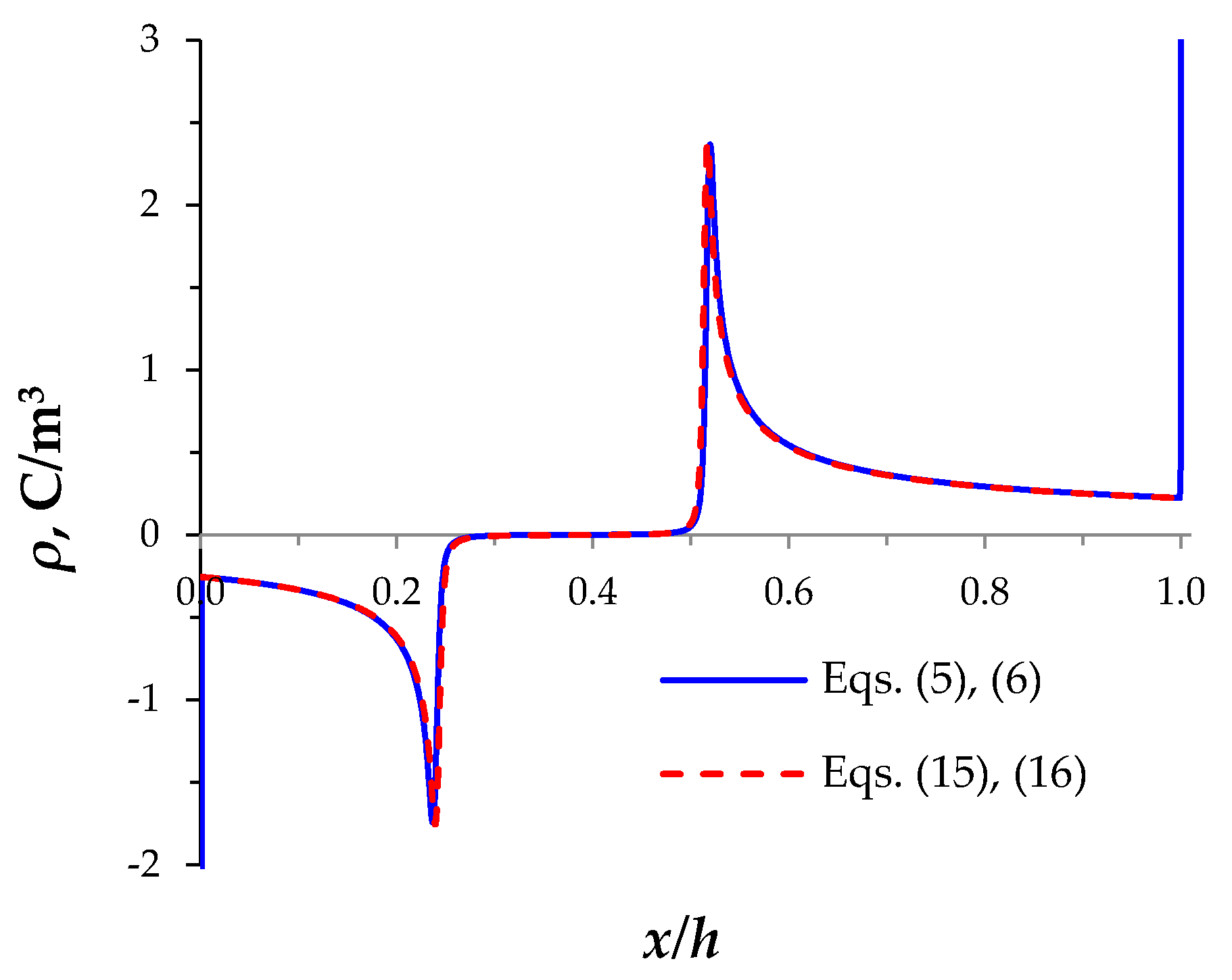
3.1. Space-Charge Breakdown
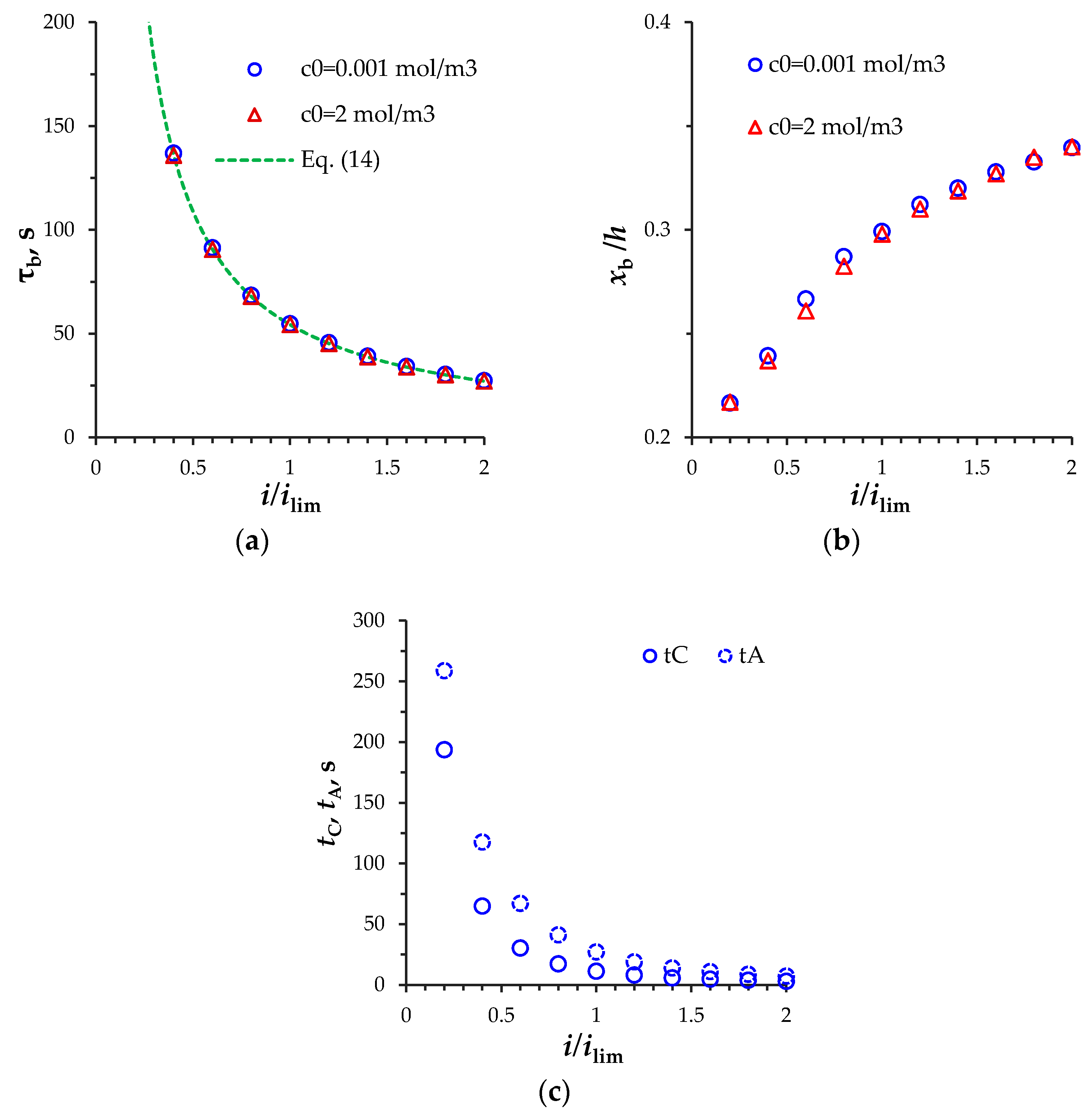
3.2. Estimation of the Space-Charge Breakdown Time
3.3. Simplification of the Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Mariñas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nat. Cell Biol. 2008, 452, 301–310. [Google Scholar] [CrossRef]
- Kim, S.J.; Song, Y.-A.; Han, J. Nanofluidic concentration devices for biomolecules utilizing ion concentration polarization: Theory, fabrication, and applications. Chem. Soc. Rev. 2010, 39, 912–922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elimelech, M.; Phillip, W.A. The Future of Seawater Desalination: Energy, Technology, and the Environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmental Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes 2020, 10, 146. [Google Scholar] [CrossRef]
- Wilson, J.R. Demineralization by Electrodialysis; Butterworths Scientific Publ.: London, UK, 1960. [Google Scholar]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Zaltzman, B.; Rubinstein, I. Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 2007, 579, 173–226. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Shaposhnik, V.; Vasil’Eva, V.; Praslov, D. Concentration fields of solutions under electrodialysis with ion-exchange membranes. J. Membr. Sci. 1995, 101, 23–30. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasil’Eva, V.I.; Grigorchuk, O.V. The interferometric investigations of electromembrane processes. Adv. Colloid Interface Sci. 2008, 139, 74–82. [Google Scholar] [CrossRef]
- Frilette, V.J. Electrogravitational Transport at Synthetic Ion Exchange Membrane Surfaces. J. Phys. Chem. 1957, 61, 168–174. [Google Scholar] [CrossRef]
- Balster, J.; Yildirim, M.H.; Stamatialis, D.F.; Ibanez, R.; Lammertink, R.G.; Jordan, V.; Wessling, M. Morphology and Microtopology of Cation-Exchange Polymers and the Origin of the Overlimiting Current. J. Phys. Chem. B 2007, 111, 2152–2165. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Mareev, S.; Pis’Menskaya, N.D.; Uzdenova, A.; Kovalenko, A.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Shi, P. Shear electroconvective instability in electrodialysis channel under extreme depletion and its scaling laws. Phys. Rev. E 2020, 101, 043105. [Google Scholar] [CrossRef] [PubMed]
- Urtenov, M.; Chubyr, N.; Gudza, V. Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes 2020, 10, 189. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A.; Wessling, M.; Nikonenko, V.; Mareev, S.; Moroz, I.; Evdochenko, E.; Urtenov, M.K. Space-Charge breakdown phenomenon and spatio-temporal ion concentration and fluid flow patterns in overlimiting current electrodialysis. J. Membr. Sci. 2021, 636, 119583. [Google Scholar] [CrossRef]
- Barros, K.S.; Martí-Calatayud, M.C.; Scarazzato, T.; Bernardes, A.M.; Espinosa, D.C.R.; Pérez-Herranz, V. Investigation of ion-exchange membranes by means of chronopotentiometry: A comprehensive review on this highly informative and multipurpose technique. Adv. Colloid Interface Sci. 2021, 293, 102439. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Murphy, W.D.; Mafe, S.; Reiss, H. Numerical simulation of the nonequilibrium diffuse double layer in ion-exchange membranes. J. Phys. Chem. 1993, 97, 8524–8530. [Google Scholar] [CrossRef]
- Brumleve, T.R.; Buck, R.P. Numerical solution of the Nernst-Planck and poisson equation system with applications to membrane electrochemistry and solid state physics. J. Electroanal. Chem. Interfacial Electrochem. 1978, 90, 1–31. [Google Scholar] [CrossRef]
- Larchet, C.; Nouri, S.; Auclair, B.; Dammak, L.; Nikonenko, V. Application of chronopotentiometry to determine the thickness of diffusion layer adjacent to an ion-exchange membrane under natural convection. Adv. Colloid Interface Sci. 2008, 139, 45–61. [Google Scholar] [CrossRef]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef] [Green Version]
- Nikonenko, V.V.; Zabolotsky, V.I.; Gnusin, N.P. Electromigration of ions through a diffusion layer with broken electroneutrality. Sov. J. Electrochem. 1989, 25, 301–305. [Google Scholar]
- Larchet, C.; Auclair, B.; Nikonenko, V. Approximate evaluation of water transport number in ion-exchange membranes. Electrochim. Acta 2004, 49, 1711–1717. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdenova, A.; Urtenov, M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes 2021, 11, 873. https://doi.org/10.3390/membranes11110873
Uzdenova A, Urtenov M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes. 2021; 11(11):873. https://doi.org/10.3390/membranes11110873
Chicago/Turabian StyleUzdenova, Aminat, and Makhamet Urtenov. 2021. "Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel" Membranes 11, no. 11: 873. https://doi.org/10.3390/membranes11110873
APA StyleUzdenova, A., & Urtenov, M. (2021). Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes, 11(11), 873. https://doi.org/10.3390/membranes11110873






