An Empirical Modeling of Gate Voltage-Dependent Behaviors of Amorphous Oxide Semiconductor Thin-Film Transistors including Consideration of Contact Resistance and Disorder Effects at Room Temperature
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Mathematical Formulations for AOS TFTs
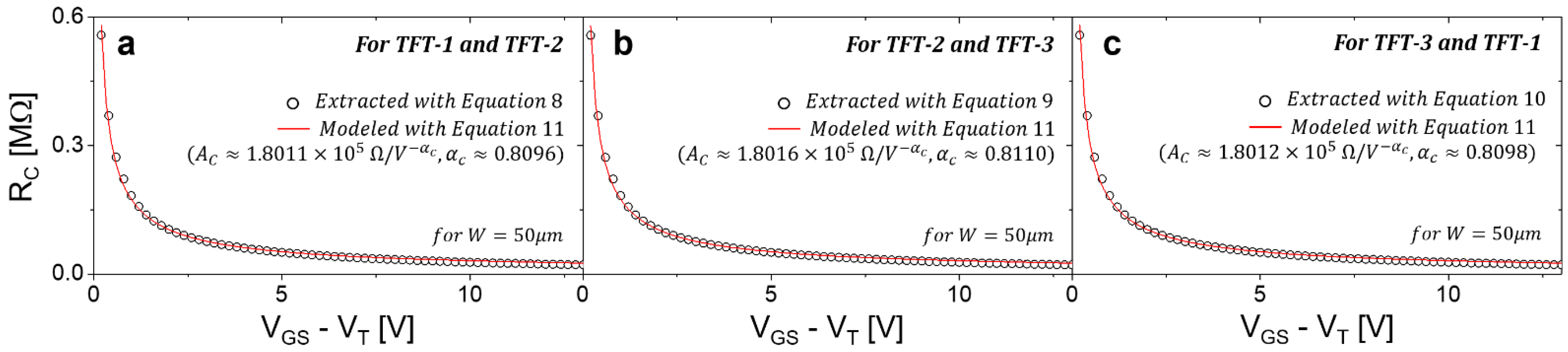
3.2. Contact Resistance and Transfer Characteristics of two TFTs
3.3. Intrinsic Channel Conductance and Tail States
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hosono, H. How we made the IGZO transistor. Nat. Electron. 2018, 1, 428. [Google Scholar] [CrossRef]
- Lee, S.; Nathan, A. Subthreshold Schottky-barrier thin-film transistors with ultralow power and high intrinsic gain. Science 2016, 354, 302–304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nomura, K.; Kamiya, T.; Hosono, H. Ambipolar oxide thin-film transistor. Adv. Mater. 2011, 23, 3431–3434. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.-H.; Jang, J.-H.; Kim, J.-J.; Han, M.-K. Low-temperature organic (CYTOP) passivation for improvement of electric characteristics and reliability in IGZO TFTs. IEEE Electron Device Lett. 2012, 33, 381–383. [Google Scholar] [CrossRef]
- Yu, M.-C.; Ruan, D.-B.; Liu, P.-T.; Chien, T.-C.; Chiu, Y.-C.; Gan, K.-J.; Sze, S.M. High performance transparent a-IGZO thin film transistors with ALD-HfO2 gate insulator on colorless polyimide substrate. IEEE Trans. Nanotechnol. 2020, 19, 481–485. [Google Scholar] [CrossRef]
- Lee, S.; Nathan, A.; Robertson, J.; Ghaffarzadeh, K.; Pepper, M.; Jeon, S.; Kim, C.; Song, I.-H.; Chung, U.-I.; Kim, K. Temperature dependent electron transport in amorphous oxide semiconductor thin film transistors. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011. [Google Scholar] [CrossRef]
- Mondal, S. Controllable surface contact resistance in solution-processed thin-film transistors due to dimension modification. Semicond. Sci. Technol. 2020, 35, 10LT02. [Google Scholar] [CrossRef]
- Cha, H.-S.; Jeong, H.-S.; Hwang, S.-H.; Lee, D.-H.; Kwon, H.-I. Electrical performance and stability improvements of high-mobility indium–gallium–tin oxide thin-film transistors using an oxidized aluminum capping layer of optimal thickness. Electronics 2020, 9, 2196. [Google Scholar] [CrossRef]
- Cheng, X.; Lee, S.; Nathan, A. TFT small signal model and analysis. IEEE Electron Device Lett. 2016, 37, 890–893. [Google Scholar] [CrossRef] [Green Version]
- Kanicki, J.; Libsch, F.R.; Griffith, J.; Polastre, R. Performance of thin hydrogenated amorphous silicon thin-film transistors. J. Appl. Phys. 1991, 69, 2339–2345. [Google Scholar] [CrossRef]
- Lee, S. Bias-dependent subthreshold characteristics and interface states in disordered semiconductor thin-film transistors. Semicond. Sci. Technol. 2019, 34, 11LT01. [Google Scholar] [CrossRef]
- Lee, S. A semiphysical current–voltage model with a contact ideality factor for disordered thin-film transistors. J. Comput. Electron. 2018, 17, 1615–1620. [Google Scholar] [CrossRef]
- Kamiya, T.; Nomura, K.; Hosono, H. Electronic structures above mobility edges in crystalline and amorphous In-Ga-Zn-O: Percolation conduction examined by analytical model. J. Disp. Technol. 2009, 5, 462–467. [Google Scholar] [CrossRef]
- Kimura, M.; Kamiya, T.; Nakanishi, T.; Nomura, K.; Hosono, H. Intrinsic carrier mobility in amorphous In–Ga–Zn–O thin-film transistors determined by combined field-effect technique. Appl. Phys. Lett. 2010, 96, 262105. [Google Scholar] [CrossRef]
- Lee, S.; Ghaffarzadeh, K.; Nathan, A.; Robertson, J.; Jeon, S.; Kim, C.; Song, I.-H.; Chung, U.-I. Trap-limited and percolation conduction mechanisms in amorphous oxide semiconductor thin film transistors. Appl. Phys. Lett. 2011, 98, 203508. [Google Scholar] [CrossRef]
- Lee, S.; Nathan, A. Conduction threshold in accumulation-mode InGaZnO thin film transistors. Sci. Rep. 2016, 6, 22567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Zhang, X.; Wang, L.; Zhang, L.; Chan, M. Gate-controlled electron injection in tunneling contact IGZO TFTs. In Proceedings of the 2017 International Conference on Electron Devices and Solid-State Circuits (EDSSC), Hsinchu, Taiwan, 18–20 October 2017. [Google Scholar] [CrossRef]
- Lee, S.; Nathan, A. Localized tail state distribution in amorphous oxide transistors deduced from low temperature measurements. Appl. Phys. Lett. 2012, 101, 113502. [Google Scholar] [CrossRef]
- Powell, M.J. Charge trapping instabilities in amorphous silicon-silicon nitride thin-film transistors. Appl. Phys. Lett. 1983, 43, 597–599. [Google Scholar] [CrossRef]
- Shur, M.; Hack, M. Physics of amorphous silicon based alloy field-effect transistors. J. Appl. Phys. 1984, 55, 3831–3842. [Google Scholar] [CrossRef]
- Kimura, M.; Matsuda, T. (Invited) extraction of trap densities in tfts using C-V characteristics. ECS Trans. 2014, 64, 45–50. [Google Scholar] [CrossRef]
- Kamiya, T.; Hosono, H. Material characteristics and applications of transparent amorphous oxide semiconductors. NPG Asia Mater. 2010, 2, 15–22. [Google Scholar] [CrossRef] [Green Version]



| Examined IGZO TFTs | Channel Length (L) | Channel Width (W) |
|---|---|---|
| TFT-1 | L1= 10 μm | W = 50 μm (common) (W = W1 = W2 = W3) |
| TFT-2 | L2= 20 μm | |
| TFT-3 | L3= 30 μm |
| Non-Ideal Effects | Model Equations | Model Parameters |
|---|---|---|
| Contact Resistance | (for example of TFT-1 and TFT-2) | AC ≈ 1.8 × 105 for W = 50 μm αc ≈ 0.81 |
| Disorder (Traps) | Kn ≈ 8.29 × 10−8 αt ≈ 0.18 kTt ≈ 4.7 meV i.e., Tt ≈ 54 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S. An Empirical Modeling of Gate Voltage-Dependent Behaviors of Amorphous Oxide Semiconductor Thin-Film Transistors including Consideration of Contact Resistance and Disorder Effects at Room Temperature. Membranes 2021, 11, 954. https://doi.org/10.3390/membranes11120954
Lee S. An Empirical Modeling of Gate Voltage-Dependent Behaviors of Amorphous Oxide Semiconductor Thin-Film Transistors including Consideration of Contact Resistance and Disorder Effects at Room Temperature. Membranes. 2021; 11(12):954. https://doi.org/10.3390/membranes11120954
Chicago/Turabian StyleLee, Sungsik. 2021. "An Empirical Modeling of Gate Voltage-Dependent Behaviors of Amorphous Oxide Semiconductor Thin-Film Transistors including Consideration of Contact Resistance and Disorder Effects at Room Temperature" Membranes 11, no. 12: 954. https://doi.org/10.3390/membranes11120954
APA StyleLee, S. (2021). An Empirical Modeling of Gate Voltage-Dependent Behaviors of Amorphous Oxide Semiconductor Thin-Film Transistors including Consideration of Contact Resistance and Disorder Effects at Room Temperature. Membranes, 11(12), 954. https://doi.org/10.3390/membranes11120954






