Removal of Sulfadiazine by Polyamide Nanofiltration Membranes: Measurement, Modeling, and Mechanisms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Membranes and Chemicals
2.2. Membrane Pore Size Determination
2.3. Experiment System and Operations
2.4. Analytical Methods
2.5. Membrane Characterization
2.6. Solute Transport Model
3. Results and Discussion
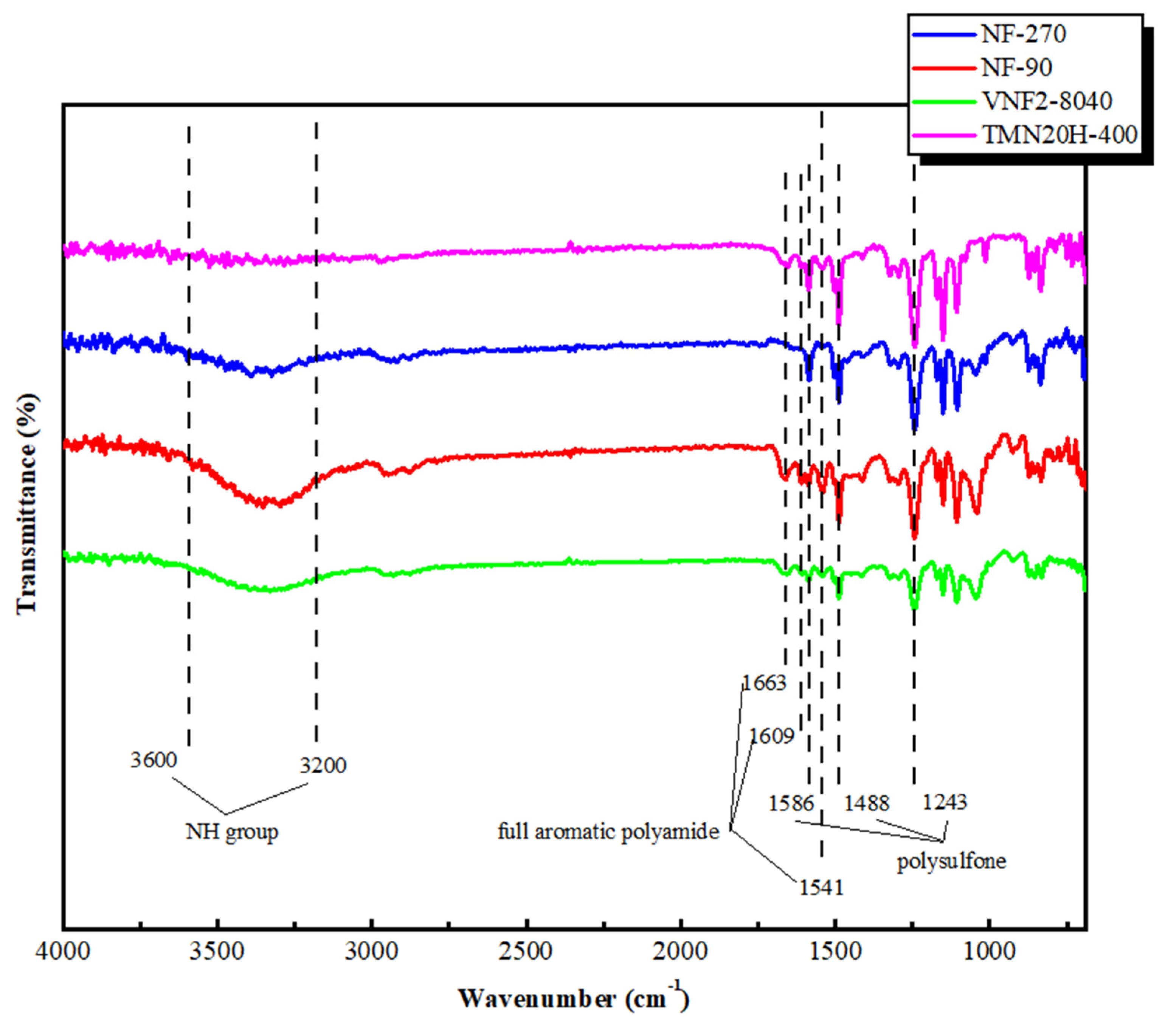
3.1. ATR-FTIR Analysis
3.2. XPS Analysis
3.3. NF Membrane Pore Size Estimation
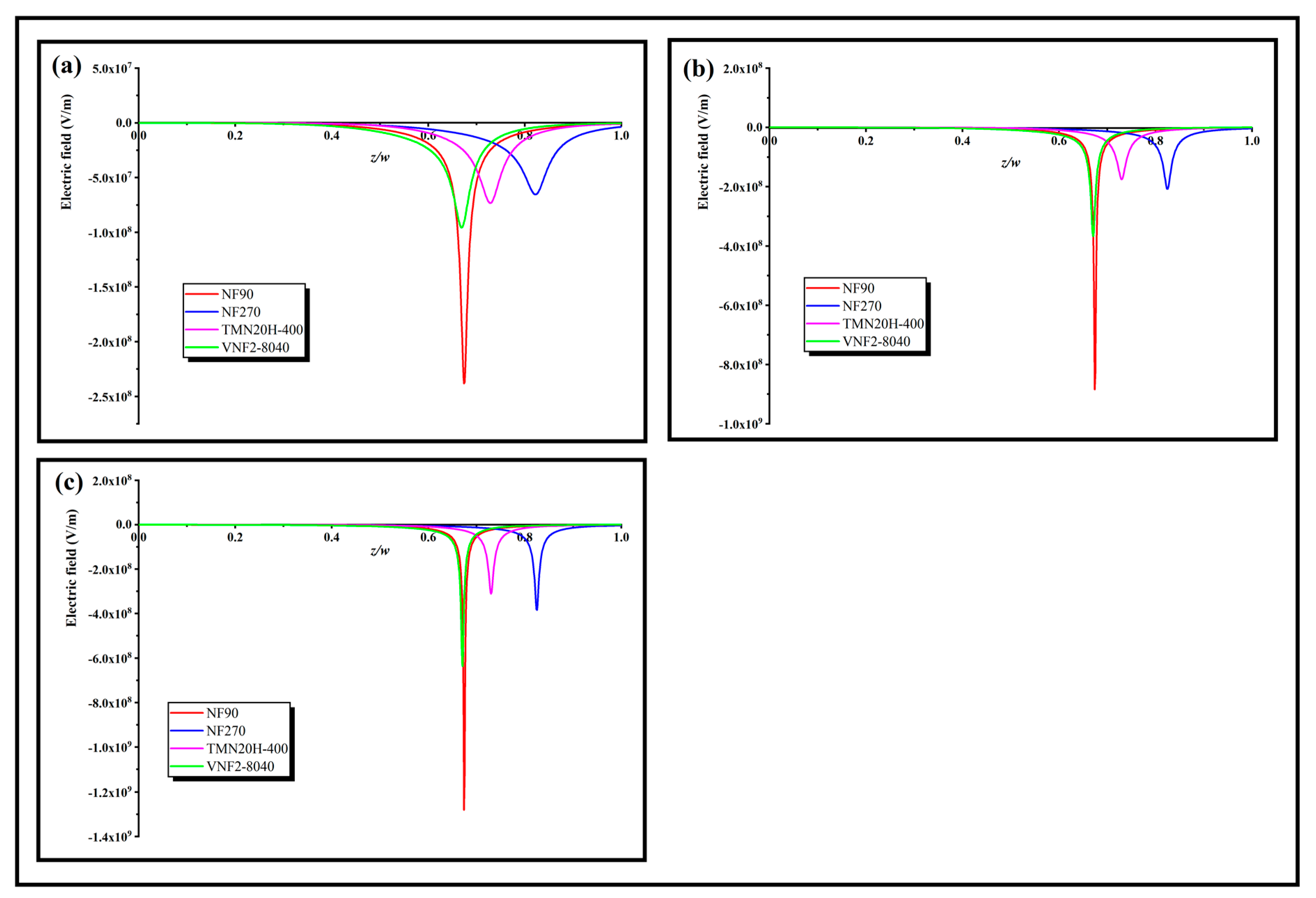
3.4. Pore Dielectric Constant Calculation
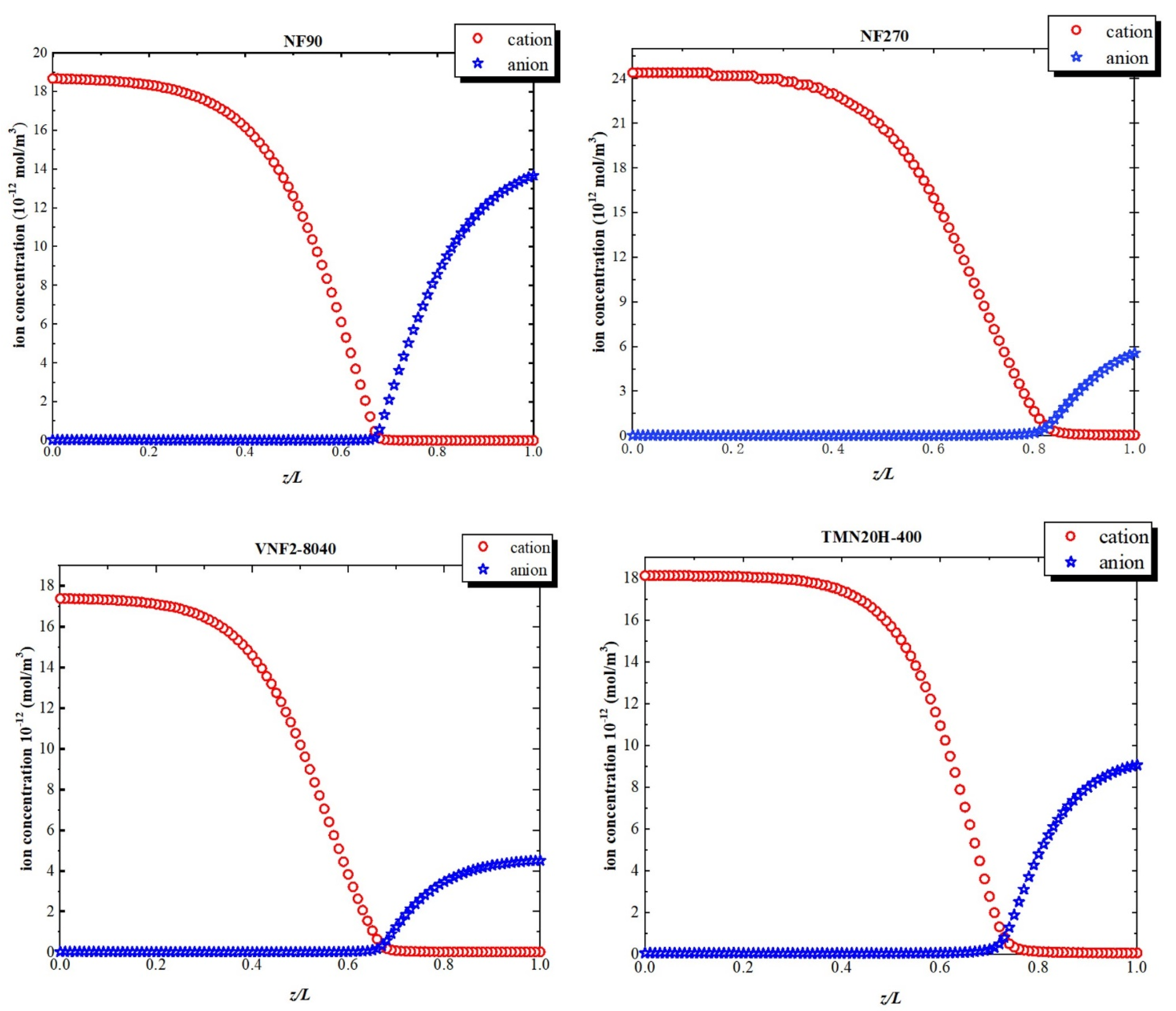
3.5. Surface Fixed Charge Analysis
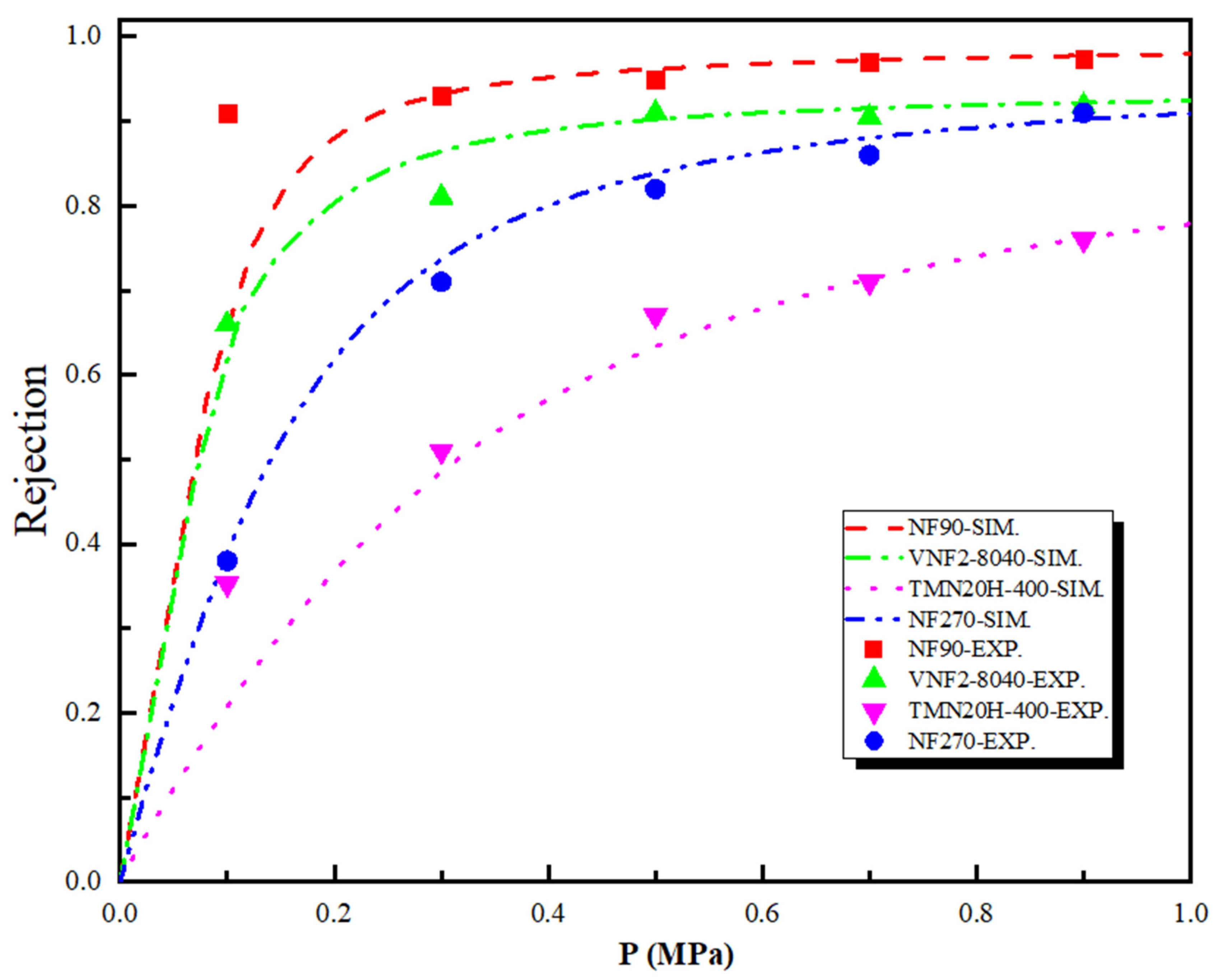
3.6. Separation Performance and Mechanism of Sulfadiazine
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petrie, B.; Barden, R.; Kasprzyk-Hordern, B. A review on emerging contaminants in wastewaters and the environment: Current knowledge, understudied areas and recommendations for future monitoring. Water Res. 2015, 72, 3–27. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Liu, G.; Lv, W.; Yao, K.; Zhang, X.; Xiao, H. Photodegradation of naproxen in water under simulated solar radiation: Mechanism, kinetics, and toxicity variation. Environ. Sci. Pollut. Res. 2014, 21, 7797–7804. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Niu, X.; Yang, J.; Wang, C.; Lu, M. Retentions of bisphenol A and norfloxacin by three different ultrafiltration membranes in regard to drinking water treatment. Chem. Eng. J. 2016, 294, 410–416. [Google Scholar] [CrossRef]
- Radjenović, J.; Petrović, M.; Ventura, F.; Barceló, D. Rejection of pharmaceuticals in nanofiltration and reverse osmosis membrane drinking water treatment. Water Res. 2008, 42, 3601–3610. [Google Scholar] [CrossRef]
- Mamo, J.; García-Galán, M.J.; Stefani, M.; Rodríguez-Mozaz, S.; Barceló, D.; Monclús, H.; Rodriguez-Roda, I.; Comas, J. Fate of pharmaceuticals and their transformation products in integrated membrane systems for wastewater reclamation. Chem. Eng. J. 2018, 331, 450–461. [Google Scholar] [CrossRef] [Green Version]
- Andrade, L.H.; Ricci, B.C.; Grossi, L.B.; Pires, W.L.; Aguiar, A.O.; Amaral, M.C.S. Nanofiltration applied in gold mining effluent treatment: Evaluation of chemical cleaning and membrane stability. Chem. Eng. J. 2017, 323, 545–556. [Google Scholar] [CrossRef]
- Wei, X.; Shi, Y.; Fei, Y.; Chen, J.; Lv, B.; Chen, Y.; Zheng, H.; Shen, J.; Zhu, L. Removal of trace phthalate esters from water by thin-film composite nanofiltration hollow fiber membranes. Chem. Eng. J. 2016, 292, 382–388. [Google Scholar] [CrossRef]
- Xu, Y.C.; Wang, Z.X.; Cheng, X.Q.; Xiao, Y.C.; Shao, L. Positively charged nanofiltration membranes via economically mussel-substance-simulated co-deposition for textile wastewater treatment. Chem. Eng. J. 2016, 303, 555–564. [Google Scholar] [CrossRef]
- Freger, V. Nanoscale Heterogeneity of Polyamide Membranes Formed by Interfacial Polymerization. Langmuir 2003, 19, 4791–4797. [Google Scholar] [CrossRef]
- Bowen, W.R.; Mohammad, A.W.; Hilal, N. Characterisation of nanofiltration membranes for predictive purposes—Use of salts, uncharged solutes and atomic force microscopy. J. Membr. Sci. 1997, 126, 91–105. [Google Scholar] [CrossRef]
- Berg, P.; Hagmeyer, G.; Gimbel, R. Removal of pesticides and other micropollutants by nanofiltration. Desalination 1997, 113, 205–208. [Google Scholar] [CrossRef]
- Yoon, Y.; Westerhoff, P.; Snyder, S.A.; Wert, E.C.; Yoon, J. Removal of endocrine disrupting compounds and pharmaceuticals by nanofiltration and ultrafiltration membranes. Desalination 2007, 202, 16–23. [Google Scholar] [CrossRef]
- Shah, A.D.; Huang, C.-H.; Kim, J.-H. Mechanisms of antibiotic removal by nanofiltration membranes: Model development and application. J. Membr. Sci. 2012, 389, 234–244. [Google Scholar] [CrossRef]
- Ouyang, Z.; Huang, Z.; Tang, X.; Xiong, C.; Tang, M.; Lu, Y. A dually charged nanofiltration membrane by pH-responsive polydopamine for pharmaceuticals and personal care products removal. Sep. Purif. Technol. 2019, 211, 90–97. [Google Scholar] [CrossRef]
- Yaroshchuk, A.E. Dielectric exclusion of ions from membranes. Adv. Colloid Interface Sci. 2000, 85, 193–230. [Google Scholar] [CrossRef]
- Yaroshchuk, A.E. Non-steric mechanisms of nanofiltration: Superposition of Donnan and dielectric exclusion. Sep. Purif. Technol. 2001, 22–23, 143–158. [Google Scholar] [CrossRef]
- Bandini, S.; Vezzani, D. Nanofiltration modeling: The role of dielectric exclusion in membrane characterization. Chem. Eng. Sci. 2003, 58, 3303–3326. [Google Scholar] [CrossRef]
- Wadekar, S.S.; Vidic, R.D. Influence of Active Layer on Separation Potentials of Nanofiltration Membranes for Inorganic Ions. Environ. Sci. Technol. 2017, 51, 5658–5665. [Google Scholar] [CrossRef]
- Yaroshchuk, A.; Bruening, M.L.; Zholkovskiy, E. Modelling nanofiltration of electrolyte solutions. Adv. Colloid Interface Sci. 2019, 268, 39–63. [Google Scholar] [CrossRef]
- Bandini, S.; Mazzoni, C. Modelling the amphoteric behaviour of polyamide nanofiltration membranes. Desalination 2005, 184, 327–336. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, H.; Li, G.; Mai, Z.; Gu, Y. The effect of dielectric exclusion on the rejection performance of inhomogeneously charged polyamide nanofiltration membranes. J. Nanoparticle Res. 2019, 21, 217. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, H.; Li, A.; Li, G.; Mai, Z.; Gu, Y. Investigating the effect of inhomogeneous fixed charge distribution on dielectric exclusion in nanofiltration membranes. Desalination Water Treat. 2019, 166, 1–8. [Google Scholar] [CrossRef]
- Escoda, A.; Fievet, P.; Lakard, S.; Szymczyk, A.; Déon, S. Influence of salts on the rejection of polyethyleneglycol by an NF organic membrane: Pore swelling and salting-out effects. J. Membr. Sci. 2010, 347, 174–182. [Google Scholar] [CrossRef]
- Simon, A.; Price, W.E.; Nghiem, L.D. Influence of formulated chemical cleaning reagents on the surface properties and separation efficiency of nanofiltrationmembranes. J. Membr. Sci. 2013, 432, 73–82. [Google Scholar] [CrossRef] [Green Version]
- Nghiem, L.D.; Simon, H. Effects of Membrane Fouling on the Nanofiltration of Pharmaceutically Active Compounds (Phacs): Mechanisms and Role of Membrane Pore Size. Sep. Purif. Technol. 2007, 57, 176–184. [Google Scholar] [CrossRef]
- Kong, F.-X.; Yang, H.-W.; Wu, Y.-Q.; Wang, X.-M.; Xie, Y.F. Rejection of pharmaceuticals during forward osmosis and prediction by using the solution–diffusion model. J. Membr. Sci. 2015, 476, 410–420. [Google Scholar] [CrossRef]
- Sukul, P.; Lamshöft, M.; Zühlke, S.; Spiteller, M. Sorption and Desorption of Sulfadiazine in Soil and Soil-Manure Systems. Chemosphere 2008, 73, 1344–1350. [Google Scholar] [CrossRef]
- Leal, R.M.P.; Alleoni, L.R.F.; Tornisielo, V.L.; Regitano, J.B. Sorption of Fluoroquinolones and Sulfonamides in 13 Brazilian Soils. Chemosphere 2013, 92, 979–985. [Google Scholar] [CrossRef] [Green Version]
- Thiele-Bruhn, S.; Seibicke, T.; Schulten, H.-R.; Leinweber, P. Sorption of Sulfonamide Pharmaceutical Antibiotics on Whole Soils and Particle-Size Fractions. J. Environ. Qual. 2004, 33, 1331–1342. [Google Scholar] [CrossRef]
- Al-Zoubi, H.; Omar, W. Rejection of salt mixtures from high saline by nanofiltration membranes. Korean J. Chem. Eng. 2009, 26, 799–805. [Google Scholar] [CrossRef]
- Szymczyk, A.; Fievet, P. Investigating transport properties of nanofiltration membranes by means of a steric, electric and dielectric exclusion model. J. Membr. Sci. 2005, 252, 77–88. [Google Scholar] [CrossRef]
- Plecis, A.; Schoch, R.B.; Renaud, P. Ionic Transport Phenomena in Nanofluidics: Experimental and Theoretical Study of the Exclusion-Enrichment Effect on a Chip. Nano Lett. 2005, 5, 1147–1155. [Google Scholar] [CrossRef] [PubMed]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic Press: Cambridge, MA, USA, 2013; Volume 2. [Google Scholar]
- de Lint, W.S.; Benes, N.E. Predictive charge-regulation transport model for nanofiltration from the theory of irreversible processes. J. Membr. Sci. 2004, 243, 365–377. [Google Scholar] [CrossRef]
- Deen, W. Hindered transport of large molecules in liquid-filled pores. AIChE J. 1987, 33, 1409–1425. [Google Scholar] [CrossRef]
- Born, M. Volumen und hydratationswärme der ionen. Z. Phys. 1920, 1, 45–48. [Google Scholar] [CrossRef]
- Vogel, D.; Simon, A.; Alturki, A.A.; Bilitewski, B.; Price, W.E.; Nghiem, L.D. Effects of fouling and scaling on the retention of trace organic contaminants by a nanofiltration membrane: The role of cake-enhanced concentration polarisation. Sep. Purif. Technol. 2010, 73, 256–263. [Google Scholar] [CrossRef]
- Schnitzer, C.; Ripperger, S. Influence of Surface Roughness on Streaming Potential Method. Chem. Eng. Technol. 2008, 31, 1696–1700. [Google Scholar] [CrossRef]
- Mänttäri, M.; Pihlajamäki, A.; Nyström, M. Effect of pH on hydrophilicity and charge and their effect on the filtration efficiency of NF membranes at different pH. J. Membr. Sci. 2006, 280, 311–320. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Song, J.; Guan, Y.; Yu, H.; Pan, X.; Wu, F.; Zhang, M. Influence of silica nanospheres on the separation performance of thin film composite poly(piperazine-amide) nanofiltration membranes. Appl. Surf. Sci. 2015, 324, 757–764. [Google Scholar] [CrossRef]
- Tang, C.Y.; Kwon, Y.-N.; Leckie, J.O. Effect of membrane chemistry and coating layer on physiochemical properties of thin film composite polyamide RO and NF membranes: I. FTIR and XPS characterization of polyamide and coating layer chemistry. Desalination 2009, 242, 149–167. [Google Scholar] [CrossRef]
- Lin, Y.-L. In situ concentration-polarization-enhanced radical graft polymerization of NF270 for mitigating silica fouling and improving pharmaceutical and personal care product rejection. J. Membr. Sci. 2018, 552, 387–395. [Google Scholar] [CrossRef]
- Kwon, Y.-N.; Leckie, J.O. Hypochlorite degradation of crosslinked polyamide membranes: II. Changes in hydrogen bonding behavior and performance. J. Membr. Sci. 2006, 282, 456–464. [Google Scholar] [CrossRef]
- Kwon, Y.-N.; Shih, K.; Tang, C.; Leckie, J.O. Adsorption of perfluorinated compounds on thin-film composite polyamide membranes. J. Appl. Polym. Sci. 2012, 124, 1042–1049. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Bassler, G.C. Spectrometric identification of organic compounds. J. Chem. Educ. 1962, 39, 546. [Google Scholar] [CrossRef]
- Tang, C.Y.; Kwon, Y.-N.; Leckie, J.O. Probing the nano- and micro-scales of reverse osmosis membranes—A comprehensive characterization of physiochemical properties of uncoated and coated membranes by XPS, TEM, ATR-FTIR, and streaming potential measurements. J. Membr. Sci. 2007, 287, 146–156. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Wei, W.; Wang, X.-M.; Yang, H.-W.; Xie, Y.F. Relating the rejections of oligomeric ethylene glycols and saccharides by nanofiltration: Implication for membrane pore size determination. Sep. Purif. Technol. 2018, 205, 151–158. [Google Scholar] [CrossRef]
- Bungay, P.M.; Brenner, H. The motion of a closely-fitting sphere in a fluid-filled tube. Int. J. Multiph. Flow 1973, 1, 25–56. [Google Scholar] [CrossRef]
- Noordman, T.R.; Wesselingh, J.A. Transport of large molecules through membranes with narrow pores: The Maxwell–Stefan description combined with hydrodynamic theory. J. Membr. Sci. 2002, 210, 227–243. [Google Scholar] [CrossRef]
- Senapati, S.; Chandra, A. Dielectric Constant of Water Confined in a Nanocavity. J. Phys. Chem. B 2001, 105, 5106–5109. [Google Scholar] [CrossRef]
- Déon, S.; Dutournié, P.; Bourseau, P. Modeling nanofiltration with Nernst-Planck approach and polarization layer. AIChE J. 2007, 53, 1952–1969. [Google Scholar] [CrossRef]
- Cavaco Morão, A.I.; Szymczyk, A.; Fievet, P.; Brites Alves, A.M. Modelling the separation by nanofiltration of a multi-ionic solution relevant to an industrial process. J. Membr. Sci. 2008, 322, 320–330. [Google Scholar] [CrossRef]
- Bouranene, S.; Szymczyk, A.; Fievet, P.; Vidonne, A. Effect of salts on the retention of polyethyleneglycol by a nanofiltration ceramic membrane. Desalination 2009, 240, 94–98. [Google Scholar] [CrossRef]
- Bowen, W.R.; Welfoot, J.S. Modelling the performance of membrane nanofiltration—critical assessment and model development. Chem. Eng. Sci. 2002, 57, 1121–1137. [Google Scholar] [CrossRef]
- Zhu, H.; Szymczyk, A.; Balannec, B. On the salt rejection properties of nanofiltration polyamide membranes formed by interfacial polymerization. J. Membr. Sci. 2011, 379, 215–223. [Google Scholar] [CrossRef]
- Szymczyk, A.; Zhu, H.; Balannec, B. Ion Rejection Properties of Nanopores with Bipolar Fixed Charge Distributions. J. Phys. Chem. B 2010, 114, 10143–10150. [Google Scholar] [CrossRef] [PubMed]
- Szymczyk, A.; Zhu, H.; Balannec, B. Pressure-Driven Ionic Transport through Nanochannels with Inhomogenous Charge Distributions. Langmuir 2010, 26, 1214–1220. [Google Scholar] [CrossRef]
- Szymczyk, A.; Sbaï, M.; Fievet, P.; Vidonne, A. Transport Properties and Electrokinetic Characterization of an Amphoteric Nanofilter. Langmuir 2006, 22, 3910–3919. [Google Scholar] [CrossRef]




| Membrane | NF90 | NF270 | VNF2-8040 | TMN20H-400 |
|---|---|---|---|---|
| Surface material | Phenylenediamine and benzentricarbonyl trichloride | Semi-aromatic piperazine-based polyamide | Polyamide | Polyamide |
| The molecular weight cut off (MWCO) (Da) | 200 | 150~200 | <300 | 200 |
| pH range | 2~12 a | 3~10 a | 2~12 b | 2~11 c |
| Maximum operation pressure (MPa) | 0.48~4.41 a | 0.69~4.14 a | 0.69~4.14 b | 0.69~2.5 c |
| Temperature resistance (°C) | 5~45 a | 5~45 a | 5~45 b | 5~45 c |
| MgSO4 rejection (%) | ≥97 a | 85~95 a | ≥96 b | ≥97 c |
| NaCl rejection (%) | 85~90 d | 40 d | 90~98 b | 50 c |
| Compound | Sulfadiazine (SDZ) |
|---|---|
| Formula | C10H10N4O2S |
| Chemical Structure | 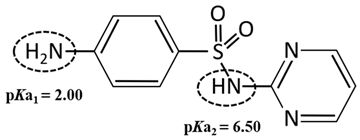 |
| MW | 250.28 g mol−1 |
| pKa | 2.00/6.50 a |
| log Kow | −0.09 a |
| Water solubility | 77 mg·L−1 (25 °C) b |
| Diffusion coefficient | 0.605 × 10−9 m2s−1 |
| Stokes radius | 0.40 nm |
| Speciation | 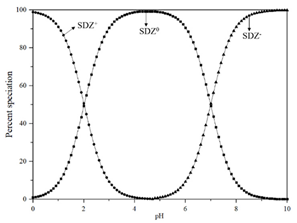 |
| Ionization equilibria |  |
| Organic Tracer | Molecular Weight (g/mol) | Diffusivity (10−10 m2/s) | Stokes Radius (nm) |
|---|---|---|---|
| dioxane | 88 | 9.1 | 0.234 |
| erythritol | 120 | 8.1 | 0.263 |
| xylose | 150 | 7.4 | 0.290 |
| Organic Tracer | ||||
|---|---|---|---|---|
| NF90 | ||||
| dioxane | 0.234 | 0.691 | 0.34 | |
| erythritol | 0.263 | 0.790 | 0.33 | |
| xylose | 0.290 | 0.820 | 0.35 | |
| average | 0.34 | 33.4 | ||
| NF270 | ||||
| dioxane | 0.234 | 0.509 | 0.46 | |
| erythritol | 0.263 | 0.584 | 0.45 | |
| xylose | 0.290 | 0.829 | 0.35 | |
| average | 0.42 | 35.7 | ||
| VNF2-8040 | ||||
| dioxane | 0.234 | 0.616 | 0.38 | |
| erythritol | 0.263 | 0.731 | 0.36 | |
| xylose | 0.290 | 0.935 | 0.31 | |
| average | 0.35 | 33.7 | ||
| TMN20H-400 | ||||
| dioxane | 0.234 | 0.498 | 0.47 | |
| erythritol | 0.263 | 0.598 | 0.44 | |
| xylose | 0.290 | 0.707 | 0.41 | |
| average | 0.44 | 36.4 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Hu, B.; Yang, F. Removal of Sulfadiazine by Polyamide Nanofiltration Membranes: Measurement, Modeling, and Mechanisms. Membranes 2021, 11, 104. https://doi.org/10.3390/membranes11020104
Zhu H, Hu B, Yang F. Removal of Sulfadiazine by Polyamide Nanofiltration Membranes: Measurement, Modeling, and Mechanisms. Membranes. 2021; 11(2):104. https://doi.org/10.3390/membranes11020104
Chicago/Turabian StyleZhu, Haochen, Bo Hu, and Fengrui Yang. 2021. "Removal of Sulfadiazine by Polyamide Nanofiltration Membranes: Measurement, Modeling, and Mechanisms" Membranes 11, no. 2: 104. https://doi.org/10.3390/membranes11020104
APA StyleZhu, H., Hu, B., & Yang, F. (2021). Removal of Sulfadiazine by Polyamide Nanofiltration Membranes: Measurement, Modeling, and Mechanisms. Membranes, 11(2), 104. https://doi.org/10.3390/membranes11020104






