Optimization of Fuel Cell Performance Using Computational Fluid Dynamics
Abstract
:1. Introduction
2. Geometry Design
2.1. Computational Domain
2.2. Boundary Conditions
3. Mathematical Modelling
| Governing Equations | Mathematical Expressions | Ref. |
|---|---|---|
| Continuity | + + = | [22] |
| Momentum transport | + + = + + = + + = | [23] |
| Energy | + + = | [24] |
| Hydrogen transport (anode region) | + + + + | [25] |
| Water transport (anode region) | + + + + | [26] |
| Oxygen transport (cathode region) | ++ ++ | [27] |
| Water transport (cathode region) | ++ ++ | [28] |
| Source terms | Sm = Sm = | [29] |
| Spx = − Spy = − Spz = − | [30] | |
| = − | [31] | |
| Sh = I2Rohm + hreact + | [32] | |
| [33] | ||
| [34] | ||
| [35] | ||
| [36] | ||
| Charge transport | ∇·(σsol ∇øsol) + Rsol = 0 ∇·(σmem ∇ømem) + Rmem= 0 | [37] [38] |
4. Results and Discussion
4.1. Effects of Operating Temperature Variation
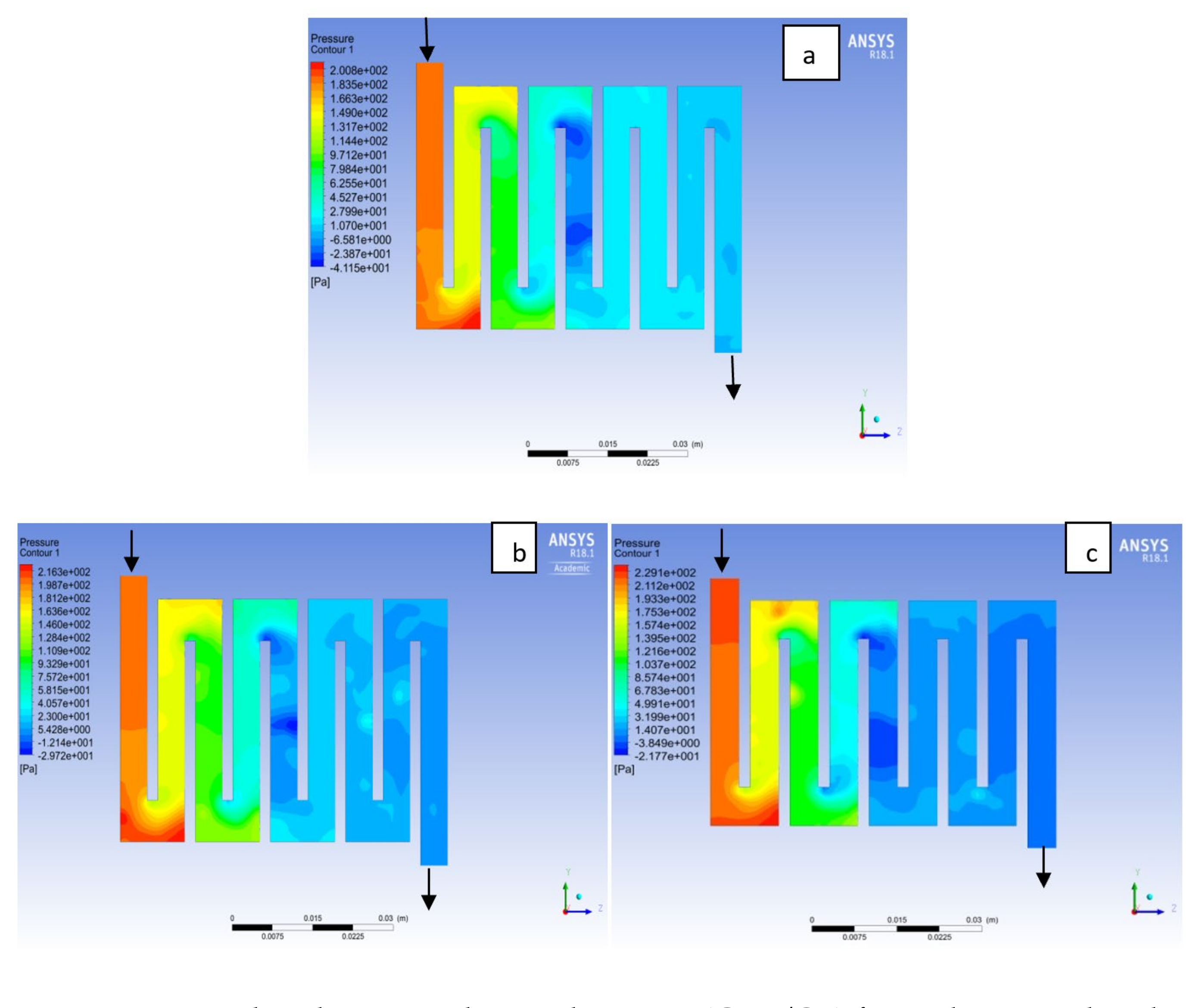
4.2. Effects of Operating Pressure Variation
4.3. Mass Fraction
4.4. Modeling Results Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Abdelkareem, M.A.; Lootah, M.A.; Sayed, E.T.; Wilberforce, T.; Alawadhi, H.; Yousef, B.A.A.; Olabi, A.G. Fuel cells for carbon capture applications. Sci. Total Environ. 2021, 769, 144243. [Google Scholar] [CrossRef] [PubMed]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A. Fuel cell application in the automotive industry and future perspective. Energy 2021, 214, 118955. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Wilberforce, T.; Elsaid, K.; Sayed, E.T.; Abdelghani, E.A.M.; Olabi, A.G. Transition metal carbides and nitrides as oxygen reduction reaction catalyst or catalyst support in proton exchange membrane fuel cells (PEMFCs). Int. J. Hydrog. Energy 2020, in press. [Google Scholar] [CrossRef]
- Wilberforce, T.; El-Hassan, Z.; Khatib, F.N.; Al Makky, A.; Baroutaji, A.; Carton, J.G.; Olabi, A.G. Developments of electric cars and fuel cell hydrogen electric cars. Int. J. Hydrogen Energy 2017, 42, 25695–25734. [Google Scholar] [CrossRef] [Green Version]
- Olabi, A.G.; Wilberforce, T.; Sayed, E.T.; Elsaid, K.; Abdelkareem, M.A. Prospects of Fuel Cell Combined Heat and Power Systems. Energies 2020, 13, 4104. [Google Scholar] [CrossRef]
- Wilberforce, T.; Khatib, F.N.; Ijaodola, O.; Ogungbemi, E.; El Hassan, Z.; Durrant, A.; Thompson, J.; Olabi, A.G. Numerical modelling and CFD simulation of a polymer electrolyte membrane (PEM) fuel cell flow channel using an open pore cellular foam material. Sci. Total Environ. 2019, 678, 728740. [Google Scholar] [CrossRef]
- Baroutaji, A.; Arjunan, A.; Alaswad, A.; Praveen, A.S.; Wilberforce, T.; Abdelkareem, M.A.; Olabi, A.G. Materials for fuel cell membranes. Ref. Modul. Mater. Sci. Mater. Eng. 2020. [Google Scholar] [CrossRef]
- Karimi, S.; Fraser, N.; Roberts, B.; Foulkes, F.R. A review of metallic bipolar plates for proton exchange membrane fuel cells: Materials and fabrication methods. Adv. Mater. Sci. Eng. 2012. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Cooke, K.; Eitzinger, G.; Hamilton, P.; Pollet, B. Development of PVD coatings for PEMFC metallic bipolar plates. Thin Solid Films 2013, 528, 199–204. [Google Scholar] [CrossRef]
- Wilberforce, T.; El Hassan, Z.; Khatib, F.N.; Ahmed, A.M.; Jim, M.; Ahmad, B.; Carton, J.G.; Olabi, A.G. Development of Bi-polar plate design of PEM fuel cell using CFD techniques. Int. J. Hydrog. Energy 2017, 42, 25663–25685. [Google Scholar] [CrossRef] [Green Version]
- Hong, L.; Peiwen, L.; Jon, V.L. CFD study on flow distribution uniformity in fuel distributors having multiple structural bifurcations of flow channels. Int. J. Hydrog. Energy 2010, 35, 9186–9198. [Google Scholar] [CrossRef]
- Jason, P.K.; Xia, W.; Joan, L.; Zhongying, S.; Laila, G. Investigation of bio-inspired flow channel designs for bipolar plates in proton exchange membrane fuel cells. J. Power Sources 2009, 188, 132–140. [Google Scholar] [CrossRef]
- Mohammad, H.A.; Behzad, R. Numerical investigation of flow field configuration and contact resistance for PEM fuel cell. Renew. Energy 2008, 33, 1775–1783. [Google Scholar] [CrossRef]
- Sierra, J.M.; Figueroa-Ramirez Diaz, S.E.; Vargas, J.; Sebastian, P.J. Numerical evaluation of a PEM fuel cell with conventional flow fields adapted to tubular plates. Int. J. Hydrog. Energy 2014, 39, 16694–16705. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y. Three-dimensional analysis of transport and electrochemical reactions in polymer electrolyte fuel cells. J. Power Sources 2004, 125, 40–51. [Google Scholar] [CrossRef]
- Yousef, V.; Kurosh, S. Numerical investigation of a novel compound flow-field for PEMFC performance improvement. Int. J. Hydrog. Energy 2015, 40, 15032–15039. [Google Scholar] [CrossRef]
- Bladimir, R.A.; Abel, H.G.; Daniel, J.R.; Peiwen, L. Numerical investigation of the performance of symmetric flow distributors as flow channels for PEM fuel cells. Int. J. Hydrog. Energy 2012, 37, 436–448. [Google Scholar] [CrossRef]
- Tabbi Wilberforce, A.G.O. Design of Experiment (DOE) Analysis of 5-Cell Stack Fuel Cell Using Three Bipolar Plate Geometry Design. Sustainability 2020, 12, 4488. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y.; Chen, K.S. Computational fluid dynamics modeling of proton exchange membrane fuel cells. J. Electrochem. Soc. 2000, 147, 4485e93. [Google Scholar] [CrossRef]
- Atul, K.; Ramana, G.R. Effect of channel dimensions and shape in the flow-field distributor on the performance of polymer electrolytemembranefuel cells. J. Power Sources 2003, 113, 11–18. [Google Scholar] [CrossRef]
- Miguel, P.A.; Enzo, S.; Contreras, J. Renewable energy policy performance in reducing CO2 emissions. Energy Econ. 2016, 54, 272–280. [Google Scholar] [CrossRef]
- Negin, H.; Joshua, M.P. A review of greenhouse gas emission liabilities as the value of renewable energy for mitigating lawsuits for climate change related damages. Renew. Sustain. Energy Rev. 2016, 55, 899–908. [Google Scholar] [CrossRef] [Green Version]
- Bladimir, R.A.; Peiwen, L.; Hong, L.; Abel, H.G. CFD study of liquid-cooled heat sinks with micro-channel flow field configurations for electronics, fuel cells, and concentrated solar cells. Appl. Therm. Eng. 2011, 31, 2494–2507. [Google Scholar] [CrossRef]
- Guilin, H.; Jianren, F.; Song, C.; Yongjiang, L.; Kefa, C. Three-dimensional numerical analysis of proton exchange membrane fuel cells (PEMFCs) with conventional and interdigitated flow fields. J. Power Sources 2004, 136, 1–9. [Google Scholar] [CrossRef]
- Zheng, C.H.; Oh, C.E.; Park, Y.I.; Cha, S.W. Fuel economy evaluation of fuel cell hybrid vehicles based on equivalent fuel consumption. Int. J. Hydrog. Energy 2012, 37, 1790–1796. [Google Scholar] [CrossRef]
- Yuh, M.F.; Ay, S. A three-dimensional full-cell CFD model used to investigate the effects of different flow channel designs on PEMFC performance. Int. J. Hydrog. Energy 2007, 32, 4466–4476. [Google Scholar] [CrossRef]
- Elif, E.H.; Imdat, T. Assessment of single-serpentine PEM fuel cell model developed by computational fluid dynamics. Fuel 2018, 217, 51–58. [Google Scholar] [CrossRef]
- Alizadeh, E.; Rahimi, M.; Rahgoshay, S.M.; Saadat, S.H.; Khorshidian, M. Numerical and experimental investigation of cascade type serpentine flow field of reactant gases for improving performance of PEM fuel cell. Int. J. Hydrog. Energy 2017, 42, 14708–14724. [Google Scholar] [CrossRef]
- Antonio, S.; Alfredo, I.; Felipe, R.; Elvira, T.; Eduardo, L.; Fernando, I. Optimization of a PEM fuel cell operation conditions: Obtaining the maximum performance polarization curve. Int. J. Hydrog. Energy 2016, 41, 19713–19723. [Google Scholar] [CrossRef]
- Lin, W.; Attila, H.; Tianhong, Z.; Hongtan, L. A parametric study of PEM fuel cell performances. Int. J. Hydrog. Energy 2003, 28, 1263–1272. [Google Scholar] [CrossRef]
- Falcao, D.S.; Gomes, P.J.; Pinho, C.; Pinto, A.M. 1D and 3D numerical simulations in PEM fuel cells. Int. J. Hydrog. Energy 2011, 36, 12486–12498. [Google Scholar] [CrossRef]
- Hua, M. A three-dimensional PEM fuel cell model with consistent treatment of water transport in MEA. J. Power Sources 2006, 162, 426–435. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Ribeirinha, P.; Boaventura, M.; Mendes, A. Three-dimensional modeling of PEMFC with contaminated anode fuel. Energy 2018, 152, 939–959. [Google Scholar] [CrossRef]
- Fatemeh, H.; Soosan, R.; Mashallah, R. CFD simulation of PEM fuel cell performance: Effect of straight and serpentine flow fields. Math. Comput. Model. 2012, 55, 1540–1557. [Google Scholar] [CrossRef]
- Iranzo, A.; Muñoz, M.; Rosa, F.; Pino, J. Numerical model for the performance prediction of a PEM fuel cell. Model results and experimental validation. Int. J. Hydrog. Energy 2010, 35, 11533–11550. [Google Scholar] [CrossRef]
- Guobin, Z.; Linhao, F.; Jing, S.; Kui, J. A 3D model of PEMFC considering detailed multiphase flow and anisotropic transport properties. Int. J. Heat Mass Transf. 2017, 115, 714–724. [Google Scholar] [CrossRef]
- Guobin, Z.; Kui, J. Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Convers. Manag. 2018, 176, 409–421. [Google Scholar] [CrossRef]
- Ijaodola, O.S.; El-Hassan, Z.; Ogungbemi, E.; Khatib, F.N.; Wilberforce, T.; Thompson, J.; Olabi, A.G. Energy efficiency improvements by investigating the water flooding management on proton exchange membrane fuel cell (PEMFC). Energy 2019, 179, 246–267. [Google Scholar] [CrossRef]
- Shimpalee, S.; Lilavivat, V.; McCrabb, H.; Khunatorn, Y.; Lee, H.K.; Lee, W.K.; Weidner, J.W. Investigation of bipolar plate materials for proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2016, 41, 13688–13696. [Google Scholar] [CrossRef] [Green Version]
- Wilberforce, T.; Ijaodola, O.; Khatib, F.N.; Ogungbemi, E.; El Hassan, Z.; Thompson, J.; Olabi, A.G. Effect of humidification of reactive gases on the performance of a proton exchange membrane fuel cell. Sci. Total Environ. 2019, 688, 1016–1035. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Yuanchun, H.; Zhengbing, X.; Xianwei, R. Study of Adsorption of Hydrogen on Al, Cu, Mg, Ti Surfaces in Al Alloy Melt via First Principles Calculation. Metals 2017, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Anderson, A.B. Theory of Hydrogen Deposition and Evolution on Cu(111) Electrodes. J. Electrochem. Soc. 2017, 164, H691–H695. [Google Scholar] [CrossRef] [Green Version]


















| Parameters | Value | Unit |
|---|---|---|
| Current collector width (anode side) | 45 | mm |
| Current collector width (cathode side) | 45 | mm |
| Gas flow field channel width | 45 | mm |
| Gas flow field channel depth | 2 | mm |
| Cell electrode length | 65 | mm |
| Gas diffusion layer thickness (anode region) | 0.39 | mm |
| Gas diffusion layer thickness (cathode region) | 0.39 | mm |
| Catalyst layer thickness (anode side) | 0.08 | mm |
| Catalyst layer thickness (cathode side) | 0.08 | mm |
| Active area | 25 | cm2 |
| Membrane thickness | 0.6 | mm |
| Gas diffusion layer porosity (anode side) | 0.5 | − |
| Gas diffusion layer porosity (cathode side) | 0.5 | − |
| Catalyst layer porosity (anode region) | 0.5 | − |
| Catalyst layer porosity (cathode region) | 0.5 | − |
| Parameters | Value | Unit |
|---|---|---|
| Operating temperature | 298/323/338 | K |
| Operating pressure | 1.5/2/2.5 | Bar |
| Mole fractions for hydrogen and water vapor (anode region) | 0.6/0.4 | − |
| Mole fractions for oxygen and water vapor (cathode region) | 0.2/0.15 | − |
| Relative humidity at anode side | 100 | % |
| Relative humidity at cathode side | 100 | % |
| Open circuit voltage | 0.7 | V |
| Materials | Peak Power (Simulation) | Peak Power (Experimental) | % Deviation b/w Simulation and Experimental Results |
|---|---|---|---|
| Aluminium | 0.36 | 0.33 | 8.33 |
| Copper | 0.3 | 0.28 | 6.67 |
| Steel | 0.25 | 0.23 | 8.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilberforce, T.; Ijaodola, O.; Emmanuel, O.; Thompson, J.; Olabi, A.G.; Abdelkareem, M.A.; Sayed, E.T.; Elsaid, K.; Maghrabie, H.M. Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes 2021, 11, 146. https://doi.org/10.3390/membranes11020146
Wilberforce T, Ijaodola O, Emmanuel O, Thompson J, Olabi AG, Abdelkareem MA, Sayed ET, Elsaid K, Maghrabie HM. Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes. 2021; 11(2):146. https://doi.org/10.3390/membranes11020146
Chicago/Turabian StyleWilberforce, Tabbi, Oluwatosin Ijaodola, Ogungbemi Emmanuel, James Thompson, Abdul Ghani Olabi, Mohammad Ali Abdelkareem, Enas Taha Sayed, Khaled Elsaid, and Hussein M. Maghrabie. 2021. "Optimization of Fuel Cell Performance Using Computational Fluid Dynamics" Membranes 11, no. 2: 146. https://doi.org/10.3390/membranes11020146
APA StyleWilberforce, T., Ijaodola, O., Emmanuel, O., Thompson, J., Olabi, A. G., Abdelkareem, M. A., Sayed, E. T., Elsaid, K., & Maghrabie, H. M. (2021). Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes, 11(2), 146. https://doi.org/10.3390/membranes11020146










