Evaluating Critical Influencing Factors of Desalination by Membrane Distillation Process—Using Multi-Criteria Decision-Making
Abstract
1. Introduction
- Direct Contact Membrane Distillation (DCMD): The membrane in this method is directly in contact with the hot feed solution and cold permeate stream [6]. Difference in temperature and partial pressure between the two sides across the membrane causes the molecules of water to evaporate at the interface of the membrane and the hot feed stream. Condensation of the formed vapor takes place at the interface of the membrane and the cold stream, after passing through the membrane pores [7].
- Air Gap Membrane Distillation (AGMD): In this type of MD, an air gap is insinuated between the membrane and the condensation surface where the generated water vapor condenses. The other side of the condensation surface is cooled by a cold stream [8].
- Sweep Gas Membrane Distillation (SGMD): In this method of MD, a carrier in the form of a cold inert gas is used to sweep the generated water vapor formed on the permeate membrane side [9]. The condensation takes place in a separate chamber outward from the membrane module.
- Vacuum Membrane Distillation (VMD): A vacuum pressure is applied to increase the partial pressure difference across the membrane to maximize the driving force of the water evaporation, wherein a vacuum pump is used to apply vacuum on the permeate side of the membrane [10]. As the saturation vapor pressure is higher than the applied vacuum pressure, the evaporation rate is augmented. The condensation of the produced water vapor takes place in a condenser outside the membrane module [11].
- MD process is a reliable alternative to other desalination methods as it functions at reduced pressure leading to decreased equipment cost and improved safety process.
- MD is an environmentally friendly and cost-efficient process, as it can utilizes energy from solar sources and even the waste heat from other processes.
- MD is successfully being used in food industry for the concentration of juices and milk.
- MD has low organic fouling, low energy cost, and the absence of limitations caused by osmotic pressure effect.
2. Methodology
- Detailed analysis of literature on membrane technologies and effect of different factors influencing membrane distillation.
- Identification of critical factors which influence the performance of the MD process.
2.1. Analytic Hierarchy Process (AHP) Theory
2.2. Fuzzy-AHP Theory
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saleem, H.; Trabzon, L.; Kilic, A.; Zaidi, S.J. Recent advances in nanofibrous membranes: Production and applications in water treatment and desalination. Desalination 2020, 478, 114178. [Google Scholar] [CrossRef]
- Shafieian, A.; Khiadani, M. A novel solar-driven direct contact membrane-based water desalination system. Energy Convers. Manag. 2019, 199, 112055. [Google Scholar] [CrossRef]
- Chen, Q.; Muhammad, B.; Akhtar, F.H.; Ybyraiymkul, D.; Muhammad, W.S.; Li, Y.; Ng, K.C. Thermo-economic analysis and optimization of a vacuum multi-effect membrane distillation system. Desalination 2020, 483, 114413. [Google Scholar] [CrossRef]
- El-Bourawi, M.S.; Ding, Z.; Ma, R.; Khayet, M. A framework for better understanding membrane distillation separation process. J. Memb. Sci. 2006, 285, 4–29. [Google Scholar] [CrossRef]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Khumalo, N.; Nthunya, L.; Derese, S.; Motsa, M.; Verliefde, A.; Kuvarega, A.; Mamba, B.B.; Mhlanga, S.; Dlamini, D.S. Water recovery from hydrolysed human urine samples via direct contact membrane distillation using PVDF/PTFE membrane. Sep. Purif. Technol. 2019, 211, 610–617. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Florido-Díaz, F.J. Desalination of brines by membrane distillation. Desalination 2001, 137, 267–273. [Google Scholar] [CrossRef]
- Lu, K.J.; Chen, Y.; Chung, T.S. Design of omniphobic interfaces for membrane distillation—A review. Water Res. 2019, 162, 64–77. [Google Scholar] [CrossRef]
- Belessiotis, V.; Kalogirou, S.; Delyannis, E. Chapter Four—Membrane Distillation. In Thermal Solar Desalination; Belessiotis, V., Kalogirou, S., Delyannis, E., Eds.; Academic Press: London, UK, 2016; pp. 191–251. ISBN 978-0-12-809656-7. [Google Scholar]
- Anqi, A.E.; Usta, M.; Krysko, R.; Lee, J.G.; Ghaffour, N.; Oztekin, A. Numerical study of desalination by vacuum membrane distillation—Transient three-dimensional analysis. J. Memb. Sci. 2020, 596. [Google Scholar] [CrossRef]
- Urtiaga, A.M.; Ruiz, G.; Ortiz, I. Kinetic analysis of the vacuum membrane distillation of chloroform from aqueous solutions. J. Memb. Sci. 2000, 165, 99–110. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in seawater desalination: Thermal efficiency, sensitivity study and cost estimation. J. Memb. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Naveed, Q.N.; Qureshi, M.R.N.; Tairan, N.; Mohammad, A.H.; Shaikh, A.; Alsayed, A.O.; Shah, A.; Alotaibi, F.M. Evaluating critical success factors in implementing E-learning system using multi-criteria decision-making. PLoS ONE 2020, 15, e231465. [Google Scholar] [CrossRef] [PubMed]
- Srdjevic, Z.; Samardzic, M.; Srdjevic, B. Robustness of AHP in selecting wastewater treatment method for the coloured metal industry: Serbian case study. Civ. Eng. Environ. Syst. 2012, 29, 147–161. [Google Scholar] [CrossRef]
- Manekar, P.; Nandy, T.; Sargaonkar, A.; Rathi, B.; Karthik, M. FAHP ranking and selection of pretreatment module for membrane separation processes in textile cluster. Bioresour. Technol. 2011, 102, 558–566. [Google Scholar] [CrossRef]
- Chamblás, O.; Pradeñas, L. Multi-criteria optimization for seawater desalination. Tecnol. y Ciencias del Agua 2018, 9, 198–213. [Google Scholar] [CrossRef]
- Al-Araidah, O.; Hayajneh, M.T.; Al-Rwabdah, R.A. Desalination membrane selection using group fuzzy analytical hierarchy process. Desalin. WATER Treat. 2020, 174, 79–89. [Google Scholar] [CrossRef]
- Talaeipour, M.; Mahvi, A.H.; Nouri, J.; Hassani, A.H. A Comprehensive Evaluation Optimal Ground Water Desalination Process with Membranes and Integrated Process Using AHP Method in Qom Province, Iran. Arch. Hyg. Sci. 2018, 7, 216–224. [Google Scholar] [CrossRef]
- Abu-Zeid, M.A.E.R.; Zhang, Y.; Dong, H.; Zhang, L.; Chen, H.L.; Hou, L. A comprehensive review of vacuum membrane distillation technique. Desalination 2015, 356, 1–14. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Vázquez-González, M.I. Temperature and concentration polarization in membrane distillation of aqueous salt solutions. J. Memb. Sci. 1999, 156, 265–273. [Google Scholar] [CrossRef]
- Criscuoli, A.; Carnevale, M.C.; Drioli, E. Evaluation of energy requirements in membrane distillation. Chem. Eng. Process. Process Intensif. 2008, 47, 1098–1105. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, P.; Mengual, J.I. Nature of flow on sweeping gas membrane distillation. J. Memb. Sci. 2000, 170, 243–255. [Google Scholar] [CrossRef]
- Ji, Z.; Wang, J.; Hou, D.; Yin, Z.; Luan, Z. Effect of microwave irradiation on vacuum membrane distillation. J. Memb. Sci. 2013, 429, 473–479. [Google Scholar] [CrossRef]
- Ullah, R.; Khraisheh, M.; Esteves, R.J.; McLeskey, J.T.; AlGhouti, M.; Gad-el-Hak, M.; Vahedi Tafreshi, H. Energy efficiency of direct contact membrane distillation. Desalination 2018, 433, 56–67. [Google Scholar] [CrossRef]
- Jun, D.U.; Zuohua, L.I.U.; Lihua, G.A.N.; Changyuan, T.A.O.; Renlong, L.I.U. A method for experimental determination of mass transfer resistance across membrane in VMD. Desalination 2006, 200, 606–608. [Google Scholar] [CrossRef]
- Imdakm, A.O.; Khayet, M.; Matsuura, T. A Monte Carlo simulation model for vacuum membrane distillation process. J. Memb. Sci. 2007, 306, 341–348. [Google Scholar] [CrossRef]
- Liu, G.; Pan, J.; Xu, X.; Wang, Z.; Cui, Z. Preparation of ECTFE porous membrane with a green diluent TOTM and performance in VMD process. J. Memb. Sci. 2020, 612, 118375. [Google Scholar] [CrossRef]
- Jiao, L.; Yan, K.; Wang, J.; Lin, S.; Li, G.; Bi, F.; Zhang, L. Low surface energy nanofibrous membrane for enhanced wetting resistance in membrane distillation process. Desalination 2020, 476. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, F.; Cao, W.; Wan, Y. Hydrophilic/hydrophobic Janus membranes with a dual-function surface coating for rapid and robust membrane distillation desalination. Desalination 2020, 491, 114561. [Google Scholar] [CrossRef]
- Sun, Q.; Yang, Z.; Hu, C.; Li, C.; Yan, G.; Wang, Z. Facile preparation of superhydrophobic PVDF microporous membranes with excellent anti-fouling ability for vacuum membrane distillation. J. Memb. Sci. 2020, 605, 118106. [Google Scholar] [CrossRef]
- Xu, K.; Cai, Y.; Hassankiadeh, N.T.; Cheng, Y.; Li, X.; Wang, X.; Wang, Z.; Drioli, E.; Cui, Z. ECTFE membrane fabrication via TIPS method using ATBC diluent for vacuum membrane distillation. Desalination 2019, 456, 13–22. [Google Scholar] [CrossRef]
- Jacob, P.; Zhang, T.; Laborie, S.; Cabassud, C. Influence of operating conditions on wetting and wettability in membrane distillation using Detection of Dissolved Tracer Intrusion (DDTI). Desalination 2019, 468, 114086. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. I. Module design and performance evaluation using vacuum membrane distillation. J. Memb. Sci. 1996, 120, 111–121. [Google Scholar] [CrossRef]
- Cai, J.; Yin, H.; Guo, F. Transport analysis of material gap membrane distillation desalination processes. Desalination 2020, 481, 114361. [Google Scholar] [CrossRef]
- Khayet, M.; Khulbe, K.C.; Matsuura, T. Characterization of membranes for membrane distillation by atomic force microscopy and estimation of their water vapor transfer coefficients in vacuum membrane distillation process. J. Memb. Sci. 2004, 238, 199–211. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T.; Mengual, J.I.; Qtaishat, M. Design of novel direct contact membrane distillation membranes. Desalination 2006, 192, 105–111. [Google Scholar] [CrossRef]
- Gryta, M. Influence of polypropylene membrane surface porosity on the performance of membrane distillation process. J. Memb. Sci. 2007, 287, 67–78. [Google Scholar] [CrossRef]
- Qtaishat, M.R.; Banat, F. Desalination by solar powered membrane distillation systems. Desalination 2013, 308, 186–197. [Google Scholar] [CrossRef]
- Laganà, F.; Barbieri, G.; Drioli, E. Direct contact membrane distillation: Modelling and concentration experiments. J. Memb. Sci. 2000, 166, 1–11. [Google Scholar] [CrossRef]
- Xia, Q.C.; Liu, M.L.; Cao, X.L.; Wang, Y.; Xing, W.; Sun, S.P. Structure design and applications of dual-layer polymeric membranes. J. Memb. Sci. 2018, 562, 85–111. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, P.; Mengual, J.I. Theory and experiments on sweeping gas membrane distillation. J. Memb. Sci. 2000, 165, 261–272. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Membrane Distillation: Principles and Applications; Elsevier: Amesterdam, The Netherlands, 2011; ISBN 0444531262. [Google Scholar]
- Bandini, S.; Saavedra, A.; Sarti, G.C. Vacuum membrane distillation: Experiments and modeling. AIChE J. 1997, 43, 398–408. [Google Scholar] [CrossRef]
- Bandini, S.; Sarti, G.C. Heat and mass transport resistances in vacuum membrane distillation per drop. AIChE J. 1999, 45, 1422–1433. [Google Scholar] [CrossRef]
- Safavi, M.; Mohammadi, T. High-salinity water desalination using VMD. Chem. Eng. J. 2009, 149, 191–195. [Google Scholar] [CrossRef]
- Banat, F.; Al-Rub, F.A.; Bani-Melhem, K. Desalination by vacuum membrane distillation: Sensitivity analysis. Sep. Purif. Technol. 2003, 33, 75–87. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Z.; Feng, S.; Li, Y. Application of vacuum membrane distillation to lithium bromide absorption refrigeration system. Int. J. Refrig. 2009, 32, 1587–1596. [Google Scholar] [CrossRef]
- EL-Bourawi, M.S.; Khayet, M.; Ma, R.; Ding, Z.; Li, Z.; Zhang, X. Application of vacuum membrane distillation for ammonia removal. J. Memb. Sci. 2007, 301, 200–209. [Google Scholar] [CrossRef]
- Wu, B.; Li, K.; Teo, W.K. Preparation and characterization of poly(vinylidene fluoride) hollow fiber membranes for vacuum membrane distillation. J. Appl. Polym. Sci. 2007, 106, 1482–1495. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Theoretical and experimental study in membrane distillation. Desalination 1994, 95, 39–52. [Google Scholar] [CrossRef]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Separation efficiency in vacuum membrane distillation. J. Mem. Sci. 1992, 73, 217–229. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Heat transport and membrane distillation coefficients in direct contact membrane distillation. J. Memb. Sci. 2003, 212, 177–193. [Google Scholar] [CrossRef]
- Feng, C.; Shi, B.; Li, G.; Wu, Y. Preparation and properties of microporous membrane from poly(vinylidene fluoride-co-tetrafluoroethylene) (F2.4) for membrane distillation. J. Memb. Sci. 2004, 237, 15–24. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Membrane distillation for propanone removal from aqueous streams. J. Chem. Technol. Biotechnol. 2000, 75, 168–178. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, G.L.; Cheung, C.S.; Leung, C.W.; Zhu, Z.C. Ultrasonic stimulation on enhancement of air gap membrane distillation. J. Memb. Sci. 1999, 161, 85–93. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G.; Halim, C. Mass flux enhancement using spacer filled channels in direct contact membrane distillation. J. Memb. Sci. 2001, 187, 193–201. [Google Scholar] [CrossRef]
- Martínez, L.; Florido-Díaz, F.J.; Hernández, A.; Prádanos, P. Characterisation of three hydrophobic porous membranes used in membrane distillation: Modelling and evaluation of their water vapour permeabilities. J. Memb. Sci. 2002, 203, 15–27. [Google Scholar] [CrossRef]
- Karakulski, K.; Gryta, M.; Morawski, A. Membrane processes used for potable water quality improvement. Desalination 2002, 145, 315–319. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, F.; Wang, S. Experimental study of membrane distillation with brine circulated in the cold side. J. Memb. Sci. 2001, 183, 171–179. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, M.P.; Mengual, J.I. Possibility of nuclear desalination through various membrane distillation configurations: A comparative study. Int. J. Nucl. Desalin. 2003, 1, 30–46. [Google Scholar] [CrossRef]
- Tanudjaja, H.J.; Hejase, C.A.; Tarabara, V.V.; Fane, A.G.; Chew, J.W. Membrane-based separation for oily wastewater: A practical perspective. Water Res. 2019, 156, 347–365. [Google Scholar] [CrossRef]
- Chew, N.G.P.; Zhao, S.; Wang, R. Recent advances in membrane development for treating surfactant- and oil-containing feed streams via membrane distillation. Adv. Colloid Interface Sci. 2019, 273, 102022. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Sun, W.; Hu, Y.; Tang, H. Membrane technologies for Li+/Mg2+ separation from salt-lake brines and seawater: A comprehensive review. J. Ind. Eng. Chem. 2020, 81, 7–23. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Memb. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Kong, Y.; Lin, X.; Wu, Y.; Chen, J.; Xu, J. Plasma polymerization of octafluorocyclobutane and hydrophobic microporous composite membranes for membrane distillation. J. Appl. Polym. Sci. 1992, 46, 191–199. [Google Scholar] [CrossRef]
- Wu, Y.; Kong, Y.; Lin, X.; Liu, W.; Xu, J. Surface-modified hydrophilic membranes in membrane distillation. J. Memb. Sci. 1992, 72, 189–196. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Application of surface modifying macromolecules for the preparation of membranes for membrane distillation. Desalination 2003, 158, 51–56. [Google Scholar] [CrossRef]
- Koschikowski, J.; Wieghaus, M.; Rommel, M. Solar thermal-driven desalination plants based on membrane distillation. Desalination 2003, 156, 295–304. [Google Scholar] [CrossRef]
- Suk, D.E.; Matsuura, T.; Park, H.B.; Lee, Y.M. Development of novel surface modified phase inversion membranes having hydrophobic surface-modifying macromolecule (nSMM) for vacuum membrane distillation. Desalination 2010, 261, 300–312. [Google Scholar] [CrossRef]
- García-Payo, M.C.; Izquierdo-Gil, M.A.; Fernández-Pineda, C. Air gap membrane distillation of aqueous alcohol solutions. J. Memb. Sci. 2000, 169, 61–80. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wang, Y.; Ji, X.; Zhang, L.; Mi, X.; Huang, H. Removal of inhibitors from lignocellulosic hydrolyzates by vacuum membrane distillation. Bioresour. Technol. 2013, 144, 680–683. [Google Scholar] [CrossRef]
- Hoffmann, E.; Pfenning, D.M.; Philippsen, E.; Schwahn, P.; Sieber, M.; Wehn, R.; Woermann, D.; Wiedner, G. Evaporation of alcohol/water mixtures through hydrophobic porous membranes. J. Memb. Sci. 1987, 34, 199–206. [Google Scholar] [CrossRef]
- Al-Asheh, S.; Banat, F.; Qtaishat, M.; Al-Khateeb, M. Concentration of sucrose solutions via vacuum membrane distillation. Desalination 2006, 195, 60–68. [Google Scholar] [CrossRef]
- Yun, Y.; Ma, R.; Zhang, W.; Fane, A.G.; Li, J. Direct contact membrane distillation mechanism for high concentration NaCl solutions. Desalination 2006, 188, 251–262. [Google Scholar] [CrossRef]
- Diban, N.; Voinea, O.C.; Urtiaga, A.; Ortiz, I. Vacuum membrane distillation of the main pear aroma compound: Experimental study and mass transfer modeling. J. Memb. Sci. 2009, 326, 64–75. [Google Scholar] [CrossRef]
- Zhao, Z.-P.; Zhu, C.-Y.; Liu, D.-Z.; Liu, W.-F. Concentration of ginseng extracts aqueous solution by vacuum membrane distillation 2. Theory analysis of critical operating conditions and experimental confirmation. Desalination 2011, 267, 147–153. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M.; Karakulski, K. Wastewater treatment by membrane distillation. Desalination 2006, 198, 67–73. [Google Scholar] [CrossRef]
- Sivakumar, M.; Ramezanianpour, M.; O’Halloran, G. Mine Water Treatment Using a Vacuum Membrane Distillation System. APCBEE Procedia 2013, 5, 157–162. [Google Scholar] [CrossRef]
- Zakrzewska-Trznadel, G.; Harasimowicz, M.; Chmielewski, A.G. Concentration of radioactive components in liquid low-level radioactive waste by membrane distillation. J. Memb. Sci. 1999, 163, 257–264. [Google Scholar] [CrossRef]
- Criscuoli, A.; Zhong, J.; Figoli, A.; Carnevale, M.C.; Huang, R.; Drioli, E. Treatment of dye solutions by vacuum membrane distillation. Water Res. 2008, 42, 5031–5037. [Google Scholar] [CrossRef] [PubMed]
- Macedonio, F.; Drioli, E. Pressure-driven membrane operations and membrane distillation technology integration for water purification. Desalination 2008, 223, 396–409. [Google Scholar] [CrossRef]
- Criscuoli, A.; Bafaro, P.; Drioli, E. Vacuum membrane distillation for purifying waters containing arsenic. Desalination 2013, 323, 17–21. [Google Scholar] [CrossRef]
- Tang, N.; Zhang, H.; Wang, W. Computational fluid dynamics numerical simulation of vacuum membrane distillation for aqueous NaCl solution. Desalination 2011, 274, 120–129. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.A.; Jonsson, G. Factors affecting flux and ethanol separation performance in vacuum membrane distillation (VMD). J. Memb. Sci. 2003, 214, 113–130. [Google Scholar] [CrossRef]
- Couffin, N.; Cabassud, C.; Lahoussine-Turcaud, V. A new process to remove halogenated VOCs for drinking water production: Vacuum membrane distillation. Desalination 1998, 117, 233–245. [Google Scholar] [CrossRef]
- Khayet, M.; Velázquez, A.; Mengual, J.I. Direct contact membrane distillation of humic acid solutions. J. Memb. Sci. 2004, 240, 123–128. [Google Scholar] [CrossRef]
- Khayet, M.; Mengual, J.I. Effect of salt concentration during the treatment of humic acid solutions by membrane distillation. Desalination 2004, 168, 373–381. [Google Scholar] [CrossRef]
- Cath, T.Y.; Adams, V.D.; Childress, A.E. Experimental study of desalination using direct contact membrane distillation: A new approach to flux enhancement. J. Memb. Sci. 2004, 228, 5–16. [Google Scholar] [CrossRef]
- Khayet, M.; Mengual, J.I.; Matsuura, T. Porous hydrophobic/hydrophilic composite membranes: Application in desalination using direct contact membrane distillation. J. Memb. Sci. 2005, 252, 101–113. [Google Scholar] [CrossRef]
- Li, B.; Sirkar, K.K. Novel Membrane and Device for Direct Contact Membrane Distillation-Based Desalination Process. Ind. Eng. Chem. Res. 2004, 43, 5300–5309. [Google Scholar] [CrossRef]
- Peng, P.; Fane, A.G.; Li, X. Desalination by membrane distillation adopting a hydrophilic membrane. Desalination 2005, 173, 45–54. [Google Scholar] [CrossRef]
- Zeng, H.; Liu, S.; Wang, J.; Li, Y.; Zhu, L.; Xu, M.; Wang, C. Hydrophilic SPEEK/PES composite membrane for pervaporation desalination. Sep. Purif. Technol. 2020, 250, 117265. [Google Scholar] [CrossRef]
- Li, Q.; Lian, B.; Zhong, W.; Omar, A.; Razmjou, A.; Dai, P.; Guan, J.; Leslie, G.; Taylor, R.A. Improving the performance of vacuum membrane distillation using a 3D-printed helical baffle and a superhydrophobic nanocomposite membrane. Sep. Purif. Technol. 2020, 248. [Google Scholar] [CrossRef]
- Hubadillah, S.K.; Tai, Z.S.; Othman, M.H.D.; Harun, Z.; Jamalludin, M.R.; Rahman, M.A.; Jaafar, J.; Ismail, A.F. Hydrophobic ceramic membrane for membrane distillation: A mini review on preparation, characterization, and applications. Sep. Purif. Technol. 2019, 217, 71–84. [Google Scholar] [CrossRef]
- Choudhury, M.R.; Anwar, N.; Jassby, D.; Rahaman, M.S. Fouling and wetting in the membrane distillation driven wastewater reclamation process—A review. Adv. Colloid Interface Sci. 2019, 269, 370–399. [Google Scholar] [CrossRef] [PubMed]
- Alsebaeai, M.K.; Ahmad, A.L. Membrane distillation: Progress in the improvement of dedicated membranes for enhanced hydrophobicity and desalination performance. J. Ind. Eng. Chem. 2020, 86, 13–34. [Google Scholar] [CrossRef]
- Yao, M.; Tijing, L.D.; Naidu, G.; Kim, S.H.; Matsuyama, H.; Fane, A.G.; Shon, H.K. A review of membrane wettability for the treatment of saline water deploying membrane distillation. Desalination 2020, 479, 114312. [Google Scholar] [CrossRef]
- Rezaei, M.; Warsinger, D.M.; Duke, M.C.; Matsuura, T.; Samhaber, W.M. Wetting phenomena in membrane distillation: Mechanisms, reversal, and prevention. Water Res. 2018, 139, 329–352. [Google Scholar] [CrossRef]
- González, D.; Amigo, J.; Suárez, F. Membrane distillation: Perspectives for sustainable and improved desalination. Renew. Sustain. Energy Rev. 2017, 80, 238–259. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Yuan, X.; Zhang, J.; Chew, J.W. Metal-organic framework membranes for wastewater treatment and water regeneration. Coord. Chem. Rev. 2020, 404, 213116. [Google Scholar] [CrossRef]
- Khayet, M.; Mengual, J.I.; Zakrzewska-Trznadel, G. Direct contact membrane distillation for nuclear desalination Part I: Review of membranes used in membrane distillation and methods for their characterisation. Int. J. Nucl. Desalin. 2005, 1, 435–449. [Google Scholar] [CrossRef]
- Donato, L.; Garofalo, A.; Drioli, E.; Alharbi, O.; Aljlil, S.A.; Criscuoli, A.; Algieri, C. Improved performance of vacuum membrane distillation in desalination with zeolite membranes. Sep. Purif. Technol. 2020, 237, 116376. [Google Scholar] [CrossRef]
- de Sousa Silva, R.; Ramlow, H.; Cavalcanti, C.D.; Valle, R.D.; Machado, R.A.; Marangoni, C. Steady state evaluation with different operating times in the direct contact membrane distillation process applied to water recovery from dyeing wastewater. Sep. Purif. Technol. 2020, 230, 115892. [Google Scholar] [CrossRef]
- Feng, C.; Khulbe, K.C.; Matsuura, T.; Tabe, S.; Ismail, A.F. Preparation and characterization of electro-spun nanofiber membranes and their possible applications in water treatment. Sep. Purif. Technol. 2013, 102, 118–135. [Google Scholar] [CrossRef]
- Tijing, L.D.; Choi, J.S.; Lee, S.; Kim, S.H.; Shon, H.K. Recent progress of membrane distillation using electrospun nanofibrous membrane. J. Memb. Sci. 2014, 453, 435–462. [Google Scholar] [CrossRef]
- Fuwad, A.; Ryu, H.; Malmstadt, N.; Min, S.; Jeon, T. Biomimetic membranes as potential tools for water puri fi cation: Preceding and future avenues. Desalination 2019, 458, 97–115. [Google Scholar] [CrossRef]
- Pabby, A.K.; Sastre, A.M. State-of-the-art review on hollow fibre contactor technology and membrane-based extraction processes. J. Memb. Sci. 2013, 430, 263–303. [Google Scholar] [CrossRef]
- Goh, P.S.; Ismail, A.F. A review on inorganic membranes for desalination and wastewater treatment. Desalination 2018, 434, 60–80. [Google Scholar] [CrossRef]
- Tibi, F.; Charfi, A.; Cho, J.; Kim, J. Fabrication of polymeric membranes for membrane distillation process and application for wastewater treatment: Critical review. Process Saf. Environ. Prot. 2020, 141, 190–201. [Google Scholar] [CrossRef]
- Ravi, J.; Othman, M.H.D.; Matsuura, T.; Ro’il Bilad, M.; El-badawy, T.H.; Aziz, F.; Ismail, A.F.; Rahman, M.A.; Jaafar, J. Polymeric membranes for desalination using membrane distillation: A review. Desalination 2020, 490, 114530. [Google Scholar] [CrossRef]
- Pan, C.Y.; Xu, G.R.; Xu, K.; Zhao, H.L.; Wu, Y.Q.; Su, H.C.; Xu, J.M.; Das, R. Electrospun nanofibrous membranes in membrane distillation: Recent developments and future perspectives. Sep. Purif. Technol. 2019, 221, 44–63. [Google Scholar] [CrossRef]
- Wang, P.; Chung, T.S. Recent advances in membrane distillation processes: Membrane development, configuration design and application exploring. J. Memb. Sci. 2015, 474, 39–56. [Google Scholar] [CrossRef]
- Feng, S.; Zhong, Z.; Wang, Y.; Xing, W.; Drioli, E. Progress and perspectives in PTFE membrane: Preparation, modification, and applications. J. Memb. Sci. 2018, 549, 332–349. [Google Scholar] [CrossRef]
- Bhattacharjee, C.; Saxena, V.K.; Dutta, S. Fruit juice processing using membrane technology: A review. Innov. Food Sci. Emerg. Technol. 2017, 43, 136–153. [Google Scholar] [CrossRef]
- Chiam, C.K.; Sarbatly, R. Vacuum membrane distillation processes for aqueous solution treatment-A review. Chem. Eng. Process. Process Intensif. 2013, 74, 27–54. [Google Scholar] [CrossRef]
- Khayet, M. Membranes and theoretical modeling of membrane distillation: A review. Adv. Colloid Interface Sci. 2011, 164, 56–88. [Google Scholar] [CrossRef] [PubMed]
- Naidu, G.; Tijing, L.; Johir, M.A.H.; Shon, H.; Vigneswaran, S. Hybrid membrane distillation: Resource, nutrient and energy recovery. J. Memb. Sci. 2020, 599, 117832. [Google Scholar] [CrossRef]
- Kimura, S.; Nakao, S.-I.; Shimatani, S.-I. Transport phenomena in membrane distillation. J. Memb. Sci. 1987, 33, 285–298. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Preparation and Characterization of Polyvinylidene Fluoride Membranes for Membrane Distillation. Ind. Eng. Chem. Res. 2001, 40, 5710–5718. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, M.P.; Mengual, J.I. Thermal boundary layers in sweeping gas membrane distillation processes. AIChE J. 2002, 48, 1488–1497. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.A.; García-Payo, M.C.; Fernández-Pineda, C. Air gap membrane distillation of sucrose aqueous solutions. J. Memb. Sci. 1999, 155, 291–307. [Google Scholar] [CrossRef]
- Ugrozov, V.V.; Elkina, I.B. Mathematical modeling of influence of porous structure a membrane on its vapour-conductivity in the process of membrane distillation. Desalination 2002, 147, 167–171. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Pervaporation and vacuum membrane distillation processes: Modeling and experiments. AIChE J. 2004, 50, 1697–1712. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Transport analysis of air-gap membrane distillation. J. Memb. Sci. 2005, 255, 239–253. [Google Scholar] [CrossRef]
- Khayet, M.; Velázquez, A.; Mengual, J.I. Modelling mass transport through a porous partition: Effect of pore size distribution. J. Non-Equilibrium Thermodyn. 2004, 29, 279–299. [Google Scholar] [CrossRef]
- Ding, Z.; Ma, R.; Fane, A.G. A new model for mass transfer in direct contact membrane distillation. Desalination 2003, 151, 217–227. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Memb. Sci. 2003, 215, 75–85. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Cheng, L.-H.; Xu, X.; Chen, H. Concentration of lignocellulosic hydrolyzates by solar membrane distillation. Bioresour. Technol. 2012, 123, 382–385. [Google Scholar] [CrossRef]
- Khan, E.U.; Nordberg, Å. Membrane distillation process for concentration of nutrients and water recovery from digestate reject water. Sep. Purif. Technol. 2018, 206, 90–98. [Google Scholar] [CrossRef]
- Raza, W.; Lee, J.; Raza, N.; Luo, Y.; Kim, K.H.; Yang, J. Removal of phenolic compounds from industrial waste water based on membrane-based technologies. J. Ind. Eng. Chem. 2019, 71, 1–18. [Google Scholar] [CrossRef]
- Criscuoli, A.; Drioli, E. Date juice concentration by vacuum membrane distillation. Sep. Purif. Technol. 2020, 117301. [Google Scholar] [CrossRef]
- Zhang, J.; Dow, N.; Duke, M.; Ostarcevic, E.; Li, J.-D.; Gray, S. Identification of material and physical features of membrane distillation membranes for high performance desalination. J. Memb. Sci. 2010, 349, 295–303. [Google Scholar] [CrossRef]
- Jönsson, A.-S.; Wimmerstedt, R.; Harrysson, A.-C. Membrane distillation—A theoretical study of evaporation through microporous membranes. Desalination 1985, 56, 237–249. [Google Scholar] [CrossRef]
- Naidu, G.; Choi, Y.; Jeong, S.; Hwang, T.M.; Vigneswaran, S. Experiments and modeling of a vacuum membrane distillation for high saline water. J. Ind. Eng. Chem. 2014, 20, 2174–2183. [Google Scholar] [CrossRef]
- Martínez, L. Comparison of membrane distillation performance using different feeds. Desalination 2004, 168, 359–365. [Google Scholar] [CrossRef]
- Martínez, L.; Rodríguez-Maroto, J.M. On transport resistances in direct contact membrane distillation. J. Memb. Sci. 2007, 295, 28–39. [Google Scholar] [CrossRef]
- Wirth, D.; Cabassud, C. Water desalination using membrane distillation: Comparison between inside/out and outside/in permeation. Desalination 2002, 147, 139–145. [Google Scholar] [CrossRef]
- Qtaishat, M.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- García-Payo, M.C.; Rivier, C.A.; Marison, I.W.; von Stockar, U. Separation of binary mixtures by thermostatic sweeping gas membrane distillation: II. Experimental results with aqueous formic acid solutions. J. Memb. Sci. 2002, 198, 197–210. [Google Scholar] [CrossRef]
- Tun, C.M.; Fane, A.G.; Matheickal, J.T.; Sheikholeslami, R. Membrane distillation crystallization of concentrated salts—flux and crystal formation. J. Memb. Sci. 2005, 257, 144–155. [Google Scholar] [CrossRef]
- Drioli, E.; Criscuoli, A.; Curcio, E. Integrated membrane operations for seawater desalination. Desalination 2002, 147, 77–81. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, M.P.; Mengual, J.I. Study of Asymmetric Polarization in Direct Contact Membrane Distillation. Sep. Sci. Technol. 2005, 39, 125–147. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, L.; El-Bourawi, M.S.; Ma, R. Analysis of a solar-powered membrane distillation system. Desalination 2005, 172, 27–40. [Google Scholar] [CrossRef]
- Mengual, J.I.; Khayet, M.; Godino, M.P. Heat and mass transfer in vacuum membrane distillation. Int. J. Heat Mass Transf. 2004, 47, 865–875. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R. Direct contact membrane distillation: Effect of mass transfer on heat transfer. J. Memb. Sci. 2001, 188, 137–143. [Google Scholar] [CrossRef]
- Rivier, C.A.; García-Payo, M.C.; Marison, I.W.; von Stockar, U. Separation of binary mixtures by thermostatic sweeping gas membrane distillation: I. Theory and simulations. J. Memb. Sci. 2002, 201, 1–16. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Membrane distillation for dilute ethanol: Separation from aqueous streams. J. Memb. Sci. 1999, 163, 333–348. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, G. Modeling of ultrasonic enhancement on membrane distillation. J. Memb. Sci. 2000, 176, 31–41. [Google Scholar] [CrossRef]
- Cabassud, C.; Wirth, D. Membrane distillation for water desalination: How to chose an appropriate membrane? Desalination 2003, 157, 307–314. [Google Scholar] [CrossRef]
- Anvari, A.; Yancheshme, A.A.; Kekre, K.M.; Ronen, A. State-of-the-Art Methods for Overcoming Temperature Polarization in Membrane Distillation Process: A Review. J. Memb. Sci. 2020, 616, 118413. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.A.; Abildskov, J.; Jonsson, G. The use of VMD data/model to test different thermodynamic models for vapour-liquid equilibrium. J. Memb. Sci. 2004, 239, 227–241. [Google Scholar] [CrossRef]
- Yao, K.; Qin, Y.; Yuan, Y.; Liu, L.; He, F.; Wu, Y. A continuous-effect membrane distillation process based on hollow fiber AGMD module with internal latent-heat recovery. AIChE J. 2013, 59, 1278–1297. [Google Scholar] [CrossRef]
- Nassrullah, H.; Anis, S.F.; Hashaikeh, R.; Hilal, N. Energy for desalination: A state-of-the-art review. Desalination 2020, 491, 114569. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Ji, S.; Li, Z.; Chen, P. Review of thermal ef fi ciency and heat recycling in membrane distillation processes. DES 2015, 367, 223–239. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Florido-Díaz, F.J.; Vázquez-González, M.I. Study of evaporation efficiency in membrane distillation. Desalination 1999, 126, 193–198. [Google Scholar] [CrossRef]
- Ugrozov, V.V.; Elkina, I.B.; Nikulin, V.N.; Kataeva, L.I. Theoretical and experimental research of liquid-gap membrane distillation process in membrane module. Desalination 2003, 157, 325–331. [Google Scholar] [CrossRef]
- Chen, T.-C.; Ho, C.-D.; Yeh, H.-M. Theoretical modeling and experimental analysis of direct contact membrane distillation. J. Memb. Sci. 2009, 330, 279–287. [Google Scholar] [CrossRef]
- Ramon, G.; Agnon, Y.; Dosoretz, C. Heat transfer in vacuum membrane distillation: Effect of velocity slip. J. Memb. Sci. 2009, 331, 117–125. [Google Scholar] [CrossRef]
- Li, B.; Sirkar, K.K. Novel membrane and device for vacuum membrane distillation-based desalination process. J. Memb. Sci. 2005, 257, 60–75. [Google Scholar] [CrossRef]
- Gunko, S.; Verbych, S.; Bryk, M.; Hilal, N. Concentration of apple juice using direct contact membrane distillation. Desalination 2006, 190, 117–124. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Duke, M.; Xie, Z.; Gray, S. Performance of asymmetric hollow fibre membranes in membrane distillation under various configurations and vacuum enhancement. J. Memb. Sci. 2010, 362, 517–528. [Google Scholar] [CrossRef]
- Li, J.M.; Xu, Z.K.; Liu, Z.M.; Yuan, W.F.; Xiang, H.; Wang, S.Y.; Xu, Y.Y. Microporous polypropylene and polyethylene hollow fiber membranes. Part 3. Experimental studies on membrane distillation for desalination. Desalination 2003, 155, 153–156. [Google Scholar] [CrossRef]
- Mohammadi, T.; Safavi, M.A. Application of Taguchi method in optimization of desalination by vacuum membrane distillation. Desalination 2009, 249, 83–89. [Google Scholar] [CrossRef]
- Pangarkar, B.L.; Sane, M.G.; Guddad, M. Reverse Osmosis and Membrane Distillation for Desalination of Groundwater: A Review. ISRN Mater. Sci. 2011, 2011, 523124. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, B.; Xu, Y. Pilot test of vacuum membrane distillation for seawater desalination on a ship. Desalination 2006, 189, 165–169. [Google Scholar] [CrossRef]
- Simone, S.; Figoli, A.; Criscuoli, A.; Carnevale, M.C.; Rosselli, A.; Drioli, E. Preparation of hollow fibre membranes from PVDF/PVP blends and their application in VMD. J. Memb. Sci. 2010, 364, 219–232. [Google Scholar] [CrossRef]
- Mohammadi, T.; Akbarabadi, M. Separation of ethylene glycol solution by vacuum membrane distillation (VMD). Desalination 2005, 181, 35–41. [Google Scholar] [CrossRef]
- Ahmed, F.E.; Lalia, B.S.; Hashaikeh, R.; Hilal, N. Enhanced performance of direct contact membrane distillation via selected electrothermal heating of membrane surface. J. Memb. Sci. 2020, 610, 118224. [Google Scholar] [CrossRef]
- Martínez, L.; Florido-Díaz, F.J.; Hernández, A.; Prádanos, P. Estimation of vapor transfer coefficient of hydrophobic porous membranes for applications in membrane distillation. Sep. Purif. Technol. 2003, 33, 45–55. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-making with the AHP: Why is the principal eigenvector necessary. Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Naveed, Q.N.; Rafik, M.; Mohamed, N.; Shaikh, A.; Alsayed, A.O.; Sanober, S.; Mohiuddin, K. Evaluating and Ranking Cloud-Based E-Learning Critical Success Factors (CSFs) Using Combinatorial Approach. IEEE Access 2019, 7, 157145–157157. [Google Scholar] [CrossRef]


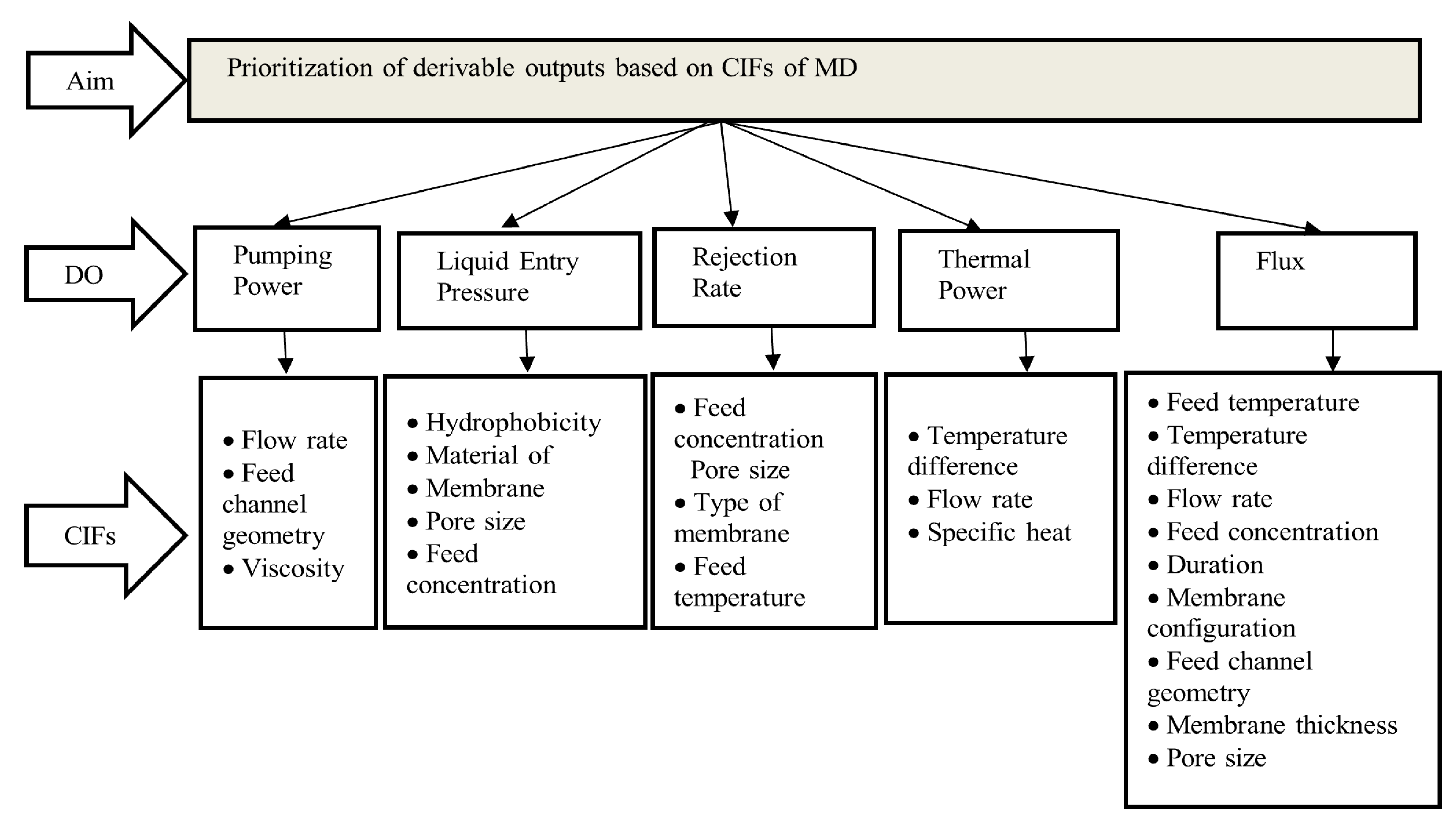

| Derivable Outputs | Critically Influencing Factors | References |
|---|---|---|
| Pumping Power | Flow rate/Reynold’s number | [10,19,20,21,22,23,24,25,26,27,28,29,30,31,32] |
| Feed channel geometry | [10,22,23,24,33,34,35,36,37,38,39,40] | |
| Pressure difference along the feed channel | [21,22,33,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59] | |
| Feed solution properties (like viscosity of liquid which is dependent on temperature and concentration of liquid) | [22,24,31,35,60,61,62,63] | |
| Liquid entry pressure | Hydrophobicity of the membrane (like Contact angle) | [8,11,21,23,24,27,28,29,30,45,47,48,49,57,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100] |
| Material of membrane | [1,8,22,29,33,35,40,92,93,94,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116] | |
| Pore size | [22,27,28,30,31,33,35,39,41,44,50,57,64,70,88,89,94,100,117,118,119,120,121,122,123,124,125,126,127] | |
| Feed solution properties, like concentration and surface tension of the feed | [23,24,29,30,35,48,60,63,112,127,128,129] | |
| Rejection Rate | Feed Concentration | [12,28,29,30,33,39,43,45,48,52,54,59,60,63,70,73,86,88,89,100,119,123,127,129,130,131,132,133,134,135,136,137,138,139,140,141] |
| Pore size of membrane | [12,21,22,27,28,30,31,33,35,39,41,44,50,57,64,70,88,89,94,100,117,118,119,120,121,122,123,124,125,130] | |
| Type of membrane | [1,8,22,26,33,37,39,45,98,99,100,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123] | |
| Feed temperature | [22,23,27,33,39,41,43,46,48,51,52,54,57,59,60,68,70,86,88,89,90,100,118,119,122,123,126,130,138,139,140,141,142,143,144,145,146,147,148,149,150] | |
| Thermal Power | Temperature Difference (between the inlet and at the outlet of the feed channel) | [12,19,21,22,33,34,39,43,52,60,119,138,145,146,149,150,151,152,153] |
| Flow rate/Reynold’s number | [10,20,21,22,24,25,26,27,28,29,30,31,32,151,154,155,156,157] | |
| Specific heat of feed liquid | [19,22,35,73,118,151,152,158] | |
| Flux | Feed temperature (Temperature of the tank) | [19,21,22,23,33,39,41,43,45,46,47,48,51,52,54,57,59,60,68,70,73,86,88,89,90,100,118,119,122,123,126,127,130,133,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,159,160,161] |
| Flow rate/Reynold’s number | [4,10,20,21,22,24,25,26,27,28,29,30,31,32,33,34,35,36,47,50,53,57,79,94,137,140,162,163,164,165,166] | |
| Feed Concentration | [12,28,29,33,39,43,45,48,52,54,59,60,63,70,73,86,88,89,100,118,122,123,127,129,131,132,133,134,135,136,137,139,140,141] | |
| Duration of the experiment | [22,28,29,30,31,50,80,130,164,165,166,167] | |
| Membrane Configuration (Air gap, VMD, etc.) | [5,33,34,40,42,43,44,45,46,47,48,49,70,106,114,116,119,123,168] | |
| Feed channel geometry | [8,10,19,24,33,35,40,103,104,162] | |
| Type of membrane (varying thickness) | [22,24,28,30,34,35,36,37,38,39,64,89,94,117,121,124,126,130] | |
| Type of membrane (varying pore size) | [4,22,30,31,33,35,39,41,44,50,64,70,88,89,94,100,117,118,119,120,121,122,123,124,125,159,169] |
| Pumping Power | Liquid Entry Pressure | Rejection Rate | Thermal Power | Flux | Weightages | |
|---|---|---|---|---|---|---|
| Pumping Power | 1.00 | 0.50 | 0.33 | 3.00 | 0.33 | 0.1280135 |
| Liquid Entry pressure | 2.00 | 1.00 | 2.00 | 0.50 | 0.50 | 0.1929312 |
| Rejection Rate | 3.00 | 0.50 | 1.00 | 2.00 | 0.50 | 0.1894944 |
| Thermal Power | 0.33 | 2.00 | 0.50 | 1.00 | 0.20 | 0.1241332 |
| Flux | 3.00 | 2.00 | 2.00 | 5.00 | 1.00 | 0.3654277 |
| Pumping Power | Liquid Entry Pressure | Rejection Rate | Thermal Power | Flux | Weightages | |
|---|---|---|---|---|---|---|
| Pumping Power | 1.00 | 0.33 | 0.33 | 2.00 | 0.33 | 0.103005549 |
| Liquid Entry pressure | 3.00 | 1.00 | 2.00 | 0.50 | 0.50 | 0.210475692 |
| Rejection Rate | 3.00 | 0.50 | 1.00 | 4.00 | 0.50 | 0.218381505 |
| Thermal Power | 0.50 | 2.00 | 0.25 | 1.00 | 0.25 | 0.123796605 |
| Flux | 3.00 | 2.00 | 2.00 | 4.00 | 1.00 | 0.344340649 |
| Pumping Power | Liquid Entry Pressure | Rejection Rate | Thermal Power | Flux | Weightages | |
|---|---|---|---|---|---|---|
| Pumping Power | 1.00 | 0.25 | 0.33 | 2.00 | 0.50 | 0.118000588 |
| Liquid Entry pressure | 4.00 | 1.00 | 2.00 | 0.50 | 0.33 | 0.212988213 |
| Rejection Rate | 3.00 | 0.50 | 1.00 | 3.00 | 0.50 | 0.208436462 |
| Thermal Power | 0.50 | 2.00 | 0.25 | 1.00 | 0.33 | 0.123790924 |
| Flux | 2.00 | 3.00 | 2.00 | 3.00 | 1.00 | 0.336783813 |
| Pumping Power | Liquid Entry Pressure | Rejection Rate | Thermal Power | Flux | Weightages | |
|---|---|---|---|---|---|---|
| Pumping Power | 1.00 | 0.35 | 0.33 | 2.29 | 0.38 | 0.116112164 |
| Liquid Entry pressure | 2.88 | 1.00 | 2.00 | 0.50 | 0.44 | 0.204823141 |
| Rejection Rate | 3.00 | 0.50 | 1.00 | 2.88 | 0.50 | 0.205390803 |
| Thermal Power | 0.44 | 2.00 | 0.31 | 1.00 | 0.26 | 0.123864583 |
| Flux | 2.62 | 2.29 | 2.00 | 3.91 | 1.00 | 0.349809308 |
| S.No | Main DOs | Weightages | CIF | Local Weights | Global Weights | Overall Ranking |
|---|---|---|---|---|---|---|
| 1 | Pumping Power | 0.116112164 | Flow Rate | 0.4381 | 0.0509 | 7 |
| Feed Channel Geometry | 0.1846 | 0.0214 | 20 | |||
| Pressure Difference | 0.2677 | 0.0311 | 17 | |||
| Viscosity | 0.1096 | 0.0127 | 23 | |||
| 2 | Liquid Entry pressure | 0.204823141 | Hydrophobicity | 0.4081 | 0.0836 | 2 |
| Material Of Membrane | 0.2062 | 0.0422 | 12 | |||
| Pore size | 0.2156 | 0.0442 | 10 | |||
| Feed Properties (concentration and Surface tension) | 0.1701 | 0.0348 | 15 | |||
| 3 | Rejection Rate | 0.205390803 | Feed Concentration | 0.2554 | 0.0525 | 6 |
| Pore size | 0.2229 | 0.0458 | 9 | |||
| Type of Membrane | 0.1064 | 0.0219 | 19 | |||
| Feed Temperature | 0.4153 | 0.0853 | 1 | |||
| 4 | Thermal Power | 0.123864583 | Temperature Difference | 0.3212 | 0.0398 | 13 |
| Flow rate | 0.5228 | 0.0648 | 5 | |||
| Specific Heat | 0.1560 | 0.0193 | 22 | |||
| 5 | Flux | 0.349809308 | Feed Temperature | 0.1882 | 0.0658 | 4 |
| Flow Rate | 0.2034 | 0.0711 | 3 | |||
| Feed concentration | 0.1365 | 0.0477 | 8 | |||
| Duration | 0.0602 | 0.0211 | 21 | |||
| Membrane Configuration | 0.0841 | 0.0294 | 18 | |||
| Feed channel Geometry | 0.0962 | 0.0337 | 16 | |||
| Membrane thickness | 0.1102 | 0.0385 | 14 | |||
| Pore Size | 0.1213 | 0.0424 | 11 |
| Pumping Power | Liquid Entry Pressure | Rejection Rate | Thermal Power | Flux | Weightages | |
|---|---|---|---|---|---|---|
| Pumping Power | (1.00,1.00,1.00) | (0.25,0.33,0.50) | (0.25,0.33,0.50) | (1.00,2.00,3.00) | (0.25,0.33,0.50) | 0.1050 |
| Liquid Entry pressure | (2.00,3.00,4.00) | (1.00,1.00,1.00) | (1.00,2.00,3.00) | (0.33,0.50,1.00) | (0.33,0.50,1.00) | 0.2001 |
| Rejection Rate | (2.00,3.00,4.00) | (0.33,0.50,1.00) | (1.00,1.00,1.00) | (3.00,4.00,5.00) | (0.33,0.50,1.00) | 0.2276 |
| Thermal Power | (0.33,0.50,1.00) | (1.00,2.00,3.00) | (0.20,0.25,0.33) | (1.00,1.00,1.00) | (0.20,0.25,0.33) | 0.1022 |
| Flux | (2.00,3.00,4.00) | (1.00,2.00,3.00) | (1.00,2.00,3.00) | (3.00,4.00,5.00) | (1.00,1.00,1.00) | 0.3651 |
| S.No | Main DOs | Weightages | CIFs | Local Weights | Global Weights | Overall Ranking |
|---|---|---|---|---|---|---|
| 1 | Pumping Power | 0.1050 | Flow Rate | 0.4309 | 0.0452 | 10 |
| Feed Channel Geometry | 0.1497 | 0.0157 | 21 | |||
| Pressure Difference | 0.2914 | 0.0306 | 15 | |||
| Viscosity | 0.1280 | 0.0134 | 23 | |||
| 2 | Liquid Entry pressure | 0.2001 | Hydrophobicity | 0.4085 | 0.0817 | 3 |
| Material of Membrane | 0.2062 | 0.0413 | 12 | |||
| Pore size | 0.2420 | 0.0484 | 8 | |||
| Feed Properties (concentration and Surface tension) | 0.1432 | 0.0287 | 16 | |||
| 3 | Rejection Rate | 0.2276 | Feed Concentration | 0.2693 | 0.0613 | 6 |
| Pore size | 0.2203 | 0.0501 | 7 | |||
| Type of Membrane | 0.1131 | 0.0257 | 17 | |||
| Feed Temperature | 0.3973 | 0.0904 | 2 | |||
| 4 | Thermal Power | 0.1022 | Temperature Difference | 0.2415 | 0.0247 | 18 |
| Flow rate | 0.6131 | 0.0627 | 5 | |||
| Specific Heat | 0.1454 | 0.0149 | 22 | |||
| 5 | Flux | 0.3651 | Feed Temperature | 0.1928 | 0.0704 | 4 |
| Flow Rate | 0.2568 | 0.0938 | 1 | |||
| Feed concentration | 0.1310 | 0.0478 | 9 | |||
| Duration | 0.0562 | 0.0205 | 20 | |||
| Membrane Configuration | 0.0675 | 0.0246 | 19 | |||
| Feed channel Geometry | 0.0915 | 0.0334 | 13 | |||
| Membrane thickness | 0.0847 | 0.0309 | 14 | |||
| Pore Size | 0.1195 | 0.0436 | 11 |
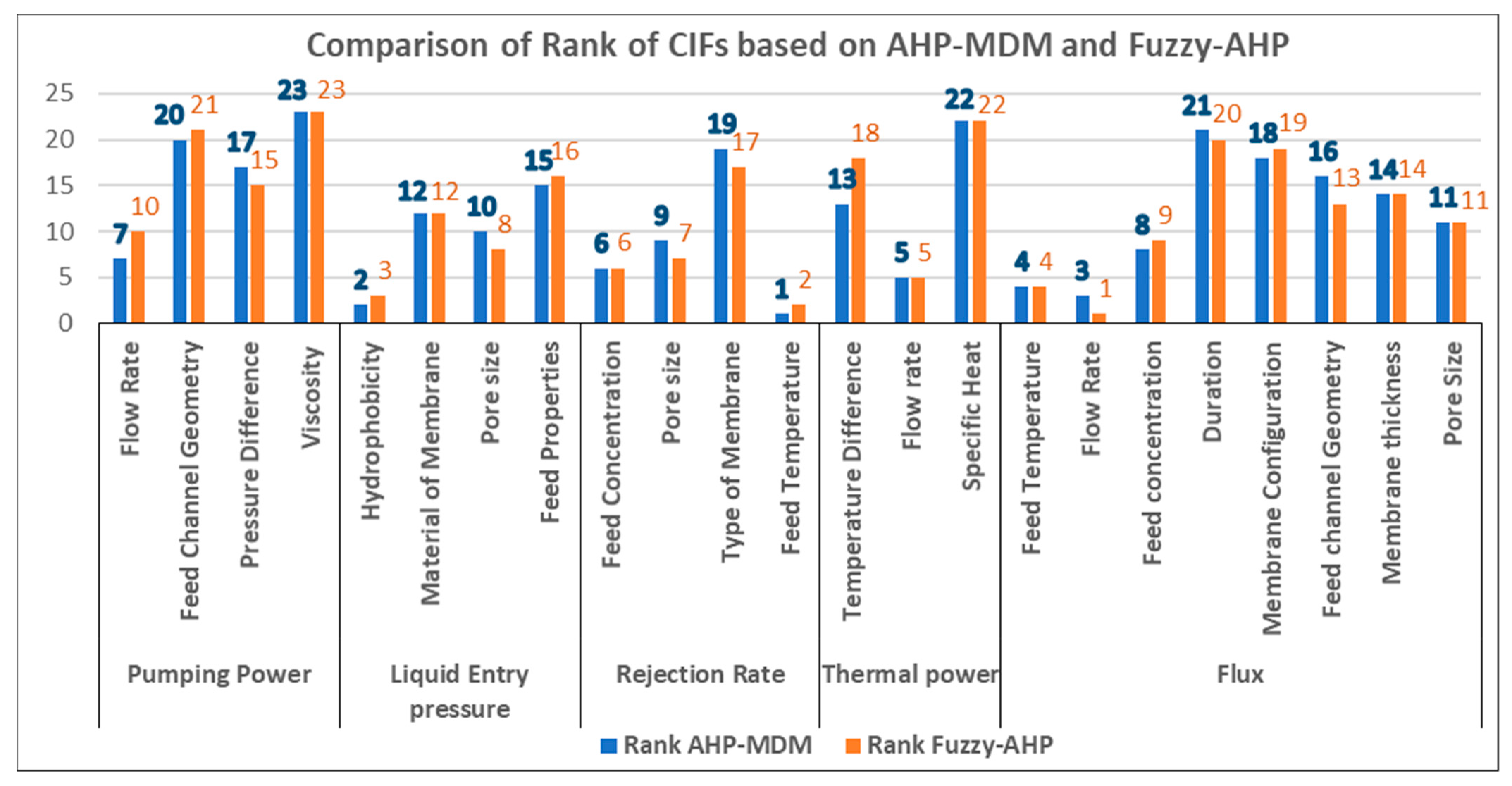
| CIF | AHP-MDM | AHP-MDM RANKS | AHP-MDM Classification | Fuzzy-AHP | Fuzzy-AHP RANKS | Fuzzy AHP Classification |
|---|---|---|---|---|---|---|
| Flow Rate | 0.1868 | 1 | *** | 0.2017 | 1 | *** |
| Feed Temperature | 0.1511 | 2 | *** | 0.1608 | 2 | *** |
| Pore size | 0.1324 | 3 | *** | 0.1422 | 3 | *** |
| Feed Concentration | 0.1002 | 4 | *** | 0.1091 | 4 | *** |
| Hydrophobicity | 0.0836 | 5 | *** | 0.0817 | 5 | *** |
| Feed Channel Geometry | 0.0551 | 6 | *** | 0.0491 | 6 | *** |
| Material of Membrane | 0.0422 | 7 | ** | 0.0413 | 7 | ** |
| Temperature Difference | 0.0398 | 8 | ** | 0.0247 | 12 | * |
| Membrane thickness | 0.0385 | 9 | ** | 0.0309 | 8 | ** |
| Feed Properties (concentration and Surface tension) | 0.0348 | 10 | ** | 0.0287 | 10 | ** |
| Pressure Difference | 0.0311 | 11 | ** | 0.0306 | 9 | ** |
| Membrane Configuration | 0.0294 | 12 | * | 0.0246 | 13 | * |
| Type of Membrane | 0.0219 | 13 | * | 0.0257 | 11 | ** |
| Duration | 0.0211 | 14 | * | 0.0205 | 14 | * |
| Specific Heat | 0.0193 | 15 | * | 0.0149 | 15 | * |
| Viscosity | 0.0127 | 16 | * | 0.0134 | 16 | * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anqi, A.E.; Mohammed, A.A. Evaluating Critical Influencing Factors of Desalination by Membrane Distillation Process—Using Multi-Criteria Decision-Making. Membranes 2021, 11, 164. https://doi.org/10.3390/membranes11030164
Anqi AE, Mohammed AA. Evaluating Critical Influencing Factors of Desalination by Membrane Distillation Process—Using Multi-Criteria Decision-Making. Membranes. 2021; 11(3):164. https://doi.org/10.3390/membranes11030164
Chicago/Turabian StyleAnqi, Ali E., and Azam A. Mohammed. 2021. "Evaluating Critical Influencing Factors of Desalination by Membrane Distillation Process—Using Multi-Criteria Decision-Making" Membranes 11, no. 3: 164. https://doi.org/10.3390/membranes11030164
APA StyleAnqi, A. E., & Mohammed, A. A. (2021). Evaluating Critical Influencing Factors of Desalination by Membrane Distillation Process—Using Multi-Criteria Decision-Making. Membranes, 11(3), 164. https://doi.org/10.3390/membranes11030164






