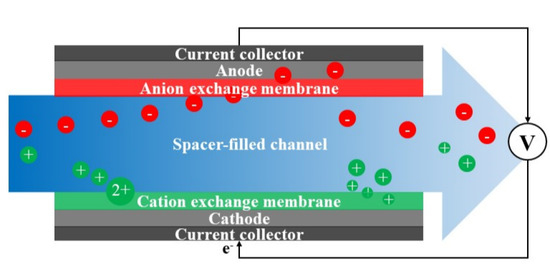
Theoretical Analysis of Constant Voltage Mode Membrane Capacitive Deionization for Water Softening
Abstract
:1. Introduction
2. Model Framework
3. Results and Discussion
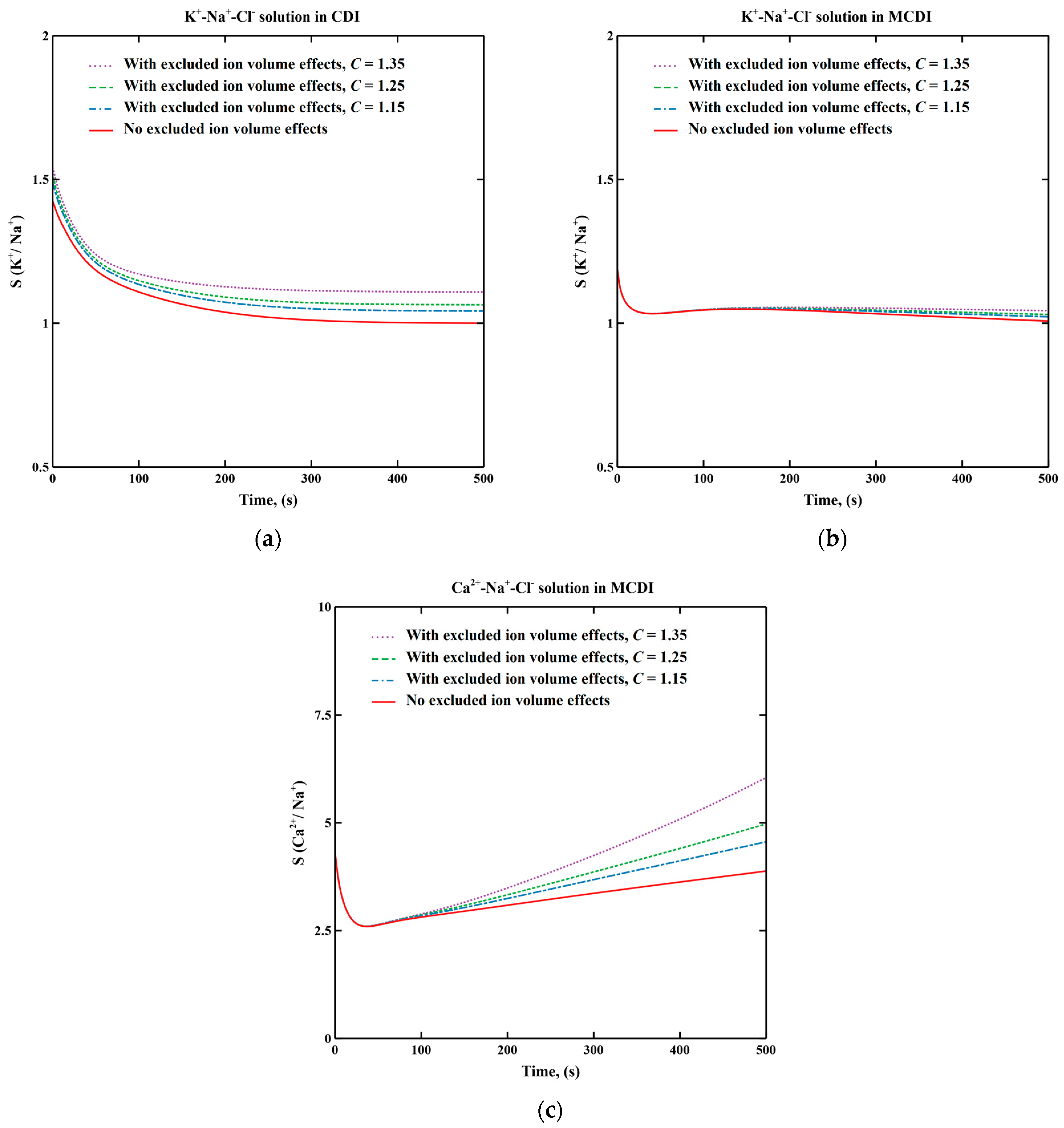
3.1. Excluded Ion Volume Effects
3.2. Trade-Offs between Selectivity and Removal Efficiency of Calcium Ions
3.3. Case Studies
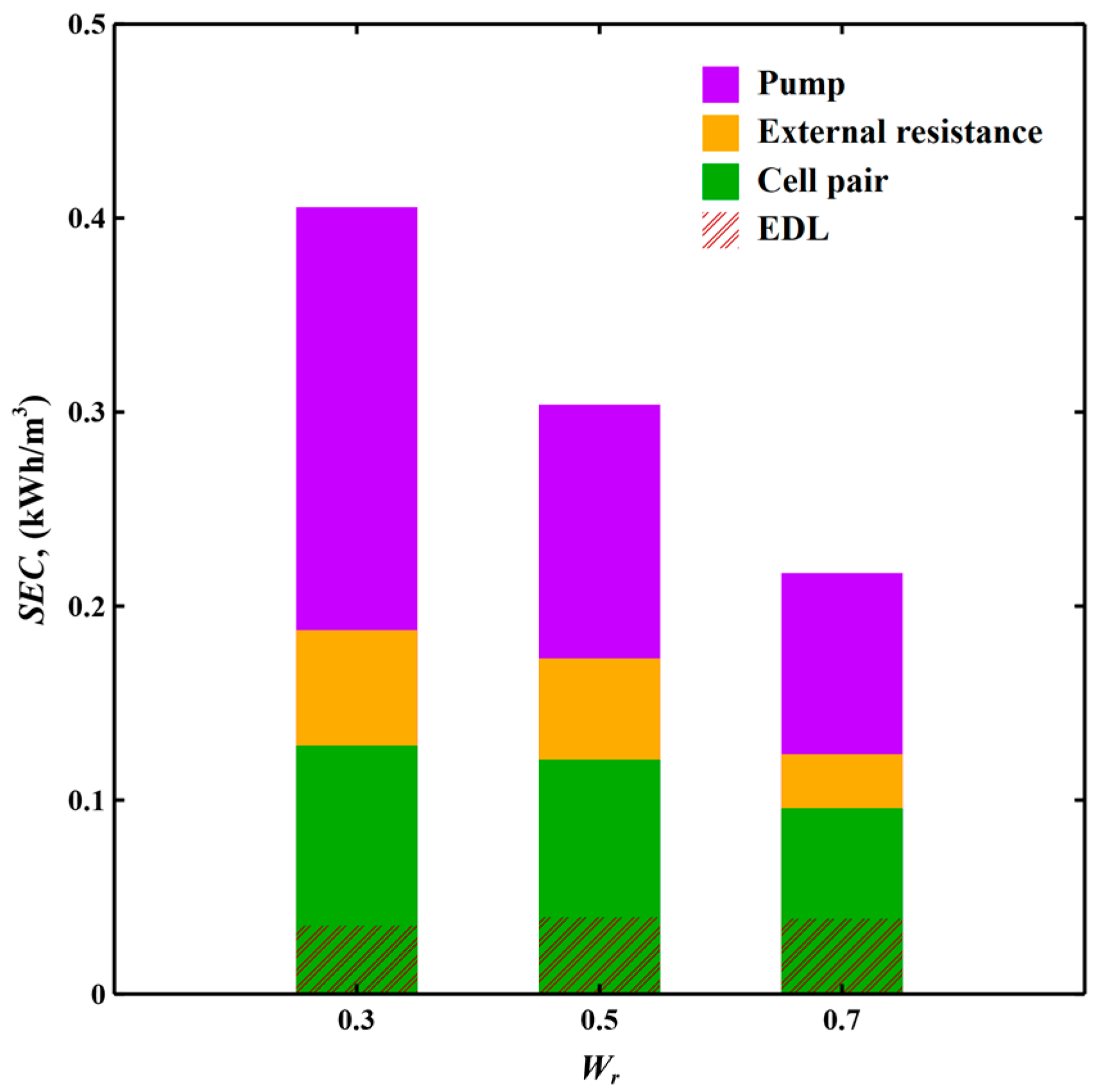
3.3.1. Industrial Cooling Tower Blowdown Water Softening Scenario
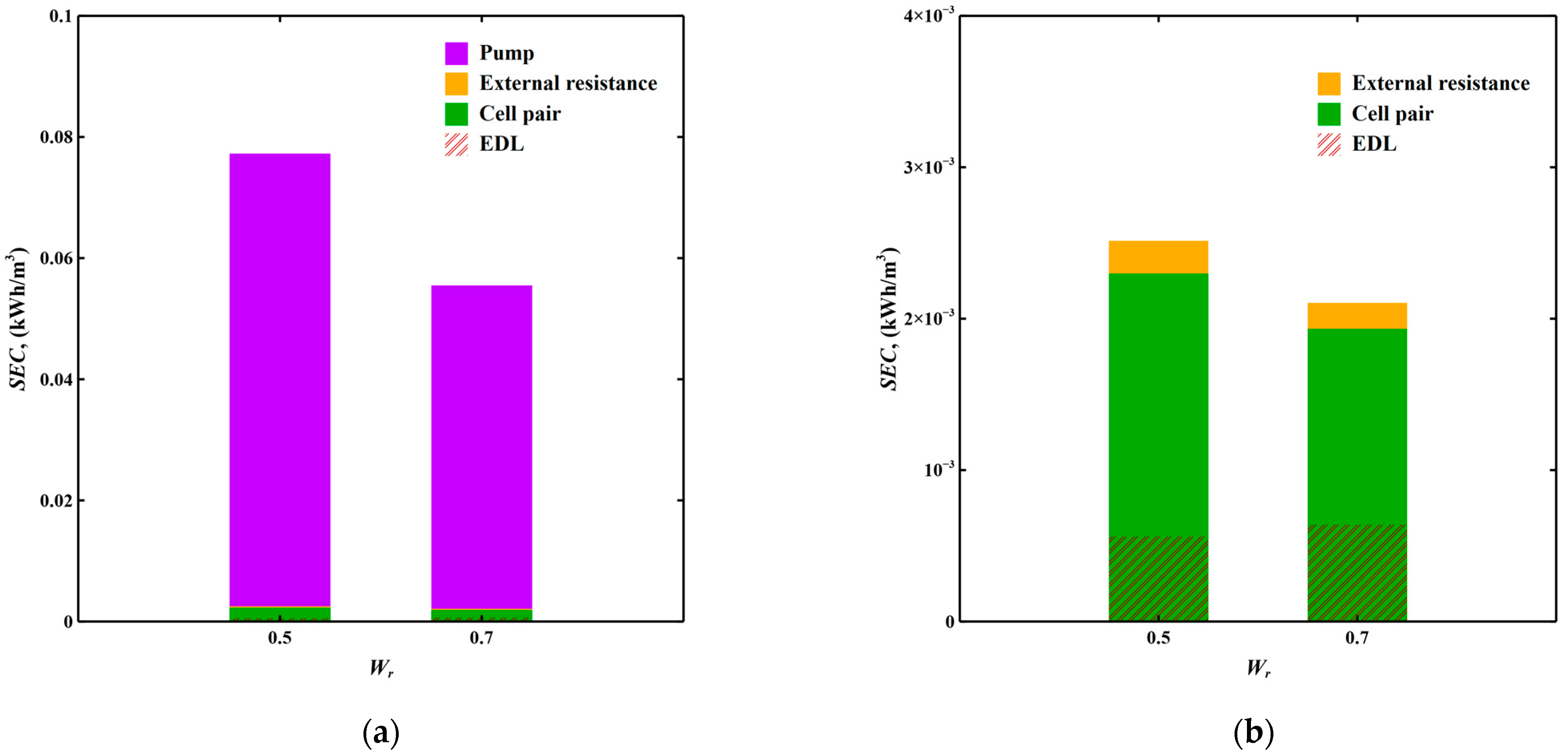
3.3.2. Domestic Tap Water Softening Scenario
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cotruvo, J.A.; Bartram, J. Calcium and Magnesium in Drinking-Water: Public Health Significance; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Greenleaf, J.E.; Lin, J.C.; Sengupta, A.K. Two novel applications of ion exchange fibers: Arsenic removal and chemical-free softening of hard water. Environ. Prog. 2006, 25, 300–311. [Google Scholar] [CrossRef]
- Wang, L.K.; Vaccari, D.A.; Li, Y.; Shammas, N.K. Chemical Precipitation. In Physicochemical Treatment Processes; Springer: Berlin/Heidelberg, Germany, 2005; pp. 141–197. [Google Scholar]
- Gabrielli, C.; Maurin, G.; Francy-Chausson, H.; Thery, P.; Tran, T.; Tlili, M. Electrochemical water softening: Principle and application. Desalination 2006, 201, 150–163. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-H. Effect of operating conditions on CaSO4 scale formation mechanism in nanofiltration for water softening. Water Res. 2000, 34, 3854–3866. [Google Scholar] [CrossRef]
- Rahimpour, A.; Jahanshahi, M.; Mortazavian, N.; Madaeni, S.S.; Mansourpanah, Y. Preparation and characterization of asymmetric polyethersulfone and thin-film composite polyamide nanofiltration membranes for water softening. Appl. Surf. Sci. 2010, 256, 1657–1663. [Google Scholar] [CrossRef]
- Park, J.-S.; Song, J.-H.; Yeon, K.-H.; Moon, S.-H. Removal of hardness ions from tap water using electromembrane processes. Desalination 2007, 202, 1–8. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Tewari, S. Capacitive deionization: Processes, materials and state of the technology. J. Electroanal. Chem. 2018, 813, 178–192. [Google Scholar] [CrossRef]
- Honarparvar, S.; Zhang, X.; Chen, T.; Na, C.; Reible, D. Modeling technologies for desalination of brackish water—toward a sustainable water supply. Curr. Opin. Chem. Eng. 2019, 26, 104–111. [Google Scholar] [CrossRef]
- Choi, J.; Dorji, P.; Shon, H.K.; Hong, S. Applications of capacitive deionization: Desalination, softening, selective removal, and energy efficiency. Desalination 2019, 449, 118–130. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Leonard, K.C.; Genthe, J.R.; Sanfilippo, J.L.; Zeltner, W.A.; Anderson, M.A. Synthesis and characterization of asymmetric electrochemical capacitive deionization materials using nanoporous silicon dioxide and magnesium doped aluminum oxide. Electrochim. Acta 2009, 54, 5286–5291. [Google Scholar] [CrossRef]
- Seo, S.-J.; Jeon, H.; Lee, J.K.; Kim, G.-Y.; Park, D.; Nojima, H.; Lee, J.; Moon, S.-H. Investigation on removal of hardness ions by capacitive deionization (CDI) for water softening applications. Water Res. 2010, 44, 2267–2275. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Van Soestbergen, M.; Rijnaarts, H.; Van der Wal, A.; Bazant, M.; Biesheuvel, P. Time-dependent ion selectivity in capacitive charging of porous electrodes. J. Colloid Interface Sci. 2012, 384, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Hou, C.-H.; Huang, C.-Y. A comparative study of electrosorption selectivity of ions by activated carbon electrodes in capacitive deionization. Desalination 2013, 314, 124–129. [Google Scholar] [CrossRef]
- Yoon, H.; Lee, J.; Kim, S.-R.; Kang, J.; Kim, S.; Kim, C.; Yoon, J. Capacitive deionization with Ca-alginate coated-carbon electrode for hardness control. Desalination 2016, 392, 46–53. [Google Scholar] [CrossRef]
- Lado, J.J.; Zornitta, R.L.; Vázquez Rodríguez, I.s.; Malverdi Barcelos, K.; Ruotolo, L.A. Sugarcane Biowaste-Derived Biochars as Capacitive Deionization Electrodes for Brackish Water Desalination and Water-Softening Applications. ACS Sustain. Chem. Eng. 2019, 7, 18992–19004. [Google Scholar] [CrossRef]
- Leong, Z.Y.; Yang, H.Y. Capacitive Deionization of Divalent Cations for Water Softening Using Functionalized Carbon Electrodes. ACS Omega 2020, 5, 2097–2106. [Google Scholar] [CrossRef]
- Biesheuvel, P.; Van der Wal, A. Membrane capacitive deionization. J. Membr. Sci. 2010, 346, 256–262. [Google Scholar] [CrossRef]
- Wang, L.; Lin, S. Mechanism of selective ion removal in membrane capacitive deionization for water softening. Environ. Sci. Technol. 2019, 53, 5797–5804. [Google Scholar] [CrossRef]
- Hassanvand, A.; Chen, G.; Webley, P.; Kentish, S. An investigation of the impact of fouling agents in capacitive and membrane capacitive deionisation. Desalination 2019, 457, 96–102. [Google Scholar] [CrossRef]
- Van Limpt, B.; Van der Wal, A. Water and chemical savings in cooling towers by using membrane capacitive deionization. Desalination 2014, 342, 148–155. [Google Scholar] [CrossRef]
- He, C.; Ma, J.; Zhang, C.; Song, J.; Waite, T.D. Short-circuited closed-cycle operation of flow-electrode CDI for brackish water softening. Environ. Sci. Technol. 2018, 52, 9350–9360. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.; Dykstra, J.E.; Zuilhof, H.; Zornitta, R.L.; de Smet, L.C. Modification of Cation-Exchange Membranes with Polyelectrolyte Multilayers to Tune Ion Selectivity in Capacitive Deionization. ACS Appl. Mater. Interfaces 2020, 12, 34746–34754. [Google Scholar] [CrossRef] [PubMed]
- Sata, T.; Sata, T.; Yang, W. Studies on cation-exchange membranes having permselectivity between cations in electrodialysis. J. Membr. Sci. 2002, 206, 31–60. [Google Scholar] [CrossRef]
- Lado, J.J.; Pérez-Roa, R.E.; Wouters, J.J.; Tejedor-Tejedor, M.I.; Federspill, C.; Ortiz, J.M.; Anderson, M.A. Removal of nitrate by asymmetric capacitive deionization. Sep. Purif. Technol. 2017, 183, 145–152. [Google Scholar] [CrossRef]
- Hemmatifar, A.; Stadermann, M.; Santiago, J.G. Two-dimensional porous electrode model for capacitive deionization. J. Phys. Chem. C 2015, 119, 24681–24694. [Google Scholar] [CrossRef]
- Rommerskirchen, A.; Ohs, B.; Hepp, K.A.; Femmer, R.; Wessling, M. Modeling continuous flow-electrode capacitive deionization processes with ion-exchange membranes. J. Membr. Sci. 2018, 546, 188–196. [Google Scholar] [CrossRef]
- Singh, K.; Bouwmeester, H.; de Smet, L.; Bazant, M.; Biesheuvel, P. Theory of water desalination with intercalation materials. Phys. Rev. Appl. 2018, 9, 064036. [Google Scholar] [CrossRef]
- He, F.; Biesheuvel, P.; Bazant, M.Z.; Hatton, T.A. Theory of water treatment by capacitive deionization with redox active porous electrodes. Water Res. 2018, 132, 282–291. [Google Scholar] [CrossRef]
- Oyarzun, D.I.; Hemmatifar, A.; Palko, J.W.; Stadermann, M.; Santiago, J.G. Ion selectivity in capacitive deionization with functionalized electrode: Theory and experimental validation. Water Res. X 2018, 1, 100008. [Google Scholar] [CrossRef]
- Zhang, X.; Reible, D. Exploring the Function of Ion-Exchange Membrane in Membrane Capacitive Deionization via a Fully Coupled Two-Dimensional Process Model. Processes 2020, 8, 1312. [Google Scholar] [CrossRef]
- Biesheuvel, P.; Van Soestbergen, M. Counterion volume effects in mixed electrical double layers. J. Colloid Interface Sci. 2007, 316, 490–499. [Google Scholar] [CrossRef]
- Suss, M.E. Size-based ion selectivity of micropore electric double layers in capacitive deionization electrodes. J. Electrochem. Soc. 2017, 164, E270. [Google Scholar] [CrossRef]
- Guyes, E.N.; Malka, T.; Suss, M.E. Enhancing the ion-size-based selectivity of capacitive deionization electrodes. Environ. Sci. Technol. 2019, 53, 8447–8454. [Google Scholar] [CrossRef]
- Nightingale, E., Jr. Phenomenological theory of ion solvation. Effective radii of hydrated ions. J. Phys. Chem. 1959, 63, 1381–1387. [Google Scholar] [CrossRef]
- Vanysek, P. Ionic conductivity and diffusion at infinite dilution. CRC Handb. Chem. Phys. 2000, 83, 76–78. [Google Scholar]
- Zhang, C.; Tang, J.; Zhao, G.; Tang, Y.; Li, J.; Li, F.; Zhuang, H.; Chen, J.; Lin, H.; Zhang, Y. Investigation on an electrochemical pilot equipment for water softening with an automatic descaling system: Parameter optimization and energy consumption analysis. J. Clean. Prod. 2020, 276, 123178. [Google Scholar] [CrossRef]
- Luan, J.; Wang, L.; Sun, W.; Li, X.; Zhu, T.; Zhou, Y.; Deng, H.; Chen, S.; He, S.; Liu, G. Multi-meshes coupled cathodes enhanced performance of electrochemical water softening system. Sep. Purif. Technol. 2019, 217, 128–136. [Google Scholar] [CrossRef]
- Altman, S.J.; Jensen, R.P.; Cappelle, M.A.; Sanchez, A.L.; Everett, R.L.; Anderson Jr, H.L.; McGrath, L.K. Membrane treatment of side-stream cooling tower water for reduction of water usage. Desalination 2012, 285, 177–183. [Google Scholar] [CrossRef]
- Wagner, T.V.; de Wilde, V.; Willemsen, B.; Mutaqin, M.; Putri, G.; Opdam, J.; Parsons, J.R.; Rijnaarts, H.H.; de Voogt, P.; Langenhoff, A.A. Pilot-scale hybrid constructed wetlands for the treatment of cooling tower water prior to its desalination and reuse. J. Environ. Manag. 2020, 271, 110972. [Google Scholar] [CrossRef]
- Clauwaert, P.; De Paepe, J.; Jiang, F.; Alonso-Fariñas, B.; Vaiopoulou, E.; Verliefde, A.; Rabaey, K. Electrochemical tap water softening: A zero chemical input approach. Water Res. 2020, 169, 115263. [Google Scholar] [CrossRef] [PubMed]
- Patterson, K.Y.; Pehrsson, P.R.; Perry, C.R. The mineral content of tap water in United States households. J. Food Compos. Anal. 2013, 31, 46–50. [Google Scholar] [CrossRef]


| Components | Hydrated Radii, (nm) [36] | Diffusion Coefficients, (m2/s) [37] |
|---|---|---|
| Na+ | 0.358 | 1.33 × 10−9 |
| K+ | 0.331 | 1.96 × 10−9 |
| Ca2+ | 0.412 | 0.79 × 10−9 |
| Mg2+ | 0.428 | 0.71 × 10−9 |
| Cl− | 0.332 | 2.03 × 10−9 |
| NO3− | 0.335 | 1.90 × 10−9 |
| SO42− | 0.379 | 1.07 × 10−9 |
| Parameter | Value | Unit |
|---|---|---|
| Cell length | 10 | [cm] |
| Cell width | 10 | [cm] |
| Electrode thickness | 0.15 | [mm] |
| Macropore porosity | 0.4 [27] | - |
| Micropore porosity | 0.3 [27] | - |
| Micropore capacitance | 1.5 [27] | [GF/m3] |
| IEM thickness | 0.15 | [mm] |
| IEM water content volume fraction | 0.4 | [L(water)/L(swollen IEM)] |
| IEM fixed charge density | 1000 | [mol/m3] |
| Spacer-filled channel thickness | 0.3 | [mm] |
| Spacer porosity | 0.71 | - |
| Spacer permeability | 1.23 × 10−12 | [m2] |
| External resistance | 0.6 | [Ω] |
| C = di/dh,i | 1.15–1.35, 1.25 * # [34] | - |
| Flow rate | 0.3, 0.35 *, 0.2 # | [L/h] |
| Applied voltage | 0.1–0.3, 0.4 *, 0.08 # | [V] |
| Parameter | Value | |||
|---|---|---|---|---|
| Concentration of ionic species in the feed water, (mM) [41] | Na+ | 24.35 | ||
| Ca2+ | 7.48 | |||
| Cl− | 14.95 | |||
| NO3− | 0.98 | |||
| SO42− | 11.69 | |||
| Water recovery | ||||
| 0.3 | 0.5 | 0.7 | ||
| Concentration of ionic species in the product water, (mM) | Na+ | 13.21 | 17.44 | 22.64 |
| Ca2+ | 1.28 | 2.50 | 5.19 | |
| Cl− | 9.23 | 11.53 | 14.19 | |
| NO3− | 0.62 | 0.76 | 0.93 | |
| SO42− | 2.96 | 5.07 | 8.95 | |
| Ion removal efficiency, (%) | Na+ | 45.76 | 28.37 | 7.03 |
| Ca2+ | 82.88 | 66.64 | 30.62 | |
| Cl− | 38.25 | 22.89 | 5.09 | |
| NO3− | 37.21 | 22.37 | 5.22 | |
| SO42− | 74.68 | 56.61 | 23.43 | |
| Ca2+ selectivity | 1.81 | 2.35 | 4.36 | |
| SEC, (kWh/m3) | 0.406 | 0.304 | 0.217 | |
| SECmole, (kWh/mole) | 0.065 | 0.061 | 0.095 | |
| Parameter | Value | ||
|---|---|---|---|
| Concentration of ionic species in the feed water, (mM) [43] | Na+ | 1.65 | |
| Ca2+ | 0.75 | ||
| K+ | 0.13 | ||
| Mg2+ | 0.38 | ||
| Cl− | 4.04 | ||
| Water recovery | |||
| 0.5 | 0.7 | ||
| Concentration of ionic species in the product water, (mM) | Na+ | 1.44 | 1.58 |
| Ca2+ | 0.53 | 0.66 | |
| K+ | 0.11 | 0.13 | |
| Mg2+ | 0.27 | 0.34 | |
| Cl− | 3.16 | 3.71 | |
| Ion removal efficiency, (%) | Na+ | 12.94 | 4.38 |
| Ca2+ | 28.90 | 11.43 | |
| K+ | 12.80 | 1.63 | |
| Mg2+ | 28.58 | 10.78 | |
| Cl− | 21.80 | 8.12 | |
| Ca2+ selectivity | 2.23 | 2.61 | |
| Mg2+ selectivity | 2.21 | 2.46 | |
| SEC, (kWh/m3) | 0.077 | 0.055 | |
| SECmole, (kWh/mole) | 0.356 | 0.256 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Reible, D. Theoretical Analysis of Constant Voltage Mode Membrane Capacitive Deionization for Water Softening. Membranes 2021, 11, 231. https://doi.org/10.3390/membranes11040231
Zhang X, Reible D. Theoretical Analysis of Constant Voltage Mode Membrane Capacitive Deionization for Water Softening. Membranes. 2021; 11(4):231. https://doi.org/10.3390/membranes11040231
Chicago/Turabian StyleZhang, Xin, and Danny Reible. 2021. "Theoretical Analysis of Constant Voltage Mode Membrane Capacitive Deionization for Water Softening" Membranes 11, no. 4: 231. https://doi.org/10.3390/membranes11040231
APA StyleZhang, X., & Reible, D. (2021). Theoretical Analysis of Constant Voltage Mode Membrane Capacitive Deionization for Water Softening. Membranes, 11(4), 231. https://doi.org/10.3390/membranes11040231