An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation
Abstract
:1. Introduction
- To develop and validate a semi-empirical model that is able to capture downstream variables, including transmembrane water flux, Temperature Polarisation Coefficient (TPC), Concentration Polarisation Coefficient (CPC), and thermal efficiency on a DCMD module;
- To model DCMD with a self-sustained water flux equation which allows to systematically investigate different membranes with few assumptions;
- To conduct a sensitivity analysis to understand which parameters have more significant effects on DCMD performance;
- To analyse 22 commercially available membranes in terms of performance metric evaluation to assess the suitability of these membranes for DCMD application.
2. Governing Equations
2.1. Transmembrane Transport
2.1.1. Transmembrane Mass Transport
2.1.2. Transmembrane Heat Transfer
2.2. Channel Flow Governing Equations
2.2.1. Semi-Empirical Approximation Using Nusselt Correlation
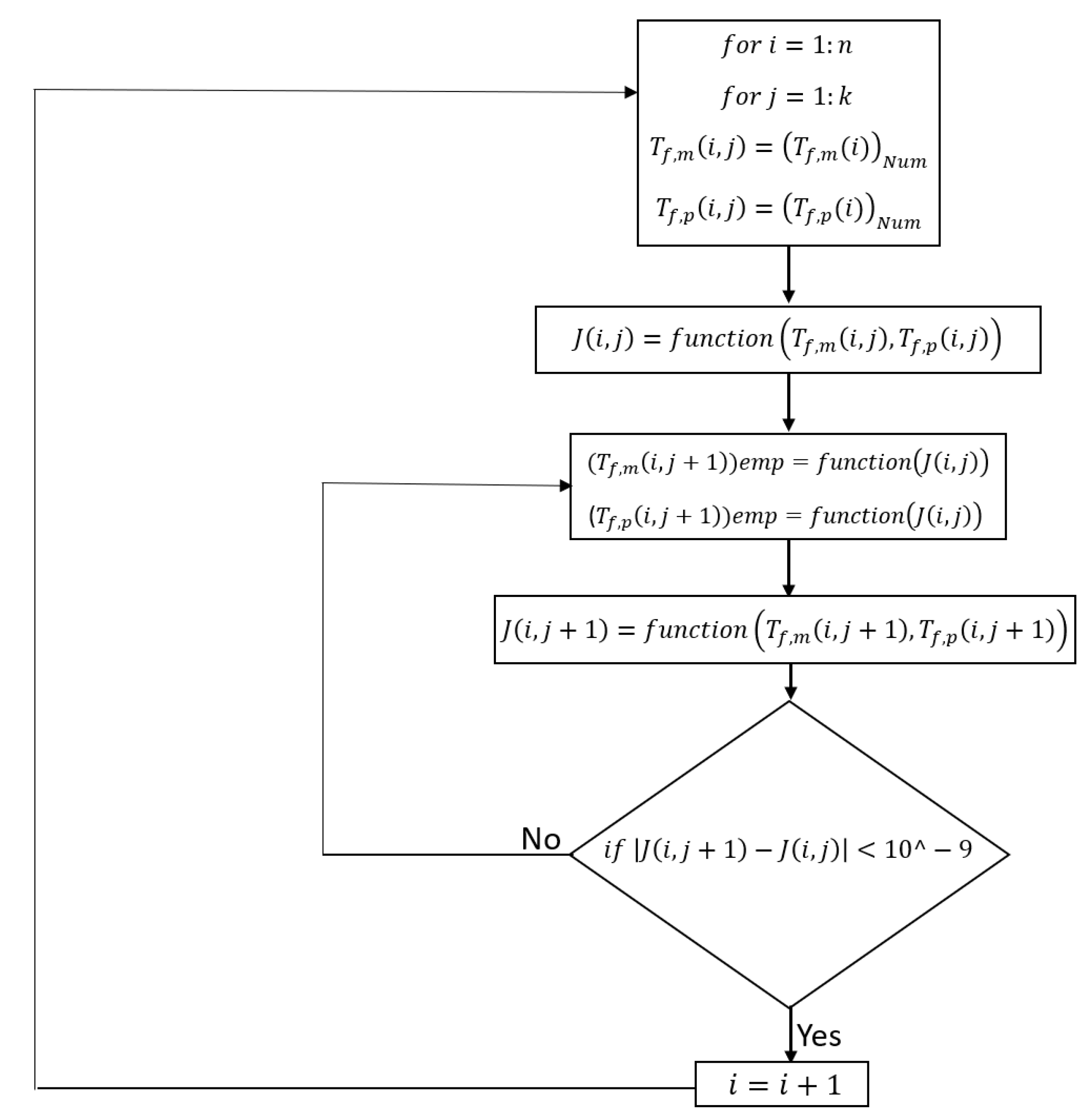
2.2.2. Numerical Method
3. Materials and Methods
3.1. Process Modelling
3.2. System Performance Metrics
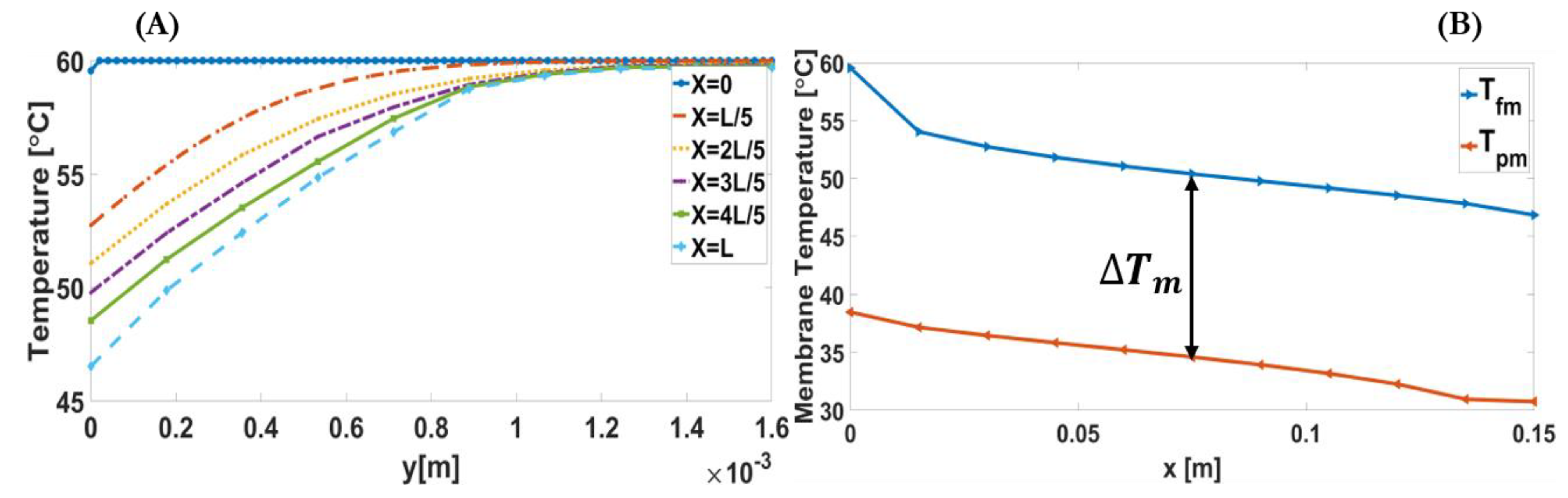
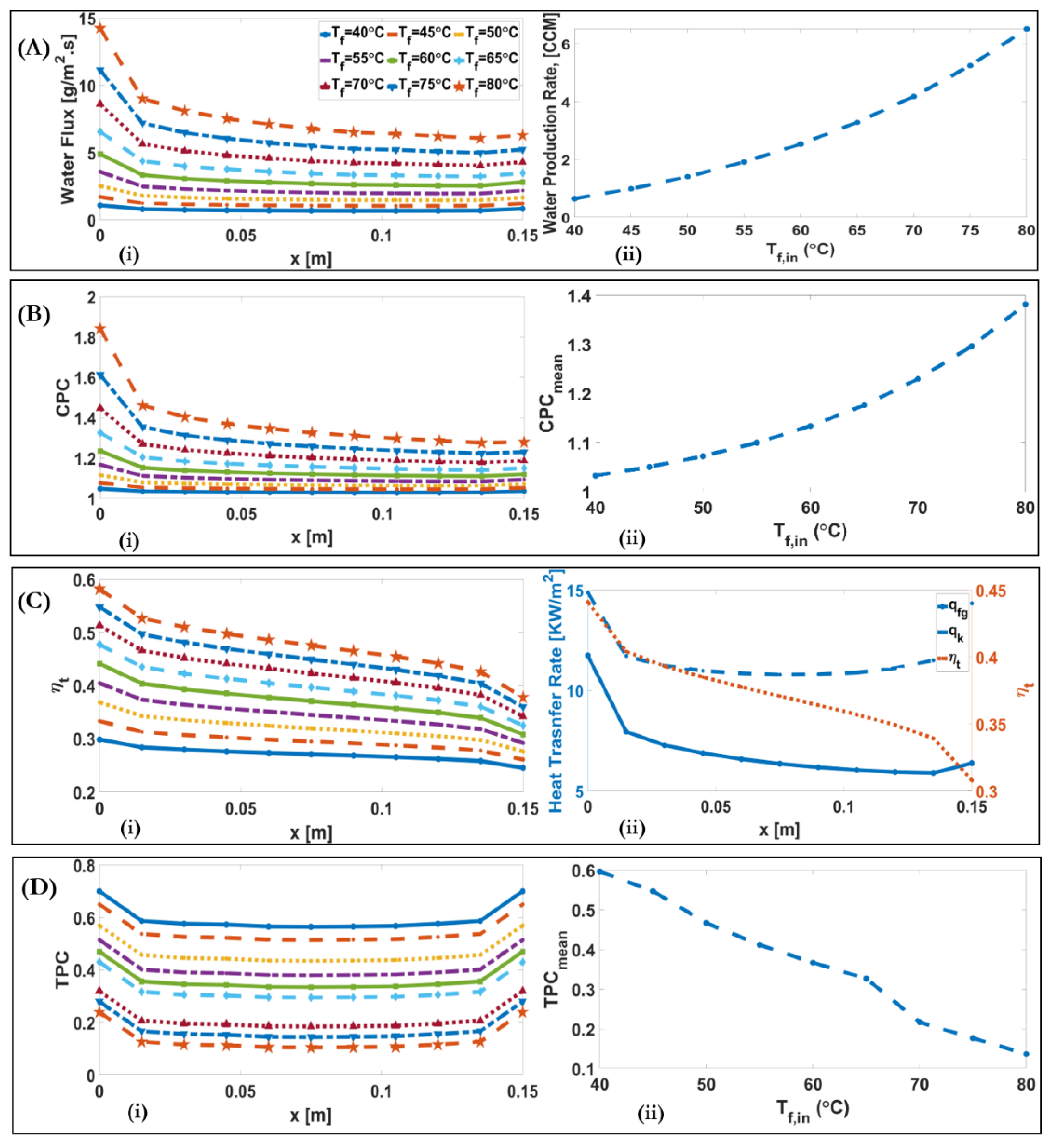
3.2.1. Temperature Polarisation Coefficient (TPC)
3.2.2. Concentration Polarisation Coefficient (CPC)
3.2.3. Thermal Efficiency
4. Results and Discussion
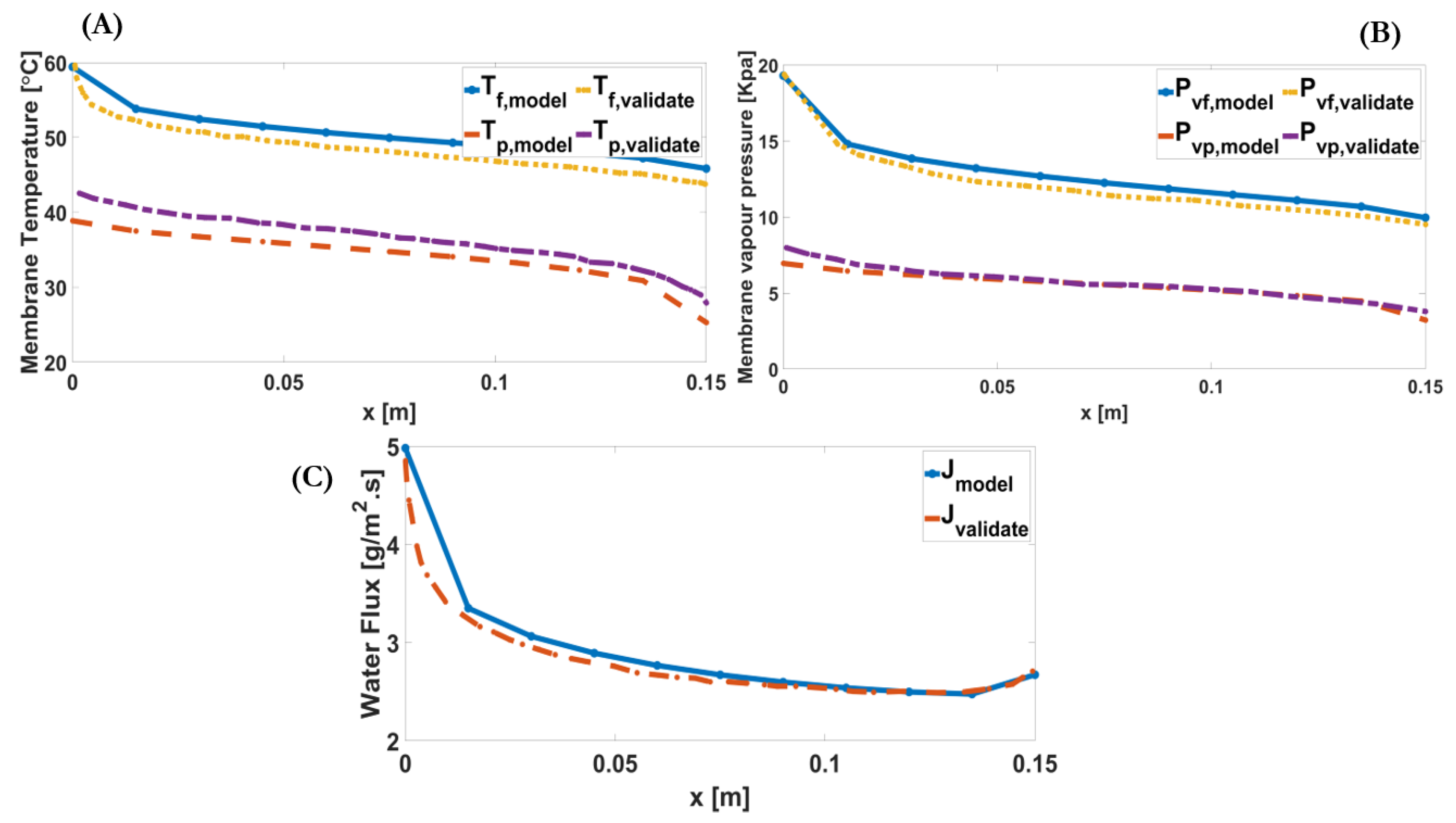
4.1. Model Validation
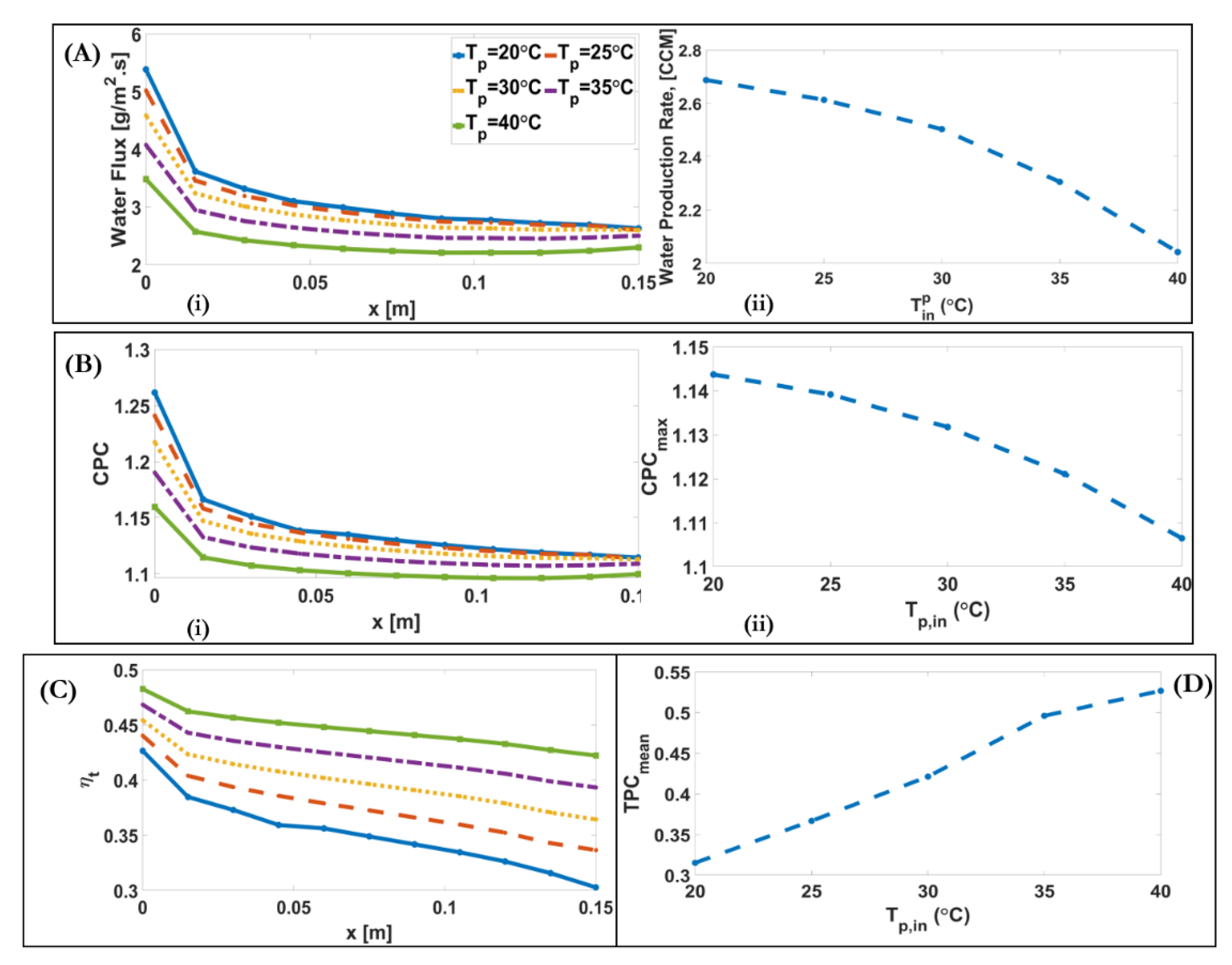
4.2. Influence of Inlet Feed and Permeate Temperature
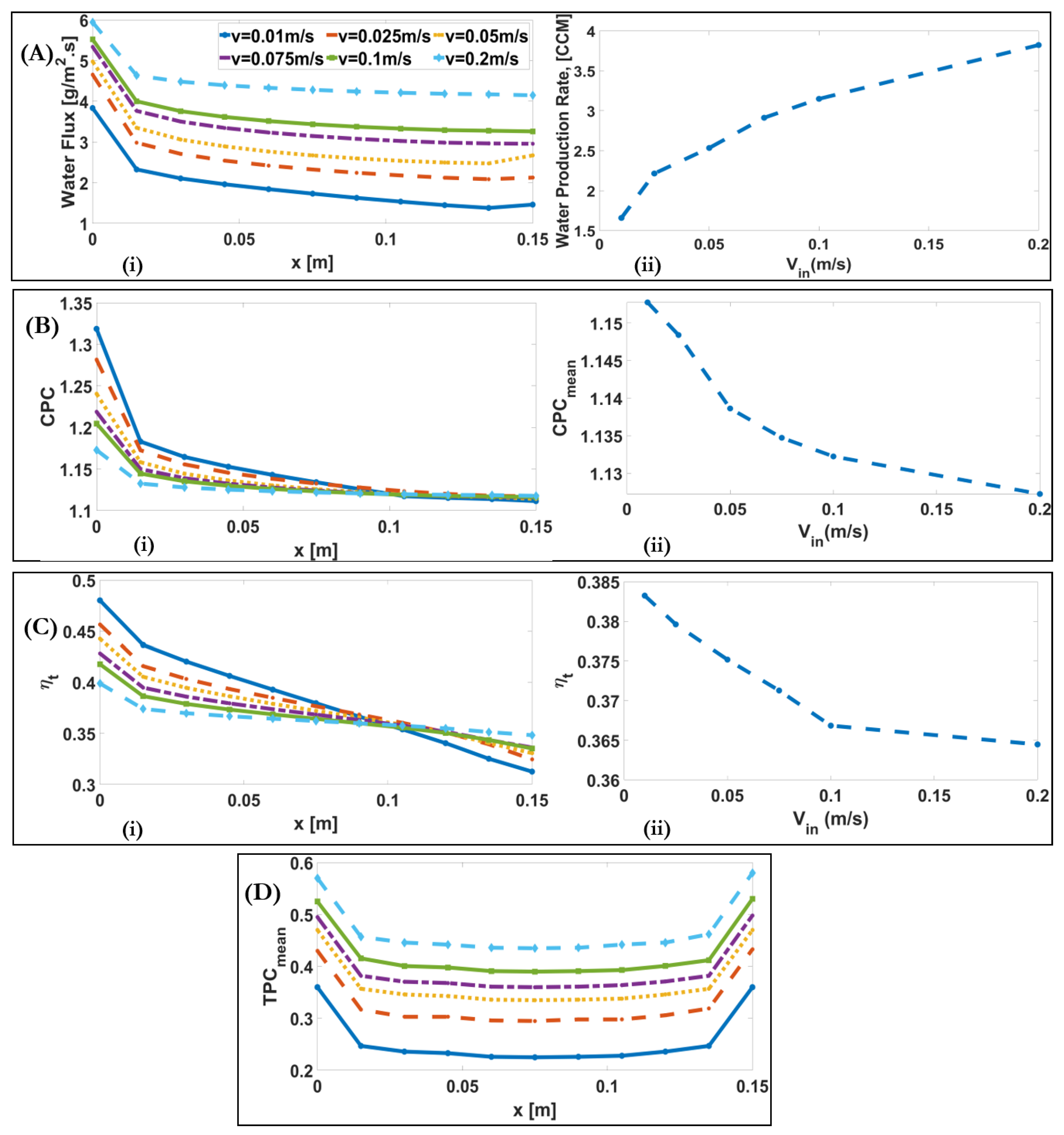
4.3. Influence of Inlet Velocity
4.4. Influence of Inlet Feed Concentration
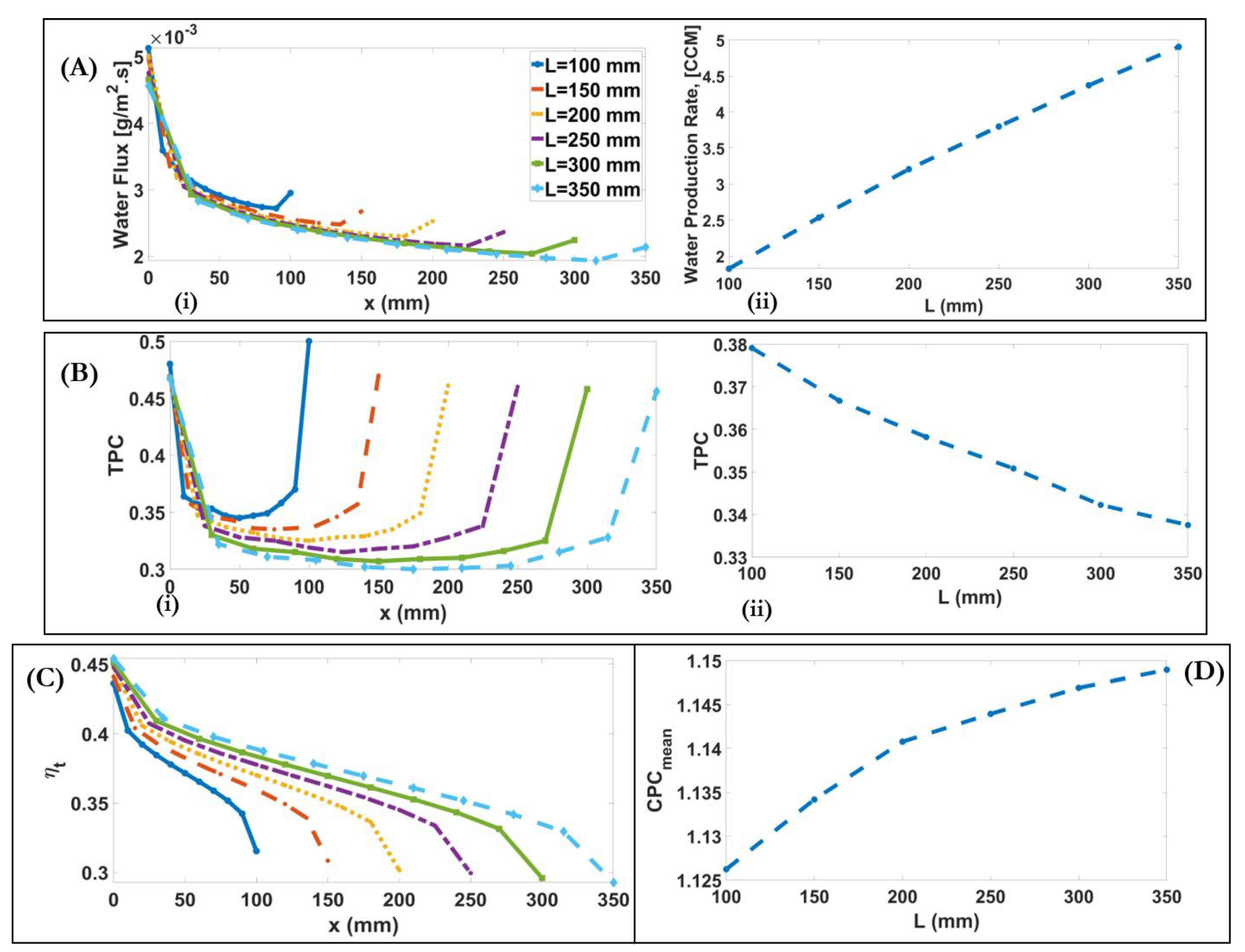
4.5. Influence of Channel Length
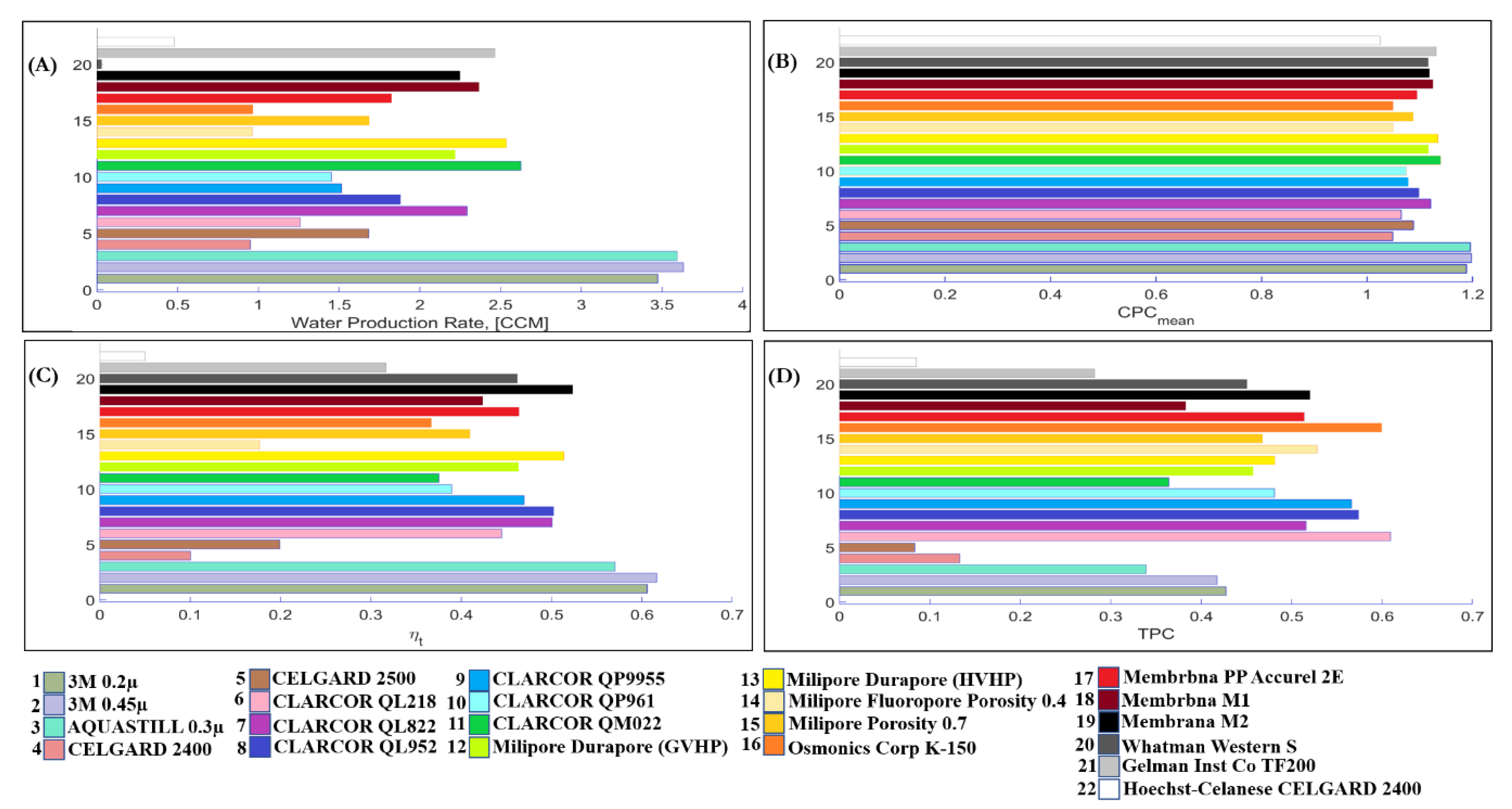
4.6. Commercial Membranes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Karagiannis, I.C.; Soldatos, P.G. Water desalination cost literature: Review and assessment. Desalination 2008, 223, 448–456. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The Future of Seawater Desalination: Energy, Technology, and the Environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef]
- Kummu, M.; Ward, P.J.; De Moel, H.; Varis, O. Is physical water scarcity a new phenomenon? Global assessment of water shortage over the last two millennia. Environ. Res. Lett. 2010, 5, 034006. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudi, F.; Goodarzi, G.M.; Dehghani, S.; Akbarzadeh, A. Experimental and theoretical study of a lab scale permeate gap membrane distillation setup for desalination. Desalination 2017, 419, 197–210. [Google Scholar] [CrossRef]
- Kumar, M.; Culp, T.; Shen, Y. Water Desalination: History, Advances, and Challenges. In Frontiers of Engineering: Reports on Leading-Edge Engineering from the 2016 Symposium; National Academies Press: Washington, DC, USA, 2017. [Google Scholar]
- Mahmoudi, F.; Date, A.; Akbarzadeh, A. Further investigation of simultaneous fresh water production and power generation concept by permeate gap membrane distillation system. J. Membr. Sci. 2019, 572, 230–245. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Thu, K.; Ghaffour, N.; Ng, K.C. Performance investigation of a solar-assisted direct contact membrane distillation system. J. Membr. Sci. 2013, 427, 345–364. [Google Scholar] [CrossRef] [Green Version]
- Ali, E.; Orfi, J.; AlAnsary, H.; Lee, J.-G.; Alpatova, A.; Ghaffour, N. Integration of multi effect evaporation and membrane distillation desalination processes for enhanced performance and recovery ratios. Desalination 2020, 493, 114619. [Google Scholar] [CrossRef]
- Ruiz-Aguirre, A.; Andrés-Mañas, J.A.; Zaragoza, G. Evaluation of Permeate Quality in Pilot Scale Membrane Distillation Systems. Membranes 2019, 9, 69. [Google Scholar] [CrossRef] [Green Version]
- Soukane, S.; Elcik, H.; Alpatova, A.; Orfi, J.; Ali, E.; AlAnsary, H.; Ghaffour, N. Scaling sets the limits of large scale membrane distillation modules for the treatment of high salinity feeds. J. Clean. Prod. 2021, 287, 125555. [Google Scholar] [CrossRef]
- Dudchenko, A.V.; Hardikar, M.; Xin, R.; Joshi, S.; Wang, R.; Sharma, N.; Mauter, M.S. Impact of module design on heat transfer in membrane distillation. J. Membr. Sci. 2020, 601, 117898. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Ahmed, Z.; Cha, D.K.; Cho, J. Flux model for the membrane distillation process to treat wastewater: Effect of solids concentration. J. Membr. Sci. 2018, 566, 396–405. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A. Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Membr. Sci. 2003, 215, 75–85. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A. Effects of net-type spacers on heat and mass transfer in direct contact membrane distillation and comparison with ultrafiltration studies. J. Membr. Sci. 2003, 217, 193–206. [Google Scholar] [CrossRef]
- Qtaishat, M.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- Bouchrit, R.; Boubakri, A.; Hafiane, A.; Bouguecha, S.A.-T. Direct contact membrane distillation: Capability to treat hyper-saline solution. Desalination 2015, 376, 117–129. [Google Scholar] [CrossRef]
- Manawi, Y.M.; Khraisheh, M.; Fard, A.K.; Benyahia, F.; Adham, S. Effect of operational parameters on distillate flux in direct contact membrane distillation (DCMD): Comparison between experimental and model predicted performance. Desalination 2014, 336, 110–120. [Google Scholar] [CrossRef]
- Yang, X.; Wang, R.; Fane, A.G. Novel designs for improving the performance of hollow fiber membrane distillation modules. J. Membr. Sci. 2011, 384, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Lou, J.; Johnston, J.; Cath, T.Y.; Martinand, D.; Tilton, N. Computational fluid dynamics simulations of unsteady mixing in spacer-filled direct contact membrane distillation channels. J. Membr. Sci. 2020, 622, 118931. [Google Scholar] [CrossRef]
- Lou, J.; Vanneste, J.; DeCaluwe, S.C.; Cath, T.Y.; Tilton, N. Computational fluid dynamics simulations of polarization phenomena in direct contact membrane distillation. J. Membr. Sci. 2019, 591, 117150. [Google Scholar] [CrossRef]
- Park, D.J.; Norouzi, E.; Park, C. Experimentally-validated computational simulation of direct contact membrane distillation performance. Int. J. Heat Mass Transf. 2019, 129, 1031–1042. [Google Scholar] [CrossRef]
- Fard, A.K.; Rhadfi, T.; Khraisheh, M.; Atieh, M.A.; Khraisheh, M.; Hilal, N. Reducing flux decline and fouling of direct contact membrane distillation by utilizing thermal brine from MSF desalination plant. Desalination 2016, 379, 172–181. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Francis, L.; Lee, J.-G.; Ham, M.-G.; Ghaffour, N. Effect of non-woven net spacer on a direct contact membrane distillation performance: Experimental and theoretical studies. J. Membr. Sci. 2018, 564, 193–203. [Google Scholar] [CrossRef]
- Lee, J.G.; Jang, Y.; Fortunato, L.; Jeong, S.; Lee, S.; Leiknes, T.; Ghaffour, N. An advanced online monitoring approach to study the scaling behavior in direct contact membrane distillation. J. Membr. Sci. 2018, 546, 50–60. [Google Scholar] [CrossRef] [Green Version]
- Soukane, S.; Naceur, M.W.; Francis, L.; Alsaadi, A.; Ghaffour, N. Effect of feed flow pattern on the distribution of permeate fluxes in desalination by direct contact membrane distillation. Desalination 2017, 418, 43–59. [Google Scholar] [CrossRef]
- Elcik, H.; Fortunato, L.; Alpatova, A.; Soukane, S.; Orfi, J.; Ali, E.; Al Ansary, H.; Leiknes, T.; Ghaffour, N. Multi-effect distillation brine treatment by membrane distillation: Effect of antiscalant and antifoaming agents on membrane performance and scaling control. Desalination 2020, 493, 114653. [Google Scholar] [CrossRef]
- Elmarghany, M.R.; El-Shazly, A.H.; Salem, M.S.; Sabry, M.N.; Nady, N. Thermal analysis evaluation of direct contact membrane distillation system. Case Stud. Therm. Eng. 2019, 13, 100377. [Google Scholar] [CrossRef]
- Janajreh, I.; Suwwan, D.; Hashaikeh, R. Assessment of direct contact membrane distillation under different configurations, velocities and membrane properties. Appl. Energy 2017, 185, 2058–2073. [Google Scholar] [CrossRef]
- Salem, M.S.; El-Shazly, A.H.; Nady, N.; Elmarghany, M.R.; Shouman, M.A.; Sabry, M.N. 3-D numerical investigation on commercial PTFE membranes for membrane distillation: Effect of inlet conditions on heat and mass transfer. Case Stud. Ther. Eng. 2019, 13, 100396. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.M.; Kim, J.H. Spacer optimization strategy for direct contact membrane distillation: Shapes, configurations, diameters, and numbers of spacer filaments. Desalination 2017, 417, 9–18. [Google Scholar] [CrossRef]
- Taamneh, Y.; Bataineh, K. Improving the performance of direct contact membrane distillation utilizing spacer-filled channel. Desalination 2017, 408, 25–35. [Google Scholar] [CrossRef]
- Katsandri, A. A theoretical analysis of a spacer filled flat plate membrane distillation modules using CFD: Part II: Temperature polarisation analysis. Desalination 2017, 408, 166–180. [Google Scholar] [CrossRef]
- Katsandri, A. A theoretical analysis of a spacer filled flat plate membrane distillation modules using CFD: Part I: Velocity and shear stress analysis. Desalination 2017, 408, 145–165. [Google Scholar] [CrossRef]
- Al-Sharif, S.; Albeirutty, M.; Cipollina, A.; Micale, G. Modelling flow and heat transfer in spacer-filled membrane distillation channels using open source CFD code. Desalination 2013, 311, 103–112. [Google Scholar] [CrossRef]
- Yazgan-Birgi, P.; Ali, M.I.H.; Arafat, H.A. Comparative performance assessment of flat sheet and hollow fiber DCMD processes using CFD modeling. Sep. Purif. Technol. 2019, 212, 709–722. [Google Scholar] [CrossRef]
- Orfi, J.; Loussif, N.; Davies, P.A. Heat and mass transfer in membrane distillation used for desalination with slip flow. Desalination 2016, 381, 135–142. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudi, F.; Date, A.; Akbarzadeh, A. Examining the commercially available hydrophobic membranes in combined desalination and power generation through permeate gap membrane distillation. Desalination 2020, 474, 114149. [Google Scholar] [CrossRef]
- Gryta, M. Effectiveness of Water Desalination by Membrane Distillation Process. Membranes 2012, 2, 415–429. [Google Scholar] [CrossRef] [Green Version]
- García, J.V.; Dow, N.; Milne, N.; Zhang, J.; Naidoo, L.; Gray, S.; Duke, M. Membrane Distillation Trial on Textile Wastewater Containing Surfactants Using Hydrophobic and Hydrophilic-Coated Polytetrafluoroethylene (PTFE) Membranes. Membranes 2018, 8, 31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Furaiji, M.; Arena, J.T.; Ren, J.; Benes, N.; Nijmeijer, A.; McCutcheon, J.R. Triple-Layer Nanofiber Membranes for Treating High Salinity Brines Using Direct Contact Membrane Distillation. Membranes 2019, 9, 60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ray, S.S.; Bakshi, H.S.; Dangayach, R.; Singh, R.; Deb, C.K.; Ganesapillai, M.; Chen, S.-S.; Purkait, M.K. Recent Developments in Nanomaterials-Modified Membranes for Improved Membrane Distillation Performance. Membranes 2020, 10, 140. [Google Scholar] [CrossRef]
- Intrchom, W.; Roy, S.; Humoud, M.S.; Mitra, S. Immobilization of Graphene Oxide on the Permeate Side of a Membrane Distillation Membrane to Enhance Flux. Membranes 2018, 8, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elmarghany, M.R.; El-Shazly, A.H.; Rajabzadeh, S.; Salem, M.S.; Shouman, M.A.; Sabry, M.N.; Matsuyama, H.; Nady, N. Triple-Layer Nanocomposite Membrane Prepared by Electrospinning Based on Modified PES with Carbon Nanotubes for Membrane Distillation Applications. Membranes 2020, 10, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, F.Y.C.; Arning, A. Performance Comparison between Polyvinylidene Fluoride and Polytetrafluoroethylene Hollow Fiber Membranes for Direct Contact Membrane Distillation. Membranes 2019, 9, 52. [Google Scholar] [CrossRef] [Green Version]
- Yazgan-Birgi, P.; Ali, M.I.H.; Arafat, H.A. Estimation of liquid entry pressure in hydrophobic membranes using CFD tools. J. Membr. Sci. 2018, 552, 68–76. [Google Scholar] [CrossRef]
- Vanneste, J.; Bush, J.A.; Hickenbottom, K.L.; Marks, C.A.; Jassby, D.; Turchi, C.S.; Cath, T.Y. Novel thermal efficiency-based model for determination of thermal conductivity of membrane distillation membranes. J. Membr. Sci. 2018, 548, 298–308. [Google Scholar] [CrossRef]
- Najib, A.; Orfi, J.; Ali, E.; Saleh, J. Thermodynamics analysis of a direct contact membrane distillation with/without heat recovery based on experimental data. Desalination 2019, 466, 52–67. [Google Scholar] [CrossRef]
- Kast, W.; Hohenthanner, C.-R. Mass transfer within the gas-phase of porous media. Int. J. Heat Mass Transf. 2000, 43, 807–823. [Google Scholar] [CrossRef]
- Hitsov, I.; Maere, T.; De Sitter, K.; Dotremont, C.; Nopens, I. Modelling approaches in membrane distillation: A critical review. Sep. Purif. Technol. 2015, 142, 48–64. [Google Scholar] [CrossRef]
- Johnson, R.A.; Nguyen, M.H. Understanding Membrane Distillation and Osmotic Distillation; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- ANSYS Fluent. ANSYS Fluent Theory Guide; Release 18.0; Ansys. Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- ANSYS Fluent®. ANSYS [ANSYS Fluent], 15.0, Help System. In User’s Guide/Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2017; p. 2019. [Google Scholar]
- Chiam, C.-K.; Sarbatly, R. Vacuum membrane distillation processes for aqueous solution treatment—A review. Chem. Eng. Process. Process. Intensif. 2013, 74, 27–54. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Carvalho, G.; Chenlo, F.; Moreira, R.; Telis-Romero, J. Physicothermal Properties of Aqueous Sodium Chloride Solutions. J. Food Process. Eng. 2014, 38, 234–242. [Google Scholar] [CrossRef]
- Ramires, M.L.V.; De Castro, C.A.N.; Fareleira, J.M.N.A.; Wakeham, W.A. Thermal conductivity of aqueous sodium chloride solutions. J. Chem. Eng. Data 1994, 39, 186–190. [Google Scholar] [CrossRef]
- Harned, H.S.; Hildreth, C.L. The Differential Diffusion Coefficients of Lithium and Sodium Chlorides in Dilute Aqueous Solution at 25°. J. Am. Chem. Soc. 1951, 73, 650–652. [Google Scholar] [CrossRef]




| Feed Inlet Temperature | Permeate Inlet Temperature | Inlet Velocity | Feed Concentration | Channel Length | Membrane Type | |
|---|---|---|---|---|---|---|
| Baseline condition | 60 | 25 | 0.05 | 10 | 150 | CLARCOR, QM0200 |
| Feed inlet temperature study | 40–80 | 25 | 0.05 | 10 | 150 | CLARCOR, QM0200 |
| Permeate inlet temperature study | 60 | 20–40 | 0.05 | 10 | 150 | CLARCOR, QM0200 |
| Inlet velocity study | 60 | 25 | 0.01–0.2 | 10 | 150 | CLARCOR, QM0200 |
| Feed concentration study | 60 | 25 | 0.05 | 0–250 | 150 | CLARCOR, QM0200 |
| Channel length study | 60 | 25 | 0.05 | 10 | 100–400 | CLARCOR, QM0200 |
| Membrane type study | 60 | 25 | 0.05 | 10 | 150 | Table 2 |
| Manufacturer | Model Number | Membrane Type | Nominal Pore Size (µm) | Thickness (µm) | Porosity (%) | Reference |
|---|---|---|---|---|---|---|
| 3M | 0.2 µm | PP | 0.59 | 110 | 85 | [46] |
| 3M | 0.45 µm | PP | 0.79 | 110 | 85 | [46] |
| AQUASTILL | 0.3 µm | PE | 0.3 | 76 | 85 | [46] |
| CELGARD | 2400 | PP | 0.043 | 25 | 41 | [46] |
| CELGARD | 2500 | PP | 0.064 | 25 | 55 | [46] |
| CLARCOR | QL218 | PTFE | 0.2 | 254–305 (280) | 70–85 (75) | [46] |
| CLARCOR | QL822 | PTFE | 0.45 | 127–203 (165) | 70–85 (75) | [46] |
| CLARCOR | QP952 | PTFE | 0.45 | 150–300 (223) | 70–85 (75) | [46] |
| CLARCOR | QP9955 | PES | 0.2 | 127–305 (216) | 70–85 (75) | [46] |
| CLARCOR | QP961 | PES | 0.1 | 76–203 (140) | 70–85 (75) | [46] |
| CLARCOR | QM022 | PTFE | 0.36 | 84 | 0.62 | [21] |
| Milipore | Durapore (GVHP) | PVDF | 0.22 | 125 | 75 | [53] |
| Milipore | Durapore (HVHP) | PVDF | 0.45 | 140 | 75 | [53] |
| Milipore | Fluoropore | PTFE | 0.22 | 175 | 40 | [53] |
| Milipore | Fluoropore | PTFE | 0.22 | 175 | 70 | [53] |
| Osmonics Corp | k-150 | PTFE | 0.1 | 260 | 75 | [53] |
| Membrana, Germany | PP Accurel 2E | PP | 0.2 | 163 | 75 | [53] |
| Membrana, Germany | M1 | PP | 0.2 | 91 | 70 | [53] |
| Membrana, Germany | M2 | PP | 0.45 | 170 | 75 | [53] |
| Whatman, Germany | Westran S | PVDF | 0.2 | 121 | 76 | [53] |
| Gelman Inst Co | TF200 | PTFE | 0.2 | 60 | 60 | [53] |
| Hoechst-Celanese | CELGARD 2400 | PP | 0.02 | 25 | 38 | [53] |
| Parameter Study | System Performance Metrics | |||||
|---|---|---|---|---|---|---|
| Alteration Range | Water Flux | CPC | TPC | Thermal Efficiency | ||
| Operating Conditions | Inlet Temperature [] | 40–80 | +10-fold | +0.34% | −0.48% | +0.27% |
| Inlet velocity [] /Reynolds number | 0.01–0.2 80–1600 | +2.3-fold | −2% | +21% | −5% | |
| Inlet Concentration [] | 0–250 | −0.26% | −5% | +30% | −7% | |
| Length [mm] | 100–350 | +2.7-fold | +2% | −10% | +8% | |
| Membrane Properties | Thickness [µm] | M1 with 91 [µm] and Membrana PP Accurel 2E with 163 [µm] | −22% | −3% | +25% | +4% |
| Pore size [µm] | 3M with 0.59 [µm] and 3M with 0.79 [µm] | +3% | +1.5% | −1.5% | +1% | |
| Porosity [%] | Milipore with 0.4 and Milipore with 0.7 Porosity | +73% | +3% | −17% | +23% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansari, A.; Kavousi, S.; Helfer, F.; Millar, G.; Thiel, D.V. An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation. Membranes 2021, 11, 308. https://doi.org/10.3390/membranes11050308
Ansari A, Kavousi S, Helfer F, Millar G, Thiel DV. An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation. Membranes. 2021; 11(5):308. https://doi.org/10.3390/membranes11050308
Chicago/Turabian StyleAnsari, Abolfazl, Saman Kavousi, Fernanda Helfer, Graeme Millar, and David V. Thiel. 2021. "An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation" Membranes 11, no. 5: 308. https://doi.org/10.3390/membranes11050308
APA StyleAnsari, A., Kavousi, S., Helfer, F., Millar, G., & Thiel, D. V. (2021). An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation. Membranes, 11(5), 308. https://doi.org/10.3390/membranes11050308







