The Origin of the Non-Constancy of the Bulk Resistance of Ion-Selective Electrode Membranes within the Nernstian Response Range
Abstract
:1. Introduction
2. Materials and Methods
3. Results
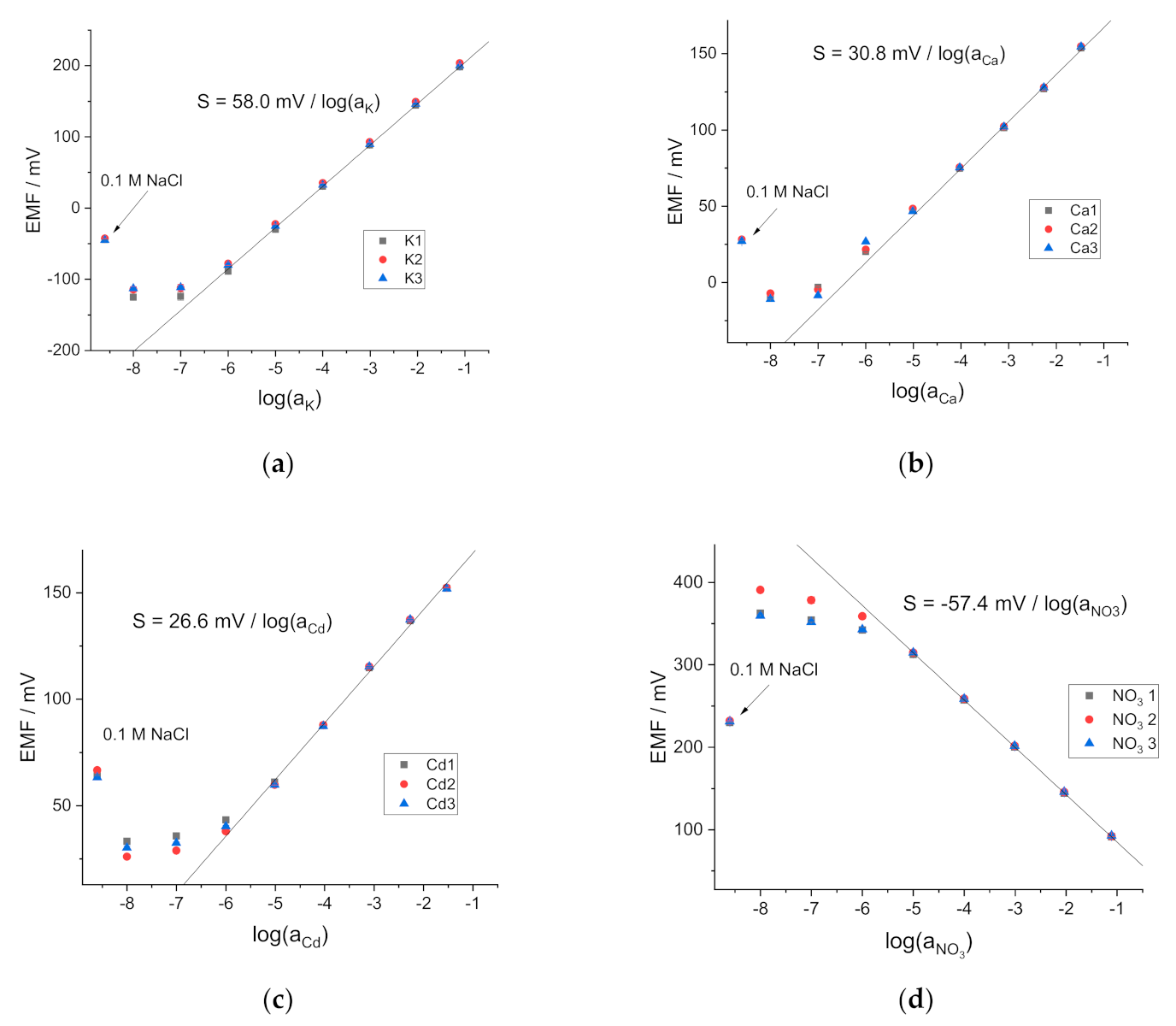
3.1. Potentiometric Response of the ISEs
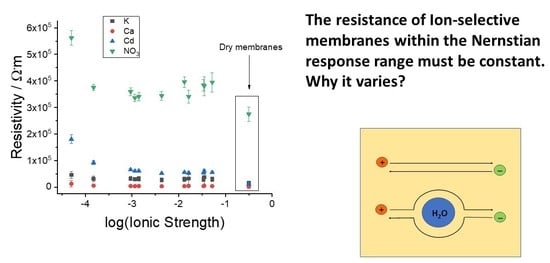
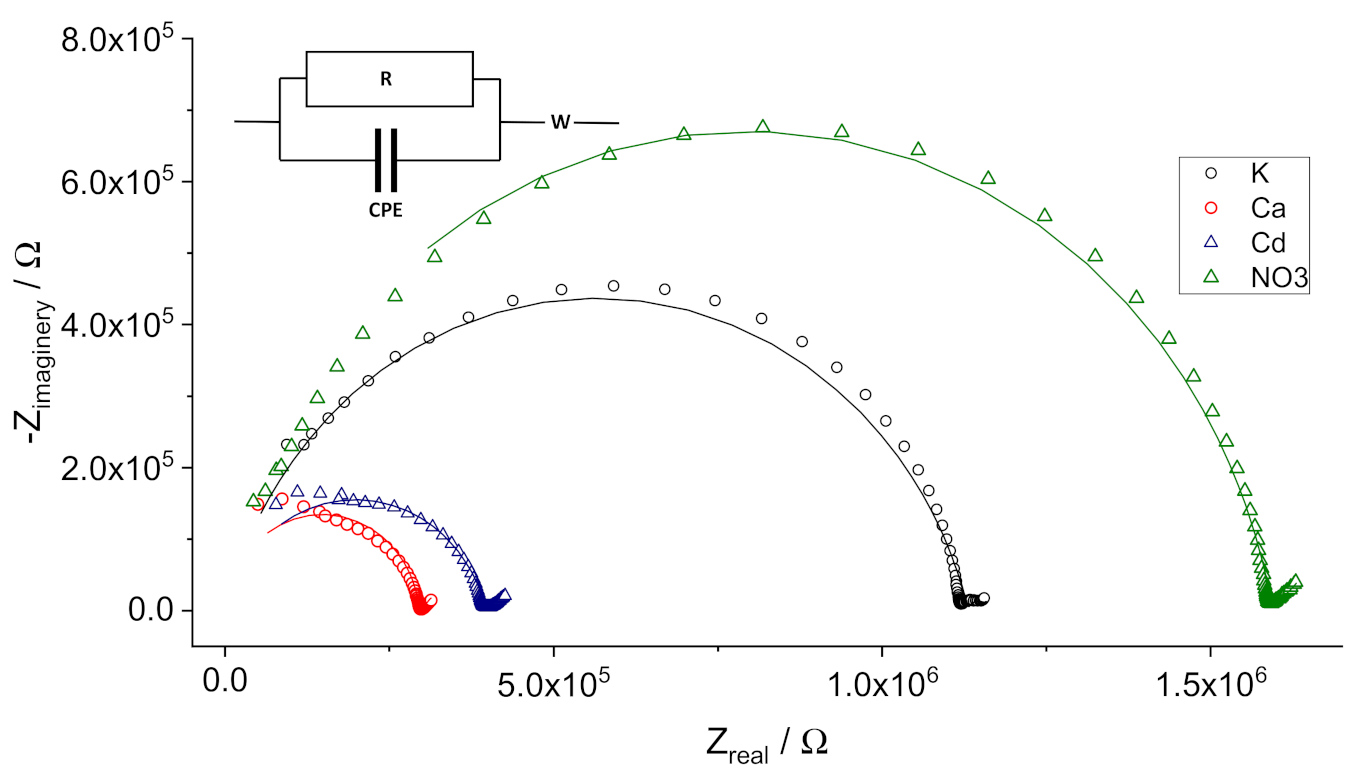
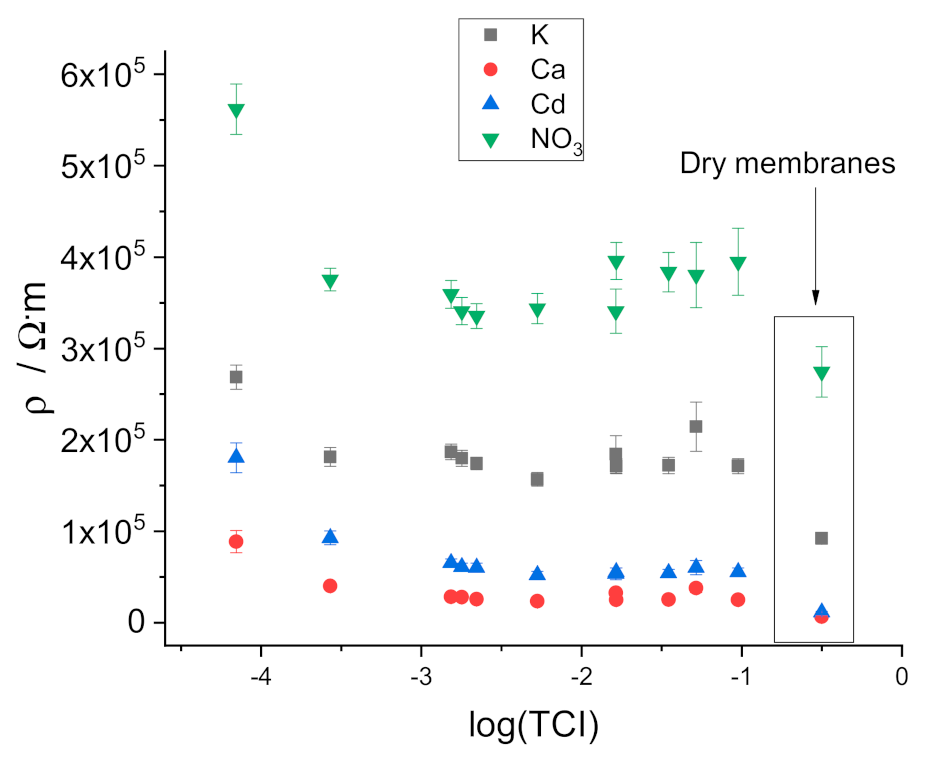
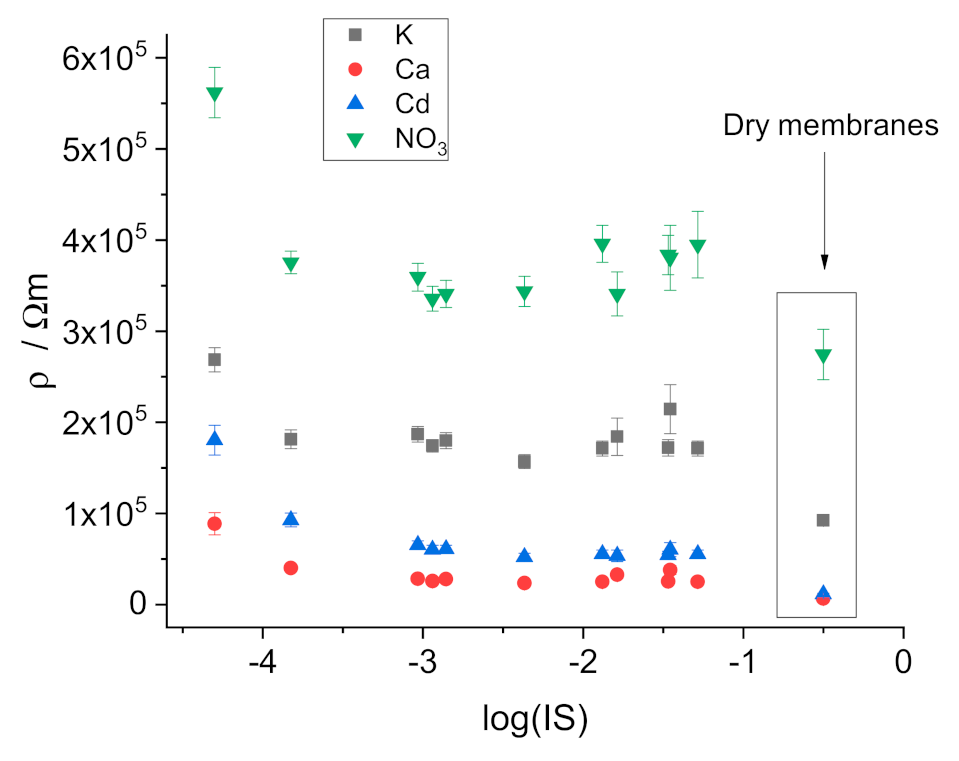
3.2. Resistivity of the Membranes
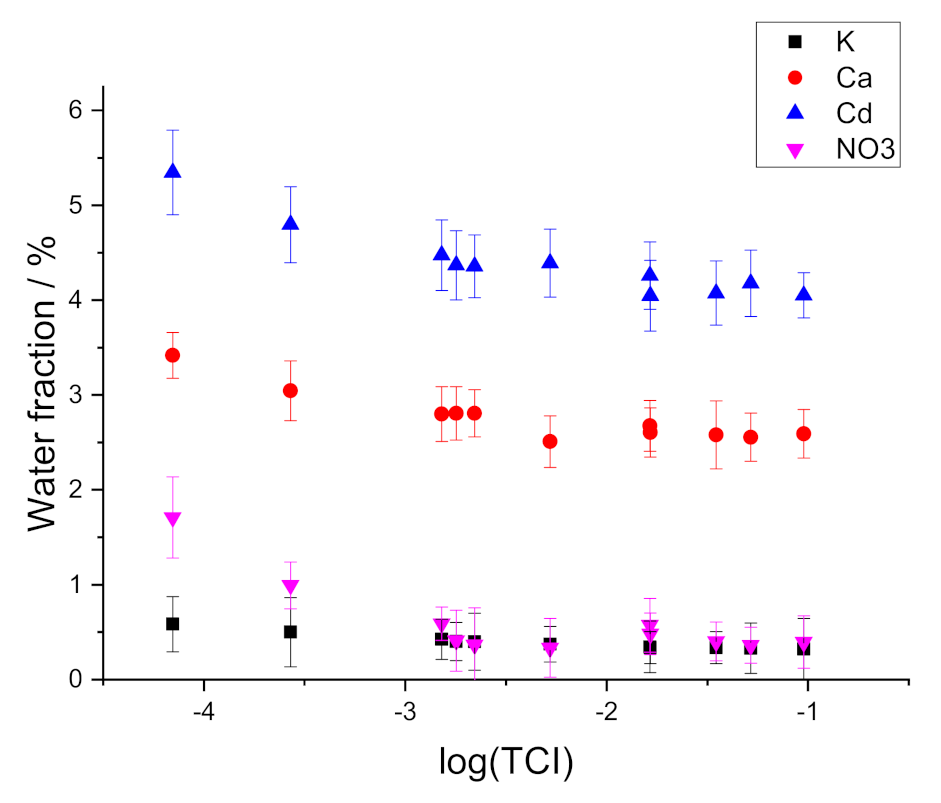
3.3. Water Uptake
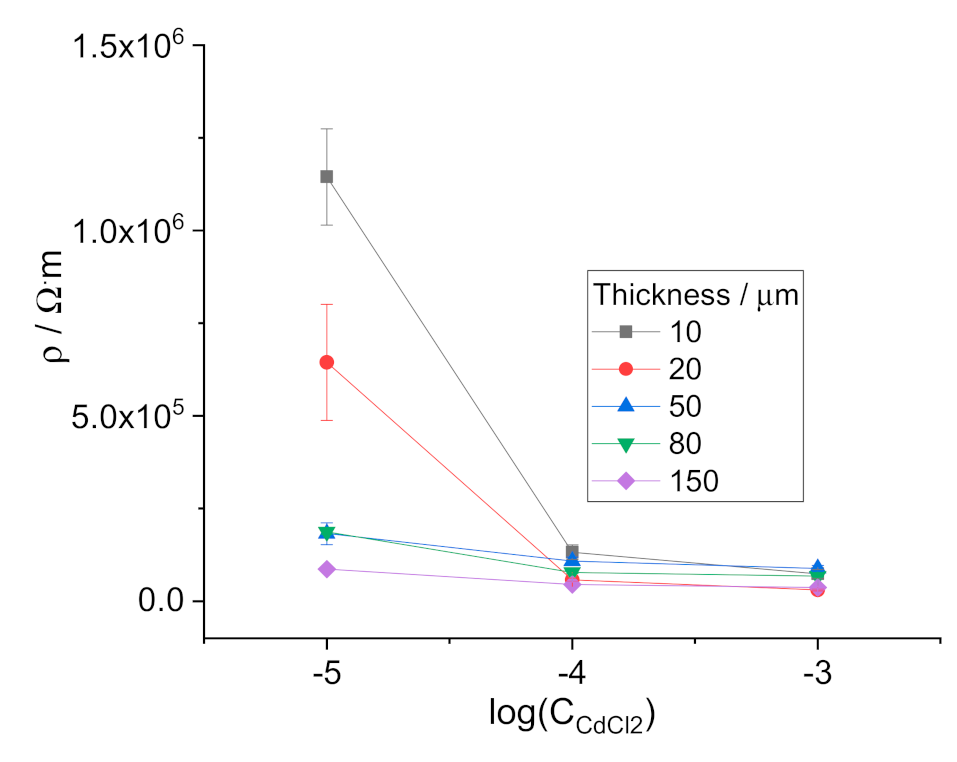
3.4. Measurements with Thin Membranes
4. Discussion of the Role of Water Droplets in the ISE Membrane Resistance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zdrachek, E.; Bakker, E. Potentiometric Sensing. Anal. Chem. 2019, 91, 2–26. [Google Scholar] [CrossRef] [Green Version]
- Bobacka, J.; Ivaska, A.; Lewenstam, A. Potentiometric ion sensors. Chem. Rev. 2008, 108, 329–351. [Google Scholar] [CrossRef] [PubMed]
- Mikhelson, K.N.; Peshkova, M.A. Advances and trends in ionophore-based chemical sensors. Russ. Chem. Rev. 2015, 84, 555–578. [Google Scholar] [CrossRef]
- Kabagambe, B.; Izadyar, A.; Amemiya, S. Stripping Voltammetry of Nanomolar Potassium and Ammonium Ions Using a Valinomycin-Doped Double-Polymer Electrode. Anal. Chem. 2012, 84, 7979–7986. [Google Scholar] [CrossRef]
- Crespo, G.A.; Cuartero, M.; Bakker, E. Thin Layer Ionophore-Based Membrane for Multianalyte Ion Activity Detection. Anal. Chem. 2015, 87, 7729–7737. [Google Scholar] [CrossRef]
- Yuan, D.; Cuartero, M.; Crespo, G.A.; Bakker, E. Voltammetric Thin-Layer Ionophore-Based Films: Part 1. Experimental Evidence and Numerical Simulations. Anal. Chem. 2017, 89, 586–594. [Google Scholar] [CrossRef]
- Yuan, D.; Cuartero, M.; Crespo, G.A.; Bakker, E. Voltammetric Thin-Layer Ionophore-Based Films: Part 2. Semi-Empirical Treatment. Anal. Chem. 2017, 89, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Hupa, E.; Vanamo, U.; Bobacka, J. Novel Ion-to-Electron Transduction Principle for Solid-Contact ISEs. Electroanalysis 2015, 27, 591–594. [Google Scholar] [CrossRef]
- Han, T.; Mattinen, U.; Bobacka, J. Improving the sensitivity of solid-contact ion-selective electrodes by using coulometric signal transduction. ACS Sens. 2019, 4, 900–906. [Google Scholar] [CrossRef] [Green Version]
- Kondratyeva, Y.O.; Tolstopjatova, E.G.; Kirsanov, D.O.; Mikhelson, K.N. Chronoamperometric and coulometric analysis with ionophore-based ionselective electrodes: A modified theory and the potassium ion assay in serum samples. Sens. Actuators B 2020, 310, 127894. [Google Scholar] [CrossRef]
- Han, T.; Mousavi, Z.; Mattinen, U.; Bobacka, J. Coulometric response characteristics of solid contact ion-selective electrodes for divalent cations. J. Solid State Electrochem. 2020, 24, 2975–2983. [Google Scholar] [CrossRef]
- Han, T.; Mattinen, U.; Mousavi, Z.; Bobacka, J. Coulometric response of solid-contact anion-sensitive electrodes. Electrochim. Acta 2021, 367, 137566. [Google Scholar] [CrossRef]
- Kraikaew, P.; Sailapu, S.K.; Bakker, E. Rapid Constant Potential Capacitive Measurements with Solid-Contact Ion-Selective Electrodes Coupled to Electronic Capacitor. Anal. Chem. 2020, 92, 14174–14180. [Google Scholar] [CrossRef] [PubMed]
- Kondratyeva, Y.O.; Solovyeva, E.V.; Khripoun, G.A.; Mikhelson, K.N. Non-constancy of the bulk resistance of ionophore-based ion-selective electrode: A result of electrolyte co-extraction or of something else? Electrochim. Acta 2018, 259, 458–465. [Google Scholar] [CrossRef]
- Ivanova, A.; Mikhelson, K. Electrochemical Properties of Nitrate-Selective Electrodes: The Dependence of Resistance on the Solution Concentration. Sensors 2018, 18, 2062. [Google Scholar] [CrossRef] [Green Version]
- Kondratyeva, Y.O.; Solovyeva, E.V.; Khripoun, G.A.; Mikhelson, K.N. Paradox of the variation of the bulk resistance of potassium ion-selective electrode membranes within the Nernstian potentiometric response range. Russ. J. Electrochem. 2019, 55, 1118–1126. [Google Scholar] [CrossRef]
- Kalinichev, A.V.; Solovyeva, E.V.; Ivanova, A.R.; Khripoun, G.A.; Mikhelson, K.N. Non-constancy of the bulk resistance of ionophore-based Cd2+-selective electrode: A correlation with the water uptake by the electrode membrane. Electrtochim. Acta 2019, 334, 135541. [Google Scholar] [CrossRef]
- Morf, W.E. The Principles of Ion-Selective Electrodes and of Membrane Transport; Akademiai Kiado: Budapest, Hungary, 1981. [Google Scholar]
- Bakker, E.; Bühlmann, P.; Pretsch, E. Carrier-based ion-selective electrodes and bulk optodes. 1. General characteristics. Chem. Rev. 1997, 97, 3083–3112. [Google Scholar] [CrossRef] [PubMed]
- Mikhelson, K.N. Ion-Selective Electrodes; Lecture Notes in Chemistry; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2013; Volume 81, p. 162. [Google Scholar] [CrossRef]
- Solovyeva, E.V.; Lu, H.; Khripoun, G.A.; Mikhelson, K.N.; Kazarian, S.G. In situ ATR-FTIR spectroscopic imaging of PVC, plasticizer and water in solvent-polymeric ion-selective membrane containing Cd2+-selective neutral ionophore. J. Membr. Sci. 2020, 619, 118798. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Petrovic, S.; Harrison, J.D. Dual-sorption model of water uptake in poly (vinyl chloride)-based ion-selective membranes: Experimental water concentration and transport parameters. Anal. Chem. 1996, 68, 1717–1725. [Google Scholar] [CrossRef]
- He, N.; Lindfors, T. Determination of water uptake of polymeric ion-selective membranes with the coulometric Karl Fischer and FT-IR-attenuated total reflection techniques. Anal. Chem. 2013, 85, 1006–1012. [Google Scholar] [CrossRef]
- Bobacka, J. Potential Stability of All-Solid-State Ion-Selective Electrodes Using Conducting Polymers as Ion-to-Electron Transducers. Anal. Chem. 1999, 71, 4932–4937. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.D.; Horvai, G. Properties of PVC based membranes used in ion-selective electrodes. Electrochim. Acta 1990, 35, 1–7. [Google Scholar] [CrossRef]
- Harrison, J.D.; Li, X. Measurement of concentration profiles inside a nitrite ion selective electrode membrane. Anal. Chem. 1991, 63, 2168–2174. [Google Scholar] [CrossRef]
- Chan, A.D.C.; Li, X.; Harrison, J.D. Evidence for a water-rich surface region in poli(vinyl chloride)-based ion-selective electrode membranes. Anal. Chem. 1992, 64, 2512–2517. [Google Scholar] [CrossRef]
- Zwickl, T.; Schneider, B.; Lindner, E.; Sokalski, T.; Schaller, U.; Pretsch, E. Chromoionophore-mediated imaging of water transport in ion-selective membranes. Anal. Sci. 1998, 14, 57–61. [Google Scholar] [CrossRef] [Green Version]
- Chan, A.D.C.; Harrison, J.D. NMR study of the water in ion-selective electrode membrane. Anal. Chem. 1993, 65, 32–36. [Google Scholar] [CrossRef]
- Lindfors, T.; Sundfors, F.; Höfler, L.; Gyurcsányi, R.E. FTIR-ATR study of water uptake and diffusion through ion-selective membranes based on plasticized poly (vinyl chloride). Electroanalysis 2009, 21, 1914–1922. [Google Scholar] [CrossRef]
- Lindfors, T.; Höfler, L.; Jágerszki, G.; Gyurcsányi, R.E. Hyphenated FT-IR-attenuated total reflection and electrochemical impedance spectroscopy technique to study the water uptake and potential stability of polymeric solid-contact ion-selective electrodes. Anal. Chem. 2011, 83, 4902–4908. [Google Scholar] [CrossRef] [PubMed]
- Sundfors, F.; Lindfors, T.; Höfler, L.; Bereczki, R.; Gyurcsányi, R.E. FTIR-ATR Study of Water Uptake and Diffusion through Ion-Selective Membranes Based on Poly (acrylates) and Silicone Rubber. Anal. Chem. 2009, 81, 5925–5934. [Google Scholar] [CrossRef]
- Qin, D.; Liu, Z.; Bai, H.; Song, X.; Sun, D.D. Fine-tuning selective layer architecture of hydrogel membrane towards high separation performances for engineered osmosis. J. Membr. Sci. 2019, 592, 117370. [Google Scholar] [CrossRef]
- Lee, D.; Woo, Y.C.; Park, K.H.; Phuntsho, S.; Tijing, L.D.; Yao, M.; Shim, W.-G.; Shon, H.K. Polyvinylidene fluoride phase design by two-dimensional boron nitride enables enhanced performance and stability for seawater desalination. J. Membr Sci. 2020, 598, 117669. [Google Scholar] [CrossRef]
- Guan, K.; Zhang, L.; Wang, S.; Takagi, R.; Matsuyama, H. Controlling the formation of porous polyketone membranes via a cross-linkable alginate additive for oil-in-water emulsion separations. J. Membr. Sci. 2020, 611, 118362. [Google Scholar] [CrossRef]
- Desmond, P.; Böni, L.; Fischer, P.; Morgenroth, E.; Derlon, N. Stratification in the physical structure and cohesion of membrane biofilms—Implications for hydraulic resistance. J. Membr. Sci. 2018, 564, 897–904. [Google Scholar] [CrossRef]


| Ion | Neutral Ionophore | Ion Exchanger | Plasticizer | PVC |
|---|---|---|---|---|
| K+ | Valinomycin 1.5%, 0.02 M | KClTPB, 0.3%, 0.01 M | BBPA 65.5% | 32.7% |
| Ca2+ | ETH 1001 0.9%, 0.02 M | KClTPB 0.3%, 0.01 M | oNPOE 65.9% | 32.9% |
| Cd2+ | ETH 1062 0.6%, 0.02 M | KClTPB 0.3%, 0.01 M | oNPOE 66.1% | 33.0% |
| NO3− | - | TDABr 2.2%, 0.05 M | DOP 65.2%, | 32.6 % |
| Solution | Concentration, mM | log(IS) | log(TCI) | ||||
|---|---|---|---|---|---|---|---|
| KCl | CaCl2 | CdCl2 | KNO3 | NaCl | |||
| 1 | 10.0 | 3.00 | 0.00 | 3.00 | 30.0 | −1.28 | −1.02 |
| 2 | 6.00 | 2.00 | 4.00 | 1.00 | 10.0 | −1.46 | −1.28 |
| 3 | 0.00 | 1.00 | 10.0 | 1.00 | 0.00 | −1.47 | −1.46 |
| 4 | 3.00 | 0.30 | 3.00 | 0.30 | 0.00 | −1.88 | −1.78 |
| 5 | 0.10 | 0.40 | 5.00 | 0.00 | 0.00 | −1.79 | −1.79 |
| 6 | 1.00 | 0.10 | 1.00 | 0.00 | 0.00 | −2.37 | −2.28 |
| 7 | 0.03 | 0.00 | 0.03 | 0.03 | 1.00 | −2.94 | −2.66 |
| 8 | 0.30 | 0.03 | 0.30 | 0.10 | 0.00 | −2.86 | −2.75 |
| 9 | 0.10 | 0.01 | 0.10 | 0.00 | 0.50 | −3.03 | −2.82 |
| 10 | 0.01 | 0.00 | 0.01 | 0.01 | 0.10 | −3.82 | −3.57 |
| 11 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | −4.30 | −4.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keresten, V.; Solovyeva, E.; Mikhelson, K. The Origin of the Non-Constancy of the Bulk Resistance of Ion-Selective Electrode Membranes within the Nernstian Response Range. Membranes 2021, 11, 344. https://doi.org/10.3390/membranes11050344
Keresten V, Solovyeva E, Mikhelson K. The Origin of the Non-Constancy of the Bulk Resistance of Ion-Selective Electrode Membranes within the Nernstian Response Range. Membranes. 2021; 11(5):344. https://doi.org/10.3390/membranes11050344
Chicago/Turabian StyleKeresten, Valentina, Elena Solovyeva, and Konstantin Mikhelson. 2021. "The Origin of the Non-Constancy of the Bulk Resistance of Ion-Selective Electrode Membranes within the Nernstian Response Range" Membranes 11, no. 5: 344. https://doi.org/10.3390/membranes11050344
APA StyleKeresten, V., Solovyeva, E., & Mikhelson, K. (2021). The Origin of the Non-Constancy of the Bulk Resistance of Ion-Selective Electrode Membranes within the Nernstian Response Range. Membranes, 11(5), 344. https://doi.org/10.3390/membranes11050344