Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part II, Diffusivity of C6 Hydrocarbon in Micropore
Abstract
:1. Introduction
2. Materials and Methods
2.1. Membrane Preparation
2.2. Vapor Permeation Test
3. Results and Discussion
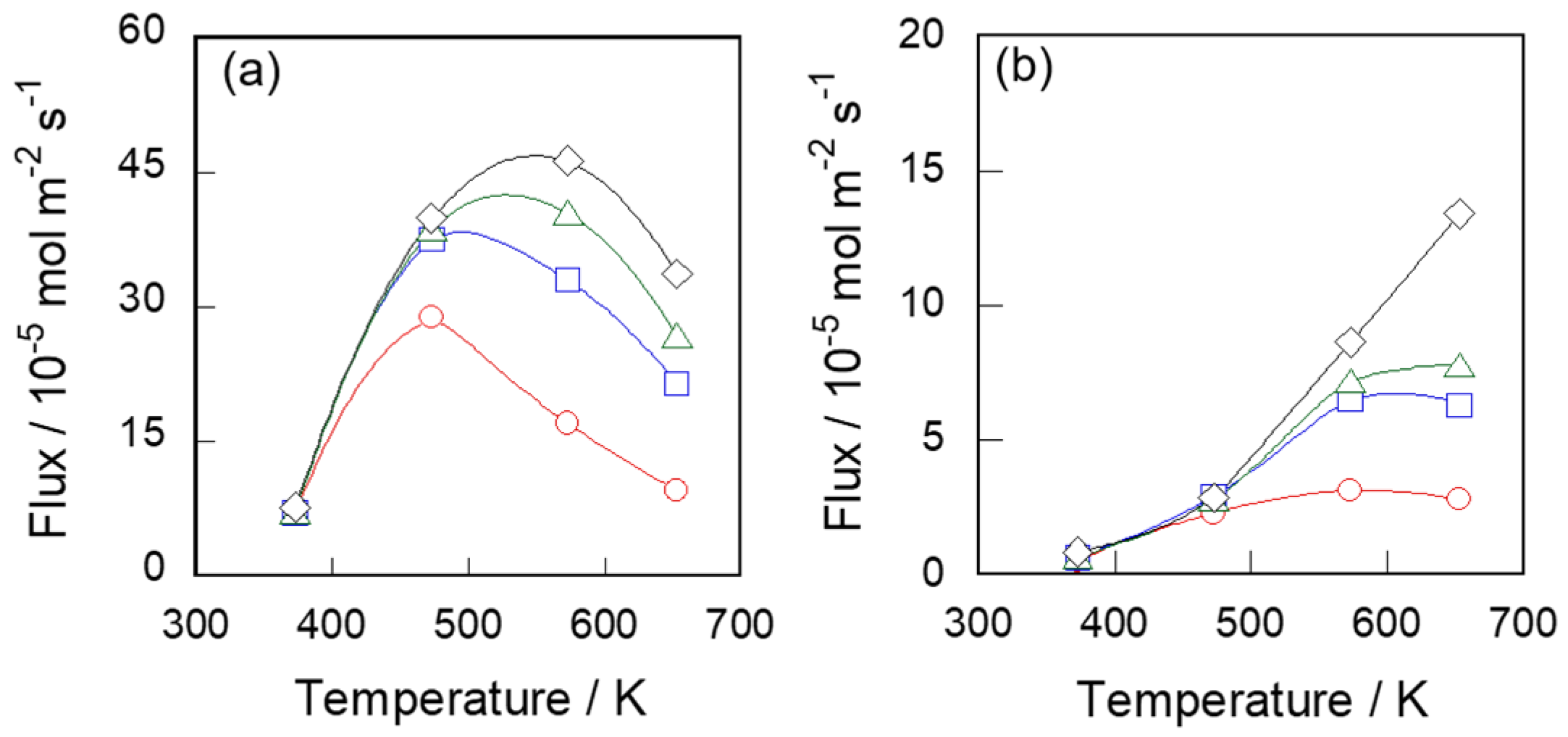
3.1. Vapor Permeation Properties of Silicalite-1 Membrane for C6 Hydrocarbons
3.2. Modeling of Hydrocarbon Permeation through Silicalite-1 Membrane
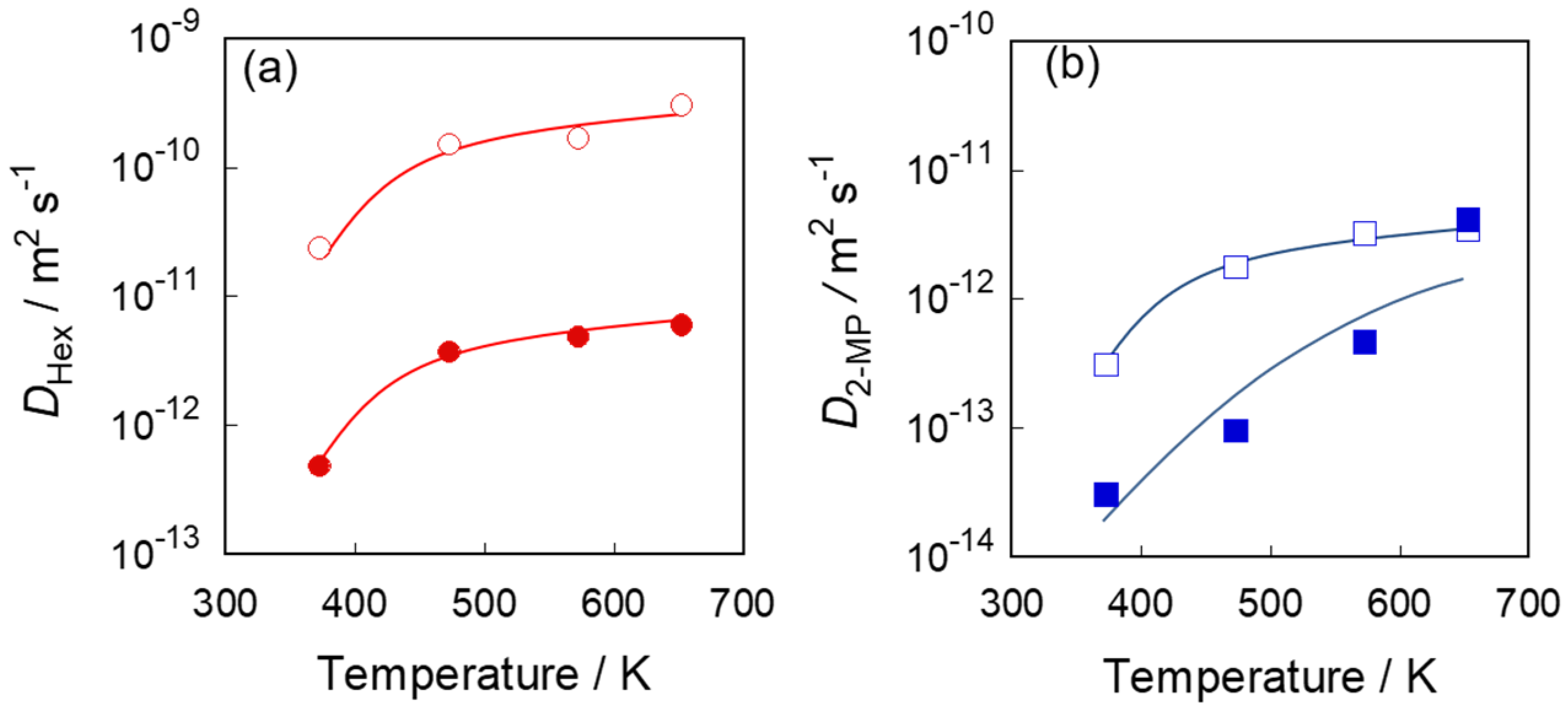
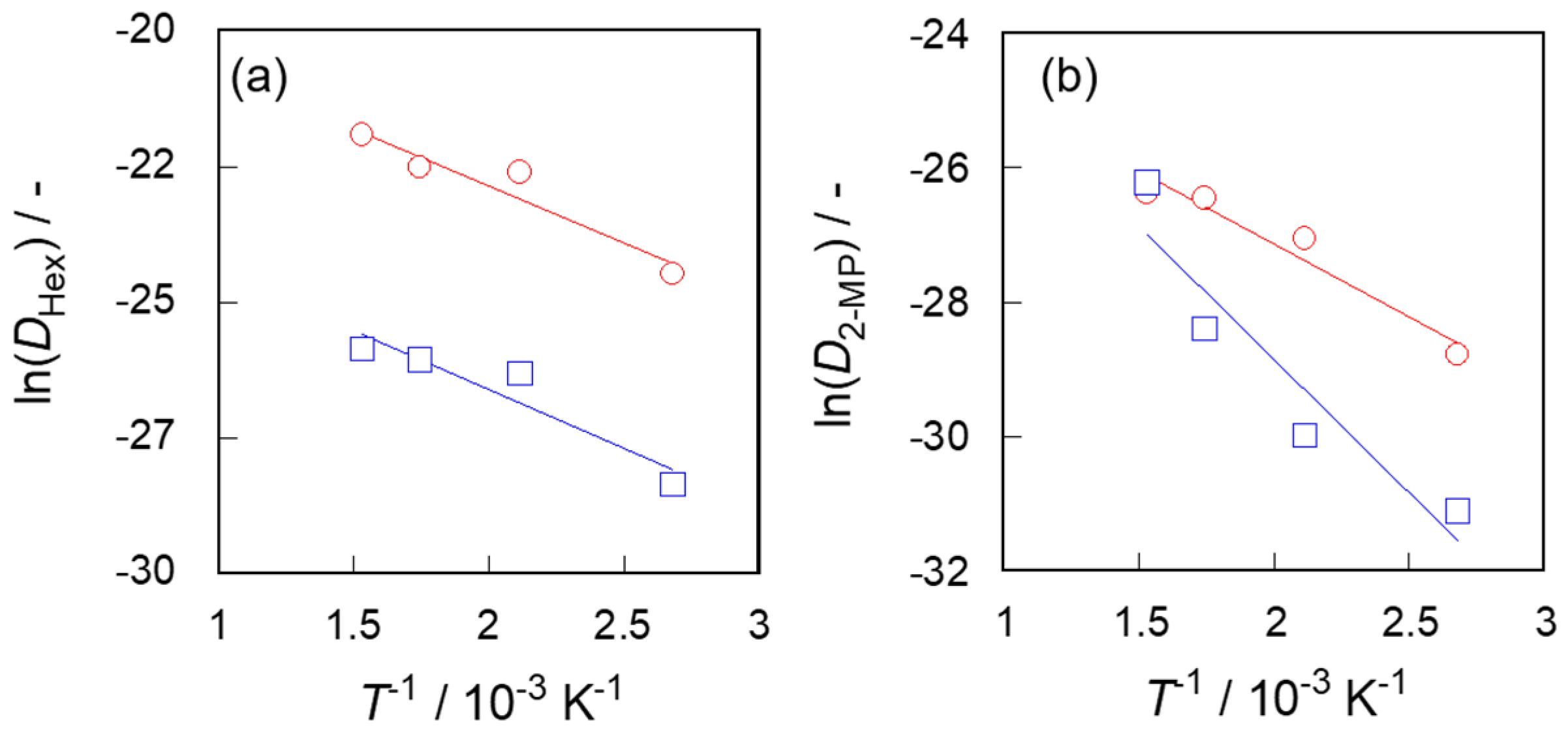
3.3. Diffusivities in Two Types of Silicalite-1 Membranes
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | Saturated adsorption amount (mol m−3) |
| A | Effective membrane area (m2) |
| b | Adsorption equilibrium constant (-) |
| C | Concentration (mol m−3) |
| D | Diffusion coefficient (m2 s−1) |
| D′ | Term including diffusion coefficient (=aDL−1) |
| J | Permeation flux (mol m−2 s−1) |
| L | Membrane thickness (m) |
| P | Partial pressure of hydrocarbon in feed side (Pa) |
| R | Gas constant (J mol−1 K−1) |
| u | Flow rate (mol s−1) |
| VF | Adsorption amount on the membrane in feed side (mol m−3) |
| VP | Adsorption amount on the membrane in permeate side (mol m−3) |
References
- Hedlund, J.; Sterte, J.; Anthonis, M.; Bons, A.-J.; Carstensen, B.; Corcoran, N.; Cox, D.; Deckman, H.; Gijnst, W.D.; Moor, P.-P. High-flux MFI membranes. Microporous Mesoporous Mater. 2002, 52, 179–189. [Google Scholar] [CrossRef]
- Funke, H.H.; Argo, A.M.; Falconer, J.L.; Noble, R.D. Separations of Cyclic, Branched, and Linear Hydrocarbon Mixtures through Silicalite Membranes. Ind. Eng. Chem. Res. 1997, 334, 137–143. [Google Scholar] [CrossRef]
- Tarditi, A.M.; Lombardo, E.A. Influence of exchanged cations (Na+, Cs+, Sr2+ and Ba2+) on xylene permeation through ZSM-5/SS tubular membranes. Sep. Purif. Technol. 2008, 61, 136–147. [Google Scholar] [CrossRef]
- Daramola, M.O.; Burger, A.J.; Giroir-Fendler, A.; Miachon, S.; Lorenzen, L. Extractor-type catalytic membrane reactor with nanocomposite MFI-alumina membrane tube as separation unit: Prospect for ultra-pure para-Xylene production from m-Xylene isomerization over Pt-HZSM-5 catalyst. Appl. Catal. A 2010, 386, 109–115. [Google Scholar] [CrossRef]
- Sakai, M.; Kaneko, T.; Sasaki, Y.; Sekigawa, M.; Matsukata, M. Formation Process of Columnar Grown (101)-Oriented Silicalite-1 Membrane and Its Separation Property for Xylene Isomer. Crystals 2020, 10, 949. [Google Scholar] [CrossRef]
- Lai, Z.; Bonilla, G.; Diaz, I.; Nery, J.G.; Sujaoti, K.; Amat, M.A.; Kokkoli, E.; Terasaki, O.; Thompson, R.W.; Tsapatsis, M.; et al. Microstructural Optimization of a Zeolite Membrane for Organic Vapor Separation. Science 2003, 300, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.; Jeong, H.-K. Synthesis and gas permeation properties of highly b-oriented MFI silicalite-1 thin membranes with controlled microstructure. Microporous Mesopor Mater. 2011, 141, 175–183. [Google Scholar] [CrossRef]
- Kumar, P.; Kim, D.W.; Rangnekar, N.; Xu, H.; Fetisov, E.O.; Ghosh, S.; Zhang, H.; Xiao, Q.; Shete, M.; Siepmann, J.I.; et al. One-dimensional intergrowths in two-dimensional zeolite nanosheets and their effect on ultra-selective transport. Nat. Mater. 2020, 19, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Choi, J.; Tsapatsis, M. On the performance of c-oriented MFI zeolite Membranes treated by rapid thermal processing. J. Membr. Sci. 2013, 436, 79–89. [Google Scholar] [CrossRef]
- Pham, T.C.T.; Kim, H.S.; Yoon, K.B. Growth of Uniformly Oriented Silica MFI and BEA Zeolite Films on Substrates. Science 2011, 334, 1533–1538. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Grahn, M.; Ye, P.; Hedlund, J. Ultra-thin MFI membranes for olefin/nitrogen separation. J. Membr. Sci. 2017, 524, 428–435. [Google Scholar] [CrossRef]
- Agrawal, K.V.; Topuz, B.; Pham, T.C.T.; Nguyen, T.H.; Sauer, N.; Rangnekar, N.; Zhang, H.; Narasimharao, K.; Basahel, S.N.; Francis, L.F.; et al. Oriented MFI Membranes by Gel-Less Secondary Growth of Sub-100 nm MFI-Nanosheet Seed Layers. Adv. Mater. 2015, 27, 3243–3249. [Google Scholar] [CrossRef]
- Sakai, M.; Sasaki, Y.; Kaneko, T.; Matsukata, M. Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part I, Pore Volume and Effective Pore Size. Membranes 2021, 11, 382. [Google Scholar] [CrossRef]
- Bakker, W.J.W.; Van Den Broeke, L.J.P.; Kapteijn, F.; Moulijn, J.A. Temperature dependence of one-component permeation through a silicalite-1 membrane. AIChE J. 1997, 43, 2203–2214. [Google Scholar] [CrossRef]
- Nomura, M.; Yamaguchi, T.; Nakao, S. Transport phenomena through intercrystalline and intracrystalline pathways of silicalite zeolite membranes. J. Memb. Sci. 2001, 187, 203–212. [Google Scholar] [CrossRef]
- Shindo, Y.; Hakuta, T.; Yoshitome, H.; Inoue, H. Gas diffusion in microporous media in Knudsen’s regime. J. Chem. Eng. J. 1983, 16, 120–126. [Google Scholar] [CrossRef] [Green Version]
- Silvestre-Albero, J.; Silvestre-Albero, A.; Rodríguez-Reinoso, F.; Thommes, M. Physical characterization of activated carbons with narrow microporosity by nitrogen (77.4 K), carbon dioxide (273 K) and argon (87.3 K) adsorption in combination with immersion calorimetry. Carbon 2012, 50, 3128–3133. [Google Scholar] [CrossRef]
- Bárcia, P.S.; Guimarães, D.; Mendes, P.A.P.; Silva, J.A.C.; Guillerm, V.; Chevreau, H.; Serre, C.; Rodrigues, A.E. Reverse shape selectivity in the adsorption of hexane and xylene isomers in MOF UiO-66. Microporous Mesoporous Mater. 2011, 139, 67–73. [Google Scholar] [CrossRef] [Green Version]
- Runnebaum, R.C.; Maginn, E.J. Molecular Dynamics Simulations of Alkanes in the Zeolite Silicalite: Evidence for Resonant Diffusion Effects. J. Phys. Chem. B 1997, 101, 6394–6408. [Google Scholar] [CrossRef]
- June, R.L.; Bell, A.T.; Theodorou, D.N. Molecular Dynamics Studies of Butane and Hexane in Siiicalite. J. Phys. Chem. 1992, 96, 1051–1060. [Google Scholar] [CrossRef]
- Sun, M.S.; Talu, O.; Shah, D.B. Diffusion measurements through embedded zeolite crystals. AIChE J. 1996, 42, 3001–3007. [Google Scholar] [CrossRef]
- Nijhuis, T.A.; van den Broeke, L.J.P.; Linders, M.J.G.; van de Graaf, J.M.; Kapteijn, F.; Makkee, M.; Moulijn, J.A. Measurement and modeling of the transient adsorption, desorption and diffusion processes in microporous materials. Chem. Eng. Sci. 1999, 54, 4423–4436. [Google Scholar] [CrossRef]
- Heink, W.; Karger, J.; Pfeifer, H.; Datema, K.P.; Nowak, A.K. High-temperature pulsed field gradient nuclear magnetic resonance self-diffusion measurements of n-alkanes in MFl-type zeolites. J. Chem. Soc. Faraday Trans. 1992, 88, 3505–3509. [Google Scholar] [CrossRef]
- Song, L.; Sun, Z.; Duan, L.; Gui, J.; McDougall, G.S. Adsorption and diffusion properties of hydrocarbons in zeolites. Microporous Mesoporous Mater. 2007, 104, 115–128. [Google Scholar] [CrossRef]



| Methods | Temperature/K | Species | Self-Diffusivity /10−10 m2 s−1 | References |
|---|---|---|---|---|
| MD | 300 | n-hexane | 30 | [18] |
| 300 | n-butane | 45 | ||
| MD | 300 | n-hexane | 22 | [19] |
| 300 | n-butane | 32 | ||
| Wicke–Kallenbach | 303 | n-butane | 0.31 | [20] |
| Pulse–response | - | n-butane | 45.6 | [21] |
| PFG NMR | - - | n-hexane n-pentane | 2.9 | [22] |
| 10 | ||||
| Frequency–response | 303 303 | n-butane n-hexane | 5.2 4.1 | [23] |
| Unary permeation test | 373 373 | n-hexane | 0.23 | S-1S (This work) S-1M (This work) |
| n-hexane | 0.0048 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakai, M.; Sasaki, Y.; Kaneko, T.; Matsukata, M. Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part II, Diffusivity of C6 Hydrocarbon in Micropore. Membranes 2021, 11, 399. https://doi.org/10.3390/membranes11060399
Sakai M, Sasaki Y, Kaneko T, Matsukata M. Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part II, Diffusivity of C6 Hydrocarbon in Micropore. Membranes. 2021; 11(6):399. https://doi.org/10.3390/membranes11060399
Chicago/Turabian StyleSakai, Motomu, Yukichi Sasaki, Takuya Kaneko, and Masahiko Matsukata. 2021. "Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part II, Diffusivity of C6 Hydrocarbon in Micropore" Membranes 11, no. 6: 399. https://doi.org/10.3390/membranes11060399






