Simulation on Pore Formation from Polymer Solution at Surface in Contact with Solid Substrate via Thermally Induced Phase Separation
Abstract
:1. Introduction
2. Numerical Simulation
2.1. TIPS Simulation
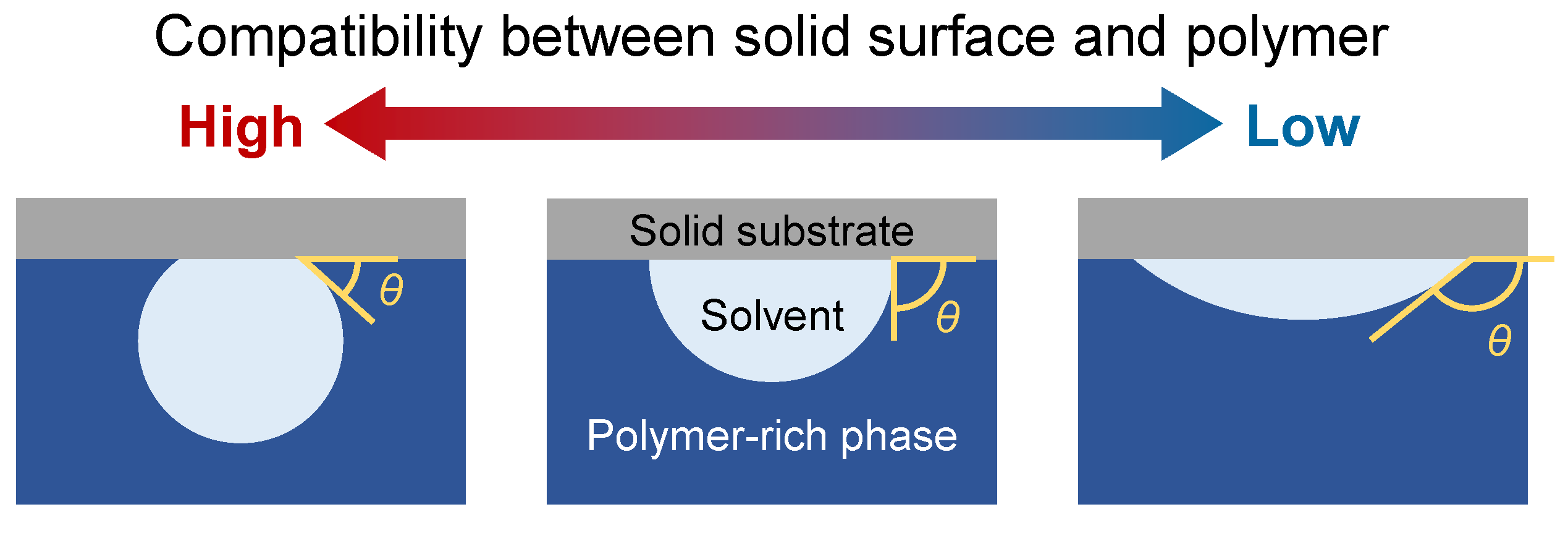
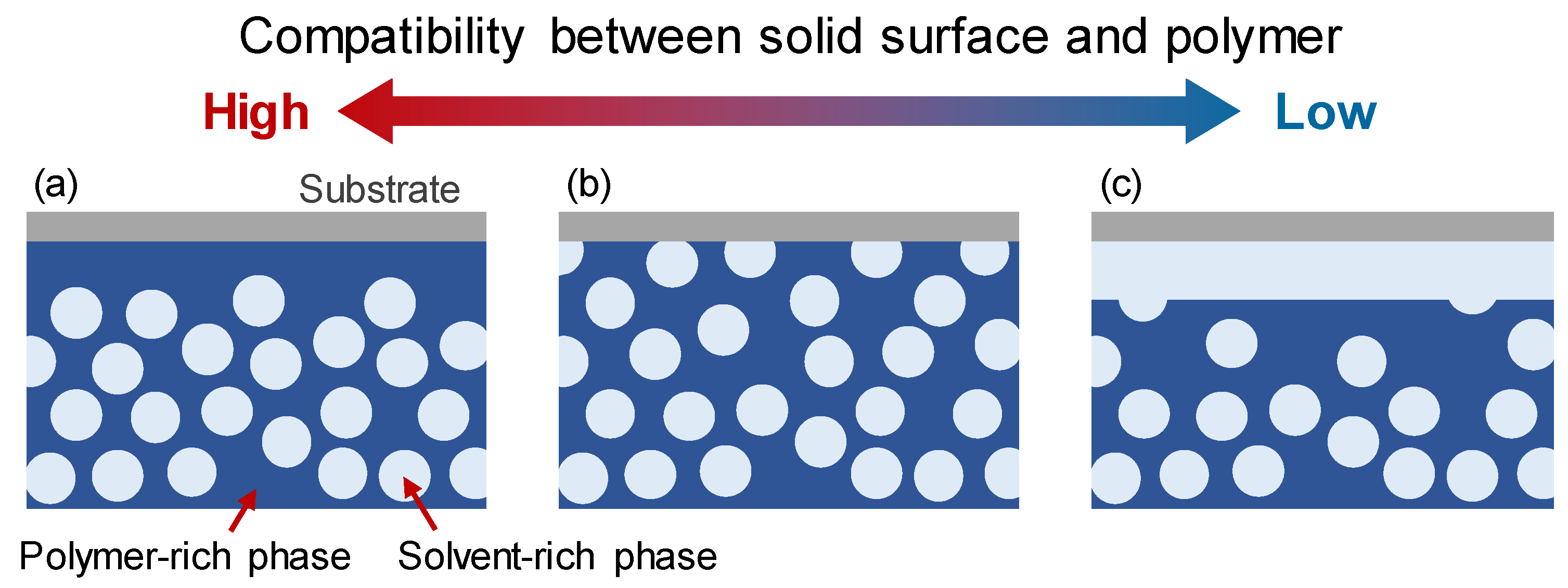
2.2. Boundary Conditions for Solid Surfaces with Various Compatibilities for Polymers and Solvents
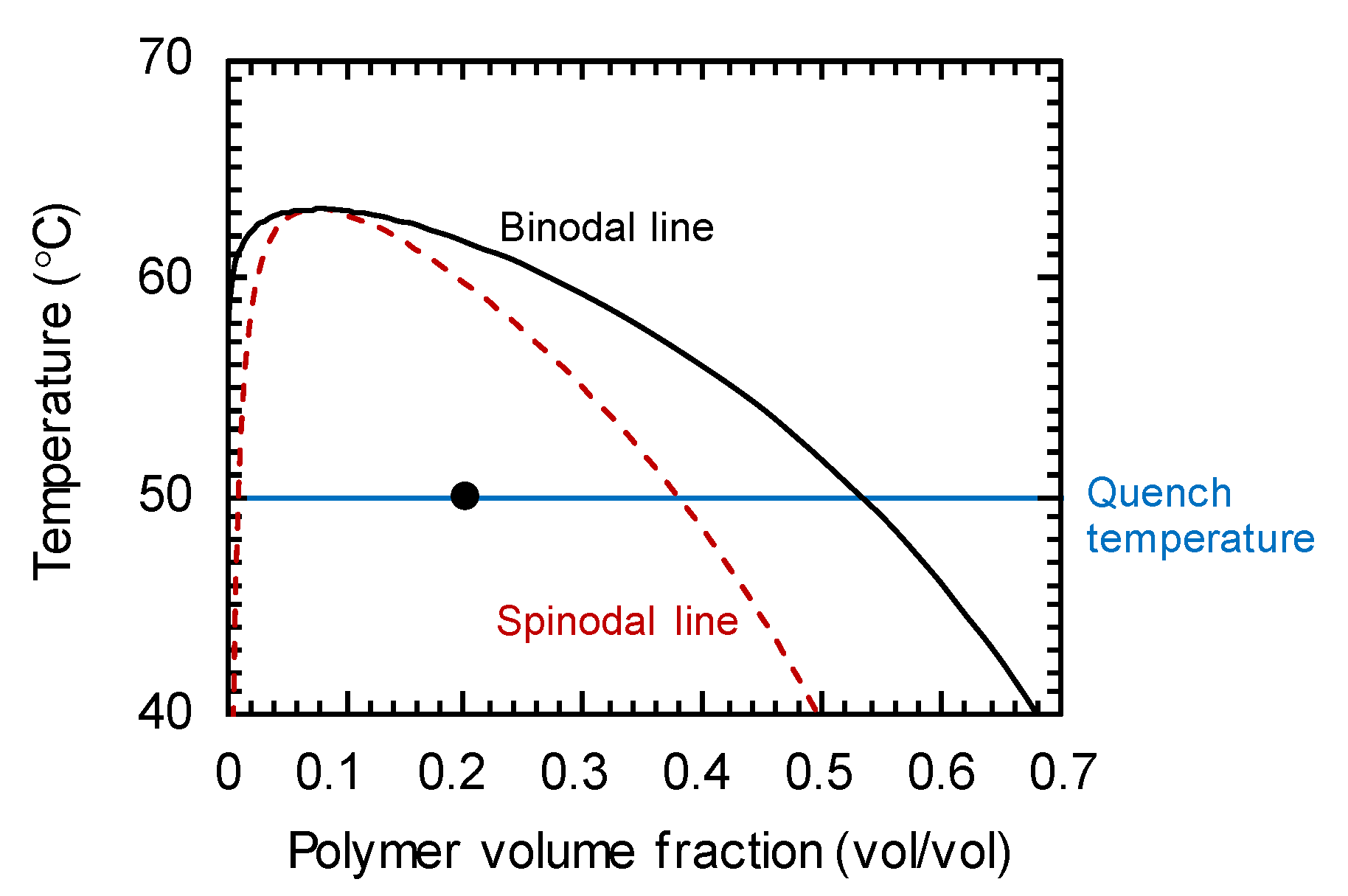
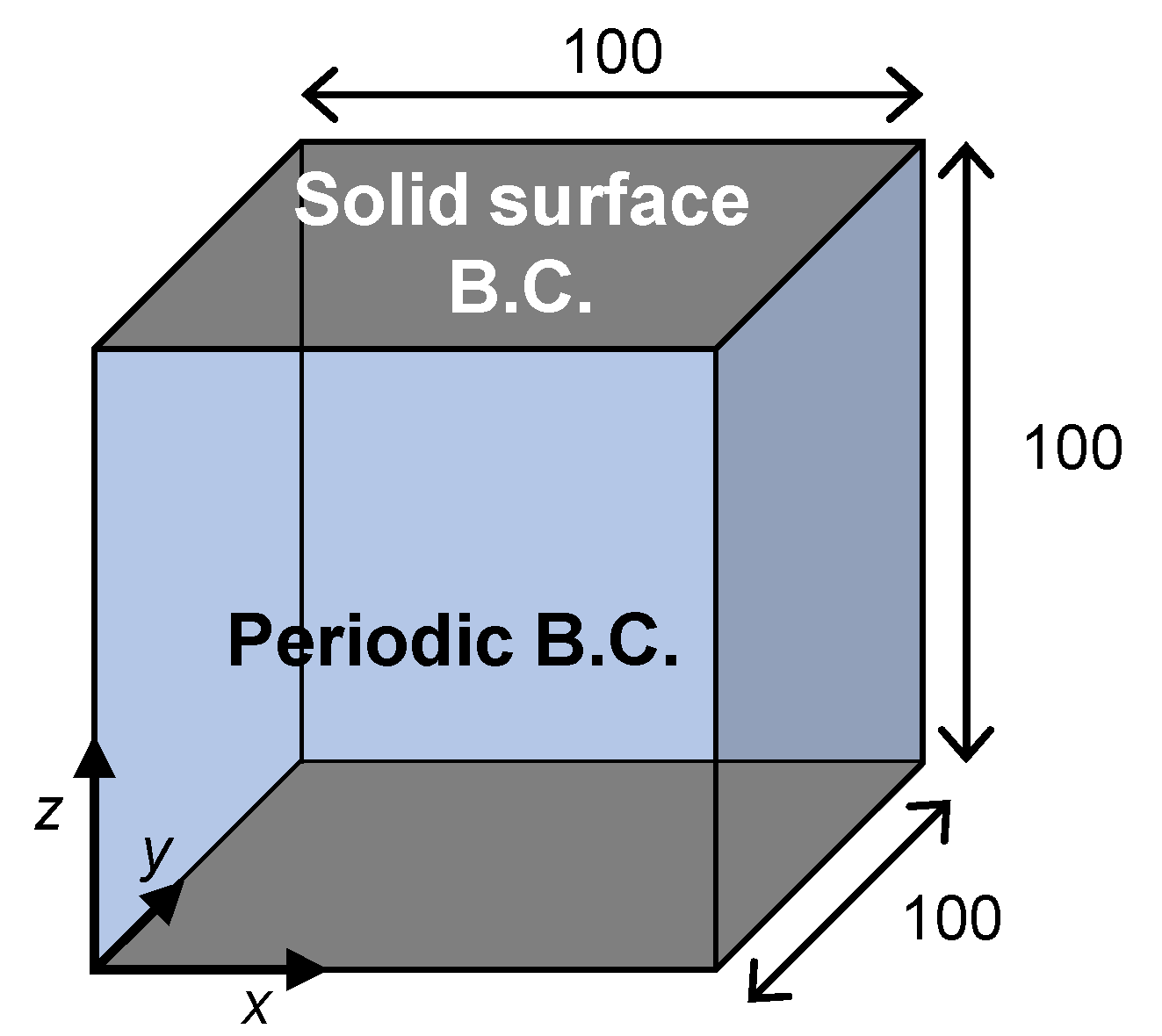
2.3. Simulaation Condition
3. Results and Discussion
3.1. Evolution of Membrane Morphology in Bulk of Membrane
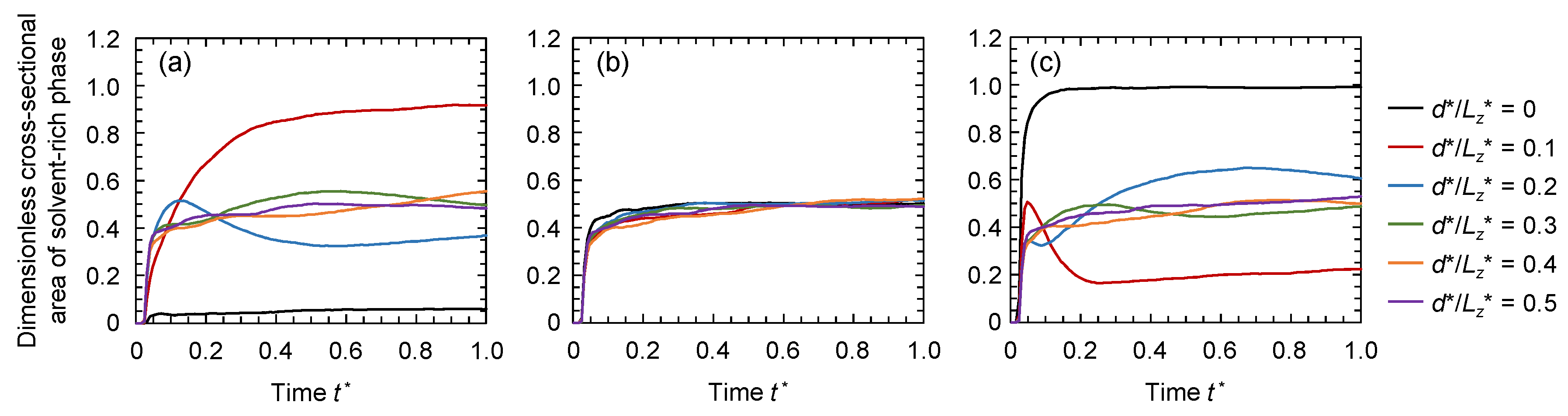
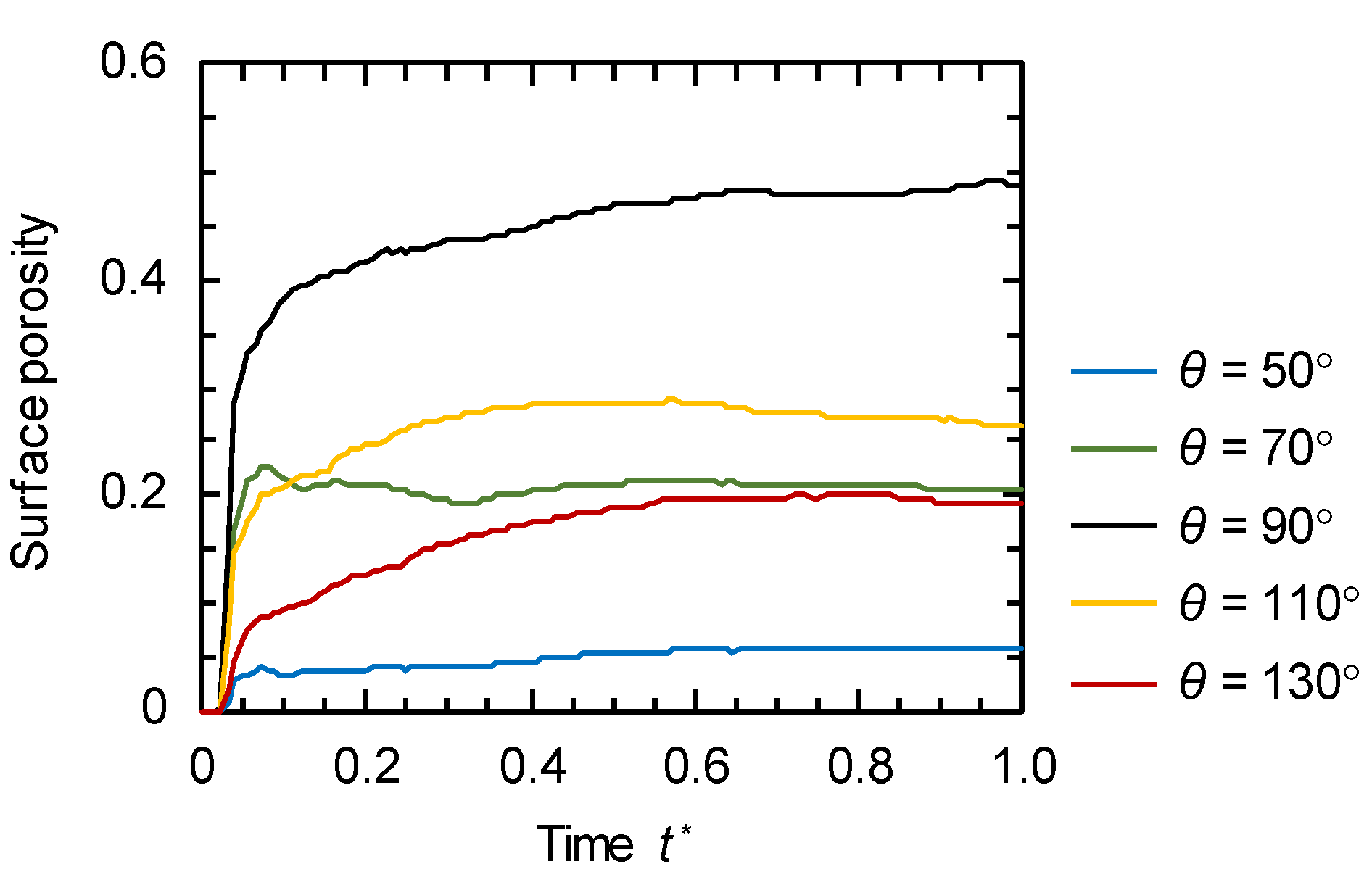
3.2. Evolution of Membrane Morphology at Surface of Membrane
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Caneba, G.T.; Soong, D.S. Polymer membrane formation through the thermal-inversion process. 1. Experimental study of membrane structure formation. Macromolecules 1985, 18, 2538–2545. [Google Scholar] [CrossRef]
- Lloyd, D.R.; Kinzer, K.E.; Tseng, H.S. Microporous membrane formation via thermally induced phase separation. I. Solid-liquid phase separation. J. Membr. Sci. 1990, 52, 239–261. [Google Scholar] [CrossRef]
- Lloyd, D.R.; Kim, S.S.; Kinzer, K.E. Microporous membrane formation via thermally-induced phase separation. II. Liquid-liquid phase separation. J. Membr. Sci. 1991, 64, 1–11. [Google Scholar] [CrossRef]
- Caneba, G.T.; Soong, D.S. Polymer membrane formation through the thermal-inversion process. 2. Mathematical modeling of membrane structure formation. Macromolecules 1985, 18, 2545–2555. [Google Scholar] [CrossRef]
- Rajabzadeh, S.; Maruyama, T.; Sotani, T.; Matsuyama, H. Preparation of PVDF hollow fiber membrane from a ternary polymer/solvent/nonsolvent system via thermally induced phase separation (TIPS) method. Sep. Purif. Technol. 2008, 63, 415–423. [Google Scholar] [CrossRef]
- Kang, G.D.; Cao, Y.M. Application and modification of poly(vinylidene fluoride) (PVDF) membranes—A review. J. Membr. Sci. 2014, 463, 145–165. [Google Scholar] [CrossRef]
- Kim, J.F.; Kim, J.H.; Lee, Y.M.; Drioli, E. Thermally induced phase separation and electrospinning methods for emerging membrane applications: A review. AIChE J. 2016, 62, 461–490. [Google Scholar] [CrossRef]
- Ma, T.; Cui, Z.; Wu, Y.; Qin, S.; Wang, H.; Yan, F.; Han, N.; Li, J. Preparation of PVDF based blend microporous membranes for lithium ion batteries by thermally induced phase separation: I. Effect of PMMA on the membrane formation process and the properties. J. Membr. Sci. 2013, 444, 213–222. [Google Scholar] [CrossRef]
- Wu, Q.Y.; Liang, H.Q.; Gu, L.; Yu, Y.; Huang, Y.Q.; Xu, Z.K. PVDF/PAN blend separators via thermally induced phase separation for lithium ion batteries. Polymer 2016, 107, 54–60. [Google Scholar] [CrossRef]
- Zuo, J.; Bonyadi, S.; Chung, T.S. Exploring the potential of commercial polyethylene membranes for desalination by membrane distillation. J. Membr. Sci. 2016, 497, 239–247. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, L.; Loh, C.H.; Wang, R. Preparation of PVDF/PTFE hollow fiber membranes for direct contact membrane distillation via thermally induced phase separation method. Desalination 2018, 430, 86–97. [Google Scholar] [CrossRef]
- Ho, C.C.; Zydney, A.L. Effect of membrane morphology on the initial rate of protein fouling during microfiltration. J. Membr. Sci. 1999, 155, 261–275. [Google Scholar] [CrossRef]
- Hwang, K.J.; Liao, C.Y.; Tung, K.L. Effect of membrane pore size on the particle fouling in membrane filtration. Desalination 2008, 234, 16–23. [Google Scholar] [CrossRef]
- Fu, X.; Maruyama, T.; Sotani, T.; Matsuyama, H. Effect of surface morphology on membrane fouling by humic acid with the use of cellulose acetate butyrate hollow fiber membranes. J. Membr. Sci. 2008, 320, 483–491. [Google Scholar] [CrossRef]
- Van der Marel, P.; Zwijnenburg, A.; Kemperman, A.; Wessling, M.; Temmink, H.; van der Meer, W. Influence of membrane properties on fouling in submerged membrane bioreactors. J. Membr. Sci. 2010, 348, 66–74. [Google Scholar] [CrossRef]
- Cha, B.J.; Yang, J.M. Preparation of poly (vinylidene fluoride) hollow fiber membranes for microfiltration using modified TIPS process. J. Membr. Sci. 2007, 291, 191–198. [Google Scholar] [CrossRef]
- Ji, G.L.; Zhu, L.P.; Zhu, B.K.; Zhang, C.F.; Xu, Y.Y. Structure formation and characterization of PVDF hollow fiber membrane prepared via TIPS with diluent mixture. J. Membr. Sci. 2008, 319, 264–270. [Google Scholar] [CrossRef]
- Shang, M.; Matsuyama, H.; Teramoto, M.; Lloyd, D.R.; Kubota, N. Effect of glycerol content in cooling bath on performance of poly (ethylene-co-vinyl alcohol) hollow fiber membranes. Sep. Purif. Technol. 2005, 45, 208–212. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, C.; Liu, G.; Li, X.; Guan, Y.; Lv, J. Effect of TEP content in cooling bath on porous structure, crystalline and mechanical properties of PVDF hollow fiber membranes. Polym. Eng. Sci. 2014, 54, 2207–2214. [Google Scholar] [CrossRef]
- Rascón, C.; Parry, A.O. Geometry-dominated fluid adsorption on sculpted solid substrates. Nature 2000, 407, 986–989. [Google Scholar] [CrossRef] [Green Version]
- Murata, K.; Tanaka, H. Surface-wetting effects on the liquid–liquid transition of a single-component molecular liquid. Nat. Commun. 2010, 1, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Böltau, M.; Walheim, S.; Mlynek, J.; Krausch, G.; Steiner, U. Surface-induced structure formation of polymer blends on patterned substrates. Nature 1998, 391, 877–879. [Google Scholar] [CrossRef]
- Chan, P.K.; Rey, A.D. Computational analysis of spinodal decomposition dynamics in polymer solutions. Macromol. Theory Simul. 1995, 4, 873–899. [Google Scholar] [CrossRef]
- Barton, B.F.; Graham, P.D.; McHugh, A.J. Dynamics of spinodal decomposition in polymer solutions near a glass transition. Macromolecules 1998, 31, 1672–1679. [Google Scholar] [CrossRef]
- Mino, Y.; Ishigami, T.; Kagawa, Y.; Matsuyama, H. Three-dimensional phase-field simulations of membrane porous structure formation by thermally induced phase separation in polymer solutions. J. Membr. Sci. 2015, 483, 104–111. [Google Scholar] [CrossRef]
- Manzanarez, H.; Mericq, J.P.; Guenoun, P.; Chikina, J.; Bouyer, D. Modeling phase inversion using Cahn-Hilliard equations—Influence of the mobility on the pattern formation dynamics. Chem. Eng. Sci. 2017, 173, 411–427. [Google Scholar] [CrossRef]
- Chan, P.K. Effect of concentration gradient on the thermal-induced phase separation phenomenon in polymer solutions. Model. Simul. Mater. Sci. Eng. 2006, 14, 41–51. [Google Scholar] [CrossRef]
- Jiang, B.T.; Chan, P.K. Effect of concentration gradient on the morphology development in polymer solutions undergoing thermally induced phase separation. Macromol. Theory Simul. 2007, 16, 690–702. [Google Scholar] [CrossRef]
- Lee, K.W.D.; Chan, P.K.; Feng, X. Morphology development and characterization of the phase-separated structure resulting from the thermal-induced phase separation phenomenon in polymer solutions under a temperature gradient. Chem. Eng. Sci. 2004, 59, 1491–1504. [Google Scholar] [CrossRef]
- Kukadiya, S.B.; Chan, P.K.; Mehrvar, M. The Ludwig-Soret effect on the thermally induced phase separation process in polymer solutions: A computational study. Macromol. Theory Simul. 2009, 18, 97–107. [Google Scholar] [CrossRef]
- Cervellere, M.R.; Tang, Y.H.; Qian, X.; Ford, D.M.; Millett, P.C. Mesoscopic simulations of thermally-induced phase separation in PVDF/DPC solutions. J. Membr. Sci. 2019, 577, 266–273. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: New York, NY, USA, 1953. [Google Scholar]
- Debye, P. Angular dissymmetry of the critical opalescence in liquid mixtures. J. Chem. Phys. 1959, 31, 680–687. [Google Scholar] [CrossRef]
- Zielinski, J.M.; Duda, J.L. Predicting polymer/solvent diffusion coefficients using free-volume theory. AIChE J. 1992, 38, 405–415. [Google Scholar] [CrossRef]
- Vrentas, J.S.; Vrentas, C.M. Solvent self-diffusion in rubbery polymer-solvent systems. Macromolecules 1994, 27, 4684–4690. [Google Scholar] [CrossRef]
- Jamet, D.; Lebaigue, O.; Coutris, N.; Delhaye, J.M. The second gradient method for the direct numerical simulation of liquid–vapor flows with phase change. J. Comput. Phys. 2001, 169, 624–651. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mino, Y.; Fukukawa, N.; Matsuyama, H. Simulation on Pore Formation from Polymer Solution at Surface in Contact with Solid Substrate via Thermally Induced Phase Separation. Membranes 2021, 11, 527. https://doi.org/10.3390/membranes11070527
Mino Y, Fukukawa N, Matsuyama H. Simulation on Pore Formation from Polymer Solution at Surface in Contact with Solid Substrate via Thermally Induced Phase Separation. Membranes. 2021; 11(7):527. https://doi.org/10.3390/membranes11070527
Chicago/Turabian StyleMino, Yasushi, Naruki Fukukawa, and Hideto Matsuyama. 2021. "Simulation on Pore Formation from Polymer Solution at Surface in Contact with Solid Substrate via Thermally Induced Phase Separation" Membranes 11, no. 7: 527. https://doi.org/10.3390/membranes11070527
APA StyleMino, Y., Fukukawa, N., & Matsuyama, H. (2021). Simulation on Pore Formation from Polymer Solution at Surface in Contact with Solid Substrate via Thermally Induced Phase Separation. Membranes, 11(7), 527. https://doi.org/10.3390/membranes11070527






