Model-Based Analysis of Low Stoichiometry Operation in Proton Exchange Membrane Water Electrolysis
Abstract
:1. Introduction
2. Model Description
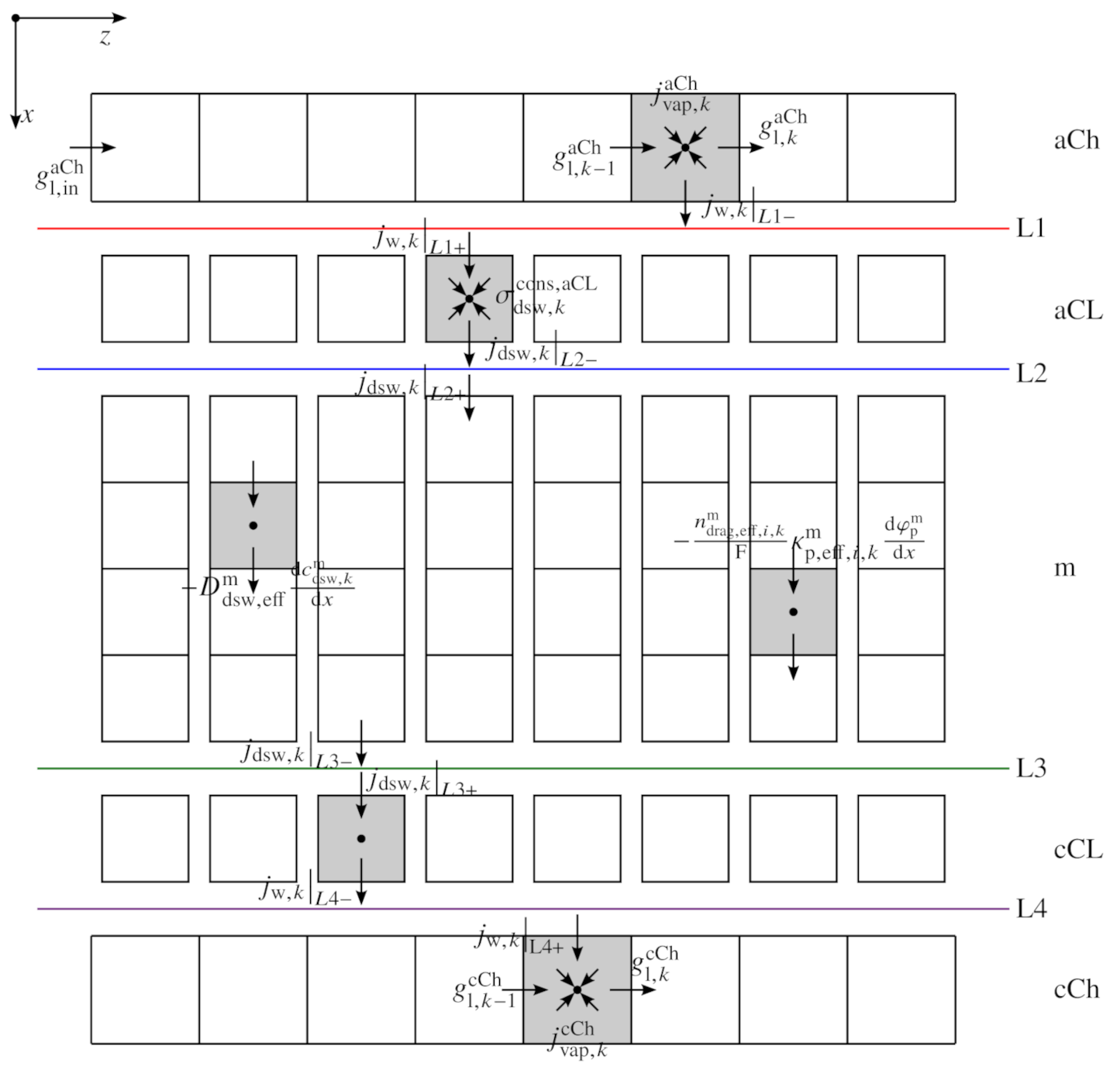
2.1. Sandwich Model
2.1.1. Charge Balances
Electron Potential
Proton Potential
Further Equations to Solve the Charge Balances
2.1.2. Dissolved Gases
Further Equations
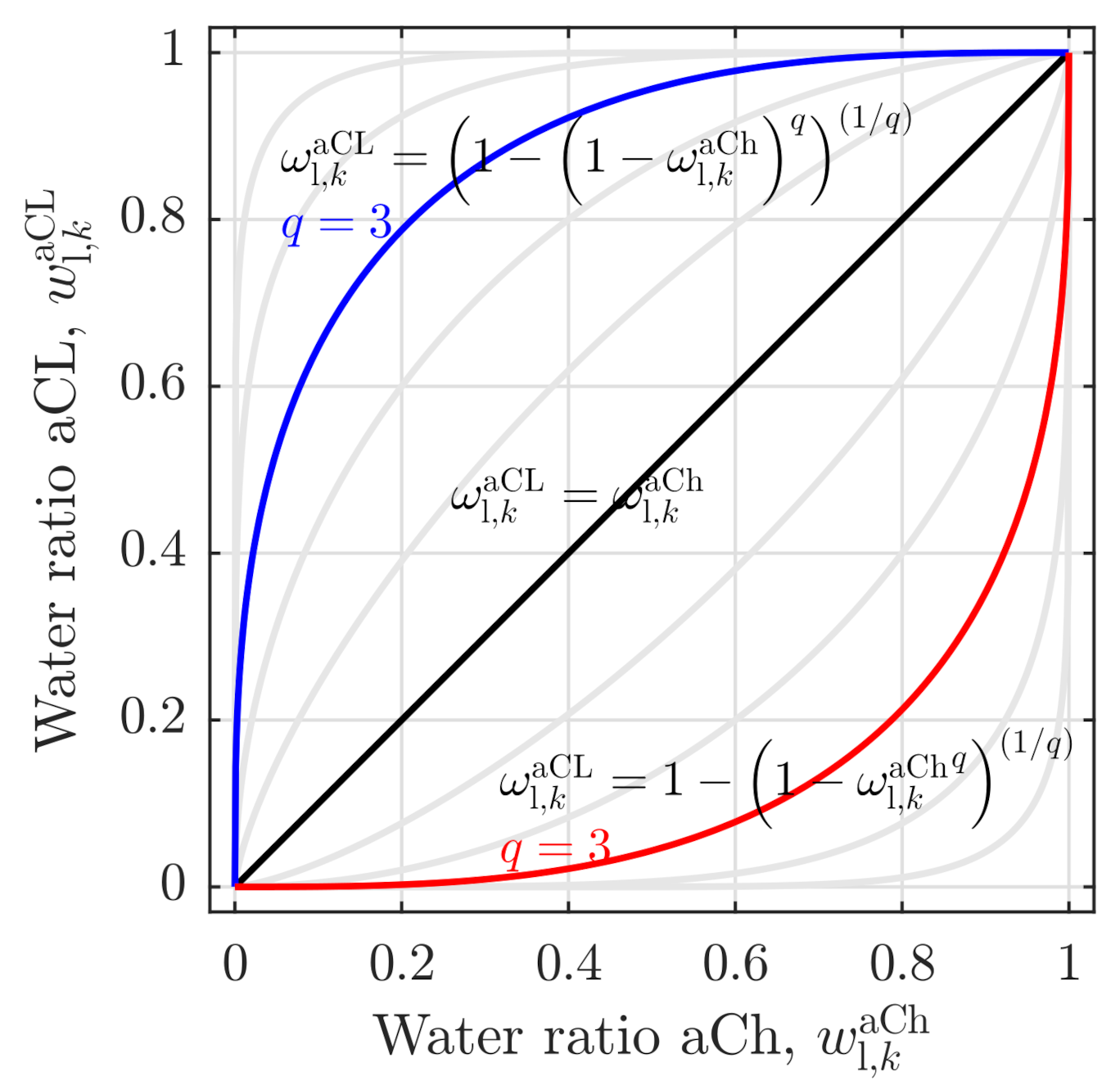
2.1.3. Dissolved Water Model
2.2. Channel Model
2.3. Coupling of Channel and Sandwich Model
3. Results and Discussion
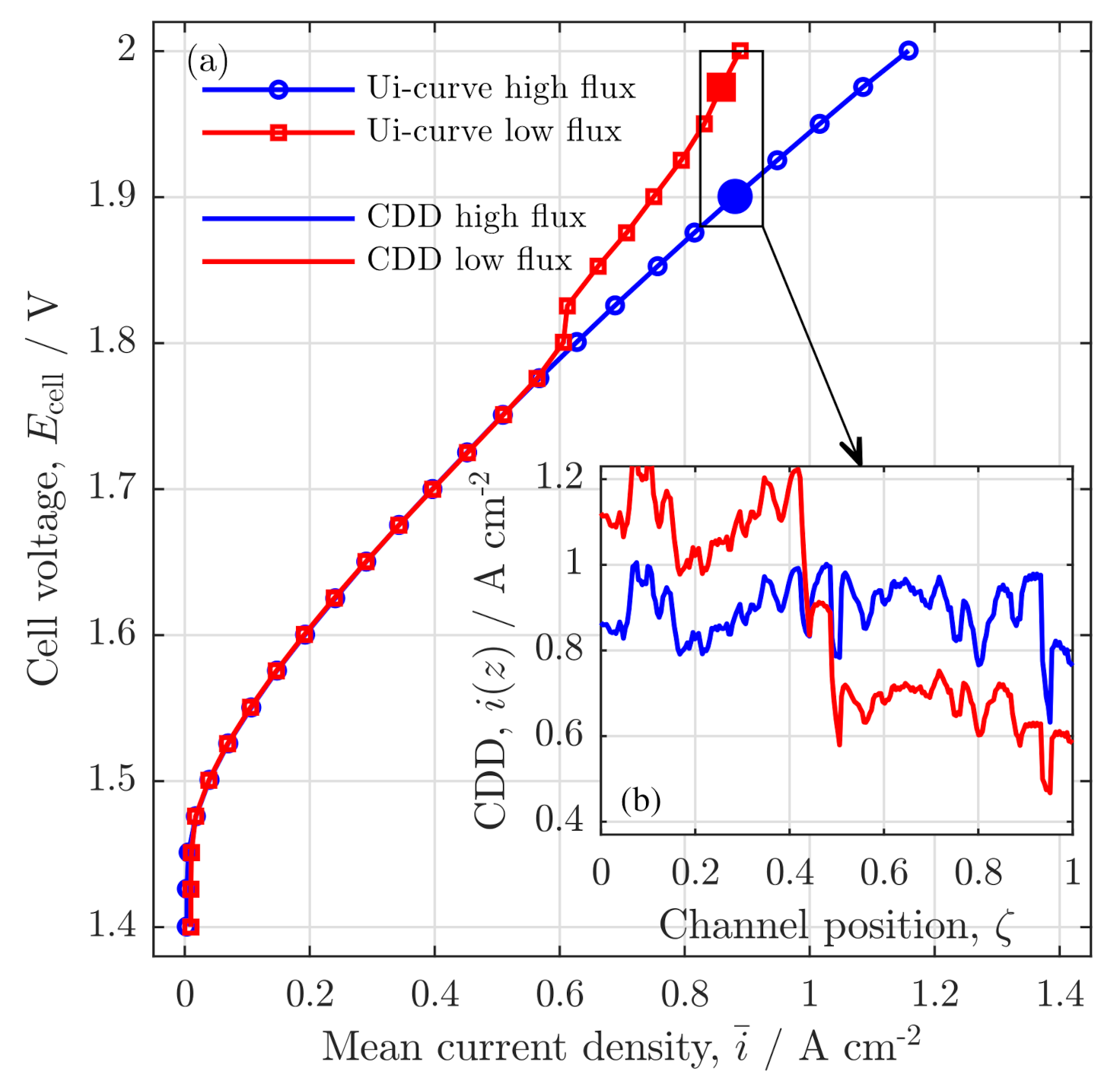
3.1. Experimental Validation
Polarization Curve
Validation of Current Density Distribution Profiles
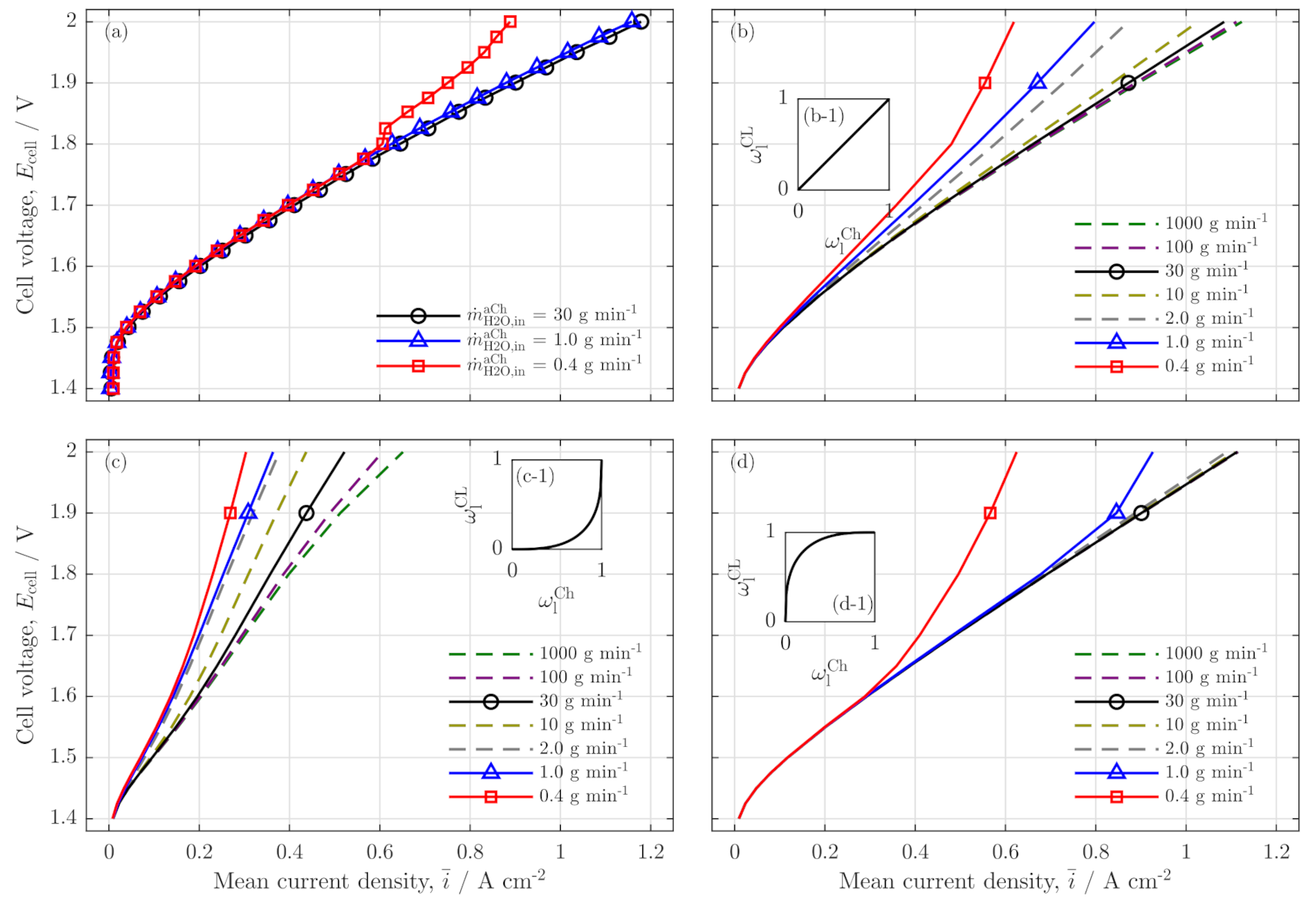
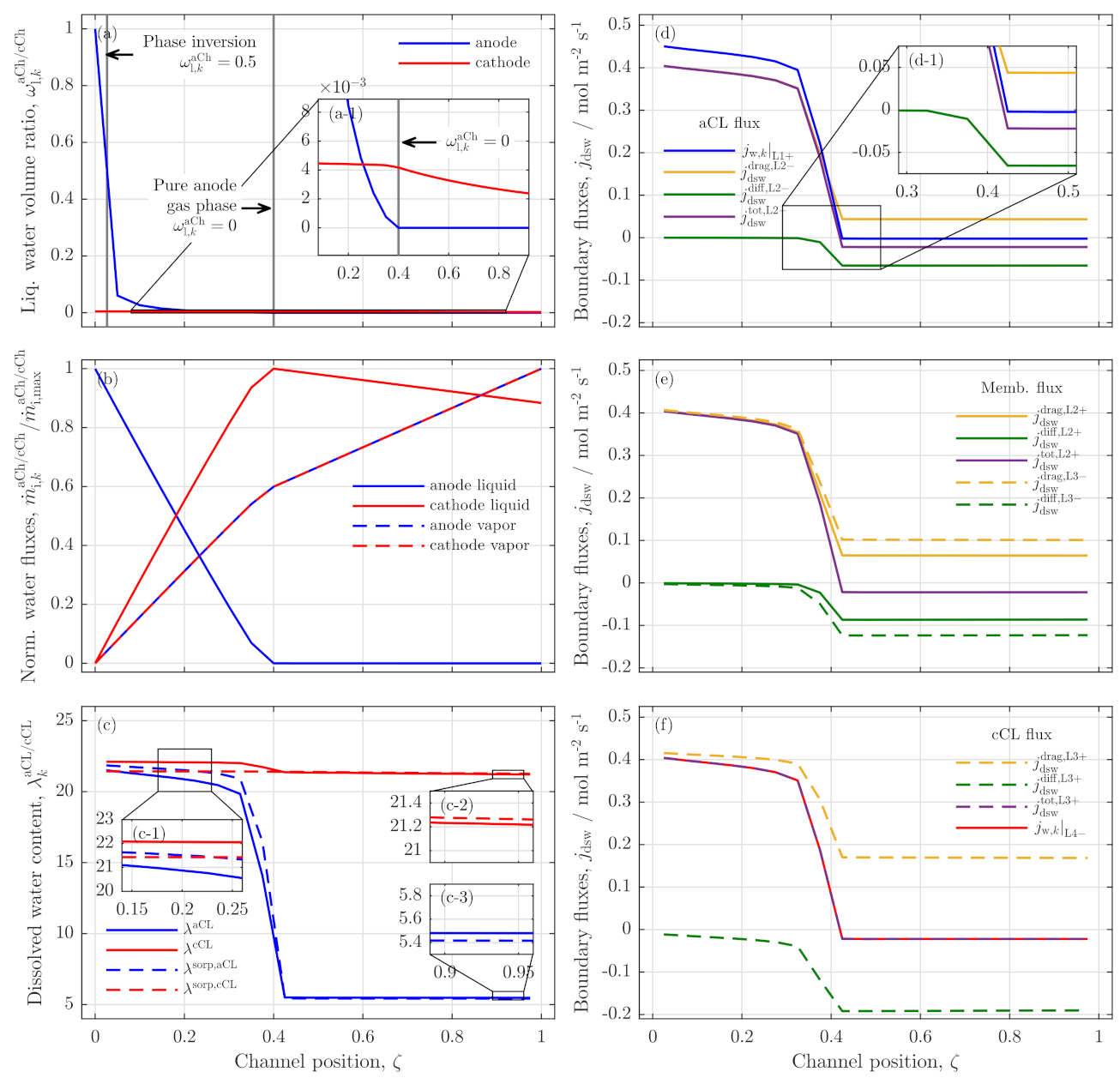
3.2. Further Analysis of Low Stoichiometry Operation
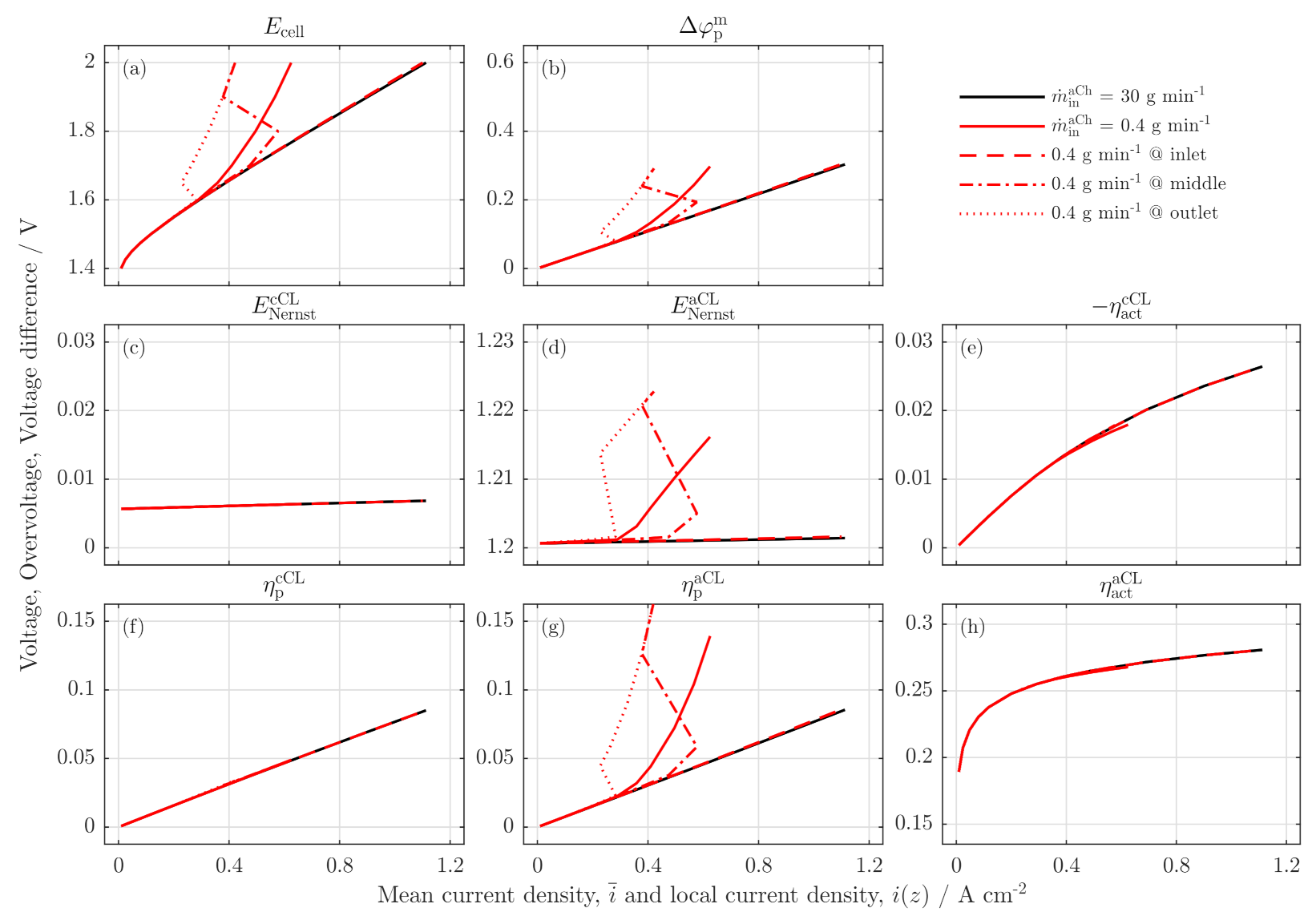
3.3. Local Cell Potential Analysis
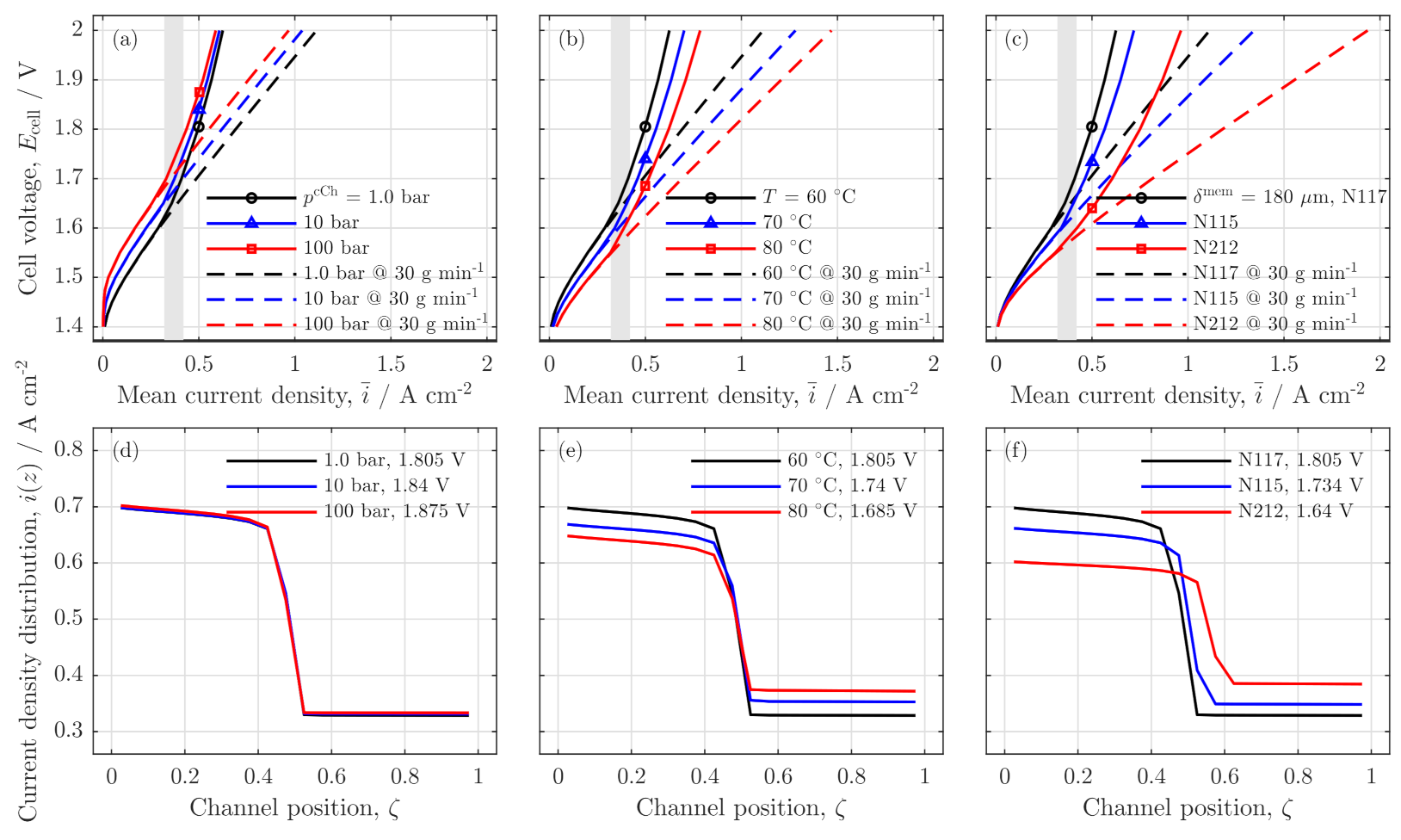
3.4. Parameter Variation
Influences of Pressure, Temperature and Membrane Thickness
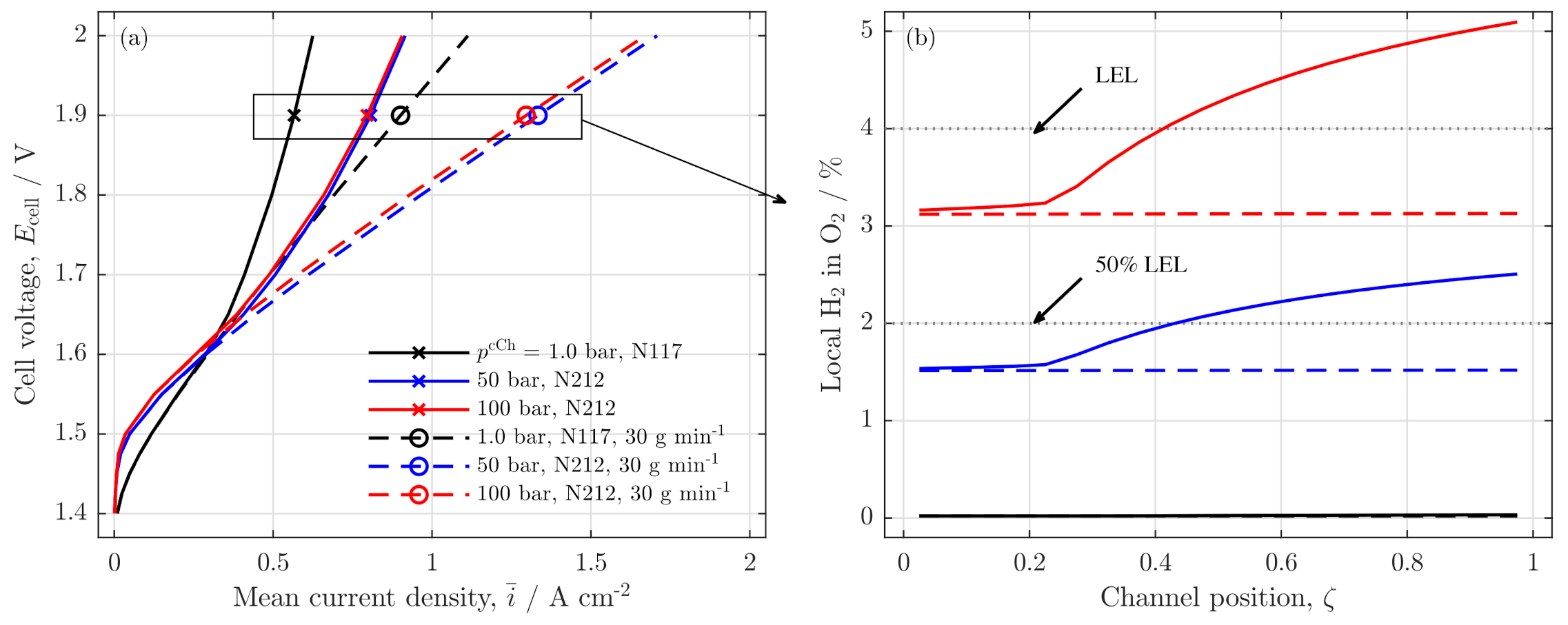
Influence on Safety and Crossover
3.5. Remarks on Low Stoichiometry Operation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Model
| Unit | Equation |
|---|---|
| Potential field electron conductor | |
| Potential field proton conductor | |
| Dissolved gases | |
| Dissolved water | |
| Unit | Equation |
|---|---|
| Cathode channel fluxes | |
| Further equations | |
| Variable | Symbol | aCL | m | cCL | Unit | Source |
|---|---|---|---|---|---|---|
| Temperature | T | 60 | ||||
| Pressure | p | 1.0 | 1.0 | |||
| Faraday’s constant | 96,485 | |||||
| Layer thickness | 5.432 | 180 | 5.556 | calc. in [15] | ||
| Electron conductivity | 22.2 | - | 25 | [15] | ||
| Ex. current dens. | - | 700 | chosen s. [35] | |||
| Ref. hydrogen conc. | 0.3921 | calc. in [15] | ||||
| Ref. oxygen conc. | 0.6368 | calc. in [15] | ||||
| Ref. liq. water content | 22 | [17] | ||||
| Activation energy | 54 | 54 | [36] | |||
| Apparent charge trans. coef., ox | 1.5 | - | 2 | - | chosen by [15] | |
| Apparent charge trans. coef., red | 1.5 | - | 2 | - | chosen by [15] | |
| Ionomer porosity | 0.2 | 1 | 0.2 | - | [37] | |
| Ionomer tortuosity | 2.236 | 1.5 | 2.2361 | - | [18,37] | |
| Mass transfer coef. O2 | 0.0441 | calc. in [15], data from [31] | ||||
| Mass transfer coef. H2 | 0.0992 | calc. in [15], data from [31] | ||||
| Sorption coef. vapor | [38] | |||||
| Sorption coef. liquid | calc. with [39], data from [38] | |||||
| Spec. ionomer surface | 2.470 | calc. in [15] | ||||
| Spec. pore surface | 2.470 | assumed as | ||||
| Vapor diffusivity | [40] | |||||
| CL Pore diameter | [37] | |||||
| Sherwood number | - | [41] | ||||
| Ref. O2 diffusivity | [31] | |||||
| Ref. H2 diffusivity | [31] | |||||
| Act. Energy O2 diff. | [31] | |||||
| Act. Energy H2 diff. | [31] | |||||
| Vap. enthalpy | 40.96 | for [15] | ||||
| Entropy change | 159.685 | for [15] |
Appendix B. Temperature Approximation
Appendix C. Experimental Setup
Abbreviations
| Latin Symbols | |
| a | Volume specific surface, () |
| Active geometrical cell area, () | |
| Activity of vapor | |
| b | Width of layer, () |
| c | Concentration, () |
| Reference concentration, () | |
| Molar heat capacity, () | |
| Pore diameter, () | |
| D | Diffusion coefficient, () |
| E | Voltage, () |
| Reference Nernst potential, () | |
| Activation energy, () | |
| Cell voltage, () | |
| Equivalent weight of Nafion®, () | |
| Faraday’s constant, () | |
| g | Molar flux density in z-direction, () |
| Specific vaporization enthalpy, () | |
| i | Current density, () |
| Exchange current density, () | |
| j | Molar flux density in x-direction, () |
| k | Mass transfer coefficient, () |
| Mass flow, () | |
| Molar mass, () | |
| Electro-osmotic drag coefficient | |
| p | Pressure, () |
| q | Coupling exponent |
| Q | Heat flux, () |
| Universal gas constant, () | |
| Entropy change () | |
| S | Solubility, () |
| Electrochemical dimensionless Sherwood number | |
| T | Temperature, () |
| v | Volume flux density, () |
| x | Sandwich coordinate, () |
| z | Channel coordinate, () |
| Greek symbols | |
| Apparent charge transfer coefficient | |
| Thickness, () | |
| Porosity | |
| Dimensionless channel coordinate | |
| Overpotential, () | |
| Conductivity, () | |
| Water content | |
| Stoichiometric water ratio | |
| Density, () | |
| Source term, () resp. () | |
| Tortuosity | |
| Potential, () | |
| Volume specific phase ratio | |
| Abbreviations | |
| aCh | Anode channel |
| aCL | Anode catalyst layer |
| cCh | Cathode channel |
| cCL | Cathode catalyst layer |
| CCM | Catalyst coated membrane |
| CDD | Current density distribution |
| CL | Catalyst layer |
| LEL | Lower explosion limit |
| m | Membrane |
| PEM | Proton exchange membrane |
| PEMWE | Proton exchange membrane water electrolysis |
| PTL | Porous transport layer |
| Sub- and superscripts | |
| act | Activation |
| cons | Consumed |
| conv | Convective |
| dry | Dry |
| dsg | Dissolved gases |
| dsw | Dissolved water |
| e | Electron |
| eff | Effective |
| entr | Entropy |
| evo | Evolved |
| g | Gaseous water |
| H2 | Hydrogen |
| i | Counter variable for membrane elements |
| ion | Ionomer |
| j | Placeholder variable for substances |
| joule | Joule heat |
| k | Counter variable in channel direction |
| l | Liquid water |
| L1, L2, L3, L4 | Boundaries 1–4 |
| L1−, L1+ | Into boundary L1, out of boundary L1 |
| m | Number of channel elements |
| n | Number of membrane elements |
| O2 | Oxygen |
| ox | Oxidation |
| p | Proton |
| red | Reduction |
| ref | Reference |
| sat | Saturation |
| set | Set |
| sorp | Sorption |
| v | Placeholder variable for layers |
| vap | Vapor |
| w | Water |
References
- Olesen, A.C.; Rømer, C.; Kær, S.K. A numerical study of the gas-liquid, two-phase flow maldistribution in the anode of a high pressure PEM water electrolysis cell. Int. J. Hydrog. Energy 2016, 41, 52–68. [Google Scholar] [CrossRef] [Green Version]
- Famouri, P.; Gemmen, R.S. Electrochemical circuit model of a PEM fuel cell. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; pp. 1436–1440. [Google Scholar] [CrossRef]
- Villagra, A.; Millet, P. An analysis of PEM water electrolysis cells operating at elevated current densities. Int. J. Hydrog. Energy 2019, 44, 9708–9717. [Google Scholar] [CrossRef]
- Immerz, C.; Schweins, M.; Trinke, P.; Bensmann, B.; Paidar, M.; Bystroň, T.; Bouzek, K.; Hanke-Rauschenbach, R. Experimental characterization of inhomogeneity in current density and temperature distribution along a single-channel PEM water electrolysis cell. Electrochim. Acta 2018, 260, 582–588. [Google Scholar] [CrossRef]
- Immerz, C.; Bensmann, B.; Trinke, P.; Suermann, M.; Hanke-Rauschenbach, R. Local Current Density and Electrochemical Impedance Measurements within 50 cm Single-Channel PEM Electrolysis Cell. J. Electrochem. Soc. 2018, 165, F1292–F1299. [Google Scholar] [CrossRef]
- Nie, J.; Chen, Y. Numerical modeling of three-dimensional two-phase gas–liquid flow in the flow field plate of a PEM electrolysis cell. Int. J. Hydrog. Energy 2010, 35, 3183–3197. [Google Scholar] [CrossRef]
- Lafmejani, S.S.; Olesen, A.C.; Kær, S.K. VOF modelling of gas–liquid flow in PEM water electrolysis cell micro-channels. Int. J. Hydrog. Energy 2017, 42, 16333–16344. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Xing, X. Simulation and experiment of heat and mass transfer in a proton exchange membrane electrolysis cell. Int. J. Hydrog. Energy 2020, 45, 20184–20193. [Google Scholar] [CrossRef]
- Rho, K.H.; Na, Y.; Ha, T.; Kim, D.K. Performance Analysis of Polymer Electrolyte Membrane Water Electrolyzer Using OpenFOAM®: Two-Phase Flow Regime, Electrochemical Model. Membranes 2020, 10, 441. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Yang, F.; Xu, H. Two-dimensional multi-physics modeling of porous transport layer in polymer electrolyte membrane electrolyzer for water splitting. Int. J. Hydrog. Energy 2020, 45, 32984–32994. [Google Scholar] [CrossRef]
- Ma, Z.; Witteman, L.; Wrubel, J.A.; Bender, G. A comprehensive modeling method for proton exchange membrane electrolyzer development. Int. J. Hydrog. Energy 2021, 46, 17627–17643. [Google Scholar] [CrossRef]
- Onda, K.; Murakami, T.; Hikosaka, T.; Kobayashi, M.; Notu, R.; Ito, K. Performance Analysis of Polymer-Electrolyte Water Electrolysis Cell at a Small-Unit Test Cell and Performance Prediction of Large Stacked Cell. J. Electrochem. Soc. 2002, 149, A1069–A1078. [Google Scholar] [CrossRef]
- Dedigama, I.; Angeli, P.; van Dijk, N.; Millichamp, J.; Tsaoulidis, D.; Shearing, P.R.; Brett, D.J. Current density mapping and optical flow visualisation of a polymer electrolyte membrane water electrolyser. J. Power Sources 2014, 265, 97–103. [Google Scholar] [CrossRef]
- Sun, S.; Xiao, Y.; Liang, D.; Shao, Z.; Yu, H.; Hou, M.; Yi, B. Behaviors of a proton exchange membrane electrolyzer under water starvation. RSC Adv. 2015, 5, 14506–14513. [Google Scholar] [CrossRef]
- Trinke, P. Experimental and Model-Based Investigations on Gas Crossover in Polymer Electrolyte Membrane Water Electrolyzers: Experimental and Model-Based Investigations on Gas Crossover in Polymer Electrolyte Membrane Water Electrolyzers. Ph.D. Thesis, Institutionelles Repositorium der Leibniz Universität Hannover, Hannover, Germany, 2021. [Google Scholar] [CrossRef]
- Nič, M.; Jirát, J.; Košata, B.; Jenkins, A.; McNaught, A. IUPAC Compendium of Chemical Terminology; IUPAC: Research Triagle Park, NC, USA, 2009. [Google Scholar]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Fimrite, J.; Carnes, B.; Struchtrup, H.; Djilali, N. Transport Phenomena in Polymer Electrolyte Membranes. J. Electrochem. Soc. 2005, 152, A1815. [Google Scholar] [CrossRef]
- Schmidt, G.; Suermann, M.; Bensmann, B.; Hanke-Rauschenbach, R.; Neuweiler, I. Modeling Overpotentials Related to Mass Transport Through Porous Transport Layers of PEM Water Electrolysis Cells. J. Electrochem. Soc. 2020, 167, 114511. [Google Scholar] [CrossRef]
- Schuler, T.; Schmidt, T.J.; Büchi, F.N. Polymer Electrolyte Water Electrolysis: Correlating Performance and Porous Transport Layer Structure: Part II. Electrochemical Performance Analysis. J. Electrochem. Soc. 2019, 166, F555–F565. [Google Scholar] [CrossRef]
- Lopata, J.; Kang, Z.; Young, J.; Bender, G.; Weidner, J.W.; Shimpalee, S. Effects of the Transport/Catalyst Layer Interface and Catalyst Loading on Mass and Charge Transport Phenomena in Polymer Electrolyte Membrane Water Electrolysis Devices. J. Electrochem. Soc. 2020, 167, 064507. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Millet, P.; Korobtsev, S.V.; Porembskiy, V.I.; Pepic, M.; Etievant, C.; Puyenchet, C.; Fateev, V.N. Hydrogen safety aspects related to high-pressure polymer electrolyte membrane water electrolysis. Int. J. Hydrog. Energy 2009, 34, 5986–5991. [Google Scholar] [CrossRef]
- Takenaka, H.; Torikai, E.; Kawami, Y.; Wakabayashi, N. Solid polymer electrolyte water electrolysis. Int. J. Hydrog. Energy 1982, 7, 397–403. [Google Scholar] [CrossRef]
- Ayers, K.E.; Anderson, E.B.; Capuano, C.; Carter, B.; Dalton, L.; Hanlon, G.; Manco, J.; Niedzwiecki, M. Research Advances towards Low Cost, High Efficiency PEM Electrolysis. ECS Trans. 2010, 33, 3–15. [Google Scholar] [CrossRef]
- Han, B.; Steen, S.M.; Mo, J.; Zhang, F.Y. Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy. Int. J. Hydrog. Energy 2015, 40, 7006–7016. [Google Scholar] [CrossRef] [Green Version]
- Babic, U.; Suermann, M.; Büchi, F.N.; Gubler, L.; Schmidt, T.J. Critical Review—Identifying Critical Gaps for Polymer Electrolyte Water Electrolysis Development. J. Electrochem. Soc. 2017, 164, F387–F399. [Google Scholar] [CrossRef] [Green Version]
- Janssen, H. Safety-related studies on hydrogen production in high-pressure electrolysers. Int. J. Hydrog. Energy 2004, 29, 759–770. [Google Scholar] [CrossRef]
- Möckl, M.; Bernt, M.; Schröter, J.; Jossen, A. Proton exchange membrane water electrolysis at high current densities: Investigation of thermal limitations. Int. J. Hydrog. Energy 2020, 45, 1417–1428. [Google Scholar] [CrossRef]
- Olesen, A.C.; Frensch, S.H.; Kær, S.K. Towards uniformly distributed heat, mass and charge: A flow field design study for high pressure and high current density operation of PEM electrolysis cells. Electrochim. Acta 2019, 293, 476–495. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. NIST Chemistry WebBook, NIST Standard Reference Database 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1997. [Google Scholar]
- Ito, H.; Maeda, T.; Nakano, A.; Takenaka, H. Properties of Nafion membranes under PEM water electrolysis conditions. Int. J. Hydrog. Energy 2011, 36, 10527–10540. [Google Scholar] [CrossRef]
- Zhao, Q.; Majsztrik, P.; Benziger, J. Diffusion and interfacial transport of water in Nafion. J. Phys. Chem. B 2011, 115, 2717–2727. [Google Scholar] [CrossRef] [PubMed]
- Weber, A.Z.; Newman, J. Transport in Polymer-Electrolyte Membranes. J. Electrochem. Soc. 2004, 151, A311. [Google Scholar] [CrossRef]
- Stull, D.R. Vapor Pressure of Pure Substances. Organic and Inorganic Compounds. Ind. Eng. Chem. 1947, 39, 517–540. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrog. Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- García-Valverde, R.; Espinosa, N.; Urbina, A. Simple PEM water electrolyser model and experimental validation. Int. J. Hydrog. Energy 2012, 37, 1927–1938. [Google Scholar] [CrossRef]
- Inoue, G.; Yokoyama, K.; Ooyama, J.; Terao, T.; Tokunaga, T.; Kubo, N.; Kawase, M. Theoretical examination of effective oxygen diffusion coefficient and electrical conductivity of polymer electrolyte fuel cell porous components. J. Power Sources 2016, 327, 610–621. [Google Scholar] [CrossRef]
- Berg, P.; Promislow, K.; St Pierre, J.; Stumper, J.; Wetton, B. Water Management in PEM Fuel Cells. J. Electrochem. Soc. 2004, 151, A341. [Google Scholar] [CrossRef]
- Ge, S.; Li, X.; Yi, B.; Hsing, I.M. Absorption, Desorption, and Transport of Water in Polymer Electrolyte Membranes for Fuel Cells. J. Electrochem. Soc. 2005, 152, A1149. [Google Scholar] [CrossRef]
- Nam, J.H.; Kaviany, M. Effective diffusivity and water-saturation distribution in single- and two-layer PEMFC diffusion medium. Int. J. Heat Mass Transf. 2003, 46, 4595–4611. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Berg, P. On the modeling of water transport in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6913–6927. [Google Scholar] [CrossRef]
- Liste der Spezifischen Wärmekapazitäten. Available online: https://www.chemie.de/lexikon/Liste_der_spezifischen_W%C3%A4rmekapazit%C3%A4ten.html (accessed on 30 April 2021).


| Charge balances | |
|---|---|
| Electron potential anode, state equations | Equations (1)–(3) |
| Proton potential anode, state equations | Equations (4)–(6) |
| Proton potential membrane, state equations | Equations (7)–(9) |
| Constitutive and closing equations | Equations (10)–(16) |
| Electron potential cathode, state equations | Equations (A20)–(A22) |
| Proton potential cathode, state equations | Equations (A23)–(A25) |
| Additional electrical equations | Equations (A1)+(A2) |
| Dissolved gases | |
| H2, O2 concentrations anode, state equations | Equations (17)–(19) |
| H2, O2 concentrations membrane, state equations | Equations (20)–(22) |
| Constitutive and closing equations | Equations (23)–(26) |
| H2, O2 concentrations cathode, state equations | Equations (A26)–(A28) |
| Additional dissolved gases equations | Equations (A3)–(A7) |
| Dissolved water | |
| Water concentrations anode, state equations | Equations (27)–(29) |
| Constitutive and closing equations | Equations (30)–(33) |
| Water concentrations membrane, state equations | Equations (A29)–(A31) |
| Water concentrations cathode, state equations | Equations (A32)–(A34) |
| Additional dissolved water equations | Equations (A8)–(A15) |
| Channel model | |
| Channel fluxes, state equations | Equations (34)–(36) |
| Constitutive and closing equations | Equations (37)–(38) |
| Coupling equations | Equations (39)–(40) |
| Channel volume fluxes | Equations (A16)–(A19) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Immerz, C.; Bensmann, B.; Hanke-Rauschenbach, R. Model-Based Analysis of Low Stoichiometry Operation in Proton Exchange Membrane Water Electrolysis. Membranes 2021, 11, 696. https://doi.org/10.3390/membranes11090696
Immerz C, Bensmann B, Hanke-Rauschenbach R. Model-Based Analysis of Low Stoichiometry Operation in Proton Exchange Membrane Water Electrolysis. Membranes. 2021; 11(9):696. https://doi.org/10.3390/membranes11090696
Chicago/Turabian StyleImmerz, Christoph, Boris Bensmann, and Richard Hanke-Rauschenbach. 2021. "Model-Based Analysis of Low Stoichiometry Operation in Proton Exchange Membrane Water Electrolysis" Membranes 11, no. 9: 696. https://doi.org/10.3390/membranes11090696
APA StyleImmerz, C., Bensmann, B., & Hanke-Rauschenbach, R. (2021). Model-Based Analysis of Low Stoichiometry Operation in Proton Exchange Membrane Water Electrolysis. Membranes, 11(9), 696. https://doi.org/10.3390/membranes11090696






