Feasibility of Adsorption Kinetic Models to Study Carrier-Mediated Transport of Heavy Metal Ions in Emulsion Liquid Membranes
Abstract
:1. Introduction
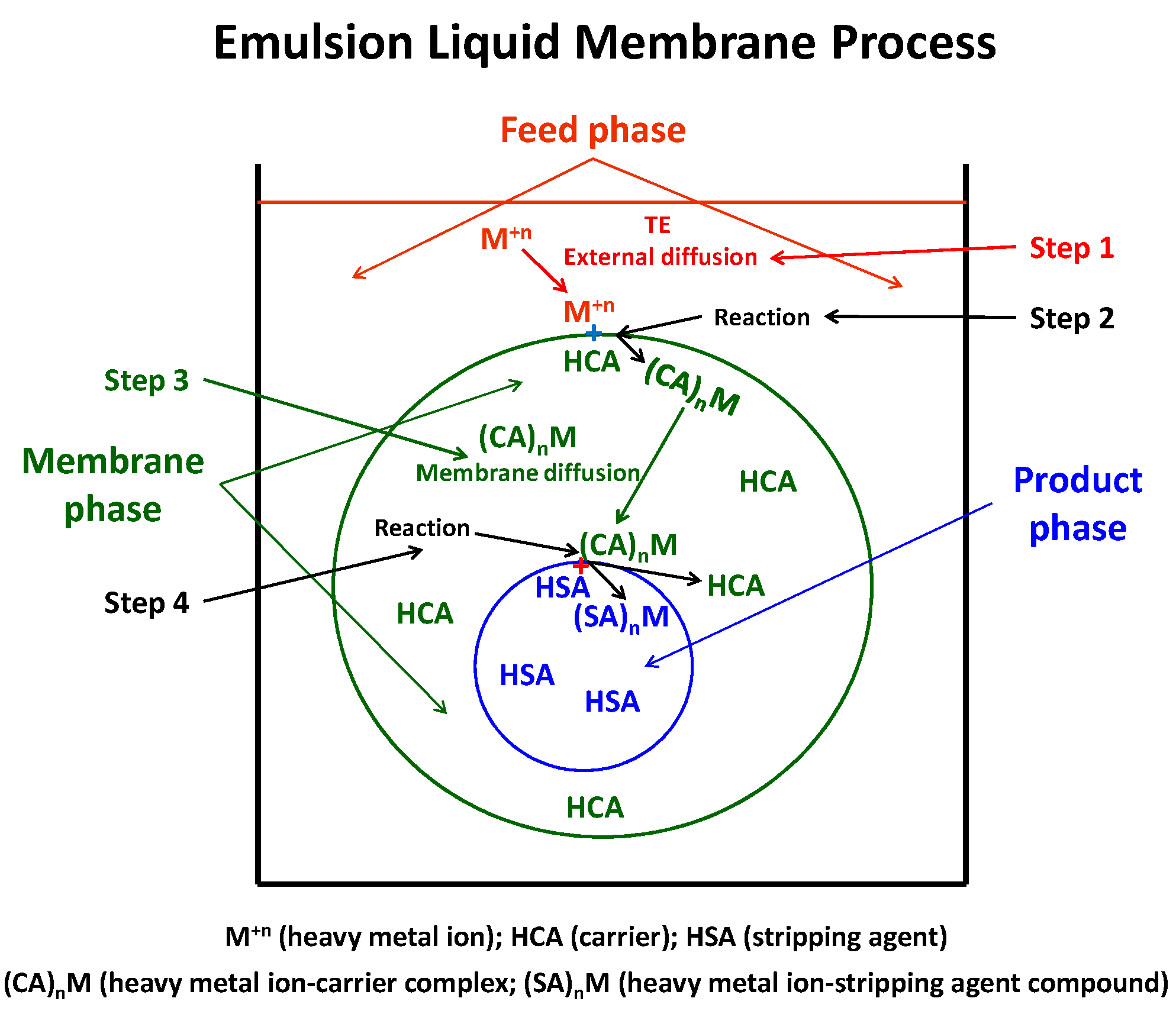
- Step 1. Heavy metal ion diffusion through the boundary layer of the feed phase to the feed/membrane interface.
- Step 2. Heavy metal ion reaction, at the feed/membrane interface, with the carrier present in the membrane phase forming a metal-carrier complex soluble in the membrane phase.
- Step 3. Complex diffusion, in the membrane phase, from the feed/membrane interface toward the membrane/product interface.
- Step 4. Complex breakdown at the membrane/product interface due to the reaction between the heavy metal ion and stripping agent present in the product phase and carrier regeneration.
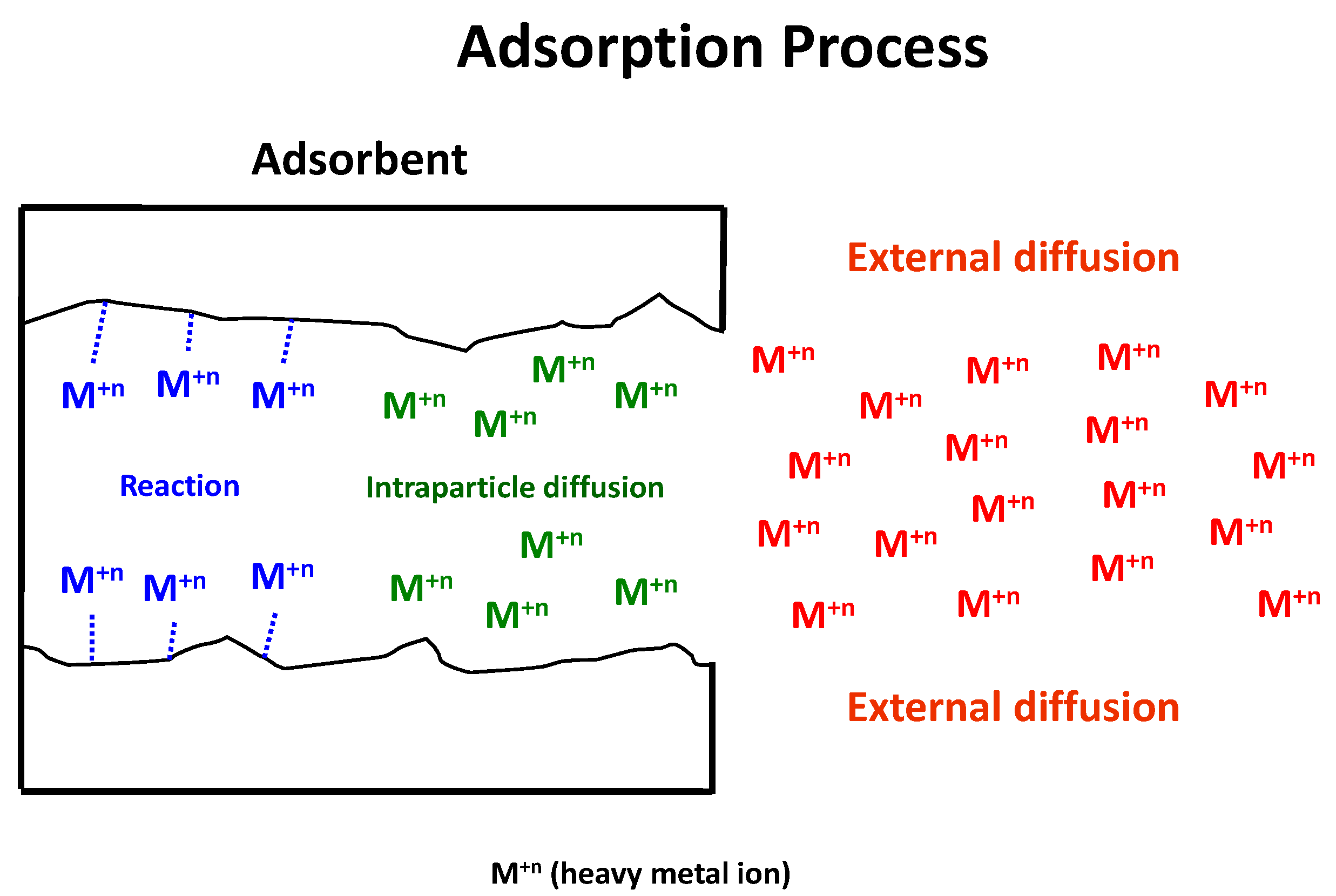
- Step 1. External diffusion (film diffusion), which is the transport of the heavy metal ion from the bulk phase to the external surface of the adsorbent.
- Step 2. Intraparticle diffusion (pore diffusion), which is the transport of the heavy metal ion from the external surface into the pores.
- Step 3. Surface reaction, which is the attachment of the heavy metal ion to the internal surface of the sorbent.
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussion
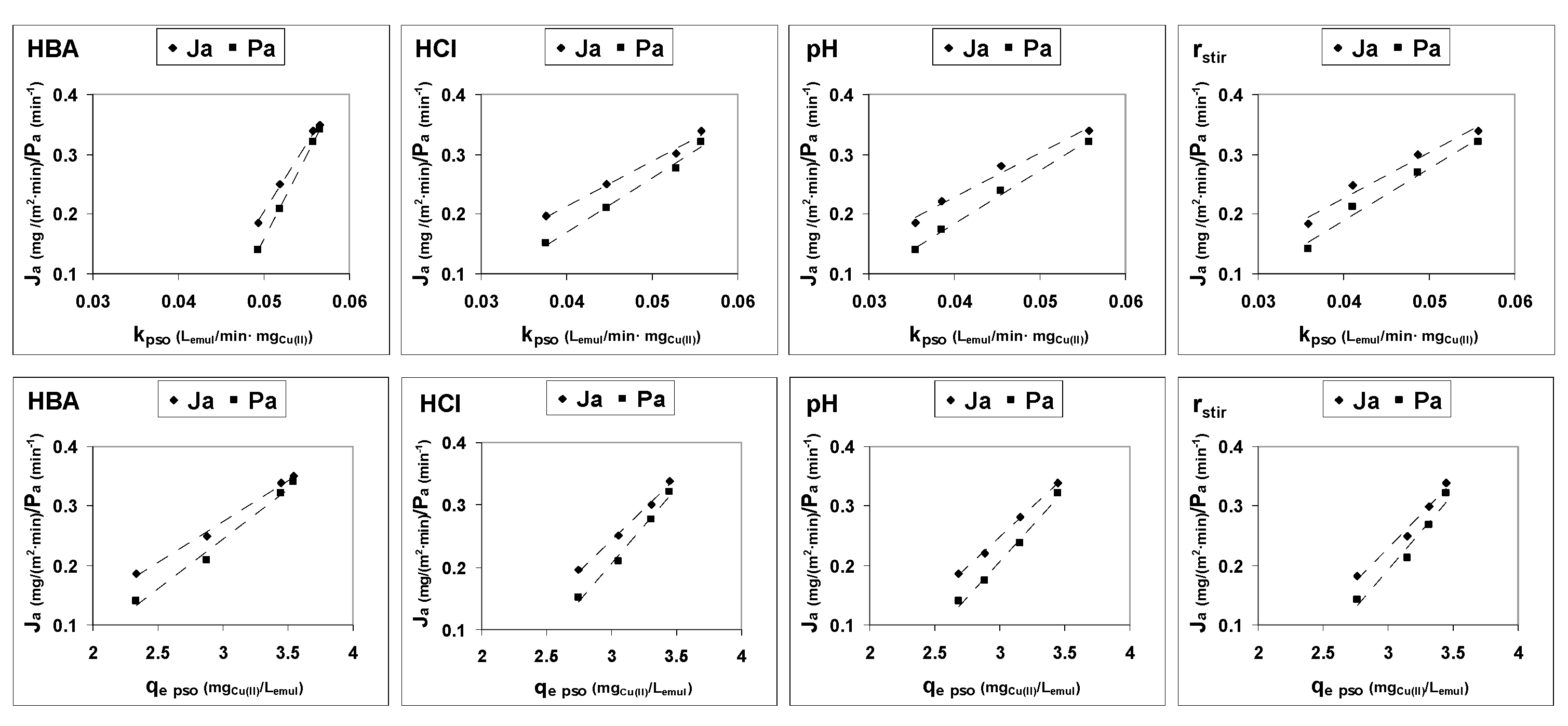
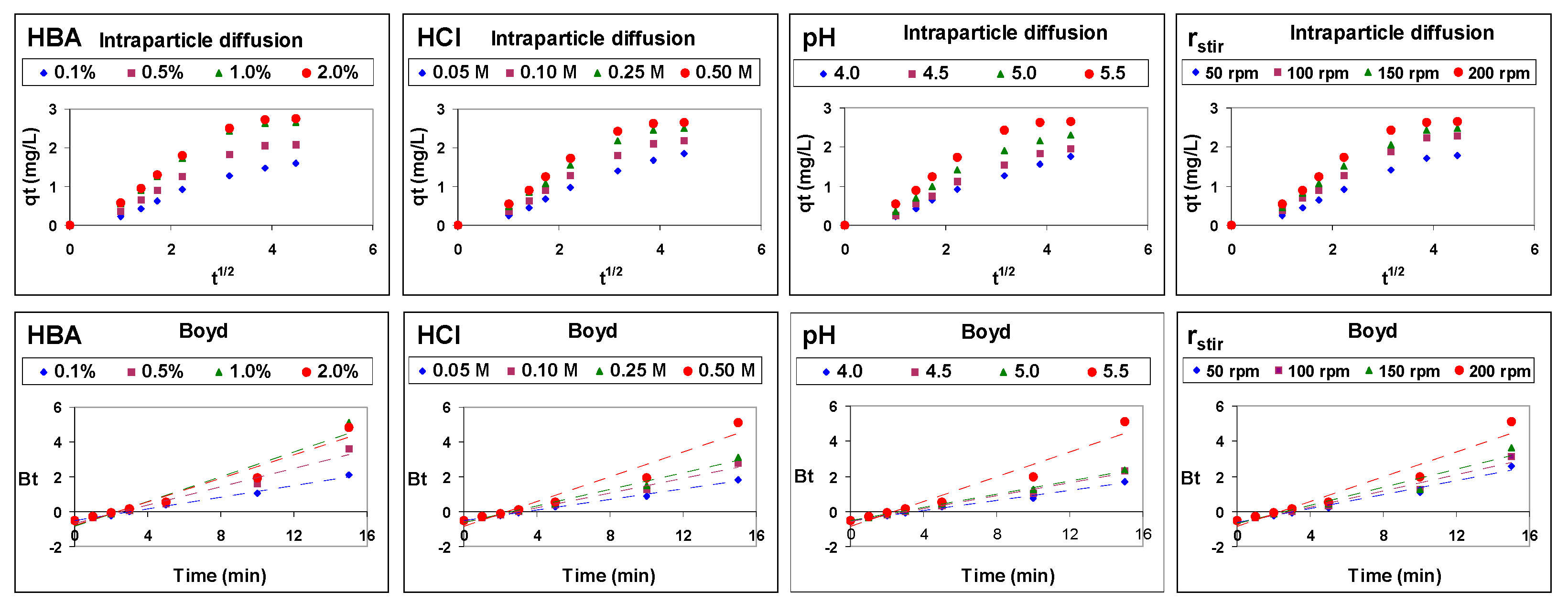
3.1. Kinetics of Cu(II) Transport
3.2. Mechanism of Cu(II) Transport
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Srivastava, N.K.; Majumder, C.B. Novel biofiltration methods for the treatment of heavy metals from industrial wastewater. J. Hazard. Mater. 2008, 151, 1–8. [Google Scholar] [CrossRef]
- Han, R.; Zhou, B.; Huang, Y.; Lu, X.; Li, S.; Li, N. Bibliometric overview of research trends on heavy metal health risks and impacts in 1989–2018. J. Clean. Prod. 2020, 276, 123249. [Google Scholar] [CrossRef]
- Zaynab, M.; Al-Yahyai, R.; Ameen, A.; Sharif, Y.; Ali, L.; Fatima, M.; Khan, K.A.; Li, S. Health and environmental effects of heavy metals. J. King Saud Univ. Sci. 2022, 34, 101653. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Mohammed, R.H.; Lawal, D.U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. NPJ Clean Water 2021, 4, 36. [Google Scholar] [CrossRef]
- Kumar, M.; Seth, A.; Singh, A.K.; Rajput, M.S.; Sikandar, M. Remediation strategies for heavy metals contaminated ecosystem: A review. Environ. Sustain. Indic. 2021, 12, 100155. [Google Scholar] [CrossRef]
- Chen, Q.; Yao, Y.; Li, X.; Lu, J.; Zhou, J.; Huang, Z. Comparison of heavy metal removals from aqueous solutions by chemical precipitation and characteristics of precipitates. J. Water Process. Eng. 2018, 26, 289–300. [Google Scholar] [CrossRef]
- Ahmeda, M.S.; Zewaila, T.M.; El-Ashtoukhya, E.S.Z.; Faraga, H.A.; El Azabb, I.H.; Albatatid, F.A.; Al-Hossainye, A.F.; Zorombag, M.S.; Abdel-Azizg, M.H. Enhancement of heavy metals recovery from aqueous solutions by cementation on a rotating cylinder using a stationary wiper. J. Ind. Eng. Chem. 2021, 97, 460–465. [Google Scholar] [CrossRef]
- Shrestha, R.; Ban, S.; Devkota, S.; Sharma, S.; Joshi, R.; Tiwari, A.P.; Kim, H.Y.; Joshi, M.K. Technological trends in heavy metals removal from industrial wastewater: A review. J. Environ. Chem. Eng. 2021, 9, 105688. [Google Scholar] [CrossRef]
- Burakov, A.E.; Galunin, E.V.; Burakova, I.V.; Kucherova, A.E.; Agarwal, S.; Tkachev, A.G.; Gupta, V.K. Adsorption of heavy metals on conventional and nanostructured materials for wastewater treatment purposes: A review. Ecotoxicol. Environ. Saf. 2018, 148, 702–712. [Google Scholar] [CrossRef] [PubMed]
- Chai, W.S.; Cheun, J.Y.; Kumar, P.S.; Mubashir, M.; Majeed, Z.; Banat, F.; Ho, S.H.; Show, P.L. A review on conventional and novel materials towards heavy metal adsorption in wastewater treatment application. J. Clean. Prod. 2021, 296, 126589. [Google Scholar] [CrossRef]
- Bilal, M.; Ihsanullah, I.; Younas, M.; Shah, M.U.H. Recent advances in applications of low-cost adsorbents for the removal of heavy metals from water: A critical review. Sep. Purif. Technol. 2022, 278, 119510. [Google Scholar] [CrossRef]
- Qiu, B.; Tao, X.; Wang, H.; Li, W.; Ding, X.; Chu, H. Biochar as a low-cost adsorbent for aqueous heavy metal removal: A review. J. Anal. Appl. Pyrolysis 2021, 155, 105081. [Google Scholar] [CrossRef]
- Tran, T.K.; Chiu, K.F.; Lin, C.Y.; Leu, H.J. Electrochemical treatment of wastewater: Selectivity of the heavy metals removal process. Int. J. Hydrogen Energy 2017, 42, 27741–27748. [Google Scholar] [CrossRef]
- Ya, V.; Martin, N.; Chou, Y.H.; Chen, Y.M.; Choo, K.H.; Chen, S.S.; Li, C.W. Electrochemical treatment for simultaneous removal of heavy metals and organics from surface finishing wastewater using sacrificial iron anode. J. Taiwan Inst. Chem. Eng. 2018, 83, 107–114. [Google Scholar] [CrossRef]
- Gao, X.; Meng, X. Photocatalysis for Heavy Metal Treatment: A Review. Processes 2021, 9, 1729. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Moffitt, M.; Grieves, R.B. Charged Membrane Ultrafiltration of Toxic Metal Oxyanions and Cations from Single and Multisalt Aqueous Solutions. Sep. Sci. Technol. 1978, 13, 449–463. [Google Scholar] [CrossRef]
- Sato, T.; Imaizumi, M.; Kato, S.; Taniguchi, Y. RO Applications in wastewater reclamation for reuse. Desalination 1977, 23, 65–76. [Google Scholar] [CrossRef]
- Juang, R.S.; Xu, Y.Y.; Chen, C.L. Separation and removal of metal ions from dilute solutions using micellar-enhanced ultrafiltration. J. Membr. Sci. 2003, 218, 257–267. [Google Scholar] [CrossRef]
- Yaqub, M.; Lee, S.H. Heavy metals removal from aqueous solution through micellar enhanced ultrafiltration: A review. Environ. Eng. Res. 2019, 24, 363–375. [Google Scholar] [CrossRef]
- Al-Rashdi, B.A.M.; Johnson, D.J.; Hilal, N. Removal of heavy metal ions by nanofiltration. Desalination 2013, 315, 2–17. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Hu, S.; Yu, F.; He, Z.; Zeng, G.; Feng, Z.; Sengupta, A. Construction of Fe3O4@MXene composite nanofiltration membrane for heavy metal ions removal from wastewater. Polym. Adv. Technol. 2021, 32, 1000–1010. [Google Scholar] [CrossRef]
- Ozaki, H.; Sharma, K.; Saktaywin, W. Performance of an ultra-low-pressure reverse osmosis membrane (ULPROM) for separating heavy metal: Effects of interference parameters. Desalination 2002, 144, 287–294. [Google Scholar] [CrossRef]
- Vital, B.; Bartacek, J.; Ortega-Bravo, J.C.; Jeison, D. Treatment of acid mine drainage by forward osmosis: Heavy metal rejection and reverse flux of draw solution constituents. Chem. Eng. J. 2018, 332, 85–91. [Google Scholar] [CrossRef]
- Mohammadi, T.; Moheb, A.; Sadrzadeh, M.; Razmi, A. Modeling of metal ion removal from wastewater by electrodialysis. Sep. Purif. Technol. 2005, 41, 73–82. [Google Scholar] [CrossRef]
- Keskin, B.; Zeytuncu-Gökoğlu, B.; Koyuncu, I. Polymer inclusion membrane applications for transport of metal ions: A critical review. Chemosphere 2021, 279, 130604. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.L.; Kusumastutib, A.; Derek, C.J.C.; Ooi, B.S. Emulsion liquid membrane for heavy metal removal: An overview on emulsion stabilization and destabilization. Chem. Eng. J. 2011, 171, 870–882. [Google Scholar] [CrossRef]
- León, L.; León, G.; Senent, J.; Pérez-Sirvent, C. Optimization of Copper Removal from Aqueous Solutions Using Emulsion Liquid Membranes with Benzoylacetone as a Carrier. Metals 2017, 7, 19. [Google Scholar] [CrossRef] [Green Version]
- Amini, M.; Rahbar-Kelishami, A.; Alipour, M.; Vahidi, O. Supported Liquid Membrane in Metal Ion Separation: An Overview. J. Membr. Sci. Res. 2018, 4, 121–135. [Google Scholar]
- León, G.; Hidalgo, A.M.; Miguel, B.; Guzmán, M.A. Pertraction of Co(II) through Novel Ultrasound Prepared Supported Liquid Membranes Containing D2EHPA. Optimization and Transport Parameters. Membranes 2020, 10, 436. [Google Scholar] [CrossRef]
- Rzelewska-Piekut, M.; Regel-Rosocka, M. Liquid membranes for separation of metal ions from wastewaters. Phys. Sci. Rev. 2021, 20210049. [Google Scholar] [CrossRef]
- León, G. Facilitated transport. In Encyclopedia of Membranes, 1st ed.; Drioli, E., Giorno, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 763–764. [Google Scholar]
- Kislik, V.S. Introduction, General Description, Definitions and Classification. Overview. In Liquid Membranes. Principles and Applications in Chemical Separation and Wastewater Treatment, 1st ed.; Kislik, V.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–15. [Google Scholar]
- Ma, G.; Jiang, Y.; Kun, S.C. A general mass transfer model for liquid surfactant membrane. Chem. Eng. Sci. 1997, 52, 433–441. [Google Scholar]
- Ho, W.S.; Hatton, T.A.; Lightfoot, E.N.; Li, N.N. Liquid surfactant membranes: A diffusion controlled model. AIChE J. 1982, 28, 662–671. [Google Scholar] [CrossRef]
- Teramoto, M.; Sakai, T.; Yamagawa, K.; Ohsuga, M.; Miyake, Y. Extraction of phenol and cresol by liquid surfactant membrane. Sep. Sci. Technol. 1983, 18, 397–406. [Google Scholar] [CrossRef]
- Box, G.E.P. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Tan, K.L.; Hameed, B.H. Insight into the adsorption kinetics models for the removal of contaminants from aqueous solutions. J. Taiwan Inst. Chem. Eng. 2017, 74, 25–48. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Kulkarni, P.S.; Mahajani, V.V. Application of liquid emulsion membrane (LEM) process for enrichment of Molybdenum from aqueous solutions. J. Membr. Sci. 2002, 201, 123–135. [Google Scholar] [CrossRef]
- Lagergren, S. About the theory of so-called adsorption of soluble substances. K. Sven. Vetensk. Handl. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S. Review of second-order model for adsorption systems. J. Hazard. Mater. 2006, 136, 681–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elovich, S.Y.; Larinov, O.G. Theory of adsorption from solutions of non-electrolytes on solid (I) equation adsorption from solutions and the analysis of its simplest form, (II) verification of the equation of adsorption isotherm from solutions. Izvestyja Akad. Nauk SSSR Otd. Khimicheskikh Nauk 1962, 2, 209–216. [Google Scholar]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1940, 7, 1103–1112. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. J. Sanit. Eng. Div. 1963, 89, 31–59. [Google Scholar] [CrossRef]
- Boyd, G.E.; Adamson, A.W.; Myers, L.S. The exchange adsorption of ions from aqueous solutions by organic zeolites. II. Kinetics. J. Am. Chem. Soc. 1947, 69, 2836–2848. [Google Scholar] [CrossRef] [PubMed]
- Coleman, N.T.; McClung, A.C.; Moore, D.P. Formation constants for Cu(II)-peat complexes. Science 1956, 123, 330–331. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.S.; McKay, G. The kinetics of sorption of divalent metal ions onto sphagnum moss peat. Water Res. 2000, 34, 735–742. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León, G.; Gómez, E.; Miguel, B.; Hidalgo, A.M.; Gómez, M.; Murcia, M.D.; Guzmán, M.A. Feasibility of Adsorption Kinetic Models to Study Carrier-Mediated Transport of Heavy Metal Ions in Emulsion Liquid Membranes. Membranes 2022, 12, 66. https://doi.org/10.3390/membranes12010066
León G, Gómez E, Miguel B, Hidalgo AM, Gómez M, Murcia MD, Guzmán MA. Feasibility of Adsorption Kinetic Models to Study Carrier-Mediated Transport of Heavy Metal Ions in Emulsion Liquid Membranes. Membranes. 2022; 12(1):66. https://doi.org/10.3390/membranes12010066
Chicago/Turabian StyleLeón, Gerardo, Elisa Gómez, Beatriz Miguel, Asunción María Hidalgo, María Gómez, María Dolores Murcia, and María Amelia Guzmán. 2022. "Feasibility of Adsorption Kinetic Models to Study Carrier-Mediated Transport of Heavy Metal Ions in Emulsion Liquid Membranes" Membranes 12, no. 1: 66. https://doi.org/10.3390/membranes12010066
APA StyleLeón, G., Gómez, E., Miguel, B., Hidalgo, A. M., Gómez, M., Murcia, M. D., & Guzmán, M. A. (2022). Feasibility of Adsorption Kinetic Models to Study Carrier-Mediated Transport of Heavy Metal Ions in Emulsion Liquid Membranes. Membranes, 12(1), 66. https://doi.org/10.3390/membranes12010066







