Economic Benefits of Waste Pickling Solution Valorization
Abstract
:1. Introduction
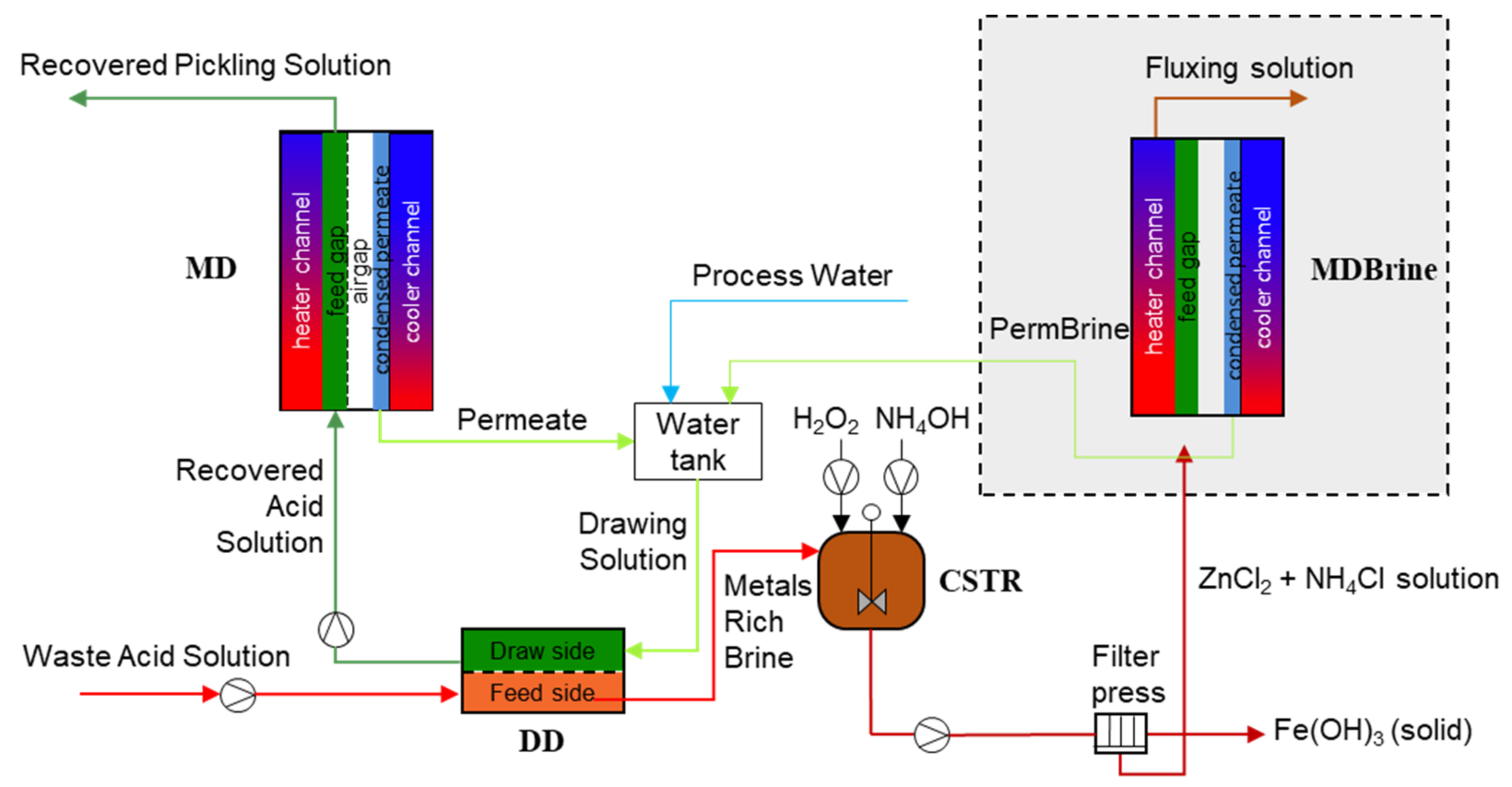
2. Process Modelling Platform
3. Engineering Economic Analysis
3.1. Capital Investment
3.2. Operating Costs
3.3. Profitability Analysis
4. Optimization Problem Formulation
4.1. Optimization and Sensitivity Analysis with Operating Variables
4.2. Optimization with Operating and Design Variables
Trade-Off Solution between Profitability and Environmental Issue
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Acronyms
| AEM | Anionic Exchange Membrane | |
| AIZ | Italian Galvanizing Association | |
| BAT | Best Available Techniques | |
| C | Cost | |
| CAPEX | Capital Expenditures | |
| CDCF | Cumulative Discounted Cash Flow | |
| CF | Cash Flow | |
| DCF | Discounted Cash Flow | |
| DCFROR | Discounted Cash Flow Rate of Return | |
| DPBP | Discounted Payback Period | |
| CSTR | Continuous Stirred Tank Reactor | |
| DCMD | Direct Contact Membrane Distillation | |
| DD | Diffusion Dialysis | |
| DPBP | Discounted Payback Period | |
| E | Expenses | |
| EGGA | European General Galvanizers Association | |
| FCI | Fixed Capital Investment | |
| IPPC | Integrated Pollution Prevention and Control | |
| MD | Membrane Distillation | |
| N | Equipment Cost Attribute | |
| NPV | Net Present Value | |
| OPEX | Operating Expenditures | |
| R | Revenues | |
| S | Selling | |
| Nomenclature | ||
| A | ] | area |
| c | molar concentration | |
| consumption/production | ||
| F | volumetric flow rate | |
| f | [-] | multiplicative factor |
| i | [%] | discount rate |
| molar flux | ||
| kinetic constant | ||
| L | length | |
| n | [y] | project duration |
| [-] | DD membranes number | |
| [-] | MD feed number | |
| W | molar mass | |
| diffusive permeability | ||
| RR | [%] | recovery ratio |
| W | width | |
| mass flow rate of the integrated process streams | ||
| [-] | amount of solution trapped in the humid cake | |
| [-] | hydration number | |
| [-] | difference of value | |
| ζ | [-] | extent of reaction |
| [bar] | osmotic pressure | |
| ρ | density | |
| υ | [-] | stoichiometric coefficient |
| [-] | conversion | |
| Subscripts and Superscripts | ||
| diffusion dialysis | ||
| draw solution | ||
| entrainment stream, inlet | ||
| entrainment stream, outlet | ||
| evaporating stream | ||
| galv.steel | galvanized steel | |
| i | pickling component i i.e., Fe2O3, Fe3O4, Fe, FeCl2, HCl, ZnCl2, H2O | |
| j | component j, i.e., HCl, FeCl2, ZnCl2, H2O | |
| k | generic year | |
| m | component m i.e., HCl, FeCl2, ZnCl2 | |
| membrane distillation | ||
| metals-rich brine | ||
| metal sludge | ||
| make-up | ||
| n | reactor components n, i.e., HCl, FeCl2, ZnCl2, H2O NH4OH, H2O2, NH4Cl | |
| p | pickling reactions | |
| perm | permeate | |
| PW | process water | |
| r | reactions | |
| recovered acid solution | ||
| recovered pickling solution | ||
| s | pickling streams | |
| tot | total | |
| u | membrane unit | |
| waste acid solution in the integrated process | ||
References
- Pernice, L.; (Associazione Italiana Zincatura (AIZ), Vienna, Austria). Personal Communication, 2017.
- Cusano, G.; Gonzalo, M.R.; Farrell, F.; Remus, R.; Roudier, S.; Sancho, L.D. Best Available Techniques (BAT) Reference Document for the Ferrous Metals Processing Industry; EU Publications: Luxembourg, 2017. [Google Scholar]
- Culcasi, A.; Gueccia, R.; Randazzo, S.; Cipollina, A.; Micale, G. Design of a novel membrane-integrated waste acid recovery process from pickling solution. J. Clean Prod. 2019, 236, 117623–117636. [Google Scholar] [CrossRef]
- Gueccia, R.; Aguirre, A.R.; Randazzo, S.; Cipollina, A.; Micale, G. Diffusion Dialysis for Separation of Hydrochloric Acid, Iron and Zinc Ions from Highly Concentrated Pickling Solutions. Membranes 2020, 10, 129. [Google Scholar] [CrossRef] [PubMed]
- Gueccia, R.; Randazzo, S.; Chillura Martino, D.; Cipollina, A.; Micale, G. Experimental investigation and modeling of diffusion dialysis for HCl recovery from waste pickling solution. J. Environ. Manag. 2019, 235, 202–212. [Google Scholar] [CrossRef] [PubMed]
- Gueccia, R.; Daniel, W.; Randazzo, S.; Cipollina, A.; Koschikowski, J.; Micale, G. An integrated approach for the HCl and metals recovery from waste pickling solutions: Pilot plant and design operations. Chem. Eng. Res. Des. 2021, 168, 383–396. [Google Scholar] [CrossRef]
- European Commission. Control Reference Document on Best Available Techniques for the Surface Treatment of Metals and Plástics. Available online: https://eippcb.jrc.ec.europa.eu/reference/surface-treatment-metals-and-plastics (accessed on 8 December 2021).
- Luo, J.; Wu, C.; Wu, Y.; Xu, T. Diffusion dialysis processes of inorganic acids and their salts: The permeability of different acidic anions. Sep. Purif. Technol. 2011, 78, 97–102. [Google Scholar] [CrossRef]
- Xu, J.; Lu, S.; Fu, D. Recovery of hydrochloric acid from the waste acid solution by diffusion dialysis. J. Hazard. Mater. 2009, 165, 832–837. [Google Scholar] [CrossRef] [PubMed]
- Cullivan, J.; Cullivan, B. Economic and chemical comparisons of hydrochloric acid recovery technologies for iron pickling operations. Wire J. Int. 2016, 49, 80–85. [Google Scholar]
- U.S. Department of Defense. Cost and Performance Report; U.S. Department of Defense: Washington, DC, USA, 1999.
- Schwantes, R.; Chavan, K.; Winter, D.; Felsmann, C.; Pfafferott, J. Techno-economic comparison of membrane distillation and MVC in a zero liquid discharge application. Desalination 2018, 428, 50–68. [Google Scholar] [CrossRef] [Green Version]
- Özdemir, T.; Öztin, C.; Kincal, N.S. Treatment of waste pickling liquors: Process synthesis and economic analysis. Chem. Eng. Commun. 2006, 193, 548–563. [Google Scholar] [CrossRef]
- Pfister, S.; Koehler, A.; Hellweg, S. Assessing the environmental impacts of freshwater consumption in LCA. Environ. Sci. Technol. 2009, 43, 4098–4104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhaskar, V.; Gupta, S.K.; Ray, A.K. Applications of multiobjective optimization in chemical engineering. Rev. Chem. Eng. 2000, 16, 1–54. [Google Scholar] [CrossRef]
- Randazzo, S.; La Corte, D.; Gueccia, R.; Cipollina, A.; Micale, G. Metals recovery from Waste Pickling Solutions by Reactive Precipitation. Chem. Eng. Trans. 2021, 86, 1045–1050. [Google Scholar]
- Laliberté, M.; Cooper, W.E. Model for calculating the density of aqueous electrolyte solutions. J. Chem. Eng. Data 2004, 49, 1141–1151. [Google Scholar] [CrossRef]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A.; Bhattacharyya, D. Profitability Analysis. In Analysis, Synthesis, and Design of Chemical Processes, 4th ed.; Pearson Education International: New York, NY, USA, 2013; pp. 261–310. [Google Scholar]
- Salaryexplorer. Available online: http://www.salaryexplorer.com/salary-survey.php?loc=105&loctype=1&job=22&jobtype=1 (accessed on 8 December 2021).
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A.; Bhattacharyya, D. Estimation of Capital Costs. In Analysis, Synthesis, and Design of Chemical Processes, 4th ed.; Pearson Education International: New York, NY, USA, 2013; pp. 157–196. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A.; Bhattacharyya, D. Estimation of Manufacturing Costs. In Analysis, Synthesis, and Design of Chemical Processes, 4th ed.; Pearson Education International: New York, NY, USA, 2013; pp. 197–226. [Google Scholar]
- Echemi. Available online: https://www.echemi.com/ (accessed on 8 December 2021).
- Campano, B.R.; (HIDADA Galvanizing Plants, Jeddah, Saudi Arabia). Personal Communication, 2012.
- Kleingarn, J.P. Pickling in hydrochloric acid. In Proceedings of the 15th International Galvanizing Conference, Rome, Italy, 5–10 June 1988. [Google Scholar]
- Depurstore. Available online: https://www.depurstore.it/mezzi-filtranti/3020-3561-gfh-idrossido-ferrico-granulare.html#/ (accessed on 8 December 2021).
- Zhao, B.; Zhang, Y.; Dou, X.; Yuan, H.; Yang, M. Granular ferric hydroxide adsorbent for phosphate removal: Demonstration preparation and field study. Water Sci. Technol. 2015, 72, 2179–2186. [Google Scholar] [CrossRef] [PubMed]
- Azichem. Available online: https://www.azichem.it/prodotti/protech-oxicrom/116 (accessed on 8 December 2021).
- Xiamen Ditai Chemicals Co. Ltd. Available online: https://it.made-in-china.com/co_ditaichem/ (accessed on 8 December 2021).
- MOLBASE. Available online: http://www.molbase.com/cas/1309-33-7.html (accessed on 8 December 2021).
- Stocks, C.; Wood, J.; Guy, S. Minimisation and recycling of spent acid wastes from galvanizing plants. Resour. Conserv. Recycl. 2005, 44, 153–166. [Google Scholar] [CrossRef]
- Chankong, V.; Haimes, Y.Y. Multiobjective Decision Making Theory and Methodology; Dover Publication Inc.: Mineola, NY, USA, 1983. [Google Scholar]
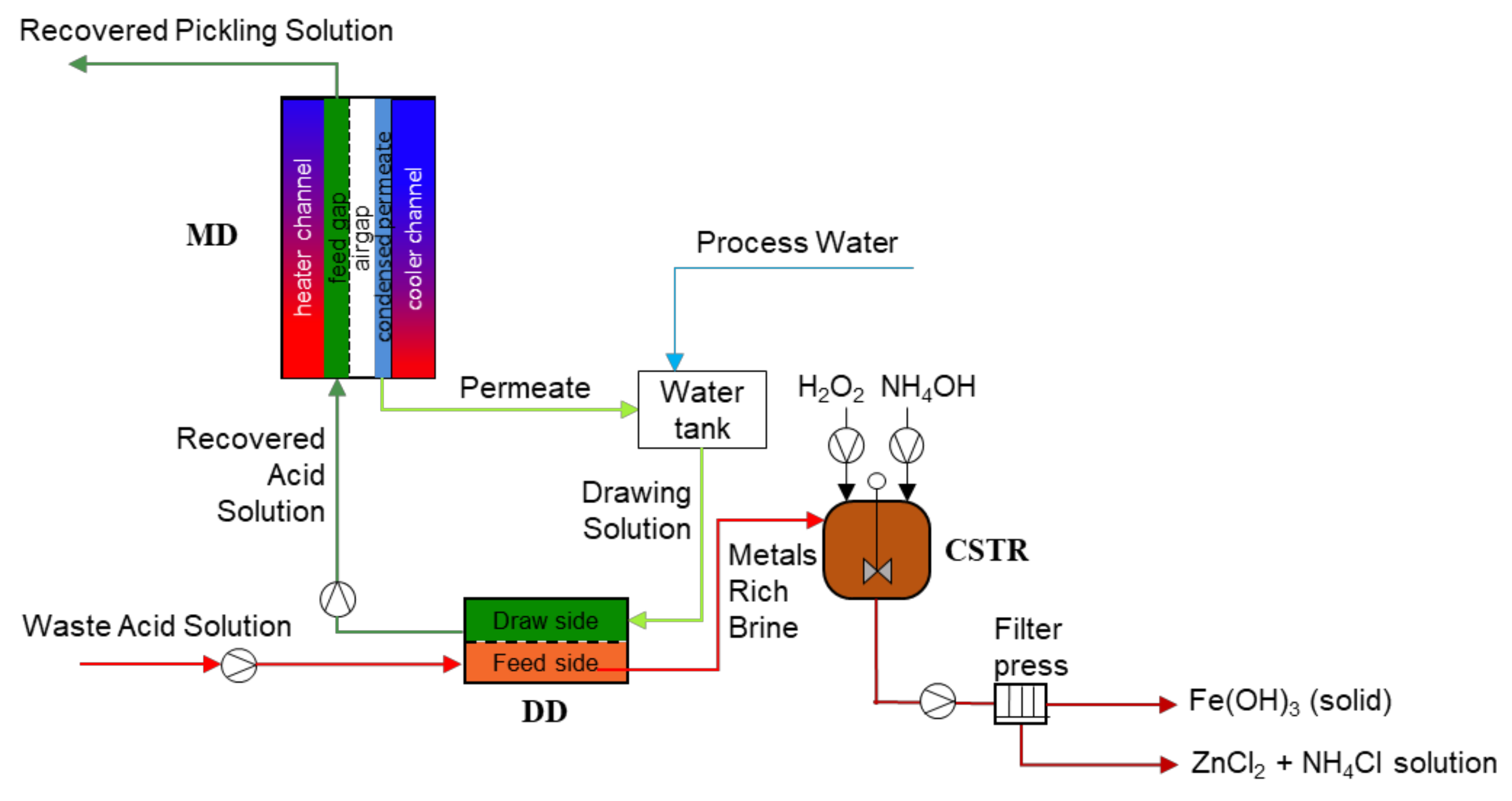

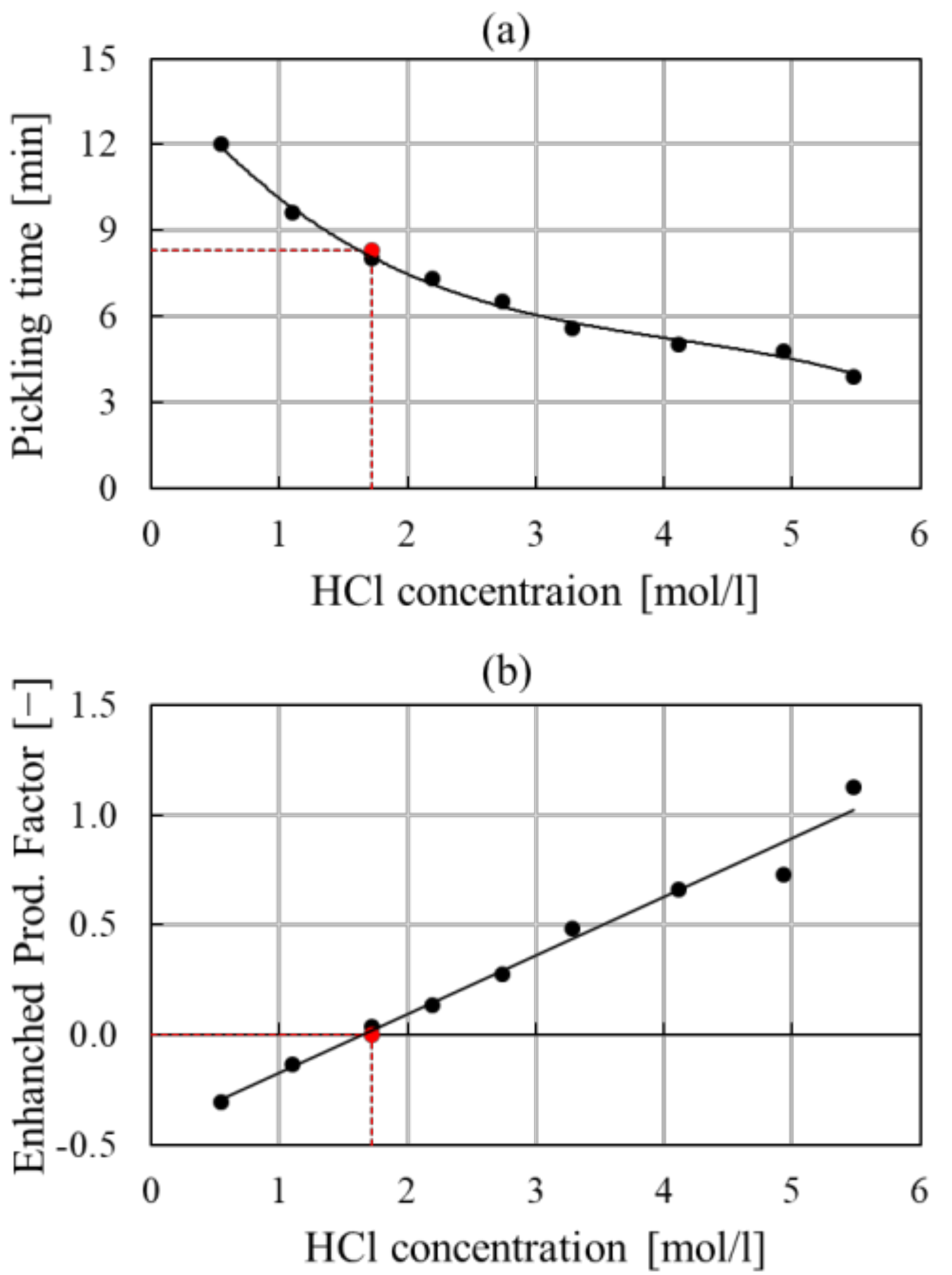

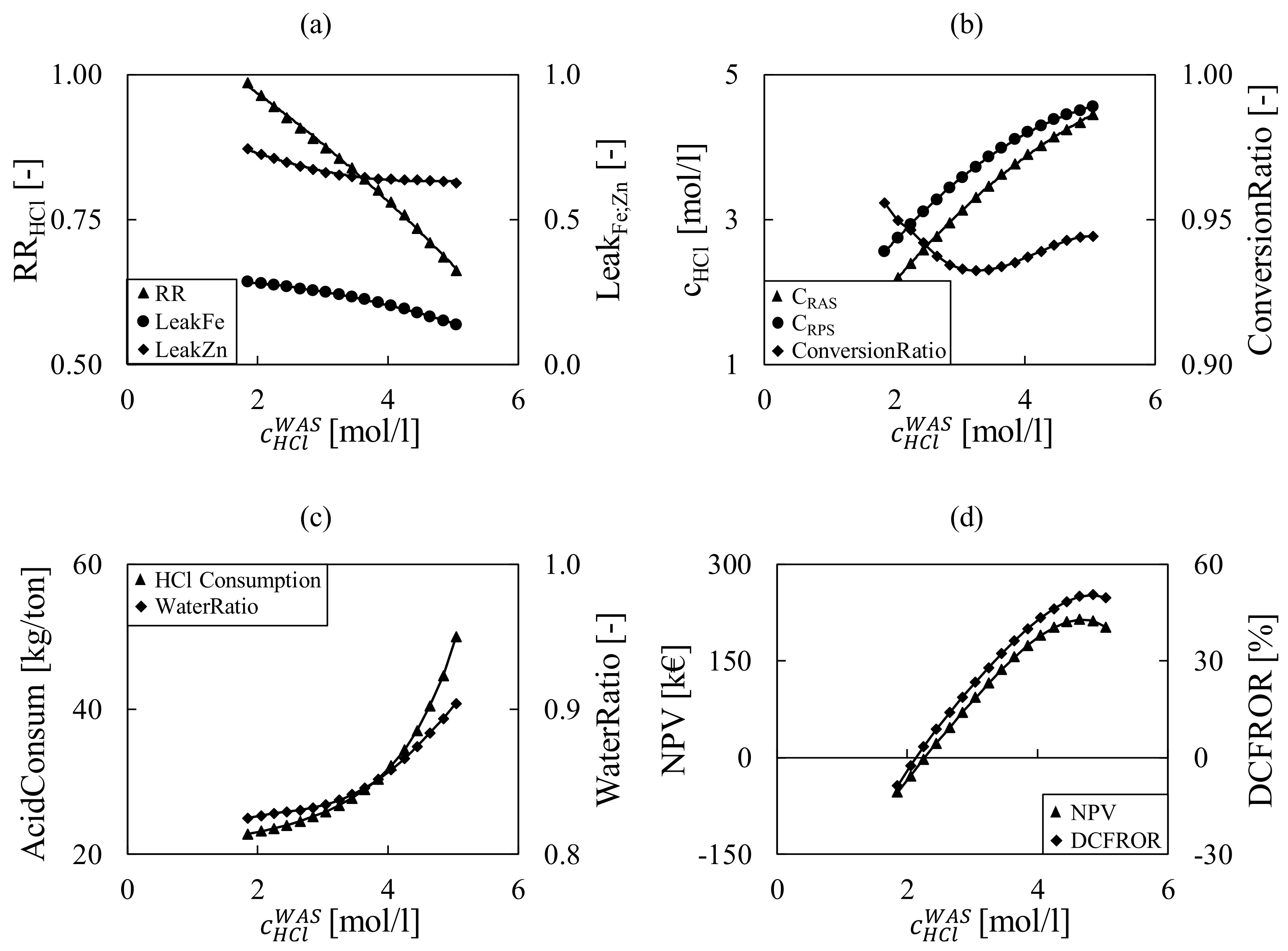
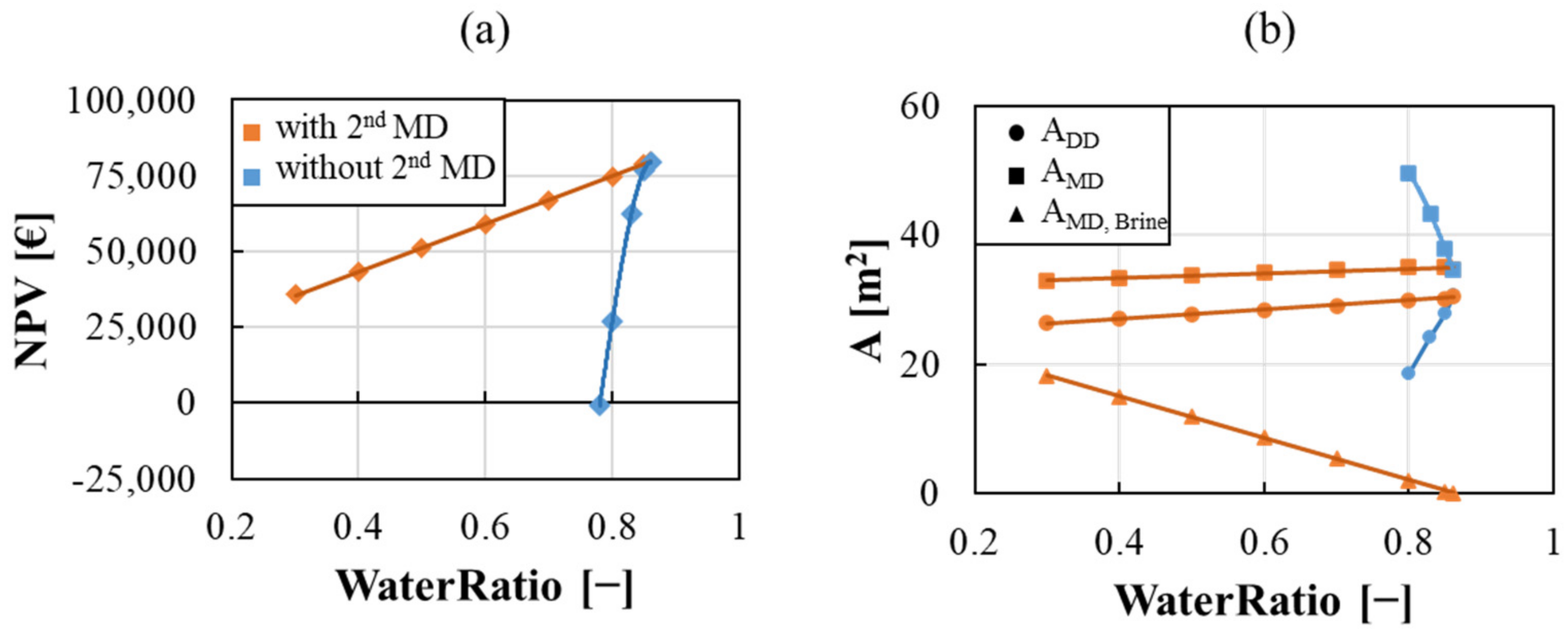
| Pickling | ||
| , Ɐ i ≠ HCl | (1) | |
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| p pickling reactions | Fe2O3 + Fe + 6HCl = 3FeCl2 + 3H2O Fe3O4 + Fe + 8HCl = 4FeCl2 + 4H2O | |
| i pickling components | Fe2O3, Fe3O4, Fe, FeCl2, HCl, ZnCl2, H2O | |
| j components | HCl, FeCl2, ZnCl2, H2O | |
| Diffusion Dialysis | ||
| Ɐ j ≠ H2O m = HCl, FeCl2, ZnCl2 | (7) | |
| (8) | ||
| Ɐ j ≠ H2O | (9) | |
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| Membrane Distillation | ||
| (15) | ||
| (16) | ||
| (17) | ||
| (18) | ||
| (19) | ||
| (20) | ||
| Reactive Crystallizer | ||
| (21) | ||
| (22) | ||
| (23) | ||
| (24) | ||
| (25) | ||
| (26) | ||
| (27) | ||
| (28) | ||
| (29) | ||
| (30) | ||
| r reactions | : HCl + NH4OH = NH4Cl + H2O : FeCl2 + 1/2 H2O2 + 2NH4OH = Fe(OH)3(s) + 2NH4Cl | |
| n reactor components | n = j + NH4OH, H2O2, NH4Cl | |
| base: | NH4OH, H2O | |
| oxidant: | H2O2, H2O | |
| Density | ||
| (31) | ||
| Integrated Process | ||
| Connectivity equations | ||
| (32) | ||
| (33) | ||
| Treatment Capacity (Feed Flow Rate) | ||||
|---|---|---|---|---|
| Cost Items [€] | Pilot Size 0.02 m3 h−1 | Future Size I 0.1 m3 h−1 | Future Up-Scaled Size II 1 m3 h−1 | Future Up-Scaled Size III 10 m3 h−1 |
| Mechanical | 6300 | 6300 | 7600 | 16,000 |
| Hydraulic | 8600 | 16,500 | 33,000 | 82,500 |
| Actuators | 4200 | 5400 | 6500 | 27,000 |
| Sensors | 13,900 | 12,500 | 12,500 | 12,500 |
| Electrical | 12,600 | 16,000 | 16,000 | 16,000 |
| Total Material Costs (excl. Modules) | 45,600 | 56,700 | 75,600 | 154,000 |
| MD Module | 10,000 | 13,500 | 36,000 | 84,000 |
| DD Module | 8000 | 9800 | 58,400 | 418,000 |
| Membrane Module cost | 18,000 | 23,300 | 94,400 | 502,000 |
| Total Material Costs (incl. Modules) | 63,600 | 80,000 | 170,000 | 656,000 |
| Freight, insurance, taxes | 2000 | 2000 | 4000 | 6000 |
| Logistics, Ordering, Desk | 5200 (1.4 × PM) 1 | 5200 (1.4 × PM) 1 | 6200 (1.7 × PM) 1 | 12,600 (3.4 × PM) 1 |
| Documentation | 2600 (0.7 × PM) 1 | 2600 (0.7 × PM) 1 | 3000 (0.8 × PM) 1 | 6200 (1.7 × PM) 1 |
| Assembly | 24,000 (8.3 × PM) 2 | 24,000 (8.3 × PM) 2 | 48,000 (8.3 × PM) × 2 2 | 240,000 (8.3 × PM) × 10 2 |
| Commissioning and Training | 8100 (1.4 × PM) 3 | 8100 (1.4 × PM) 3 | 9900 (1.7 × PM) 3 | 19,600 (3.4 × PM) 3 |
| Development | 8100 (1.4 × PM) 3 | 8100 (1.4 × PM) 3 | 9900 (1.7 × PM) 3 | 19,600 (3.4 × PM) 3 |
| Subtotal | 113,600 | 128,000 | 251,000 | 960,000 |
| Technology Provider Fee (=25% of subtotal) | 28,400 | 32,000 | 62,700 | 240,000 |
| FCI (total) | 142,000 | 160,000 | 313,700 | 1,200,000 |
| 7.9 | 6.9 | 3.3 | 2.4 | |
| Position | Salary |
|---|---|
| Engineer | EUR 44,000/year |
| Senior Engineer | EUR 70,000/year |
| Assembler | EUR 30,000/year |
| OPEX Items | Cost Position | Unitary Cost 1 | Selected Values |
|---|---|---|---|
| Raw Material (inputs for CRM calc.) | HCl Make-Up | 30–125 €/ton | 125 €/ton |
| Alkaline reactant | 0.1–0.55 €/L | 0.55 €/L | |
| Oxidizing reactant | 0.135–0.38 €/kg | 0.38 €/kg | |
| Waste treatment (inputs for CWT calc.) | - | - | - |
| Utilities (inputs for CUT calc.) | Process Water | - | 0.95 €/m3 |
| Electricity | - | 0.2 €/kWh | |
| Operating Labor COL | - | 11,000 €/year |
| Revenues Inputs | Unitary Cost | Selected Values |
|---|---|---|
| Iron (III) hydroxide | EUR 0.6–14/kg 1 | EUR 2/kg |
| Fluxing solution | EUR 0.06/kg | EUR 0.06/kg |
| Waste acid disposal saving | EUR 40–160/ton 2 | EUR 145/ton |
| Added value of the Enhanced Prod. | EUR 0.045/kg | EUR 0.045/kg |
| Profitability Analysis Inputs | Unit | |
|---|---|---|
| Feed flow rate (FWAS) | 130 | L/h |
| Process Steel | 2030 | kg/h |
| DD total area (ADD) | 25 | m2 |
| MD total area (AMD) | 43.5 | m2 |
| FCI | 160 | EUR k |
| CAPEX | 36 | EUR k/year |
| OPEX | 125 | EUR k/year |
| R | 180 | EUR k/year |
| Project duration (n) | 5 | y |
| Time for plant construction | 0.5 | y |
| Economics | |
|---|---|
| (44) | |
| (45) | |
| time to recover the FCI after start-up | (46) |
| Optimization Problem | Results | |||
|---|---|---|---|---|
| Fixed reference condition (given scenario) | ) | 2030 kg/h | ||
| Control variables | ) or | 134 L/h | ||
| 2.7 mol/L | ||||
| Objective function (to be maximised) | NPV | EUR 63,777 | ||
| Constraints | Equality | Steady state operation | ||
| Acid consumption | 25 kg/ton * | 25 kg/ton | ||
| Inequality | Channel velocity | 0.1 cm/s < vDD & vMD < 3 cm/s | vDD 0.88 cm/s vMD 0.17 cm/s | |
| FlowRatio | < 1.5 | 1.09 | ||
| Optimization Problem | Results | ||||
|---|---|---|---|---|---|
| Fixed reference condition (given scenario) | Plant throughput () | 2030 kg/h | 10,000 kg/h | ||
| Control variables | Feed flow () | 142 L/h | 842 L/h | ||
| Composition ( | 2.86 mol/L | 3.22 mol/L | |||
| ) | 30.6 m2 | 231 m2 | |||
| ) | 34.7 m2 | 217 m2 | |||
| Objective function (to be maximised) | NPV | EUR 79,631 | EUR 913,000 | ||
| Constraints | Equality | Steady state operation | |||
| Acid consumption | 25 kg/ton * | 25 kg/ton | 25 kg/ton | ||
| Inequality | Channel velocity | 0.1cm/s < vDD | vDD 0.76 cm/s | vDD 0.6 cm/s | |
| vMD < 3cm/s | vMD 0.22 cm/s | vMD 0.22 cm/s | |||
| FlowRatio | < 1.5 | 1.07 | 1.05 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gueccia, R.; Bogle, D.; Randazzo, S.; Tamburini, A.; Cipollina, A.; Winter, D.; Koschikowski, J.; Micale, G. Economic Benefits of Waste Pickling Solution Valorization. Membranes 2022, 12, 114. https://doi.org/10.3390/membranes12020114
Gueccia R, Bogle D, Randazzo S, Tamburini A, Cipollina A, Winter D, Koschikowski J, Micale G. Economic Benefits of Waste Pickling Solution Valorization. Membranes. 2022; 12(2):114. https://doi.org/10.3390/membranes12020114
Chicago/Turabian StyleGueccia, Rosa, David Bogle, Serena Randazzo, Alessandro Tamburini, Andrea Cipollina, Daniel Winter, Joachim Koschikowski, and Giorgio Micale. 2022. "Economic Benefits of Waste Pickling Solution Valorization" Membranes 12, no. 2: 114. https://doi.org/10.3390/membranes12020114
APA StyleGueccia, R., Bogle, D., Randazzo, S., Tamburini, A., Cipollina, A., Winter, D., Koschikowski, J., & Micale, G. (2022). Economic Benefits of Waste Pickling Solution Valorization. Membranes, 12(2), 114. https://doi.org/10.3390/membranes12020114










