Drying Regimes on Regenerated Cellulose Films Characteristics and Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Fabrication of Regenerated Cellulose Membrane
2.3. Regenerated Cellulose Membrane Drying Procedures
2.4. Mathematical Modeling of Drying Curve
2.5. Determination of Effective Diffusion Coefficients
2.6. Determination of Film Thickness and Density
2.7. Swelling and Pore Volume
2.8. Tensile Properties
2.9. Statistical Analysis
3. Results
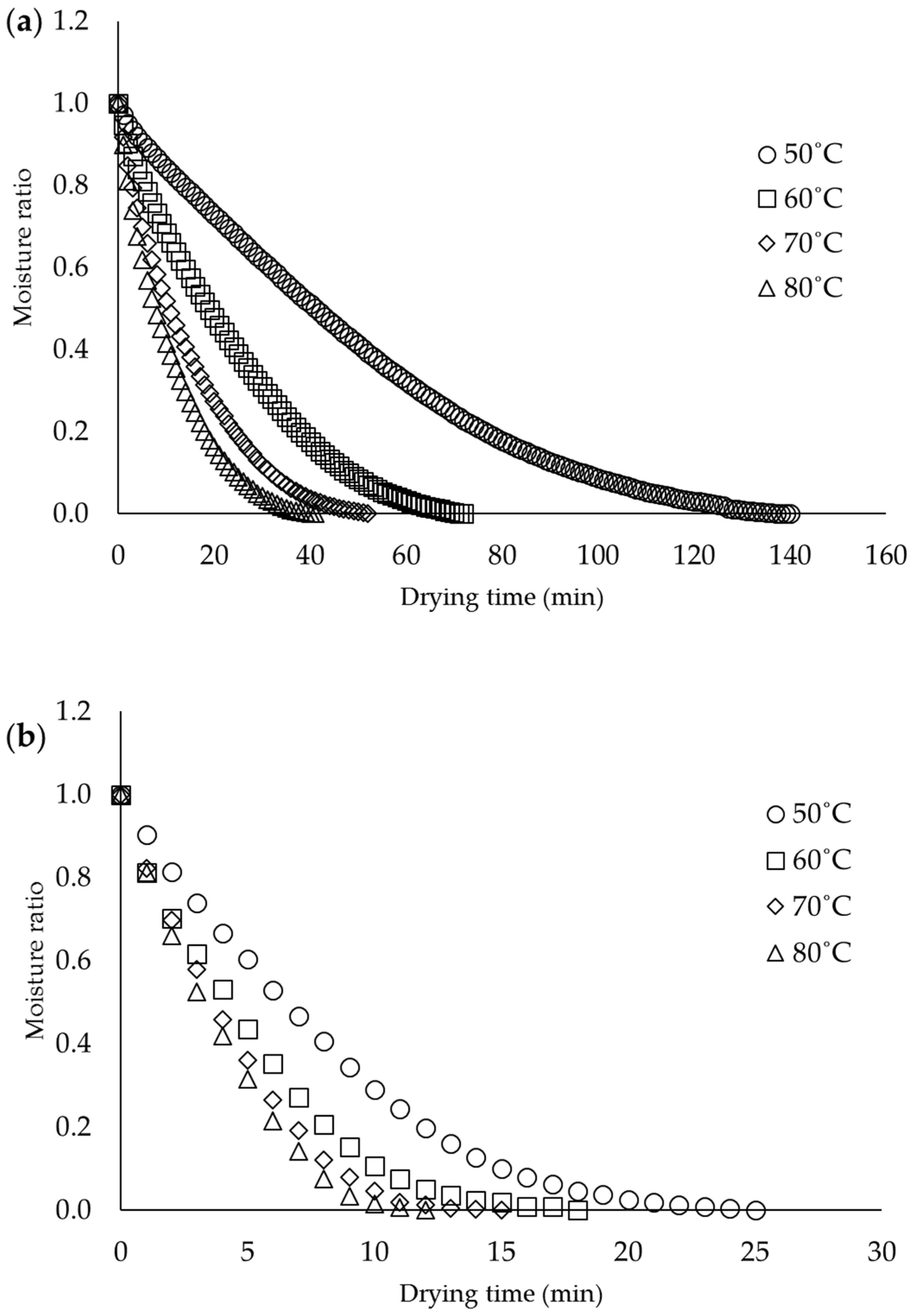
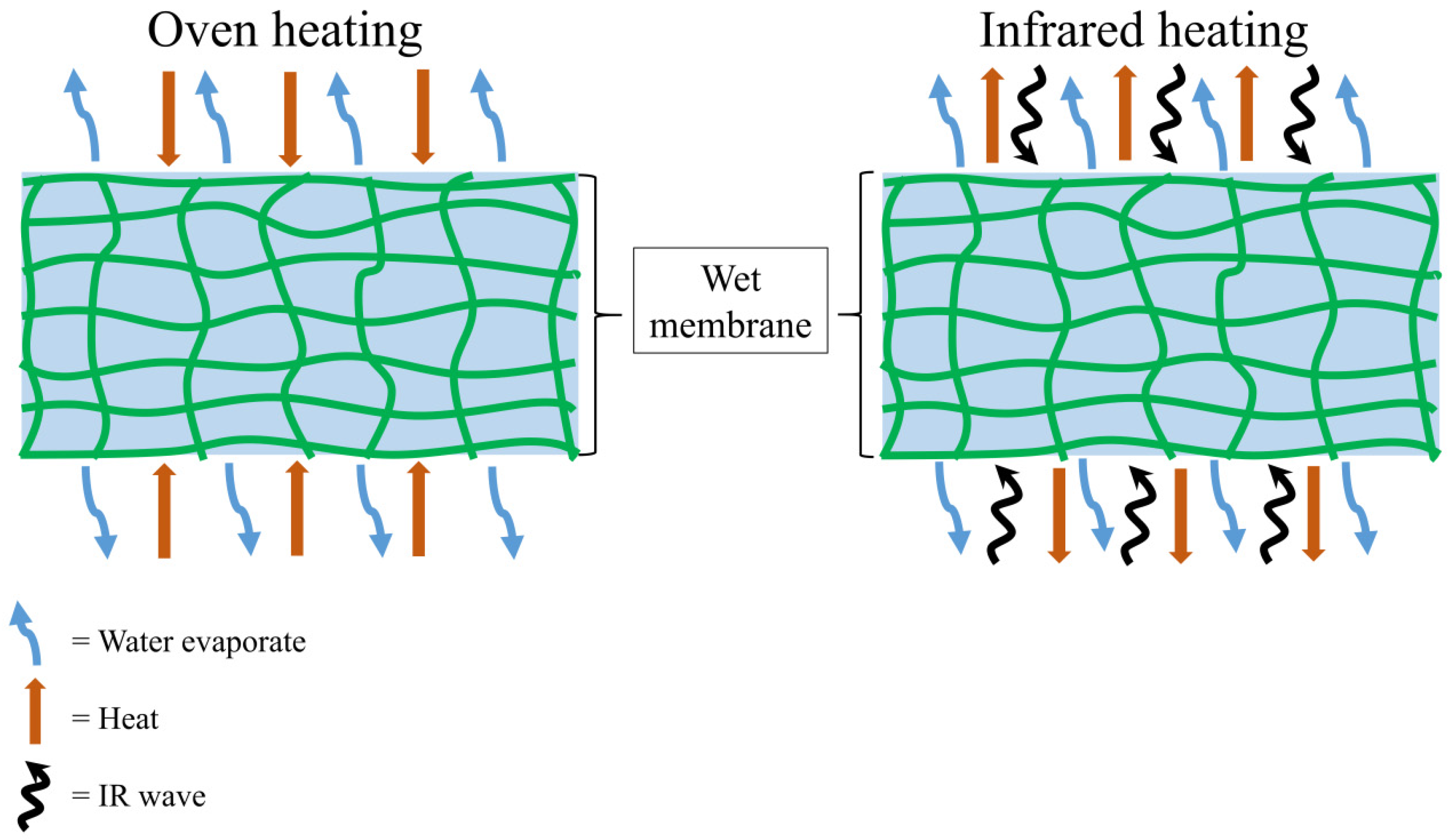
3.1. Drying Characteristic of Cellulose Membrane
3.2. Evaluation of the Models
- a = 0.3633ln (T) − 1.6256
- b = −0.438ln (T) + 2.9219
- k = 0.0023T − 0.101
- a = 0.0002T − 0.008
- b = −0.19ln (T) + 0.6522
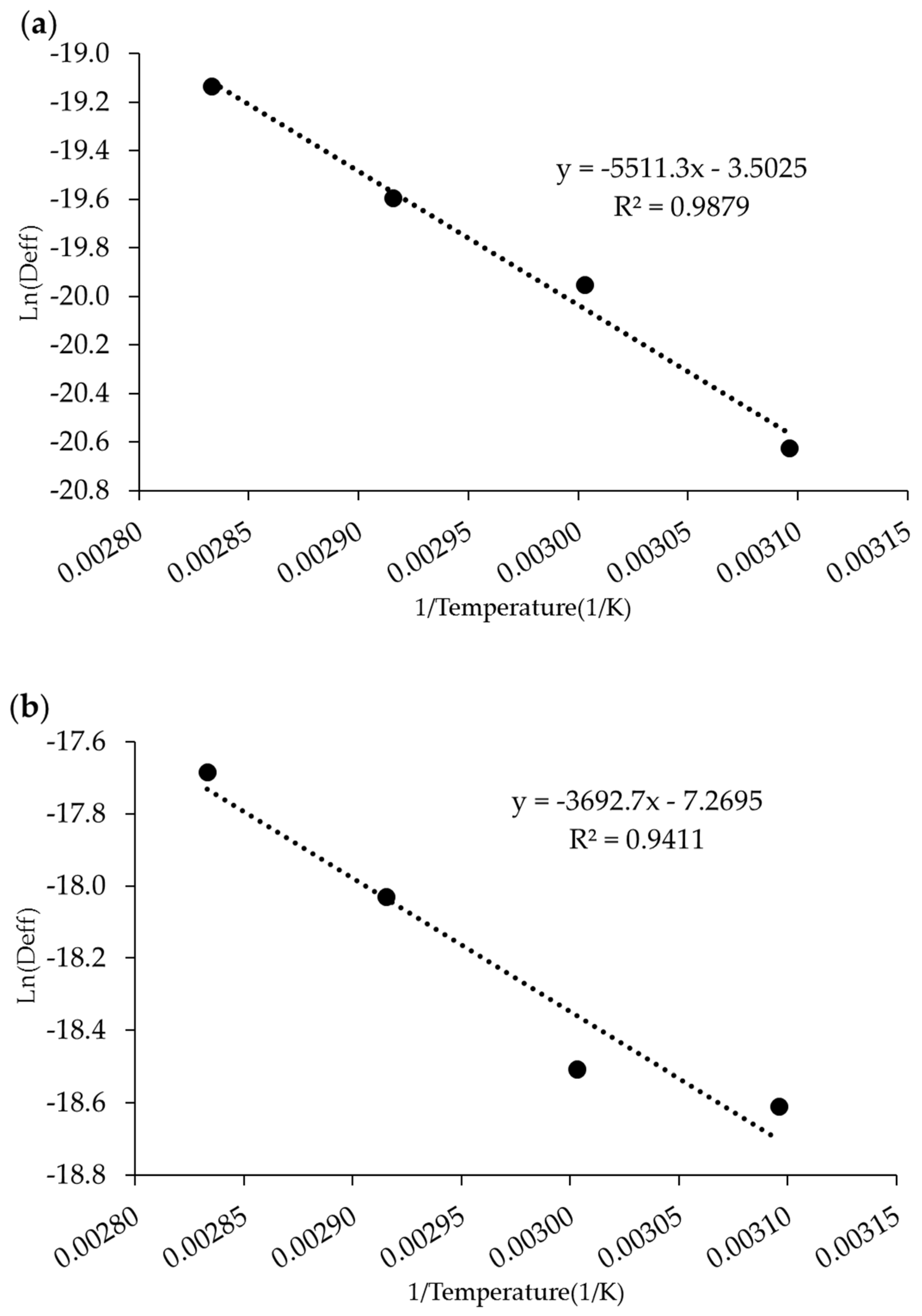
3.3. Effective Diffusion and Activation Energy
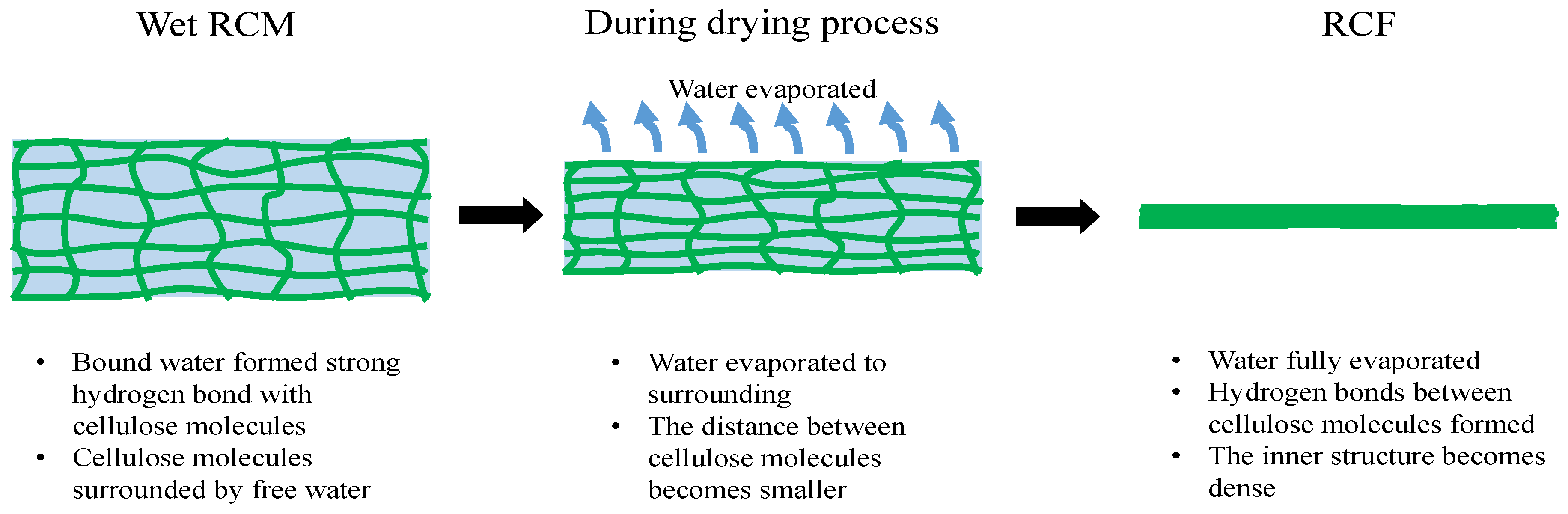
3.4. Characterization of Dried RCF
3.5. Tensile Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cervin, N.T.; Andersson, L.; Ng, J.B.S.; Olin, P.; Bergström, L.; Wågberg, L. Lightweight and strong cellulose materials made from aqueous foams stabilized by nanofibrillated cellulose. Biomacromolecules 2013, 14, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Alhamid, J.O.; Mo, C.; Zhang, X.; Wang, P.; Whiting, M.D.; Zhang, Q. Cellulose nanocrystals reduce cold damage to reproductive buds in fruit crops. Biosyst. Eng. 2018, 172, 124–133. [Google Scholar] [CrossRef]
- Salleh, K.M.; Zakaria, S.; Mostapha, M.; Amra, U.A.; Nadhari, W.N.A.W.; Ibrahim, N.A. Keterlarutan selulosa, pelarut dan produk selulosa yang dijana semula: Suatu ulasan. Sains Malays. 2021, 50, 3107–3126. [Google Scholar] [CrossRef]
- Salleh, K.M.; Armir, N.A.Z.; Mazlan, N.S.N.; Wang, C.; Zakaria, S. Cellulose and its derivatives in textiles: Primitive application to current trend. In Fundamentals of Natural Fibres and Textiles; Mondal, M.I.H., Ed.; Woodhead Publishing: Sawston, UK, 2021; pp. 33–63. ISBN 0128214848. [Google Scholar]
- Salleh, K.M.; Zakaria, S.; Sajab, M.S.; Gan, S.; Kaco, H. Superabsorbent hydrogel from oil palm empty fruit bunch cellulose and sodium carboxymethylcellulose. Int. J. Biol. Macromol. 2019, 131, 50–59. [Google Scholar] [CrossRef]
- Salleh, K.M.; Armir, N.A.Z.; Mazlan, N.S.N.; Mostapha, M.; Zakaria, S. Hydrogel- and aerogel-based composites: Biodegradable hydrogel and aerogel polymer blend-based composites. In Biodegradable Polymers, Blends and Composites; Rangappa, S.M., Parameswaranpillai, J., Siengchin, S., Ramesh, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 355–388. ISBN 9780128237915. [Google Scholar]
- Salleh, K.M.; Zakaria, S.; Sajab, M.S.; Gan, S.; Chia, C.H.; Jaafar, S.N.; Amran, U.A. Chemically crosslinked hydrogel and its driving force towards superabsorbent behaviour. Int. J. Biol. Macromol. 2018, 118, 1422–1430. [Google Scholar] [CrossRef]
- Mazlan, N.S.N.; Zakaria, S.; Gan, S.; Hua, C.C.; Baharin, K.W. Comparison of regenerated cellulose membrane coagulated in sulphate based coagulant. Cerne 2019, 25, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Li, C.; Huang, J.; Wang, W.; Liu, H.; Xu, Q. Preparation and characterization of natural cellulose packaging film. In Advanced Graphic Communications, Packaging Technology and Materials; Ouyang, Y., Xu, M., Yang, L., Ouyang, Y., Eds.; Springer: Singapore, 2016; pp. 827–835. ISBN 978-981-10-0072-0. [Google Scholar]
- Liu, X.; Xiao, W.; Ma, X.; Huang, L.; Ni, Y.; Chen, L.; Ouyang, X.; Li, J. Conductive regenerated cellulose film and its electronic devices—A review. Carbohydr. Polym. 2020, 250, 116969. [Google Scholar] [CrossRef]
- Baez, C.; Considine, J.; Rowlands, R. Influence of drying restraint on physical and mechanical properties of nanofibrillated cellulose films. Cellulose 2014, 21, 347–356. [Google Scholar] [CrossRef]
- Beaumont, M.; König, J.; Opietnik, M.; Potthast, A.; Rosenau, T. Drying of a cellulose II gel: Effect of physical modification and redispersibility in water. Cellulose 2017, 24, 1199–1209. [Google Scholar] [CrossRef] [Green Version]
- Martelli, S.M.; Motta, C.; Caon, T.; Alberton, J.; Bellettini, I.C.; Do Prado, A.C.P.; Barreto, P.L.M.; Soldi, V. Edible carboxymethyl cellulose films containing natural antioxidant and surfactants: α-tocopherol stability, in vitro release and film properties. LWT 2017, 77, 21–29. [Google Scholar] [CrossRef]
- Kaco, H.; Zakaria, S.; Chia, C.H.; Sajab, M.S.; Saidi, A.S.M. Characterization of aldehyde crosslinked kenaf regenerated cellulose film. BioResources 2015, 10, 6705–6719. [Google Scholar] [CrossRef]
- Shahari, N.A.; Hussein, S.M.; Nursabrina, M.; Hibberd, S. Mathematical modelling of cucumber (Cucumis sativus) drying. In AIP Conference Proceedings; American Institute of Physics: Penang, Malaysia, 2014; Volume 1605, pp. 307–312. [Google Scholar]
- Sorour, H.; El-Mesery, H. Effect of microwave and infrared radiation on drying of onion slices. Int. J. Res. Applied, Nat. Soc. Sci. 2014, 2, 119–130. [Google Scholar]
- Stegou-Sagia, A.; Fragkou, D.V. Influence of drying conditions and mathematical models on the drying curves and the moisture diffusivity of mushrooms. J. Therm. Eng. 2015, 1, 236–244. [Google Scholar] [CrossRef]
- Shen, F.; Peng, L.; Zhang, Y.; Wu, J.; Zhang, X.; Yang, G.; Peng, H.; Qi, H.; Deng, S. Thin-layer drying kinetics and quality changes of sweet sorghum stalk for ethanol production as affected by drying temperature. Ind. Crops Prod. 2011, 34, 1588–1594. [Google Scholar] [CrossRef]
- Torrez Irigoyen, R.M.; Giner, S.A. Modeling thin layer drying-roasting kinetics of soaked quinoa. Coupled mass and energy transfer. Biosyst. Eng. 2017, 157, 99–108. [Google Scholar] [CrossRef]
- Ekka, J.P.; Palanisamy, M. Determination of heat transfer coefficients and drying kinetics of red chilli dried in a forced convection mixed mode solar dryer. Therm. Sci. Eng. Prog. 2020, 19, 100607. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, F.; Leiva-Portilla, D.; Rodríguez-Núñez, K.; Pacheco, P.; Briones-Labarca, V. Mathematical modeling and quality parameters of Salicornia fruticosa dried by convective drying. J. Food Sci. Technol. 2021, 58, 474–483. [Google Scholar] [CrossRef]
- Lewis, W.K. The rate of drying of solid materials. J. Ind. Eng. Chem. 1921, 13, 427–432. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin Layers. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 1949. [Google Scholar]
- Henderson, S.M.; Pabis, S. Grain drying theory (I) temperature effect on drying coefficients. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Degirmencioglu, A.; Kadir Yagcioglu, A.; Cagatay, F. Drying characteristics of laurel leaves under different drying conditions. In Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, Adana, Turkey, 26–27 May 1999. [Google Scholar]
- Wang, C.Y.; Singh, R.P. Single layer drying equation for rough rice. ASAE Pap. 1978, No. 78-3001, 33. [Google Scholar]
- Bualuang, O.; Tirawanichakul, Y.; Tirawanichakul, S. Comparative study between hot air and infrared drying of parboiled rice: Kinetics and qualities aspects. J. Food Process. Preserv. 2013, 37, 1119–1132. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979; ISBN 0198534116. [Google Scholar]
- Salleh, K.M.; Zakaria, S.; Gan, S.; Baharin, K.W.; Ibrahim, N.A.; Zamzamin, R. Interconnected macropores cryogel with nano-thin crosslinked network regenerated cellulose. Int. J. Biol. Macromol. 2020, 148, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Sadin, R.; Chegini, G.-R.; Sadin, H. The effect of temperature and slice thickness on drying kinetics tomato in the infrared dryer. Heat Mass Transf. 2014, 50, 501–507. [Google Scholar] [CrossRef]
- Sridhar, D.; Madhu, G.M. Drying kinetics and mathematical modeling of casuarina equisetifolia wood chips at various temperatures. Period. Polytech. Chem. Eng. 2015, 59, 288–295. [Google Scholar] [CrossRef] [Green Version]
- Wan Nadhari, W.N.A.; Hashim, R.; Danish, M.; Sulaiman, O.; Hiziroglu, S. A model of drying kinetics of Acacia mangium wood at different temperatures. Dry. Technol. 2014, 32, 361–370. [Google Scholar] [CrossRef]
- Grdzelishvili, G.; Hoffman, P.; Penicka, M. Infrared drying of food products. Int. Congr. Chem. Process Eng. 2012, 20, 1–12. [Google Scholar]
- Pawar, S.B.; Pratape, V.M. Fundamentals of infrared heating and its application in drying of food materials: A review. J. Food Process. Eng. 2017, 40, e12308. [Google Scholar] [CrossRef]
- Nowak, D.; Lewicki, P.P. Infrared drying of apple slices. Innov. Food Sci. Emerg. Technol. 2004, 5, 353–360. [Google Scholar] [CrossRef]
- Corrêa, P.C.; Botelho, F.M.; Oliveira, G.H.H.; Goneli, A.L.D.; Resende, O.; de Campos, S.C. Mathematical modeling of the drying process of corn ears. Acta Sci. Agron. 2011, 33, 575–581. [Google Scholar] [CrossRef] [Green Version]
- Mirzaee, E.; Rafiee, S.; Keyhani, A. Evaluation and selection of thin-layer models for drying kinetics of apricot (cv. NASIRY). Agric. Eng. Int. CIGR J. 2010, 12, 111–116. [Google Scholar]
- Sacilik, K. Effect of drying methods on thin-layer drying characteristics of hull-less seed pumpkin (Cucurbita pepo L.). J. Food Eng. 2007, 79, 23–30. [Google Scholar] [CrossRef]
- Coradi, P.C.; De Castro Melo, E.; Da Rocha, R.P. Mathematical modeling of the drying kinetics of the leaves of lemon grass (Cymbopogon citratus Stapf) and its effects on quality. IDESIA 2014, 32, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Siah, W.M.; Aminah, A.; Ishak, A. Edible films from seaweed (Kappaphycus alvarezii). Int. Food Res. J. 2015, 22, 2230. [Google Scholar]

| No. | Model | Equation | References |
|---|---|---|---|
| 1 | Newton | MR = exp (−kt) | Lewis [22] |
| 2 | Page | MR = exp (−ktn) | Page [23] |
| 3 | Henderson–Pabis | MR = a.exp (−kt) | Henderson and Pabis [24] |
| 4 | Logarithmic | MR = a + bexp (−kt) | Degirmencioglu et al. [25] |
| 5 | Wang–Singh | MR = at2 + bt + 1 | Wang and Singh [26] |
| Drying Type | Model | Temperature (°C) | R2 | X2 | RMSE |
|---|---|---|---|---|---|
| Oven drying | Newton | 50 | 0.973764 | 0.320098 | 0.047647 |
| 60 | 0.984203 | 0.093485 | 0.035786 | ||
| 70 | 0.994375 | 0.022085 | 0.020413 | ||
| 80 | 0.995616 | 0.013764 | 0.018103 | ||
| Page | 50 | 0.994375 | 0.068628 | 0.022062 | |
| 60 | 0.992743 | 0.042943 | 0.024254 | ||
| 70 | 0.995135 | 0.019101 | 0.018984 | ||
| 80 | 0.995990 | 0.012590 | 0.017313 | ||
| Henderson–Pabis | 50 | 0.979333 | 0.252150 | 0.042288 | |
| 60 | 0.985545 | 0.085543 | 0.034232 | ||
| 70 | 0.994379 | 0.022070 | 0.020406 | ||
| 80 | 0.995616 | 0.013764 | 0.018103 | ||
| Logarithmic | 50 | 0.997589 | 0.029413 | 0.014443 | |
| 60 | 0.998712 | 0.007624 | 0.010220 | ||
| 70 | 0.999195 | 0.003161 | 0.007723 | ||
| 80 | 0.998957 | 0.003276 | 0.008832 | ||
| Wang–Singh | 50 | 0.999366 | 0.007740 | 0.007409 | |
| 60 | 0.995262 | 0.028038 | 0.019598 | ||
| 70 | 0.977392 | 0.088762 | 0.040924 | ||
| 80 | 0.971319 | 0.090051 | 0.046304 | ||
| IR drying | Newton | 50 | 0.978146 | 0.053920 | 0.045540 |
| 60 | 0.974252 | 0.048225 | 0.050380 | ||
| 70 | 0.979273 | 0.033343 | 0.045650 | ||
| 80 | 0.977783 | 0.029974 | 0.048018 | ||
| Page | 50 | 0.996858 | 0.007751 | 0.017266 | |
| 60 | 0.995240 | 0.008915 | 0.021661 | ||
| 70 | 0.995642 | 0.007011 | 0.020933 | ||
| 80 | 0.994323 | 0.007659 | 0.024273 | ||
| Henderson–Pabis | 50 | 0.963677 | 0.041575 | 0.039988 | |
| 60 | 0.978961 | 0.039406 | 0.045541 | ||
| 70 | 0.982395 | 0.028322 | 0.042073 | ||
| 80 | 0.980801 | 0.025902 | 0.044637 | ||
| Logarithmic | 50 | 0.995670 | 0.010684 | 0.020271 | |
| 60 | 0.996523 | 0.006503 | 0.018501 | ||
| 70 | 0.994941 | 0.008139 | 0.022554 | ||
| 80 | 0.996735 | 0.004405 | 0.018408 | ||
| Wang–Singh | 50 | 0.999068 | 0.002299 | 0.009404 | |
| 60 | 0.999438 | 0.001053 | 0.007446 | ||
| 70 | 0.998610 | 0.002236 | 0.011821 | ||
| 80 | 0.999379 | 0.000838 | 0.008031 |
| Sample | Temperature (°C) | Deff (m2/s) | Ea (kJ/mol) |
|---|---|---|---|
| Oven drying | 50 | 1.10567 × 10−9 | 45.82 |
| 60 | 2.16122 × 10−9 | ||
| 70 | 3.09148 × 10−9 | ||
| 80 | 4.89876 × 10−9 | ||
| IR drying | 50 | 8.28781 × 10−9 | 30.70 |
| 60 | 9.18049 × 10−9 | ||
| 70 | 1.47903 × 10−8 | ||
| 80 | 2.09231 × 10−8 |
| Sample | Temperature (°C) | Thickness (mm) | Density (g/cm3) | Vp (cm3/g1) | Swelling Percentage (%) |
|---|---|---|---|---|---|
| Oven drying | 50 | 0.020 a | 1.277 a | 1.106 a | 110.418 a |
| 60 | 0.020 a | 1.237 a | 1.163 a | 116.164 a | |
| 70 | 0.020 a | 1.291 a | 1.106 a | 110.423 a | |
| 80 | 0.020 a | 1.303 a | 1.162 a | 115.966 a | |
| IR drying | 50 | 0.020 a | 1.243 a | 1.157 a | 115.458 a |
| 60 | 0.019 a | 1.300 a | 1.090 a | 108.763 a | |
| 70 | 0.018 a | 1.245 a | 1.125 a | 112.284 a | |
| 80 | 0.020 a | 1.283 a | 1.153 a | 115.143 a | |
| Air drying | Room temperature | 0.018 a | 1.267 a | 1.140 a | 113.805 a |
| Sample | Temperature (°C) | Tensile Strength (MPa) | Elongation (%) |
|---|---|---|---|
| Air drying | Room temperature | 59.402 a | 5.561 a |
| Oven drying | 50 | 63.107 a | 5.196 a |
| 60 | 66.009 a | 5.409 a | |
| 70 | 50.108 b | 5.316 a | |
| 80 | 45.414 b | 6.104 a | |
| IR drying | 50 | 64.953 a | 5.221 a |
| 60 | 62.453 a | 5.875 a | |
| 70 | 62.205 a | 5.552 a | |
| 80 | 63.703 a | 5.873 a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, N.A.; Salleh, K.M.; Fudholi, A.; Zakaria, S. Drying Regimes on Regenerated Cellulose Films Characteristics and Properties. Membranes 2022, 12, 445. https://doi.org/10.3390/membranes12050445
Ibrahim NA, Salleh KM, Fudholi A, Zakaria S. Drying Regimes on Regenerated Cellulose Films Characteristics and Properties. Membranes. 2022; 12(5):445. https://doi.org/10.3390/membranes12050445
Chicago/Turabian StyleIbrahim, Nur Ain, Kushairi Mohd Salleh, Ahmad Fudholi, and Sarani Zakaria. 2022. "Drying Regimes on Regenerated Cellulose Films Characteristics and Properties" Membranes 12, no. 5: 445. https://doi.org/10.3390/membranes12050445
APA StyleIbrahim, N. A., Salleh, K. M., Fudholi, A., & Zakaria, S. (2022). Drying Regimes on Regenerated Cellulose Films Characteristics and Properties. Membranes, 12(5), 445. https://doi.org/10.3390/membranes12050445






