Simulation and Experimental Investigation of the Vacuum-Enhanced Direct Membrane Distillation Driven by a Low-Grade Heat Source
Abstract
:1. Introduction
2. Theoretical and CFD Model
2.1. Theoretical Model
2.1.1. Mass Transfer
2.1.2. Heat Transfer
- (1)
- Heat is transferred from the main body of feed seawater flow to the membrane surface on the feed side.
- (2)
- A part of the heat is taken away from the feed side and passes through the membrane by heat conduction and vaporization.
- (3)
- The vapor condenses on the permeate side, together with the conducted heat of the membrane, raising the temperature on the permeate side.
2.2. CFD Model for Permeate Flux Prediction
2.2.1. Governing Equations
2.2.2. Simplified Geometrical Model
2.2.3. Boundary Conditions
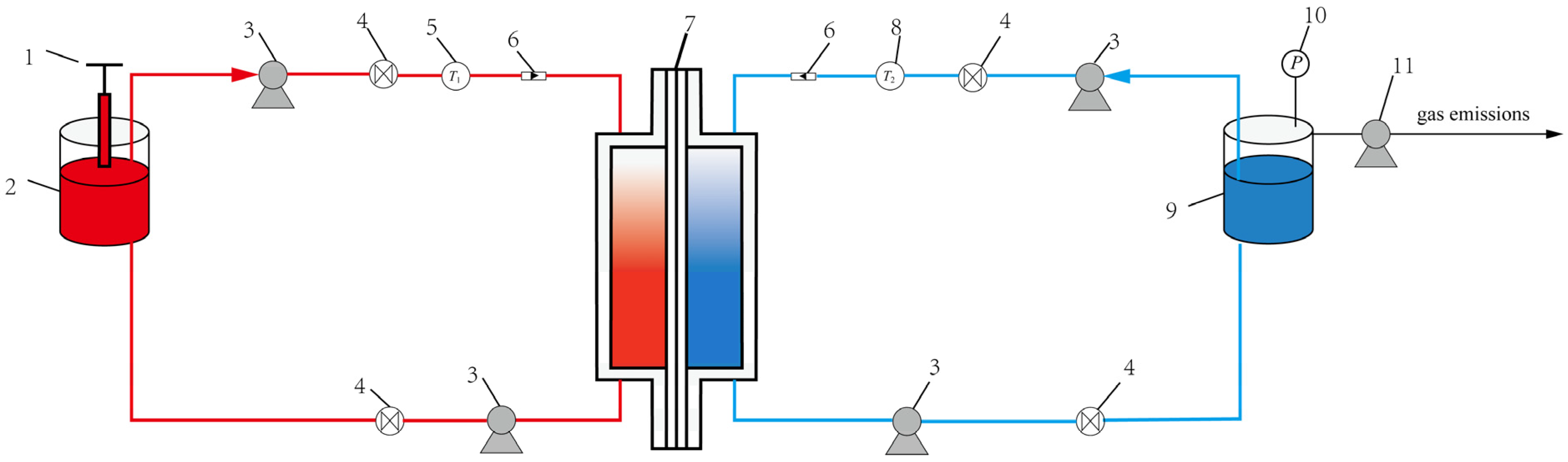
3. Experimental Setup
4. Results and Discussion
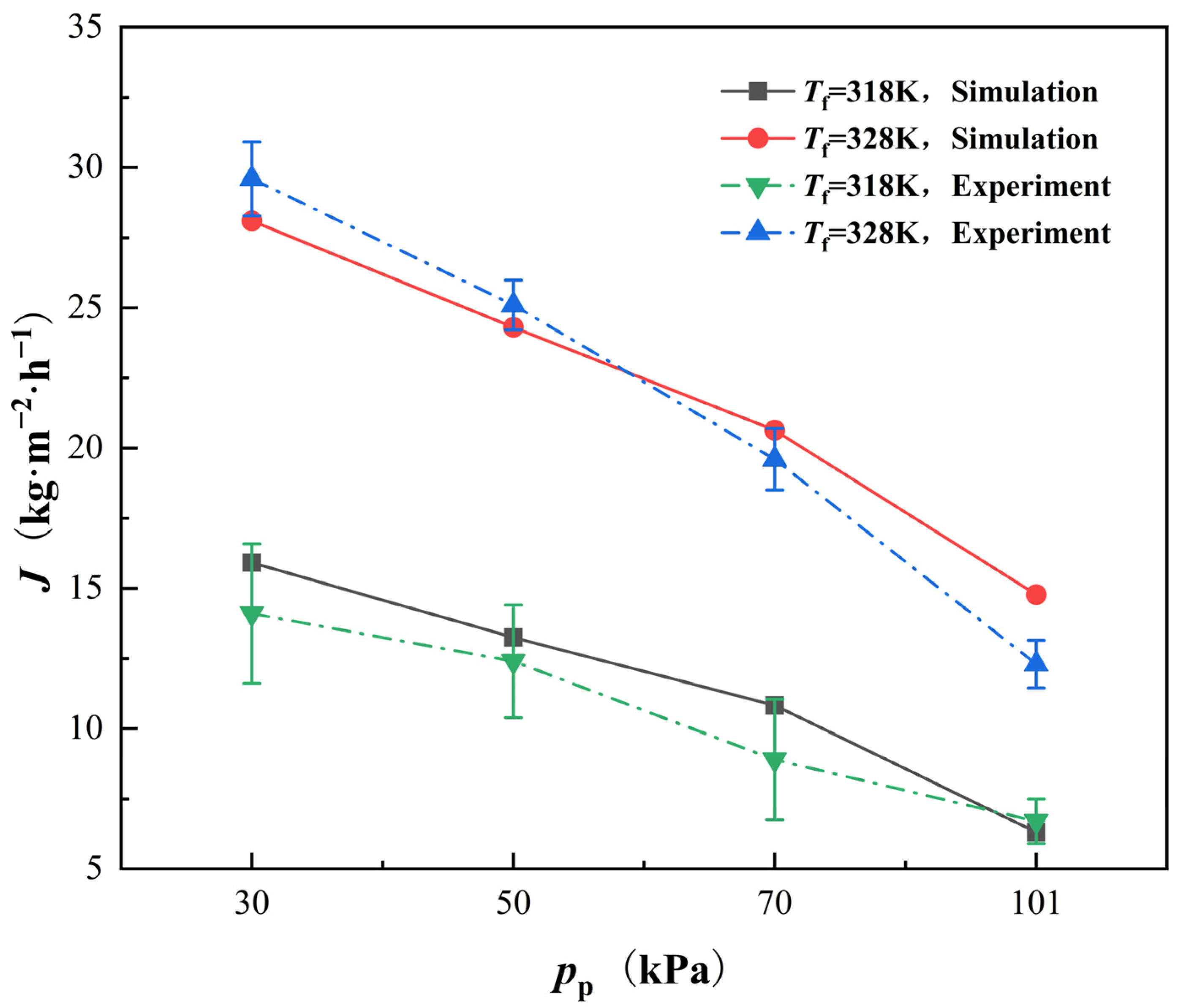
4.1. Experimental Verification of the Proposed Transmembrane Transfer Model
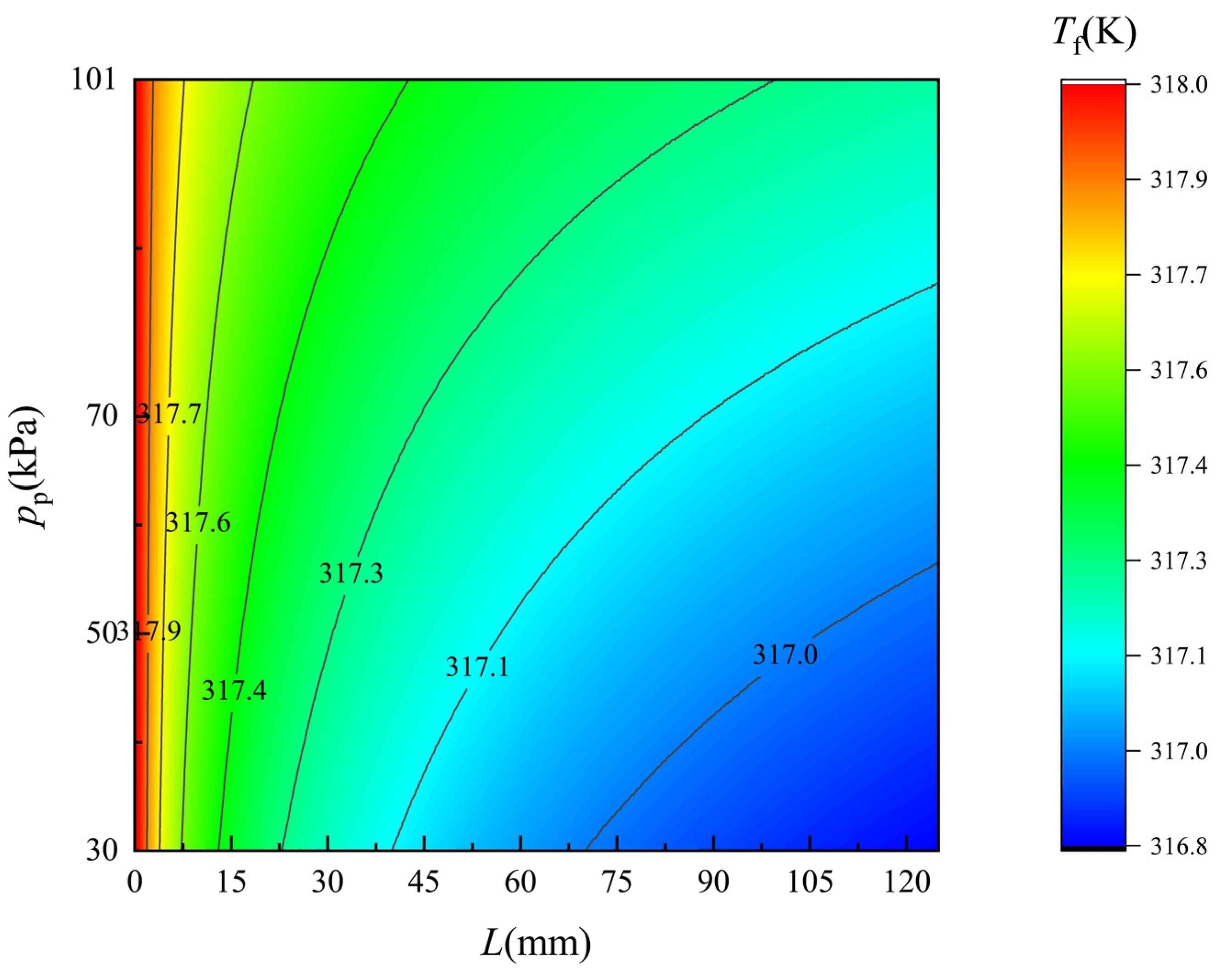
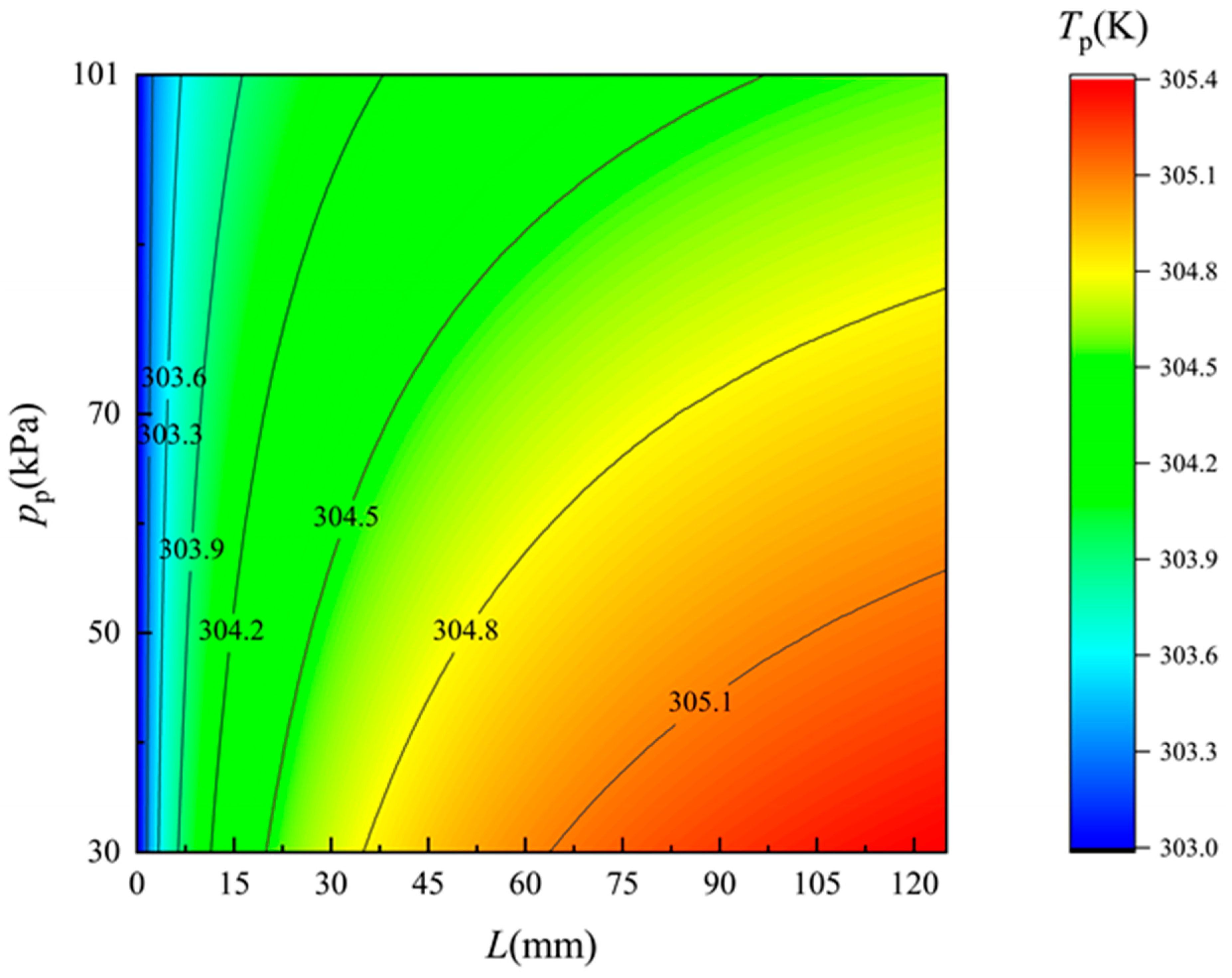
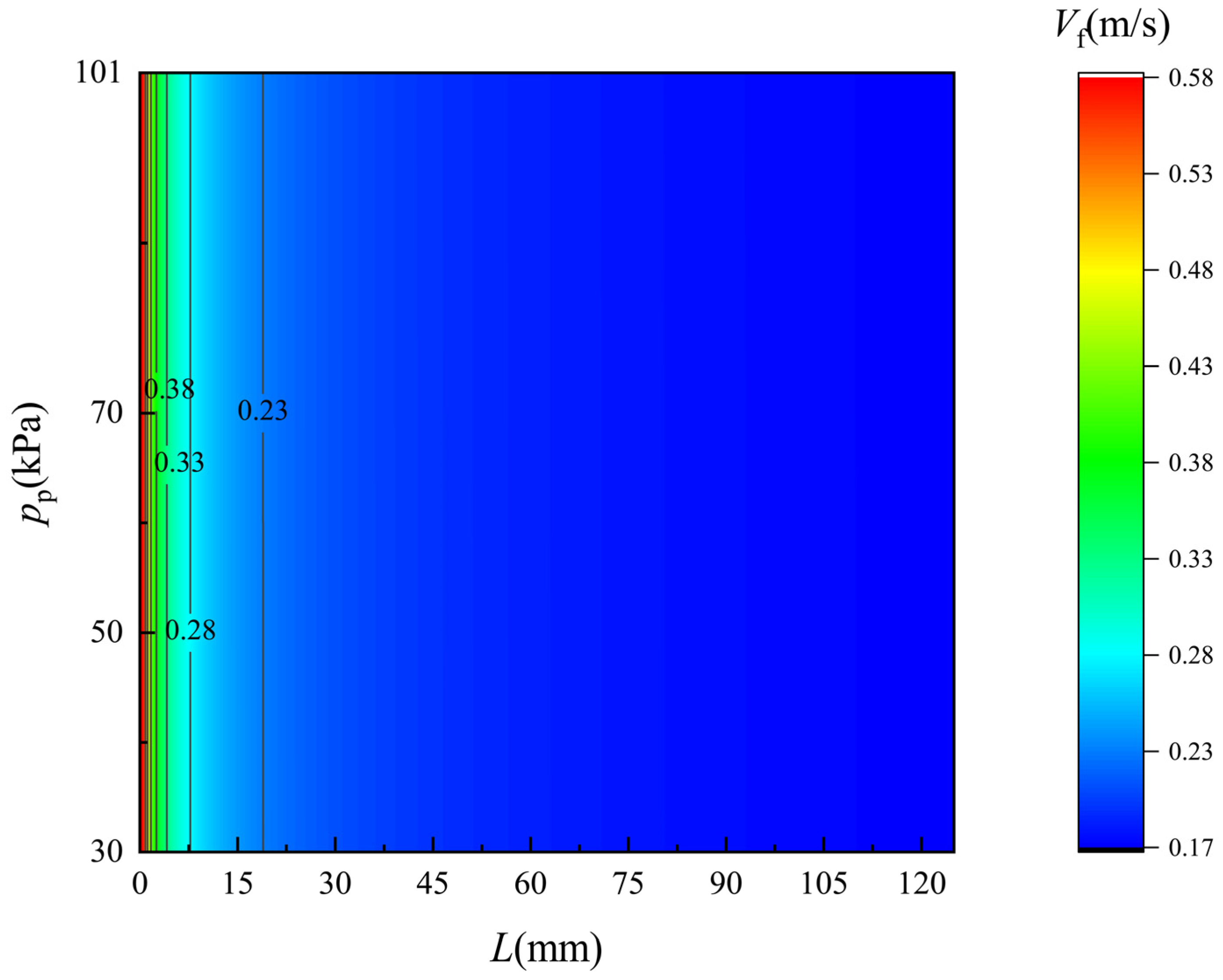
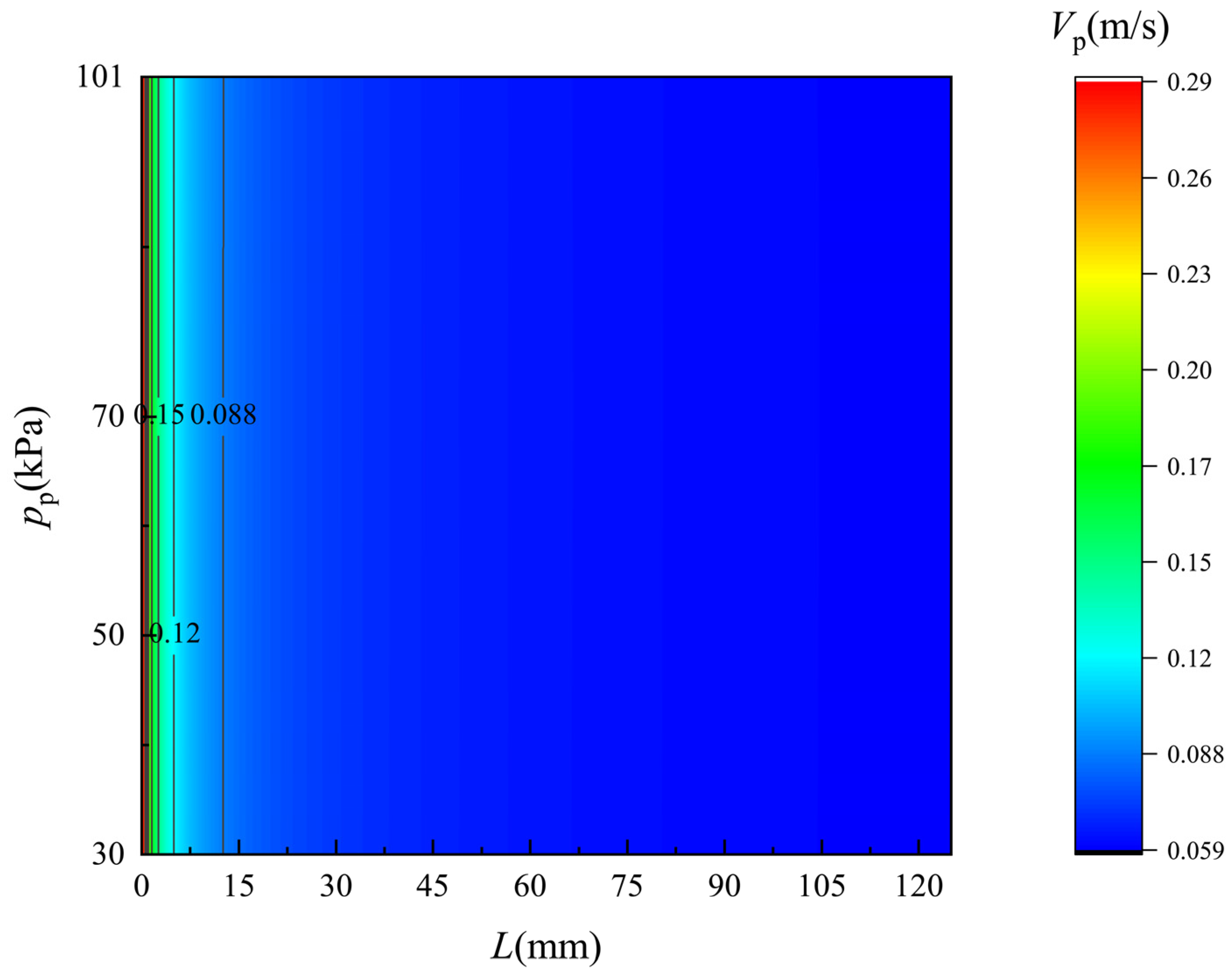
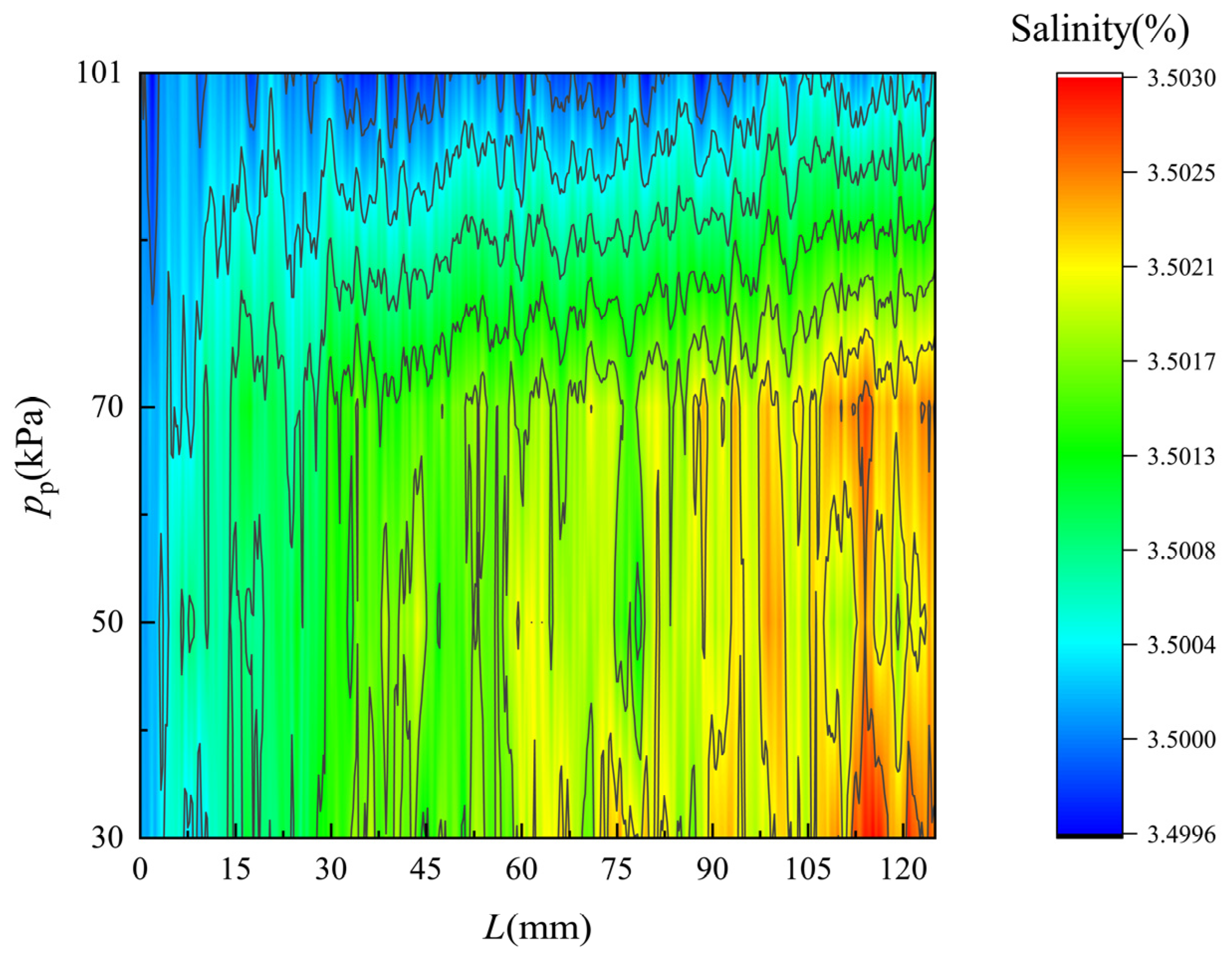
4.2. Flow Field along the Membrane Surface
5. Conclusions
- (1)
- Compared with the model introducing a semi-empirical coefficient, all the parameters of the model proposed in this paper are independent of the operating condition, and thus the model is easier for use and has better adaptability to the fluctuating operating conditions.
- (2)
- The simulation results based on the proposed model have good agreement with the experimental data. In the VEDCMD desalination, the permeate flux is significantly enhanced by decreasing the permeate side pressure. When the absolute pressure of the permeate side reaches 30 kPa, the permeate flux can be improved by nearly 200%.
- (3)
- The flow fields of the flow along each side of the membrane are revealed under different pressure of the permeate side. The permeate flux rising caused by the vacuum enhancement leads to increasing temperature rise/drop and salinity, while it can hardly influence the velocity distribution.
- (4)
- The CFD simulation results are helpful for guiding the VEDCMD operation and module structure improvement. Increasing the temperature of the feed flow and decreasing the pressure of the permeate flow can contribute to larger permeate fluxes. The length of the module should be controlled to avoid excessive heat conduction between the two sides of the membrane. In addition, the turbulence of the flow near the membrane should be enhanced for better mass transfer and smaller concentration polarization, by inserting or mounting some small obstacles near the membrane surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| J | Permeation flux (kg·m−2·s−1) |
| K | Membrane distillation coefficient (kg·m−2·s−1·pa−1) |
| p | Pressure (Pa) |
| XNaCl | Molar fraction of solute |
| T | Temperature (K) |
| γ | Activity coefficient |
| W | Mass fraction |
| M | Molar mass (kg·mol−1) |
| Kn | Knudsen number |
| λ | Average free path of water vapor (μm) |
| d | Diameter of membrane pore (μm) |
| KB | Boltzmann constant (J·mol−1·K−1) |
| β | Collision diameters(μm) |
| DWa | Diffusion coefficient of water vapor (m2·s−1) |
| pt | Gas pressure in the pore of the membrane |
| εh | Surface porosity |
| τ | Membrane tortuosity factor |
| δ | Membrane thickness (mm) |
| R | Gas constant (J·mol−1·k−1) |
| r | Membrane pore radius (μm) |
| μ | Viscosity (pa·s) |
| q | Heat flux (w·m−2) |
| ΔHV | Enthalpy of evaporation (kJ·kg−1) |
| κ | Thermal conductivity (J·m−1·k−1) |
| ρ | Density (kg·m−3) |
| S | Source term |
| b | Thickness of the first grid layer (mm) |
| Stress tensor (kg·m−1·s−1) | |
| Gravitational body force | |
| External body force | |
| k | Turbulent kinetic energy |
| σ | Turbulent Prandtl number |
| Gb | Turbulence kinetic energy (buoyancy) |
| Gk | Turbulence kinetic energy (the mean velocity gradients) |
| YM | Contribution of the fluctuating dilatation |
| C1 | constant |
| C2 | constant |
| C1e | constant |
| C3e | constant |
| Superscript | |
| S | Saturation properties |
| Subscripts | |
| m | Membrane |
| f | Feed side |
| p | Permeate side |
| W | Flow channel |
| v | Vapor |
| w | Water |
| MD | Molecular diffusion |
| K | Knudsen diffusion |
| K-MD | Knudsen-molecular diffusion |
| PO | Poiseuille flow |
| g | Gas |
| D | DCMD |
| H | Latent heat |
| C | Heat conduction |
| a | Air |
| s | Solid |
| eff | Effective |
| j | Component |
References
- Shim, W.G.; He, K.; Gray, S.; Moon, I.S. Solar energy assisted direct contact membrane distillation (DCMD) process for seawater desalination. Sep. Purif. Technol. 2015, 143, 94–104. [Google Scholar] [CrossRef]
- Drioli, E.; Ali, A.; Macedonio, F. Membrane distillation: Recent developments and perspectives. Desalination 2015, 356, 56–84. [Google Scholar] [CrossRef]
- Ji, H.; Choi, M.Y.; Lee, H.S.; Kim, A.S.; Kim, H.J. Vacuum membrane distillation for deep seawater: Experiments and theory. Desalination Water Treat. 2017, 58, 344–350. [Google Scholar] [CrossRef]
- Bamasag, A.; Alqahtani, T.; Sinha, S.; Ghaffour, N.; Phelan, P. Experimental investigation of a solar-heated direct contact membrane distillation system using evacuated tube collectors. Desalination 2020, 487, 15. [Google Scholar] [CrossRef]
- Lokare, O.R.; Tavakkoli, S.; Rodriguez, G.; Khanna, V.; Vidic, R.D. Integrating membrane distillation with waste heat from natural gas compressor stations for produced water treatment in Pennsylvania. Desalination 2017, 413, 144–153. [Google Scholar] [CrossRef]
- AbdulKadir, W.; Ahmad, A.L.; Seng, O.B. Carnauba Wax/Halloysite Nanotube with Improved Anti-Wetting and Permeability of Hydrophobic PVDF Membrane via DCMD. Membranes 2021, 11, 19. [Google Scholar] [CrossRef]
- Aljumaily, M.M.; Alsaadi, M.A.; Hashim, N.A.; Alsalhy, Q.F.; Das, R.; Mjalli, F.S. Embedded high-hydrophobic CNMs prepared by CVD technique with PVDF-co-HFP membrane for application in water desalination by DCMD. Desalination Water Treat. 2019, 142, 37–48. [Google Scholar] [CrossRef]
- Bonyadi, E.; Niknejad, A.S.; Ashtiani, F.Z.; Bazgir, S.; Kargari, A. A well-designed polystyrene/polycarbonate membrane for highly saline water desalination using DCMD process. Desalination 2022, 528, 9. [Google Scholar] [CrossRef]
- Fahmey, M.S.; El-Aassar, A.H.M.; Abo-Elfadel, M.M.; Orabi, A.S.; Das, R. Comparative performance evaluations of nanomaterials mixed polysulfone: A scale-up approach through vacuum enhanced direct contact membrane distillation for water desalination. Desalination 2019, 451, 111–116. [Google Scholar] [CrossRef]
- Ghorabi, S.; Ashtiani, F.Z.; Karimi, M.; Fouladitajar, A.; Yousefi, B.; Dorkalam, F. Development of a novel dual-bioinspired method for synthesis of a hydrophobic/hydrophilic polyethersulfone coated membrane for membrane distillation. Desalination 2021, 517, 17. [Google Scholar] [CrossRef]
- Hubadillah, S.K.; Othman, M.H.D.; Gani, P.; Ismail, A.F.; Rahman, M.A.; Jaafar, J.; Iop. A green membrane distillation system for seawater desalination: Response surface modelling and optimization. In Proceedings of the 9th International Conference on Mechatronics and Manufacturing (ICMM), Phuket, Thailand, 27–29 January 2018. [Google Scholar]
- Sadeghzadeh, A.; Bazgir, S.; Shirazi, M.M.A. Fabrication and characterization of a novel hydrophobic polystyrene membrane using electroblowing technique for desalination by direct contact membrane distillation. Sep. Purif. Technol. 2020, 239, 15. [Google Scholar] [CrossRef]
- Zhou, L.; Li, C.L.; Chang, P.T.; Tan, S.H.; Ahmad, A.L.; Low, S.C. Intrinsic microspheres structure of electrospun nanofibrous membrane with rational superhydrophobicity for desalination via membrane distillation. Desalination 2022, 527, 12. [Google Scholar] [CrossRef]
- Zou, L.; Gusnawan, P.; Zhang, G.; Yu, J. Novel Janus composite hollow fiber membrane-based direct contact membrane distillation (DCMD) process for produced water desalination. J. Membr. Sci. 2020, 597, 11. [Google Scholar] [CrossRef]
- Khalifa, A.; Mezghani, A.; Alawami, H. Analysis of integrated membrane distillation-heat pump system for water desalination. Desalination 2021, 510, 19. [Google Scholar] [CrossRef]
- Kuang, Z.F.; Long, R.; Liu, Z.C.; Liu, W. Analysis of temperature and concentration polarizations for performance improvement in direct contact membrane distillation. Int. J. Heat Mass Transf. 2019, 145, 11. [Google Scholar] [CrossRef]
- Soomro, M.I.; Kim, W.S. Parabolic-trough plant integrated with direct-contact membrane distillation system: Concept, simulation, performance, and economic evaluation. Sol. Energy 2018, 173, 348–361. [Google Scholar] [CrossRef]
- Ve, Q.L.; Koirala, R.; Bawahab, M.; Faqeha, H.; Do, M.C.; Nguyen, Q.L.; Date, A.; Akbarzadeh, A. Experimental investigation of the effect of the spacer and operating conditions on mass transfer in direct contact membrane distillation. Desalination 2021, 500, 11. [Google Scholar] [CrossRef]
- Ansari, A.; Kavousi, S.; Helfer, F.; Millar, G.; Thiel, D.V. An Improved Modelling Approach for the Comprehensive Study of Direct Contact Membrane Distillation. Membranes 2021, 11, 22. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, A.; Ahmad, H.; Antar, M.; Laoui, T.; Khayet, M. Experimental and theoretical investigations on water desalination using direct contact membrane distillation. Desalination 2017, 404, 22–34. [Google Scholar] [CrossRef]
- Shafieian, A.; Khiadani, M.; Nosrati, A. Performance analysis of a thermal-driven tubular direct contact membrane distillation system. Appl. Therm. Eng. 2019, 159, 13. [Google Scholar] [CrossRef]
- Cath, T.Y.; Adams, V.D.; Childress, A.E. Experimental study of desalination using direct contact membrane distillation: A new approach to flux enhancement. J. Membr. Sci. 2004, 228, 5–16. [Google Scholar] [CrossRef]
- Naidu, G.; Jeong, S.; Vigneswaran, S.; Jang, E.K.; Choi, Y.J.; Hwang, T.M. Fouling study on vacuum-enhanced direct contact membrane distillation for seawater desalination. Desalination Water Treat. 2016, 57, 10042–10051. [Google Scholar] [CrossRef]
- Okiel, K.; El-Aassar, A.H.M.; Temraz, T.; El-Etriby, S.; Shawky, H.A. Vacuum enhanced direct contact membrane distillation for oil field produced water desalination: Specific energy consumption and energy efficiency. Desalination Water Treat. 2016, 57, 11945–11955. [Google Scholar] [CrossRef]
- Plattner, J.; Naidu, G.; Wintgens, T.; Vigneswaran, S.; Kazner, C. Fluoride removal from groundwater using direct contact membrane distillation (DCMD) and vacuum enhanced DCMD (VEDCMD). Sep. Purif. Technol. 2017, 180, 125–132. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C. Gas and vapour transport through microporous membranes. I. Knudsen-Poiseuille transition. J. Membr. Sci. 1990, 53, 159–171. [Google Scholar] [CrossRef]
- Naidu, G.; Shim, W.G.; Jeong, S.; Choi, Y.; Ghaffour, N.; Vigneswaran, S. Transport phenomena and fouling in vacuum enhanced direct contact membrane distillation: Experimental and modelling. Sep. Purif. Technol. 2017, 172, 285–295. [Google Scholar] [CrossRef]
- Ibrahim, S.S.; Alsalhy, Q.F. Modeling and Simulation for Direct Contact Membrane Distillation in Hollow Fiber Modules. Aiche J. 2013, 59, 589–603. [Google Scholar] [CrossRef]
- Mason, E.A.; Malinauskas, A.P. Gas Transport in Porous Media: The Dusty-Gas Model; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Schofield, R.; Fane, A.; Fell, C. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]



| VEDCMD Module Property | Value |
|---|---|
| Membrane material | PVDF |
| Porosity | 0.75 |
| Membrane nominal pore size | 0.22 μm |
| Membrane thickness | 0.12 mm |
| Length L | 125 mm |
| Hot channel height H | 12 mm |
| Cold channel height H | 12 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Tong, L.; Wang, C.; Cao, G.; Lu, H.; Li, J.; Liu, X.; Feng, X.; Wu, Z. Simulation and Experimental Investigation of the Vacuum-Enhanced Direct Membrane Distillation Driven by a Low-Grade Heat Source. Membranes 2022, 12, 842. https://doi.org/10.3390/membranes12090842
Ma Q, Tong L, Wang C, Cao G, Lu H, Li J, Liu X, Feng X, Wu Z. Simulation and Experimental Investigation of the Vacuum-Enhanced Direct Membrane Distillation Driven by a Low-Grade Heat Source. Membranes. 2022; 12(9):842. https://doi.org/10.3390/membranes12090842
Chicago/Turabian StyleMa, Qingfen, Liang Tong, Chengpeng Wang, Guangfu Cao, Hui Lu, Jingru Li, Xuejin Liu, Xin Feng, and Zhongye Wu. 2022. "Simulation and Experimental Investigation of the Vacuum-Enhanced Direct Membrane Distillation Driven by a Low-Grade Heat Source" Membranes 12, no. 9: 842. https://doi.org/10.3390/membranes12090842
APA StyleMa, Q., Tong, L., Wang, C., Cao, G., Lu, H., Li, J., Liu, X., Feng, X., & Wu, Z. (2022). Simulation and Experimental Investigation of the Vacuum-Enhanced Direct Membrane Distillation Driven by a Low-Grade Heat Source. Membranes, 12(9), 842. https://doi.org/10.3390/membranes12090842





