Review and Analysis of Heat Transfer in Spacer-Filled Channels of Membrane Distillation Systems
Abstract
:1. Introduction
2. Theoretical
2.1. Transport across the Membrane
2.2. Transport across the Fluid Boundary Layers
3. Materials and Methods
3.1. Test Rig
3.2. Test Procedure
3.3. Experimental Evaluation
4. CFD Case Study
4.1. Setup
4.2. Numerical Results and Discussion
5. Results and Discussion
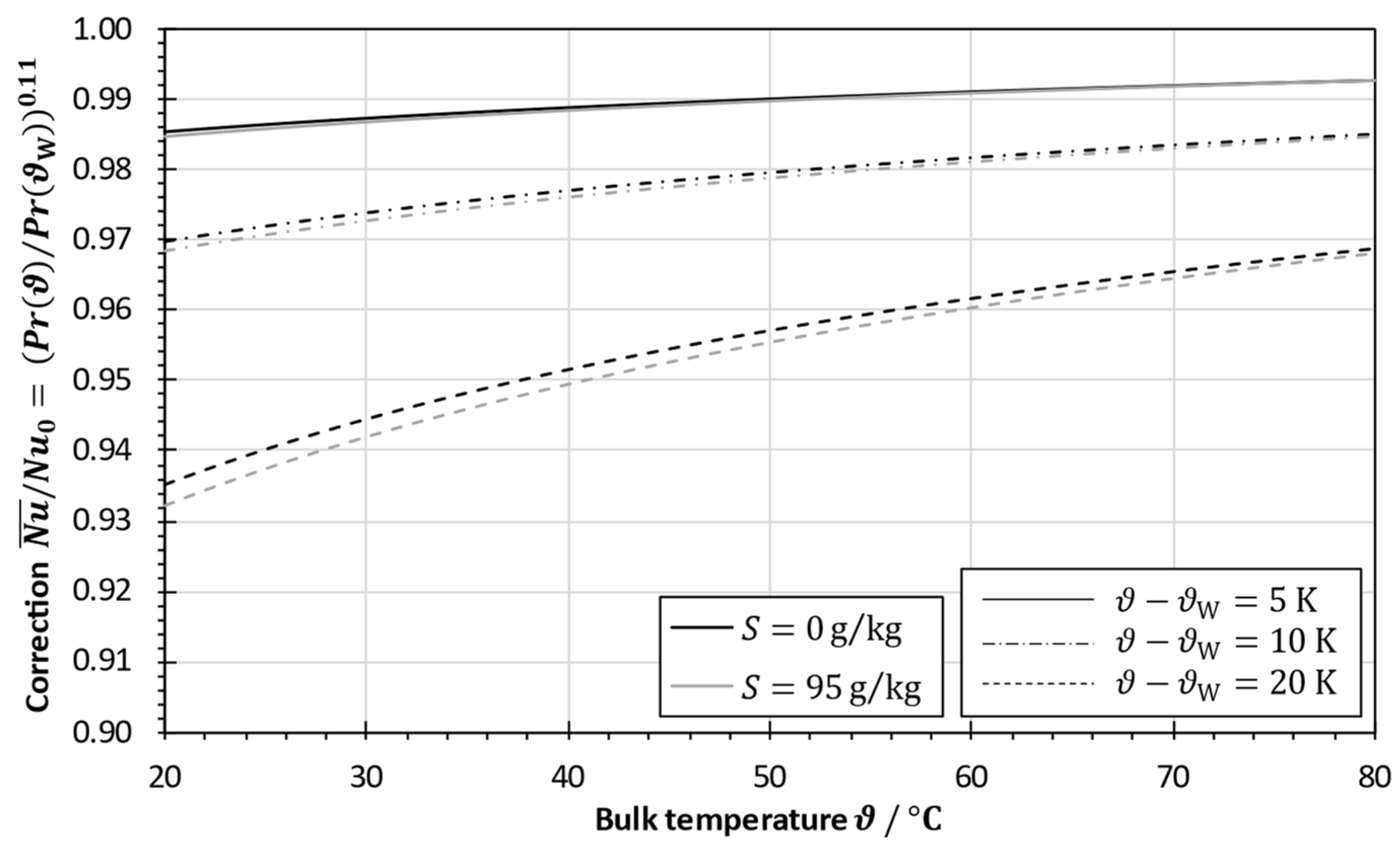
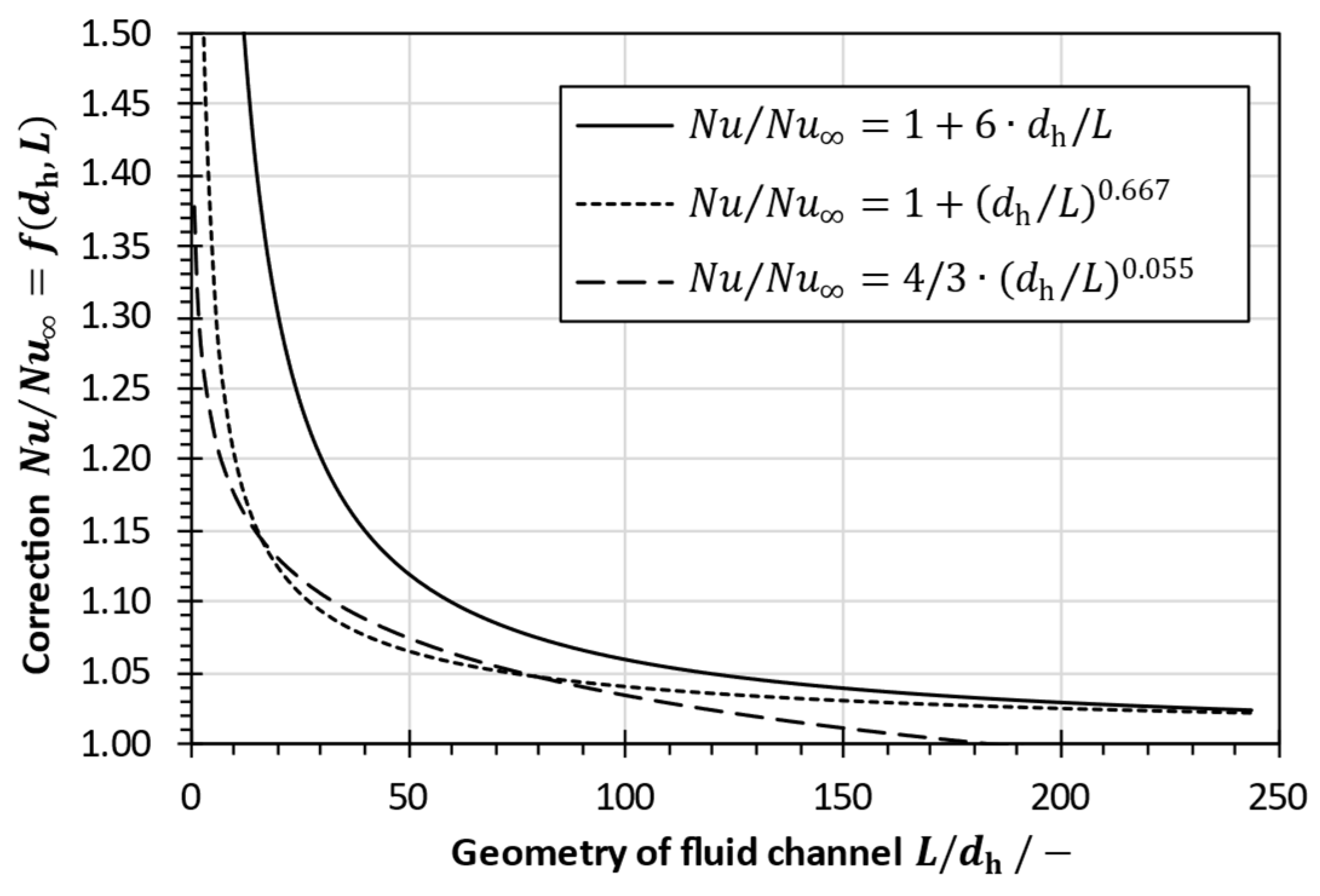
5.1. Nusselt Number Correction for Variation of Fluid Properties and Channel Geometry
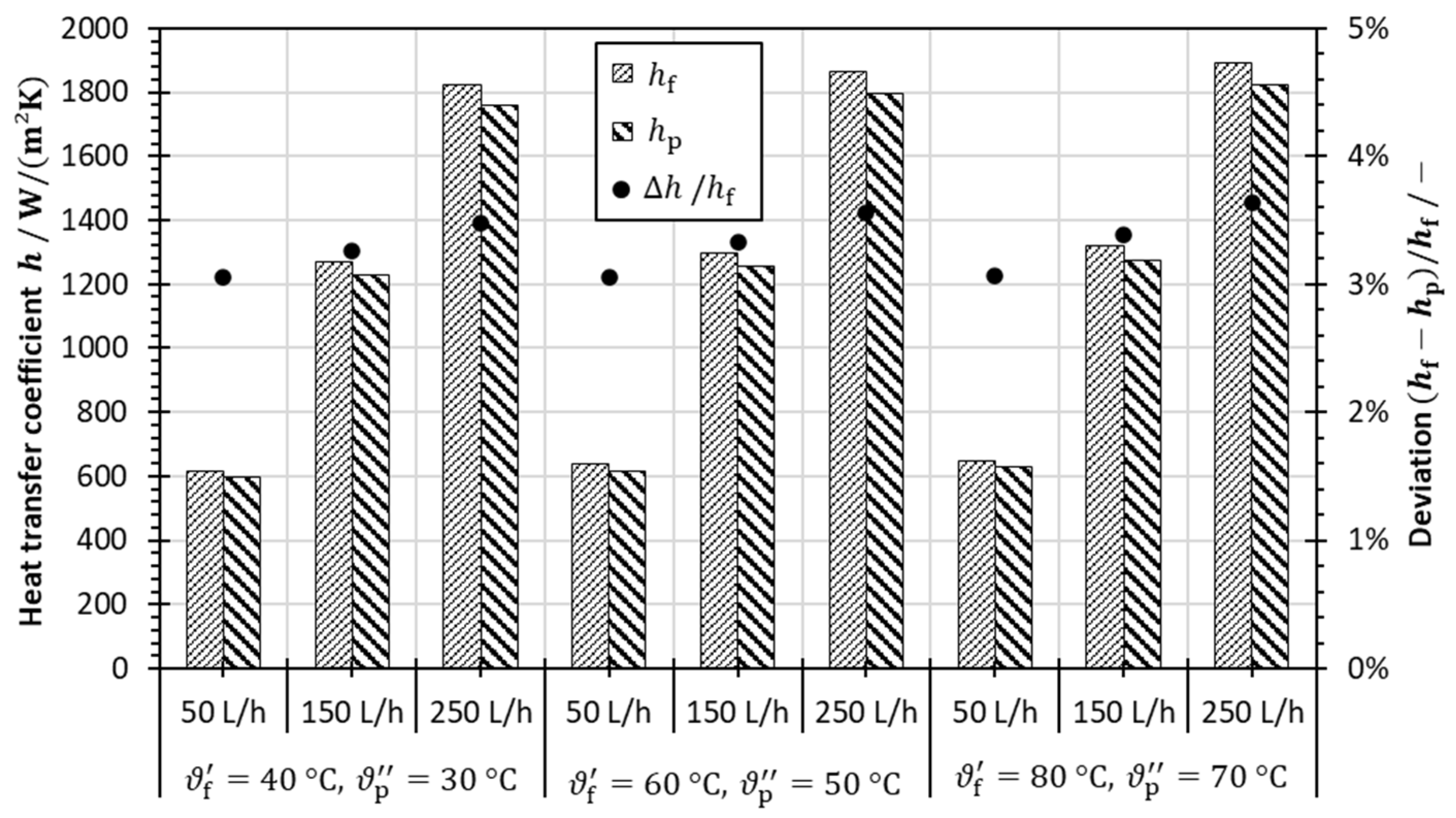
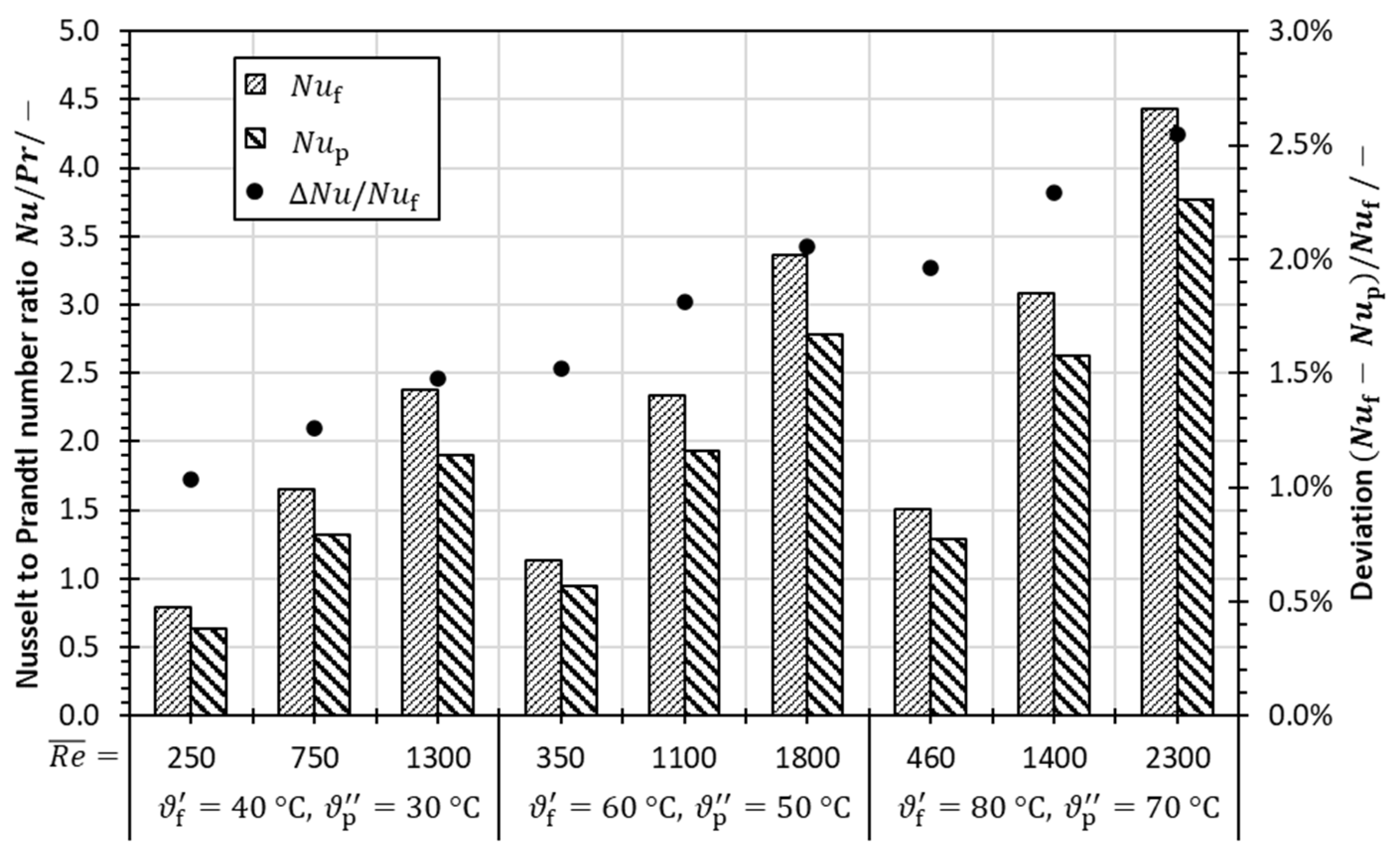
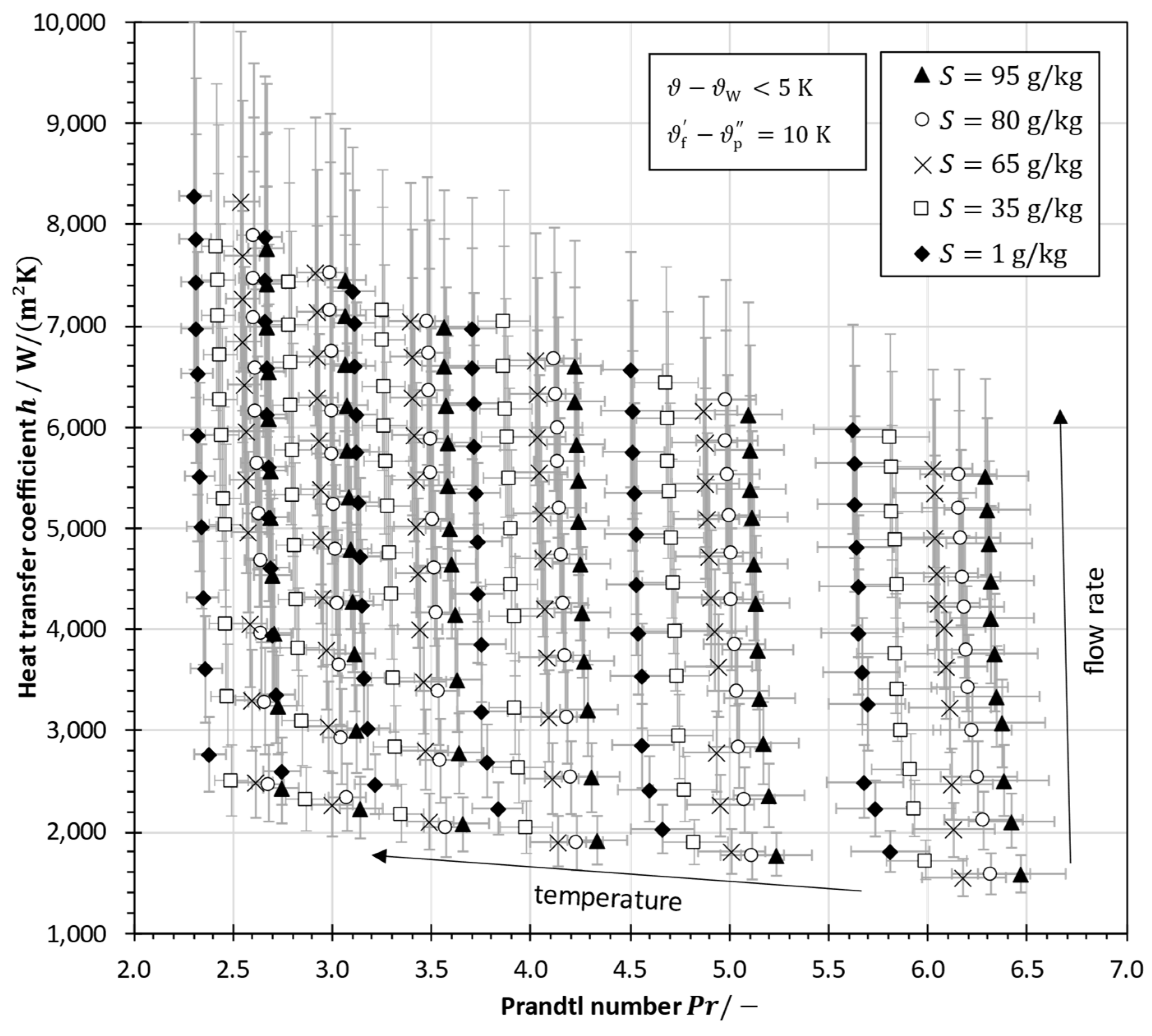
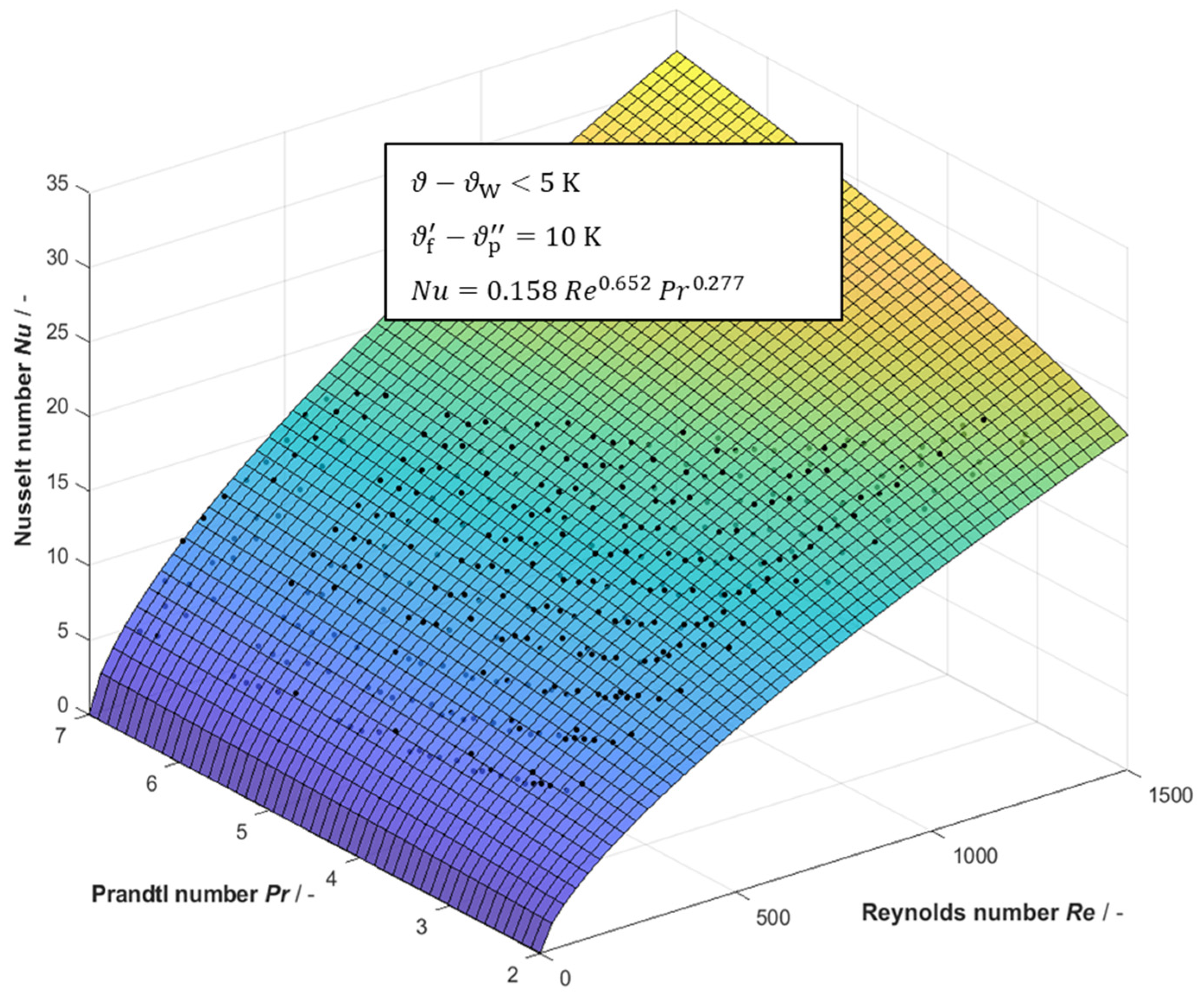
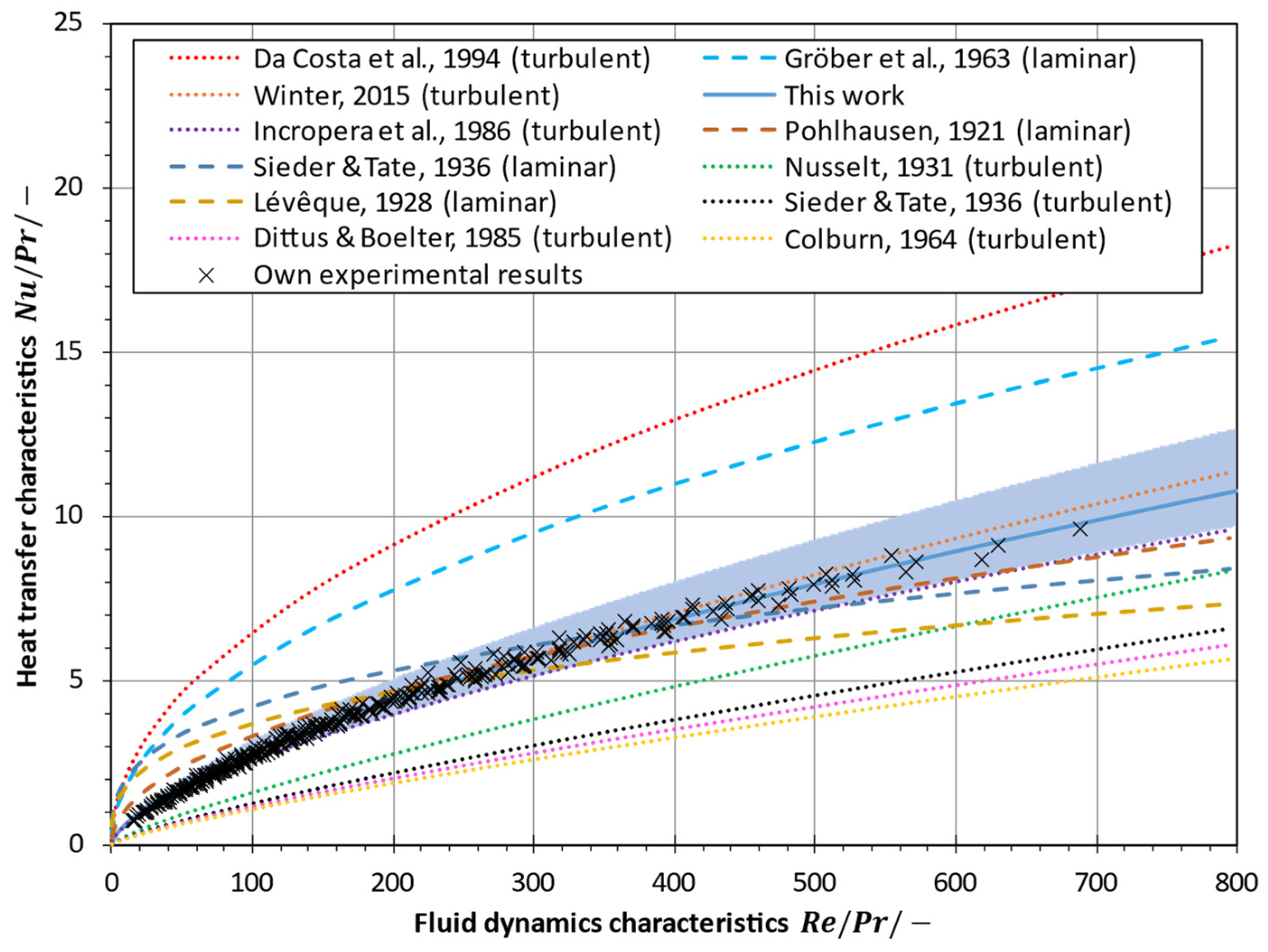
5.2. Evaluation of Heat Transfer Measurements and Derivation of a Correlation for Nusselt Number
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Area | ||
| Empirical constant | - | |
| Membrane parameter | ||
| Concentration | ||
| Specific isobaric heat capacity | ||
| Binary diffusion coefficient | ||
| Diameter | ||
| Specific total energy | ||
| Factor or function | div. | |
| Universal gravitational constant | ||
| Grashof number | - | |
| Height | ||
| Convective heat transfer coefficient | ||
| Specific enthalpy of vaporization | ||
| Thermal conductivity | ||
| Length | ||
| Mesh size | ||
| Mass flow rate | ||
| Mass flux | ||
| Nusselt number | - | |
| Perimeter | ||
| Pressure | ||
| Partial pressure | ||
| Prandtl number | - | |
| Heat flow rate | ||
| Heat flux | ||
| Coefficient of determination | - | |
| Rayleigh number | - | |
| Reynolds number | - | |
| Richardson number | - | |
| Root-mean-square error | - | |
| Salinity | ||
| Schmidt number | - | |
| Sherwood number | - | |
| Sum of squared errors | - | |
| Overall heat transfer coefficient | ||
| Fluid velocity | ||
| Fluid velocity vector | ||
| Volume | ||
| Volume flow rate | ||
| Longitudinal dimension | ||
| Convective mass transfer coefficient | ||
| Coefficient of thermal expansion | ||
| Thickness | ||
| Porosity | - | |
| Friction factor | - | |
| Dynamic viscosity | s | |
| Temperature | ||
| Kinematic viscosity | ||
| Density | ||
| Tortuosity | - | |
| Stress tensor | ||
| Angle | ||
| Sub- and Superscript | Description | |
| 0 | Initial, boundary | |
| Al | Aluminum plate | |
| corr | Correlation | |
| crit | Critical | |
| exp | Experimental | |
| f | Feed bulk | |
| flux-law | Flux law | |
| forced | Forced convection | |
| fm | Feed–membrane interface | |
| free | Free convection | |
| g | Gaseous | |
| geometric mean | Geometric mean | |
| h | Hydraulic | |
| iso-strain | Iso-strain | |
| iso-stress | Iso-stress | |
| iso-superposed | Superposed iso-strain/iso-stress | |
| L | At length | |
| lm | Logarithmic mean | |
| m | Membrane | |
| modified iso-strain | Modified iso-strain | |
| p | Permeate bulk | |
| pm | Permeate–membrane interface | |
| S | Spacer | |
| s | Solid | |
| W | Wall | |
| x | In direction of | |
| Inlet | ||
| Outlet | ||
| Infinite length | ||
| Average, mean | ||
Appendix A
| Nusselt Correlation | Application in MD Modelling | References | |
|---|---|---|---|
| (A1) | Laminar, flat-sheet/tubular (lumen side) | [2,5,13,22,27,59] | |
| (A2) | Flat-sheet, experimentally found for symmetric spacer (thickness 2.0 mm) | [16] | |
| (A3) | Flat-sheet, experimentally found for symmetric spacer (thickness 3.2 mm) | [16] | |
| (A4) | Laminar, flat-sheet | [13] | |
| (A5) | Laminar, flat-sheet/tubular (lumen side) | [13,59,108,109] | |
| (A6) | Laminar, flat-sheet | [13] | |
| (A7) | Laminar, , flat-sheet, spacer not inducing change of flow direction | [80,96,110] | |
| (A8) | Laminar, flat-sheet | [13,39] | |
| (A9) | Flat-sheet, spacer inducing change of flow direction, transition to fully developed turbulent mesh size; filament size; spacer thickness; spacer voidage; angle between spacer filaments | [5,11,16,27,32,39] | |
| (A10) | Laminar, flat-sheet | [13,108,109,111] | |
| (A11) | Laminar, tubular (shell side cross-flow) | [62,63,112,113] | |
| (A12) | Laminar, , flat-sheet/tubular (lumen side) | [2,5,6,18,20,59,60,66,67,80,108,109,114] | |
| (A13) | Laminar, flat-sheet | [13] | |
| (A14) | Laminar, , , flat-sheet/tubular | [3,6,13,27,57,61,62,63,65,68,70,71,72,73,74,80,108] | |
| (A15) | Laminar, experimentally found, flat-sheet | [17,108] | |
| (A16) | Laminar, flat-sheet | [27] | |
| (A17) | Laminar, flat-sheet | [13,27] | |
| (A18) | Laminar, , tubular (lumen side) | [2,5,6,12,18,43,80,115,116] | |
| (A19) | Laminar, tubular (lumen side) | [3,6,18,27,84,108,111,114,117] | |
| (A20) | Transition, tubular (lumen side) | [2,5,18,59] | |
| (A21) | Turbulent, , flat-sheet/tubular (lumen side) | [5,10,12,13,19,22,27,59,60,80,82,83,84,97,108,118,119,120] | |
| (A22) | Turbulent, , flat-sheet/tubular (lumen side) | [2,6,18,61,65,73,74,80,86,96,108] | |
| (A23) | Turbulent, flat-sheet | [6,66,121] | |
| (A24) | Turbulent, , flat-sheet/tubular (lumen side) | [3,5,6,18,22,27,43,59,71,80] | |
| (A25) | Turbulent, flat-sheet | [22,108,122] | |
| (A26) | Turbulent, flat-sheet | [22] | |
| (A27) | Turbulent, flat-sheet/tubular (lumen side) | [5,27,59,80,108] | |
| (A28) | Turbulent, flat-sheet, experimentally found | [17,108] | |
| (A29) | Turbulent, tubular (shell side), experimentally found | [18] | |
| (A30) | Turbulent, flat-sheet/tubular (lumen side) | [2,5,13,22,27,59,83,88,119] | |
| (A31) | Turbulent, tubular (shell side, simultaneous cross- and parallel flow) , | [2,18] | |
| (A32) | Turbulent, tubular (shell side crossflow) | [62,63,112,113] | |
| (A33) | Turbulent, , flat-sheet | [22,27,43,89,90] | |
| (A34) | Turbulent, , flat-sheet | [22,27,80] | |
| (A35) | Turbulent, flat-sheet | [22,80,89] | |
| (A36) | Turbulent, flat-sheet | [27,123] | |
References
- Tong, T.; Elimelech, M. The Global Rise of Zero Liquid Discharge for Wastewater Management: Drivers, Technologies, and Future Directions. Environ. Sci. Technol. 2016, 50, 6846–6855. [Google Scholar] [CrossRef]
- Khayet, M. Membranes and theoretical modeling of membrane distillation: A review. Adv. Colloid Interface Sci. 2011, 164, 56–88. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Membrane Distillation: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 9780444531261. [Google Scholar]
- Drioli, E.; Ali, A.; Macedonio, F. Membrane distillation: Recent developments and perspectives. Desalination 2015, 356, 56–84. [Google Scholar] [CrossRef]
- Curcio, E.; Drioli, E. Membrane Distillation and Related Operations-A Review. Sep. Purif. Rev. 2005, 34, 35–86. [Google Scholar] [CrossRef]
- Abu-Zeid, M.A.E.-R.; Zhang, Y.; Dong, H.; Zhang, L.; Chen, H.-L.; Hou, L. A comprehensive review of vacuum membrane distillation technique. Desalination 2015, 356, 1–14. [Google Scholar] [CrossRef]
- Song, L.; Ma, Z.; Liao, X.; Kosaraju, P.B.; Irish, J.R.; Sirkar, K.K. Pilot plant studies of novel membranes and devices for direct contact membrane distillation-based desalination. J. Membr. Sci. 2008, 323, 257–270. [Google Scholar] [CrossRef]
- He, F.; Gilron, J.; Lee, H.; Song, L.; Sirkar, K.K. Potential for scaling by sparingly soluble salts in crossflow DCMD. J. Membr. Sci. 2008, 311, 68–80. [Google Scholar] [CrossRef]
- Thomas, N.; Mavukkandy, M.O.; Loutatidou, S.; Arafat, H.A. Membrane distillation research & implementation: Lessons from the past five decades. Sep. Purif. Technol. 2017, 189, 108–127. [Google Scholar] [CrossRef]
- Koschikowski, J. Entwicklung von energieautark arbeitenden Wasserentsalzungsanlagen auf Basis der Membrandestillation. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2011. [Google Scholar]
- Ray, S.S.; Chen, S.-S.; Sangeetha, D.; Chang, H.-M.; Thanh, C.N.D.; Le, Q.H.; Ku, H.-M. Developments in forward osmosis and membrane distillation for desalination of waters. Environ. Chem. Lett. 2018, 16, 1247–1265. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M.; Morawski, A.W. Membrane distillation with laminar flow. Sep. Purif. Technol. 1997, 11, 93–101. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Vázquez-González, M.I.; Florido-Díaz, F.J. Study of membrane distillation using channel spacers. J. Membr. Sci. 1998, 144, 45–56. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effects of net-type spacers on heat and mass transfer in direct contact membrane distillation and comparison with ultrafiltration studies. J. Membr. Sci. 2003, 217, 193–206. [Google Scholar] [CrossRef]
- Winter, D. Membrane Distillation: A Thermodynamic, Technological and Economic Analysis. Ph.D. Thesis, Universität Kaiserslautern, Kaiserslautern, Germany, 2015. [Google Scholar]
- Izquierdo-Gil, M.A.; Fernández-Pineda, C.; Lorenz, M.G. Flow rate influence on direct contact membrane distillation experiments: Different empirical correlations for Nusselt number. J. Membr. Sci. 2008, 321, 356–363. [Google Scholar] [CrossRef]
- Mengual, J.I.; Khayet, M.; Godino, M.P. Heat and mass transfer in vacuum membrane distillation. Int. J. Heat Mass Transf. 2004, 47, 865–875. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. I. Module design and performance evaluation using vacuum membrane distillation. J. Membr. Sci. 1996, 120, 111–121. [Google Scholar] [CrossRef]
- Bandini, S.; Saavedra, A.; Sarti, G.C. Vacuum membrane distillation: Experiments and modeling. Am. Inst. Chem. Eng. 1997, 43, 398–408. [Google Scholar] [CrossRef]
- Bhaumik, D.; Majumdar, S.; Sirkar, K.K. Absorption of CO2 in a transverse flow hollow fiber membrane module having a few wraps of the fiber mat. J. Membr. Sci. 1998, 138, 77–82. [Google Scholar] [CrossRef]
- Qtaishat, M.R.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- International Association for the Properties of Water and Steam. Release on the IAPWS Formulation 2008 for the Thermodynamic Properties of Seawater; International Association for the Properties of Water and Steam: Berlin, Germany, 2008. [Google Scholar]
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, V.J.H. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Hömig, H.E. Seawater and Seawater Distillation; Vulkan: Essen, Germany, 1978; ISBN 9783802727597. [Google Scholar]
- Osswald, T.A.; Baur, E.; Brinkmann, S. International Plastics Handbook: The Resource for Plastics Engineers, 4th ed.; Carl Hanser: München, Germany, 2006; ISBN 3446229051. [Google Scholar]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Heat transport and membrane distillation coefficients in direct contact membrane distillation. J. Membr. Sci. 2003, 212, 177–193. [Google Scholar] [CrossRef]
- Garcia-Payo, M.C.; Izquierdo-Gil, M.A. Thermal resistance technique for measuring the thermal conductivity of thin microporous membranes. J. Phys. D Appl. Phys. 2004, 37, 3008–3016. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D.; Macoun, R. Factors affecting flux in membrane distillation. Desalination 1990, 77, 279–294. [Google Scholar] [CrossRef]
- Krischer, O.; Kast, W.; Kröll, K. Die Wissenschaftlichen Grundlagen der Trocknungstechnik, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 3540082808. [Google Scholar]
- Neubronner, M.; Bodmer, T.; Hübner, C.; Kempa, P.B.; Tsotsas, E.; Eschner, A.; Kasparek, G.; Ochs, F.; Müller-Steinhagen, H.; Werner, H.; et al. D6 Properties of Solids and Solid Materials. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 551–614. ISBN 978-3-540-77877-6. [Google Scholar]
- Nikolaus, K. Trink- und Reinstwassergewinnung mittels Membrandestillation. Ph.D. Thesis, Universität Kaiserslautern, Kaiserslautern, Germany, 2013. [Google Scholar]
- Hagedorn, A.; Fieg, G.; Winter, D.; Koschikowski, J.; Grabowski, A.; Mann, T. Membrane and spacer evaluation with respect to future module design in membrane distillation. Desalination 2017, 413, 154–167. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.A.; Garcia-Payo, M.C.; Fernández-Pineda, C. Air gap membrane distillation of sucrose aqueous solutions. J. Membr. Sci. 1999, 155, 291–307. [Google Scholar] [CrossRef]
- Qiu, L.; Zheng, X.H.; Yue, P.; Zhu, J.; Tang, D.W.; Dong, Y.J.; Peng, Y.L. Adaptable thermal conductivity characterization of microporous membranes based on freestanding sensor-based 3ω technique. Int. J. Therm. Sci. 2015, 89, 185–192. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Gnielinski, V. G1 Heat Transfer in Pipe Flow. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 693–699. ISBN 978-3-540-77877-6. [Google Scholar]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G.; Halim, C. Mass flux enhancement using spacer filled channels in direct contact membrane distillation. J. Membr. Sci. 2001, 187, 193–201. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modelling in spacer-filled channels for ultrafiltration. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Flow and mass transfer in spacer-filled channels for reverse electrodialysis: A CFD parametrical study. J. Membr. Sci. 2016, 497, 300–317. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Yiantsios, S.G.; Karabelas, A.J. Direct numerical simulation of flow in spacer-filled channels: Effect of spacer geometrical characteristics. J. Membr. Sci. 2007, 291, 53–69. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2007; ISBN 0-471-45728-0. [Google Scholar]
- Feron, P.; Solt, G.S. The influence of separators on hydrodynamics and mass transfer in narrow cells: Flow visualisation. Desalination 1991, 84, 137–152. [Google Scholar] [CrossRef]
- Ranade, V.V.; Kumar, A. Fluid dynamics of spacer filled rectangular and curvilinear channels. J. Membr. Sci. 2006, 271, 1–15. [Google Scholar] [CrossRef]
- Kang, I.S.; Chang, H.N. The effect of turbulence promoters on mass transfer—Numerical analysis and flow visualization. Int. J. Heat Mass Transf. 1982, 25, 1167–1181. [Google Scholar] [CrossRef]
- Mojab, S.M.; Pollard, A.; Pharoah, J.G.; Beale, S.B.; Hanff, E.S. Unsteady Laminar to Turbulent Flow in a Spacer-Filled Channel. Flow Turbul. Combust. 2014, 92, 563–577. [Google Scholar] [CrossRef]
- Qamar, A.; Bucs, S.; Picioreanu, C.; Vrouwenvelder, J.S.; Ghaffour, N. Hydrodynamic flow transition dynamics in a spacer filled filtration channel using direct numerical simulation. J. Membr. Sci. 2019, 590, 117264–117276. [Google Scholar] [CrossRef]
- Almeida, A.; Geraldes, V.; Semiao, V. Microflow hydrodynamics in slits: Effects of the walls relative roughness and spacer inter-filaments distance. Chem. Eng. Sci. 2010, 65, 3660–3670. [Google Scholar] [CrossRef]
- Santos, J.; Geraldes, V.; Velizarov, S.; Crespo, J.G. Investigation of flow patterns and mass transfer in membrane module channels filled with flow-aligned spacers using computational fluid dynamics (CFD). J. Membr. Sci. 2007, 305, 103–117. [Google Scholar] [CrossRef]
- Thess, A. F1 Heat Transfer by Free Convection: Fundamentals. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 661–666. ISBN 978-3-540-77877-6. [Google Scholar]
- Hunt, J.C.R. Lewis Fry Richardson and His Contributions to Mathematics, Meteorology, and Models of Conflict. Annu. Rev. Fluid Mech. 1998, 30, 13–36. [Google Scholar] [CrossRef]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006. [Google Scholar]
- Kast, W.; Klan, H.; Thess, A. F2 Heat Transfer by Free Convection: External Flows. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 667–672. ISBN 978-3-540-77877-6. [Google Scholar]
- Siebers, D.L.; Schwind, R.G.; Moffatt, R.J. Experimental mixed convection heat transfer from a large, vertical surface in a horizontal flow. In Sandia Report; United States Department of Energy: Albuquerque, NJ, USA; Livermore, CA, USA, 1983. [Google Scholar] [CrossRef]
- Churchill, S.W. A comprehensive correlating equation for laminar, assisting, forced and free convection. Am. Inst. Chem. Eng. 1977, 23, 10–16. [Google Scholar] [CrossRef]
- Lévêque, A.M. Les lois de la transmission de chaleur par convection. Ann. Des Mines 1928, 13, 201–415. [Google Scholar]
- Sieder, E.N.; Tate, G.E. Heat Transfer and Pressure Drop of Liquids in Tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Drioli, E.; Di Profio, G.; Curcio, E. Membrane-Assisted Crystallization Technology; Imperial College Press: London, UK, 2015; ISBN 978-1-78326-331-8. [Google Scholar]
- Criscuoli, A.; Carnevale, M.C.; Drioli, E. Modeling the performance of flat and capillary membrane modules in vacuum membrane distillation. J. Membr. Sci. 2013, 447, 369–375. [Google Scholar] [CrossRef]
- Banat, F.A.; Al-Rub, F.A.A.; Jumah, R.; Al-Shannag, M. Modeling of Desalination Using Tubular Direct Contact Membrane Distillation Modules. Sep. Sci. Technol. 1999, 34, 2191–2206. [Google Scholar] [CrossRef]
- Li, B.; Sirkar, K.K. Novel membrane and device for vacuum membrane distillation-based desalination process. J. Membr. Sci. 2005, 257, 60–75. [Google Scholar] [CrossRef]
- Song, L.; Li, B.; Sirkar, K.K.; Gilron, J.L. Direct Contact Membrane Distillation-Based Desalination: Novel Membranes, Devices, Larger-Scale Studies, and a Model. Ind. Eng. Chem. Res. 2007, 46, 2307–2323. [Google Scholar] [CrossRef]
- Martin, H. The generalized Lévêque equation and its practical use for the prediction of heat and mass transfer rates from pressure drop. Chem. Eng. Sci. 2002, 57, 3217–3223. [Google Scholar] [CrossRef]
- Srisurichan, S.; Jiraratananon, R.; Fane, A.G. Mass transfer mechanisms and transport resistances in direct contact membrane distillation process. J. Membr. Sci. 2006, 277, 186–194. [Google Scholar] [CrossRef]
- Kimura, S.; Nakao, S.-I.; Shimatani, S.-I. Transport phenomena in membrane distillation. J. Membr. Sci. 1987, 33, 285–298. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Vázquez-González, M.I. Effects of Polarization on Mass Transport through Hydrophobic Porous Membranes. Ind. Eng. Chem. Res. 1998, 37, 4128–4135. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Florido-Díaz, F.J.; Vázquez-González, M.I. Study of Polarization Phenomena in Membrane Distillation of Aqueous Salt Solutions. Sep. Sci. Technol. 2000, 35, 1485–1501. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Vázquez-González, M.I. Temperature and concentration polarization in membrane distillation of aqueous salt solutions. J. Membr. Sci. 1999, 156, 265–273. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Florido-Díaz, F.J. Theoretical and experimental studies on desalination using membrane distillation. Desalination 2001, 139, 373–379. [Google Scholar] [CrossRef]
- Tomaszewska, M.; Gryta, M.; Morawski, A.W. A study of separation by the direct-contact membrane distillation process. Sep. Technol. 1994, 4, 244–248. [Google Scholar] [CrossRef]
- Tun, C.M.; Fane, A.G.; Matheickal, J.T.; Sheikholeslami, R. Membrane distillation crystallization of concentrated salts—Flux and crystal formation. J. Membr. Sci. 2005, 257, 144–155. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Desalination by Membrane Distillation: A Parametric Study. Sep. Sci. Technol. 1998, 33, 201–226. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Membrane distillation for dilute ethanol: Separation from aqueous streams. J. Membr. Sci. 1999, 163, 333–348. [Google Scholar] [CrossRef]
- Gröber, H.; Erk, S.; Grigull, U. Die Grundgesetze der Wärmeübertragung, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1963; ISBN 978-3-662-27528-3. [Google Scholar]
- Gnielinski, V. G4 Heat Transfer in Flow Past a Plane Wall. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 713–715. ISBN 978-3-540-77877-6. [Google Scholar]
- Pohlhausen, E. Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibung und kleiner Wärmeleitung. Z. Angew. Math. Mech. 1921, 1, 115–121. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Fell, C.J.D.; Franken, A.C.M. Optimal channel spacer design for ultrafiltration. J. Membr. Sci. 1991, 62, 275–291. [Google Scholar] [CrossRef]
- Hausen, H. Darstellung des Wärmeüberganges in Rohren durch verallgemeinerte Potenzbeziehungen. Z. VDI—Beih. Verfahrenstechnik 1943, 8, 91–98. [Google Scholar]
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill: Boston, MA, USA, 2010; ISBN 0073529362. [Google Scholar]
- Colburn, A.P. A method of correlating forced convection heat-transfer data and a comparison with fluid friction. Int. J. Heat Mass Transf. 1964, 7, 1359–1384. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Pervaporation and vacuum membrane distillation processes: Modeling and experiments. Am. Inst. Chem. Eng. 2004, 50, 1697–1712. [Google Scholar] [CrossRef]
- Lovineh, S.G.; Asghari, M.; Rajaei, B. Numerical simulation and theoretical study on simultaneous effects of operating parameters in vacuum membrane distillation. Desalination 2013, 314, 59–66. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Membr. Sci. 2003, 215, 75–85. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Nußelt, W. Der Wärmeaustausch zwischen Wand und Wasser im Rohr. Forsch. Geb. Ingenieurwesens A 1931, 2, 309–313. [Google Scholar] [CrossRef]
- Incropera, F.P.; Kerby, J.S.; Moffatt, D.F.; Ramadhyani, S. Convection heat transfer from discrete heat sources in a rectangular channel. Int. J. Heat Mass Transf. 1986, 29, 1051–1058. [Google Scholar] [CrossRef]
- Gnielinski, V. Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forsch. Ingenieurwesen A 1975, 41, 8–16. [Google Scholar] [CrossRef]
- Warsinger, D.E.M. Thermodynamic Design and Fouling of Membrane Distillation Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2015. [Google Scholar]
- Kast, W. L1 Pressure Drop in Single Phase Flow. In VDI Heat Atlas, 2nd ed.; Verein Deutscher Ingenieure (VDI) VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1055–1115. ISBN 978-3-540-77877-6. [Google Scholar]
- Taler, D. Determining velocity and friction factor for turbulent flow in smooth tubes. Int. J. Therm. Sci. 2016, 105, 109–122. [Google Scholar] [CrossRef]
- Moody, L.F. Friction factors for pipe flow. Trans. Am. Soc. Mech. Eng. 1944, 66, 671–684. [Google Scholar] [CrossRef]
- Petukhov, B.S. Heat Transfer and Friction in Turbulent Pipe Flow with Variable Physical Properties. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1970; pp. 503–564. [Google Scholar]
- Chernyshov, M.N.; Meindersma, G.W.; de Haan, A.B. Comparison of spacers for temperature polarization reduction in air gap membrane distillation. Desalination 2005, 183, 363–374. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering, 7th ed.; McGraw-Hill: Boston, MA, USA, 2005; ISBN 0072848235. [Google Scholar]
- Hufschmidt, W.; Burck, E. Der Einfluss temperaturabhängiger Stoffwerte auf den Wärmeübergang bei turbulenter Strömung von Flüssigkeiten in Rohren bei hohen Wärmestromdichten und Prandtlzahlen. Int. J. Heat Mass Transf. 1968, 11, 1041–1048. [Google Scholar] [CrossRef]
- Rohlfs, W.; Lienhard, V.J.H. Entrance length effects on Graetz number scaling in laminar duct flows with periodic obstructions: Transport number correlations for spacer-filled membrane channel flows. Int. J. Heat Mass Transf. 2016, 97, 842–852. [Google Scholar] [CrossRef]
- Da Costa, A.R. Fluid Flow and Mass Transfer in Spacer-Filled Channels for Ultrafiltration. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 1993. [Google Scholar]
- Li, F.; Meindersma, G.W.; de Haan, A.B.; Reith, T. Experimental validation of CFD mass transfer simulations in flat channels with non-woven net spacers. J. Membr. Sci. 2004, 232, 19–30. [Google Scholar] [CrossRef]
- Ang, W.L.; Mohammad, A.W. Mathematical modeling of membrane operations for water treatment. In Advances in Membrane Technologies for Water Treatment: Materials, Processes and Applications; Basile, A.B., Cassano, A., Rastogi, N.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 379–407. ISBN 9781782421214. [Google Scholar]
- Banat, F.A.; Al-Asheh, S.; Qtaishat, M.R. Treatment of waters colored with methylene blue dye by vacuum membrane distillation. Desalination 2005, 174, 87–96. [Google Scholar] [CrossRef]
- Lin, C.-J.; Shirazi, S.; Rao, P. Mechanistic Model for CaSO4 Fouling on Nanofiltration Membrane. J. Environ. Eng. 2005, 131, 1387–1392. [Google Scholar] [CrossRef]
- Lin, C.-J.; Shirazi, S.; Rao, P.; Agarwal, S. Effects of operational parameters on cake formation of CaSO4 in nanofiltration. Water Res. 2006, 40, 806–816. [Google Scholar] [CrossRef]
- Chilton, T.H.; Colburn, A.P. Mass Transfer (Absorption) Coefficients Prediction from Data on Heat Transfer and Fluid Friction. Ind. Eng. Chem. 1934, 26, 1183–1187. [Google Scholar] [CrossRef]
- Krömer, K.; Will, S.; Loisel, K.; Nied, S.; Detering, J.; Kempter, A.; Glade, H. Scale Formation and Mitigation of Mixed Salts in Horizontal Tube Falling Film Evaporators for Seawater Desalination. Heat Transf. Eng. 2015, 36, 750–762. [Google Scholar] [CrossRef]
- Sudoh, M.; Takuwa, K.; Iizuka, H.; Nagamatsuya, K. Effects of thermal and concentration boundary layers on vapor permeation in membrane distillation of aqueous lithium bromide solution. J. Membr. Sci. 1997, 131, 1–7. [Google Scholar] [CrossRef]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Tomaszewska, M.; Gryta, M.; Morawski, A.W. Study on the concentration of acids by membrane distillation. J. Membr. Sci. 1995, 102, 113–122. [Google Scholar] [CrossRef]
- Dittscher, U.; Woermann, D.; Wiedner, G. Temperature polarization in membrane distillation of water using a porous hydrophobic membrane. Berichte Bunsenges. Phys. Chem. 1994, 98, 1056–1061. [Google Scholar] [CrossRef]
- Tomaszewska, M.; Gryta, M.; Morawski, A.W. Mass transfer of HCl and H2O across the hydrophobic membrane during membrane distillation. J. Membr. Sci. 2000, 166, 149–157. [Google Scholar] [CrossRef]
- He, F.; Sirkar, K.K.; Gilron, J.L. Studies on scaling of membranes in desalination by direct contact membrane distillation: CaCO3 and mixed CaCO3/CaSO4 systems. Chem. Eng. Sci. 2009, 64, 1844–1859. [Google Scholar] [CrossRef]
- Žukauskas, A. Heat Transfer from Tubes in Crossflow. Adv. Heat Transf. 1987, 18, 87–159. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M. Heat transport in the membrane distillation process. J. Membr. Sci. 1998, 144, 211–222. [Google Scholar] [CrossRef]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Separation efficiency in vacuum membrane distillation. J. Membr. Sci. 1992, 73, 217–229. [Google Scholar] [CrossRef]
- Sarti, G.C.; Gostoli, C.; Bandini, S. Extraction of organic components from aqueous streams by vacuum membrane distillation. J. Membr. Sci. 1993, 80, 21–33. [Google Scholar] [CrossRef]
- Gryta, M. Fouling in direct contact membrane distillation process. J. Membr. Sci. 2008, 325, 383–394. [Google Scholar] [CrossRef]
- Kurokawa, H.; Kuroda, O.; Takahashi, S.; Ebara, K. Vapor Permeate Characteristics of Membrane Distillation. Sep. Sci. Technol. 1990, 25, 1349–1359. [Google Scholar] [CrossRef]
- Asghari, M.; Harandizadeh, A.; Dehghani, M.; Harami, H.R. Persian Gulf desalination using air gap membrane distillation: Numerical simulation and theoretical study. Desalination 2015, 374, 92–100. [Google Scholar] [CrossRef]
- Termpiyakul, P.; Jiraratananon, R.; Srisurichan, S. Heat and mass transfer characteristics of a direct contact membrane distillation process for desalination. Desalination 2005, 177, 133–141. [Google Scholar] [CrossRef]
- Gekas, V.; Hallström, B. Mass transfer in the membrane concentration polarization layer under turbulent cross flow: I. Critical literature review and adaptation of existing Sherwood correlations to membrane operations. J. Membr. Sci. 1987, 30, 153–170. [Google Scholar] [CrossRef]
- Khayet, M.; Velázquez, A.; Mengual, J.I. Modelling mass transport through a porous partition: Effect of pore size distribution. J. Non-Equilib. Thermodyn. 2004, 29, 279–299. [Google Scholar] [CrossRef]
- Aravinth, S. Prediction of heat and mass transfer for fully developed turbulent fluid flow through tubes. Int. J. Heat Mass Transf. 2000, 43, 1399–1408. [Google Scholar] [CrossRef]
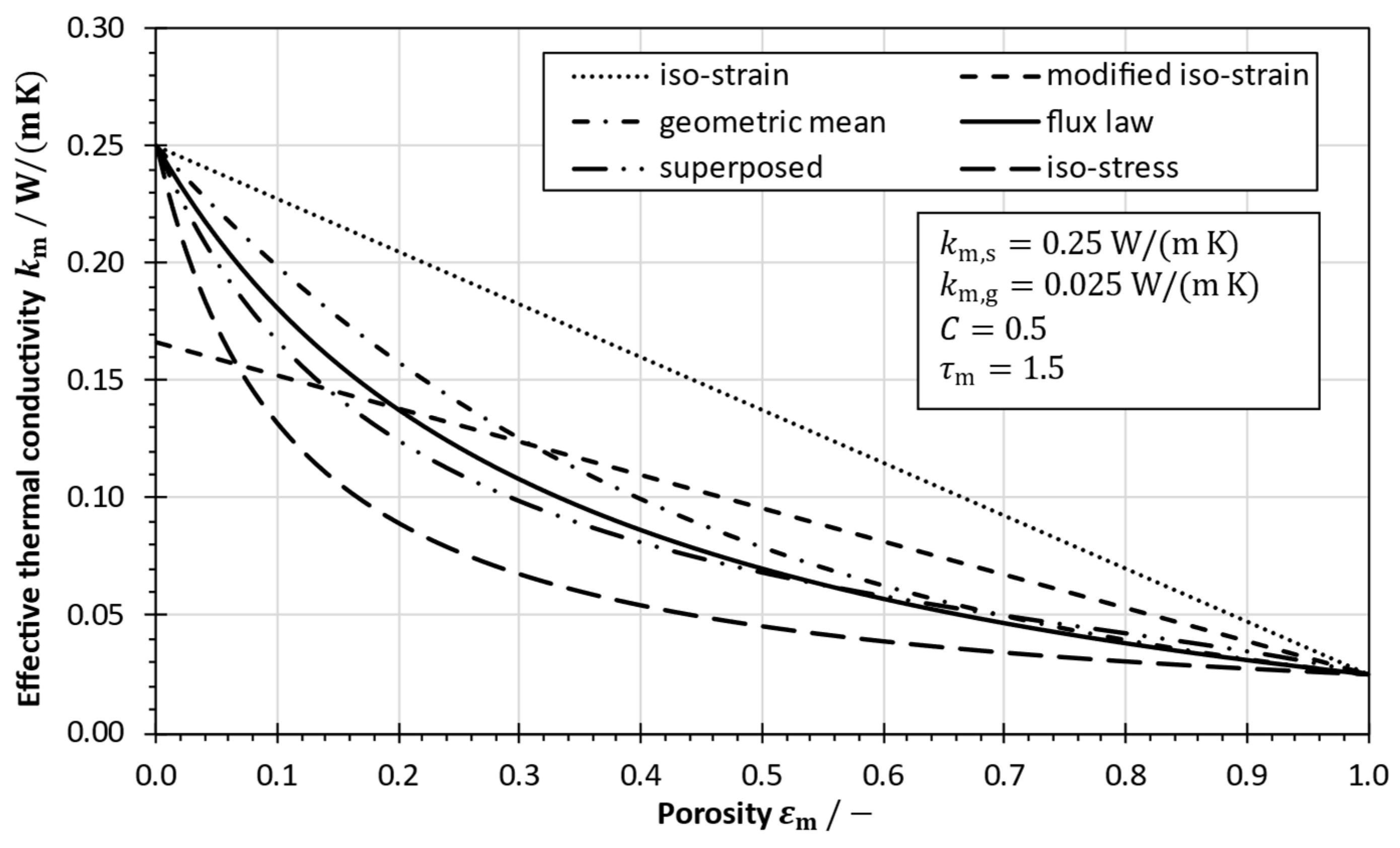
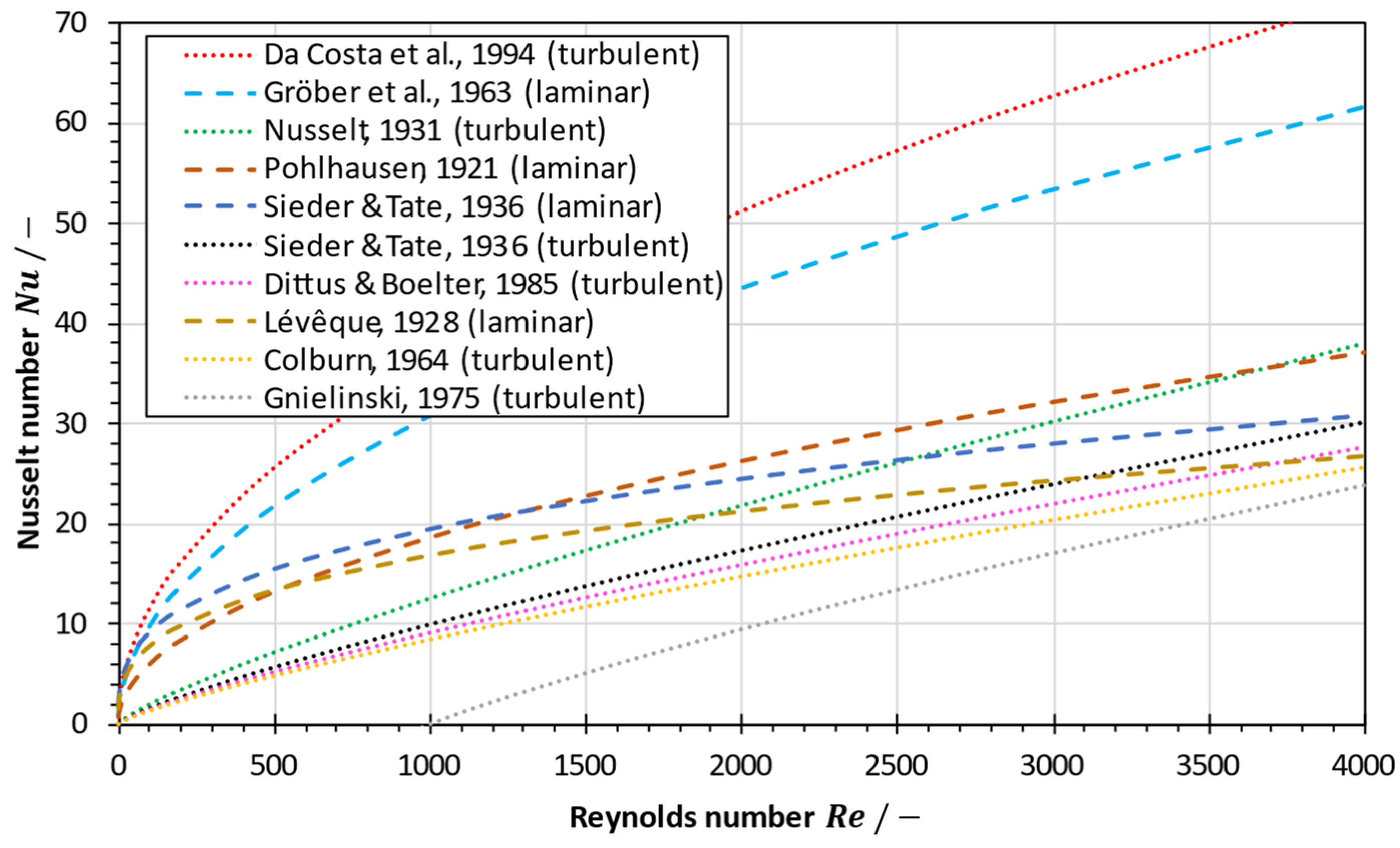

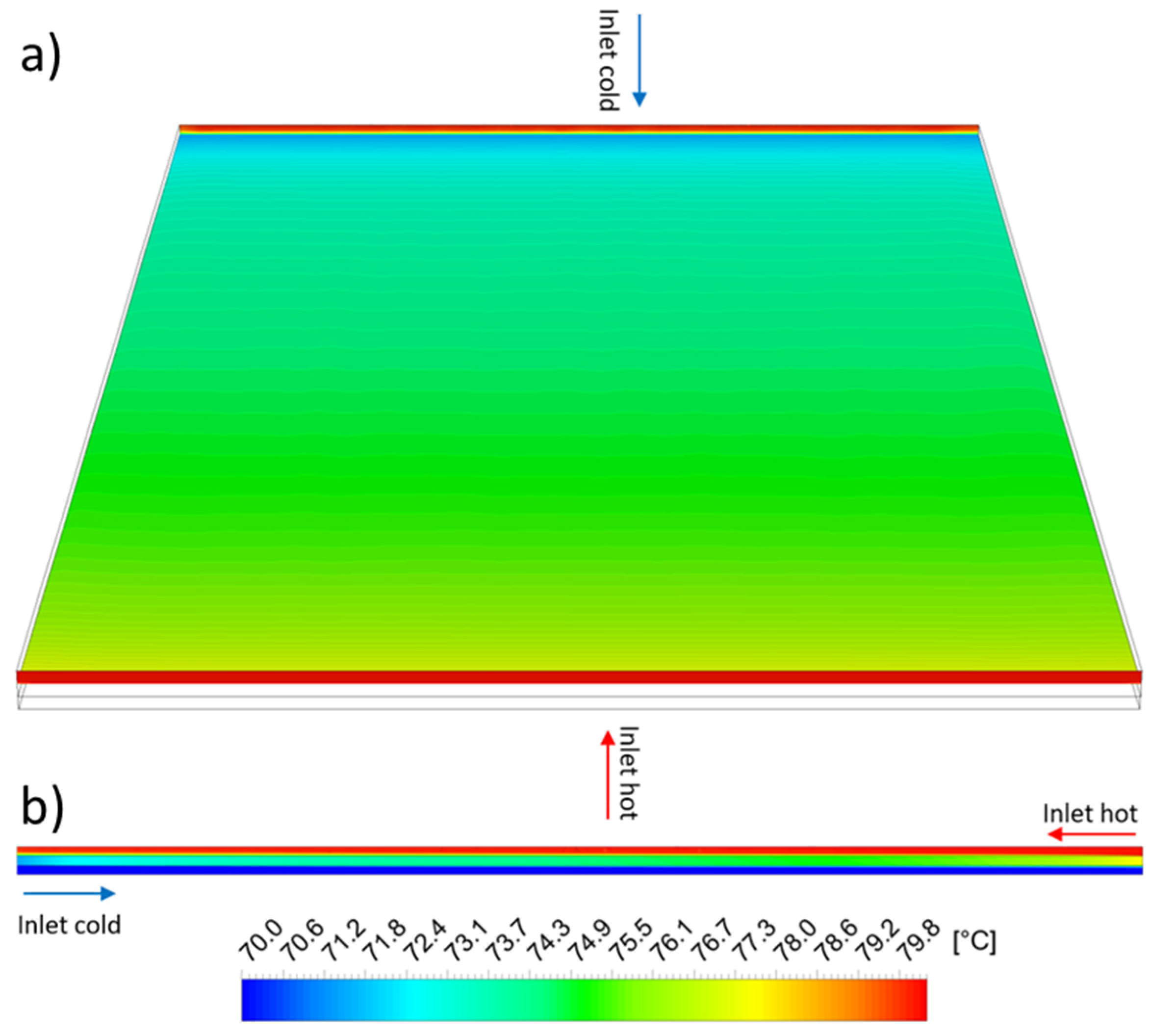
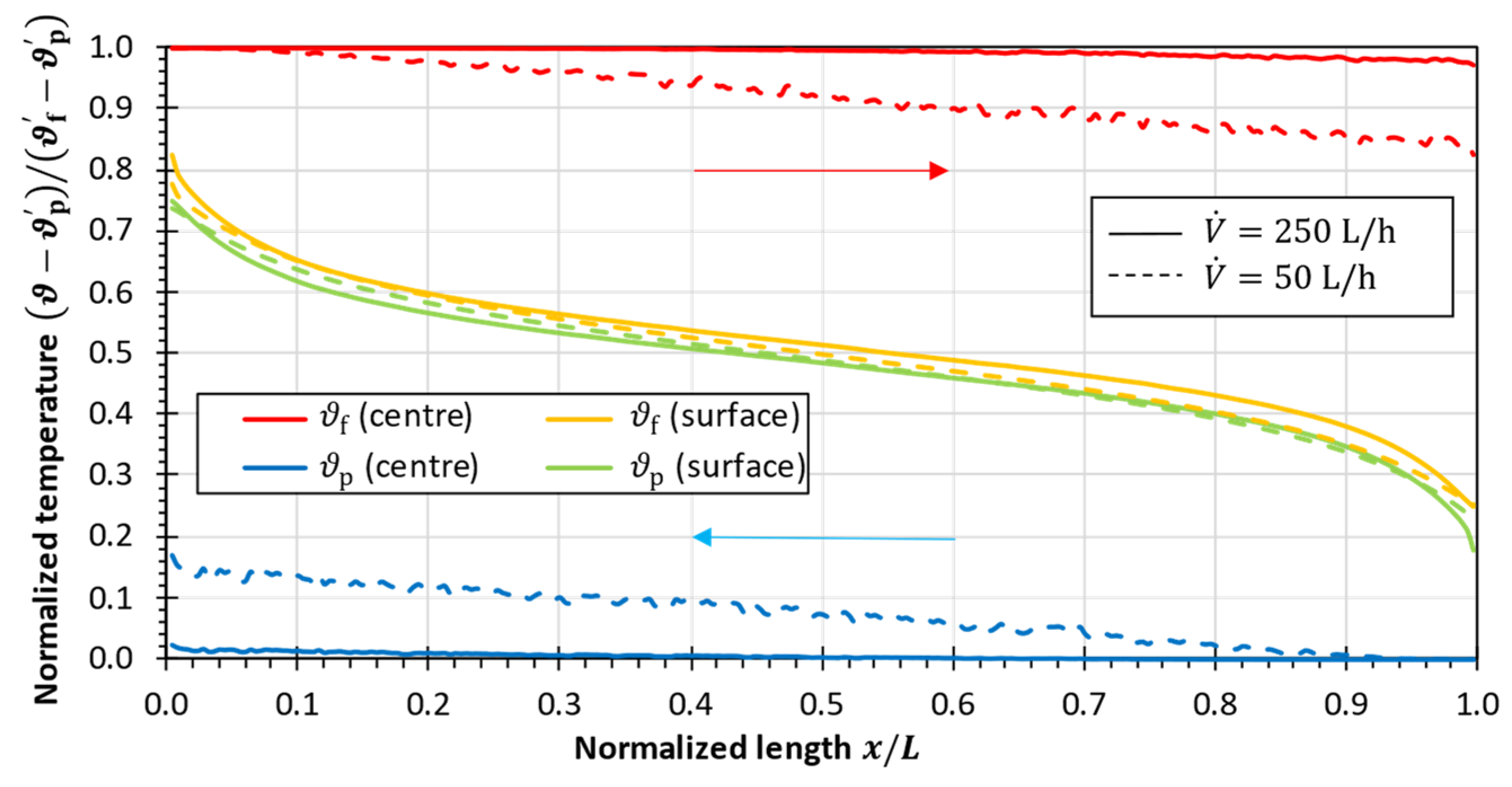


| Correlation for the Friction Factor | Comment | Reference | |
|---|---|---|---|
| (33) | Blasius equation | [80,92,93] | |
| (34) | Moody equation | [92,93] | |
| (35) | Hermann equation | [92] | |
| (36) | Konakov equation | [37] | |
| (37) | Filonienko equation | [27,43,80,90,92,94] | |
| (38) | Taler equation | [92] | |
| Constant | Value | 95% Lower Bound | 95% Upper Bound |
|---|---|---|---|
| 0.1580 | 0.1491 | 0.1669 | |
| 0.6521 | 0.6450 | 0.6592 | |
| 0.2767 | 0.2656 | 0.2877 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilling, S.; Glade, H. Review and Analysis of Heat Transfer in Spacer-Filled Channels of Membrane Distillation Systems. Membranes 2023, 13, 842. https://doi.org/10.3390/membranes13100842
Schilling S, Glade H. Review and Analysis of Heat Transfer in Spacer-Filled Channels of Membrane Distillation Systems. Membranes. 2023; 13(10):842. https://doi.org/10.3390/membranes13100842
Chicago/Turabian StyleSchilling, Sebastian, and Heike Glade. 2023. "Review and Analysis of Heat Transfer in Spacer-Filled Channels of Membrane Distillation Systems" Membranes 13, no. 10: 842. https://doi.org/10.3390/membranes13100842
APA StyleSchilling, S., & Glade, H. (2023). Review and Analysis of Heat Transfer in Spacer-Filled Channels of Membrane Distillation Systems. Membranes, 13(10), 842. https://doi.org/10.3390/membranes13100842






