Permeation Flux Prediction of Vacuum Membrane Distillation Using Hybrid Machine Learning Techniques
Abstract
:1. Introduction
2. Experimental Work
3. Artificial Intelligence-Based Models
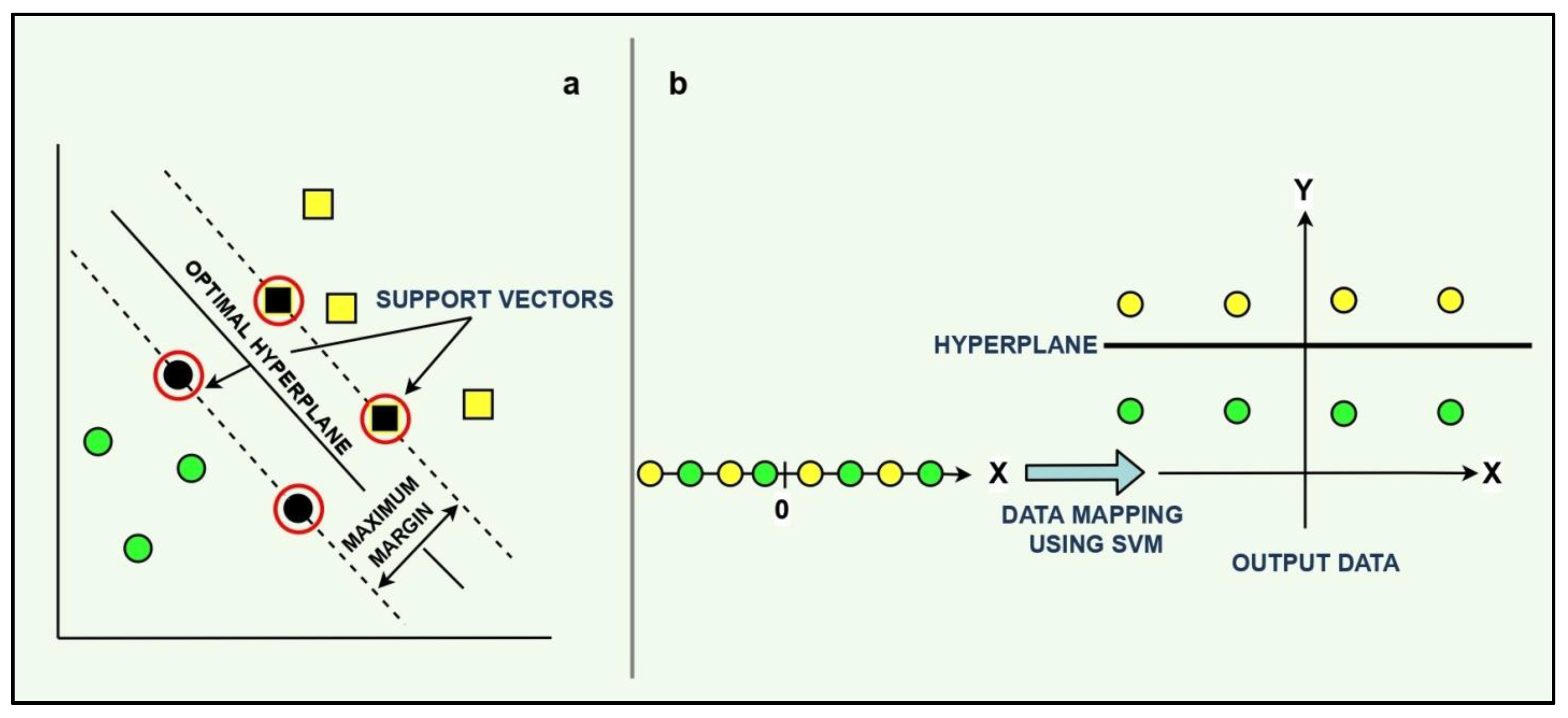
3.1. Support Vector Regression
3.2. Feed-Forward Neural Networks (FFNNs)
3.3. Multiple Linear Regression
3.4. Spotted Hyena Optimizer
3.4.1. Encircling
3.4.2. Hunting
3.4.3. Attacking
3.4.4. Searching
3.5. Model Development
4. Results and Discussion
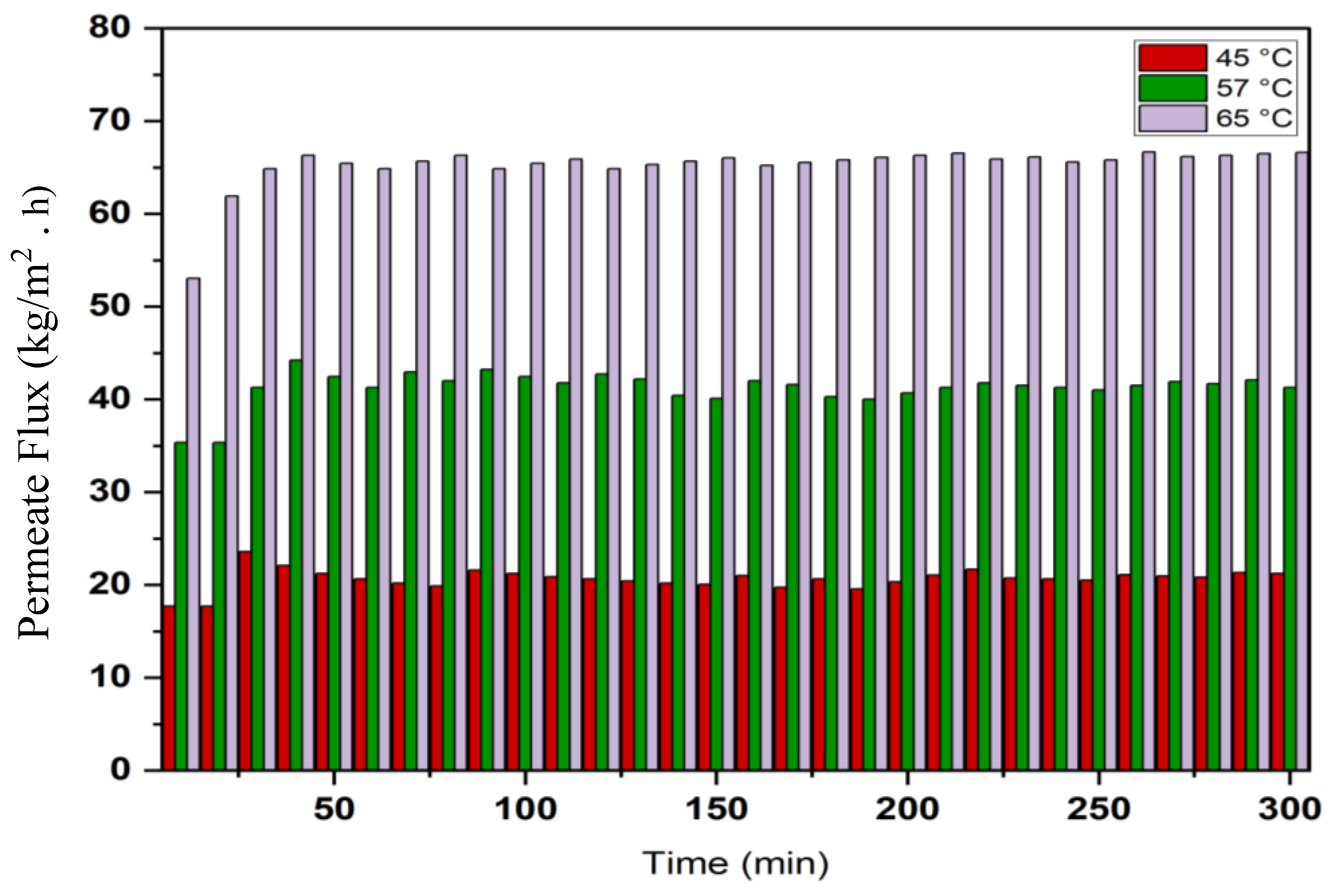
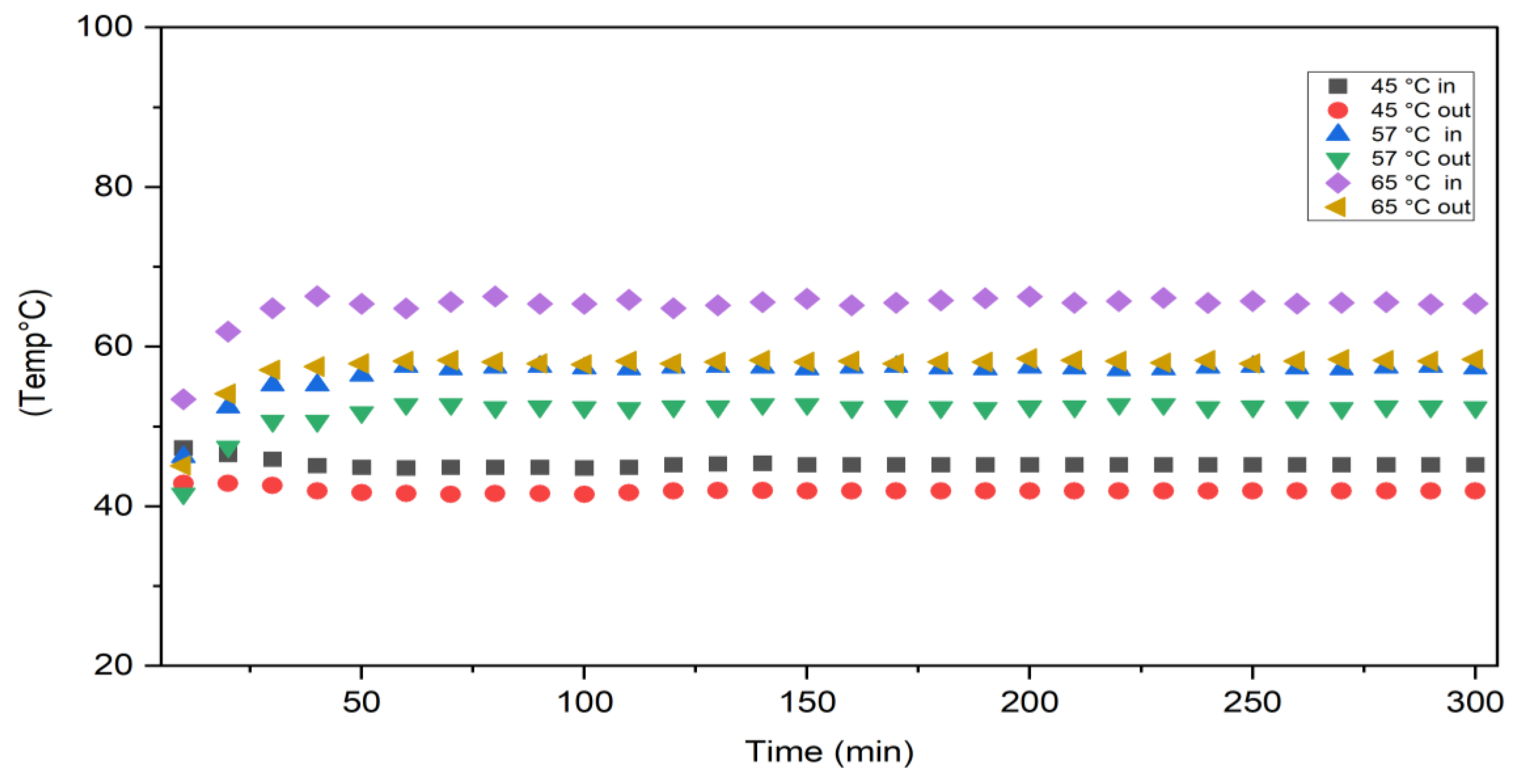
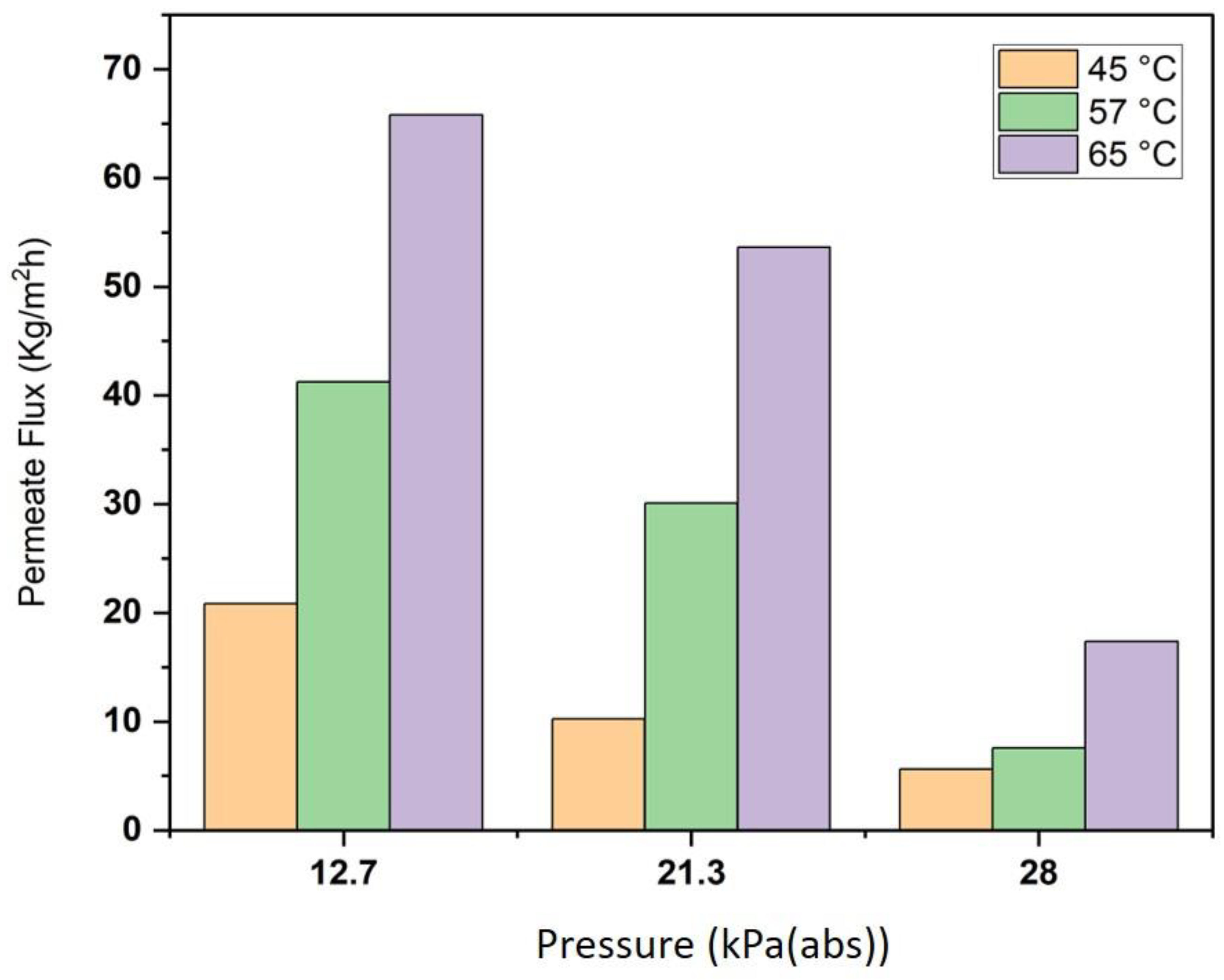
4.1. Experimental Results
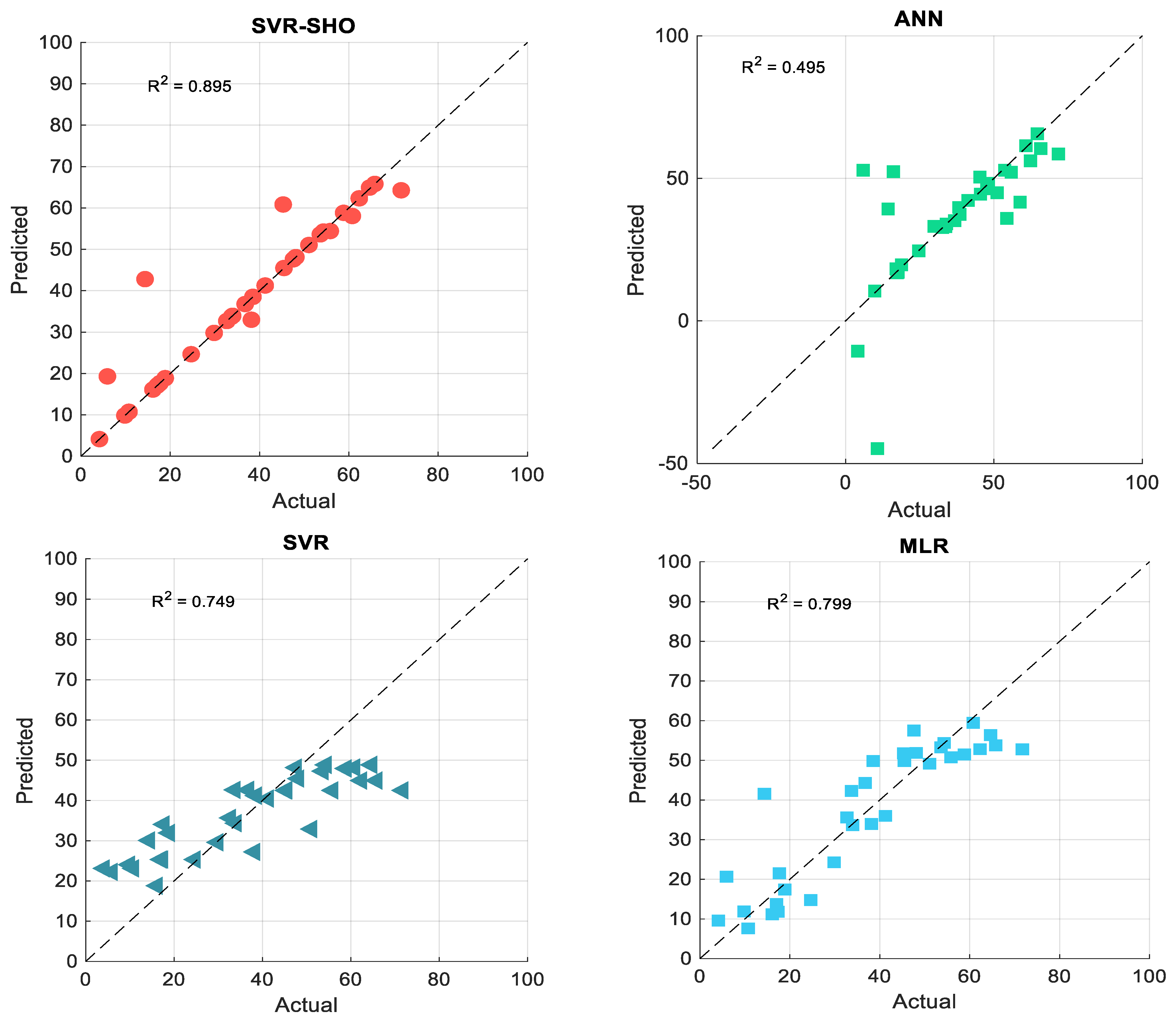
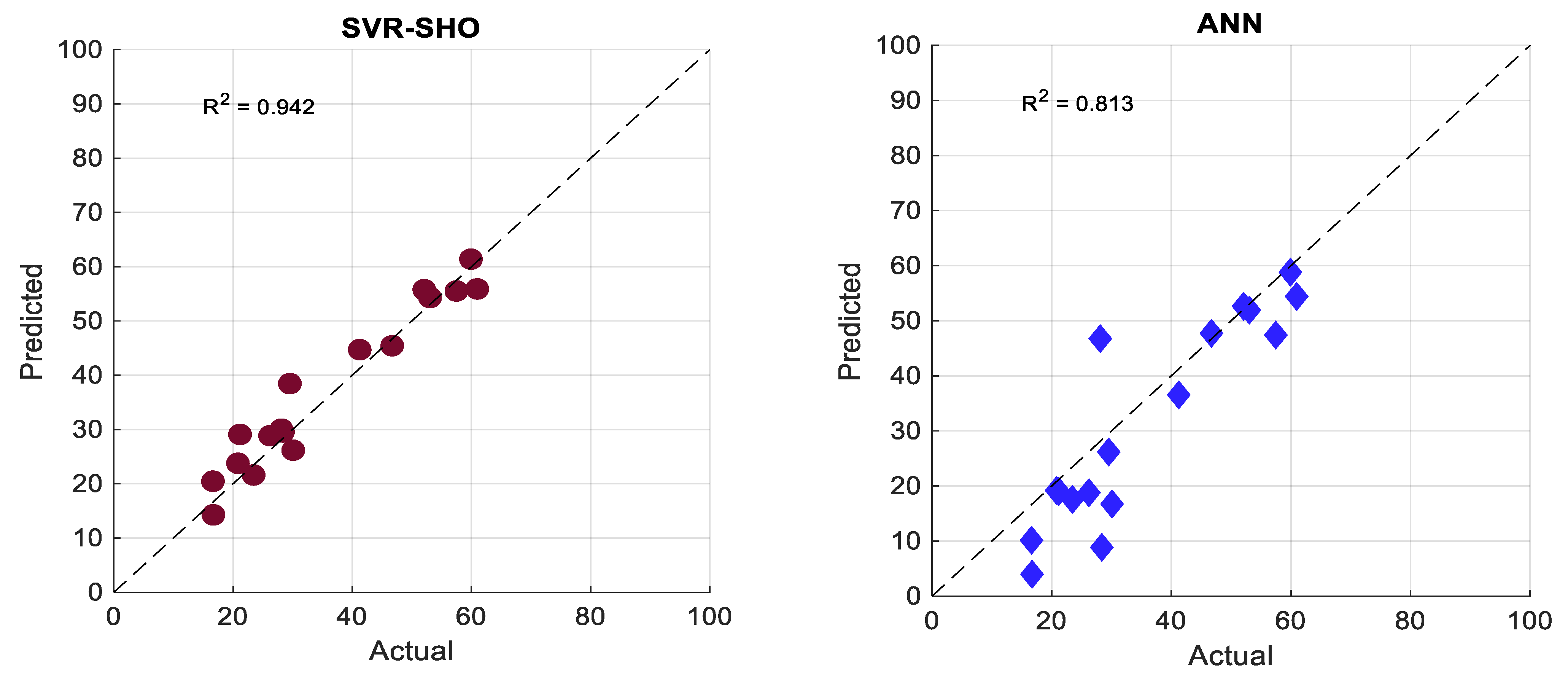
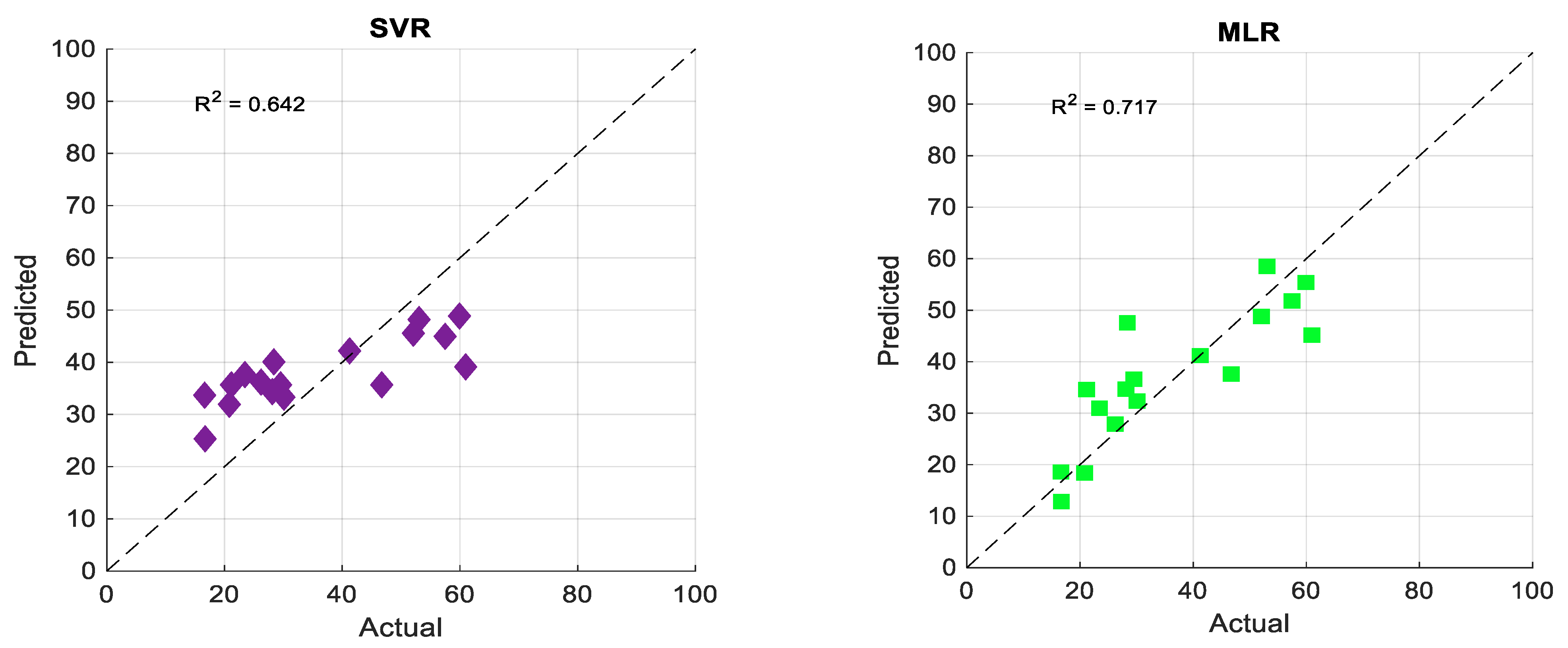
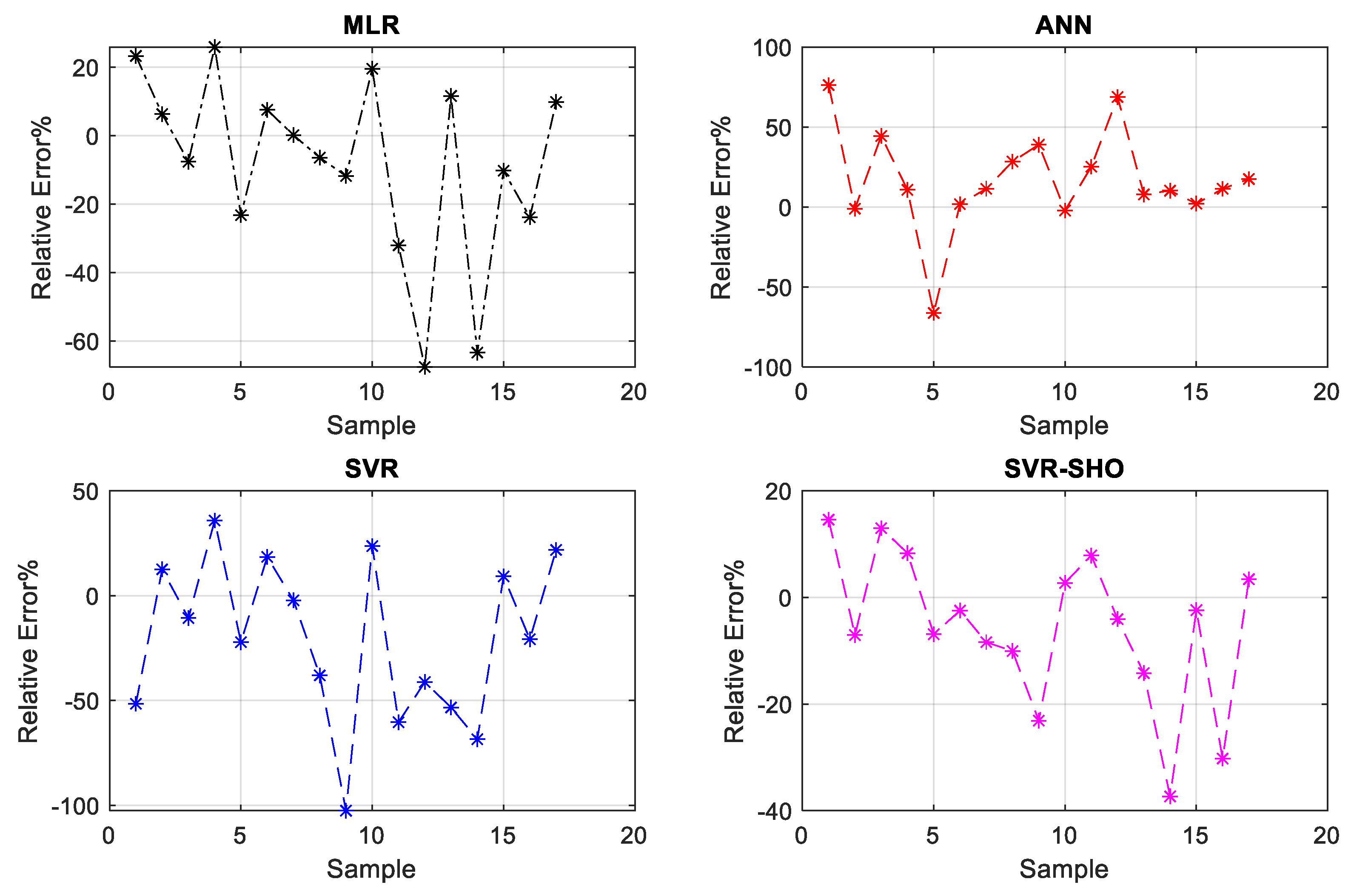
4.2. Artificial Intelligent-Based Models
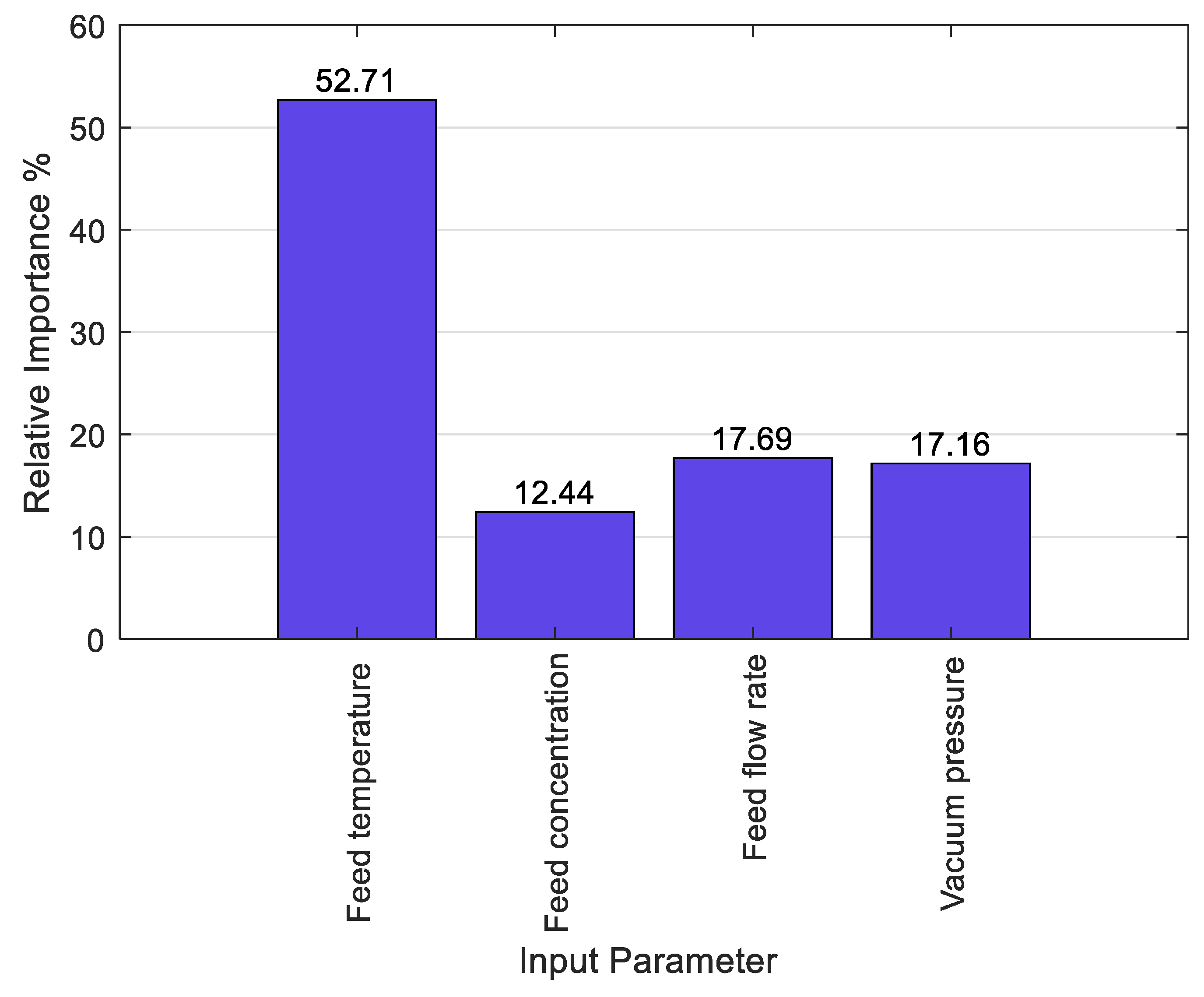
4.3. Impact of Operating Parameters on Flux
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aljumaily, M.M.; Alayan, H.M.; Mohammed, A.A.; Alsaadi, M.A.; Alsalhy, Q.F.; Figoli, A.; Criscuoli, A. The influence of coating super-hydrophobic carbon nanomaterials on the performance of membrane distillation. Appl. Water Sci. 2022, 12, 28. [Google Scholar] [CrossRef]
- Rohani, R.; Yusoff, I.I.; Khairul Zaman, N.; Mahmood Ali, A.; Rusli, N.A.B.; Tajau, R.; Basiron, S.A. Ammonia removal from raw water by using adsorptive membrane filtration process. Sep. Purif. Technol. 2021, 270, 118757. [Google Scholar] [CrossRef]
- Aljanabi, A.A.A.; Mousa, N.E.; Aljumaily, M.M.; Majdi, H.S.; Yahya, A.A.; Al-Baiati, M.N.; Hashim, N.; Rashid, K.T.; Al-Saadi, S.; Alsalhy, Q.F. Modification of Polyethersulfone Ultrafiltration Membrane Using Poly (terephthalic acid-co-glycerol-g-maleic anhydride) as Novel Pore Former. Polymers 2022, 14, 3408. [Google Scholar] [CrossRef] [PubMed]
- Altaee, A.; Alhathal Alanezi, A.; Alqahs Alanezi, Y.; Alazmi, R.; Alsalhy, Q.; Sharif, A. Enhancing Performance of the Membrane Distillation Process using Air Injection Zigzag System for Water Desalination. Desalination Water Treat. 2020, 207, 43–50. [Google Scholar]
- Abujazar, M.S.S.; Fatihah, S.; Kabeel, A.E. Seawater desalination using inclined stepped solar still with copper trays in a wet tropical climate. Desalination 2017, 423, 141–148. [Google Scholar] [CrossRef]
- Mahdavi, M.; Mahvi, A.H.; Nasseri, S.; Yunesian, M. Application of freezing to the desalination of saline water. Arab. J. Sci. Eng. 2011, 36, 1171–1177. [Google Scholar] [CrossRef]
- Aljumaily, M.M.; Ali, N.S.; Mahdi, A.E.; Alayan, H.M.; AlOmar, M.; Hameed, M.M.; Ismael, B.; Alsalhy, Q.F.; Alsaadi, M.A.; Majdi, H.S. Modification of Poly (vinylidene fluoride-co-hexafluoropropylene) Membranes with DES-Functionalized Carbon Nanospheres for Removal of Methyl Orange by Membrane Distillation. Water 2022, 14, 1396. [Google Scholar] [CrossRef]
- Jamed, M.J.; Alhathal Alanezi, A.; Alsalhy, Q.F. Effects of embedding functionalized multi-walled carbon nanotubes and alumina on the direct contact poly (vinylidene fluoride-co-hexafluoropropylene) membrane distillation performance. Chem. Eng. Commun. 2019, 206, 1035–1057. [Google Scholar] [CrossRef]
- Madalosso, H.B.; Machado, R.; Hotza, D.; Marangoni, C. Membrane Surface Modification by Electrospinning, Coating, and Plasma for Membrane Distillation Applications: A State-of-the-Art Review. Adv. Eng. Mater. 2021, 23, 2001456. [Google Scholar] [CrossRef]
- Alsalhy, Q.F.; Rashid, K.T.; Ibrahim, S.S.; Ghanim, A.H.; Van der Bruggen, B.; Luis, P.; Zablouk, M. Poly (vinylidene fluoride-co-hexafluoropropylene)(PVDF-co-HFP) hollow fiber membranes prepared from PVDF-co-HFP/PEG-600Mw/DMAC solution for membrane distillation. J. Appl. Polym. Sci. 2013, 129, 3304–3313. [Google Scholar] [CrossRef]
- Francis, L.; Ahmed, F.E.; Hilal, N. Electrospun membranes for membrane distillation: The state of play and recent advances. Desalination 2022, 526, 115511. [Google Scholar] [CrossRef]
- Alsalhy, Q.F.; Ibrahim, S.S.; Hashim, F.A. Experimental and theoretical investigation of air gap membrane distillation process for water desalination. Chem. Eng. Res. Des. 2018, 130, 95–108. [Google Scholar] [CrossRef]
- Safi, N.N.; Ibrahim, S.S.; Zouli, N.; Majdi, H.S.; Alsalhy, Q.F.; Drioli, E.; Figoli, A. A systematic framework for optimizing a sweeping gas membrane distillation (SGMD). Membranes 2020, 10, 254. [Google Scholar] [CrossRef] [PubMed]
- Ghaffour, N.; Soukane, S.; Lee, J.-G.; Kim, Y.; Alpatova, A. Membrane distillation hybrids for water production and energy efficiency enhancement: A critical review. Appl. Energy 2019, 254, 113698. [Google Scholar] [CrossRef]
- Mohanadas, D.; Nordin, P.M.I.; Rohani, R.; Dzulkharnien, N.S.F.; Mohammad, A.W.; Mohamed Abdul, P.; Abu Bakar, S. A Comparison between Various Polymeric Membranes for Oily Wastewater Treatment via Membrane Distillation Process. Membranes 2022, 13, 46. [Google Scholar] [CrossRef]
- Andrés-Mañas, J.; Ruiz-Aguirre, A.; Acién, F.; Zaragoza, G. Performance increase of membrane distillation pilot scale modules operating in vacuum-enhanced air-gap configuration. Desalination 2020, 475, 114202. [Google Scholar] [CrossRef]
- Alayan, H.M.; Aljumaily, M.M.; Alsaadi, M.A.; Mjalli, F.S.; Hashim, M.A. A review exploring the adsorptive removal of organic micropollutants on tailored hierarchical carbon nanotubes. Toxicol. Environ. Chem. 2021, 103, 295–338. [Google Scholar] [CrossRef]
- Alayan, H.; Aljumaily, M.M.; Alsaadi, M.A.; Hashim, M.A. Probing the Effect of Gaseous Hydrocarbon Precursors on the Adsorptive Efficiency of Synthesized Carbon-Based Nanomaterials. J. Eng. Res. 2020, 17, 47–58. [Google Scholar] [CrossRef]
- Ahmad, N.N.R.; Ang, W.L.; Leo, C.P.; Mohammad, A.W.; Hilal, N. Current advances in membrane technologies for saline wastewater treatment: A comprehensive review. Desalination 2021, 517, 115170. [Google Scholar] [CrossRef]
- Arumugham, T.; Kaleekkal, N.J.; Gopal, S.; Nambikkattu, J.; Rambabu, K.; Aboulella, A.M.; Wickramasinghe, S.R.; Banat, F. Recent developments in porous ceramic membranes for wastewater treatment and desalination: A review. J. Environ. Manag. 2021, 293, 112925. [Google Scholar] [CrossRef]
- Ahmed, F.E.; Hashaikeh, R.; Diabat, A.; Hilal, N. Mathematical and optimization modelling in desalination: State-of-the-art and future direction. Desalination 2019, 469, 114092. [Google Scholar] [CrossRef]
- Ibrahim, S.S.; Alsalhy, Q.F. Modeling and simulation for direct contact membrane distillation in hollow fiber modules. AIChE J. 2013, 59, 589–603. [Google Scholar] [CrossRef]
- Dong, Y.; Dai, X.; Zhao, L.; Gao, L.; Xie, Z.; Zhang, J. Review of transport phenomena and popular modelling approaches in membrane distillation. Membranes 2021, 11, 122. [Google Scholar] [CrossRef] [PubMed]
- Papapicco, D.; Demo, N.; Girfoglio, M.; Stabile, G.; Rozza, G. The Neural Network shifted-proper orthogonal decomposition: A machine learning approach for non-linear reduction of hyperbolic equations. Comput. Methods Appl. Mech. Eng. 2022, 392, 114687. [Google Scholar] [CrossRef]
- Maslahati Roudi, A.; Chelliapan, S.; Wan Mohtar, W.H.M.; Kamyab, H. Prediction and optimization of the fenton process for the treatment of landfill leachate using an artificial neural network. Water 2018, 10, 595. [Google Scholar] [CrossRef]
- Orrù, G.; Monaro, M.; Conversano, C.; Gemignani, A.; Sartori, G. Machine learning in psychometrics and psychological research. Front. Psychol. 2020, 10, 2970. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C. Artificial neural network modeling and optimization of desalination by air gap membrane distillation. Sep. Purif. Technol. 2012, 86, 171–182. [Google Scholar] [CrossRef]
- Yusuf, A.; Sodiq, A.; Giwa, A.; Eke, J.; Pikuda, O.; De Luca, G.; Di Salvo, J.L.; Chakraborty, S. A review of emerging trends in membrane science and technology for sustainable water treatment. J. Clean. Prod. 2020, 266, 121867. [Google Scholar] [CrossRef]
- Nasir, T.; Asmaela, M.; Zeeshana, Q.; Solyalib, D. Applications of machine learning to friction stir welding process optimization. J. Kejuruter. 2020, 32, 171–186. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Javaid Zaidi, S. Artificial neural network modeling of wastewater treatment and desalination using membrane processes: A review. Chem. Eng. J. 2021, 419, 129540. [Google Scholar] [CrossRef]
- Hameed, M.; Sharqi, S.S.; Yaseen, Z.M.; Afan, H.A.; Hussain, A.; Elshafie, A. Application of artificial intelligence (AI) techniques in water quality index prediction: A case study in tropical region, Malaysia. Neural Comput. Appl. 2017, 28, 893–905. [Google Scholar] [CrossRef]
- Sheikh Khozani, Z.; Hosseinjanzadeh, H.; Wan Mohtar, W.H.M. Shear force estimation in rough boundaries using SVR method. Appl. Water Sci. 2019, 9, 186. [Google Scholar] [CrossRef]
- Alomar, M.K.; Khaleel, F.; Aljumaily, M.M.; Masood, A.; Razali, S.F.M.; AlSaadi, M.A.; Al-Ansari, N.; Hameed, M.M. Data-driven models for atmospheric air temperature forecasting at a continental climate region. PLoS ONE 2022, 17, e0277079. [Google Scholar] [CrossRef] [PubMed]
- Titah, H.S.; Halmi, M.I.E.B.; Abdullah, S.R.S.; Hasan, H.A.; Idris, M.; Anuar, N. Statistical optimization of the phytoremediation of arsenic by Ludwigia octovalvis- in a pilot reed bed using response surface methodology (RSM) versus an artificial neural network (ANN). Int. J. Phytoremediation 2018, 20, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Fang, T.; Lahdelma, R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system. Appl. Energy 2016, 179, 544–552. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Dafinescu, V. Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 2021, 9, 2335. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer for solving complex and non-linear constrained engineering problems. In Harmony Search and Nature Inspired Optimization Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 857–867. [Google Scholar]
- Hameed, M.M.; Razali, S.F.M.; Mohtar, W.H.M.W.; Rahman, N.A.; Yaseen, Z.M. Machine learning models development for accurate multi-months ahead drought forecasting: Case study of the Great Lakes, North America. PLoS ONE 2023, 18, e0290891. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Dai, H.-L.; Heddam, S.; Masood, A.; Kisi, O. Enhancing accuracy of extreme learning machine in predicting river flow using improved reptile search algorithm. Stoch. Environ. Res. Risk Assess. 2023, 37, 3063–3083. [Google Scholar] [CrossRef]
- Hameed, M.M.; AlOmar, M.K.; Al-Saadi, A.A.A.; AlSaadi, M.A. Inflow forecasting using regularized extreme learning machine: Haditha reservoir chosen as case study. Stoch. Environ. Res. Risk Assess. 2022, 36, 4201–4221. [Google Scholar] [CrossRef]
- Hameed, M.M.; Khaleel, F.; AlOmar, M.K.; Mohd Razali, S.F.; AlSaadi, M.A. Optimising the Selection of Input Variables to Increase the Predicting Accuracy of Shear Strength for Deep Beams. Complexity 2022, 2022, 6532763. [Google Scholar] [CrossRef]
- AlOmar, M.K.; Hameed, M.M.; Al-Ansari, N.; AlSaadi, M.A. Data-Driven Model for the Prediction of Total Dissolved Gas: Robust Artificial Intelligence Approach. Adv. Civ. Eng. 2020, 2020, 6618842. [Google Scholar] [CrossRef]
- Hameed, M.M.; AlOmar, M.K.; Mohd Razali, S.F.; Kareem Khalaf, M.A.; Baniya, W.J.; Sharafati, A.; AlSaadi, M.A. Application of Artificial Intelligence Models for Evapotranspiration Prediction along the Southern Coast of Turkey. Complexity 2021, 2021, 8850243. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. Data-driven predictive modeling of PM2.5 concentrations using machine learning and deep learning techniques: A case study of Delhi, India. Environ. Monit. Assess. 2022, 195, 60. [Google Scholar] [CrossRef] [PubMed]
- Masood, A.; Ahmad, K. Prediction of PM2.5 concentrations using soft computing techniques for the megacity Delhi, India. Stoch. Environ. Res. Risk Assess. 2023, 37, 625–638. [Google Scholar] [CrossRef]
- Ghafori, S.; Gharehchopogh, F.S. Advances in Spotted Hyena Optimizer: A Comprehensive Survey. Arch. Comput. Methods Eng. 2022, 29, 1569–1590. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Wang, Y.; Hariri-Ardebili, M.A. Prediction, monitoring, and interpretation of dam leakage flow via adaptative kernel extreme learning machine. Measurement 2020, 166, 108161. [Google Scholar] [CrossRef]




| Data | Parameter | Type | Mean | Minimum | Maximum | Standard Deviation |
|---|---|---|---|---|---|---|
| Training data | Feed temperature (°C)) | Input | 56.85 | 45.00 | 65.00 | 8.22 |
| Feed concentration (g/L) | 51.52 | 0.00 | 100.00 | 32.12 | ||
| Feed permeate flux (L/min) | 0.52 | 0.30 | 0.60 | 0.10 | ||
| Vacuum pressure (kPa (abs)) | 15.39 | 12.70 | 28.00 | 5.10 | ||
| Permeate flux (kg/m2 h) | Output | 35.14 | 5.92 | 62.32 | 17.04 | |
| Testing data | Feed temperature (°C)) | Input | 59.83 | 50.00 | 65.00 | 6.21 |
| Feed concentration (g/L) | 63.33 | 35.00 | 100.00 | 24.83 | ||
| Feed permeate flux (L/min) | 0.55 | 0.40 | 0.60 | 0.08 | ||
| Vacuum pressure (kPa (abs)) | 12.70 | 12.70 | 12.70 | 0.00 | ||
| Permeate flux (kg/m2 h) | Output | 47.49 | 23.47 | 71.72 | 19.32 |
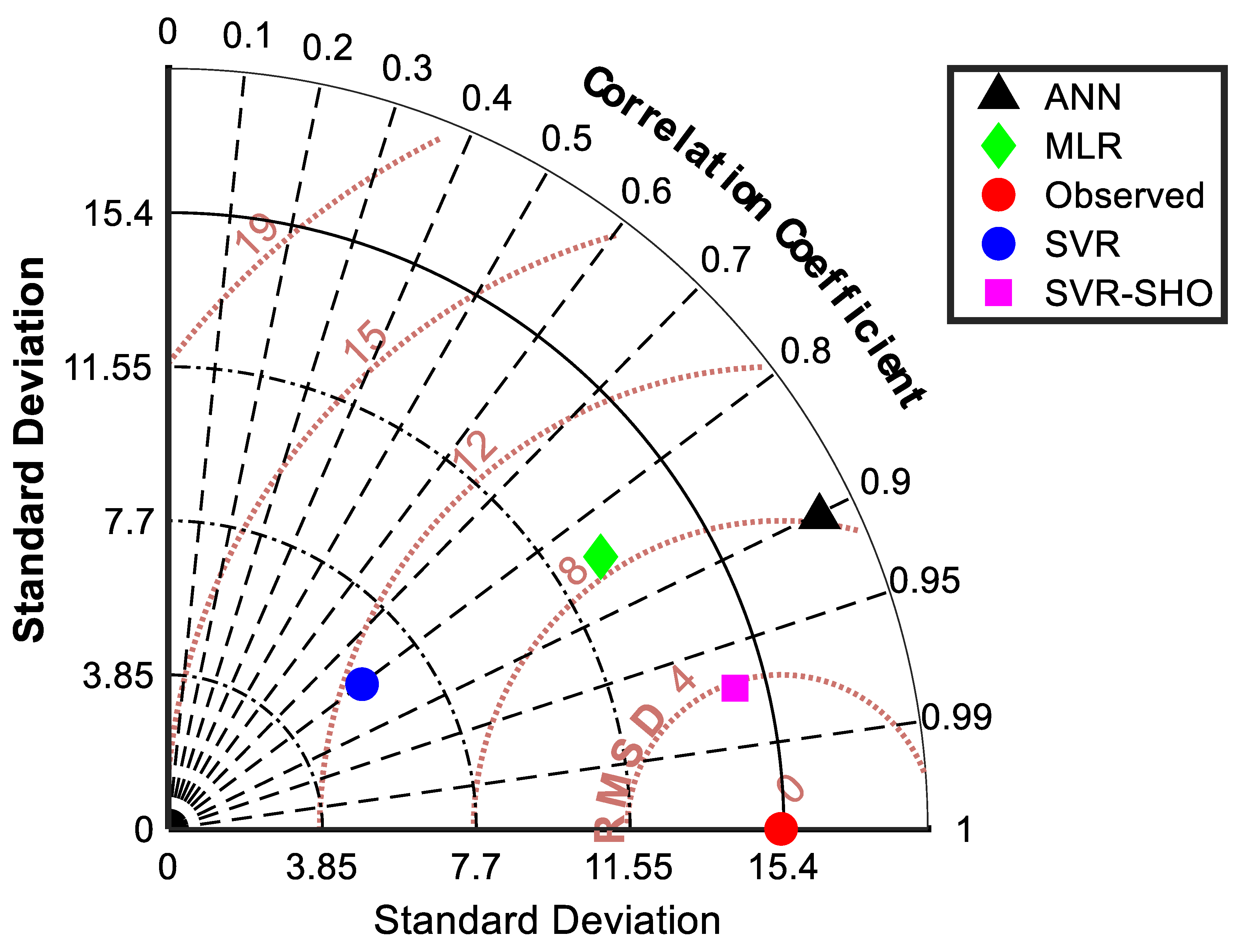
| Models/Performance Indicator | MAE | RMSE | MAPE% | R | WI |
|---|---|---|---|---|---|
| MLR | 6.554 | 8.607 | 31.9 | 0.894 | 0.942 |
| ANN | 8.238 | 15.974 | 68.4 | 0.704 | 0.834 |
| SVR | 9.651 | 12.031 | 52.6 | 0.865 | 0.815 |
| SVR–SHO | 2.262 | 6.330 | 14.9 | 0.946 | 0.971 |
| Models/Performance Indicator | MAE | RMSE | MAPE% | R | WI |
|---|---|---|---|---|---|
| MLR | 6.466 | 8.250 | 20.6 | 0.847 | 0.910 |
| ANN | 6.846 | 9.043 | 25.0 | 0.902 | 0.926 |
| SVR | 10.087 | 11.292 | 34.9 | 0.801 | 0.709 |
| SVR–SHO | 3.278 | 3.931 | 11.5 | 0.971 | 0.983 |
| Model | Hyperparameters |
|---|---|
| SVR–SHO | 1. Kernel Scale is 0.8940 |
| 2. Box Constraint is 2.2599 | |
| 3. Epsilon is 1 × 10−4 | |
| SVR | 1. Kernel Scale is 1 |
| 2. Box Constraint is 0.2684 | |
| 3. Epsilon is 0.0268 | |
| ANN | 1. Hidden Layer is 8 2. Transfer Function is hyperbolic tangent sigmoid 3. Algorithm is Levenberg–Marquardt |
| SHO | 1. Number of Search Agents (population) is 14 2. Maximum Number of Iterations is 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismael, B.H.; Khaleel, F.; Ibrahim, S.S.; Khaleel, S.R.; AlOmar, M.K.; Masood, A.; Aljumaily, M.M.; Alsalhy, Q.F.; Mohd Razali, S.F.; Al-Juboori, R.A.; et al. Permeation Flux Prediction of Vacuum Membrane Distillation Using Hybrid Machine Learning Techniques. Membranes 2023, 13, 900. https://doi.org/10.3390/membranes13120900
Ismael BH, Khaleel F, Ibrahim SS, Khaleel SR, AlOmar MK, Masood A, Aljumaily MM, Alsalhy QF, Mohd Razali SF, Al-Juboori RA, et al. Permeation Flux Prediction of Vacuum Membrane Distillation Using Hybrid Machine Learning Techniques. Membranes. 2023; 13(12):900. https://doi.org/10.3390/membranes13120900
Chicago/Turabian StyleIsmael, Bashar H., Faidhalrahman Khaleel, Salah S. Ibrahim, Samraa R. Khaleel, Mohamed Khalid AlOmar, Adil Masood, Mustafa M. Aljumaily, Qusay F. Alsalhy, Siti Fatin Mohd Razali, Raed A. Al-Juboori, and et al. 2023. "Permeation Flux Prediction of Vacuum Membrane Distillation Using Hybrid Machine Learning Techniques" Membranes 13, no. 12: 900. https://doi.org/10.3390/membranes13120900
APA StyleIsmael, B. H., Khaleel, F., Ibrahim, S. S., Khaleel, S. R., AlOmar, M. K., Masood, A., Aljumaily, M. M., Alsalhy, Q. F., Mohd Razali, S. F., Al-Juboori, R. A., Hameed, M. M., & Alsarayreh, A. A. (2023). Permeation Flux Prediction of Vacuum Membrane Distillation Using Hybrid Machine Learning Techniques. Membranes, 13(12), 900. https://doi.org/10.3390/membranes13120900











