Membranes for Osmotic Power Generation by Reverse Electrodialysis
Abstract
:1. Introduction
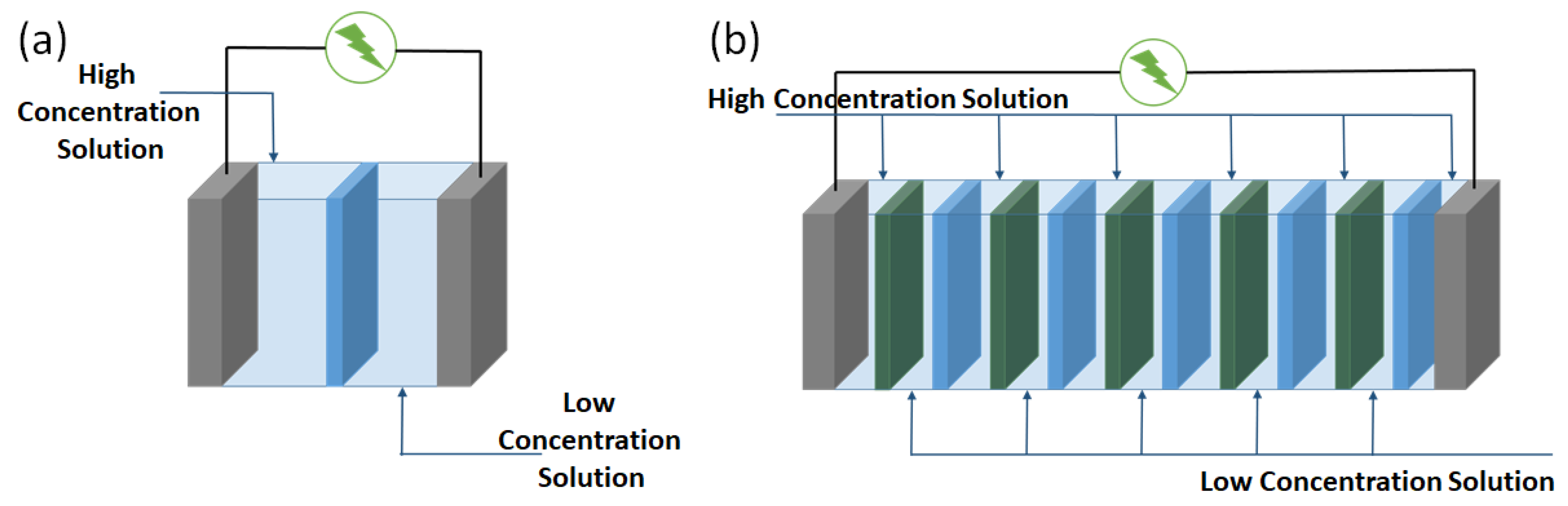
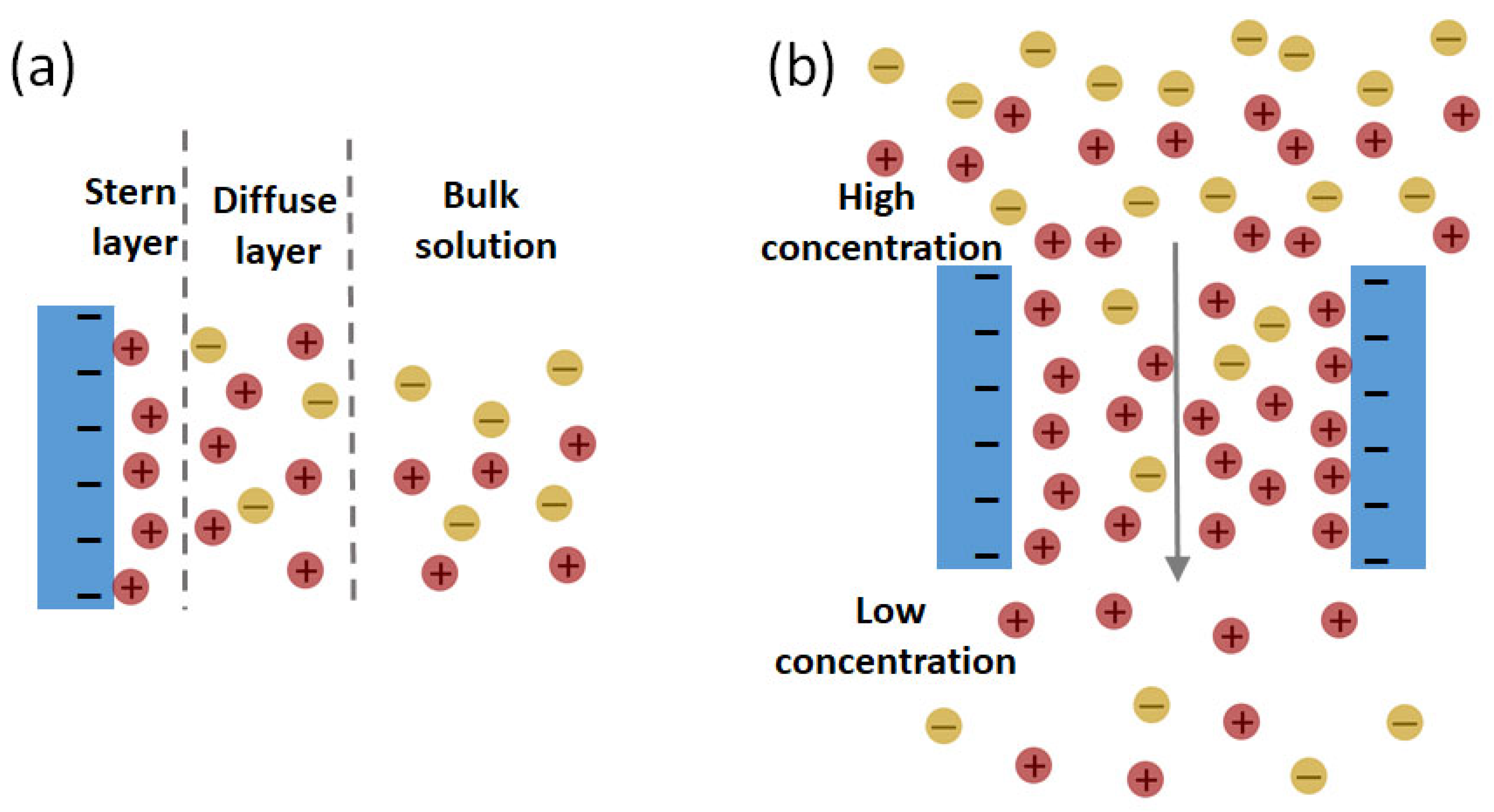
2. Principles of Reverse Electrodialysis
3. Conventional Nonporous Membranes
4. Emerging Porous Membranes
4.1. Selective Ion Transport through Porous Membranes
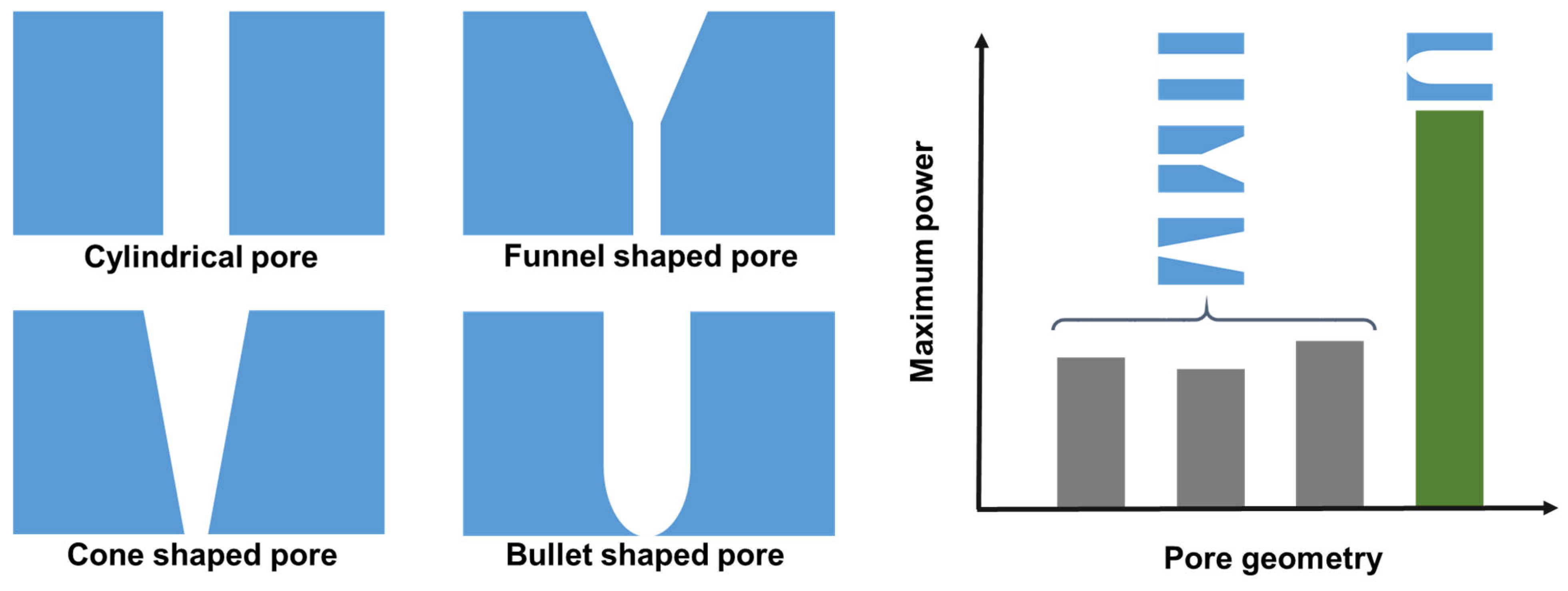
4.2. Track-Etched Polymer Membranes with 1D Pores
4.3. Porous Membranes with Atomic- and Molecular-Scale Thickness
4.4. Nanofluidic Membranes Having 2D Pores
4.5. Nanofiber-Based 3D Porous Membranes
4.6. Metal Organic Frameworks (MOF) Containing Membranes
4.7. Membranes Containing Mesoporous Carbon and a Silica Layer
4.8. Porous Block Copolymer Membranes
4.9. Other Porous Membranes
5. Summary and Outlook
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Tong, X.; Liu, S.; Crittenden, J.; Chen, Y. Nanofluidic membranes to address the challenges of salinity gradient power harvesting. ACS Nano 2021, 15, 5838–5860. [Google Scholar] [CrossRef] [PubMed]
- Ramon, G.Z.; Feinberg, B.J.; Hoek, E.M.V. Membrane-based production of salinity-gradient power. Energy Environ. Sci. 2011, 4, 4423–4434. [Google Scholar] [CrossRef]
- Tufa, R.A.; Pawlowski, S.; Veerman, J.; Bouzek, K.; Fontananova, E.; di Profio, G.; Velizarov, S.; Goulão Crespo, J.; Nijmeijer, K.; Curcio, E. Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage. Appl. Energy 2018, 225, 290–331. [Google Scholar] [CrossRef]
- Brauns, E. Towards a worldwide sustainable and simultaneous large-scale production of renewable energy and potable water through salinity gradient power by combining reversed electrodialysis and solar power. Desalination 2008, 219, 312–323. [Google Scholar] [CrossRef]
- Brauns, E. Salinity gradient power by reverse electrodialysis: Effect of model parameters on electrical power output. Desalination 2009, 237, 378–391. [Google Scholar] [CrossRef]
- Tristán, C.; Rumayor, M.; Dominguez-Ramos, A.; Fallanza, M.; Ibáñez, R.; Ortiz, I. Life cycle assessment of salinity gradient energy recovery by reverse electrodialysis in a seawater reverse osmosis desalination plant. Sustain. Energy Fuels 2020, 4, 4273–4284. [Google Scholar] [CrossRef]
- Jones, E.; Qadir, M.; van Vliet, M.T.H.; Smakhtin, V.; Kang, S.-M. The state of desalination and brine production: A global outlook. Sci. Total Environ. 2019, 657, 1343–1356. [Google Scholar] [CrossRef]
- Voutchkov, N. Energy use for membrane seawater desalination—Current status and trends. Desalination 2018, 431, 2–14. [Google Scholar] [CrossRef]
- Kim, J.; Park, K.; Yang, D.R.; Hong, S. A comprehensive review of energy consumption of seawater reverse osmosis desalination plants. Appl. Energy 2019, 254, 113652. [Google Scholar] [CrossRef]
- Sorci, M.; Gu, M.; Heldt, C.L.; Grafeld, E.; Belfort, G. A multi-dimensional approach for fractionating proteins using charged membranes. Biotechnol. Bioeng. 2013, 110, 1704–1713. [Google Scholar] [CrossRef]
- Li, W.; Krantz, W.B.; Cornelissen, E.R.; Post, J.W.; Verliefde, A.R.D.; Tang, C.Y. A novel hybrid process of reverse electrodialysis and reverse osmosis for low energy seawater desalination and brine management. Appl. Energy 2013, 104, 592–602. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Y.; Pei, Y.; Crittenden, J.C. Unique applications and improvements of reverse electrodialysis: A review and outlook. Appl. Energy 2020, 262, 114482. [Google Scholar] [CrossRef]
- Mercer, E.; Davey, C.J.; Azzini, D.; Eusebi, A.L.; Tierney, R.; Williams, L.; Jiang, Y.; Parker, A.; Kolios, A.; Tyrrel, S.; et al. Hybrid membrane distillation reverse electrodialysis configuration for water and energy recovery from human urine: An opportunity for off-grid decentralised sanitation. J. Membr. Sci. 2019, 584, 343–352. [Google Scholar] [CrossRef] [PubMed]
- Daniilidis, A.; Vermaas, D.A.; Herber, R.; Nijmeijer, K. Experimentally obtainable energy from mixing river water, seawater or brines with reverse electrodialysis. Renew. Energy 2014, 64, 123–131. [Google Scholar] [CrossRef]
- Guler, E.; Nijmeijer, K. Reverse electrodialysis for salinity gradient power generation: Challenges and future perspectives. J. Membr. Sci. Res. 2018, 4, 108–110. [Google Scholar]
- Hong, J.G.; Zhang, B.; Glabman, S.; Uzal, N.; Dou, X.; Zhang, H.; Wei, X.; Chen, Y. Potential ion exchange membranes and system performance in reverse electrodialysis for power generation: A review. J. Membr. Sci. 2015, 486, 71–88. [Google Scholar] [CrossRef]
- Chen, W.; Xiang, Y.; Kong, X.-Y.; Wen, L. Polymer-based membranes for promoting osmotic energy conversion. Giant 2022, 10, 100094. [Google Scholar] [CrossRef]
- Siria, A.; Poncharal, P.; Biance, A.-L.; Fulcrand, R.; Blase, X.; Purcell, S.T.; Bocquet, L. Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube. Nature 2013, 494, 455–458. [Google Scholar] [CrossRef]
- Mai, V.-P.; Huang, W.-H.; Yang, R.-J. Enhancing ion transport through nanopores in membranes for salinity gradient power generation. ACS EST Eng. 2021, 1, 1725–1752. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Patel, S.K.; Lin, S.; Elimelech, M. Nanopore-based power generation from salinity gradient: Why it is not viable. ACS Nano 2021, 15, 4093–4107. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Elimelech, M. Viability of harvesting salinity gradient (blue) energy by nanopore-based osmotic power generation. Engineering 2022, 9, 51–60. [Google Scholar] [CrossRef]
- Macha, M.; Marion, S.; Nandigana, V.V.R.; Radenovic, A. 2d materials as an emerging platform for nanopore-based power generation. Nat. Rev. Mater. 2019, 4, 588–605. [Google Scholar] [CrossRef]
- Mei, Y.; Tang, C.Y. Recent developments and future perspectives of reverse electrodialysis technology: A review. Desalination 2018, 425, 156–174. [Google Scholar] [CrossRef]
- Besha, A.T.; Tsehaye, M.T.; Aili, D.; Zhang, W.; Tufa, R.A. Design of monovalent ion selective membranes for reducing the impacts of multivalent ions in reverse electrodialysis. Membranes 2020, 10, 7. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-K.; Duan, C.; Chen, Y.-F.; Majumdar, A. Power generation from concentration gradient by reverse electrodialysis in ion-selective nanochannels. Microfluid. Nanofluid. 2010, 9, 1215–1224. [Google Scholar] [CrossRef]
- Xin, W.; Zhang, Z.; Huang, X.; Hu, Y.; Zhou, T.; Zhu, C.; Kong, X.-Y.; Jiang, L.; Wen, L. High-performance silk-based hybrid membranes employed for osmotic energy conversion. Nat. Commun. 2019, 10, 3876. [Google Scholar] [CrossRef] [Green Version]
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: Performance of a stack with 50 cells on the mixing of sea and river water. J. Membr. Sci. 2009, 327, 136–144. [Google Scholar] [CrossRef] [Green Version]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Doubled power density from salinity gradients at reduced intermembrane distance. Environ. Sci. Technol. 2011, 45, 7089–7095. [Google Scholar] [CrossRef] [PubMed]
- Długołęcki, P.; Dąbrowska, J.; Nijmeijer, K.; Wessling, M. Ion conductive spacers for increased power generation in reverse electrodialysis. J. Membr. Sci. 2010, 347, 101–107. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Power generation using profiled membranes in reverse electrodialysis. J. Membr. Sci. 2011, 385–386, 234–242. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Saakes, M.; Nijmeijer, K. Micro-structured membranes for electricity generation by reverse electrodialysis. J. Membr. Sci. 2014, 458, 136–148. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Enhanced mixing in the diffusive boundary layer for energy generation in reverse electrodialysis. J. Membr. Sci. 2014, 453, 312–319. [Google Scholar] [CrossRef]
- Długołȩcki, P.; Gambier, A.; Nijmeijer, K.; Wessling, M. Practical potential of reverse electrodialysis as process for sustainable energy generation. Environ. Sci. Technol. 2009, 43, 6888–6894. [Google Scholar] [CrossRef] [PubMed]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Early detection of preferential channeling in reverse electrodialysis. Electrochim. Acta 2014, 117, 9–17. [Google Scholar] [CrossRef]
- Długołęcki, P.; Nymeijer, K.; Metz, S.; Wessling, M. Current status of ion exchange membranes for power generation from salinity gradients. J. Membr. Sci. 2008, 319, 214–222. [Google Scholar] [CrossRef]
- Geise, G.M.; Curtis, A.J.; Hatzell, M.C.; Hickner, M.A.; Logan, B.E. Salt concentration differences alter membrane resistance in reverse electrodialysis stacks. Environ. Sci. Technol. Lett. 2014, 1, 36–39. [Google Scholar] [CrossRef]
- Geise, G.M.; Hickner, M.A.; Logan, B.E. Ionic resistance and permselectivity tradeoffs in anion exchange membranes. ACS Appl. Mater. Interfaces 2013, 5, 10294–10301. [Google Scholar] [CrossRef] [PubMed]
- Othman, N.H.; Kabay, N.; Guler, E. Principles of reverse electrodialysis and development of integrated-based system for power generation and water treatment: A review. Rev. Chem. Eng. 2022, 38, 921–958. [Google Scholar] [CrossRef]
- Guler, E.; Zhang, Y.; Saakes, M.; Nijmeijer, K. Tailor-made anion-exchange membranes for salinity gradient power generation using reverse electrodialysis. ChemSusChem 2012, 5, 2262–2270. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Performance-determining membrane properties in reverse electrodialysis. J. Membr. Sci. 2013, 446, 266–276. [Google Scholar] [CrossRef]
- Rijnaarts, T.; Huerta, E.; van Baak, W.; Nijmeijer, K. Effect of divalent cations on red performance and cation exchange membrane selection to enhance power densities. Environ. Sci. Technol. 2017, 51, 13028–13035. [Google Scholar] [CrossRef] [PubMed]
- Jung, D.H.; Han, E.D.; Kim, B.H.; Seo, Y.H. Ultra-thin ion exchange film on the ceramic supporter for output power improvement of reverse electrodialysis. Sci. Rep. 2019, 9, 17440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reyes-Aguilera, J.A.; Villafaña-López, L.; Rentería-Martínez, E.C.; Anderson, S.M.; Jaime-Ferrer, J.S. Electrospinning of polyepychlorhydrin and polyacrylonitrile anionic exchange membranes for reverse electrodialysis. Membranes 2021, 11, 717. [Google Scholar] [CrossRef]
- Karakoç, E.; Güler, E. Comparison of physicochemical properties of two types of polyepichlorohydrin-based anion exchange membranes for reverse electrodialysis. Membranes 2022, 12, 257. [Google Scholar] [CrossRef]
- Villafaña-López, L.; Reyes-Valadez, D.M.; González-Vargas, O.A.; Suárez-Toriello, V.A.; Jaime-Ferrer, J.S. Custom-made ion exchange membranes at laboratory scale for reverse electrodialysis. Membranes 2019, 9, 145. [Google Scholar] [CrossRef] [Green Version]
- Horkay, F.; McKenna, G.B. Polymer networks and gels. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 497–523. [Google Scholar]
- Mark, J.E. Experimental determinations of crosslink densities. Rubber Chem. Technol. 1982, 55, 762–768. [Google Scholar] [CrossRef]
- Rahman, M.M.; Abetz, V. Tailoring crosslinked polyether networks for separation of CO2 from light gases. Macromol. Rapid Commun. 2021, 42, 2100160. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Lin, X.; Hu, Y.; Fu, L.; Luo, Q.; Yang, L.; Hou, S.; Kong, X.-Y.; Jiang, L.; Wen, L. Tailoring sulfonated poly(phenyl-alkane)s of intrinsic microporosity membrane for advanced osmotic energy conversion. ACS Mater. Lett. 2022, 4, 1422–1429. [Google Scholar] [CrossRef]
- White, H.S.; Bund, A. Ion current rectification at nanopores in glass membranes. Langmuir 2008, 24, 2212–2218. [Google Scholar] [CrossRef]
- Siwy, Z.S. Ion-current rectification in nanopores and nanotubes with broken symmetry. Adv. Funct. Mater. 2006, 16, 735–746. [Google Scholar] [CrossRef]
- Guo, W.; Cao, L.; Xia, J.; Nie, F.-Q.; Ma, W.; Xue, J.; Song, Y.; Zhu, D.; Wang, Y.; Jiang, L. Energy harvesting with single-ion-selective nanopores: A concentration-gradient-driven nanofluidic power source. Adv. Funct. Mater. 2010, 20, 1339–1344. [Google Scholar] [CrossRef]
- Ma, L.; Lin, K.; Qiu, Y.; Zhuang, J.; An, X.; Yuan, Z.; Huang, C. Significantly enhanced performance of nanofluidic osmotic power generation by slipping surfaces of nanopores. J. Phys. Chem. C 2021, 125, 14195–14203. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, F.; Feng, Y.; Zhu, W.; Geng, W.; Yang, J.; Zhang, X.; Li, N.; Guo, W.; Jiang, L. Anomalous channel-length dependence in nanofluidic osmotic energy conversion. Adv. Funct. Mater. 2017, 27, 1604302. [Google Scholar] [CrossRef]
- Su, Y.-S.; Hsu, S.-C.; Peng, P.-H.; Yang, J.-Y.; Gao, M.; Yeh, L.-H. Unraveling the anomalous channel-length-dependent blue energy conversion using engineered alumina nanochannels. Nano Energy 2021, 84, 105930. [Google Scholar] [CrossRef]
- Kim, D.-K. Numerical study of power generation by reverse electrodialysis in ion-selective nanochannels. J. Mech. Sci. Technol. 2011, 25, 5–10. [Google Scholar] [CrossRef]
- Rankin, D.J.; Huang, D.M. The effect of hydrodynamic slip on membrane-based salinity-gradient-driven energy harvesting. Langmuir 2016, 32, 3420–3432. [Google Scholar] [CrossRef]
- Bocquet, L.; Charlaix, E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 2010, 39, 1073–1095. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Su, Y.; Wang, H.; Sheng, G.; Wang, W. A new slip length model for enhanced water flow coupling molecular interaction, pore dimension, wall roughness, and temperature. Adv. Polym. Technol. 2019, 2019, 6424012. [Google Scholar] [CrossRef] [Green Version]
- Williams, I.; Lee, S.; Apriceno, A.; Sear, R.P.; Battaglia, G. Diffusioosmotic and convective flows induced by a nonelectrolyte concentration gradient. Proc. Natl. Acad. Sci. USA 2020, 117, 25263–25271. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Jin, J.; Li, L.; Miller, J.D. Afm slip length measurements for water at selected phyllosilicate surfaces. Coll. Interfaces 2021, 5, 44. [Google Scholar] [CrossRef]
- Laucirica, G.; Albesa, A.G.; Toimil-Molares, M.E.; Trautmann, C.; Marmisollé, W.A.; Azzaroni, O. Shape matters: Enhanced osmotic energy harvesting in bullet-shaped nanochannels. Nano Energy 2020, 71, 104612. [Google Scholar] [CrossRef]
- Pérez-Mitta, G.; Albesa, A.; Gilles, F.M.; Toimil-Molares, M.E.; Trautmann, C.; Azzaroni, O. Noncovalent approach toward the construction of nanofluidic diodes with ph-reversible rectifying properties: Insights from theory and experiment. J. Phys. Chem. C 2017, 121, 9070–9076. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Combs, C.; Su, Y.-S.; Yeh, L.-H.; Siwy, Z.S. Rectification of concentration polarization in mesopores leads to high conductance ionic diodes and high performance osmotic power. J. Am. Chem. Soc. 2019, 141, 3691–3698. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Yameen, B.; Cervera, J.; Ramírez, P.; Neumann, R.; Ensinger, W.; Knoll, W.; Azzaroni, O. Layer-by-layer assembly of polyelectrolytes into ionic current rectifying solid-state nanopores: Insights from theory and experiment. J. Am. Chem. Soc. 2010, 132, 8338–8348. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Janot, J.-M.; Balanzat, E.; Balme, S. Mimicking ph-gated ionic channels by polyelectrolyte complex confinement inside a single nanopore. Langmuir 2017, 33, 3484–3490. [Google Scholar] [CrossRef] [PubMed]
- Lepoitevin, M.; Jamilloux, B.; Bechelany, M.; Balanzat, E.; Janot, J.-M.; Balme, S. Fast and reversible functionalization of a single nanopore based on layer-by-layer polyelectrolyte self-assembly for tuning current rectification and designing sensors. RSC Adv. 2016, 6, 32228–32233. [Google Scholar] [CrossRef]
- Balme, S.; Ma, T.; Balanzat, E.; Janot, J.-M. Large osmotic energy harvesting from functionalized conical nanopore suitable for membrane applications. J. Membr. Sci. 2017, 544, 18–24. [Google Scholar] [CrossRef]
- Ma, T.; Balanzat, E.; Janot, J.-M.; Balme, S. Nanopore functionalized by highly charged hydrogels for osmotic energy harvesting. ACS Appl. Mater. Interfaces 2019, 11, 12578–12585. [Google Scholar] [CrossRef]
- Laucirica, G.; Toimil-Molares, M.E.; Trautmann, C.; Marmisollé, W.; Azzaroni, O. Polyaniline for improved blue energy harvesting: Highly rectifying nanofluidic diodes operating in hypersaline conditions via one-step functionalization. ACS Appl. Mater. Interfaces 2020, 12, 28148–28157. [Google Scholar] [CrossRef]
- Aliprandi, A.; Pakulski, D.; Ciesielski, A.; Samorì, P. Punctured two-dimensional sheets for harvesting blue energy. ACS Nano 2017, 11, 10654–10658. [Google Scholar] [CrossRef] [Green Version]
- Garaj, S.; Hubbard, W.; Reina, A.; Kong, J.; Branton, D.; Golovchenko, J.A. Graphene as a subnanometre trans-electrode membrane. Nature 2010, 467, 190–193. [Google Scholar] [CrossRef] [PubMed]
- Garaj, S.; Liu, S.; Golovchenko, J.A.; Branton, D. Molecule-hugging graphene nanopores. Proc. Natl. Acad. Sci. USA 2013, 110, 12192–12196. [Google Scholar] [CrossRef] [Green Version]
- Russo, C.J.; Golovchenko, J.A. Atom-by-atom nucleation and growth of graphene nanopores. Proc. Natl. Acad. Sci. USA 2012, 109, 5953–5957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Hern, S.C.; Boutilier, M.S.H.; Idrobo, J.-C.; Song, Y.; Kong, J.; Laoui, T.; Atieh, M.; Karnik, R. Selective ionic transport through tunable subnanometer pores in single-layer graphene membranes. Nano Lett. 2014, 14, 1234–1241. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Graf, M.; Liu, K.; Ovchinnikov, D.; Dumcenco, D.; Heiranian, M.; Nandigana, V.; Aluru, N.R.; Kis, A.; Radenovic, A. Single-layer mos2 nanopores as nanopower generators. Nature 2016, 536, 197–200. [Google Scholar] [CrossRef] [Green Version]
- Yazda, K.; Bleau, K.; Zhang, Y.; Capaldi, X.; St-Denis, T.; Grutter, P.; Reisner, W.W. High osmotic power generation via nanopore arrays in hybrid hexagonal boron nitride/silicon nitride membranes. Nano Lett. 2021, 21, 4152–4159. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Feng, J.; Kis, A.; Radenovic, A. Atomically thin molybdenum disulfide nanopores with high sensitivity for DNA translocation. ACS Nano 2014, 8, 2504–2511. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Liu, K.; Graf, M.; Lihter, M.; Bulushev, R.D.; Dumcenco, D.; Alexander, D.T.L.; Krasnozhon, D.; Vuletic, T.; Kis, A.; et al. Electrochemical reaction in single layer mos2: Nanopores opened atom by atom. Nano Lett. 2015, 15, 3431–3438. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Su, L.; Yagmurcukardes, M.; Chen, J.; Jiang, Y.; Li, Z.; Quan, A.; Peeters, F.M.; Wang, C.; Geim, A.K.; et al. Blue energy conversion from holey-graphene-like membranes with a high density of subnanometer pores. Nano Lett. 2020, 20, 8634–8639. [Google Scholar] [CrossRef]
- Liu, X.; He, M.; Calvani, D.; Qi, H.; Gupta, K.B.S.S.; de Groot, H.J.M.; Sevink, G.J.A.; Buda, F.; Kaiser, U.; Schneider, G.F. Power generation by reverse electrodialysis in a single-layer nanoporous membrane made from core–rim polycyclic aromatic hydrocarbons. Nat. Nanotechnol. 2020, 15, 307–312. [Google Scholar] [CrossRef]
- Yang, J.; Tu, B.; Zhang, G.; Liu, P.; Hu, K.; Wang, J.; Yan, Z.; Huang, Z.; Fang, M.; Hou, J.; et al. Advancing osmotic power generation by covalent organic framework monolayer. Nat. Nanotechnol. 2022, 17, 622–628. [Google Scholar] [CrossRef] [PubMed]
- Koltonow, A.R.; Huang, J. Two-dimensional nanofluidics. Science 2016, 351, 1395–1396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raidongia, K.; Huang, J. Nanofluidic ion transport through reconstructed layered materials. J. Am. Chem. Soc. 2012, 134, 16528–16531. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Du, X.; Chen, R.; Zhou, J.; Agostini, M.; Sun, J.; Xiao, L. The combination of 2D layered graphene oxide and 3D porous cellulose heterogeneous membranes for nanofluidic osmotic power generation. Molecules 2021, 26, 5343. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.; Kang, Q.; Zhou, Y.; Feng, Y.; Chen, X.; Yuan, J.; Guo, W.; Wei, Y.; Jiang, L. Osmotic power generation with positively and negatively charged 2d nanofluidic membrane pairs. Adv. Funct. Mater. 2017, 27, 1603623. [Google Scholar] [CrossRef]
- Qin, S.; Liu, D.; Wang, G.; Portehault, D.; Garvey, C.J.; Gogotsi, Y.; Lei, W.; Chen, Y. High and stable ionic conductivity in 2D nanofluidic ion channels between boron nitride layers. J. Am. Chem. Soc. 2017, 139, 6314–6320. [Google Scholar] [CrossRef] [Green Version]
- Xiao, K.; Giusto, P.; Wen, L.; Jiang, L.; Antonietti, M. Nanofluidic ion transport and energy conversion through ultrathin free-standing polymeric carbon nitride membranes. Angew. Chem. Int. Ed. 2018, 57, 10123–10126. [Google Scholar] [CrossRef]
- Hong, S.; Ming, F.; Shi, Y.; Li, R.; Kim, I.S.; Tang, C.Y.; Alshareef, H.N.; Wang, P. Two-dimensional ti3c2tx mxene membranes as nanofluidic osmotic power generators. ACS Nano 2019, 13, 8917–8925. [Google Scholar] [CrossRef]
- Ding, L.; Zheng, M.; Xiao, D.; Zhao, Z.; Xue, J.; Zhang, S.; Caro, J.; Wang, H. Bioinspired ti3c2tx mxene-based ionic diode membrane for high-efficient osmotic energy conversion. Angew. Chem. Int. Ed. 2022, 61, e202206152. [Google Scholar]
- Zhang, Z.; Yang, S.; Zhang, P.; Zhang, J.; Chen, G.; Feng, X. Mechanically strong mxene/kevlar nanofiber composite membranes as high-performance nanofluidic osmotic power generators. Nat. Commun. 2019, 10, 2920. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Xiao, D.; Zhao, Z.; Wei, Y.; Xue, J.; Wang, H. Ultrathin and ultrastrong kevlar aramid nanofiber membranes for highly stable osmotic energy conversion. Adv. Sci. 2022, 9, 2202869. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wong, E.; Mai, Z.; Van der Bruggen, B. Fabrication of composite polyamide/kevlar aramid nanofiber nanofiltration membranes with high permselectivity in water desalination. J. Membr. Sci. 2019, 592, 117396. [Google Scholar] [CrossRef]
- Yuan, S.; Swartenbroekx, J.; Li, Y.; Zhu, J.; Ceyssens, F.; Zhang, R.; Volodine, A.; Li, J.; Van Puyvelde, P.; Van der Bruggen, B. Facile synthesis of kevlar nanofibrous membranes via regeneration of hydrogen bonds for organic solvent nanofiltration. J. Membr. Sci. 2019, 573, 612–620. [Google Scholar] [CrossRef]
- Zhang, Z.; He, L.; Zhu, C.; Qian, Y.; Wen, L.; Jiang, L. Improved osmotic energy conversion in heterogeneous membrane boosted by three-dimensional hydrogel interface. Nat. Commun. 2020, 11, 875. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Zhou, S.; Liu, J.; Qiu, B.; Liu, T.; Liang, Q.; Zheng, X.; Li, B.; Zeng, J.; Yan, M.; et al. Sequential superassembly of nanofiber arrays to carbonaceous ordered mesoporous nanowires and their heterostructure membranes for osmotic energy conversion. J. Am. Chem. Soc. 2021, 143, 6922–6932. [Google Scholar] [CrossRef]
- Cavka, J.H.; Jakobsen, S.; Olsbye, U.; Guillou, N.; Lamberti, C.; Bordiga, S.; Lillerud, K.P. A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability. J. Am. Chem. Soc. 2008, 130, 13850–13851. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, H.; Hou, J.; Li, X.; Hu, X.; Hu, Y.; Easton, C.D.; Li, Q.; Sun, C.; Thornton, A.W.; et al. Efficient metal ion sieving in rectifying subnanochannels enabled by metal–organic frameworks. Nat. Mater. 2020, 19, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-C.; Yeh, L.-H.; Zheng, M.-J.; Wu, K.C.-W. Highly selective and high-performance osmotic power generators in subnanochannel membranes enabled by metal-organic frameworks. Sci. Adv. 2021, 7, eabe9924. [Google Scholar] [CrossRef]
- Fu, L.; Wang, Y.; Jiang, J.; Lu, B.; Zhai, J. Sandwich “ion pool”—Structured power gating for salinity gradient generation devices. ACS Appl. Mater. Interfaces 2021, 13, 35197–35206. [Google Scholar] [CrossRef]
- Robertson, M.; Zagho, M.M.; Nazarenko, S.; Qiang, Z. Mesoporous carbons from self-assembled polymers. J. Polym. Sci. 2022, 60, 2015–2042. [Google Scholar] [CrossRef]
- Meng, Y.; Gu, D.; Zhang, F.; Shi, Y.; Cheng, L.; Feng, D.; Wu, Z.; Chen, Z.; Wan, Y.; Stein, A.; et al. A family of highly ordered mesoporous polymer resin and carbon structures from organic−organic self-assembly. Chem. Mater. 2006, 18, 4447–4464. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, L.; Zhang, L.; Wen, L.; Tang, J.; Zeng, J.; Liu, T.; Peng, D.; Yan, M.; Qiu, B.; et al. Interfacial super-assembly of ordered mesoporous silica–alumina heterostructure membranes with ph-sensitive properties for osmotic energy harvesting. ACS Appl. Mater. Interfaces 2021, 13, 8782–8793. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Shi, Y.; Wan, Y.; Meng, Y.; Zhang, F.; Gu, D.; Chen, Z.; Tu, B.; Zhao, D. Triconstituent co-assembly to ordered mesostructured polymer−silica and carbon-silica nanocomposites and large-pore mesoporous carbons with high surface areas. J. Am. Chem. Soc. 2006, 128, 11652–11662. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Guo, W.; Feng, D.; Wang, H.; Zhao, D.; Jiang, L. High-performance ionic diode membrane for salinity gradient power generation. J. Am. Chem. Soc. 2014, 136, 12265–12272. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Xie, L.; Li, X.; Huang, Y.; Zhang, L.; Liang, Q.; Yan, M.; Zeng, J.; Qiu, B.; Liu, T.; et al. Interfacial super-assembly of ordered mesoporous carbon-silica/aao hybrid membrane with enhanced permselectivity for temperature- and ph-sensitive smart ion transport. Angew. Chem. Int. Ed. 2021, 60, 26167–26176. [Google Scholar] [CrossRef]
- Abetz, V. Isoporous block copolymer membranes. Macromol. Rapid Commun. 2015, 36, 10–22. [Google Scholar] [CrossRef]
- Radjabian, M.; Abetz, V. Advanced porous polymer membranes from self-assembling block copolymers. Prog. Polym. Sci. 2020, 102, 101219. [Google Scholar] [CrossRef]
- Rahman, M.M. Selective swelling and functionalization of integral asymmetric isoporous block copolymer membranes. Macromol. Rapid Commun. 2021, 42, 2100235. [Google Scholar] [CrossRef]
- Zhang, Z.; Kong, X.-Y.; Xiao, K.; Liu, Q.; Xie, G.; Li, P.; Ma, J.; Tian, Y.; Wen, L.; Jiang, L. Engineered asymmetric heterogeneous membrane: A concentration-gradient-driven energy harvesting device. J. Am. Chem. Soc. 2015, 137, 14765–14772. [Google Scholar] [CrossRef]
- Zhang, Z.; Sui, X.; Li, P.; Xie, G.; Kong, X.-Y.; Xiao, K.; Gao, L.; Wen, L.; Jiang, L. Ultrathin and ion-selective janus membranes for high-performance osmotic energy conversion. J. Am. Chem. Soc. 2017, 139, 8905–8914. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Zhai, J. Gap confinement effect of a tandem nanochannel system and its application in salinity gradient power generation. ACS Appl. Mater. Interfaces 2021, 13, 41159–41168. [Google Scholar] [CrossRef]
- Yeh, L.-H.; Huang, Z.-Y.; Liu, Y.-C.; Deng, M.-J.; Chou, T.-H.; Ou Yang, H.-C.; Ahamad, T.; Saad, M.A.; Wu, K.C.-W. A nanofluidic osmotic power generator demonstrated in polymer gel electrolytes with substantially enhanced performance. J. Mater. Chem. A 2019, 7, 26791–26796. [Google Scholar] [CrossRef]
- Li, R.; Zhai, J.; Jiang, J.; Wang, Q.; Wang, S. Improved interfacial ion transport through nanofluidic hybrid membranes based on covalent organic frameworks for osmotic energy generation. ACS Appl. Energy Mater. 2022, 5, 7176–7184. [Google Scholar] [CrossRef]
- Tedesco, M.; Cipollina, A.; Tamburini, A.; Micale, G. Towards 1kw power production in a reverse electrodialysis pilot plant with saline waters and concentrated brines. J. Membr. Sci. 2017, 522, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Tedesco, M.; Scalici, C.; Vaccari, D.; Cipollina, A.; Tamburini, A.; Micale, G. Performance of the first reverse electrodialysis pilot plant for power production from saline waters and concentrated brines. J. Membr. Sci. 2016, 500, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Available online: www.reapower.eu/news.html (accessed on 27 January 2023).
- Laucirica, G.; Toimil-Molares, M.E.; Trautmann, C.; Marmisollé, W.; Azzaroni, O. Nanofluidic osmotic power generators–advanced nanoporous membranes and nanochannels for blue energy harvesting. Chem. Sci. 2021, 12, 12874–12910. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Feng, J.; Fang, M.; Wang, X.; Liu, Y.; Li, S.; Wen, L.; Zhu, Y.; Jiang, L. Large-scale, ultrastrong cu2+ cross-linked sodium alginate membrane for effective salinity gradient power conversion. ACS Appl. Polym. Mater. 2021, 3, 3902–3910. [Google Scholar] [CrossRef]


| Membrane Type | Membrane Description | Concentration Gradient | Maximum Power Density | Reference |
|---|---|---|---|---|
| Atomic and molecularly thin porous membranes | Multi-porous hexagonal boron nitride membrane | 1000-fold (KCl) | 15 Wm−2 | [77] |
| Multi-porous graphene sheets containing –NH2 groups at the pore edges | 100-fold (KCl) | 35 Wm−2 | [80] | |
| Crosslinked core–rim structure polycyclic aromatic hydrocarbon monomer hexa(2,2′-dipyridylamino)hexabenzocoronene | 50-fold (NaCl) | 67 Wm−2 | [81] | |
| metal tetraphenylporphyrin COF (MTPP-COF) monolayer | 50-fold (NaCl) 50-fold (MgCl2) 50-fold (CaCl2) | 135.8 Wm−2 317.5 Wm−2 267.7 Wm−2 | [82] | |
| Nanofluidic membranes with 2D pores | Layered carbon nitride membrane | 1000-fold (KCl) | 0.21 Wm−2 | [88] |
| Free-standing Ti3C2Tx, MXene membrane | 1000-fold (KCl) | 21 Wm−2 | [89] | |
| Diode-type membrane containing negative Ti3C2Tx, MXene nanosheets and polydiallyl dimethyl ammonium-adsorbed positive MXene nanosheets | 50-fold (NaCl) 500-fold (NaCl) | 8.6 Wm−2 17.8 Wm−2 | [90] | |
| Aramid nanofiber intercalated Ti3C2Tx, MXene nanosheets | 50-fold (NaCl) | 3.7 Wm−2 | [91] | |
| Nanofiber-based 3D porous membranes | Free-standing aramid nanofiber membrane | 50-fold (NaCl) 500-fold (NaCl) | 4.8 Wm−2 15 Wm−2 | [92] |
| Double-layer membrane containing one layer of aramid nanofiber and one layer of polyelectrolyte hydrogel | 50-fold (NaCl) | 5.06 Wm−2 | [95] | |
| Double-layer membrane containing nanowires deposited on a porous anodic alumina oxide layer | 50-fold (NaCl) | 2.78 Wm−2 | [96] | |
| Double-layer membrane containing a silk nanofibril layer and a porous anodic aluminum oxide layer | 50-fold (NaCl) | 2.86 Wm−2 | [26] | |
| Metal organic frameworks (MOF) containing membranes | Double-layer membrane containing an amino-substituted UiO-66 layer on a porous alumina layer | 5-fold (KCl) 50-fold (KCl) 500-fold (KCl) | 2.19 Wm−2 4.93 Wm−2 7.12 Wm−2 | [99] |
| “Ion Pool” membrane containing a sandwiched anodic aluminum oxide (AAO) layer between a tungsten oxide (WO3) layer and a ZIF-8 layer (WO3-AAO-ZIF-8) | 50-fold (NaCl) | 1.93 Wm−2 | [100] | |
| Membranes containing a mesoporous carbon and silica layer | Double-layer membrane with a mesoporous carbon layer on a porous alumina layer | 50-fold (NaCl) | 3.46 Wm−2 | [105] |
| Double-layer membrane with a mesoporous silica layer on a porous alumina layer | 50-fold (NaCl) | 4.5 Wm−2 | [103] | |
| Double-layer membrane with a mesoporous carbon–silica hybrid layer on a porous alumina layer | 50-fold (NaCl) 200-fold (NaCl) | 5.04 Wm−2 10.75 Wm−2 | [106] | |
| Porous block copolymer membranes | Double-layer membrane containing a spin-coated polystyrene–block–poly (4vinylpyridine) (PS-b-P4VP) layer on top of a track-etched poly(ethylene terephthalate) layer | 50-fold (NaCl) | 0.35 Wm−2 | [110] |
| Janus type membrane having a porous PS-b-P4VP layer and a porous crosslinked block copolymer substrate containing a poly (ethyelene oxide) minor block | 50-fold (NaCl) | 2.04 Wm−2 | [111] | |
| Covalent organic framework (COF)-containing membrane | Hybrid membrane with COF-LZU1 on a cellulose nanofiber support with a carbon nanotube intermediate layer | 50-fold (NaCl) | 4.26 Wm−2 | [114] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M. Membranes for Osmotic Power Generation by Reverse Electrodialysis. Membranes 2023, 13, 164. https://doi.org/10.3390/membranes13020164
Rahman MM. Membranes for Osmotic Power Generation by Reverse Electrodialysis. Membranes. 2023; 13(2):164. https://doi.org/10.3390/membranes13020164
Chicago/Turabian StyleRahman, Md. Mushfequr. 2023. "Membranes for Osmotic Power Generation by Reverse Electrodialysis" Membranes 13, no. 2: 164. https://doi.org/10.3390/membranes13020164
APA StyleRahman, M. M. (2023). Membranes for Osmotic Power Generation by Reverse Electrodialysis. Membranes, 13(2), 164. https://doi.org/10.3390/membranes13020164






