Numerical Study on Thermal Stress of High Temperature Proton Exchange Membrane Fuel Cells during Start-Up Process
Abstract
:1. Introduction
2. Model Description
2.1. Governing Equations
2.2. Numerical Procedure and Boundary Condition
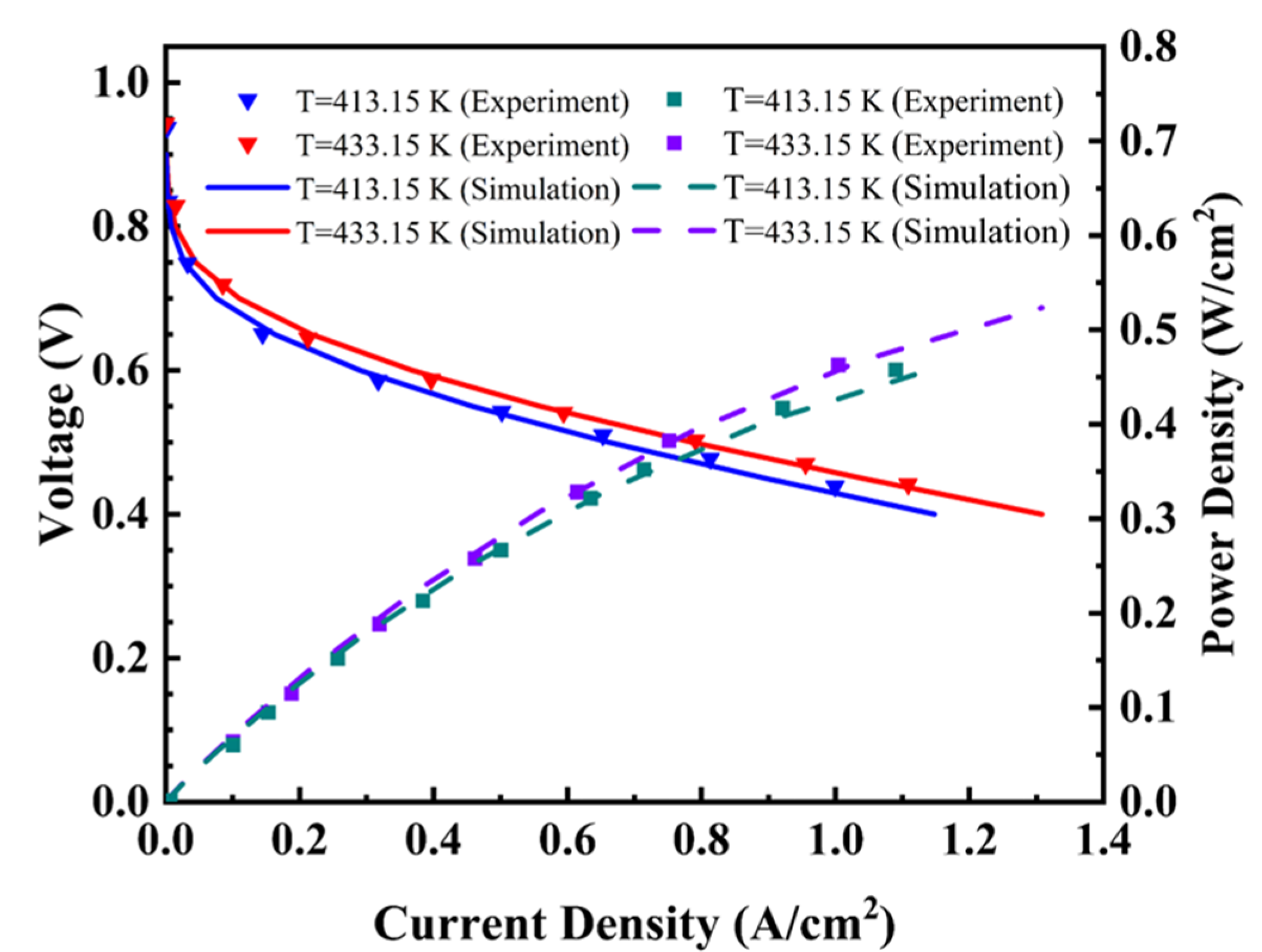
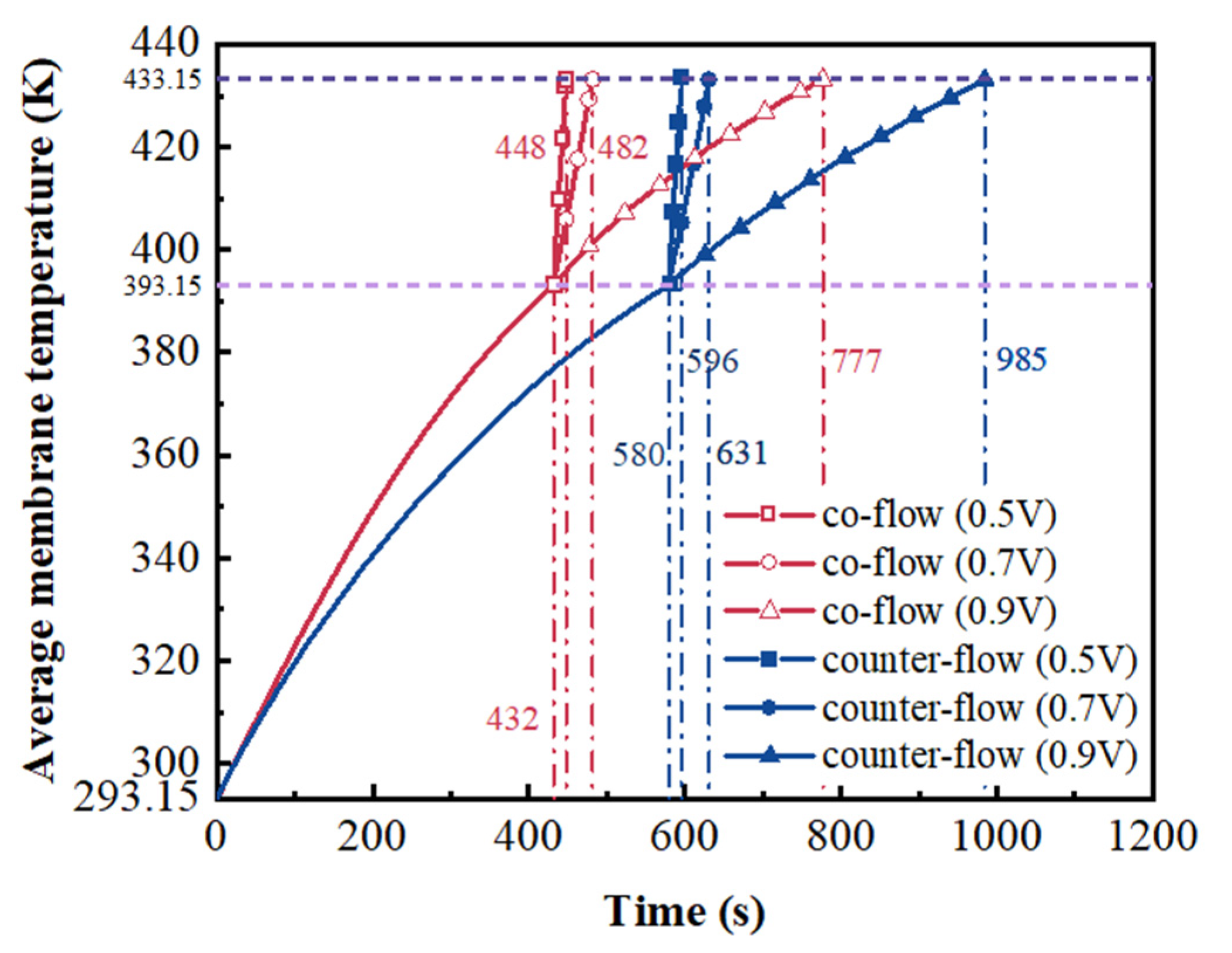
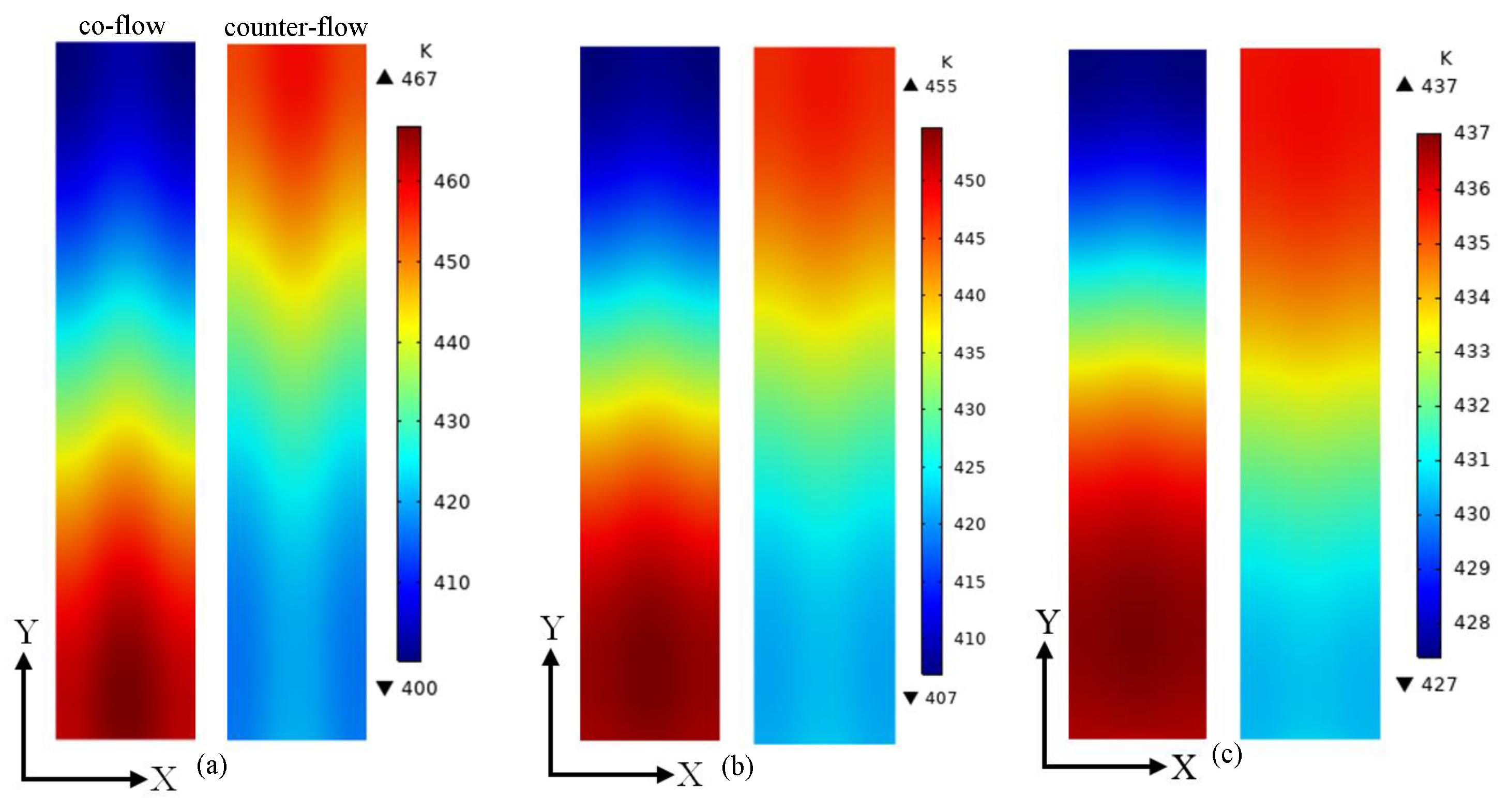
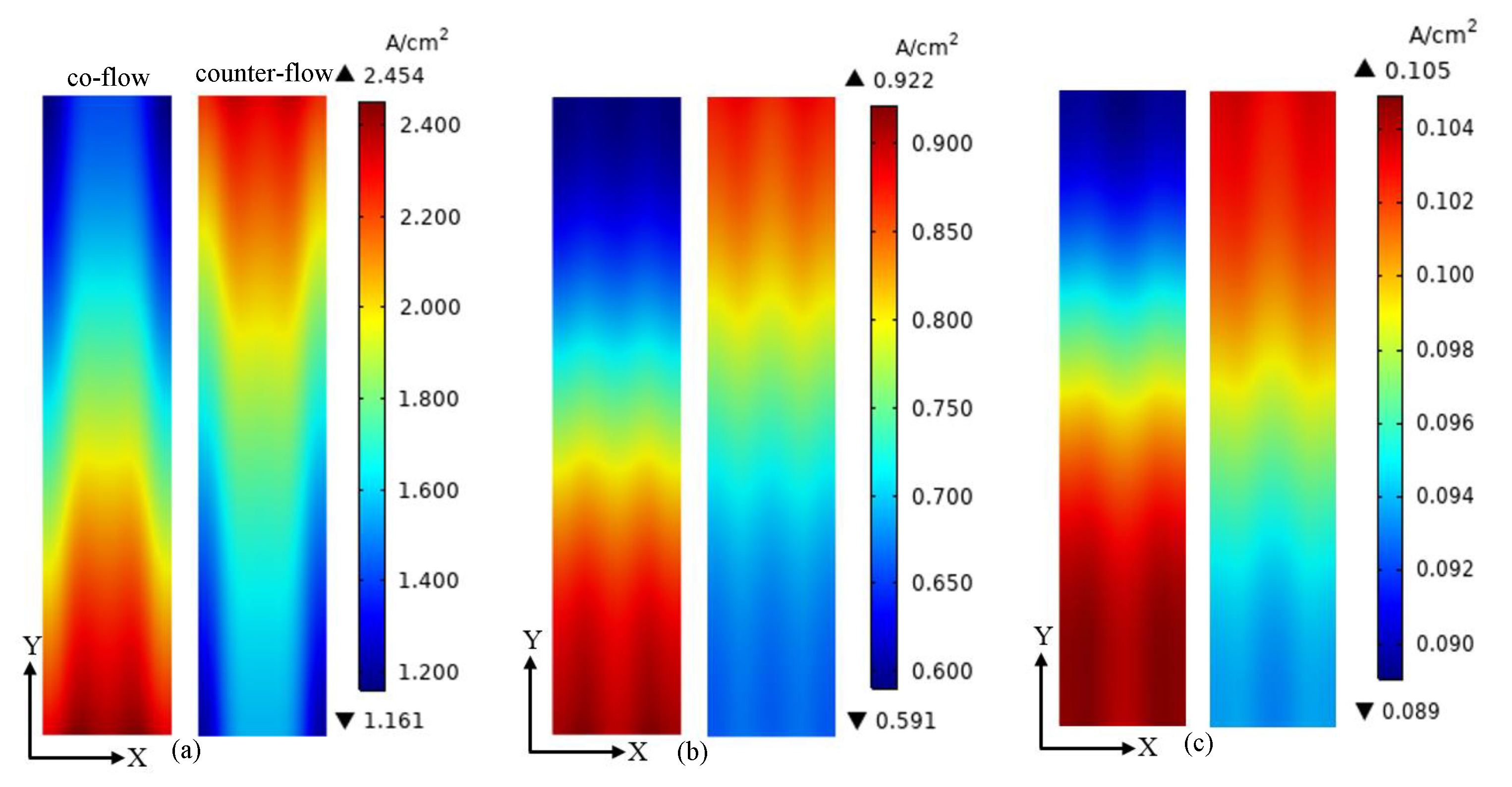
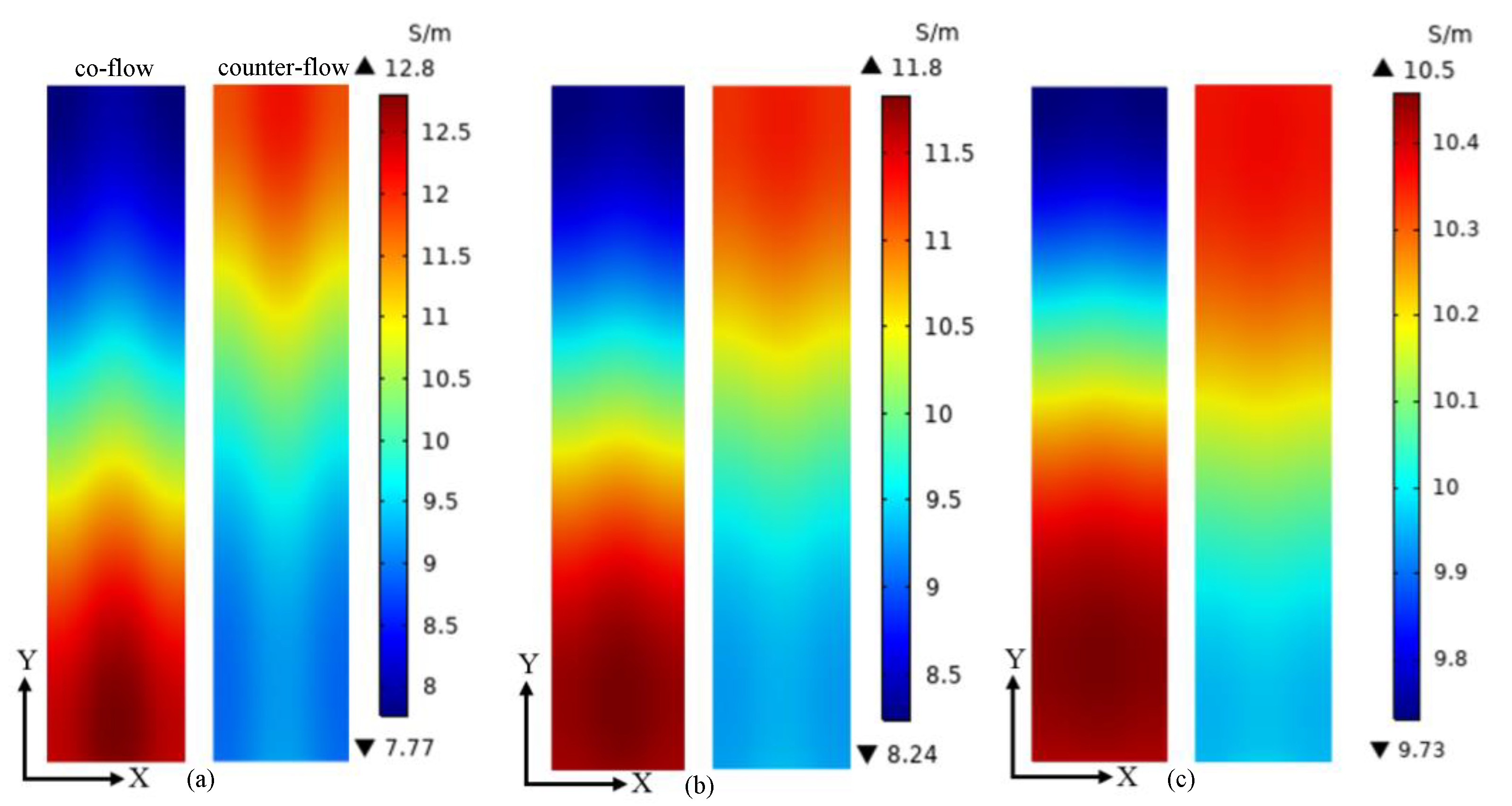
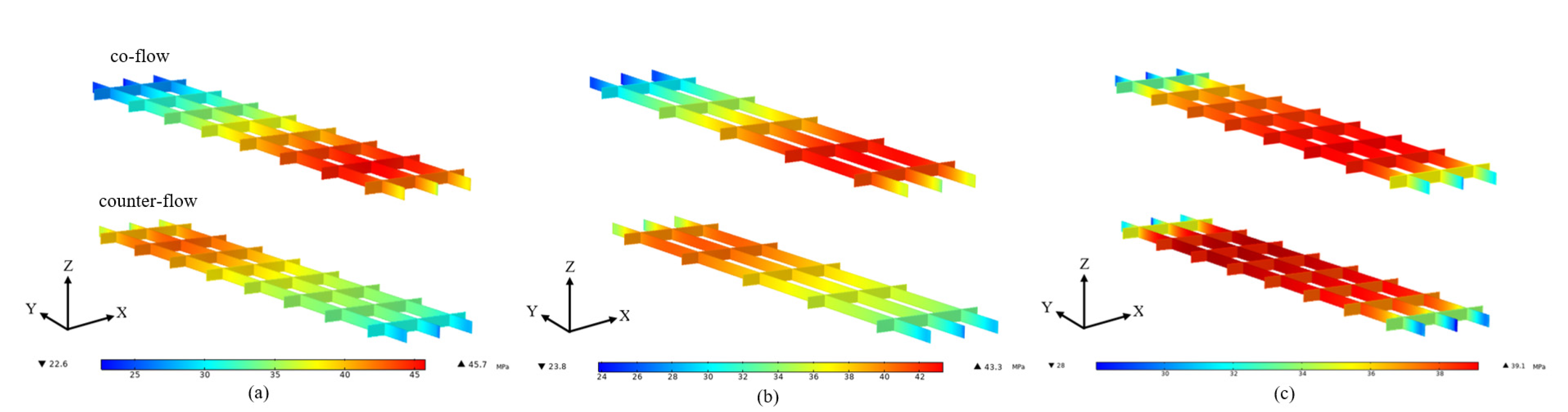
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandan, A.; Hattenberger, M.; El-Kharouf, A.; Du, S.; Dhir, A.; Self, V.; Pollet, B.G.; Ingram, A.; Bujalski, W. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)—A review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, H. Review of the development of first-generation redox flow batteries: Iron-chromium system. ChemSusChem 2022, 15, e202101798. [Google Scholar] [CrossRef]
- Lotric, A.; Sekavcnik, M.; Hočevar, S. Effectiveness of heat-integrated methanol steam reformer and polymer electrolyte membrane fuel cell stack systems for portable applications. J. Power Sources 2014, 270, 166–182. [Google Scholar] [CrossRef]
- Ubong, E.U.; Shi, Z.; Wang, X. Three-dimensional modeling and experimental study of a high temperature PBI-based PEM fuel cell. J. Electrochem. Soc. 2009, 156, B1276. [Google Scholar] [CrossRef]
- Authayanun, S.; Mamlouk, M.; Scott, K.; Arpornwichanop, A. Comparison of high-temperature and low-temperature polymer electrolyte membrane fuel cell systems with glycerol reforming process for stationary applications. Appl. Energy 2013, 109, 192–201. [Google Scholar] [CrossRef]
- Oh, K.; Jeong, G.; Cho, E.A.; Kim, W.; Ju, H. A CO poisoning model for high-temperature proton exchange membrane fuel cells comprising phosphoric acid-doped polybenzimidazole membranes. Int. J. Hydrogen Energy 2014, 39, 21915–21926. [Google Scholar] [CrossRef]
- Li, S.; Peng, C.; Shen, Q.; Wang, C.; Cheng, Y.; Yang, G. Impact of membrane phosphoric acid doping level on transport phenomena and performance in high temperature PEM fuel cells. Membranes 2021, 11, 817. [Google Scholar] [CrossRef] [PubMed]
- Oono, Y.; Sounai, A.; Hori, M. Influence of the phosphoric acid-doping level in a polybenzimidazole membrane on the cell performance of high–temperature proton exchange membrane fuel cells. J. Power Sources 2009, 189, 943–949. [Google Scholar] [CrossRef]
- Li, S.; Wei, R.; Lv, X.; Ye, W.; Shen, Q.; Yang, G. Numerical analysis on the effect of stoichiometric ratio on fuel utilization and performance of high temperature proton exchange membrane fuel cells. Int. J. Electrochem. Sci. 2020, 15, 7407–7416. [Google Scholar] [CrossRef]
- Elden, G.; Celik, M.; Genc, G.; Yapici, H. The effects of temperature on transport phenomena in phosphoric acid doped polybenzimidazole polymer electrolyte membrane fuel cell. Energy 2016, 103, 772–783. [Google Scholar] [CrossRef]
- Caglayan, D.G.; Sezgin, B.; Devrim, Y.; Eroglu, I. Three-dimensional modeling of a high temperature polymer electrolyte membrane fuel cell at different operation temperatures. Int. J. Hydrogen Energy 2016, 41, 10060–10070. [Google Scholar] [CrossRef]
- Taccani, R.; Zuliani, N. Effect of flow field design on performances of high temperature PEM fuel cells: Experimental analysis. Int. J. Hydrogen Energy 2011, 36, 10282–10287. [Google Scholar] [CrossRef]
- Li, S.; Yuan, J.; Xie, G.; Sunden, B. Numerical investigation of transport phenomena in high temperature proton exchange membrane fuel cells with different flow field designs. Numer. Heat Transf. A 2017, 72, 807–820. [Google Scholar] [CrossRef]
- Wu, H.W.; Ho, T.Y.; Han, Y.J. Parametric optimization of wall-mounted cuboid rows installed in interdigitated flow channel of HT-PEM fuel cells. Energy 2021, 216, 119261. [Google Scholar] [CrossRef]
- Sun, H.; Xie, C.; Chen, H.; Almheiri, S. A numerical study on the effects of temperature and mass transfer in high temperature PEM fuel cells with ab-PBI membrane. Appl. Energy 2015, 160, 937–944. [Google Scholar] [CrossRef]
- Kondratenko, M.S.; Gallyamov, M.O.; Khokhlov, A.R. Performance of high temperature fuel cells with different types of PBI membranes as analysed by impedance spectroscopy. Int. J. Hydrogen Energy 2012, 37, 2596–2602. [Google Scholar] [CrossRef]
- Rosli, R.E.; Sulong, A.B.; Daud, W.R.W.; Zulkifley, M.A.; Husaini, T.; Rosli, M.L.; Majlan, E.H.; Haque, M.A. A review of high- temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrogen Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Hao, D.; Ni, M.; Huang, S.; Liu, D.; Zheng, Y. 3D non-isothermal dynamic simulation of high temperature proton exchange membrane fuel cell in the start-up process. Int. J. Hydrogen Energy 2021, 46, 2577–2593. [Google Scholar] [CrossRef]
- Singdeo, D.; Dey, T.; Ghosh, P.C. Modelling of start-up time for high temperature polymer electrolyte fuel cells. Energy 2011, 36, 6081–6089. [Google Scholar] [CrossRef]
- Andreasen, S.J.; Kaer, S.K. Modelling and evaluation of heating strategies for high temperature polymer electrolyte membrane fuel cell stacks. Int. J. Hydrogen Energy 2008, 33, 4655–4664. [Google Scholar] [CrossRef]
- Wippermann, K.; Wannek, C.; Oetjen, H.F.; Mergel, J.; Lehnert, W. Cell resistances of poly (2,5-benzimidazole)-based high temperature polymer membrane fuel cell membrane electrode assemblies: Time dependence and influence of operating parameters. J. Power Sources 2010, 195, 2806–2809. [Google Scholar] [CrossRef]
- Rasheed, R.K.A.; Zhang, C.; Chan, S.H. Numerical analysis of high-temperature proton exchange membrane fuel cells during start-up by inlet gas heating and applied voltage. Int. J. Hydrogen Energy 2017, 42, 10390–10406. [Google Scholar] [CrossRef]
- Choi, M.; Kim, M.; Sohn, Y.J.; Kim, S.G. Development of preheating methodology for a 5kW HT-PEMFC system. Int. J. Hydrogen Energy 2021, 46, 36982–36994. [Google Scholar] [CrossRef]
- Wang, Y.; Sauer, D.U.; Koehne, S.; Ersoez, A. Dynamic modeling of high temperature PEM fuel cell start-up process. Int. J. Hydrogen Energy 2014, 39, 19067–19078. [Google Scholar] [CrossRef]
- Sun, C.; Zlotorowicz, A.; Nawn, G.; Negro, E.; Bertasi, F.; Pagot, G.; Vezzu, K.; Pace, G.; Guarnieri, M.; Noto, V.D. [Nafion/(WO3)x] hybrid membranes for vanadium redox flow batteries. Solid State Ion. 2018, 319, 110–116. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzu, K.; Pagot, G.; Cavinato, G.; Nale, A.; Bang, Y.H.; Noto, V.D. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Oh, K.; Chippar, P.; Ju, H. Numerical study of thermal stresses in high-temperature proton exchange membrane fuel cell (HT-PEMFC). Int. J. Hydrogen Energy 2014, 39, 2785–2794. [Google Scholar] [CrossRef]
- Varghese, G.; KP, V.B.; Joseph, T.V.; Chippar, P. A numerical investigation on thermal gradients and stresses in high temperature PEM fuel cell during start-up. Int. J. Heat Mass Transf. 2021, 175, 121365. [Google Scholar] [CrossRef]
- Nanadegani, F.S.; Lay, E.N.; Sunden, B. Computational analysis of the impact of a micro porous layer (MPL) on the characteristics of a high temperature PEMFC. Electrochim. Acta 2020, 333, 135552. [Google Scholar] [CrossRef]
- Chippar, P.; Ju, H. Three-dimensional non-isothermal modeling of a phosphoric acid-doped polybenzimidazole (PBI) membrane fuel cell. Solid State Ion. 2012, 225, 30–39. [Google Scholar] [CrossRef]
- Li, Q.; Hjuler, H.A.; Bjerrum, N.J. Phosphoric acid doped polybenzimidazole membranes: Physiochemical characterization and fuel cell applications. J. Appl. Electrochem. 2001, 31, 773–779. [Google Scholar] [CrossRef]
- Devrim, Y.; Albostan, A.; Devrim, H. Experimental investigation of CO tolerance in high temperature PEM fuel cells. Int. J. Hydrogen Energy 2018, 43, 18672–18681. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Sun, H.; He, W.; Fan, Y.; Wang, S. Investigation of dry ionomer volume fraction in cathode catalyst layer under different relative humilities and nonuniform ionomer-gradient distributions for PEM fuel cells. Electrochim. Acta 2020, 353, 136491. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. A three-dimensional non-isothermal model of high temperature proton exchange membrane fuel cells with phosphoric acid doped polybenzimidazole membranes. Fuel Cells 2010, 10, 351–362. [Google Scholar] [CrossRef]
- Li, S.; Sundén, B. Three-dimensional modeling and investigation of high temperature proton exchange membrane fuel cells with metal foams as flow distributor. Int. J. Hydrogen Energy 2017, 42, 27323–27333. [Google Scholar] [CrossRef]
- Jeong, Y.H.; Oh, K.; Ahn, S.; Kim, N.Y.; Byeon, A.; Park, H.Y.; Lee, S.Y.; Park, H.S.; Yoo, S.J.; Jang, J.H.; et al. Investigation of electrolyte leaching in the performance degradation of phosphoric acid-doped polybenzimidazole membrane-based high temperature fuel cells. J. Power Sources 2017, 363, 365–374. [Google Scholar] [CrossRef]
- Pianko-Oprych, P.; Zinko, T.; Jaworski, Z. A numerical investigation of the thermal stresses of a planar solid oxide fuel cell. Materials 2016, 9, 814. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Xu, Q.; He, Q.; Ni, M.; Seng, M. Numerical study of high temperature proton exchange membrane fuel cell (HT-PEMFC) with a focus on rib design. Int. J. Hydrogen Energy 2021, 46, 21098–21111. [Google Scholar] [CrossRef]
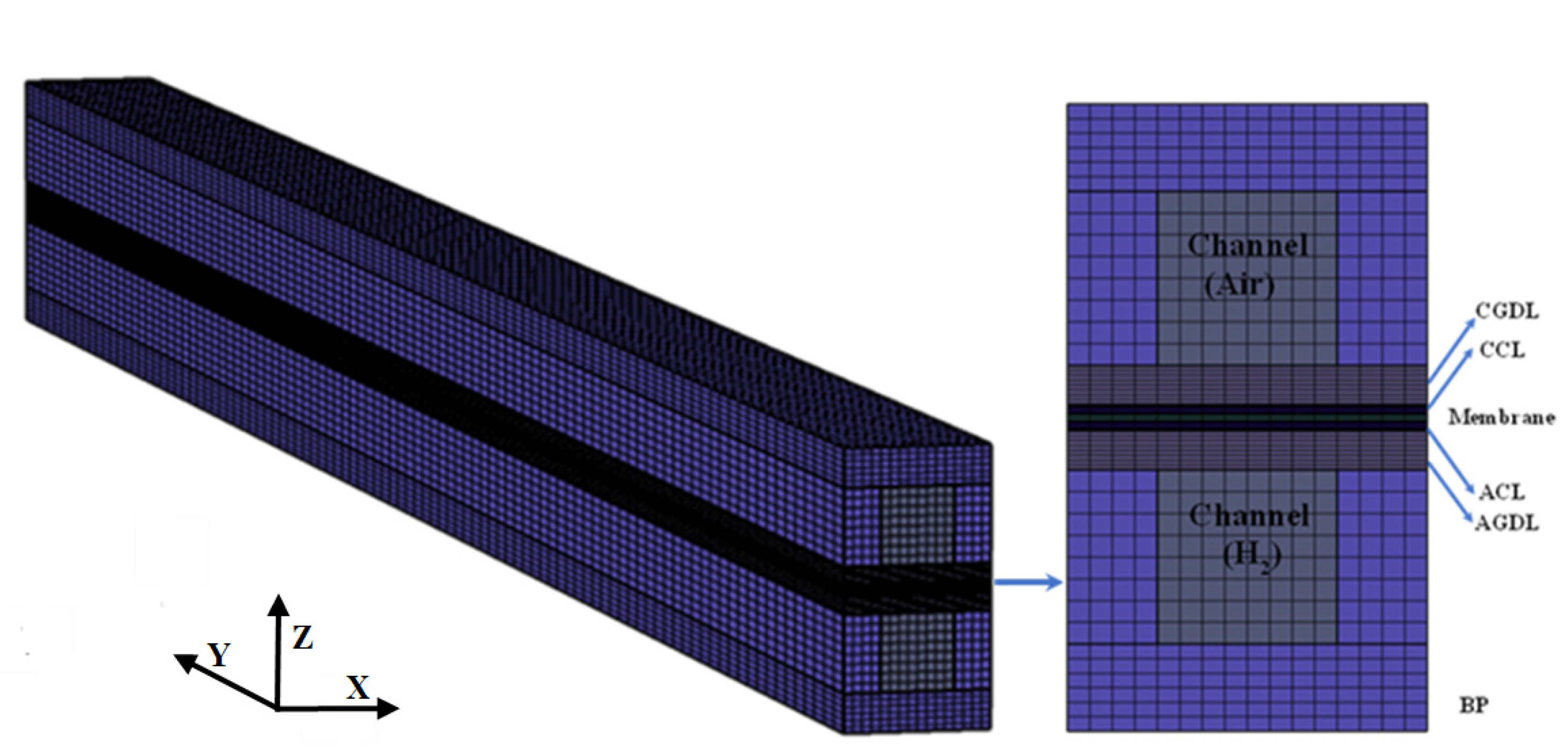


| Parameter | Value | Units |
|---|---|---|
| Channel length/width/depth | ||
| Width of rib | ||
| Thickness of CL/GDL/M | ||
| Density | ||
| Specific heat capacity | ||
| Thermal conductivity | ||
| Electrical conductivity | ||
| Young’s modulus | ||
| Poisson’s ratio | ||
| Thermal expansion coefficient | ||
| Permeability | ||
| Porosity | ||
| Volume fraction of ionomer | 0.21 |
| Description | Units |
|---|---|
| Gas Parameters | Correlation/Value | Units |
|---|---|---|
| Stoichiometry ratio | ||
| Average current density | ||
| Anode inlet mass fraction | ||
| Cathode inlet mass fraction | ||
| Reference temperature | ||
| Diffusion coefficient of species | ||
| Electrochemical Properties | Value | Units |
|---|---|---|
| Reference molar concentration | ||
| Anode and cathode transfer coefficient | ||
| Reference exchange current density | ||
| ratio of reaction surface to CL volume |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Peng, C.; Shen, Q.; Cheng, Y.; Wang, C.; Yang, G. Numerical Study on Thermal Stress of High Temperature Proton Exchange Membrane Fuel Cells during Start-Up Process. Membranes 2023, 13, 215. https://doi.org/10.3390/membranes13020215
Li S, Peng C, Shen Q, Cheng Y, Wang C, Yang G. Numerical Study on Thermal Stress of High Temperature Proton Exchange Membrane Fuel Cells during Start-Up Process. Membranes. 2023; 13(2):215. https://doi.org/10.3390/membranes13020215
Chicago/Turabian StyleLi, Shian, Chengdong Peng, Qiuwan Shen, Yuanzhe Cheng, Chongyang Wang, and Guogang Yang. 2023. "Numerical Study on Thermal Stress of High Temperature Proton Exchange Membrane Fuel Cells during Start-Up Process" Membranes 13, no. 2: 215. https://doi.org/10.3390/membranes13020215
APA StyleLi, S., Peng, C., Shen, Q., Cheng, Y., Wang, C., & Yang, G. (2023). Numerical Study on Thermal Stress of High Temperature Proton Exchange Membrane Fuel Cells during Start-Up Process. Membranes, 13(2), 215. https://doi.org/10.3390/membranes13020215







