Saline Retention and Permeability of Nanofiltration Membranes Versus Resistance and Capacitance as Obtained from Impedance Spectroscopy under a Concentration Gradient
Abstract
:1. Introduction
2. Materials and Methods
2.1. Membrane
2.2. Electrolytic Solutions
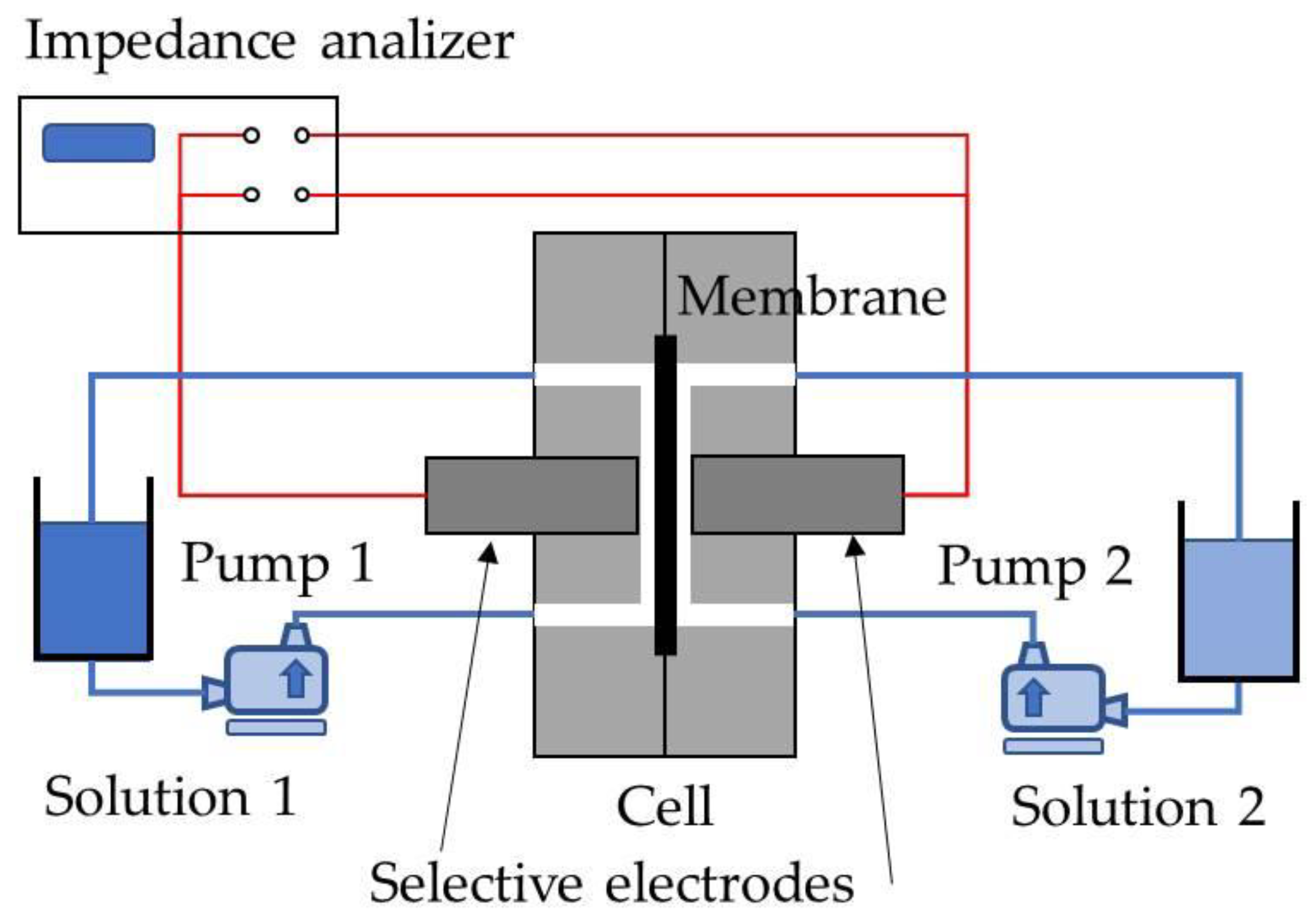
2.3. Electrochemical Impedance Spectroscopy
2.4. Retention and Permeability
2.5. Tangential Streaming Potential and Zeta Potential
3. Results and Discussion
3.1. Retention and Permeability
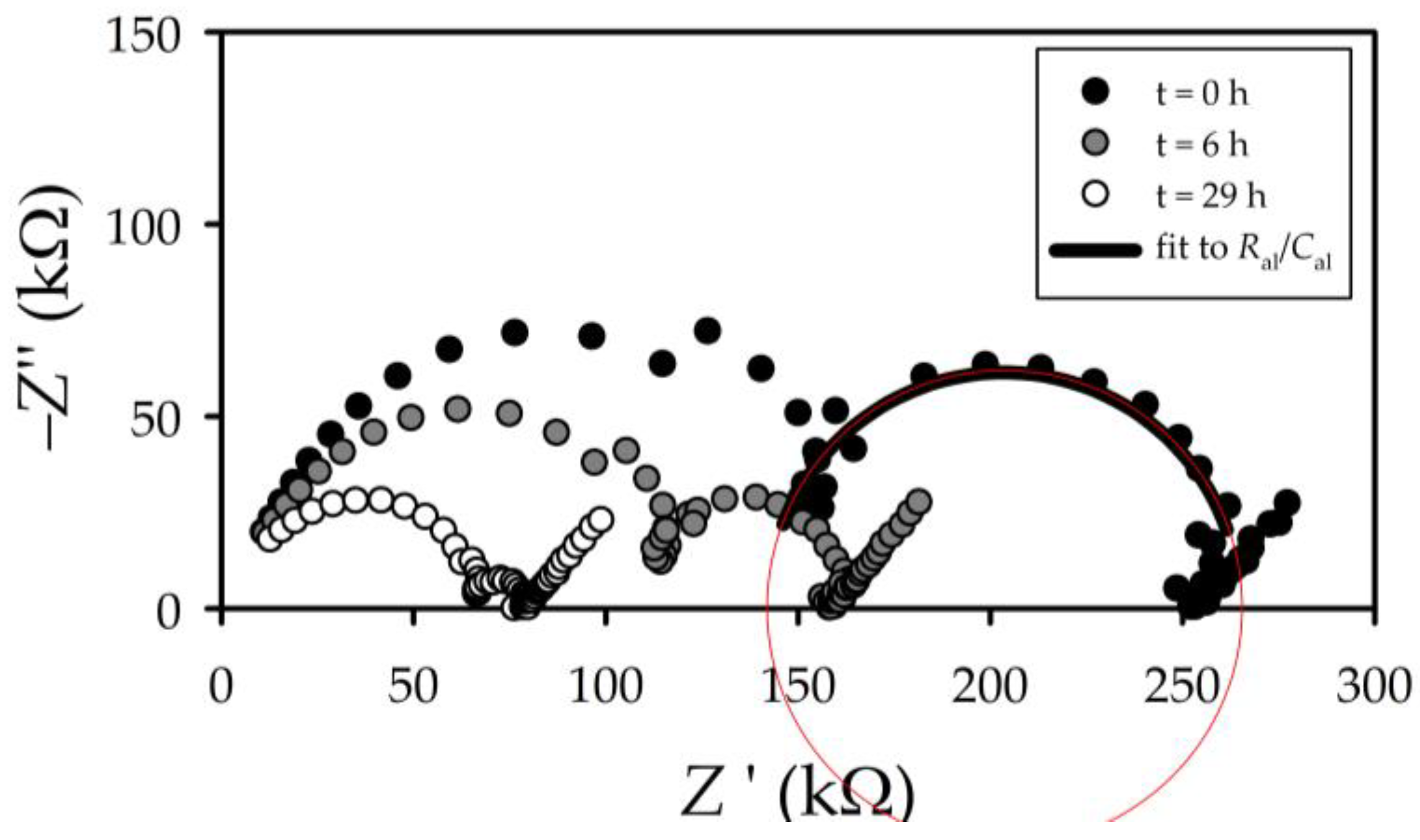
3.2. Electrochemical Impedance Spectroscopy
3.3. Zeta Potential
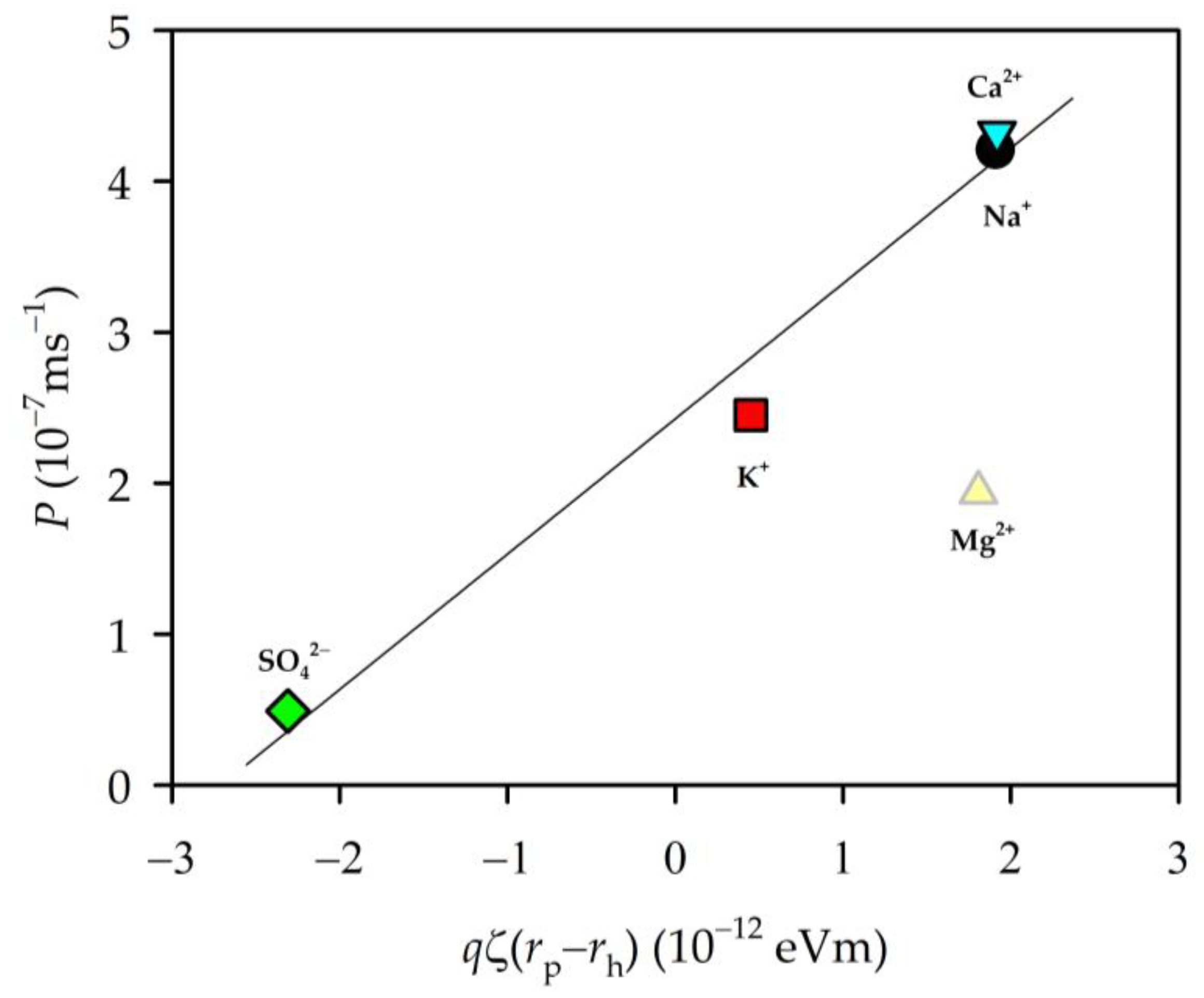
3.4. Zeta Potential and Permeability
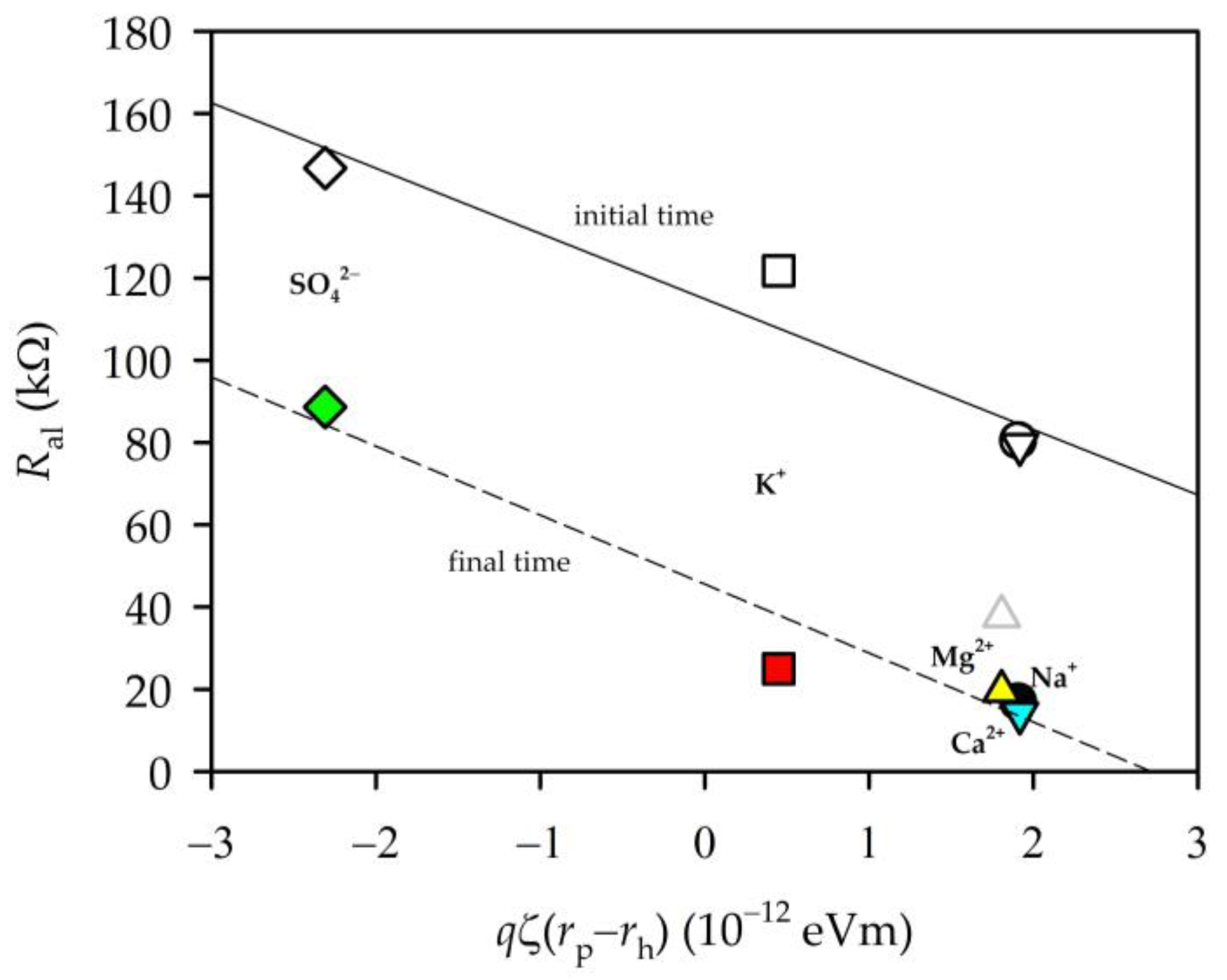
3.5. Zeta Potential and EIS Parameters
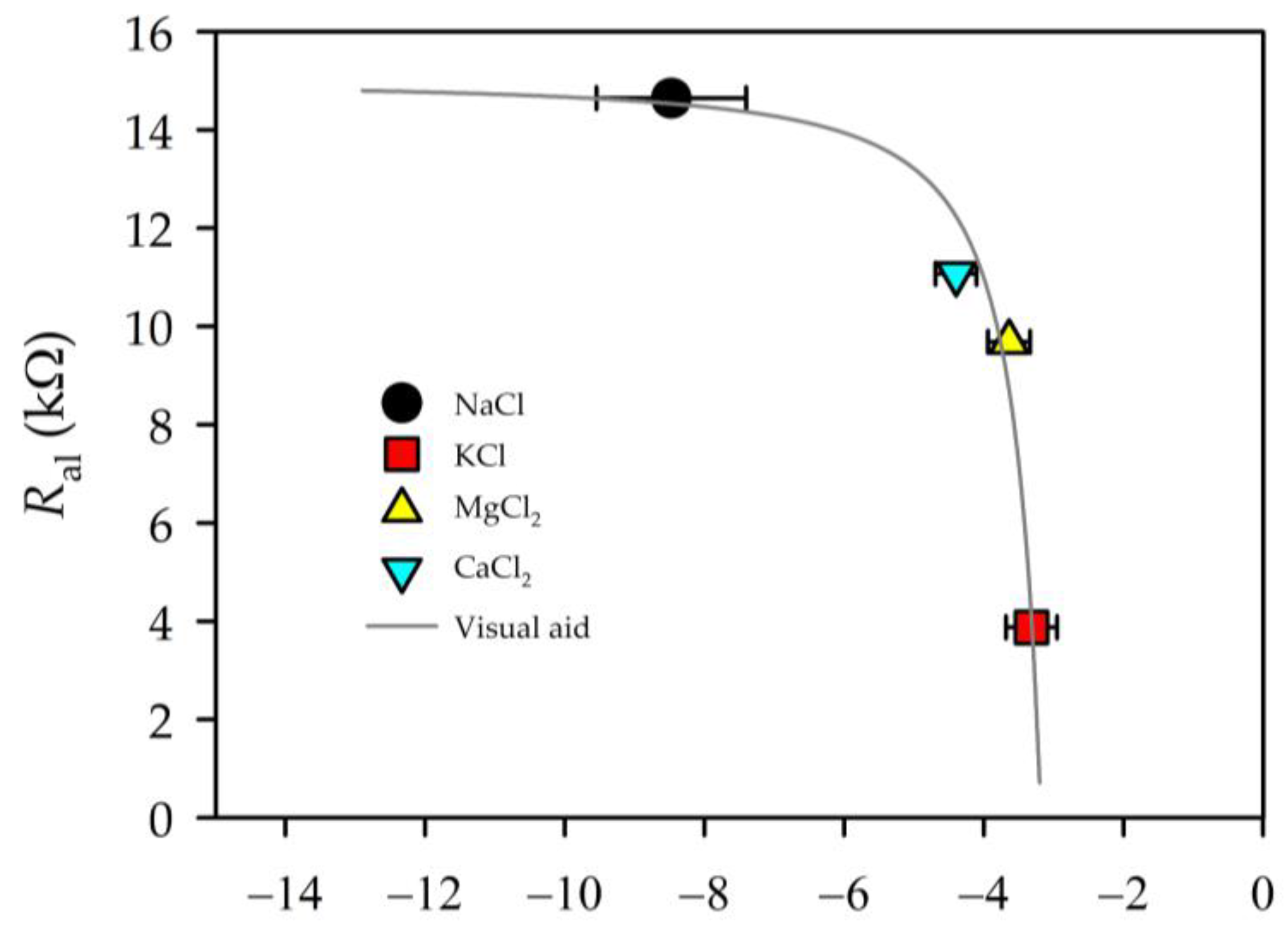
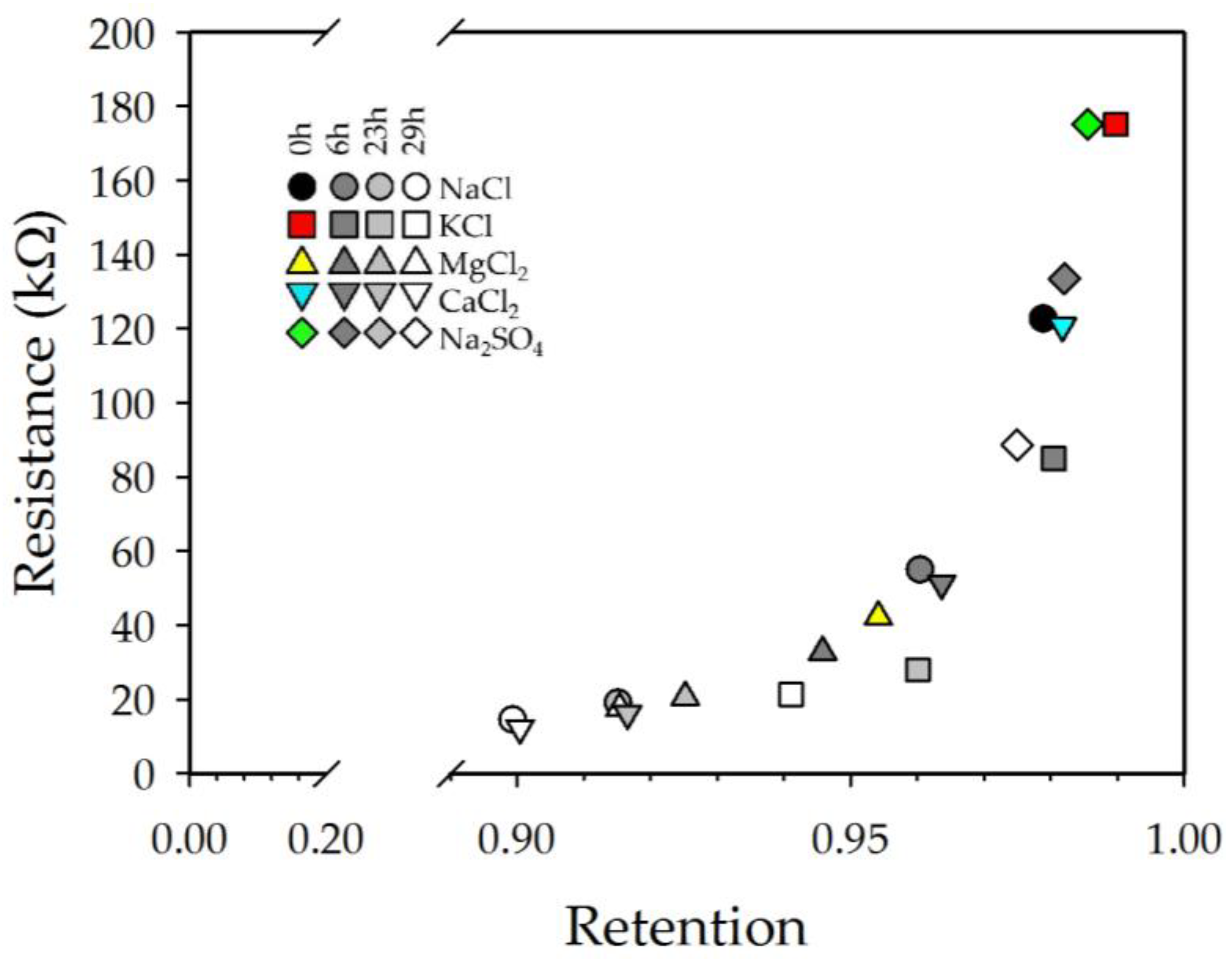
3.6. Permeability and EIS Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lanteri, Y.; Fievet, P.; Szymczyk, A. Evaluation of the steric, electric, and dielectric exclusion model on the basis of salt rejection rate and membrane potential measurements. J. Colloid Interface Sci. 2009, 331, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Fatah, M.A. Nanofiltration systems and applications in wastewater treatment: Review article. Ain Shams Eng. J. 2018, 9, 3077–3092. [Google Scholar] [CrossRef]
- Pinelo, M.; Møller, V.; Prado-Rubio, O.A.; Jonsson, G.; Meyer, A.S. Mechanisms controlling retention during ultrafiltration of charged saccharides: Molecular conformation and electrostatic forces. Sep. Purif. Technol. 2013, 118, 704–709. [Google Scholar] [CrossRef]
- Schaep, J.; Vandecasteele, C.; Leysen, R.; Doyen, W. Salt retention of Zirfon® membranes. Sep. Purif. Technol. 1998, 14, 127–131. [Google Scholar] [CrossRef]
- Tanninen, J.; Mänttäri, M.; Nyström, M. Effect of electrolyte strength on acid separation with NF membranes. J. Membr. Sci. 2007, 294, 207–212. [Google Scholar] [CrossRef]
- Tsuru, T.; Hironaka, D.; Yoshioka, T.; Asaeda, M. Titania membranes for liquid phase separation: Effect of surface charge on flux. Sep. Purif. Technol. 2001, 25, 307–314. [Google Scholar] [CrossRef]
- Labbez, C.; Fievet, P.; Szymczyk, A.; Vidonne, A.; Foissy, A.; Pagetti, J. Analysis of the salt retention of a titania membrane using the “DSPM” model: Effect of pH, salt concentration and nature. J. Membr. Sci. 2002, 208, 315–329. [Google Scholar] [CrossRef]
- Szymczyk, A.; Sbaï, M.; Fievet, P.; Vidonne, A. Transport Properties and Electrokinetic Characterization of an Amphoteric Nanofilter. Langmuir 2006, 22, 3910–3919. [Google Scholar] [CrossRef]
- Schaep, J.; Vandecasteele, C. Evaluating the charge of nanofiltration membranes. J. Membr. Sci. 2001, 188, 129–136. [Google Scholar] [CrossRef]
- Childress, A.E.; Elimelech, M. Relating Nanofiltration Membrane Performance to Membrane Charge (Electrokinetic) Characteristics. Environ. Sci. Technol. 2000, 34, 3710–3716. [Google Scholar] [CrossRef]
- Teixeira, M.R.; Rosa, M.J.; Nyström, M. The role of membrane charge on nanofiltration performance. J. Membr. Sci. 2005, 265, 160–166. [Google Scholar] [CrossRef]
- Dillmann, S.; Kaushik, S.A.; Stumme, J.; Ernst, M. Characterization and Performance of LbL-Coated Multibore Membranes: Zeta Potential, MWCO, Permeability and Sulfate Rejection. Membranes 2020, 10, 412. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Wang, H.; Zhang, Y.; Wang, M. Nanofiltration Membrane Characterization and Application: Extracting Lithium in Lepidolite Leaching Solution. Membranes 2020, 10, 178. [Google Scholar] [CrossRef] [PubMed]
- Díaz, D.R.; Carmona, F.J.; Palacio, L.; Ochoa, N.A.; Hernández, A.; Prádanos, P. Impedance spectroscopy and membrane potential analysis of microfiltration membranes. The influence of surface fractality. Chem. Eng. Sci. 2018, 178, 27–38. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Gharbi, O.; Vivier, V.; Gao, M.; Orazem, M.E. Electrochemical impedance spectroscopy. Nat. Rev. Methods Prim. 2021, 1, 1–21. [Google Scholar] [CrossRef]
- Ciucci, F. Modeling electrochemical impedance spectroscopy. Curr. Opin. Electrochem. 2018, 13, 132–139. [Google Scholar] [CrossRef]
- Macdonald, D.D. Reflections on the history of electrochemical impedance spectroscopy. Electrochimica Acta 2006, 51, 1376–1388. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. (Eds.) Impedance Spectroscopy: Theory, Experiment, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Silva, V.; Montalvillo, M.; Carmona, F.J.; Palacio, L.; Hernández, A.; Prádanos, P. Prediction of single salt rejection in nanofiltration membranes by independent measurements. Desalination 2015, 382, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Efligenir, A.; Fievet, P.; Déon, S.; Salut, R. Characterization of the isolated active layer of a NF membrane by electrochemical impedance spectroscopy. J. Membr. Sci. 2015, 477, 172–182. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, M.; Ma, Z.; Gao, C. Electrochemical impedance spectroscopy analysis of sulfonated polyethersulfone nanofiltration membrane. Desalination 2011, 271, 29–33. [Google Scholar] [CrossRef]
- Fievet, P.; Szymczyk, A.; Labbez, C.; Aoubiza, B.; Simon, C.; Foissy, A.; Pagetti, J. Determining the Zeta Potential of Porous Membranes Using Electrolyte Conductivity inside Pores. J. Colloid Interface Sci. 2001, 235, 383–390. [Google Scholar] [CrossRef]
- Zhang, Y.; Van der Bruggen, B.; Chen, G.; Braeken, L.; Vandecasteele, C. Removal of pesticides by nanofiltration: Effect of the water matrix. Sep. Purif. Technol. 2004, 38, 163–172. [Google Scholar] [CrossRef]
- Montalvillo, M.; Silva, V.; Palacio, L.; Calvo, J.I.; Carmona, F.J.; Hernández, A.; Prádanos, P. Charge and dielectric characterization of nanofiltration membranes by impedance spectroscopy. J. Membr. Sci. 2014, 454, 163–173. [Google Scholar] [CrossRef]
- Lettmann, C.; Möckel, D.; Staude, E. Permeation and tangential flow streaming potential measurements for electrokinetic characterization of track-etched microfiltration membranes. J. Membr. Sci. 1999, 159, 243–251. [Google Scholar] [CrossRef]
- Fievet, P.; Sbaï, M.; Szymczyk, A.; Vidonne, A. Determining the ζ-potential of plane membranes from tangential streaming potential measurements: Effect of the membrane body conductance. J. Membr. Sci. 2003, 226, 227–236. [Google Scholar] [CrossRef]
- Möckel, D.; Staude, E.; Dal-Cin, M.; Darcovich, K.; Guiver, M. Tangential flow streaming potential measurements: Hydrodynamic cell characterization and zeta potentials of carboxylated polysulfone membranes. J. Membr. Sci. 1998, 145, 211–222. [Google Scholar] [CrossRef] [Green Version]
- Del Valle Silva, V. Theoretical Foundations and Modelling in Nanofiltration Membrane Systems, p. 1. 2010. Available online: https://dialnet.unirioja.es/servlet/tesis?codigo=295607&info=resumen&idioma=SPA (accessed on 28 January 2023).
- Silva, V.; Martín, A.; Martínez, F.; Malfeito, J.; Prádanos, P.; Palacio, L.; Hernández, A. Electrical characterization of NF membranes. A modified model with charge variation along the pores. Chem. Eng. Sci. 2011, 66, 2898–2911. [Google Scholar] [CrossRef]
- Nyström, M.; Pihlajamäki, A.; Ehsani, N. Characterization of ultrafiltration membranes by simultaneous streaming potential and flux measurements. J. Membr. Sci. 1994, 87, 245–256. [Google Scholar] [CrossRef]
- Nyström, M.; Lindström, M.; Matthiasson, E. Streaming potential as a tool in the characterization of ultrafiltration membranes. Colloids Surf. 1989, 36, 297–312. [Google Scholar] [CrossRef]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- The Zeta Potential for Solid Surface Analysis–A Practical Guide to Streaming Potential Measurement | Web-Books in the Austria-Forum. Available online: https://austria-forum.org/web-books/en/zeta00en2014iicm (accessed on 1 February 2023).
- Starzak, M.E. The Physical Chemistry of Membranes; Academic Press: Cambridge, MA, USA, 1984; p. 334. [Google Scholar]
- Marcus, Y. Ionic radii in aqueous solutions. J. Solut. Chem. 1983, 12, 271–275. [Google Scholar] [CrossRef]
- Marcus, Y. Ionic radii in aqueous solutions. Chem. Rev. 1988, 88, 1475–1498. [Google Scholar] [CrossRef]
- Ciferri, A.; Perico, A. Ionic Interactions in Natural and Synthetic Macromolecules, 1st ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]




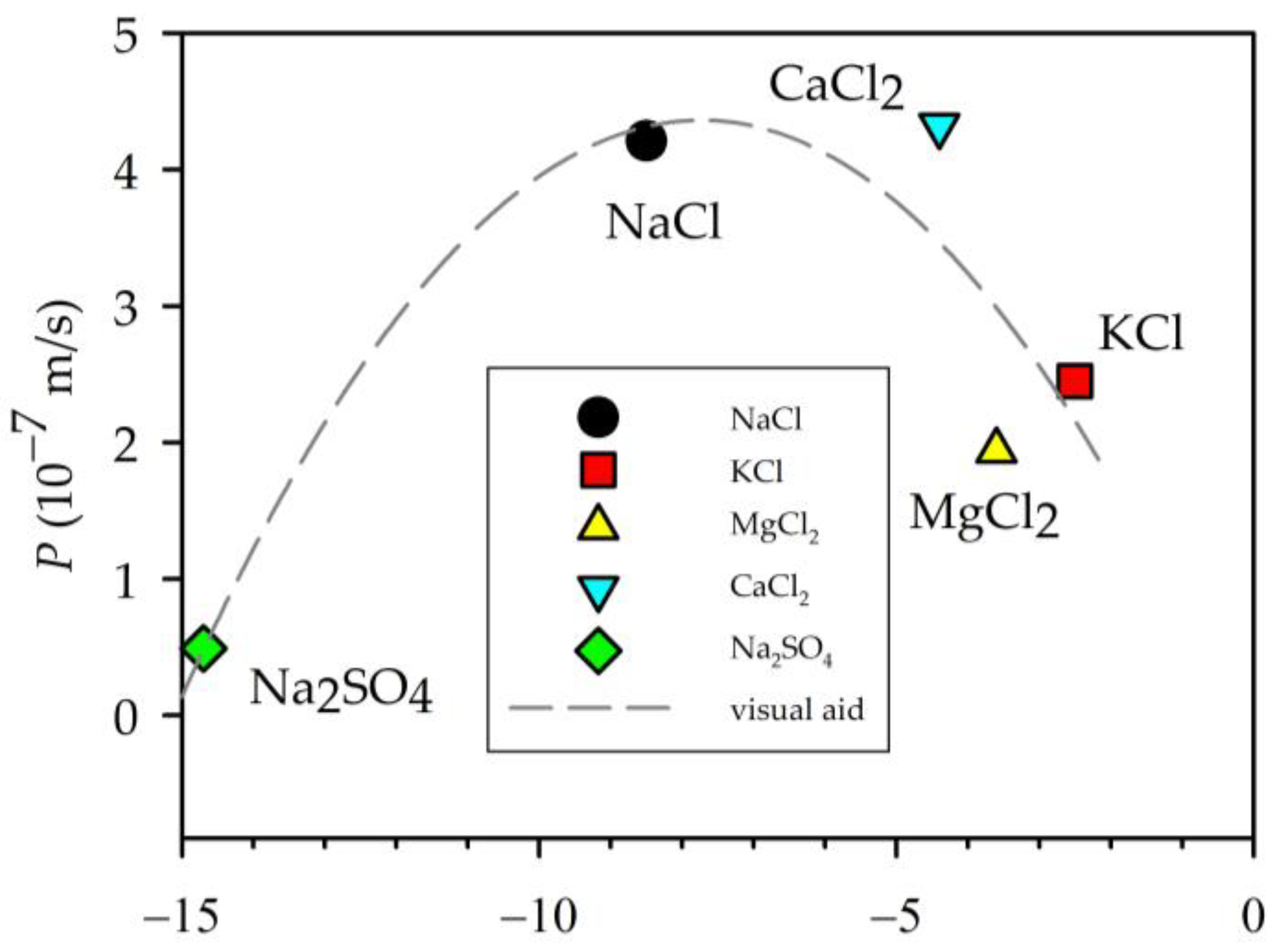

| Electrolyte Solution | Permeability (10−7 m s−1) | tc (h) |
|---|---|---|
| NaCl | 4.21 ± 0.02 | 178 |
| KCl | 2.45 ± 0.15 | 315 |
| MgCl2 | 1.94 ± 0.01 | 385 |
| CaCl2 | 4.32 ± 0.01 | 175 |
| Na2SO4 | 0.49 ± 0.14 | 1378 |
| Ion | Ionic Radius (nm) [30] | Hydrated Radius, rh. (nm) [31] | Ionic Diffusivity (10−5 cm2 s−1) [32] |
|---|---|---|---|
| Na+ | 0.098 ± 0.003 | 0.2356 ± 0.0060 | 1.334 |
| K+ | 0.134 ± 0.004 | 0.2798 ± 0.0081 | 1.957 |
| Mg2+ | 0.072 ± 0.002 | 0.2090 ± 0.0041 | 0.706 |
| Ca2+ | 0.103 ± 0.003 | 0.2422 ± 0.0052 | 0.792 |
| SO42− | 0.240 ± 0.005 | 0.3815 ± 0.0071 | 1.065 |
| Cl— | 0.183 ± 0.003 | 0.3187 ± 0.0067 | 2.032 |
| Electrolyte Solution | Streaming Potential (µV Pa−1) | Zeta Potential (mV) |
|---|---|---|
| NaCl | −0.55 ± 0.07 | −8.5 ± 1.1 |
| KCl | −0.16 ± 0.02 | −2.5 ± 0.4 |
| MgCl2 | −0.18 ± 0.02 | −3.6 ± 0.3 |
| CaCl2 | −0.20 ± 0.02 | −4.4 ± 0.3 |
| Na2SO4 | −0.83 ± 0.03 | −14.7 ± 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, M.-Á.; Gallego, S.; Palacio, L.; Hernández, A.; Prádanos, P.; Carmona, F.J. Saline Retention and Permeability of Nanofiltration Membranes Versus Resistance and Capacitance as Obtained from Impedance Spectroscopy under a Concentration Gradient. Membranes 2023, 13, 608. https://doi.org/10.3390/membranes13060608
Pérez M-Á, Gallego S, Palacio L, Hernández A, Prádanos P, Carmona FJ. Saline Retention and Permeability of Nanofiltration Membranes Versus Resistance and Capacitance as Obtained from Impedance Spectroscopy under a Concentration Gradient. Membranes. 2023; 13(6):608. https://doi.org/10.3390/membranes13060608
Chicago/Turabian StylePérez, Miguel-Ángel, Silvia Gallego, Laura Palacio, Antonio Hernández, Pedro Prádanos, and Francisco Javier Carmona. 2023. "Saline Retention and Permeability of Nanofiltration Membranes Versus Resistance and Capacitance as Obtained from Impedance Spectroscopy under a Concentration Gradient" Membranes 13, no. 6: 608. https://doi.org/10.3390/membranes13060608
APA StylePérez, M.-Á., Gallego, S., Palacio, L., Hernández, A., Prádanos, P., & Carmona, F. J. (2023). Saline Retention and Permeability of Nanofiltration Membranes Versus Resistance and Capacitance as Obtained from Impedance Spectroscopy under a Concentration Gradient. Membranes, 13(6), 608. https://doi.org/10.3390/membranes13060608









