Prediction of Flooded Compartment Damage Locations in Ships by Using Spectrum Analysis of Ship Motions in Waves
Abstract
:1. Introduction
2. Materials and Methods
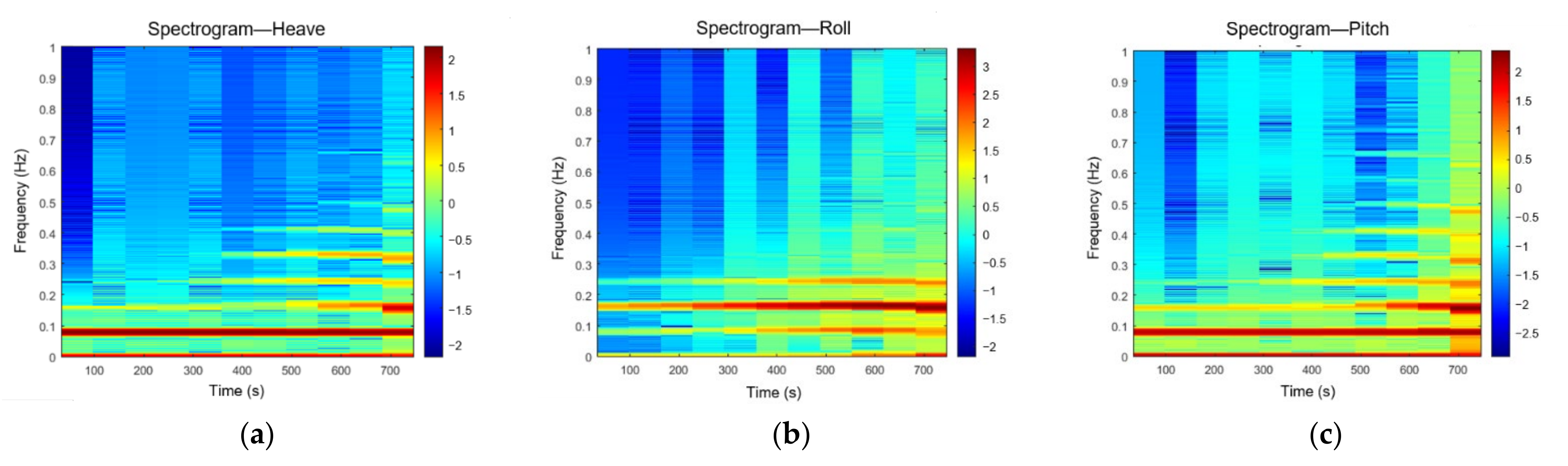
2.1. Short-Time Fourier Transform and Spectrogram
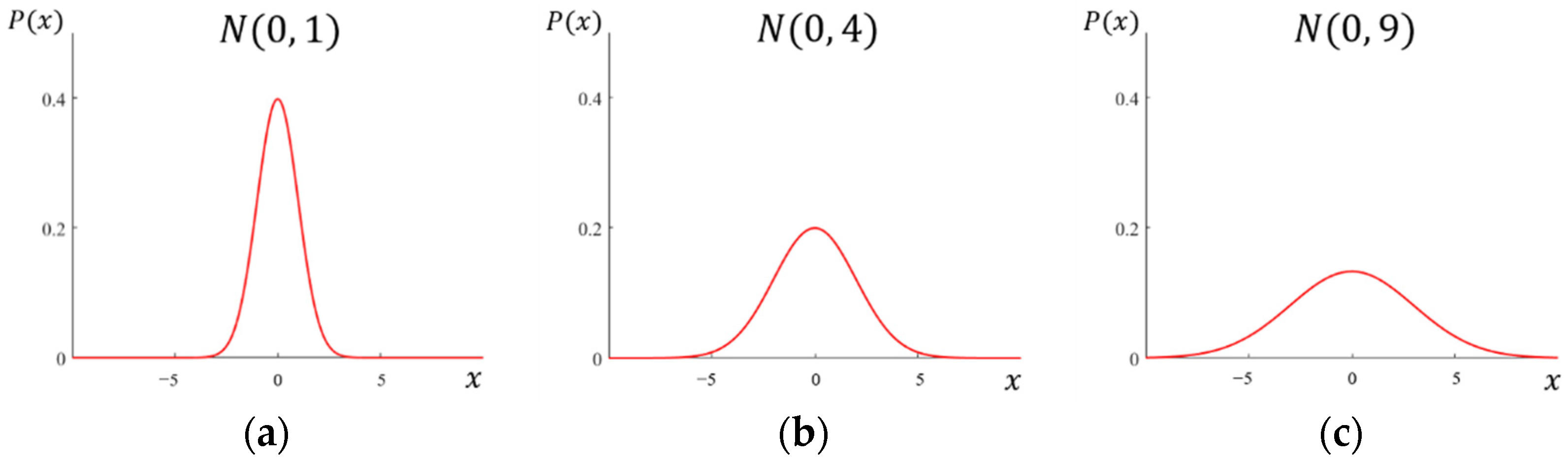
2.2. Probability Density Function of the Normal Distribution
3. Case Study
3.1. Ship Motion Data
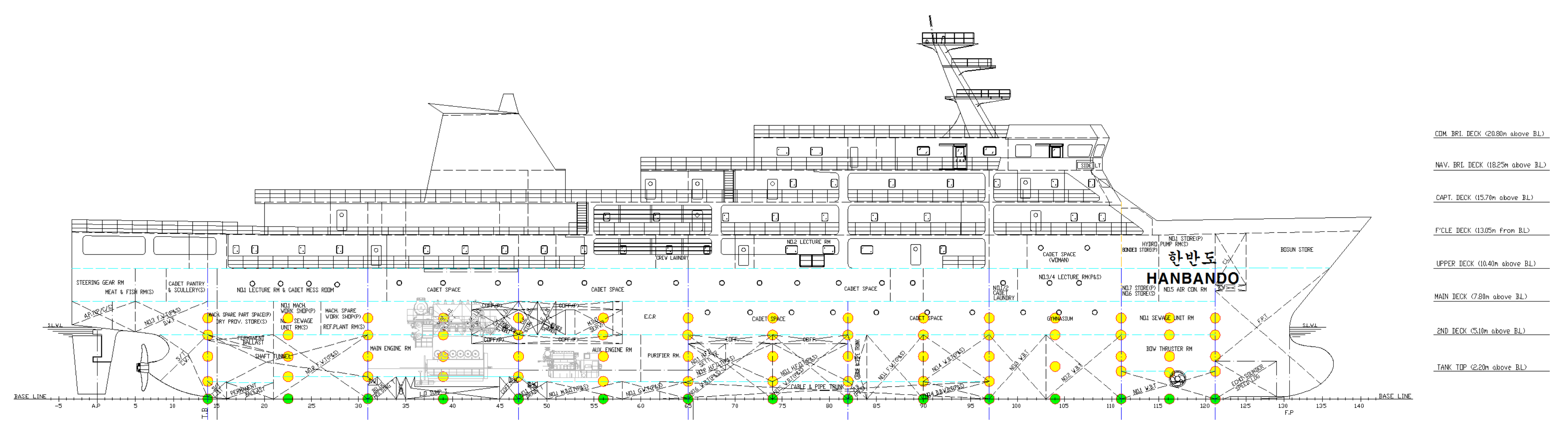
3.1.1. Ship Specifications
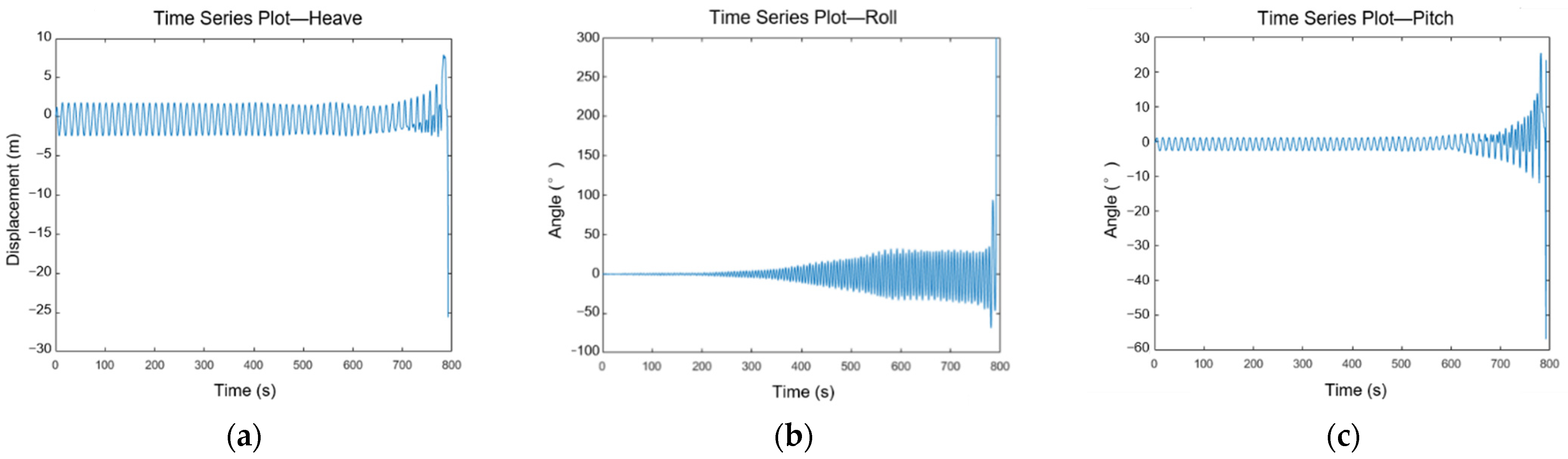
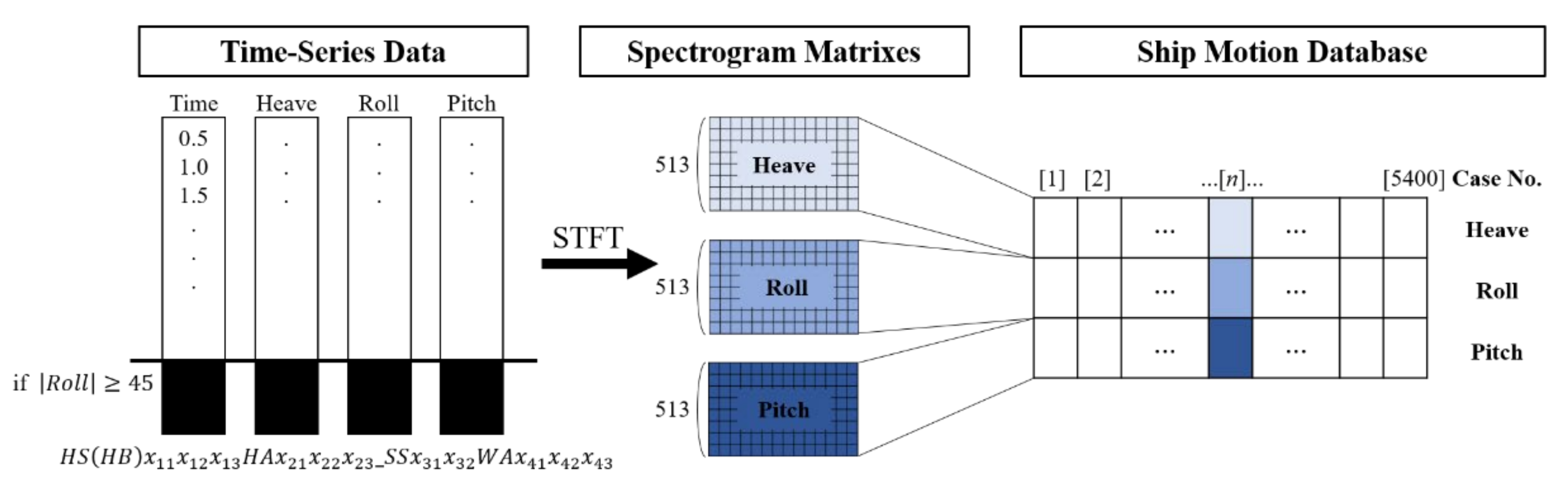
3.1.2. Construction of Ship Motion Data
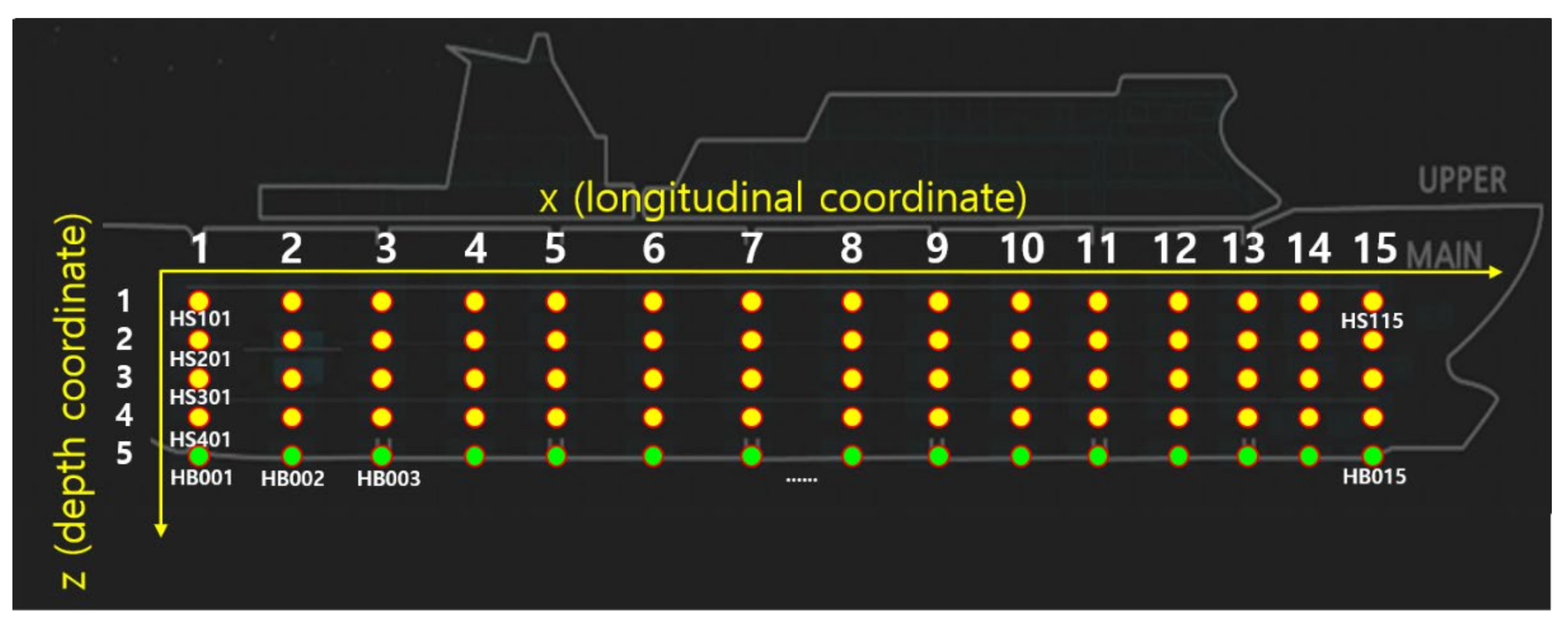
3.2. Construction of Spectrogram Database
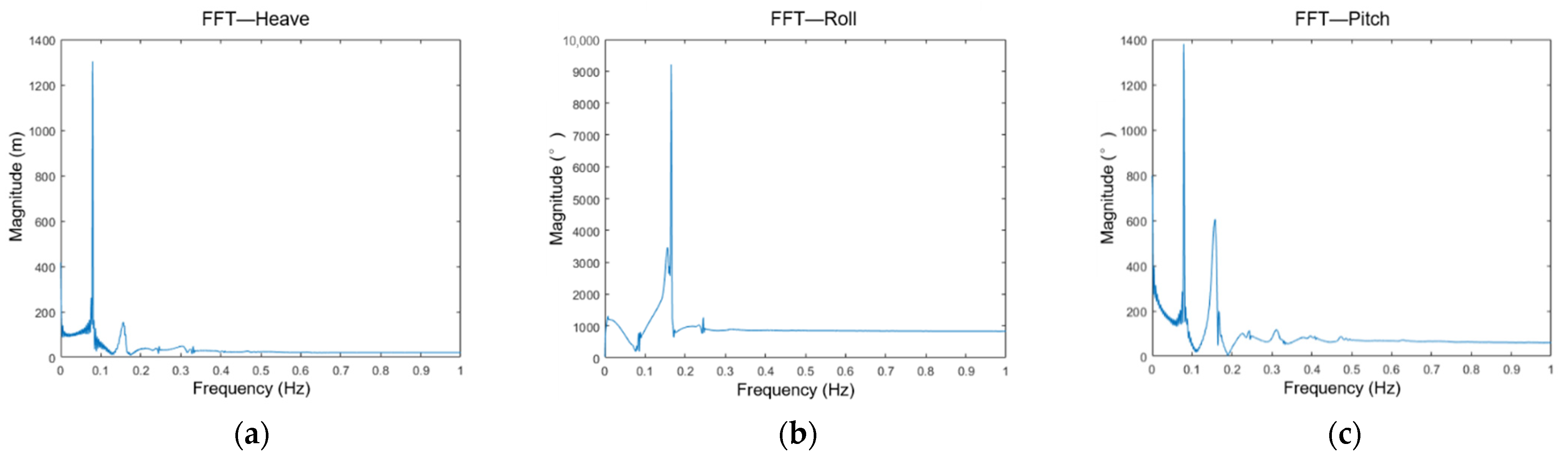
3.2.1. STFT Specifications
3.2.2. Method for Database Construction
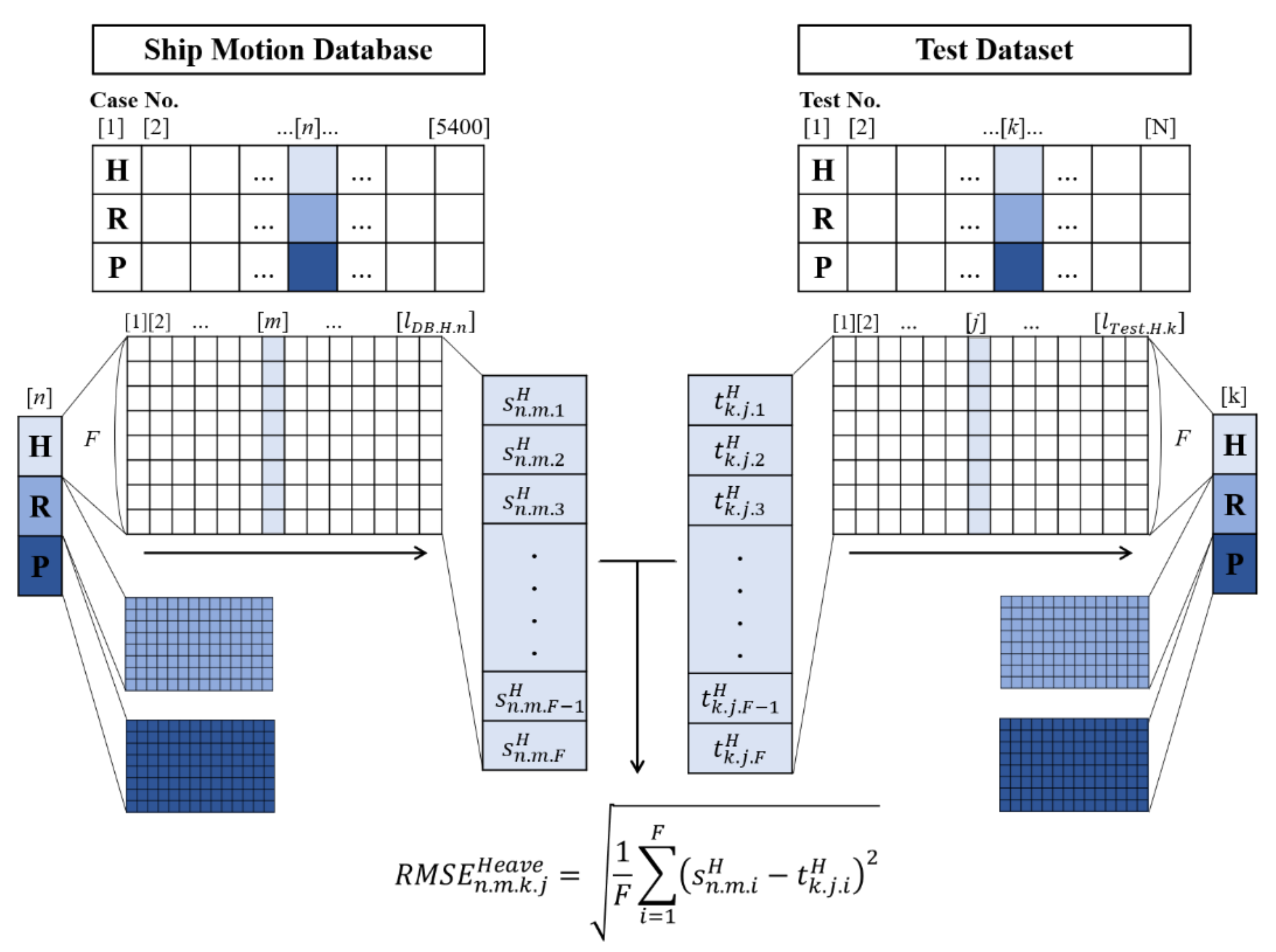
3.3. Prediction of Damage Center
3.3.1. Test Data Production
3.3.2. RMSE to Predict Damage Center
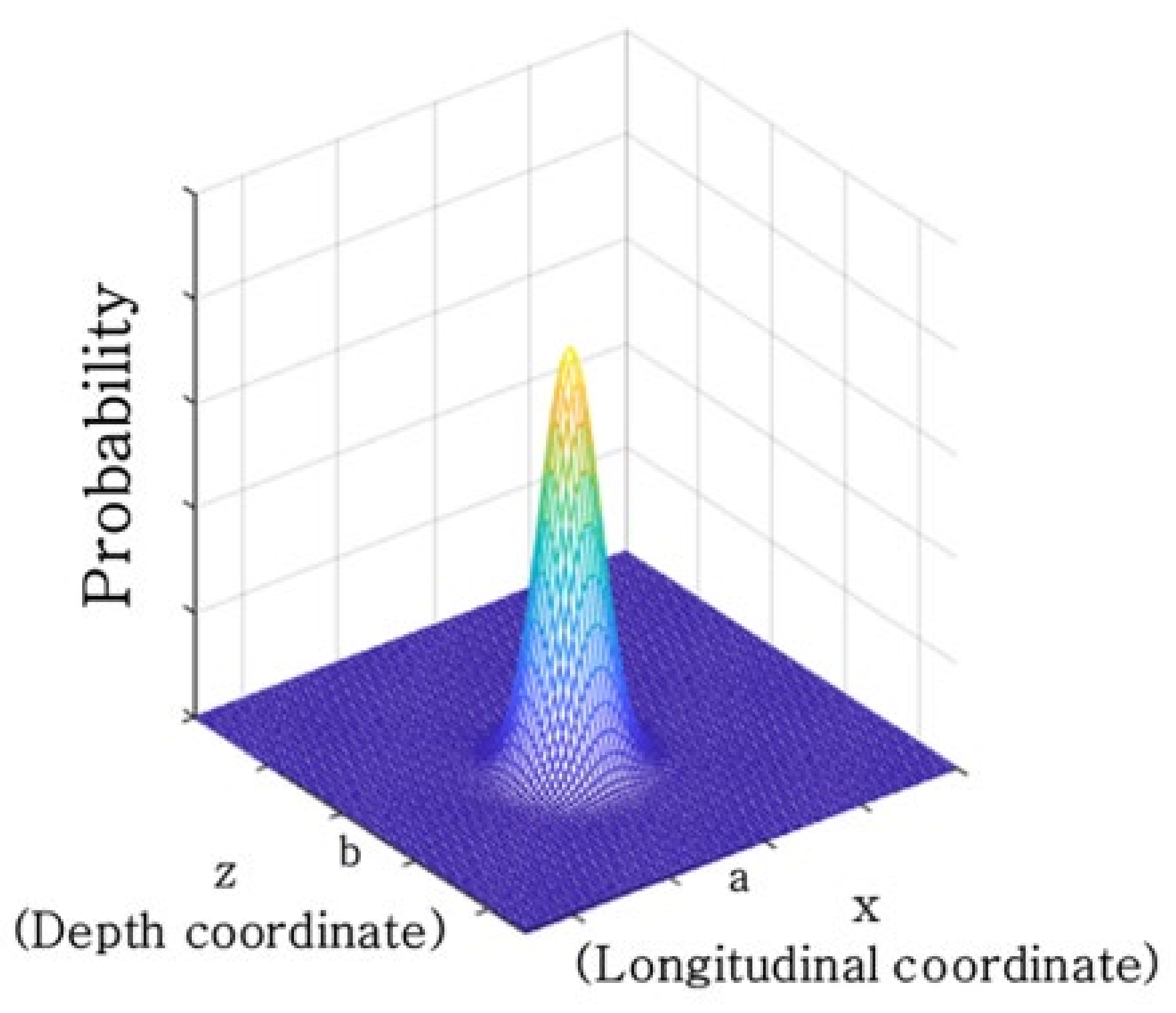
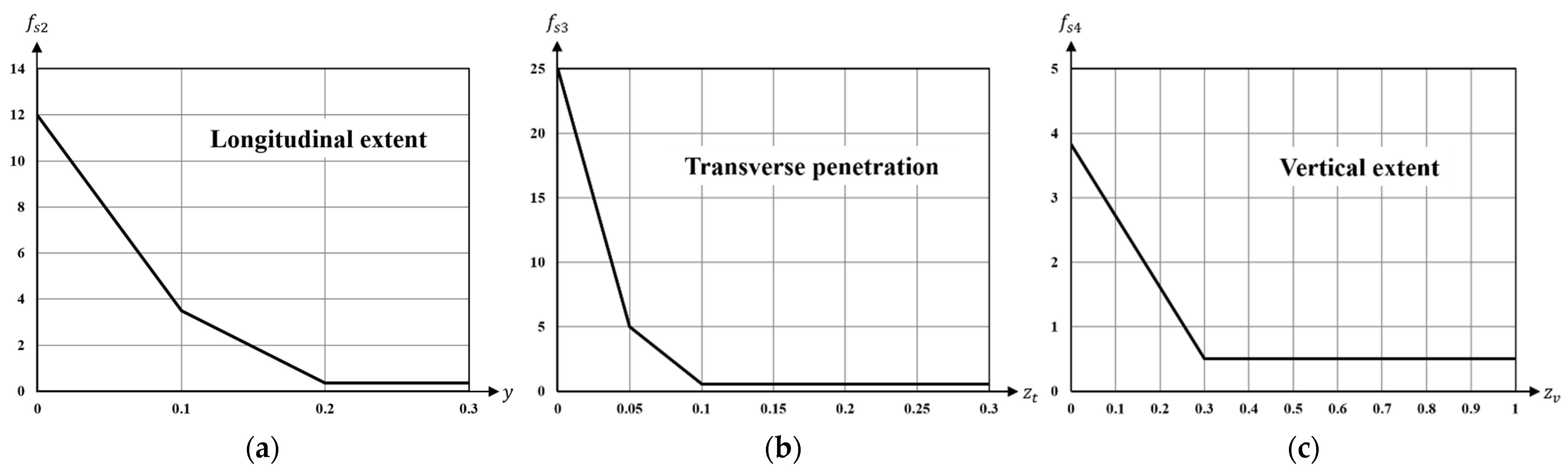
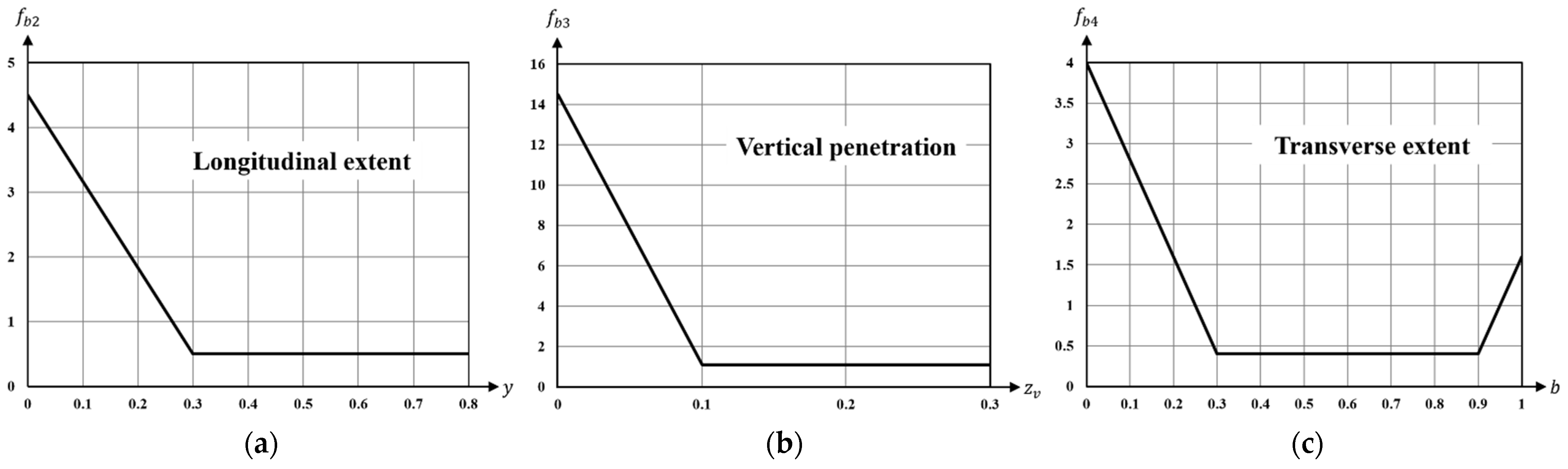
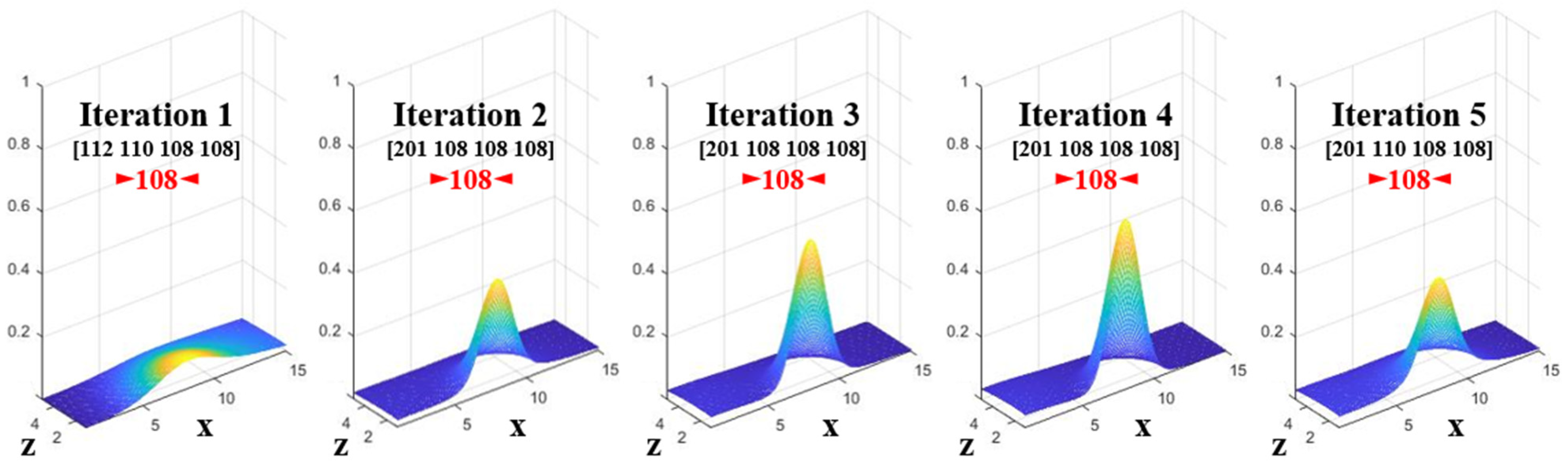
3.3.3. Probability Function for Prediction of Damage Center
4. Results and Discussion
5. Conclusions
- In 95 out of 100 tests that used heave, roll, and pitch motion data, the location of the damage center was accurately predicted. Among these, 71 cases confirmed the damage center within the initial five iterations.
- When performing the same test using only roll and pitch motion data, the damage center was predicted correctly for 94 out of 100 tests. The results showed that the heave motions did not have a significant effect on predicting the location of the damage center using ship motion characteristics.
- Prediction of the damage center in this study took approximately 4.5 to 5.5 s per iteration, where real-time ship motion data collected for 130 s was used for each iteration of the prediction. Thus, the method is valid from a time perspective.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korea Maritime Safety Tribunal. Statistics of Marine Accidents [Marine Accidents by Accident Type] 2021. Available online: https://www.kmst.go.kr/eng/com/selectHtmlPage.do?htmlName=m4_vesseltype (accessed on 1 April 2021).
- Park, H.R.; Park, H.S.; Kim, B.R. A Study on the Policy Direction related to the Introduction of Maritime Autonomous Surface Ship (MASS); KMI Research Project Report; KMI: Pusan, Korea, 2018; No 2018-07. [Google Scholar]
- Lee, D.; Kim, S.; Lee, K.; Shin, S.C.; Choi, J.; Park, B.J.; Kang, H.J. Performance-based on-board damage control system for ships. Ocean Eng. 2021, 223, 108636. [Google Scholar] [CrossRef]
- Karolius, K.; Cichowicz, J.; Vassalos, D. Risk-Based Positioning of Flooding Sensors to Reduce Prediction Uncertainty of Damage Survivability. In Proceedings of the 13th International Conference on the Stability of Ships and Ocean Vehicles-STAB 2018, Kobe, Japan, 16–21 September 2018; pp. 627–637. [Google Scholar]
- Karolius, K.B.; Cichowicz, J.; Vassalos, D. Risk-based, sensor-fused detection of flooding casualties for emergency response. Ships Offshore Struct. 2021, 16, 449–478. [Google Scholar] [CrossRef]
- Varela, J.M.; Rodrigues, J.M.; Soares, C.G. On-board decision support system for ship flooding emergency response. Procedia Comput. Sci. 2014, 29, 1688–1700. [Google Scholar] [CrossRef] [Green Version]
- Varela, J.M.; Rodrigues, J.M.; Soares, C.G. 3D simulation of ship motions to support the planning of rescue operations on damaged ships. Procedia Comput. Sci. 2015, 51, 2397–2405. [Google Scholar] [CrossRef] [Green Version]
- Ruponen, P.; Lindroth, D.; Pennanen, P. Prediction of survivability for decision support in ship flooding emergency. In Proceedings of the 12th International Conference on the Stability of Ships and Ocean Vehicles STAB 2015, Glasgow, UK, 14–19 June 2015; pp. 14–19. [Google Scholar]
- Ruponen, P.; Pulkkinen, A.; Laaksonen, J. A method for breach assessment onboard a damaged passenger ship. Appl. Ocean Res. 2017, 64, 236–248. [Google Scholar] [CrossRef]
- Kang, H.; Choi, J.; Yim, G.; Ahn, H. Time Domain Decision-Making Support Based on Ship Behavior Monitoring and Flooding Simulation Database for On-Board Damage Control. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Braidotti, L.; Mauro, F. A new calculation technique for onboard progressive flooding simulation. Ship Technol. Res. 2019, 66, 150–162. [Google Scholar] [CrossRef]
- Acanfora, M.; Begovic, E.; De Luca, F. A fast simulation method for damaged ship dynamics. J. Mar. Sci. Eng. 2019, 7, 111. [Google Scholar] [CrossRef] [Green Version]
- Braidotti, L.; Mauro, F. A fast algorithm for onboard progressive flooding simulation. J. Mar. Sci. Eng. 2020, 8, 369. [Google Scholar] [CrossRef]
- Papanikolaou, A.; Spanos, D. 24th ITTC benchmark study on numerical prediction of damage ship stability in waves preliminary analysis of results. In Proceedings of the 7th International Workshop on Stability and Operational Safety of Ships, Jiao Tong University, Shanghai, China, 1–3 November 2004. [Google Scholar]
- Ingale, R. Harmonic analysis using FFT and STFT. Int. J. Signal. Process. Image Process. Pattern Recognit. 2014, 7, 345–362. [Google Scholar] [CrossRef]
- Kehtarnavaz, N. Frequency Domain Processing. In Digital Signal Processing System Design; Elsevier: Amsterdam, The Netherlands, 2008; pp. 175–196. [Google Scholar]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Elsevier Science: Oxford, UK, 2015. [Google Scholar]
- Sairamya, N.J.; Susmitha, L.; George, S.T.; Subathra, M.S.P. Hybrid Approach for Classification of Electroencephalographic Signals Using Time–Frequency Images with Wavelets and Texture Features. In Intelligent Data Analysis for Biomedical Applications; Academic Press: Cambridge, MA, USA, 2019; pp. 253–273. [Google Scholar]
- Sugiyama, M. Examples of Continuous Probability Distributions. In Introduction to Statistical Machine Learning; Elsevier: Amsterdam, The Netherlands, 2015; pp. 37–50. [Google Scholar]
- Lee, G.J. Dynamic orifice flow model and compartment models for flooding simulation of a damaged ship. Ocean Eng. 2015, 109, 635–653. [Google Scholar] [CrossRef] [Green Version]
- IMO Res. MEPC.110(49), Revised Interim Guidelines for the Approval of Alternative Methods of Design and Construction of Oil Tankers under Regulation 13F(5) of Annex I of MARPOL 73/78). Available online: http://rise.odessa.ua/texts/MEPC110_49e.php3 (accessed on 24 October 2021).
- Rules for Classification: Ships—DNVGL-RU-SHIP, Pt.3 Ch.15. Edition July 2016, Amended January 2017, Stability. Available online: https://rules.dnv.com/docs/pdf/DNV/ru-ship/2017-01/DNVGL-RU-SHIP-Pt3Ch15.pdf (accessed on 26 October 2021).
- Jin, S.M. Introduction to the Spectrum and Spectrogram. J. Korean Soc. Laryngol. Phoniatr. Logop. 2008, 19, 101–106. [Google Scholar]
- Gautam, G.; Shrestha, S.; Cho, S. Spectral Analysis of Rectangular, Hanning, Hamming and Kaiser Window for Digital Fir Filter. Int. J. Adv. Smart Converg. 2015, 4, 138–144. [Google Scholar] [CrossRef] [Green Version]



| Human Error | Machinery Damage | Others | |
|---|---|---|---|
| 2016 | 264 | 38 | 28 |
| 2017 | 261 | 47 | 43 |
| 2018 | 189 | 46 | 28 |
| 2019 | 204 | 32 | 21 |
| 2020 | 230 | 28 | 23 |
| Rate | 77.5% | 12.9% | 9.6% |
| Sea State | Average Significant Wave Height (m) | Most Probable Spectral Peak Period (s) |
|---|---|---|
| 0–1 | 0.05 | - |
| 2 | 0.30 | 6.30 |
| 3 | 0.88 | 7.50 |
| 4 | 1.88 | 8.80 |
| 5 | 3.25 | 9.70 |
| 6 | 5.00 | 12.40 |
| 7 | 7.50 | 15.00 |
| 8 | 11.50 | 16.40 |
| Over 8 | 14.00 | 20.00 |
| Heave | Roll | Pitch | Total | |
|---|---|---|---|---|
| Count | 160,565 | 160,565 | 160,565 | 160,565 |
| Mean | 209.90 | 13.45 | 13.62 | 236.97 |
| Standard deviation | 28.99 | 6.99 | 3.93 | 29.26 |
| Min | 10.04 | 0.31 | 0.47 | 17.23 |
| 1% | 109.48 | 1.99 | 4.75 | 138.10 |
| 10% | 185.07 | 4.34 | 9.25 | 212.40 |
| 25% | 202.06 | 8.65 | 11.20 | 226.13 |
| 50% | 208.67 | 13.17 | 13.08 | 234.28 |
| Max | 364.49 | 168.74 | 28.69 | 554.86 |
| Number of Repeated Damage Centers | Standard Deviation σ | Maximum Probability |
|---|---|---|
| 4 | 0.5 | 0.8 |
| 3 | 1 | 0.4 |
| 2 | 2 | 0.2 |
| 1 | 4 | 0.1 |
| Iterations | Cases | ||
|---|---|---|---|
| Matches (95) | 1–5 | 71 | |
| 6–10 | 19 | ||
| 11–20 | 5 | ||
| Correct Location | Predicted Location | ||
| Mismatches (5) | 2 | 205 | 305 |
| 3 | 112 | 104 | |
| 5 | 206 | 306 | |
| 5 | 012 | 412 | |
| 7 | 008 | 007 | |
| Iteration | Cases | ||
|---|---|---|---|
| Matches (94) | 1–5 | 81 | |
| 6–10 | 10 | ||
| 11–20 | 3 | ||
| Correct Location | Predicted Location | ||
| Mismatches (6) | 5 | 312 | 412 |
| 5 | 306 | 206 | |
| 7 | 104 | 304 | |
| 10 | 012 | 312 | |
| 12 | 007 | 009 | |
| 13 | 401 | 001 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, H.-y.; Roh, H.-d.; Kim, G.-y.; Oh, S.-j.; Choi, J.; Lee, D.-k.; Shin, S.-c. Prediction of Flooded Compartment Damage Locations in Ships by Using Spectrum Analysis of Ship Motions in Waves. J. Mar. Sci. Eng. 2022, 10, 17. https://doi.org/10.3390/jmse10010017
Son H-y, Roh H-d, Kim G-y, Oh S-j, Choi J, Lee D-k, Shin S-c. Prediction of Flooded Compartment Damage Locations in Ships by Using Spectrum Analysis of Ship Motions in Waves. Journal of Marine Science and Engineering. 2022; 10(1):17. https://doi.org/10.3390/jmse10010017
Chicago/Turabian StyleSon, Hye-young, Hyeon-dong Roh, Gi-yong Kim, Sang-jin Oh, Jin Choi, Dong-kon Lee, and Sung-chul Shin. 2022. "Prediction of Flooded Compartment Damage Locations in Ships by Using Spectrum Analysis of Ship Motions in Waves" Journal of Marine Science and Engineering 10, no. 1: 17. https://doi.org/10.3390/jmse10010017
APA StyleSon, H.-y., Roh, H.-d., Kim, G.-y., Oh, S.-j., Choi, J., Lee, D.-k., & Shin, S.-c. (2022). Prediction of Flooded Compartment Damage Locations in Ships by Using Spectrum Analysis of Ship Motions in Waves. Journal of Marine Science and Engineering, 10(1), 17. https://doi.org/10.3390/jmse10010017







