Fatigue Assessment of Moorings for Floating Offshore Wind Turbines by Advanced Spectral Analysis Methods
Abstract
:1. Introduction
2. Model Description of Dynamic Analysis
3. Fatigue Analysis of Mooring Lines
3.1. The Combined-Spectrum Approach
3.2. Fatigue Assessment by Time-History Analysis
3.3. Fatigue Assessment by Spectral Analysis
4. Advanced Spectral Analysis
4.1. Welch Method
4.2. Thomson Method
5. Main Input Data
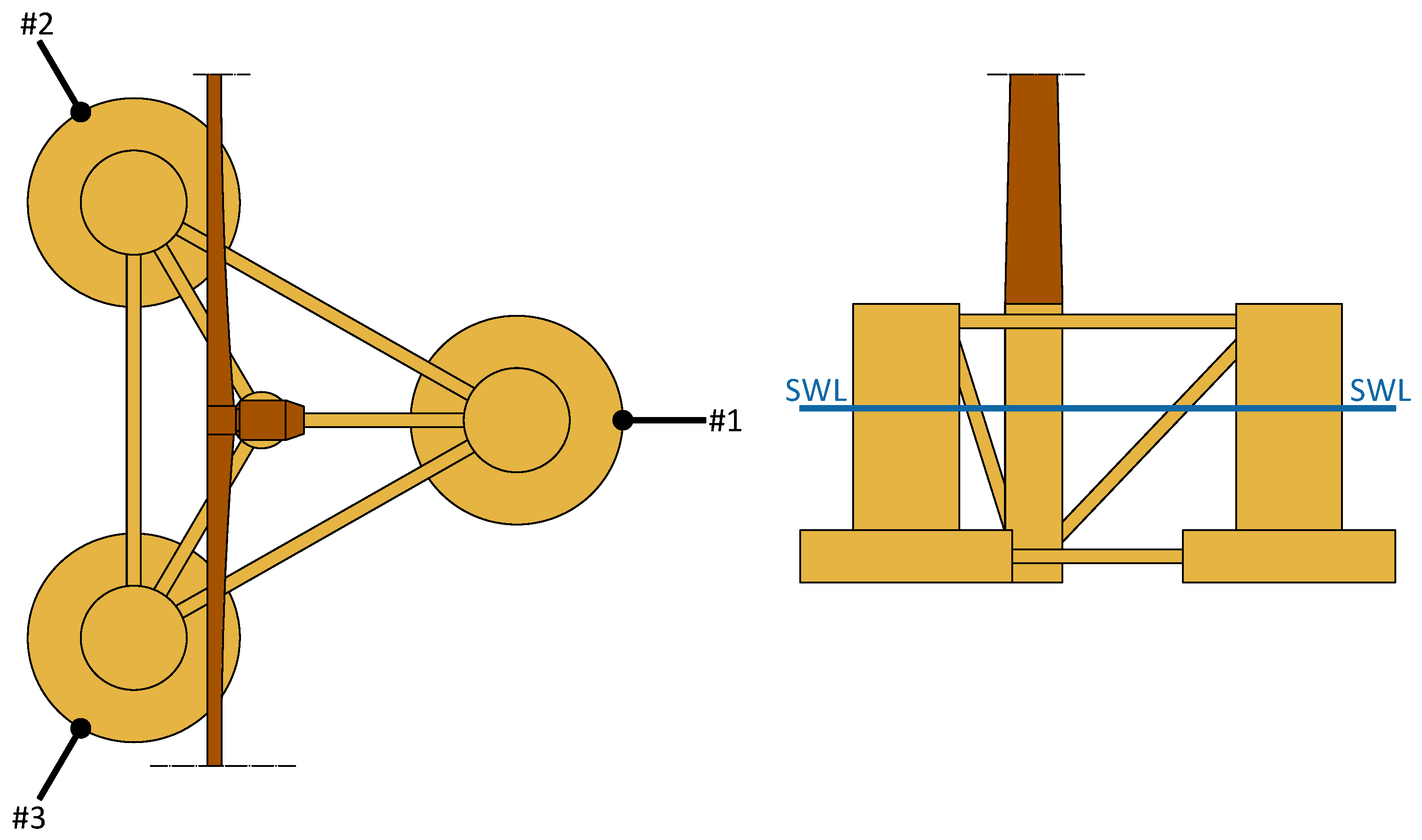
5.1. The OC4-DeepCwind Platform
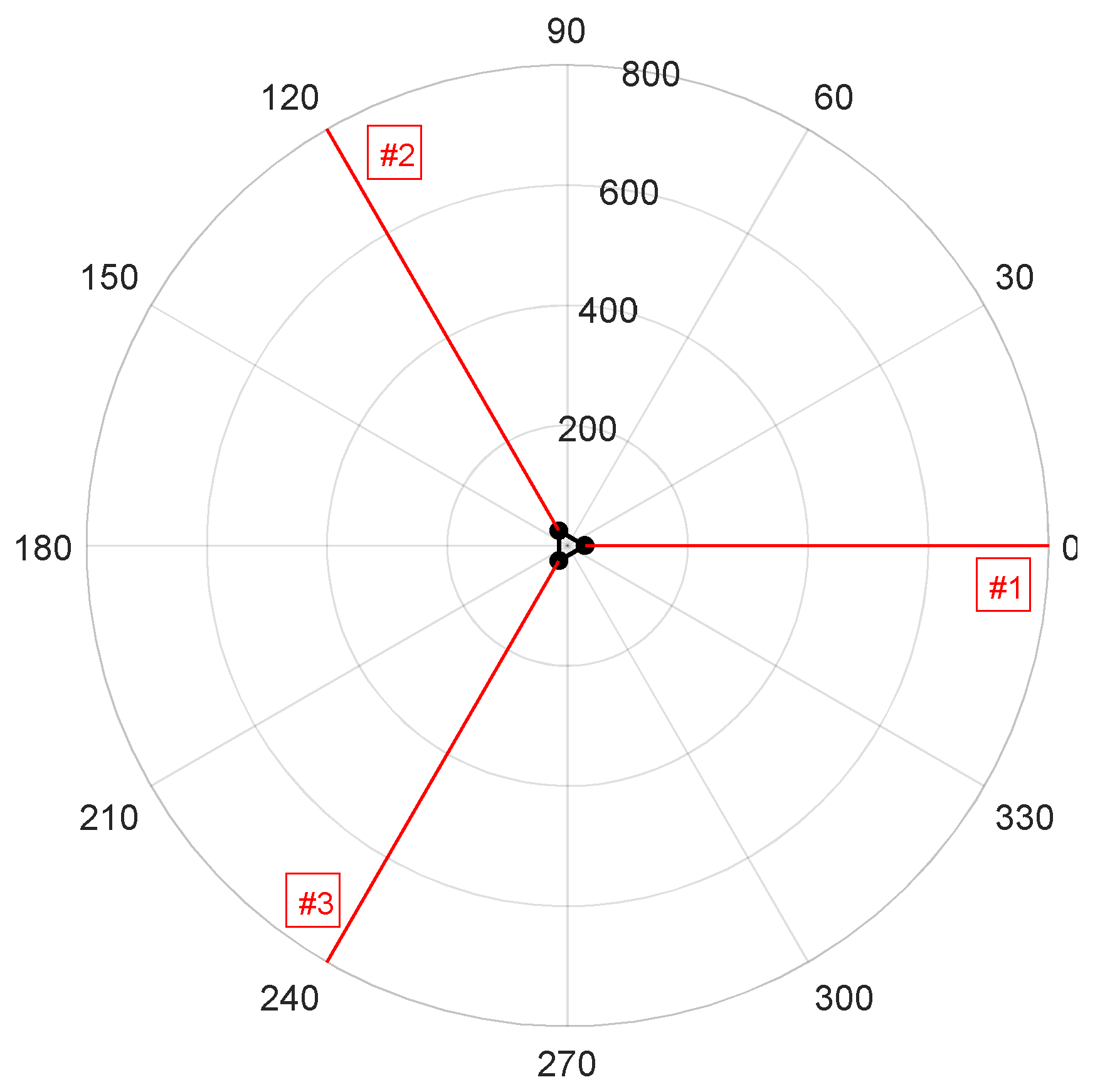
5.2. The Stationkeeping System
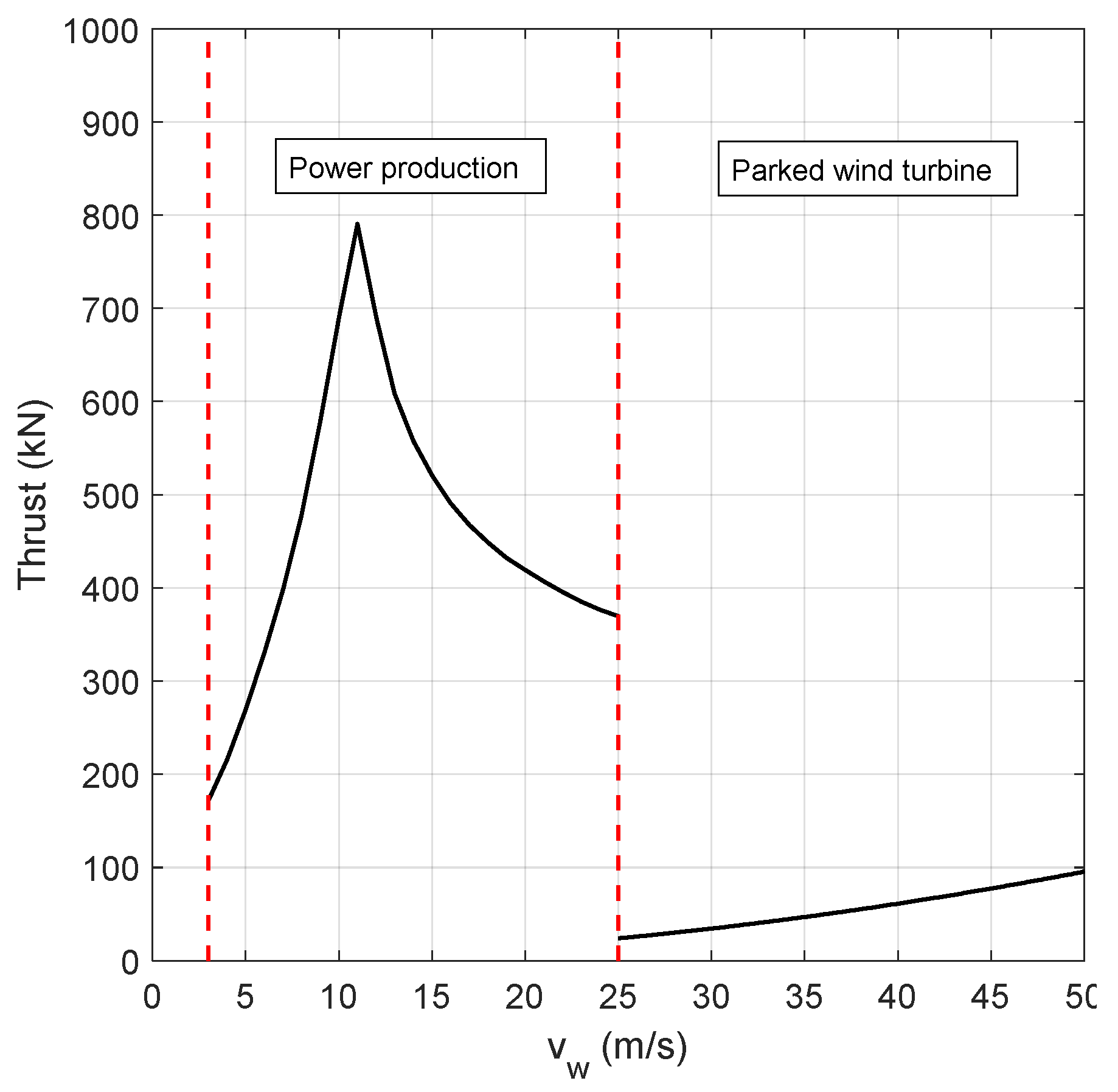
5.3. Selection of Reference Conditions
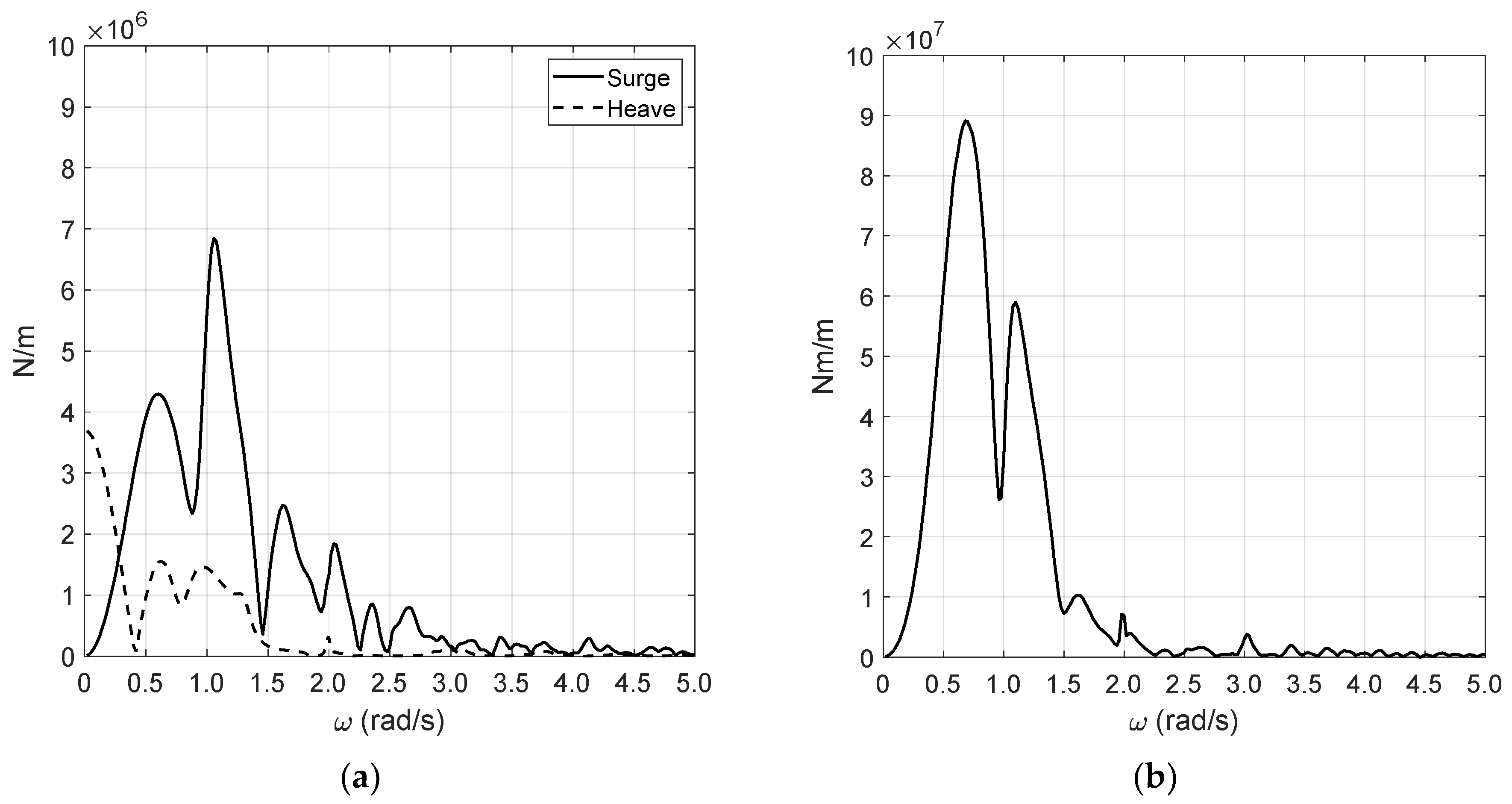
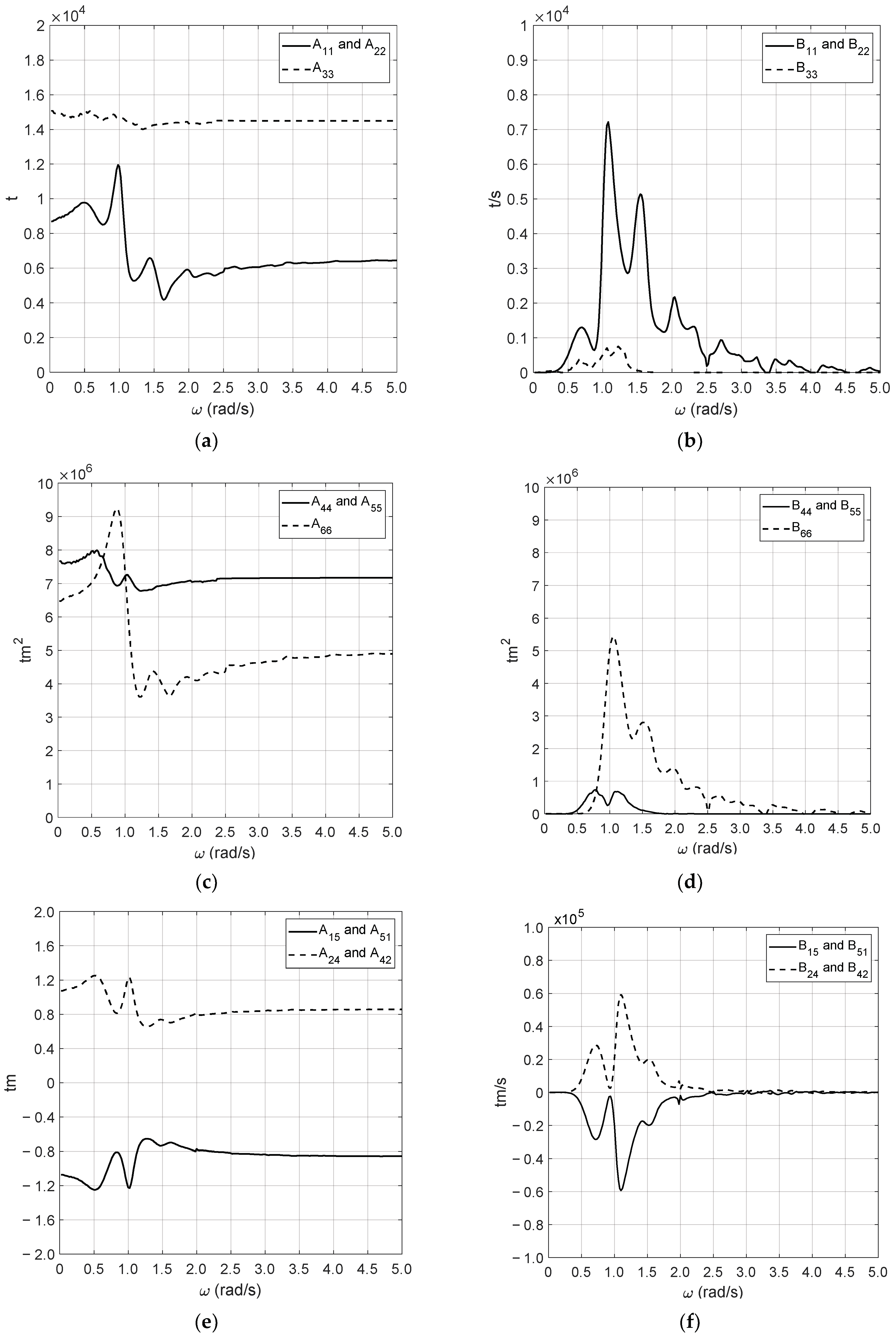
5.4. Preliminary Analysis
6. Benchmark Study
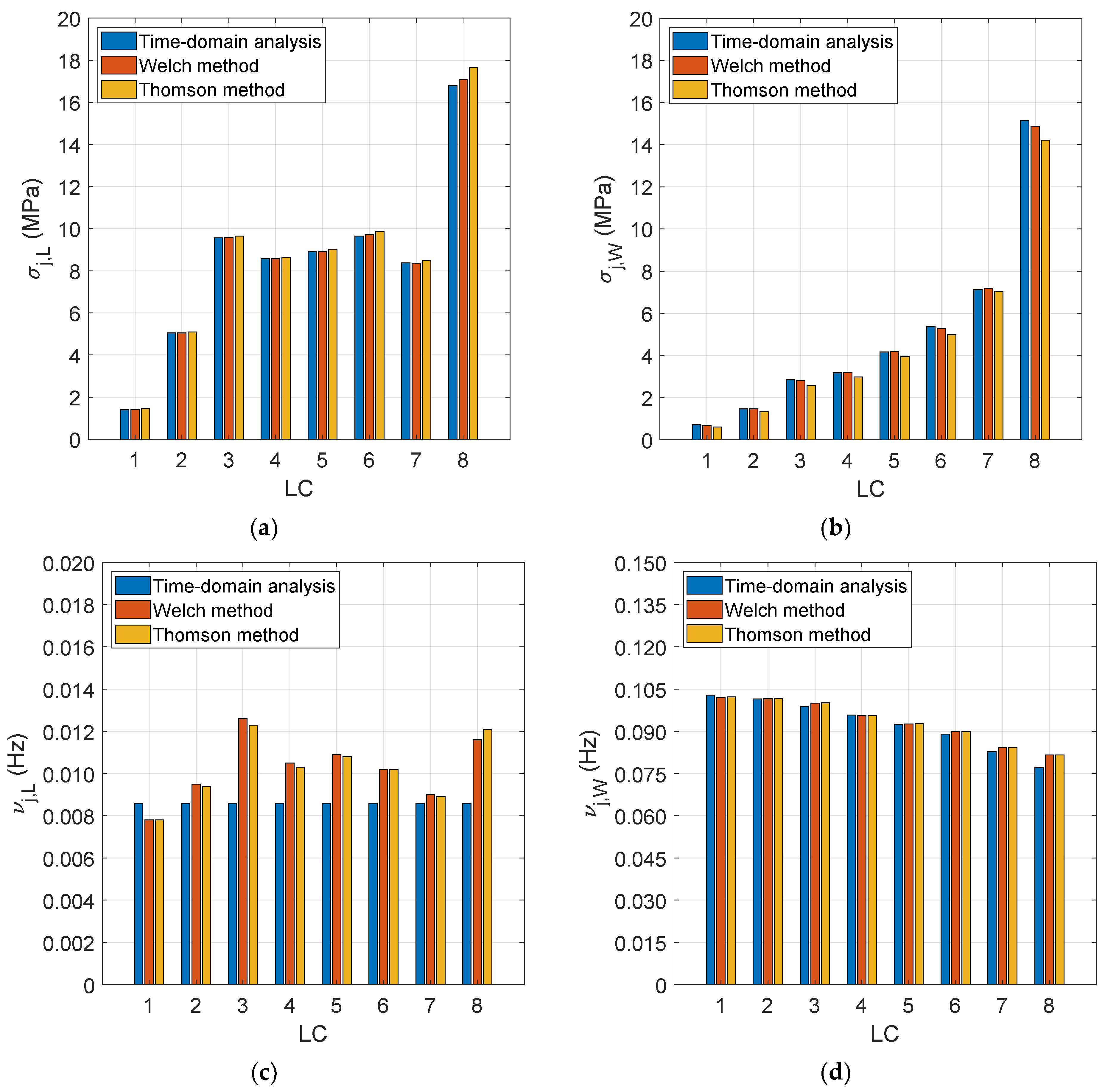
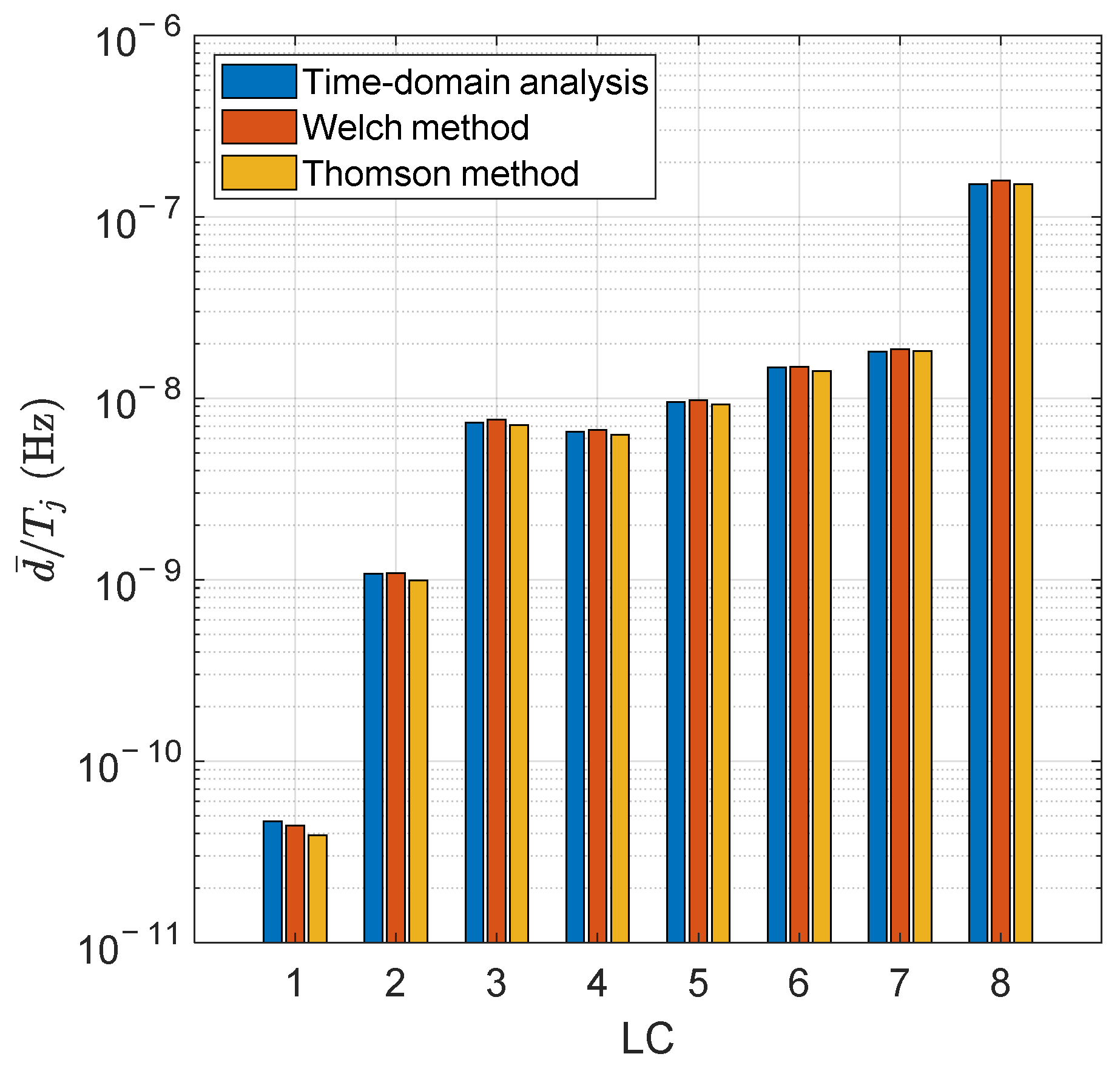
6.1. Assessment of the Stress Process in the Mooring Lines
6.2. Time-Domain Analysis of the Stress Process
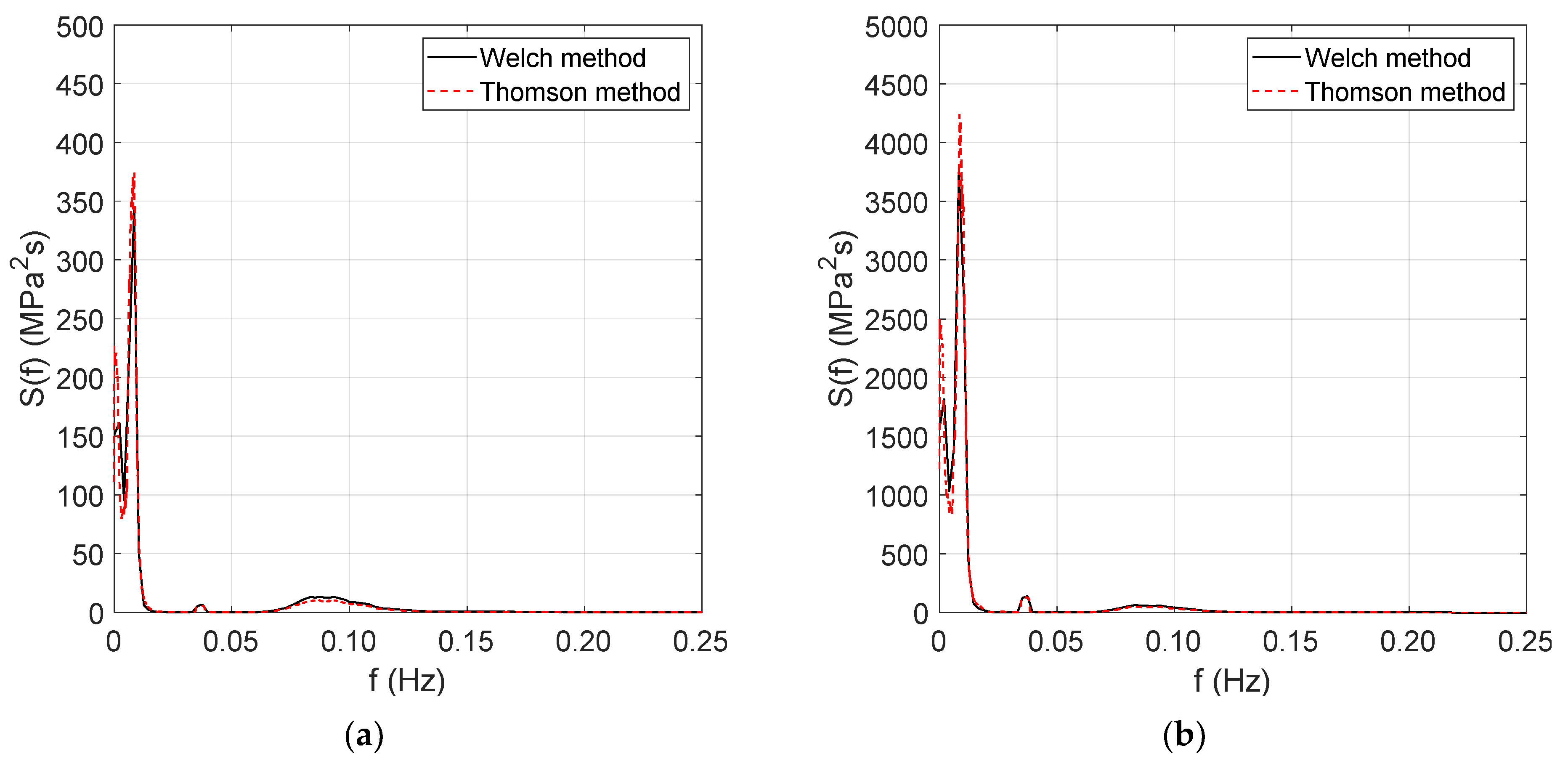
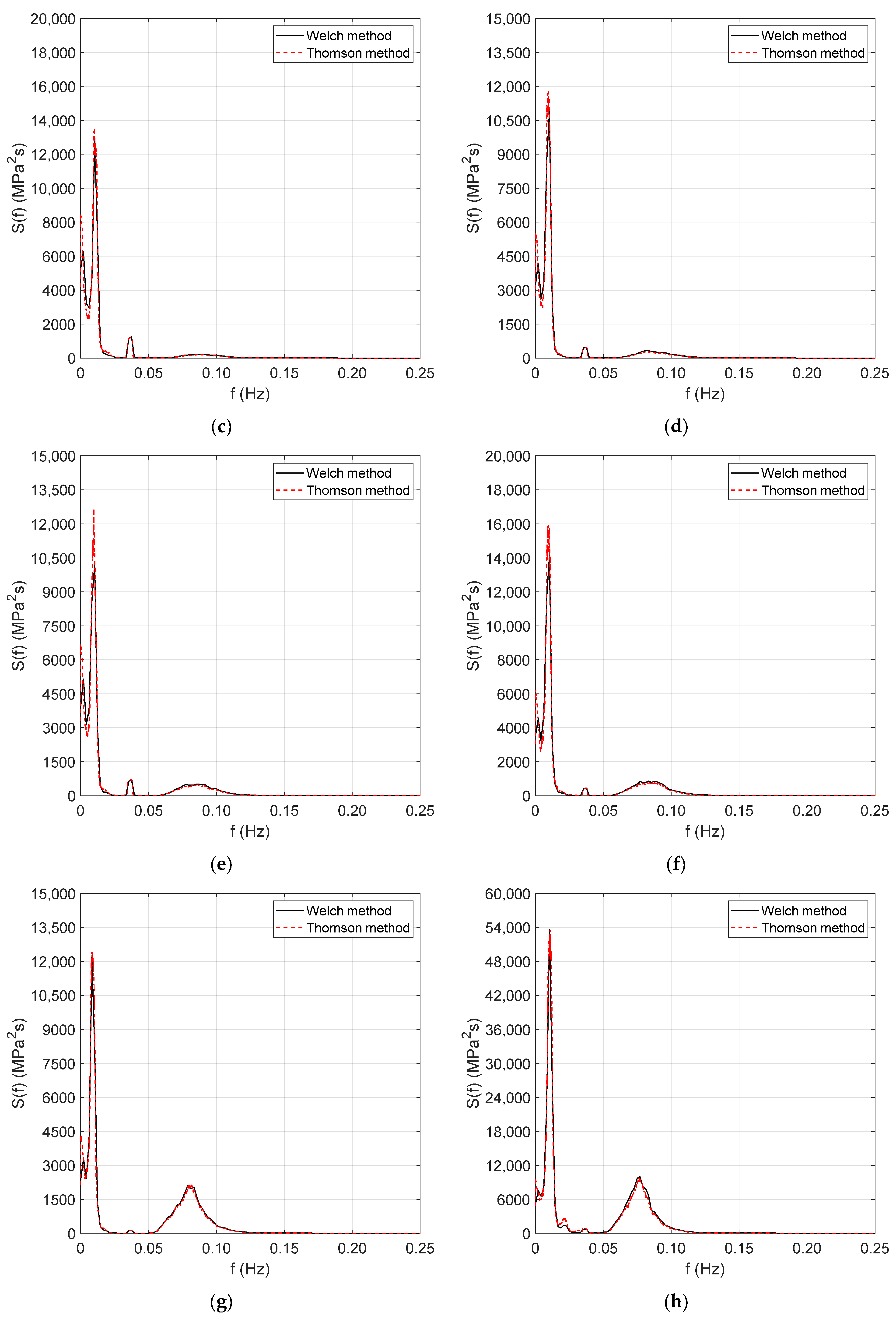
6.3. Spectral Analysis of the Stress Process
7. Discussion
- (i)
- Time-domain models are accurate enough, at least when a variety of cases need to be analysed to assess the design fatigue life of the mooring lines. In this respect, the up-crossing rate of the low- and wave-frequency components of the stress process can be assumed to be equal to the surge/sway natural period of the tri-floater platform and the wave peak period of the relevant sea state condition. These assumptions are accurate enough, as can be gathered from Figure 8c,d.
- (ii)
- Welch and Thomson methods allow accurate detection of the low- and wave-frequency components of the stress process once the partitioning frequency is provided. It was verified that the separation frequency of 0.05 Hz allowed accurate detection of the low- and wave-frequency components.
- (iii)
- It is quite challenging to identify which spectral analysis method, between the Welch and Thomson models, is the most suitable one. Presumably both methods can be applied with the same confidence, at least based on current results, provided they lead to almost the same cumulative fatigue damage per unit time in all the analysed loading conditions.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Load Condition | |||
|---|---|---|---|
| [---] | [---] | [---] | |
| LC1 | 3.0283 | −0.1652 | 0.9981 |
| LC2 | 2.9018 | −0.0050 | 0.9680 |
| LC3 | 3.9224 | 0.5524 | 1.1960 |
| LC4 | 3.0689 | 0.1633 | 1.0118 |
| LC5 | 3.9789 | 0.6189 | 1.1799 |
| LC6 | 3.6218 | 0.4005 | 1.1495 |
| LC7 | 3.2616 | 0.3834 | 1.0261 |
| LC8 | 4.2825 | 0.8995 | 1.0938 |
Appendix B
References
- Xue, X.; Chen, N.Z.; Wu, Y.; Xiong, Y.; Guo, Y. Mooring system fatigue analysis for a semi-submersible. Ocean. Eng. 2018, 156, 550–563. [Google Scholar] [CrossRef]
- European Union Commission. Horizon 2020 Work Programme 2018–2020 “Secure, Clean and Efficient Energy”; The European Commission: Bruxelles, Belgium, 2018. [Google Scholar]
- Kvitrud, A. Lessons learned from Norwegian mooring line failures 2010–2013. In Proceedings of the ASME 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- de Laval, G. Fatigue tests on anchor chain cable. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 18–20 April 1971. [Google Scholar]
- van Helvoirt, L.C. Static and fatigue tests on chain links and chain connecting links. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1982. [Google Scholar]
- Horde, G.O.; Moan, T. Fatigue and overload reliability of mooring systems. In Proceedings of the 7th International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 1997. [Google Scholar]
- Gao, Z.; Moan, T. Fatigue damage induced by nonGaussian bimodal wave loading in mooring lines. Appl. Ocean. Res. 2007, 29, 45–54. [Google Scholar] [CrossRef]
- Xu, T.J.; Zhao, Y.P.; Dong, G.H.; Bi, C.W. Fatigue analysis of mooring system for net cage under random loads. Aquac. Eng. 2014, 58, 59–68. [Google Scholar] [CrossRef]
- Brommundt, M.; Krause, L.; Merz, K.; Muskulus, M. Mooring system optimization for floating wind turbines using frequency domain analysis. Energy Procedia 2012, 24, 289–296. [Google Scholar] [CrossRef] [Green Version]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Mooring control of semi-submersible structures for wind turbines. Procedia Eng. 2014, 70, 132–141. [Google Scholar] [CrossRef]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Ultimate and accidental limit state design for mooring systems of floating offshore wind turbines. Ocean. Eng. 2014, 92, 64–74. [Google Scholar] [CrossRef]
- Kim, H.; Choung, J.; Jeon, G. Design of mooring lines of floating offshore wind turbine in Jeju offshore area. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean. Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef] [Green Version]
- Campanile, A.; Piscopo, V.; Scamardella, A. Mooring design and selection for floating offshore wind turbines on intermediate and deep-water depths. Ocean. Eng. 2018, 148, 349–360. [Google Scholar] [CrossRef]
- DnV-GL. Position Mooring. Offshore Standard DNVGL-OS-E301. 2018. Available online: https://rules.dnv.com/docs/pdf/DNV/os/2018-07/dnvgl-os-e301.pdf (accessed on 19 October 2021).
- Winterstein, S.R. Nonlinear vibration models for extremes and fatigue. J. Eng. Mech. 1988, 114, 1772–1790. [Google Scholar] [CrossRef]
- Jiao, G.; Moan, T. Probabilistic analysis of fatigue due to Gaussian load processes. Probabilistic Eng. Mech. 1990, 5, 76–83. [Google Scholar] [CrossRef]
- Fu, T.T.; Cebon, D. Predicting fatigue lives for bi-modal stress spectral densities. Int. J. Fatigue 2000, 22, 11–21. [Google Scholar] [CrossRef]
- Low, Y.M. A method for accurate estimation of the fatigue damage induced by bimodal processes. Probabilistic Eng. Mech. 2010, 25, 75–85. [Google Scholar] [CrossRef]
- Gao, Z.; Zheng, X.Y. An improved spectral discretization method for fatigue damage assessment of bimodal Gaussian processes. Int. J. Fatigue 2019, 119, 268–280. [Google Scholar] [CrossRef]
- Jun, S.-H.; Park, J.-B. Development of a novel fatigue damage model for Gaussian wide band stress responses using numerical approximation methods. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 755–767. [Google Scholar] [CrossRef]
- Ma, Y.; Han, C.; Qu, X. Fatigue assessment method of marine structures subjected to two Gaussian random loads. Ocean. Eng. 2021, 165, 107–122. [Google Scholar] [CrossRef]
- Wolfsteiner, P.; Trapp, A. Fatigue life due to non-Gaussian excitation—An analysis of the Fatigue Damage Spectrum using Higher Order Spectra. Int. J. Fatigue 2019, 127, 203–216. [Google Scholar] [CrossRef]
- Kim, H.-J.; Jang, B.-S.; Kim, J.D. Fatigue-damage prediction for ship and offshore structures under widebanded non-Gaussian random loadings Part I: Approximation of cycle distribution in wide-banded gaussian random processes. Appl. Ocean. Res. 2020, 101, 102294. [Google Scholar] [CrossRef]
- Marques, J.M.E.; Benasciutti, D. More on variance of fatigue damage in non-Gaussian random loadings—Effect of skewness and kurtosis. Procedia Struct. Integr. 2020, 25, 101–111. [Google Scholar] [CrossRef]
- Gao, S.; Zheng, X.Y.; Wang, B.; Zhao, S.; Li, W. Assessment of fatigue damage induced by Non-Gaussian bimodal processes with emphasis on spectral methods. Ocean. Eng. 2021, 220, 108489. [Google Scholar] [CrossRef]
- Kim, H.-J.; Jang, B.-S. Fatigue life prediction of ship and offshore structures under wide-banded non-Gaussian random loadings Part II: Extension to wide-banded non-Gaussian random processes. Appl. Ocean. Res. 2021, 106, 102480. [Google Scholar] [CrossRef]
- Marques, J.M.E.; Benasciutti, D. Variance of the fatigue damage in non-Gaussian stochastic processes with narrow-band power spectrum. Struct. Saf. 2021, 93, 102131. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.M.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report NREL/TP-5000-60601; National Renewable Energy Laboratory: Golden, CO, USA, 2014.
- Jonkman, J.M. Dynamics Modelling and Loads Analysis of an Offshore Floating Wind Turbine; Technical Report NREL/TP-5000-41958; National Renewable Energy Laboratory: Golden, CO, USA, 2007.
- Zhao, Z.; Wang, W.; Shi, W.; Ki, X. Effects of second-order hydrodynamics on an ultra-large semi-submersible floating offshore wind turbine. Structures 2020, 28, 2260–2275. [Google Scholar] [CrossRef]
- Barrera, C.; Battistella, T.; Guanche, R.; Lozada, I.J. Mooring system fatigue analysis of a floating offshore wind turbine. Ocean. Eng. 2020, 195, 106670. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean. Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Cummins, W.E. The impulse response function and ship motions. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- Newman, J.N. Second-order, slowly varying forces on vessels in irregular waves. In Proceedings of the International Symposium on Dynamics of Marine Vehicles and Structures in Waves, University College London, London, UK, 1–5 April 1974; pp. 182–186. [Google Scholar]
- Xu, K.; Larsen, K.; Shao, Y.; Zhang, M.; Gao, Z.; Moan, T. Design and comparative analysis of alternating mooring systems for floating wind turbines in shallow water with emphasis on ultimate limit state design. Ocean. Eng. 2021, 219, 108377. [Google Scholar] [CrossRef]
- Wan, L.; Ghao, Z.; Moan, T.; Lugni, C. Comparative experimental study of the survivability of a combined wind and wave energy converter in two testing facilities. Ocean. Eng. 2016, 111, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.O.L. Aerodynamics of Wind Turbines; Routledge: Abingdon-on-Thames, UK, 2015. [Google Scholar]
- DnV. Environmental Conditions and Environmental Loads. Recommended Practice DNV-RP-C205, 2014. Available online: https://rules.dnv.com/docs/pdf/dnvpm/codes/docs/2014-04/RP-C205.pdf (accessed on 19 October 2021).
- Jonkman, J.M. Dynamics of Offshore Floating Wind Turbines—Model Development and Verification. Wind. Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
- Trubat, P.; Molins, C.; Gironella, X. Wave hydrodynamic forces over mooring lines on floating offshore wind turbines. Ocean. Eng. 2020, 195, 106730. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Xiao, L. Wind-wave induced dynamic response analysis for motions and mooring loads of a spar-type offshore floating wind turbine. J. Hydrodyn. 2014, 26, 865–874. [Google Scholar] [CrossRef]
- MathWorks. Matlab User Guide R2020b, 2020. Available online: https://it.mathworks.com/help/matlab/ (accessed on 19 October 2021).
- Saf onov, M.G.; Chiang, R.Y. A Schur Method for Balanced Model Reduction. IEEE Trans. Autom. Control. 1989, 34, 729–733. [Google Scholar] [CrossRef]
- Kung, S.Y. A New Identification and Model Reduction Algorithm via Singular Value Decompositions. In Proceedings of the 12th Asilomar Conference on Circuits, Systems and Computers (Institute of Electrical and Electronic Engineers), New York, NY, USA, 6–8 November 1978; pp. 705–714. [Google Scholar]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open-source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–12. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
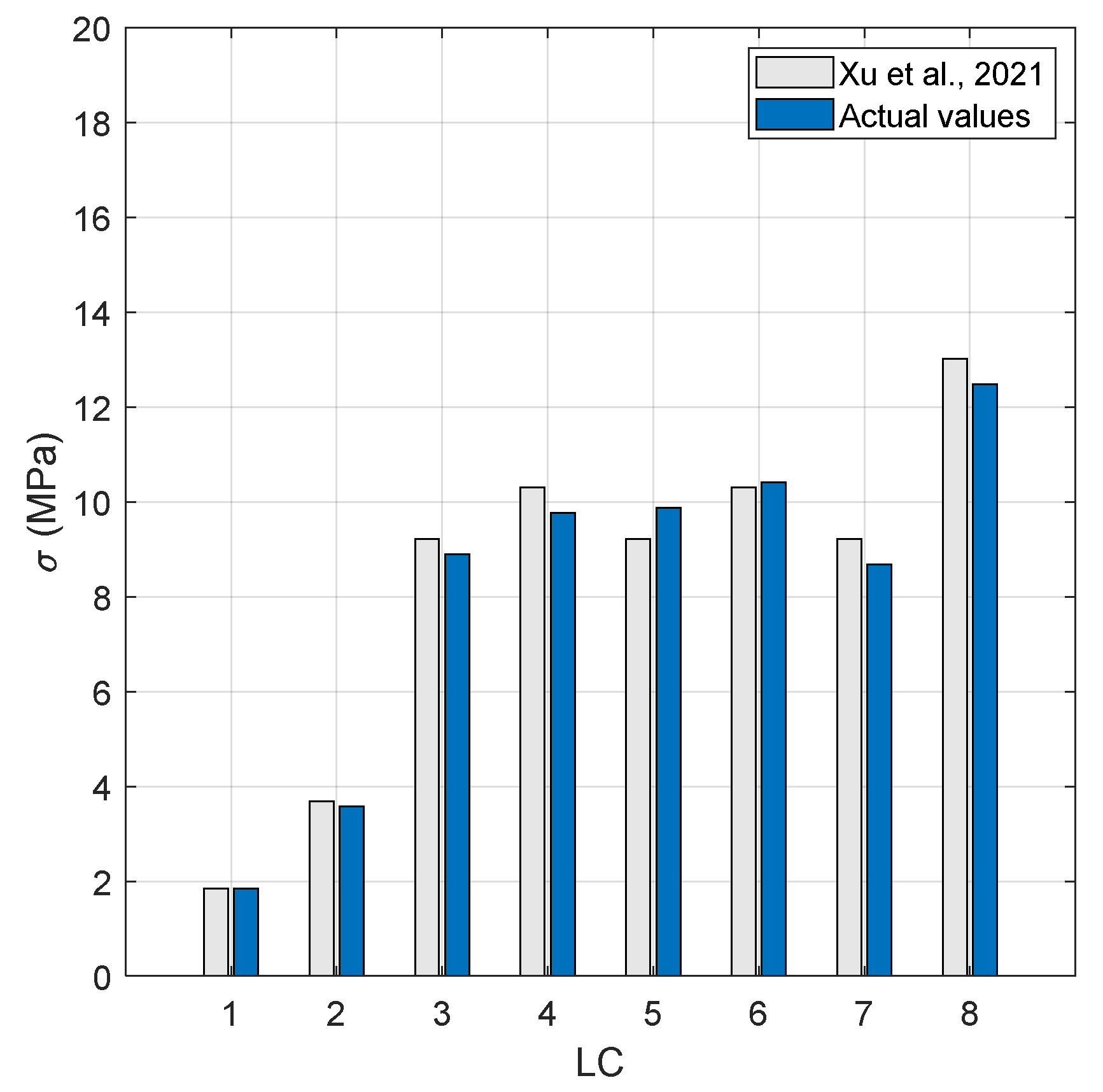
- Xu, S.; Guedes Soares, C. Evaluation of spectral methods for long term fatigue damage analysis of synthetic fibre mooring ropes based on experimental data. Ocean. Eng. 2021, 226, 108842. [Google Scholar] [CrossRef]
- DnV-GL. Standard DNVGL-ST-0437; Loads and Site Conditions for Wind Turbines. Det Norske Veritas Group: Høvik, Norway, 2016.
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Thomson, D.J. Spectrum Estimation and Harmonic Analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef] [Green Version]
- Marple, S.L. Digital Spectral Analysis; Prentice—Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Piscopo, V.; Scamardella, A. Comparative study among non-redundant and redundant stationkeeping systems for Floating Offshore Wind Turbines on intermediate water depth. Ocean. Eng. 2021, 241, 110047. [Google Scholar] [CrossRef]
- SINTEF Ocean. SIMO 4.14.0 User Guide, 2018. Available online: https://projects.dnvgl.com/sesam/status/Simo/SIMO-release-notes_4.14.0.pdf (accessed on 19 October 2021).
- Braccesi, C.; Cianetti, F.; Lori, G.; Pioli, D. The frequency domain approach in virtual fatigue estimation of non-linear systems: The problem of non-Gaussian states of stress. Int. J. Fatigue 2009, 31, 766–775. [Google Scholar] [CrossRef]
- Chuang, Z.; Liu, S.; Lu, Y. Influence of second order wave excitation loads on coupled response of an offshore floating wind turbine. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 367–375. [Google Scholar] [CrossRef]



| Total platform draught | 20.0 m |
| Elevation of tower base/hub height above SWL | 10.0/90.0 m |
| Diameter of bracings/main column | 1.6/6.50 m |
| Diameter of upper columns/base columns | 12.0/24.0 m |
| Height of upper columns/base columns | 26.0/6.0 m |
| Spacing between offset columns | 50.0 m |
| Platform displacement | 14,070 t |
| Cut-in/rated/cut-out wind speed at hub height | 3.0/11.4/25.0 m/s |
| Rotor/hub diameter | 126.0/3.0 m |
| Vertical coordinate of the centre of mass/centre of buoyancy as regards the SWL | −9.94/−13.23 m |
| Roll–pitch/yaw moment of inertia as regards the centre of mass | 1.10 × 107/1.23 × 107 tm2 |
| Surge–sway/heave added mass at infinite frequency | 6440/14,500 t |
| Roll–pitch/yaw added mass at infinite frequency | 7.17 × 106/4.90 × 106 tm2 |
| Heave restoring coefficient | 3411 t/s2 |
| Roll–pitch restoring coefficient | 1.028 × 106 tm2/s2 |
| Surge/sway natural period | 116 s |
| Drag coefficient of the submerged part of main/offset columns (viscous forces) | 0.56/0.61 |
| Drag coefficient of base columns (viscous forces) | 0.68 |
| Drag coefficient of the emerged part of main/offset columns (wind forces) | 0.42 |
| Drag coefficient of the turbine tower (wind forces) | 0.59 |
| Water Depth | 200 m |
|---|---|
| Chain cable diameter | 76.6 mm |
| Material grade | R3 |
| Material Young modulus | 81,764 MPa |
| Total line length/line length on the seabed at rest | 835.5/165.4 m |
| Fairlead horizontal/vertical coordinate as regards the local reference system | 796.6/186.0 m |
| Intercept parameter of the S–N curve | 1.2 × 1011 MPa |
| Slope parameter of the S–N curve | 3.0 |
| Seabed drag coefficient | 1.0 |
| Load Condition | Reference Scenario | |||
|---|---|---|---|---|
| LC1 | 1.96 | 9.72 | 4.0 | Power production |
| LC2 | 2.53 | 9.85 | 8.0 | Power production |
| LC3 | 3.20 | 10.11 | 12.0 | Power production |
| LC4 | 3.97 | 10.44 | 16.0 | Power production |
| LC5 | 4.80 | 10.82 | 20.0 | Power production |
| LC6 | 5.69 | 11.23 | 24.0 | Power production |
| LC7 | 7.64 | 12.08 | 32.0 | Parked wind turbine |
| LC8 | 9.77 | 12.95 | 40.0 | Parked wind turbine |
| Load Condition | |||||||
|---|---|---|---|---|---|---|---|
| [MPa] | [MPa] | [MPa] | [Hz] | [Hz] | [Hz] | [Hz] | |
| LC1 | 1.399 | 0.719 | 1.573 | 0.0086 | 0.1029 | 0.0476 | 4.649 × 10−11 |
| LC2 | 5.051 | 1.468 | 5.260 | 0.1015 | 0.0295 | 1.077 × 10−9 | |
| LC3 | 9.563 | 2.854 | 9.979 | 0.0989 | 0.0295 | 7.340 × 10−9 | |
| LC4 | 8.570 | 3.174 | 9.139 | 0.0958 | 0.0342 | 6.550 × 10−9 | |
| LC5 | 8.908 | 4.170 | 9.835 | 0.0924 | 0.0400 | 9.529 × 10−9 | |
| LC6 | 9.647 | 5.371 | 11.041 | 0.0890 | 0.0440 | 1.483 × 10−8 | |
| LC7 | 8.375 | 7.121 | 10.993 | 0.0828 | 0.0540 | 1.799 × 10−8 | |
| LC8 | 16.799 | 15.144 | 22.617 | 0.0772 | 0.0521 | 1.511 × 10−7 |
| Load Condition | |||||||
|---|---|---|---|---|---|---|---|
| [MPa] | [MPa] | [MPa] | [Hz] | [Hz] | [Hz] | [Hz] | |
| LC1 | 1.419 | 0.686 | 1.576 | 0.0078 | 0.1021 | 0.0450 | 4.415 × 10−11 |
| LC2 | 5.055 | 1.465 | 5.263 | 0.0095 | 0.1016 | 0.0297 | 1.086 × 10−9 |
| LC3 | 9.582 | 2.806 | 9.984 | 0.0126 | 0.1001 | 0.0306 | 7.643 × 10−9 |
| LC4 | 8.570 | 3.201 | 9.148 | 0.0105 | 0.0956 | 0.0348 | 6.686 × 10−9 |
| LC5 | 8.912 | 4.195 | 9.850 | 0.0109 | 0.0926 | 0.0407 | 9.742 × 10−9 |
| LC6 | 9.719 | 5.283 | 11.062 | 0.0102 | 0.0900 | 0.0439 | 1.490 × 10−8 |
| LC7 | 8.359 | 7.188 | 11.025 | 0.0090 | 0.0843 | 0.0554 | 1.860 × 10−8 |
| LC8 | 17.095 | 14.883 | 22.666 | 0.0116 | 0.0816 | 0.0543 | 1.584 × 10−7 |
| Load Condition | |||||||
|---|---|---|---|---|---|---|---|
| [MPa] | [MPa] | [MPa] | [Hz] | [Hz] | [Hz] | [Hz] | |
| LC1 | 1.457 | 0.603 | 1.576 | 0.0078 | 0.1023 | 0.0398 | 3.905 × 10−11 |
| LC2 | 5.094 | 1.325 | 5.263 | 0.0094 | 0.1017 | 0.0272 | 9.930 × 10−10 |
| LC3 | 9.643 | 2.588 | 9.985 | 0.0123 | 0.1002 | 0.0286 | 7.124 × 10−9 |
| LC4 | 8.647 | 2.987 | 9.148 | 0.0103 | 0.0957 | 0.0327 | 6.282 × 10−9 |
| LC5 | 9.025 | 3.947 | 9.850 | 0.0108 | 0.0927 | 0.0384 | 9.207 × 10−9 |
| LC6 | 9.877 | 4.982 | 11.063 | 0.0102 | 0.0899 | 0.0415 | 1.408 × 10−8 |
| LC7 | 8.488 | 7.035 | 11.025 | 0.0089 | 0.0843 | 0.0542 | 1.820 × 10−8 |
| LC8 | 17.658 | 14.211 | 22.666 | 0.0121 | 0.0816 | 0.0520 | 1.518 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piscopo, V.; Scamardella, A.; Rossi, G.B.; Crenna, F.; Berardengo, M. Fatigue Assessment of Moorings for Floating Offshore Wind Turbines by Advanced Spectral Analysis Methods. J. Mar. Sci. Eng. 2022, 10, 37. https://doi.org/10.3390/jmse10010037
Piscopo V, Scamardella A, Rossi GB, Crenna F, Berardengo M. Fatigue Assessment of Moorings for Floating Offshore Wind Turbines by Advanced Spectral Analysis Methods. Journal of Marine Science and Engineering. 2022; 10(1):37. https://doi.org/10.3390/jmse10010037
Chicago/Turabian StylePiscopo, Vincenzo, Antonio Scamardella, Giovanni Battista Rossi, Francesco Crenna, and Marta Berardengo. 2022. "Fatigue Assessment of Moorings for Floating Offshore Wind Turbines by Advanced Spectral Analysis Methods" Journal of Marine Science and Engineering 10, no. 1: 37. https://doi.org/10.3390/jmse10010037
APA StylePiscopo, V., Scamardella, A., Rossi, G. B., Crenna, F., & Berardengo, M. (2022). Fatigue Assessment of Moorings for Floating Offshore Wind Turbines by Advanced Spectral Analysis Methods. Journal of Marine Science and Engineering, 10(1), 37. https://doi.org/10.3390/jmse10010037










