Numerical Investigation on Air Film Fusion of Pressure-Equalizing Exhaust around Shoulder Ventilation of Submarine-Launched Vehicle
Abstract
:1. Introduction
2. Numerical Calculation Method
2.1. Governing Equation
2.2. Turbulence Equation
2.3. Multiphase Flow Model
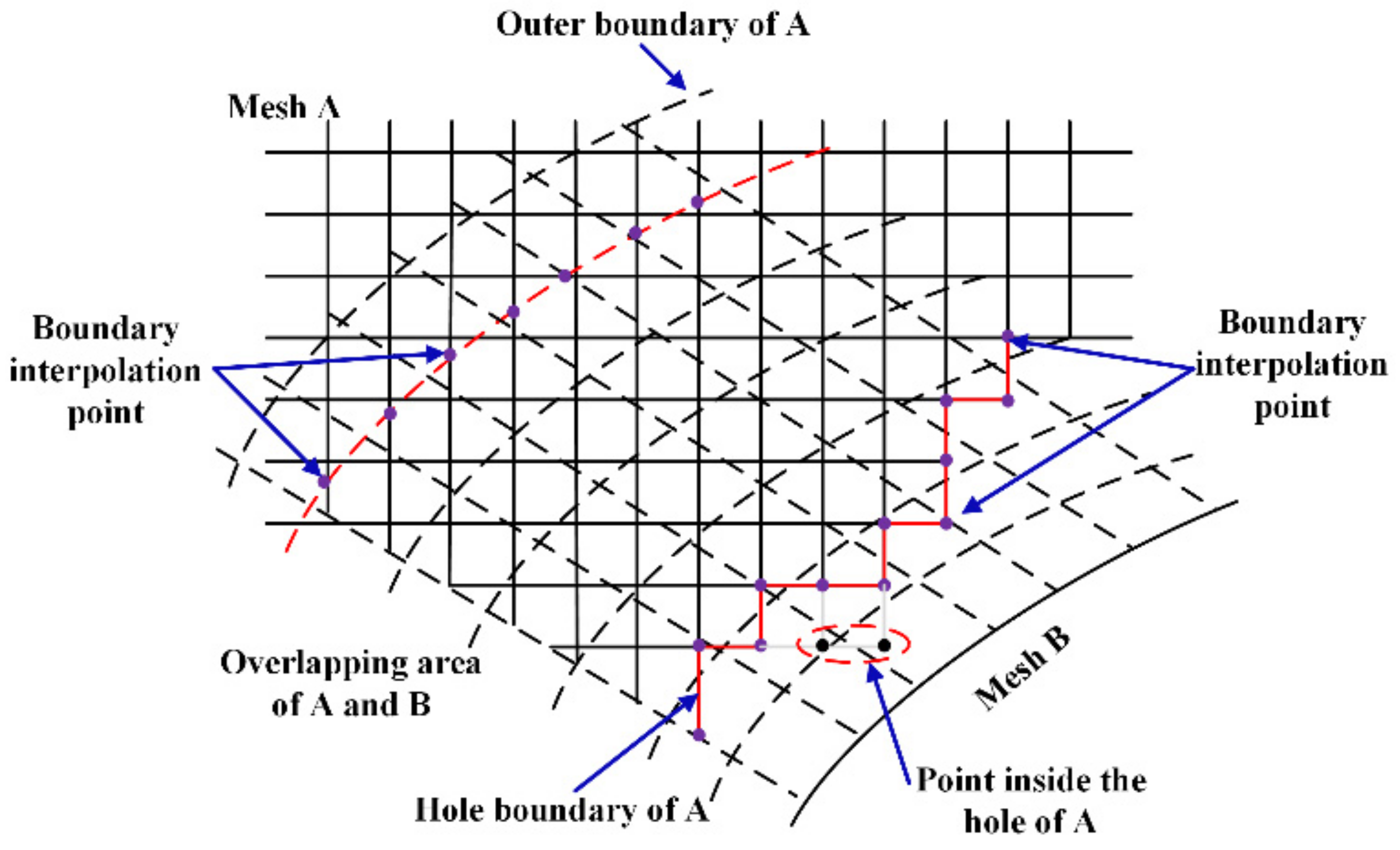
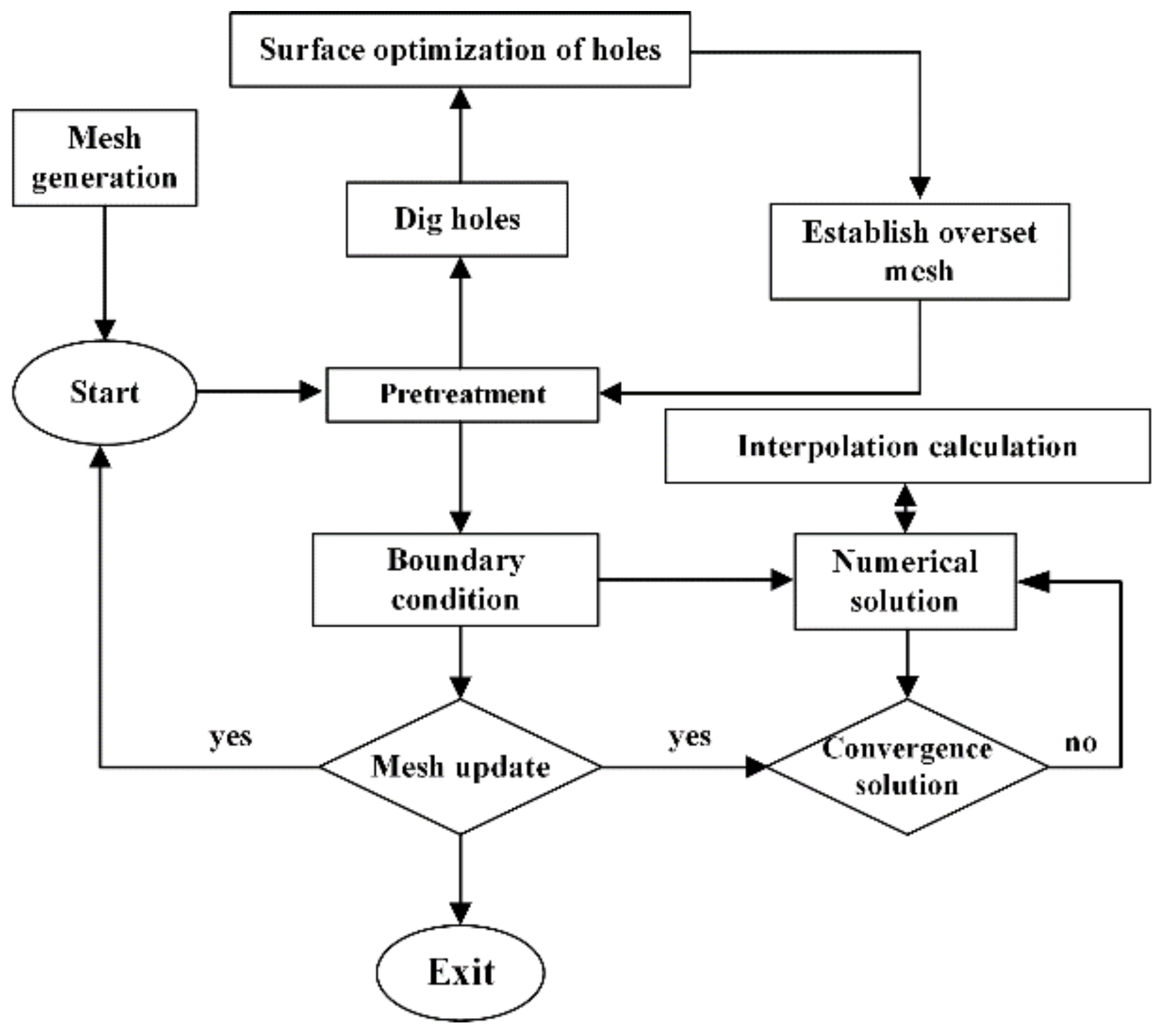
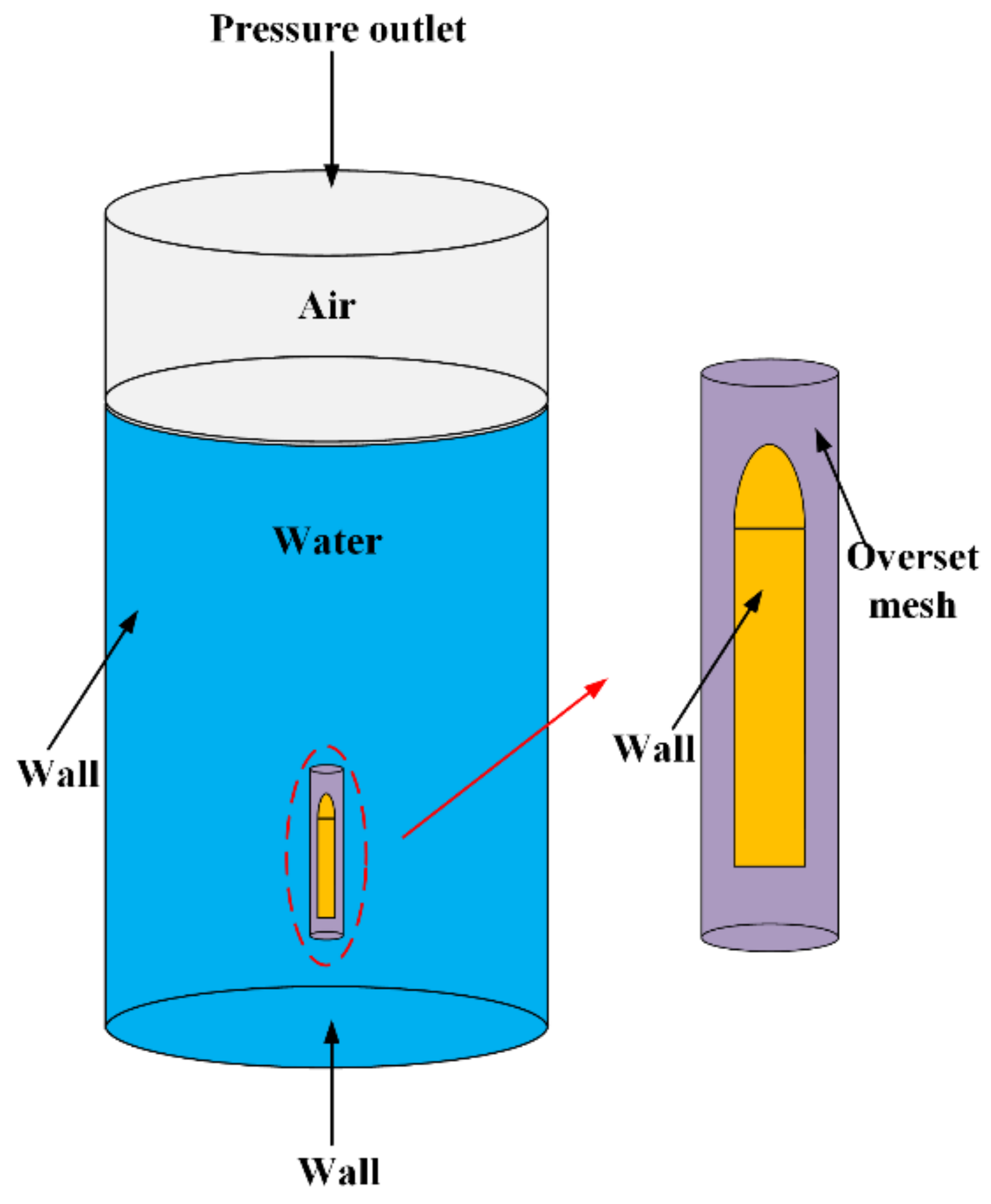
2.4. Overset Meshing
2.5. Numerical Method Verification
3. Numerical Calculation Model
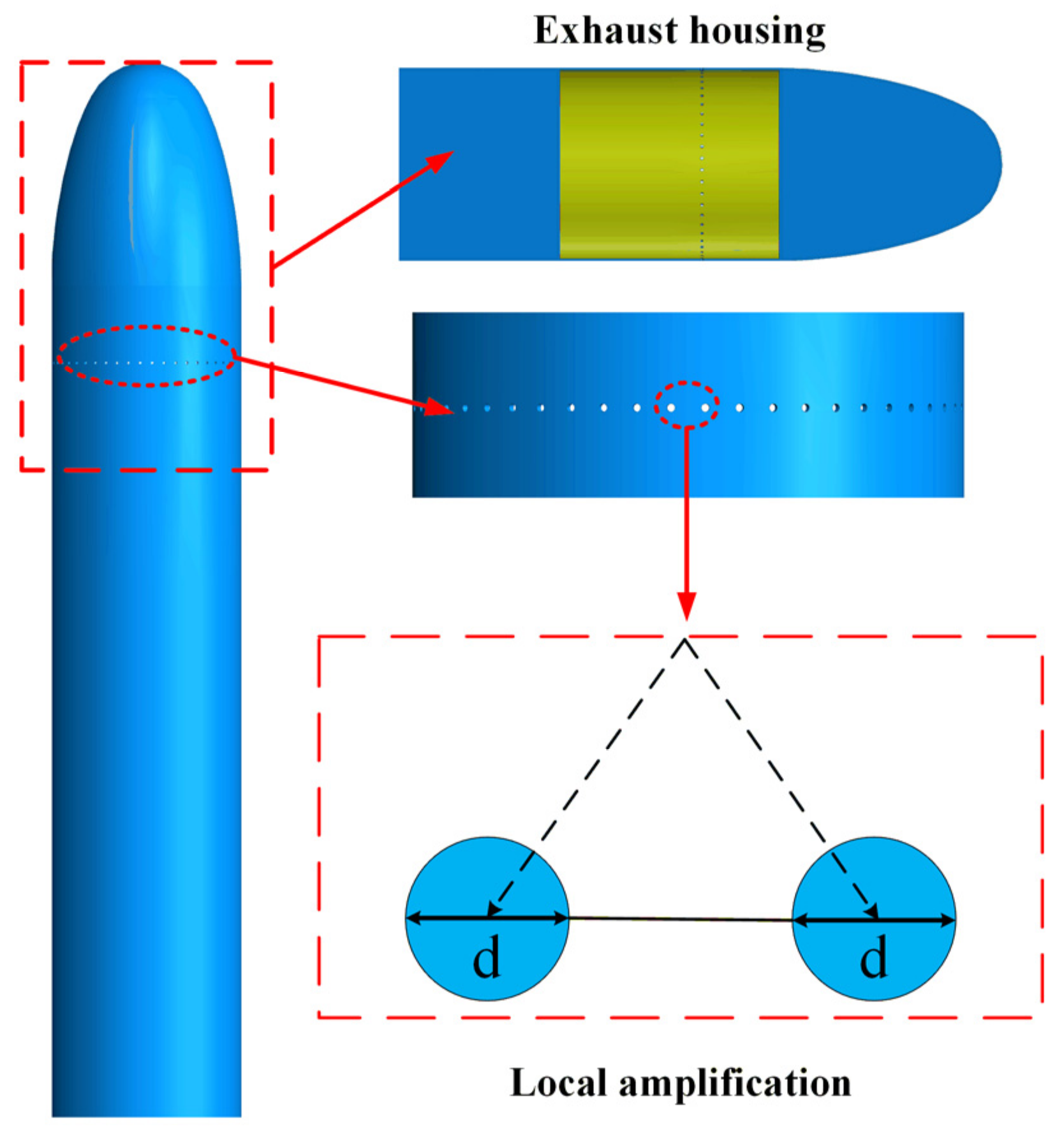
3.1. The Establishment of the Geometric Model
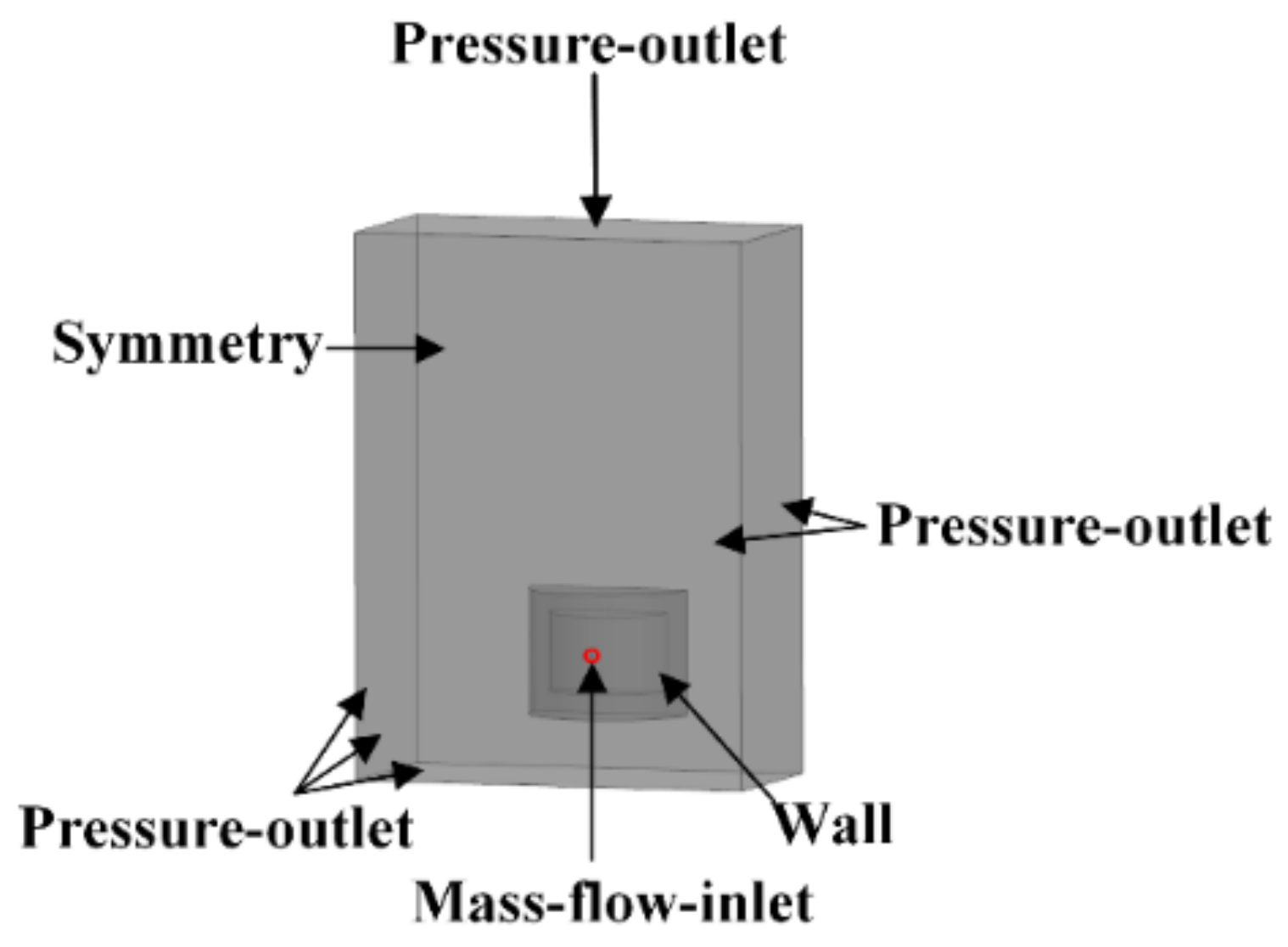
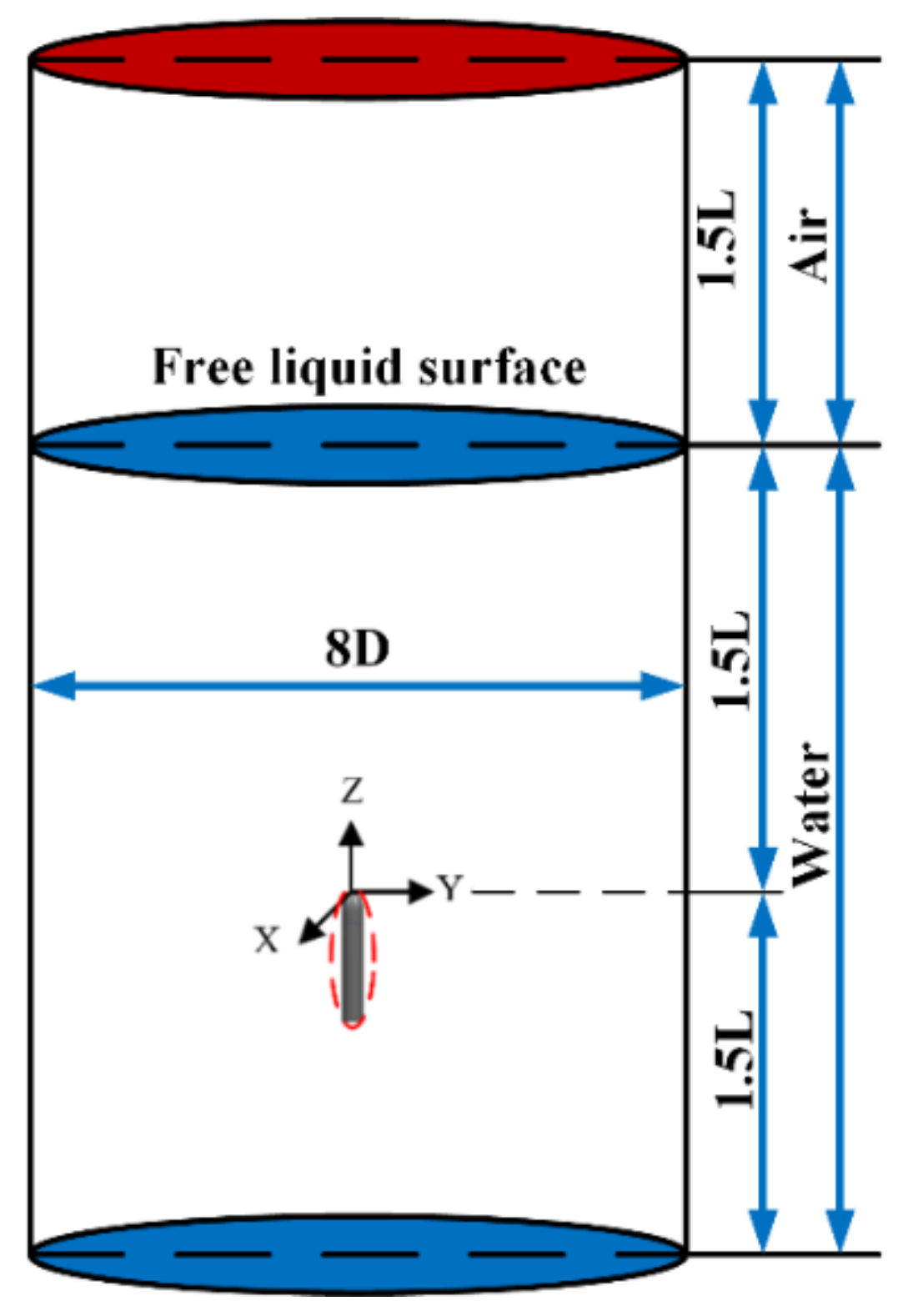
3.2. Computational Domain and Boundary Condition Division
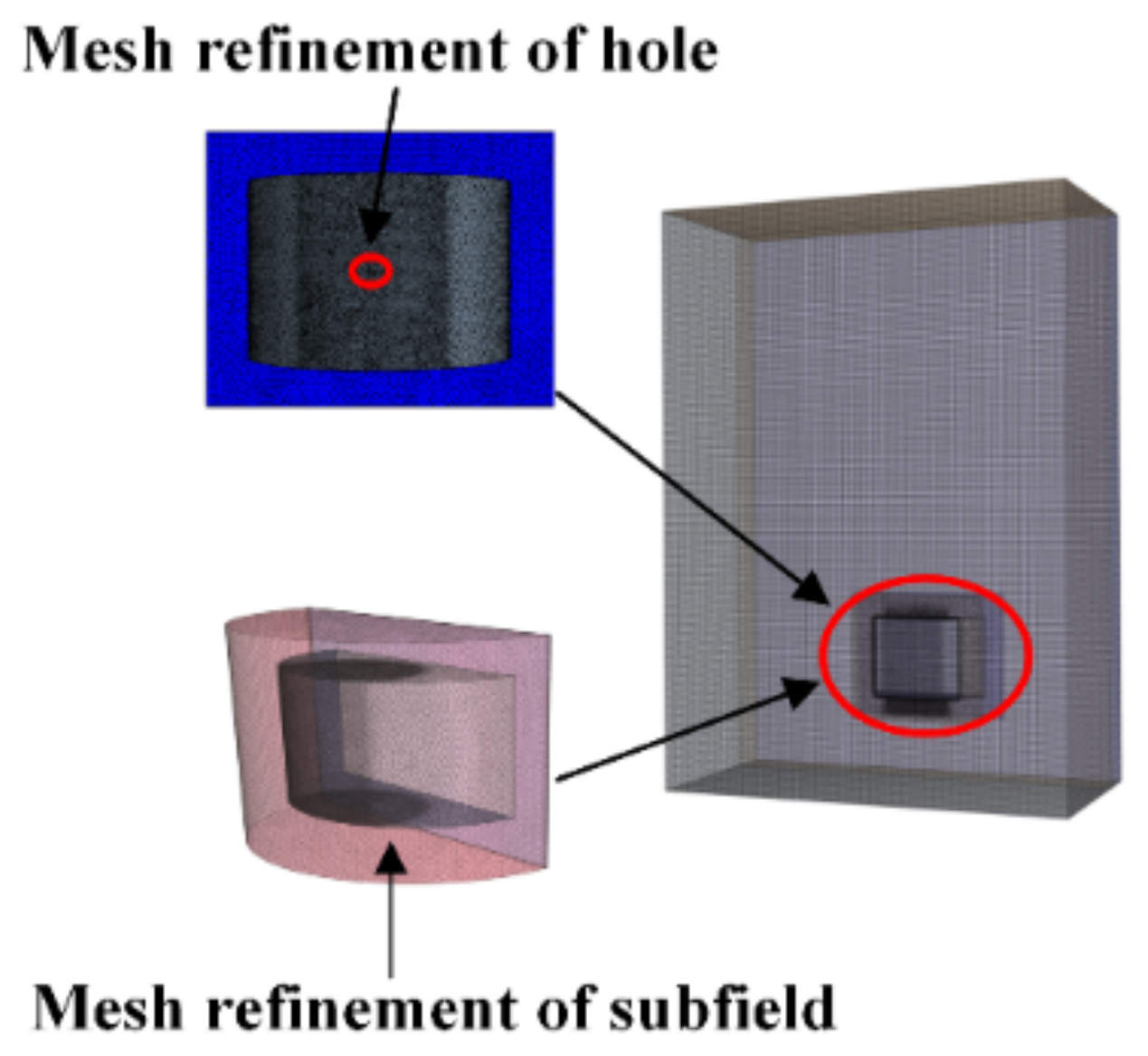
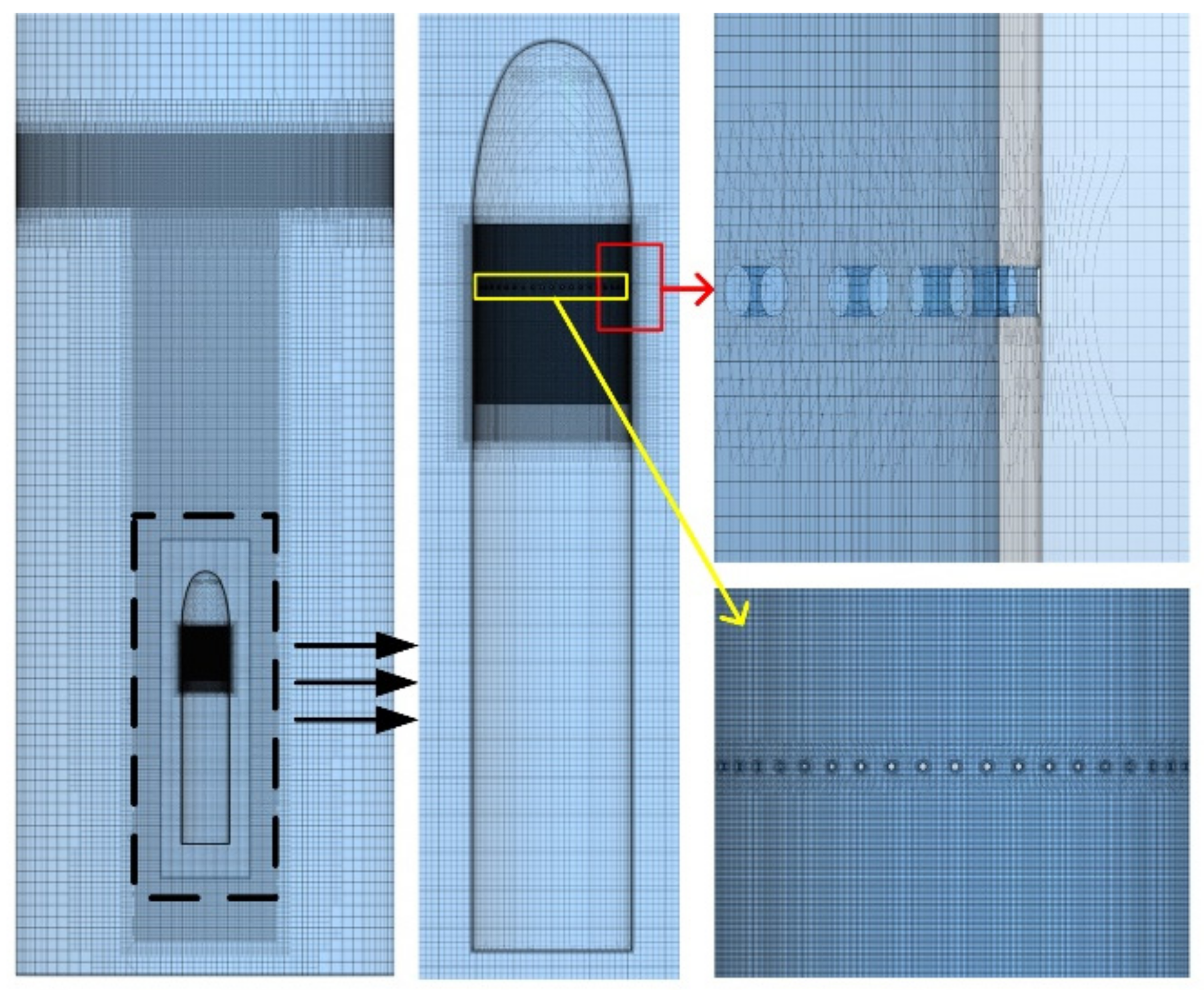
3.3. Meshing
3.4. Mesh Independence Verification
4. Analysis of Numerical Results
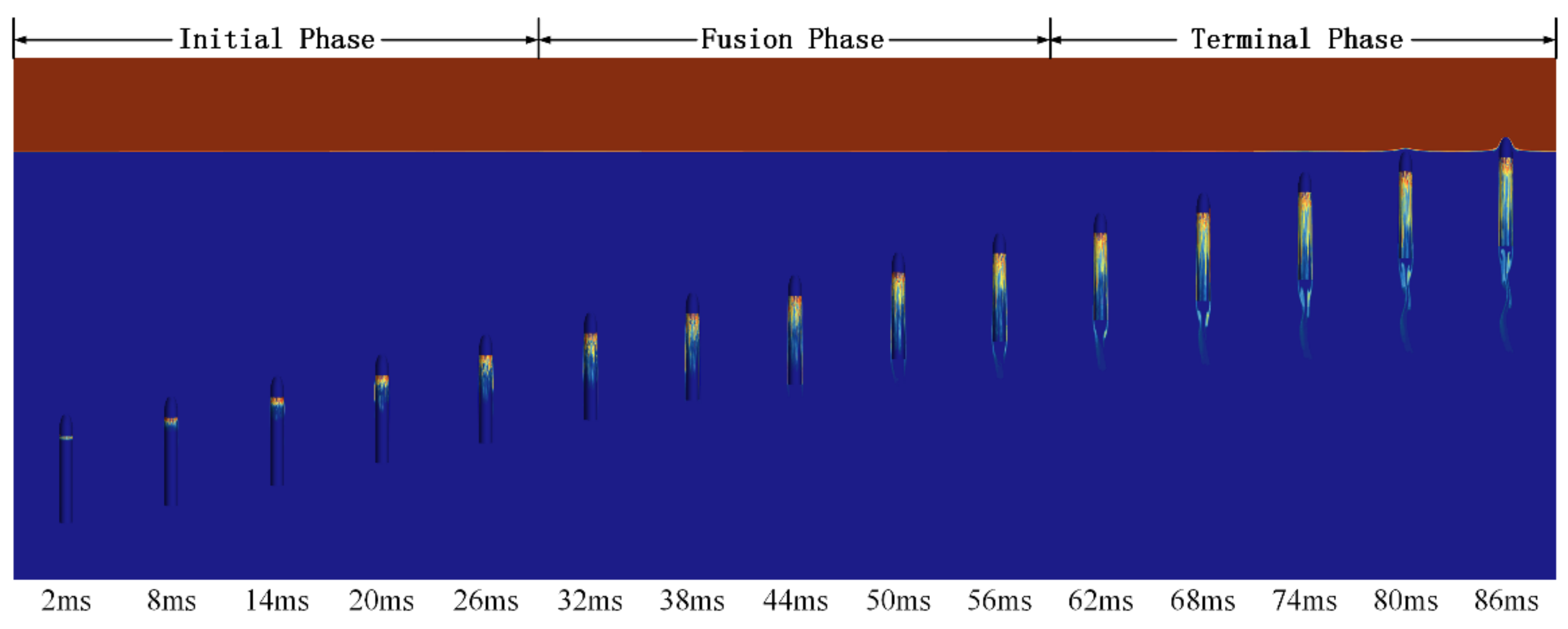
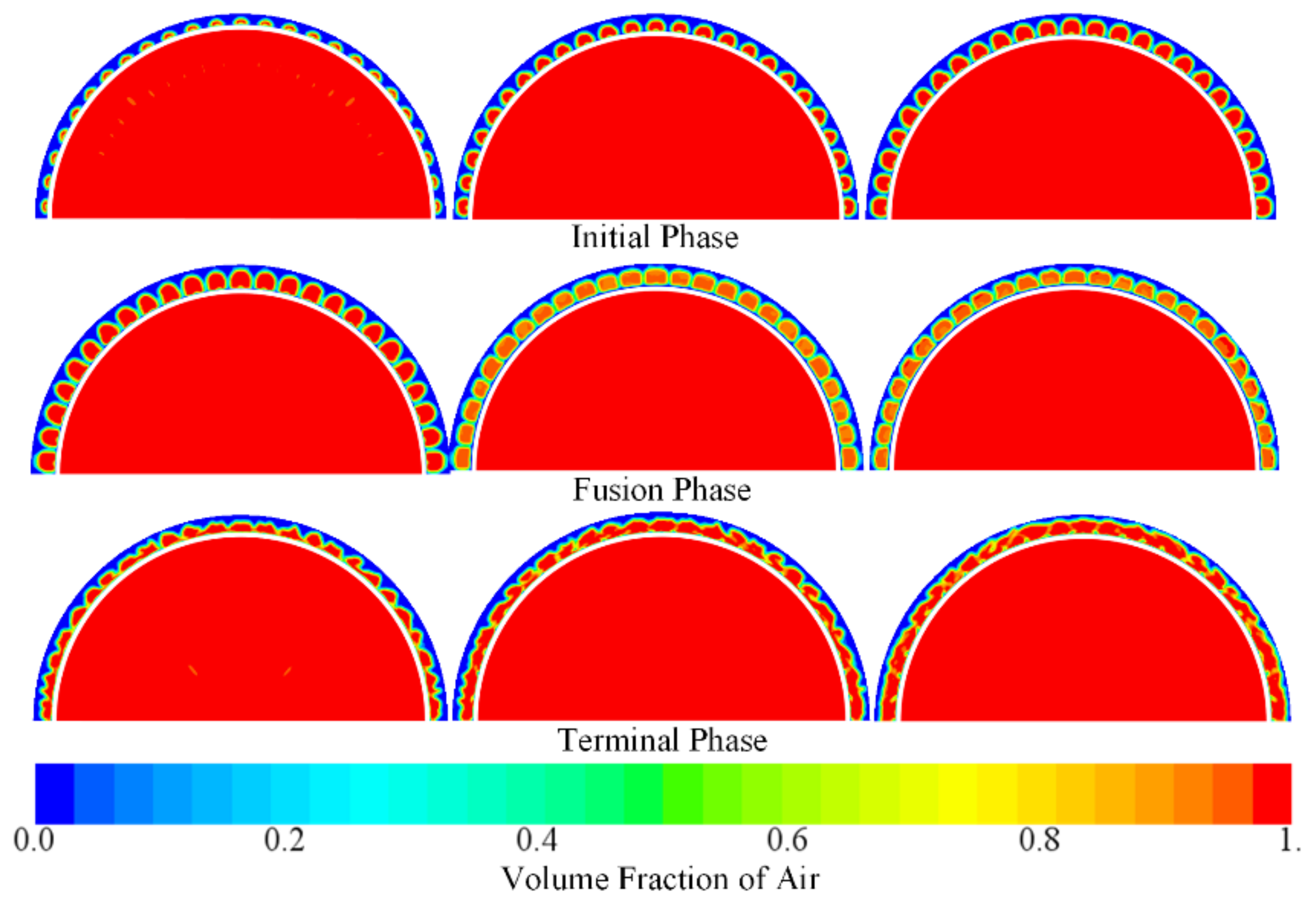
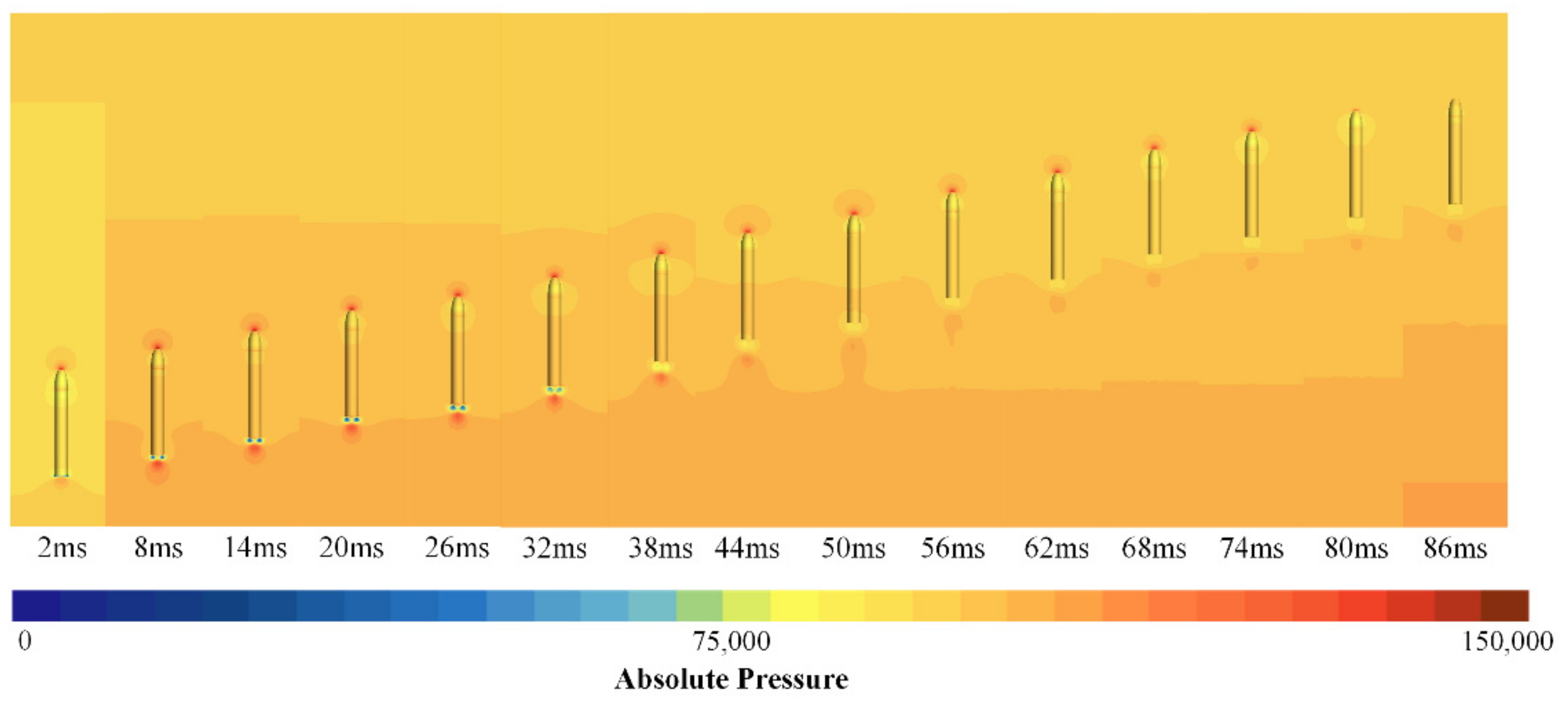
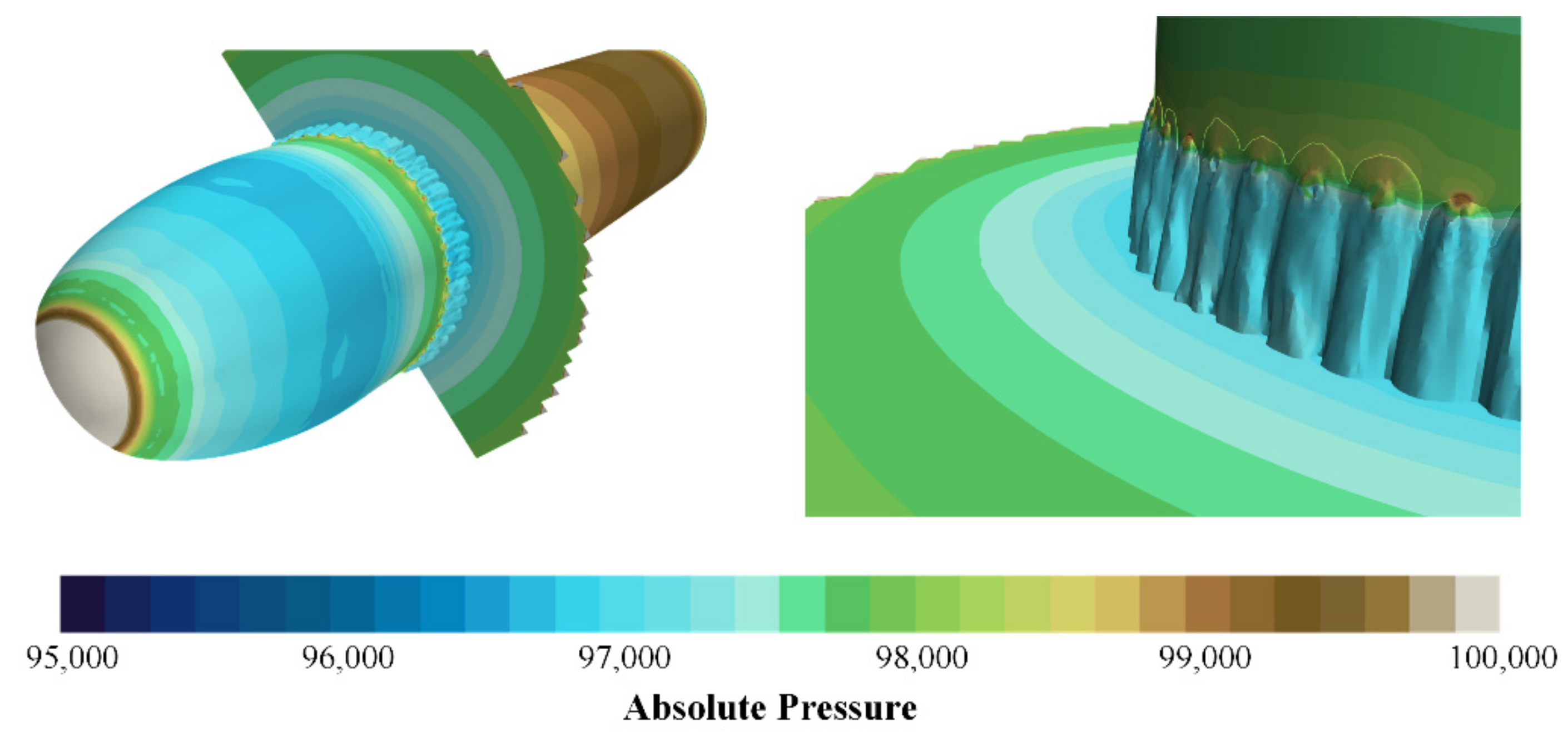
4.1. Analysis of Air Film Fusion Characteristics
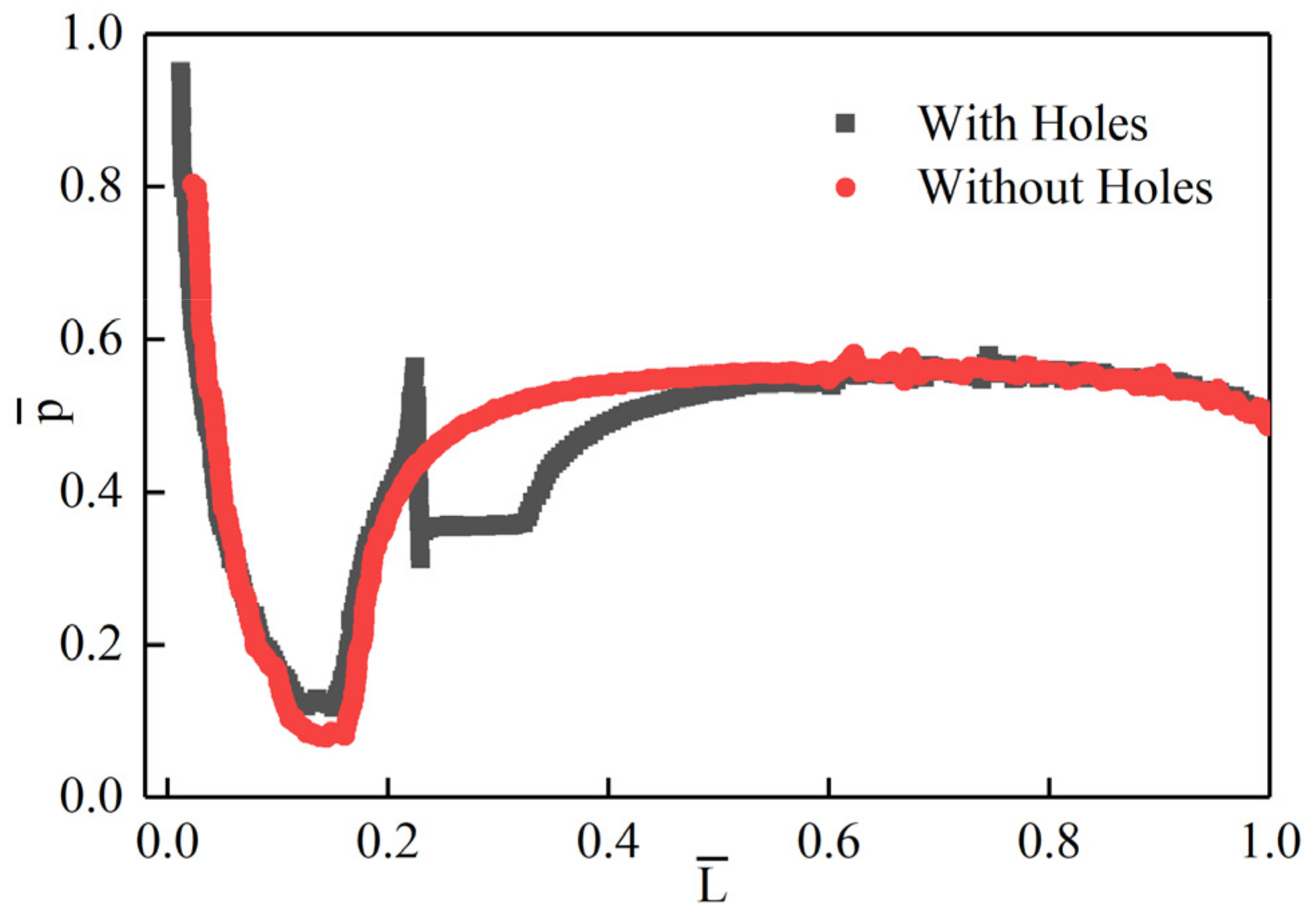
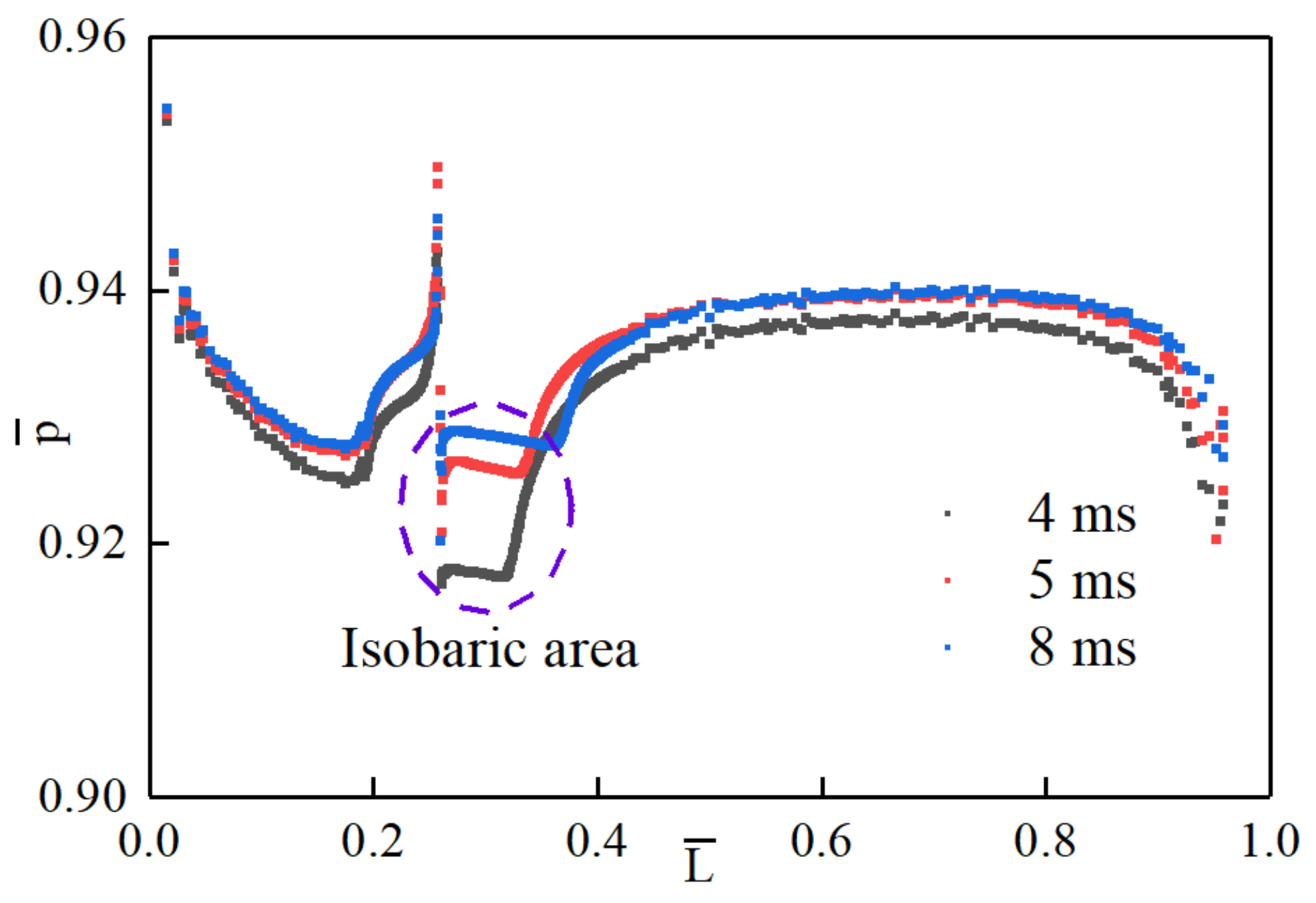
4.2. Research on the Characteristics of Surface Pressure of Vehicle
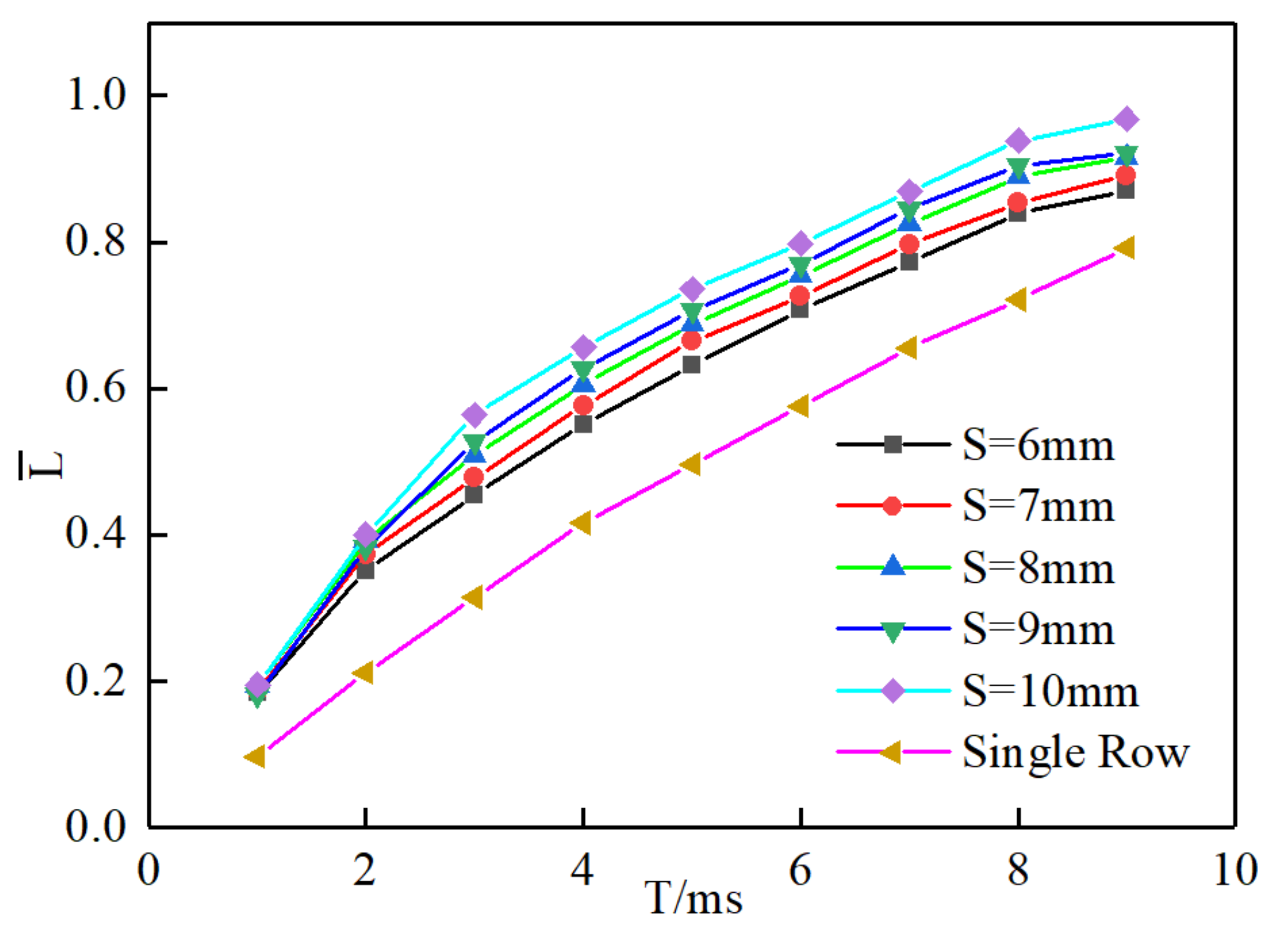
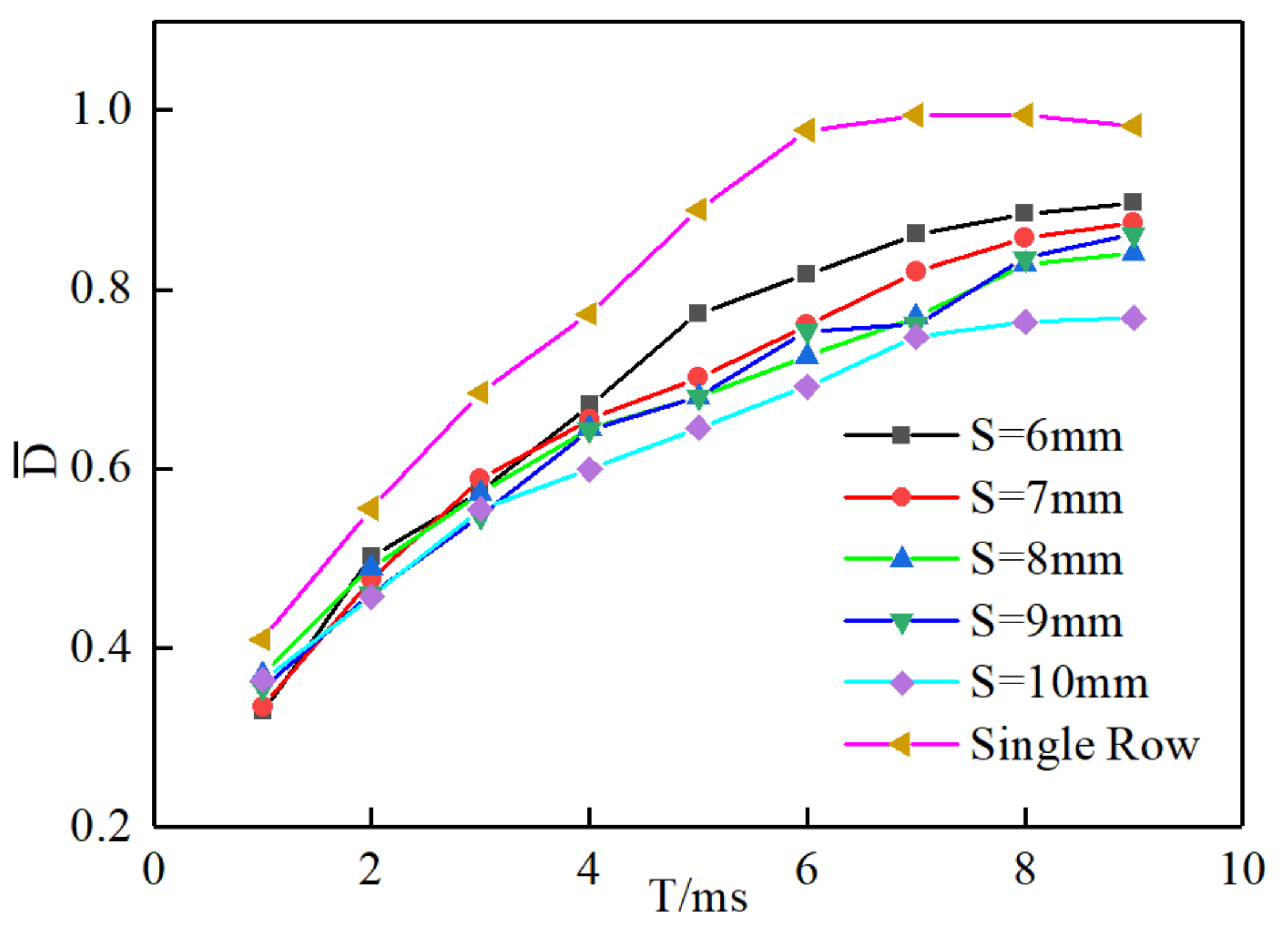
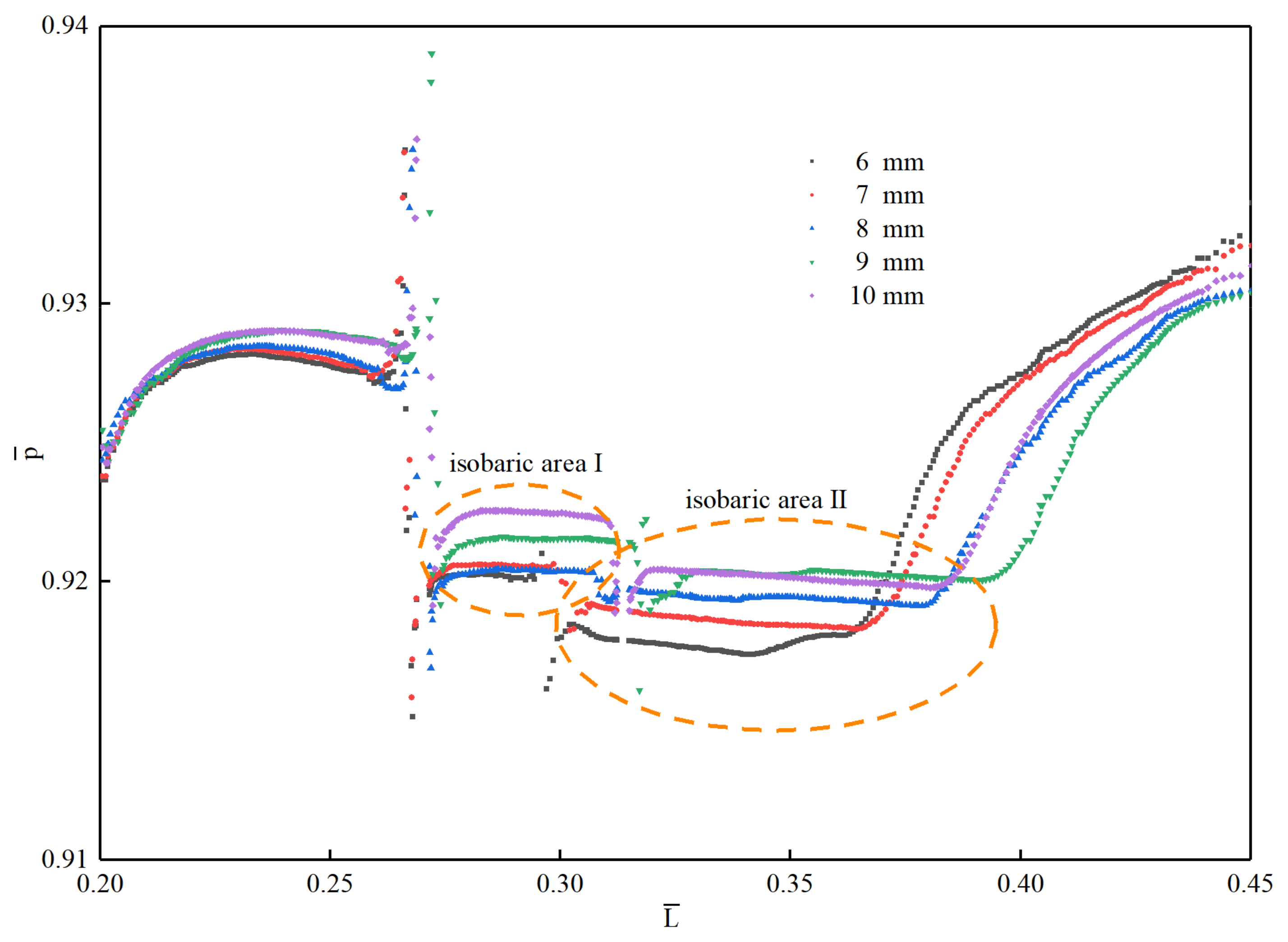
4.3. Effect of the Number of Holes on Air Film Fusion and Pressure Distribution
5. Conclusions
- (1)
- Pressure-equalizing exhaust is the passive exhaust process of gas under the joint action of the incoming shear force and the hydrostatic pressure drop of the holes. The gas morphology of the holes develops from a bundle-like to a strip-like structure, and finally develops into a sheet-like structure and achieves complete fusion.
- (2)
- The fusion film forms an isobaric zone in the coverage area, which reduces the amplitude of the surface pressure of the vehicle and effectively improves the hydrodynamic characteristics of the vehicle.
- (3)
- Compared with the single row of holes, the double row has a greater speed of axial advance, radial expansion, and circumferential fusion, and the approximate isobaric zone inside the film also develops faster, so the double row is more conducive to improving the hydrodynamic characteristics of the vehicle.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.W.; Huang, C.G. Research progress on hydrodynamics of high-speed vehicles in the underwater launching process. J. Adv. Mech. 2018, 48, 259–298. [Google Scholar]
- Wang, Y.W.; Huang, C.G.; Du, T.Z.; Fang, X.; Liang, N.G. Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical launching process. J. Chin. J. Theoretical Appl. Mech. 2012, 44, 39–48. [Google Scholar]
- Reichardt, H. The Laws of Cavitation Bubbles at Axially Symmetrical Bodies in A Flow. Kais. Wilhelm Inst. Stromungsforsch. 1945, 766, 322–326. [Google Scholar]
- Knapp, R.T.; Daily, J.W.; Hammitt, F.G. Cavitation. J. Fluid Mech. 1972, 54, 189–191. [Google Scholar]
- Zhang, N.M.; Zhao, Y.; Wei, H.P.; Cheng, S.H. Research on fusion characteristics of porous exhaust bubbles in underwater vertical launch vehicle. J. Ship Mech. 2018, 22, 135–143. [Google Scholar]
- Ma, G.H.; Chen, F.; Yu, J.Y. Research on the effect of the number of stomata on the flow around the exhausted vehicle. J. Eng. Thermophys. 2018, 39, 1945–1951. [Google Scholar]
- Huang, B.; Wang, G.Y.; Quan, X.B.; Zhang, M.D. Study on the unsteady cavitating flow dynamic characteristics around a 0-caliber ogive revolution body. J. Exp. Fluid Mech. 2011, 25, 22–28. [Google Scholar]
- Sun, T.Z.; Wei, Y.J.; Wang, C.; Cao, W. Analysis of the effect of ventilation positions on hydrodynamic characteristics of submarine-launched vehicle. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 1303–1308. [Google Scholar]
- Gao, S.; Pan, G. Characteristics Research on Unsteady Flow Field during Salvo of Submarine-launched Vehicles. J. Digital Ocean. Underw. Warf. 2020, 3, 271–275. [Google Scholar]
- Chen, F.; Ma, G.H.; Cheng, S.H.; Jiang, S. Effect of Straight or Inclined Hole Exhaust on Flow around Underwater Vehicle: Part 1-Flow Field Structure. J. Eng. Thermophys. 2016, 37, 507–513. [Google Scholar]
- Bao, W.C.; Quan, X.B.; Wei, H.P. Numerical Simulation on the Flow Dynamics of Underwater Vehicle Launching with Exhaust. J. Missiles Space Vehicles. 2014, 21, 14–18. [Google Scholar]
- Zhang, K.; Liu, G.T. Three-dimensional Numerical Simulation on Flow Field of Underwater Vehicle Launching with Air Exhaust. In Proceedings of the the 14th National Hydrodynamics Conference and the 28th National Hydrodynamics Conference, Changchun, China, 8 August 2017; Volume 7, pp. 100–106. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CPFD&dbname=CPFDLAST2017&filename=SLDX201708002012&uniplatform=NZKPT&v=tDXf9Ep8FtMAzLJpFwtYF_hgiCscmTTdN_mIZgdWM4h_5ieTIFLA8YBa_eFtqbK4YrvN9iPVPZA%3d (accessed on 25 November 2021).
- Kang, Y.Z.; Wang, C.C.; Wu, Q.; Huang, B.; Kong, D.C. Numerical Simulation on Vertical Launch of Vehicle with Pressure-equalizing. In Proceedings of the the 29th National Hydrodynamics Symposium, Zhenjiang, China, 25 August 2018; Volume 6, pp. 187–192. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CPFD&dbname=CPFDLAST2019&filename=SLDX201808001021&uniplatform=NZKPT&v=fat6wacm5-FMkZ1XaeObTnEuVKxgflFJv0_6-zTbTLak7UbHZvDUAo3vKQSQP36189W24fZQy6M%3d (accessed on 25 November 2021).
- Yan, G.J.; Liang, X.X.; Zhang, J.; Quan, X.B.; Wei, H.P. Investigation on the Vertical Launching Process of the Underwater Vehicle by Couple the Flow Field and the Hydro-ballistics. J. Energy Conserv. Technol. 2019, 37, 307–312. [Google Scholar]
- Liu, J.J. The Research of the Head-Ventilated Projectile on the Process of Water-Exit. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- Wang, K.L. Research on Gas-liquid Multiphase Flow Characteristics of Pinhole Jet Flow Field. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Li, R.F.; Hu, X.L.; Wang, Z.H.; Le, G.G. Effect of Flow Speed on Tube-exit of Submarine-launched Missile. J. Fire Control Command Control. 2019, 44, 98–101, 106. [Google Scholar]
- Zhang, Z. Study on Dynamic Simulation of Submarine High Speed Voyage Based on Mixed Mathematical Model. J. Ship Sci. Technol. 2020, 42, 31–33. [Google Scholar]
- Wu, Y.Y. Analysis of Flow Field Characteristics of Submarine Launched Vehicle during Launching Out of Cylinder. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Sun, L.Q.; Yan, H.; Ma, G.H.; Zhao, J.P. Analysis of the Promoting Effect of Annular Groove on the Coalescence of Ventilated Cavity. J. Chin. J. Theor. Appl. Mech. 2021, 53, 386–394. [Google Scholar]
- Qiu, Y. Numerical Simulation Research on the Influence of Cavity Exhaust to the Process of Vehicle Underwater Launch. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Duan, L.; Wang, G.Y.; Fu, X.N. Research on Unsteady Characteristics of Ventilated Cavitating Flow in the Form of Gas-leakage by Toroidal Vortex. Acta Armam. 2014, 35, 712–718. [Google Scholar]
- Ren, Z.Y.; Sun, L.Q.; Li, Z.P.; Xiao, W. Experimental Study on the Cavitation Development and Collapse Characteristics of Underwater Vehicle. J. Astronaut. Syst. Eng. Technol. 2021, 5, 42–49. [Google Scholar]
- Zhang, S.B.; Lu, C.J.; Chen, X. Investigation of Ventilated Cavity Shapes of a High-speed Underwater Vehicle. J. Shanghai Jiaotong Univ. 2012, 46, 329–334. [Google Scholar]
- Wei, Q.D. Research on Experimental Characteristics of Underwater Porous Exhaust. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
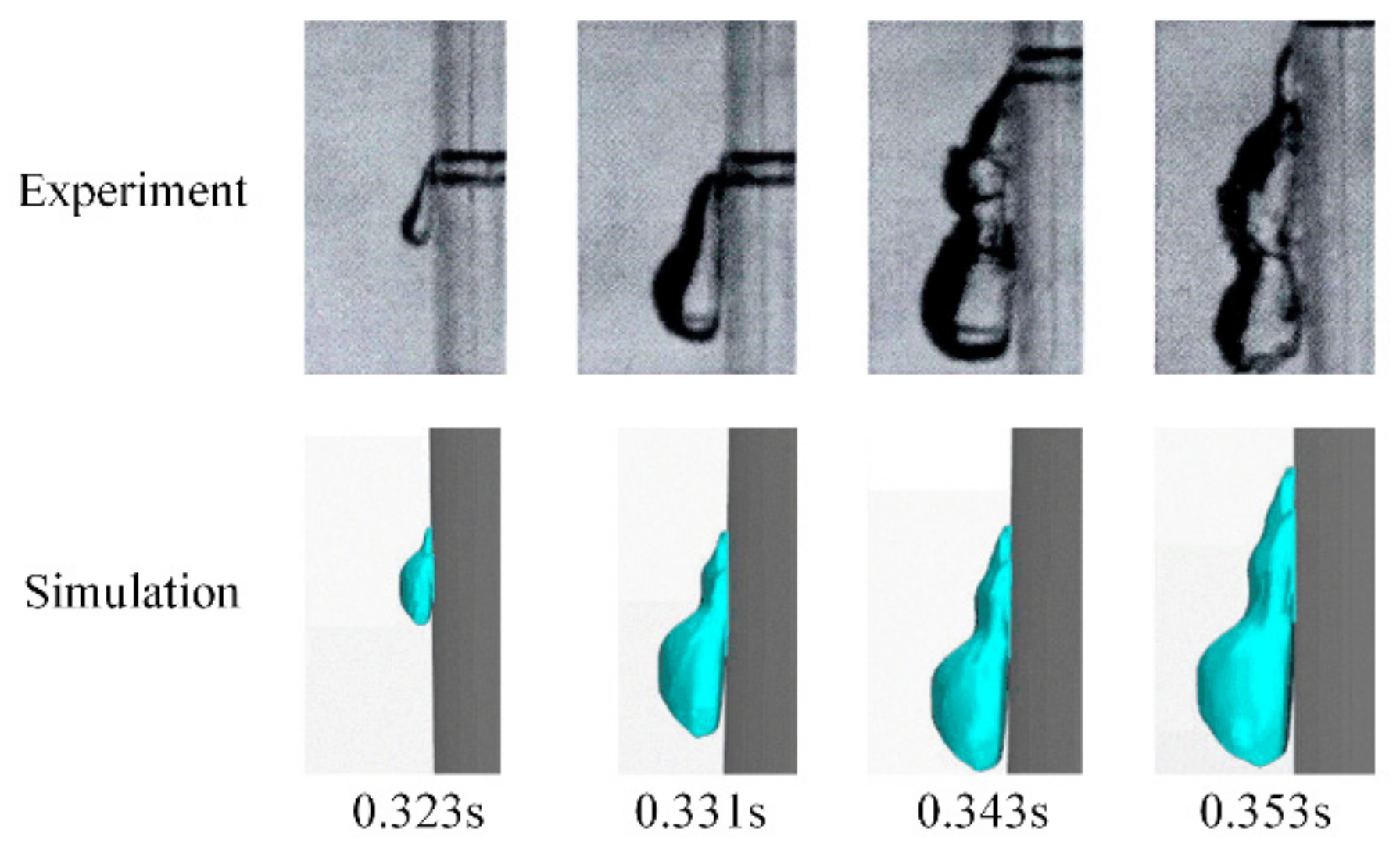


| Time | 0.067 | 0.323 | 0.331 | 0.353 | 0.357 | 0.360 | 0.363 | 0.366 |
| CFD | 13 | 18 | 23 | 34 | 38 | 42 | 45 | 46 |
| Exp | 14 | 19 | 24 | 36 | 40 | 44 | 46 | 48 |
| Error | 7.14% | 5.26% | 4.2% | 5.55% | 5% | 4.55% | 2.17% | 4.2% |
| Time | 0.067 | 0.323 | 0.331 | 0.353 | 0.357 | 0.360 | 0.363 | 0.366 |
| CFD | 3 | 5.5 | 7.5 | 10 | 10 | 11 | 11 | 11 |
| Exp | 3 | 6 | 8 | 11 | 11 | 12 | 12 | 12 |
| Error | 0 | 8.33% | 9.37% | 9.09% | 9.09% | 9.09% | 9.17% | 9.17% |
| Pressure | Time | Cavity Length | Cavity Diameter |
|---|---|---|---|
| Physic Coefficients | Coarse | Fine | Ecoarse | GCIcoarse |
|---|---|---|---|---|
| Min dimensionless pressure | 0.496 | 0.497 | 0.0042 | 1.26% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Ren, J.; Gao, S.; Pan, G. Numerical Investigation on Air Film Fusion of Pressure-Equalizing Exhaust around Shoulder Ventilation of Submarine-Launched Vehicle. J. Mar. Sci. Eng. 2022, 10, 39. https://doi.org/10.3390/jmse10010039
Shi Y, Ren J, Gao S, Pan G. Numerical Investigation on Air Film Fusion of Pressure-Equalizing Exhaust around Shoulder Ventilation of Submarine-Launched Vehicle. Journal of Marine Science and Engineering. 2022; 10(1):39. https://doi.org/10.3390/jmse10010039
Chicago/Turabian StyleShi, Yao, Jinyi Ren, Shan Gao, and Guang Pan. 2022. "Numerical Investigation on Air Film Fusion of Pressure-Equalizing Exhaust around Shoulder Ventilation of Submarine-Launched Vehicle" Journal of Marine Science and Engineering 10, no. 1: 39. https://doi.org/10.3390/jmse10010039
APA StyleShi, Y., Ren, J., Gao, S., & Pan, G. (2022). Numerical Investigation on Air Film Fusion of Pressure-Equalizing Exhaust around Shoulder Ventilation of Submarine-Launched Vehicle. Journal of Marine Science and Engineering, 10(1), 39. https://doi.org/10.3390/jmse10010039








