Two-Way Coupling Simulation of Solid-Liquid Two-Phase Flow and Wear Experiments in a Slurry Pump
Abstract
:1. Introduction
2. Parameters and Methods
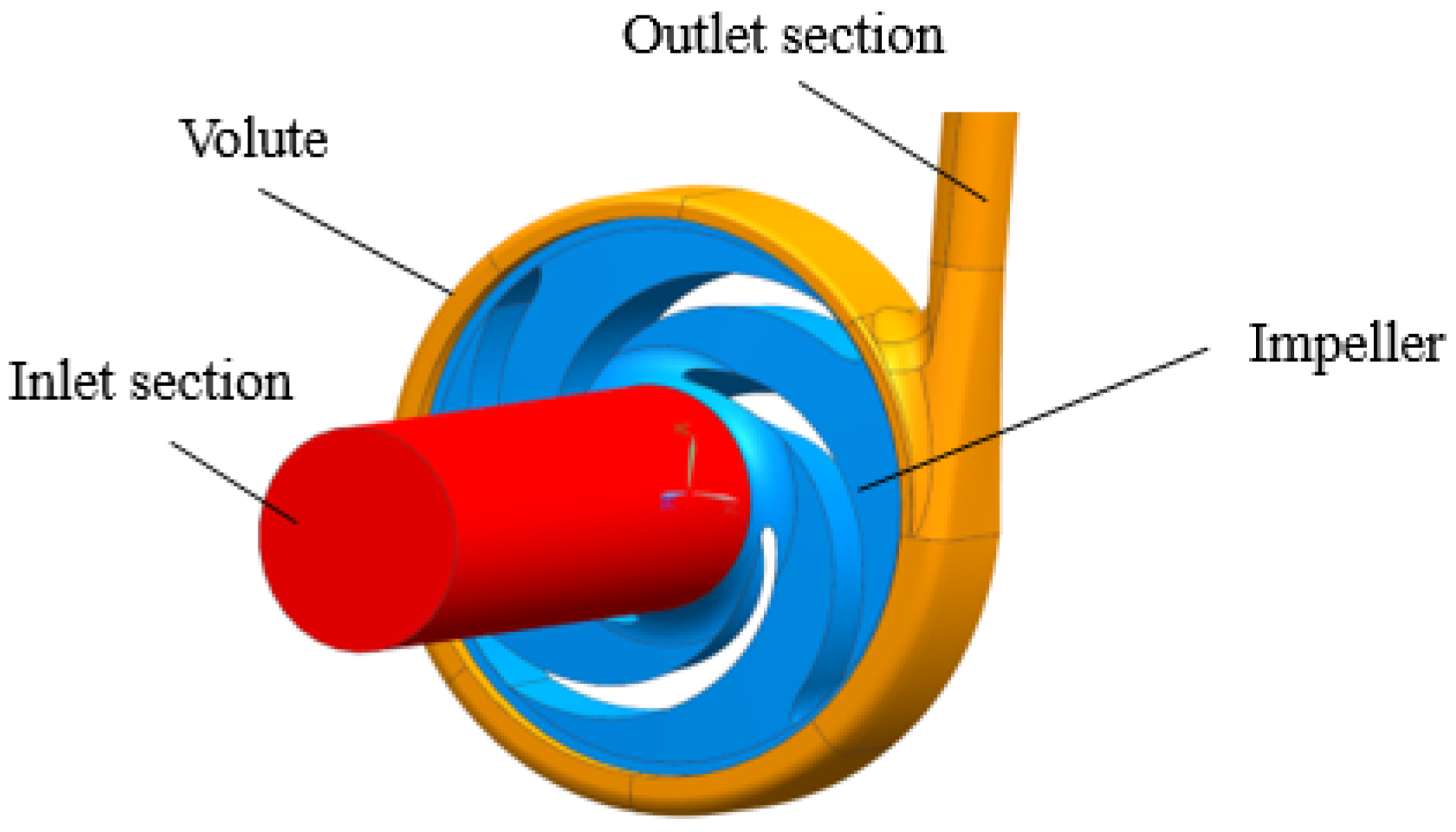
2.1. Geometry and Parameters
2.2. Grids
2.3. Numerical Methods
2.3.1. Turbulence Model
2.3.2. Discrete Phase Model
2.4. Erosion Model
2.5. Boundary Conditions
3. Experimental Verification and Simulation
3.1. Experiments
3.1.1. Performance Experiments
3.1.2. Wear Experiments
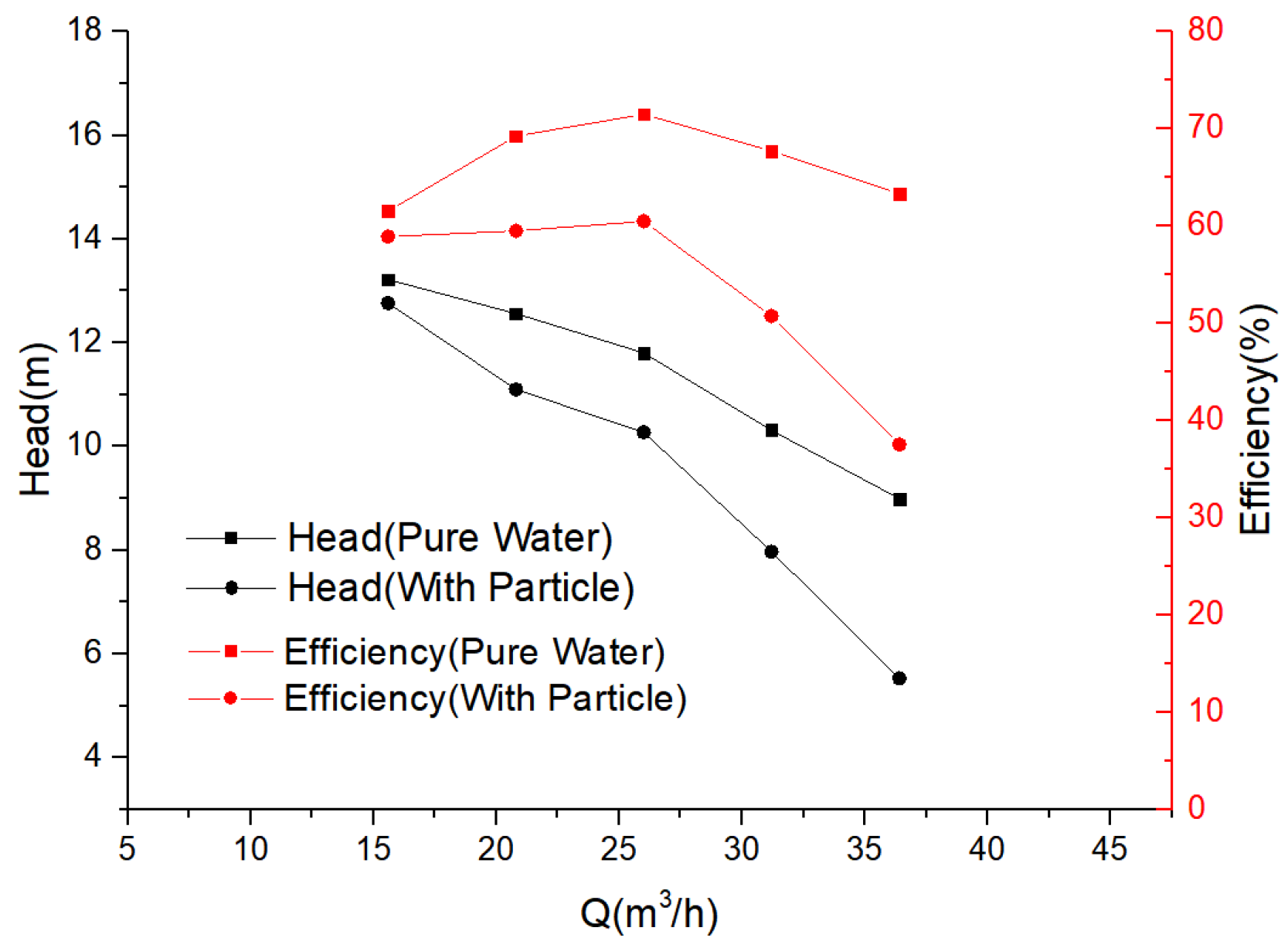
3.2. Comparison and Verification
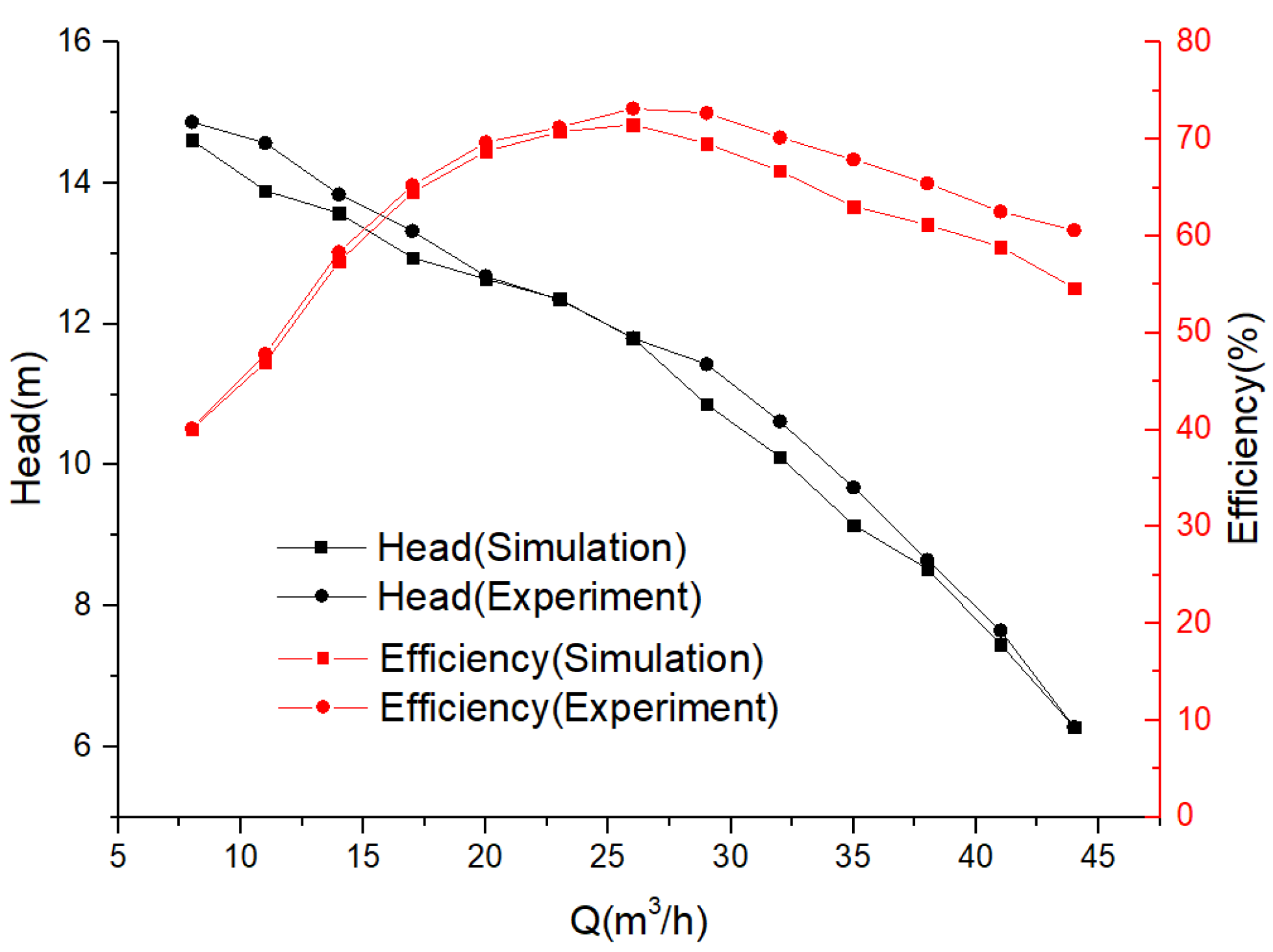
3.2.1. Performance Comparison under Pure Water Conditions
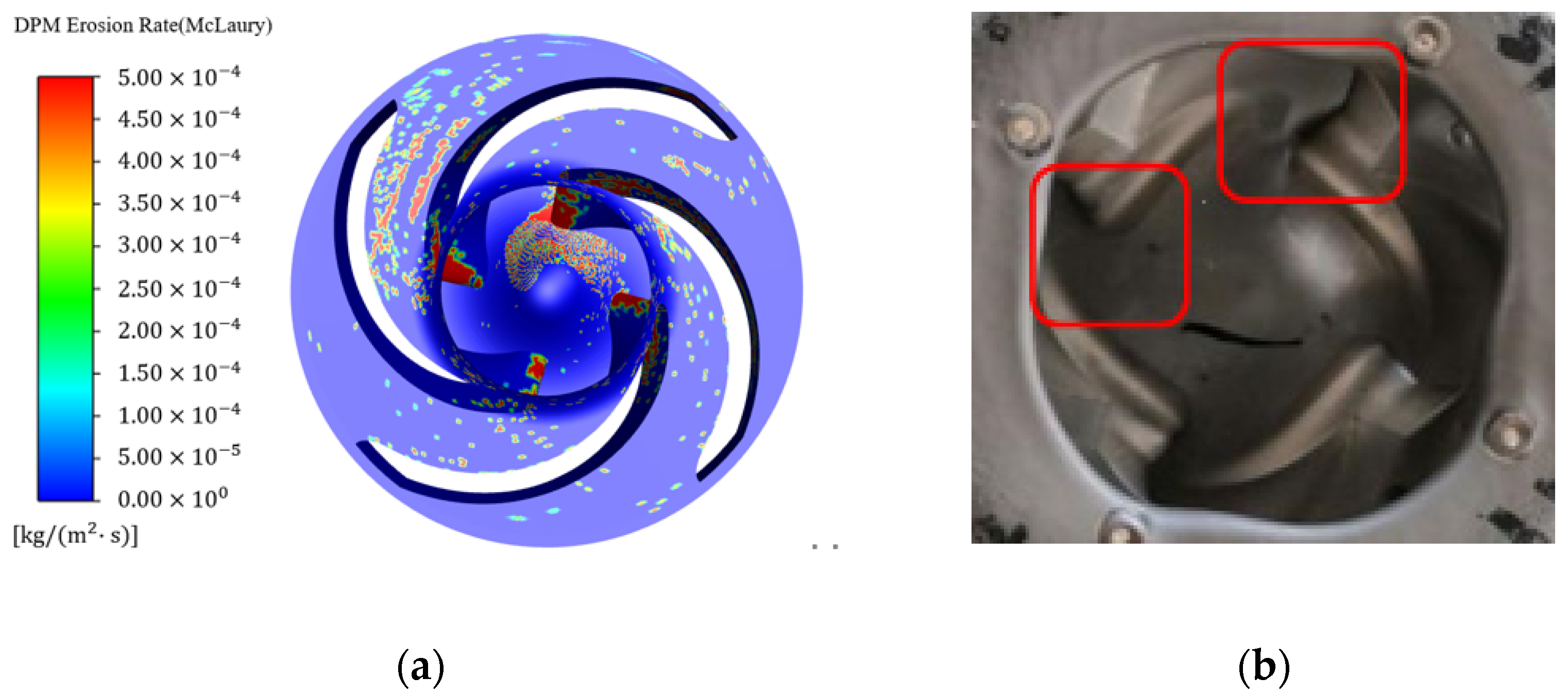
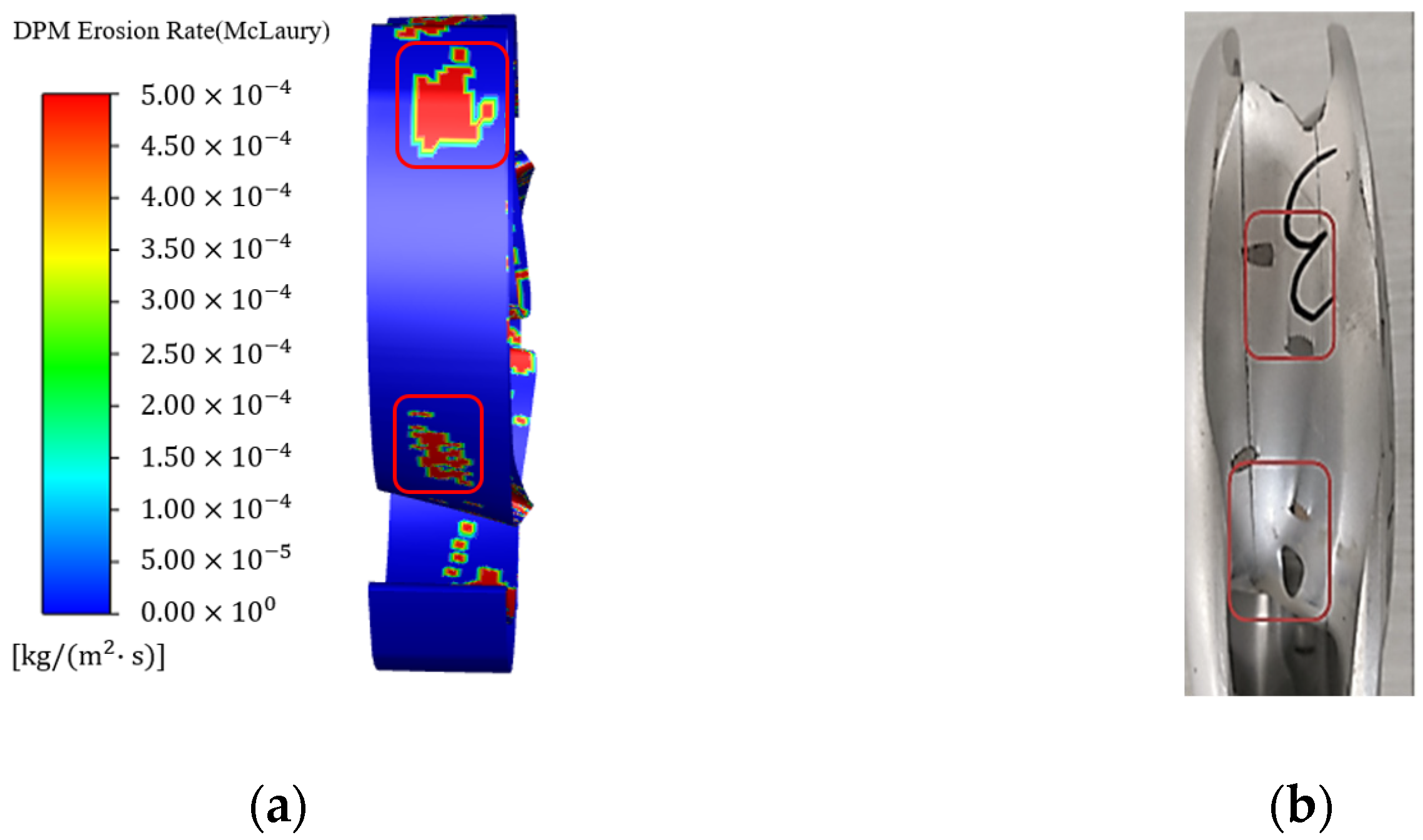
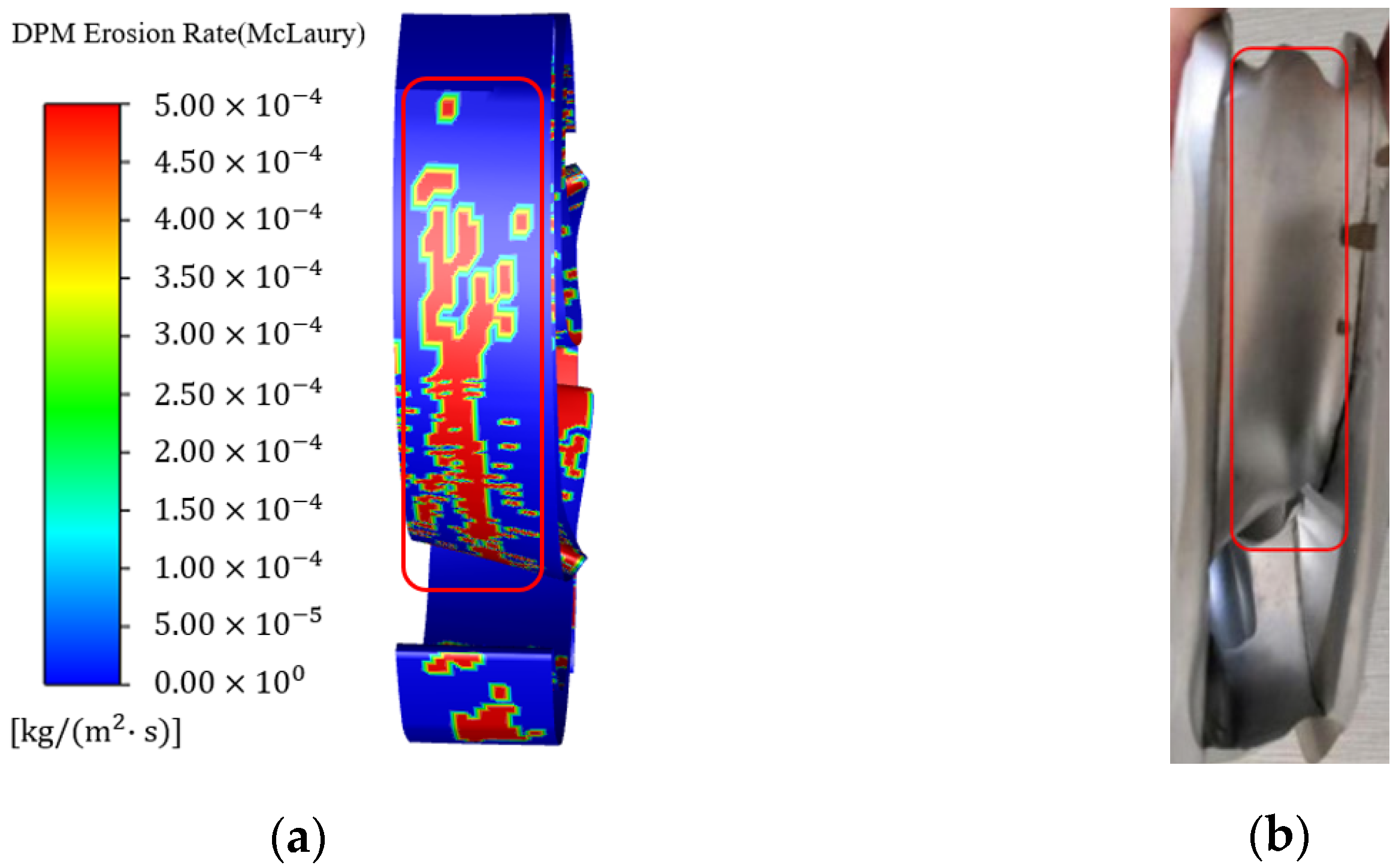
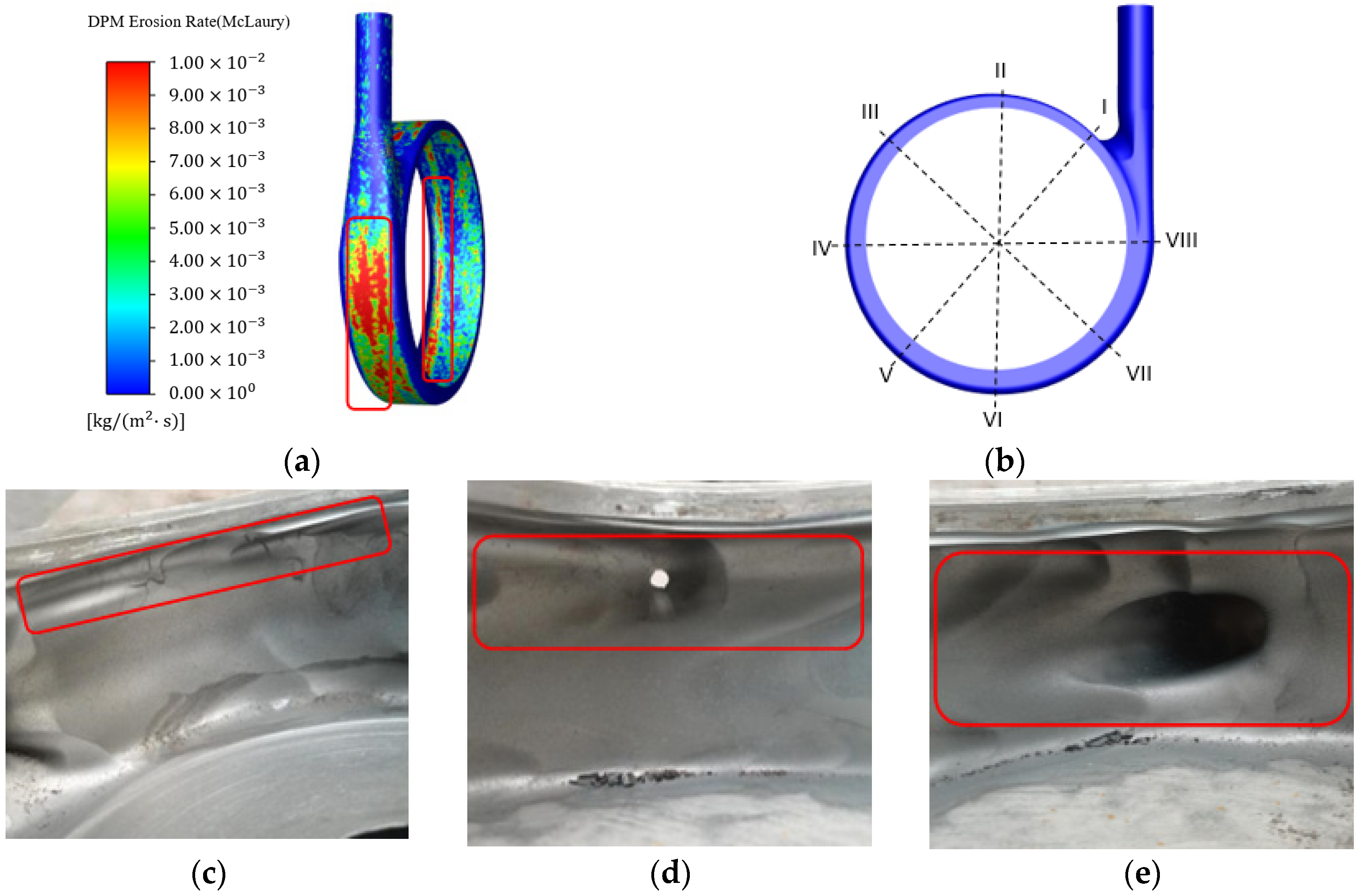
3.2.2. Wear Comparison
4. Results and Discussion
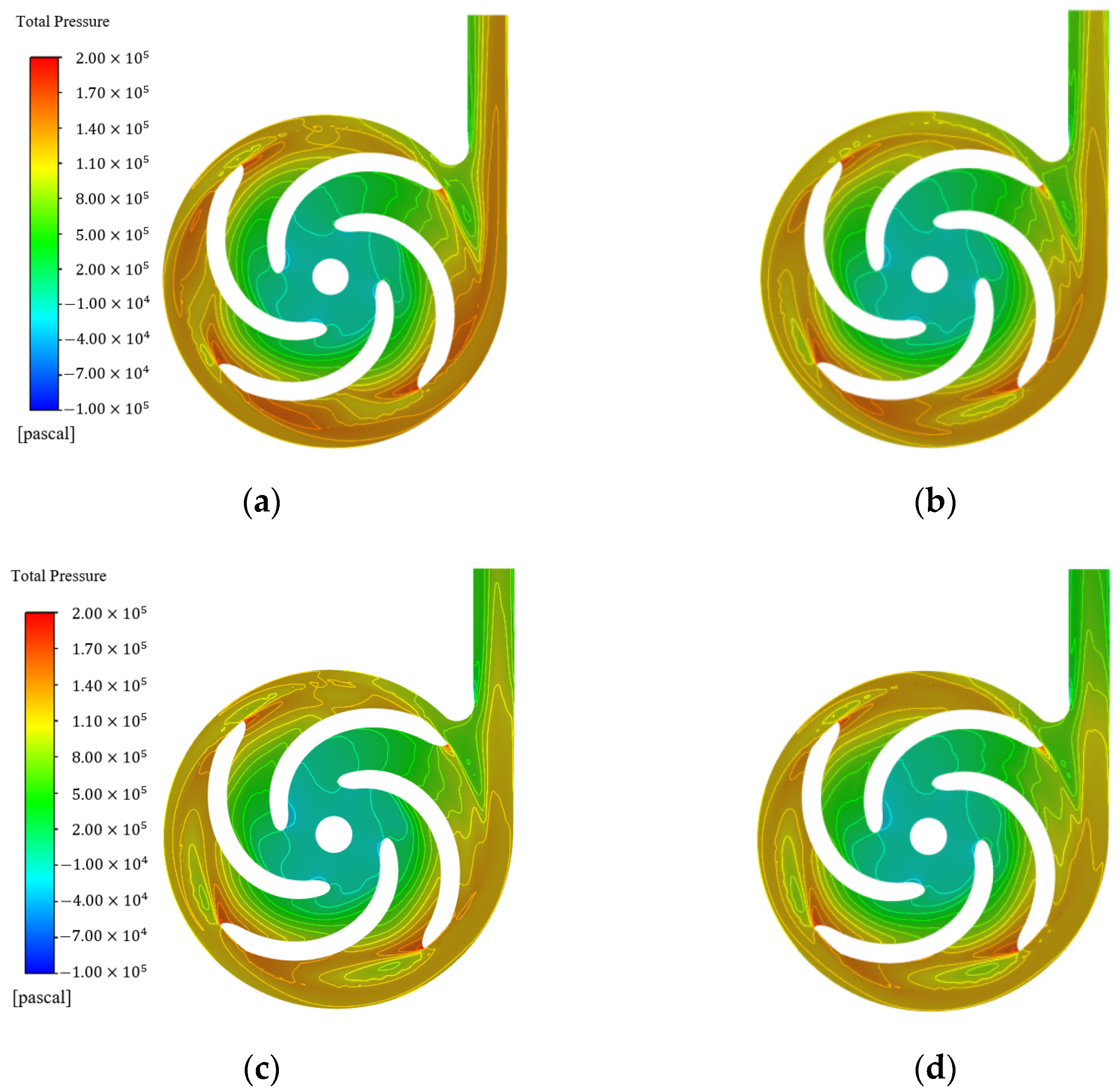
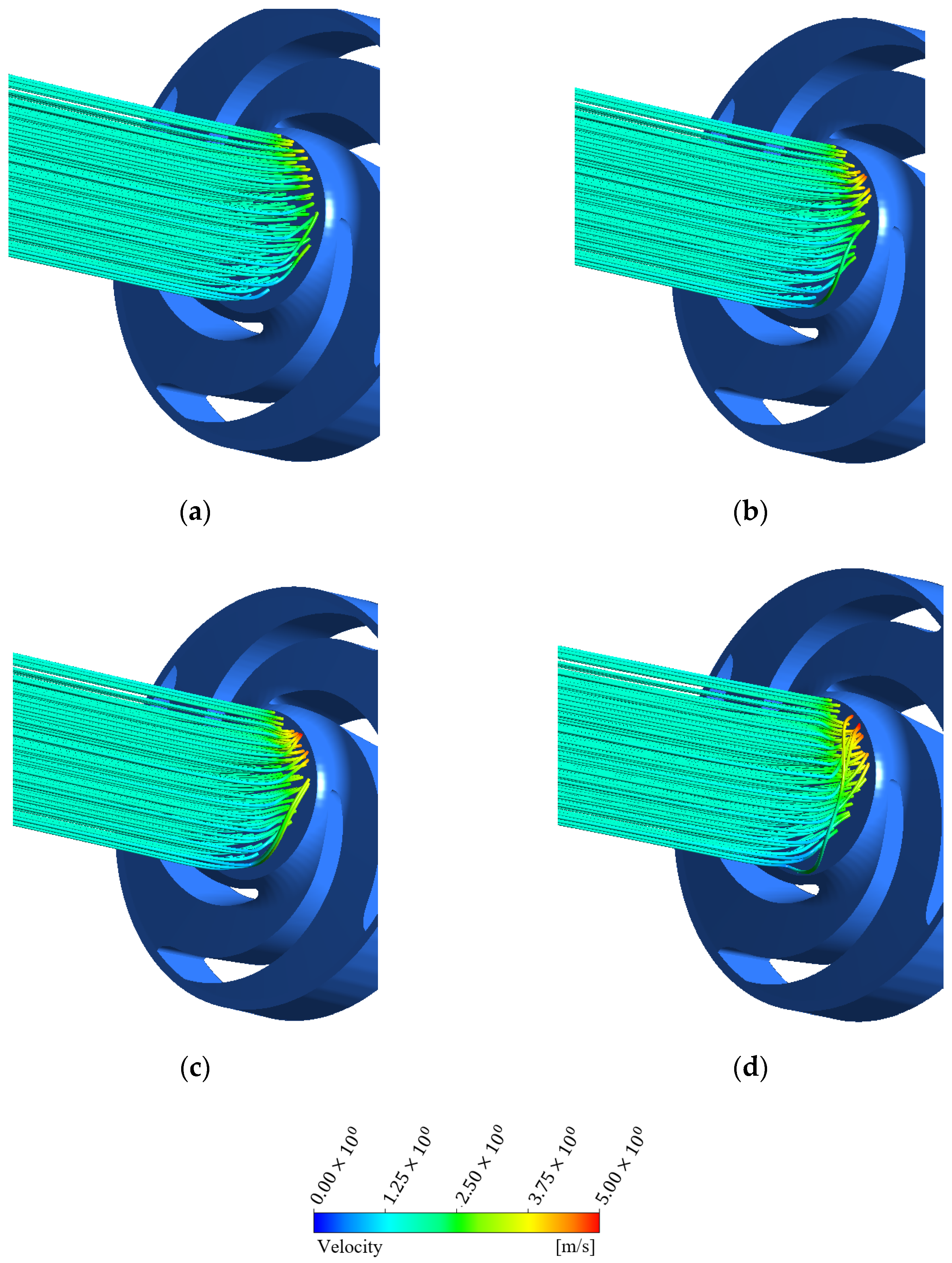
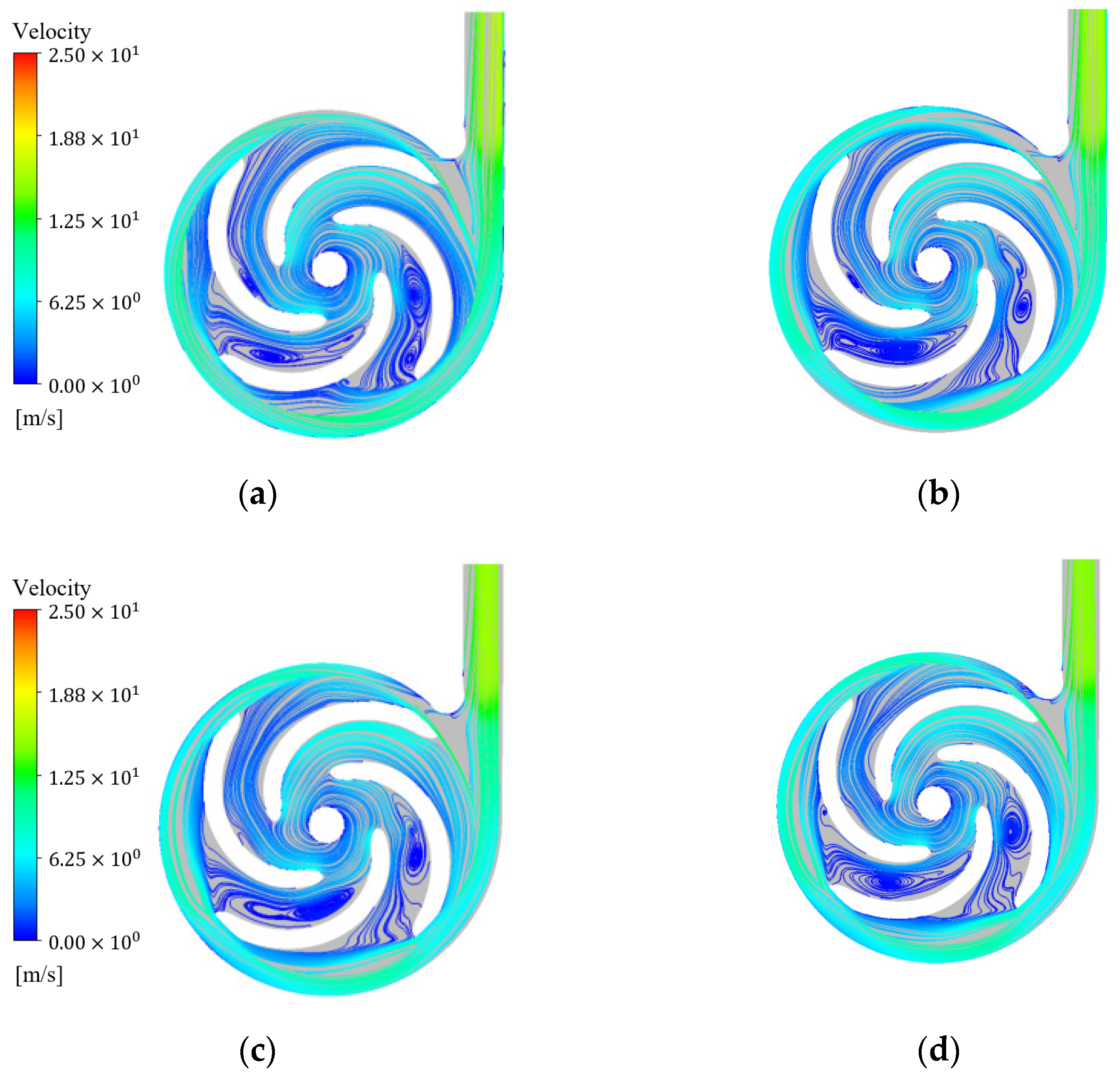
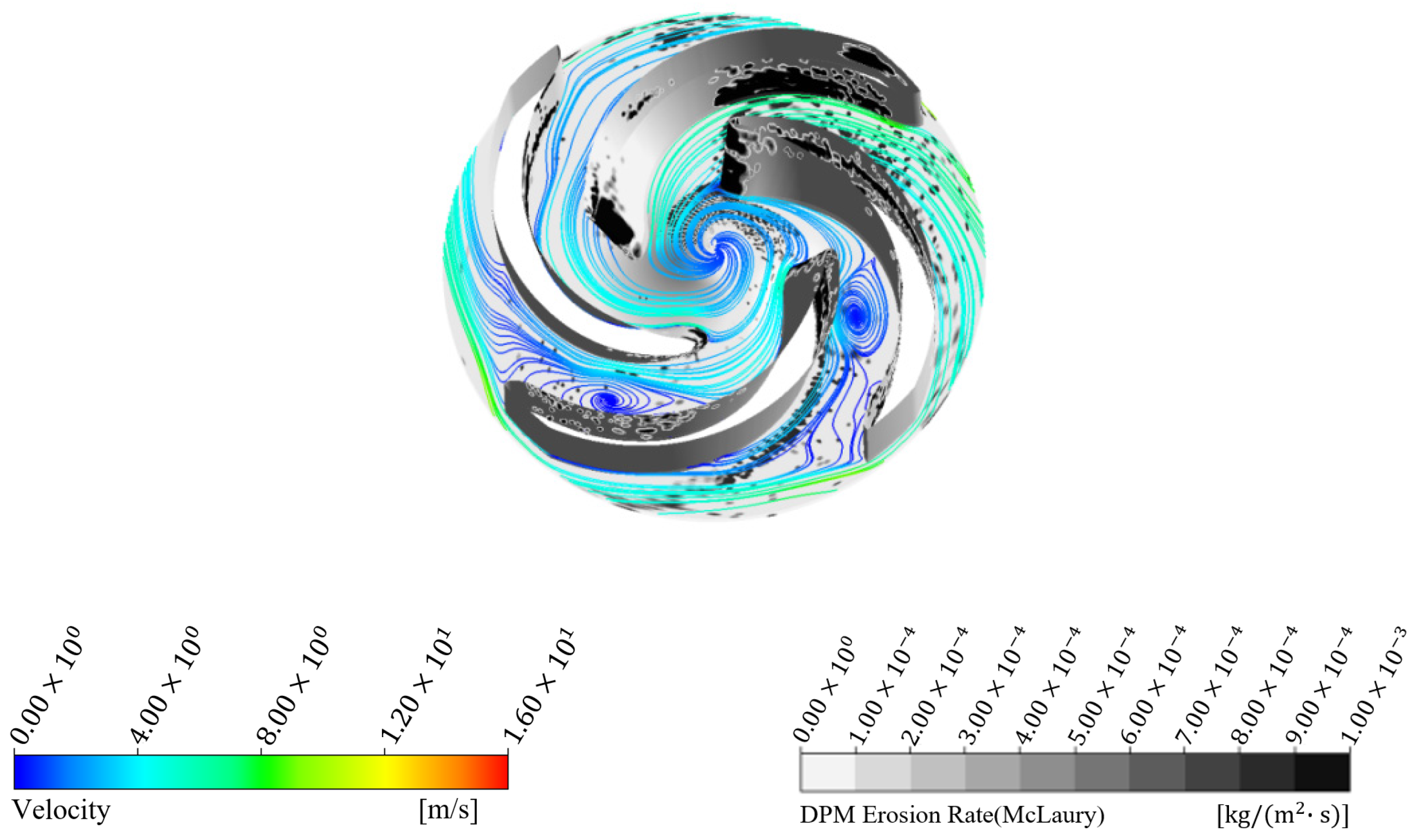
4.1. Flow Field Analysis
4.1.1. Pressure Distribution
4.1.2. Velocity Streamlines
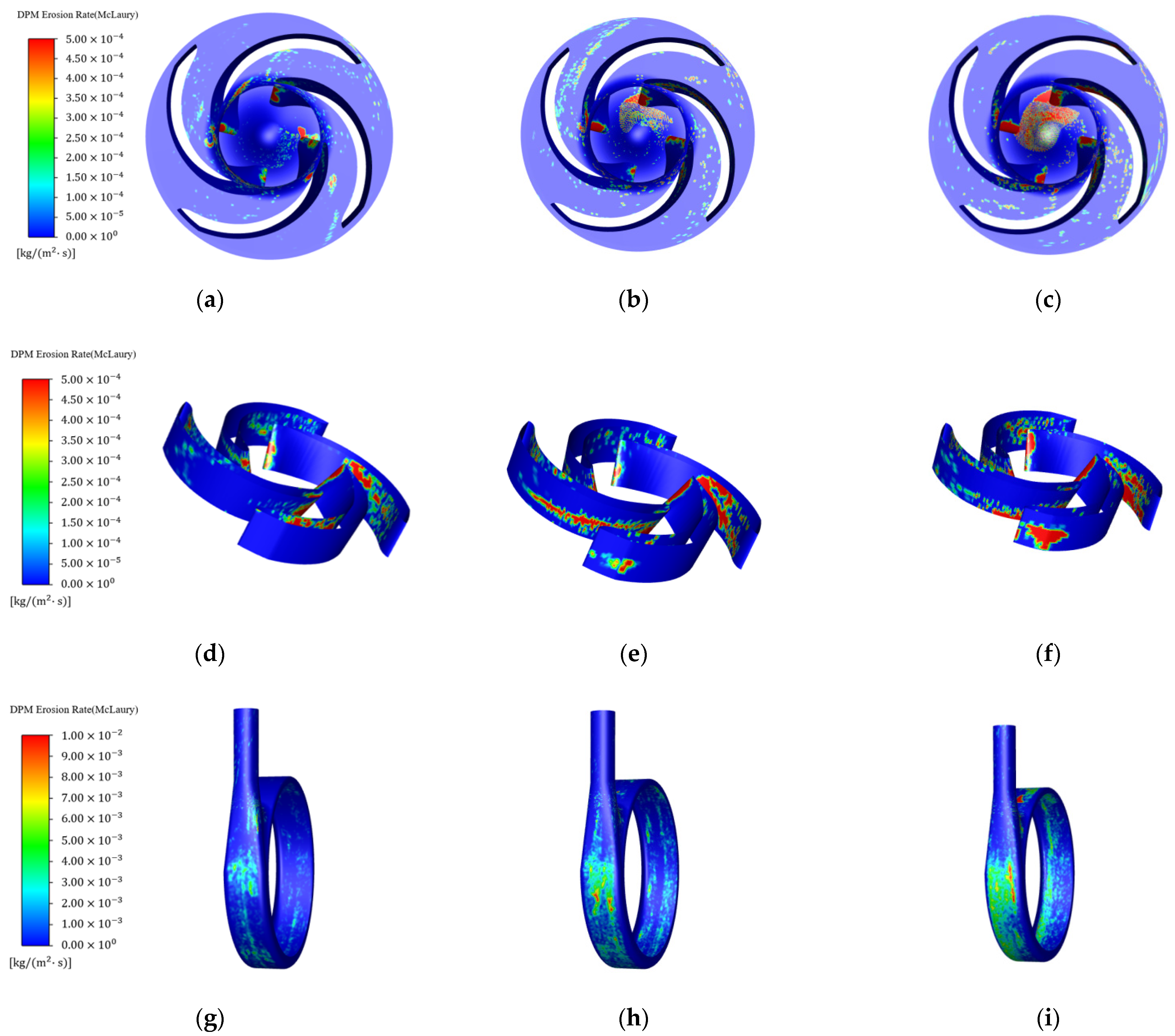
4.2. Wear Analysis
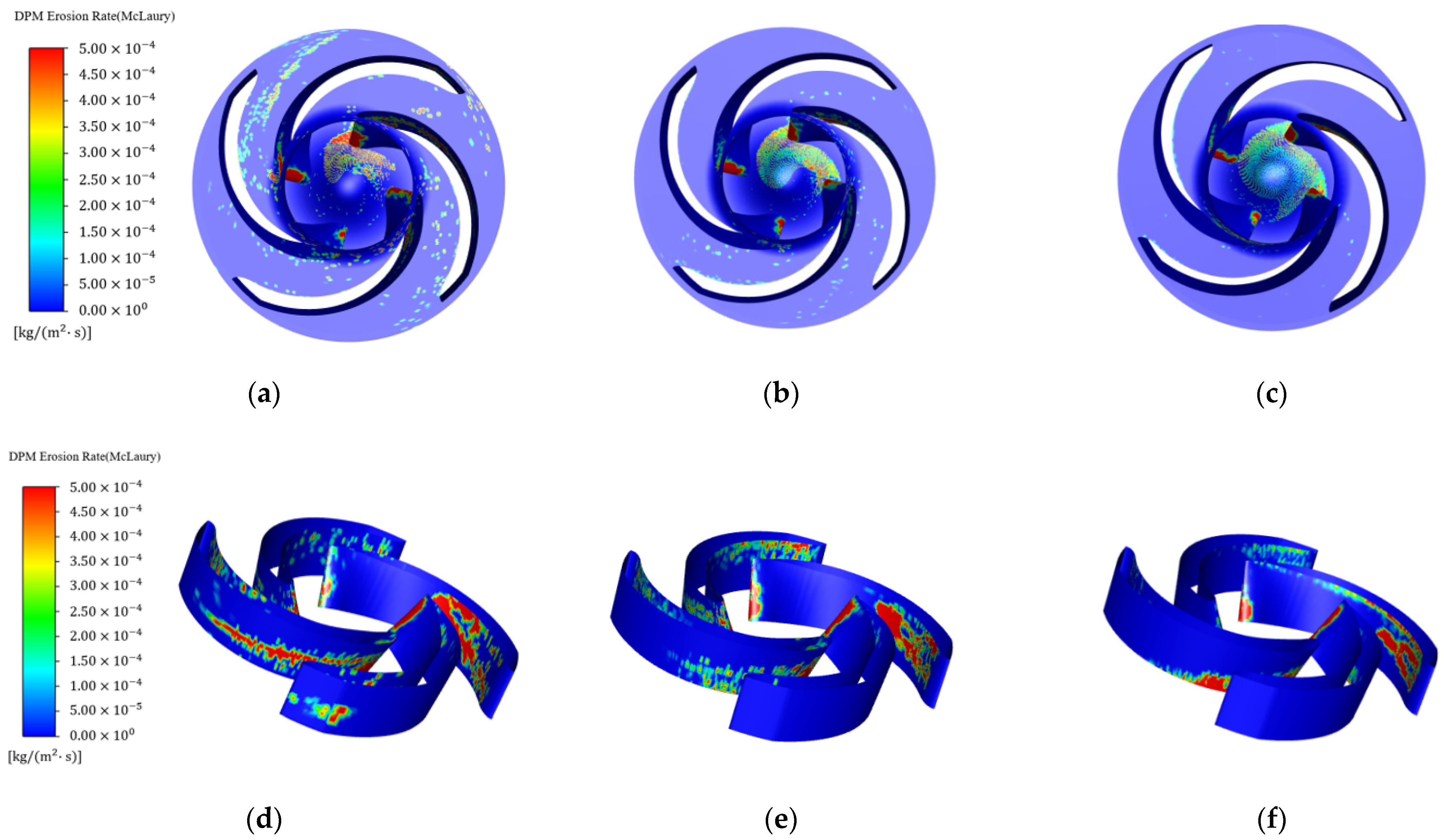
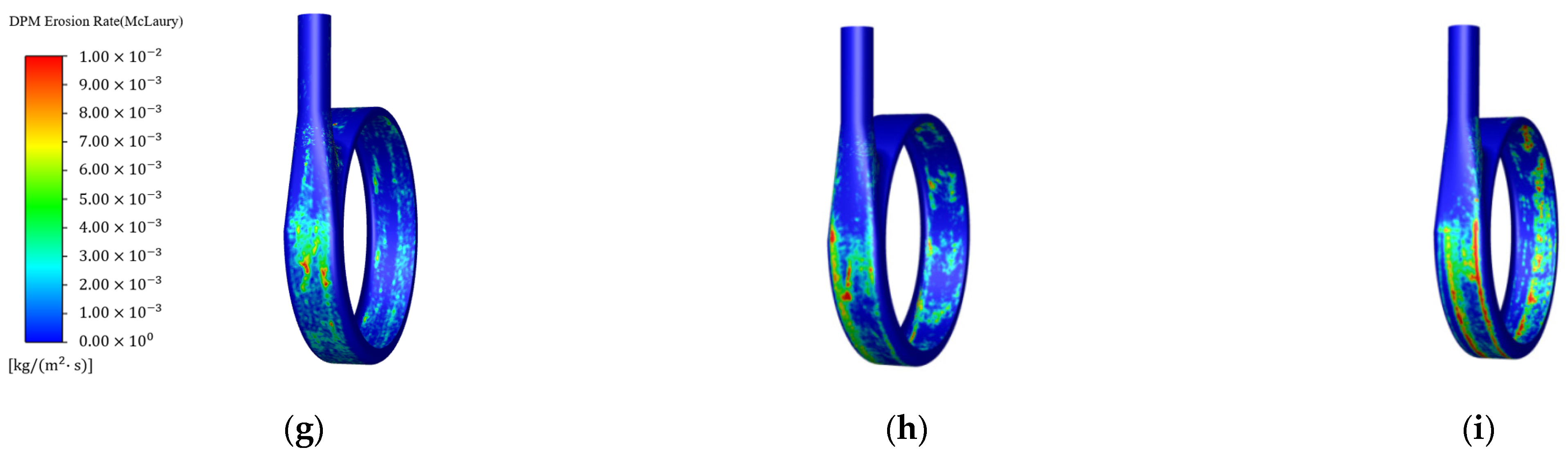
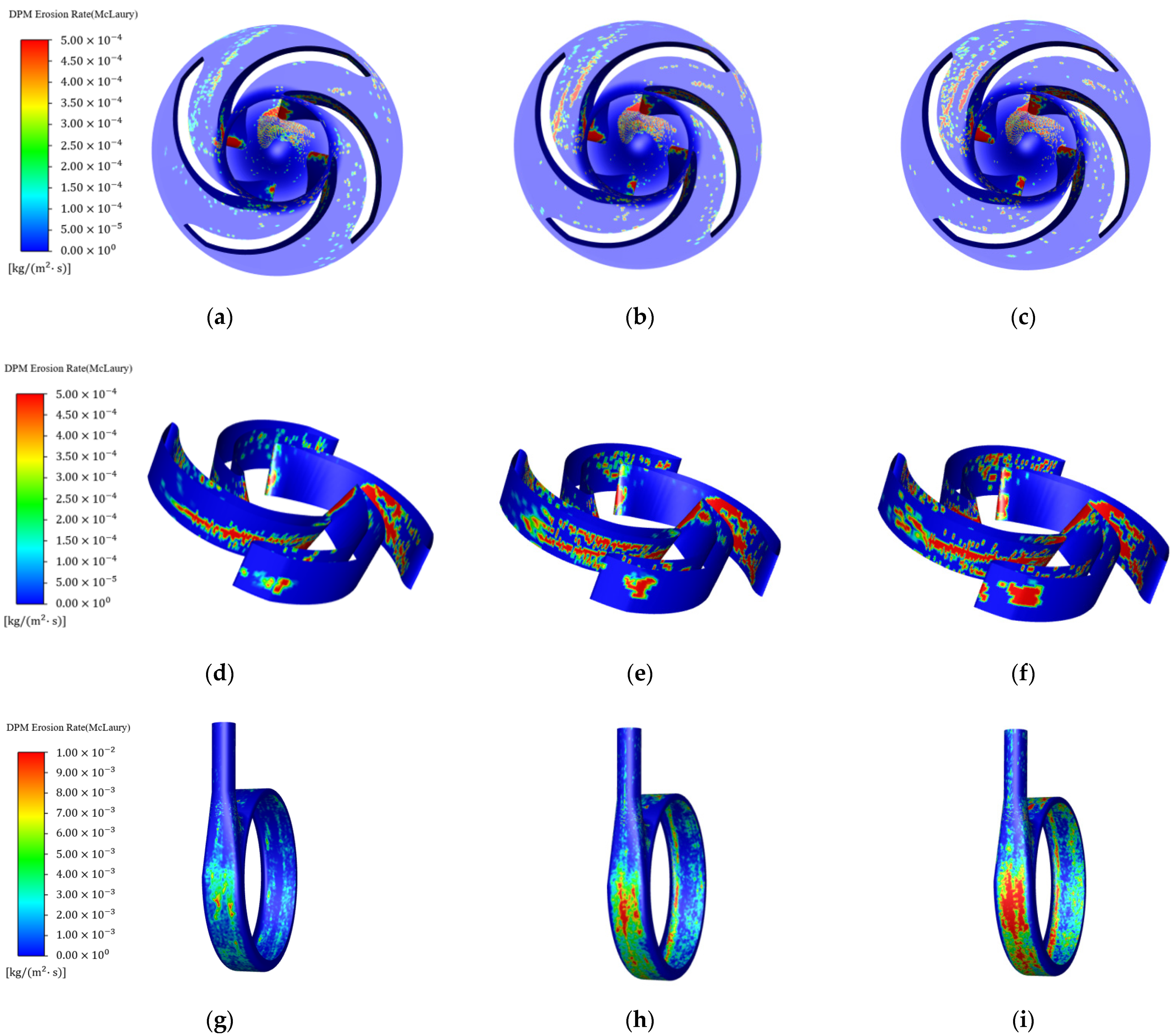
4.2.1. Effects of Volume Flow Rates
4.2.2. Effects of Particle Diameters
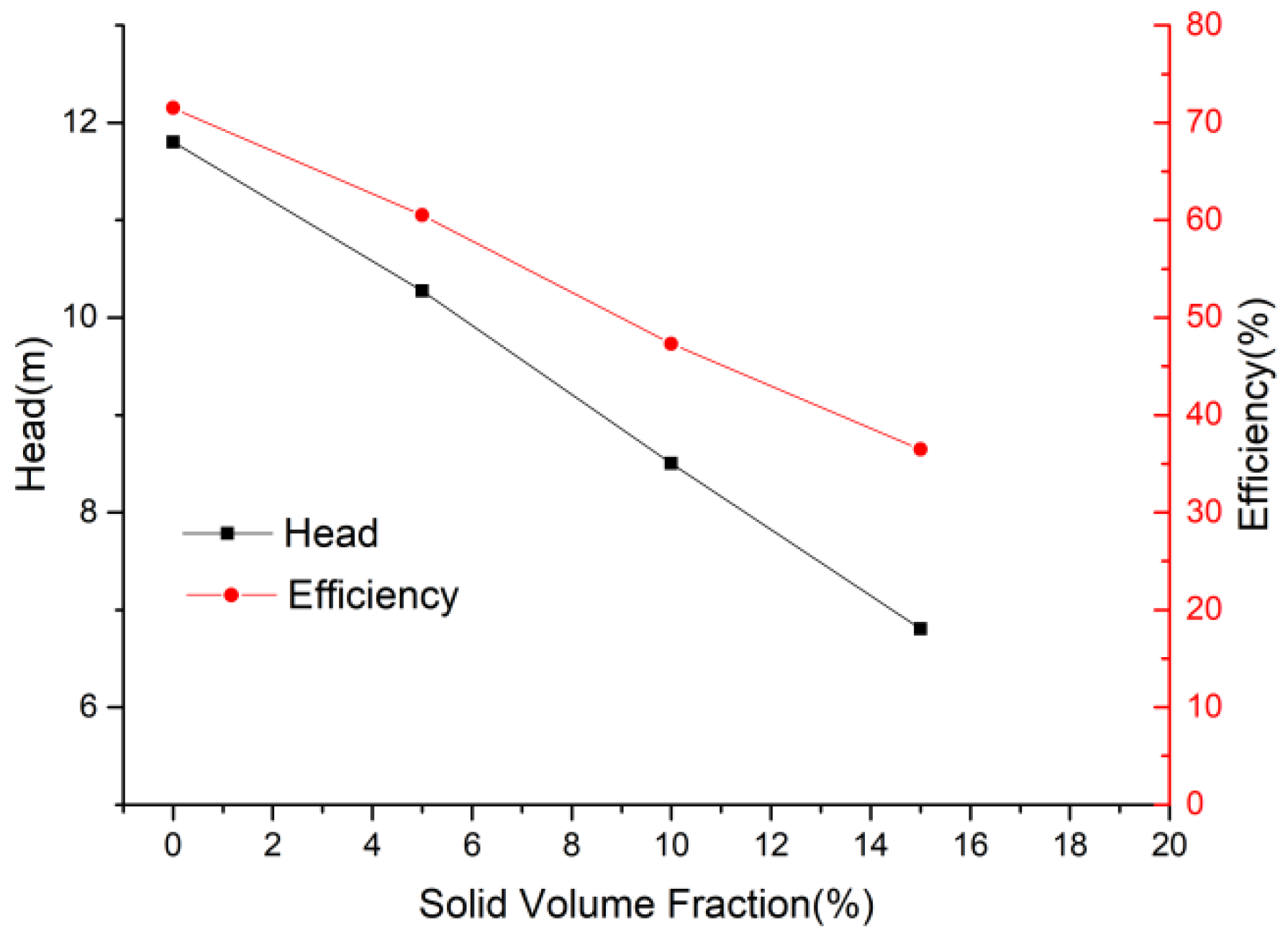
4.2.3. Effects of Solid Volume Fraction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roco, M.C.; Addie, G.R.; Visintainer, R. Study on Casing Performances in Centrifugal Slurry Pumps. Part. Sci. Technol. 1985, 3, 65–88. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Yuan, X.; Zhang, G. Influence of mixed sand on wear of centrifugal pump with semi-open impeller. J. Drain. Irrig. Mach. Eng. 2021, 39, 764–769. [Google Scholar]
- Miedema, S.A. A head loss model for slurry transport in the heterogeneous regime. Ocean Eng. 2015, 106, 360–370. [Google Scholar] [CrossRef]
- Ramirez, R.; Avila, E.; Lopez, L.; Bula, A.; Duarte Forero, J. CFD characterization and optimization of the cavitation phenomenon in dredging centrifugal pumps. Alex. Eng. J. 2020, 59, 291–309. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Gao, R.; Zheng, J.; Chen, J. Particle movement and blade erosion of diagonal flow pump for deep-sea mining. J. Drain. Irrig. Mach. Eng. 2020, 38, 1215–1220. [Google Scholar]
- Ziejewski, M.; Stanislao, J. A Study on New Centrifugal Pump for Slurries. SAE Trans. 1989, 98, 401–407. [Google Scholar]
- Williams, R.A. Slurry transport using centrifugal pumps. Powder Technol. 1997, 94, 187. [Google Scholar] [CrossRef]
- Bross, S.; Addie, G. Prediction of impeller nose wear behaviour in centrifugal slurry pumps. Exp. Therm. Fluid Sci. 2002, 26, 841–849. [Google Scholar] [CrossRef]
- El-Emam, M.A.; Zhou, L. Theories and applications of CFD–DEM coupling approach for granular flow: A review. Arch. Comput. Methods Eng. 2021, 28, 4979–5020. [Google Scholar] [CrossRef]
- Zhou, L.; Han, C.; Bai, L.; Li, W.; El-Emam, M.A.; Shi, W. CFD-DEM bidirectional coupling simulation and experimental investigation of particle ejections and energy conversion in a spouted bed. Energy 2020, 211, 118672. [Google Scholar] [CrossRef]
- Fan, A.; Long, J. Failure analysis of the impeller of a slurry pump subjected to corrosive wear. Wear 1995, 181, 876–882. [Google Scholar]
- Gandhi, B.K.; Singh, S.N. Variation of wear along the volute casing of a centrifugal slurry pump. JSME Int. J. Ser. B-Fluids Therm. Eng. 2001, 44, 231–2370. [Google Scholar] [CrossRef] [Green Version]
- Kadambi, J.R.; Mehta, M. Particulate Velocity Measurements in the Intra-Blade Passages of a Centrifugal Slurry Pump. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003. [Google Scholar]
- Khalid, Y.A.; Sapuan, S.M. Wear analysis of centrifugal slurry pump impellers. Ind. Lubr. Tribol. 2007, 59, 18–28. [Google Scholar] [CrossRef]
- Madadnia, J.; Amjad, M. Analysis of Severe Erosion in Industrial Centrifugal Slurry Pumps. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Incline Village, NV, USA, 7–11 July 2013. [Google Scholar]
- Liao, J.; Lai, X.D. Numerical Analysis of Internal Flow in Centrifugal Pump based on Solid-liquid Two-phase Modeling. J. Eng. Therm. Energy Power 2017, 32, 95–99. [Google Scholar]
- Liu, J.R.; Xu, Y.G. Analysis of Liquid-Solid Two-Phase Turbulent Flow in FGD System Pump. In Proceedings of the 10th IEEE International Conference on Computer-Aided Industrial Design and Conceptual De-sign, Wenzhou, China, 26–29 November 2009. [Google Scholar]
- Wang, P.W.; Zhao, J. Experimental study and numerical simulation of the solid-phase particles’ influence on outside characteristics of slurry pump. In Proceedings of the 26th IAHR Symposium on Hydraulic Machinery and Systems, Tsinghua University, Beijing, China, 19–23 August 2012. [Google Scholar]
- Wadnerkar, D.; Utikar, R.P. CFD simulation of solid-liquid stirred tanks. Adv. Power Technol. 2012, 23, 445–453. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Li, Y. Numerical Simulation and Analysis of Solid-liquid Two-phase Flow in Centrifugal Pump. Chin. J. Mech. Eng. 2013, 26, 53–60. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- McLaury, B.S. A Model to Predict Solid Particle Erosion in Oilfield Geometries. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 1993. [Google Scholar]
- McLaury, B.S.; Shirazi, S.A. An Alternate Method to API RP 14E for Predicting Solids Erosion in Multiphase Flow. J. Energy Resour. Technol. 2000, 122, 115–122. [Google Scholar] [CrossRef]
- Chen, X. Application of Computational Fluid Dynamics (CFD) to Flow Simulation and Erosion Prediction in Single-Phase and Multiphase Flow. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2004. [Google Scholar]
- Pagalthivarthi, K.V.; Gupta, P.K. CFD Prediction of Erosion Wear in Centrifugal Slurry Pumps for Dilute Slurry Flows. J. Comput. Multiph. Flows 2011, 3, 225–246. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhu, Z.C. Abrasion characteristic analyses of solid-liquid two-phase centrifugal pump. J. Therm. Sci. 2011, 20, 283–287. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M.-H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364, 103–111. [Google Scholar] [CrossRef]
- Shen, Z.J.; Li, R.N.; Han, W.; Zhao, W.G.; Wang, X.H. The research on particle trajectory of solid-liquid two-phase flow and erosion predicting in screw centrifugal pump. In Proceedings of the 7th International Conference on Pumps and Fans (ICPF2015), Hangzhou, China, 18–21 October 2015. [Google Scholar]
- Shen, Z.J.; Chu, W.L. Sediment erosion in the impeller of a double-suction centrifugal pump—A case study of the Jingtai Yellow River Irrigation Project, China. Wear 2019, 422, 269–279. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, J.; Zhu, J.; Rutter, R.; Zhang, H. A Numerical Study of Turbulence Model and Rebound Model Effect on Erosion Simulations in an Electrical Submersible Pump (ESP). In Proceedings of the ASME-JSME-KSME 2019 8th Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Zhu, H.; Zhu, J.; Rutter, R.; Zhang, H.-Q. A Numerical Study on Erosion Model Selection and Effect of Pump Type and Sand Characters in Electrical Submersible Pumps by Sandy Flow. J. Energy Resour. Technol.-Trans. ASME 2019, 141, 122004. [Google Scholar] [CrossRef]
- Jiang, Z.; Zeng, X.; Li, Y. Study on the Relationship between Wear and Flow Characteristics of a Centrifugal Pump at Different Mass Concentrations. Processes 2021, 9, 988. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, L.; Bai, L.; Shi, W.; Agarwal, R. Comparison and validation of various turbulence models for U-bend flow with a magnetic resonance velocimetry experiment. Phys Fluids 2021, 33, 125117. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Model of Turbulence; Academic Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow—Corrigendum. J. Fluid Mech. 1968, 31, 624. [Google Scholar] [CrossRef]
- Li, A.; Ahmadi, G. Dispersion and Deposition of Spherical Particles from Point Sources in a Turbulent Channel Flow. Aerosol Sci. Technol. 1992, 16, 209–226. [Google Scholar] [CrossRef]
- McLaury, B.S.; Shirazi, S.A. Effect of entrance shape on erosion in the throat of chokes. J. Energy Resour. Technol.-Trans. ASME 2000, 122, 198–204. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Gupta, P.K. Prediction of Erosion Wear in Multi-Size Particulate Flow through a Rotating Channel. FDMP-Fluid Dyn. Mater. Process. 2009, 5, 93–122. [Google Scholar]
- Peng, G.; Chen, Q.; Bai, L.; Hu, Z.; Zhou, L.; Huang, X. Wear mechanism investigation in a centrifugal slurry pump impeller by numerical simulation and experiments. Eng. Fail. Anal. 2021, 128, 105637. [Google Scholar] [CrossRef]
- Peng, G.; Huang, X.; Zhou, L.; Zhou, G.; Zhou, H. Solid-liquid two-phase flow and wear analysis in a large-scale centrifugal slurry pump. Eng. Fail. Anal. 2020, 114, 104602. [Google Scholar] [CrossRef]
- International Organization for Standardization. Rotodynamic Pumps—Hydraulic Performance Acceptance Tests—Grades 1, 2 and 3; ISO 99062012; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- El-Emam, M.; Zhou, L.; Shi, W.; Han, C. Performance evaluation of standard cyclone separators by using CFD–DEM simulation with realistic bio-particulate matter. Powder Technol. 2021, 385, 357–374. [Google Scholar] [CrossRef]




| Design Parameters | Value |
|---|---|
| Rotating Speed | 1500 r/min |
| Design Volume Flow Rate | 26 m3/h |
| Design Head | 11 m |
| Inlet Diameter | 75 mm |
| Number of Blades | 4 |
| Impeller Outer Diameter | 178 mm |
| Impeller Outlet Width | 30 mm |
| Number of Elements | Head/m | Efficiency/% |
|---|---|---|
| 369,713 | 12.45 | 74.43 |
| 921,493 | 12.18 | 73.24 |
| 1,565,848 | 11.95 | 72.12 |
| 3,146,214 | 11.76 | 71.27 |
| 4,041,363 | 11.78 | 71.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Bai, L.; Xue, P.; Peng, G.; Zhou, L. Two-Way Coupling Simulation of Solid-Liquid Two-Phase Flow and Wear Experiments in a Slurry Pump. J. Mar. Sci. Eng. 2022, 10, 57. https://doi.org/10.3390/jmse10010057
Jiang L, Bai L, Xue P, Peng G, Zhou L. Two-Way Coupling Simulation of Solid-Liquid Two-Phase Flow and Wear Experiments in a Slurry Pump. Journal of Marine Science and Engineering. 2022; 10(1):57. https://doi.org/10.3390/jmse10010057
Chicago/Turabian StyleJiang, Lei, Ling Bai, Peng Xue, Guangjie Peng, and Ling Zhou. 2022. "Two-Way Coupling Simulation of Solid-Liquid Two-Phase Flow and Wear Experiments in a Slurry Pump" Journal of Marine Science and Engineering 10, no. 1: 57. https://doi.org/10.3390/jmse10010057
APA StyleJiang, L., Bai, L., Xue, P., Peng, G., & Zhou, L. (2022). Two-Way Coupling Simulation of Solid-Liquid Two-Phase Flow and Wear Experiments in a Slurry Pump. Journal of Marine Science and Engineering, 10(1), 57. https://doi.org/10.3390/jmse10010057







