Consequence Analysis of Accidental LNG Release on the Collided Structure of 500 cbm LNG Bunkering Ship
Abstract
:1. Introduction
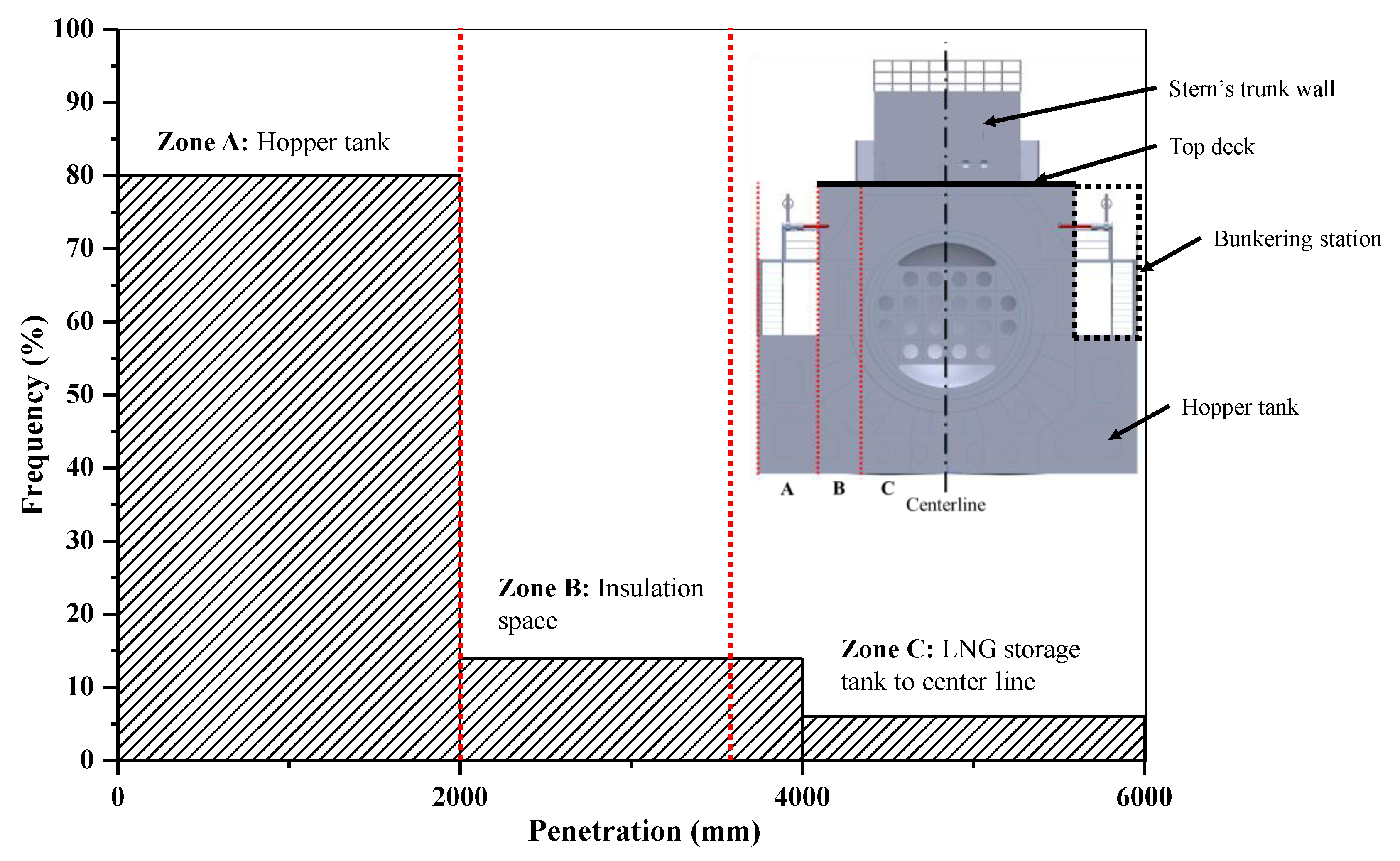
2. Determination of Leakage Scenario
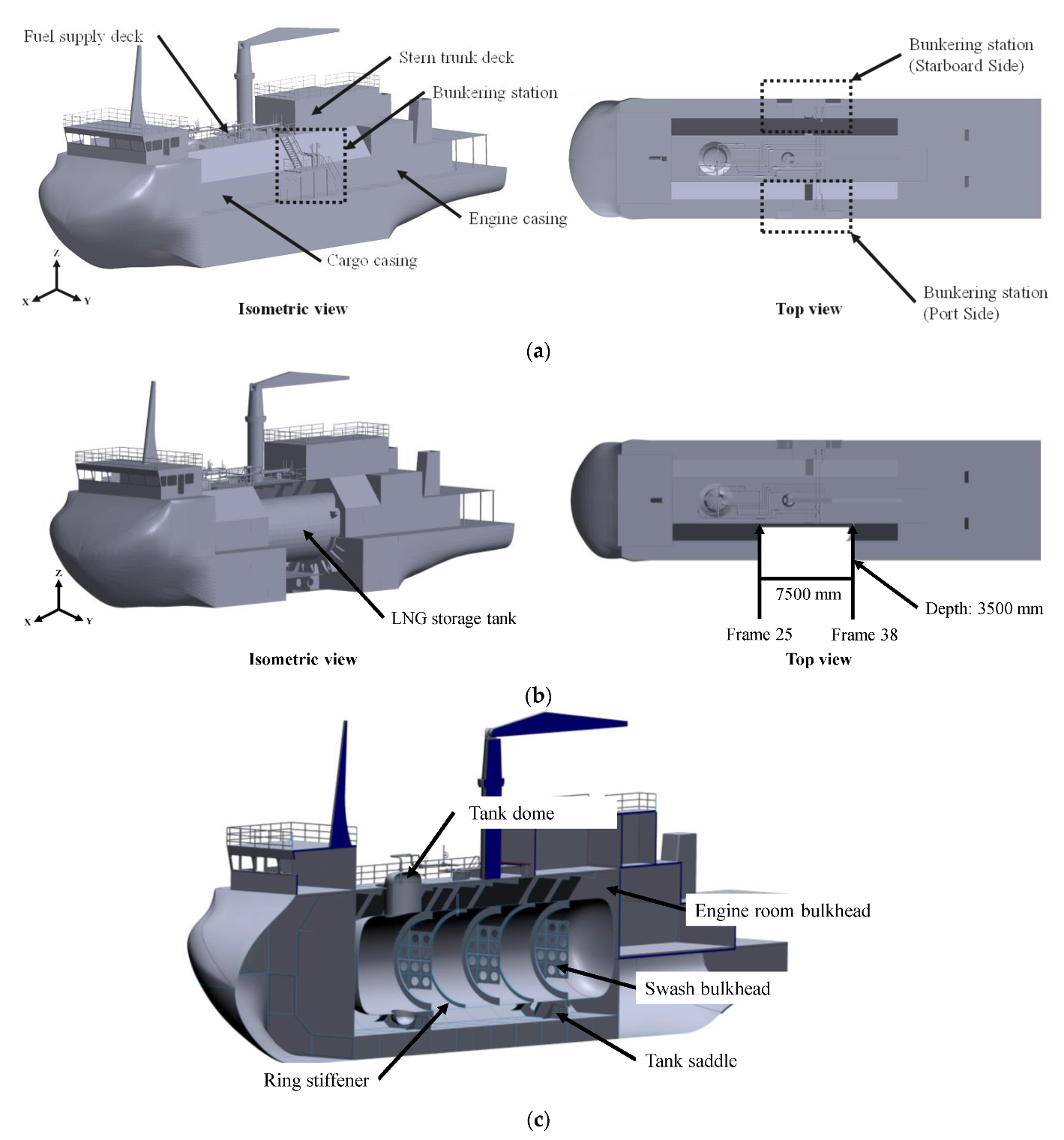
2.1. Intact and Damaged Geometries of the Ship
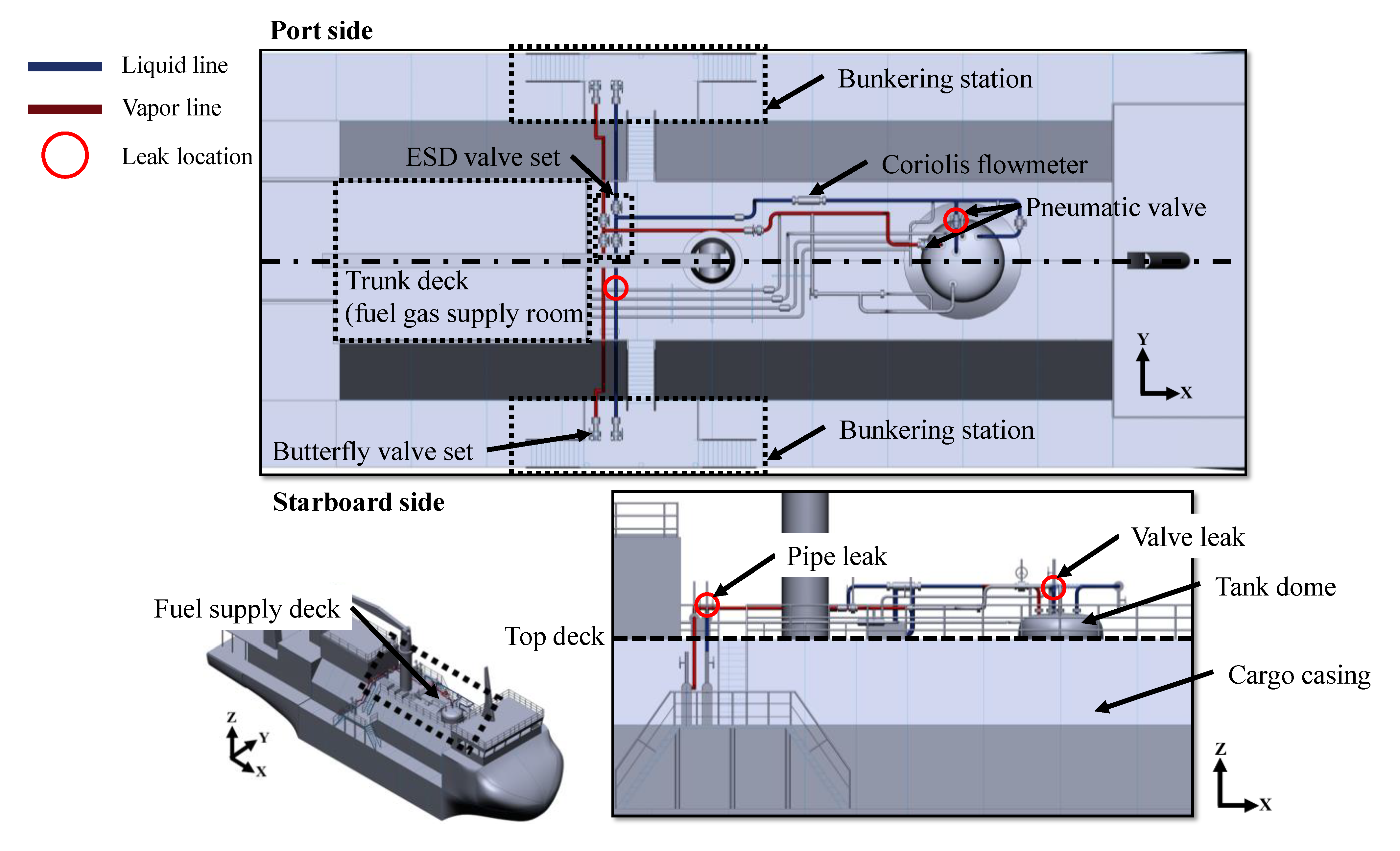
2.2. Leakage Parameter
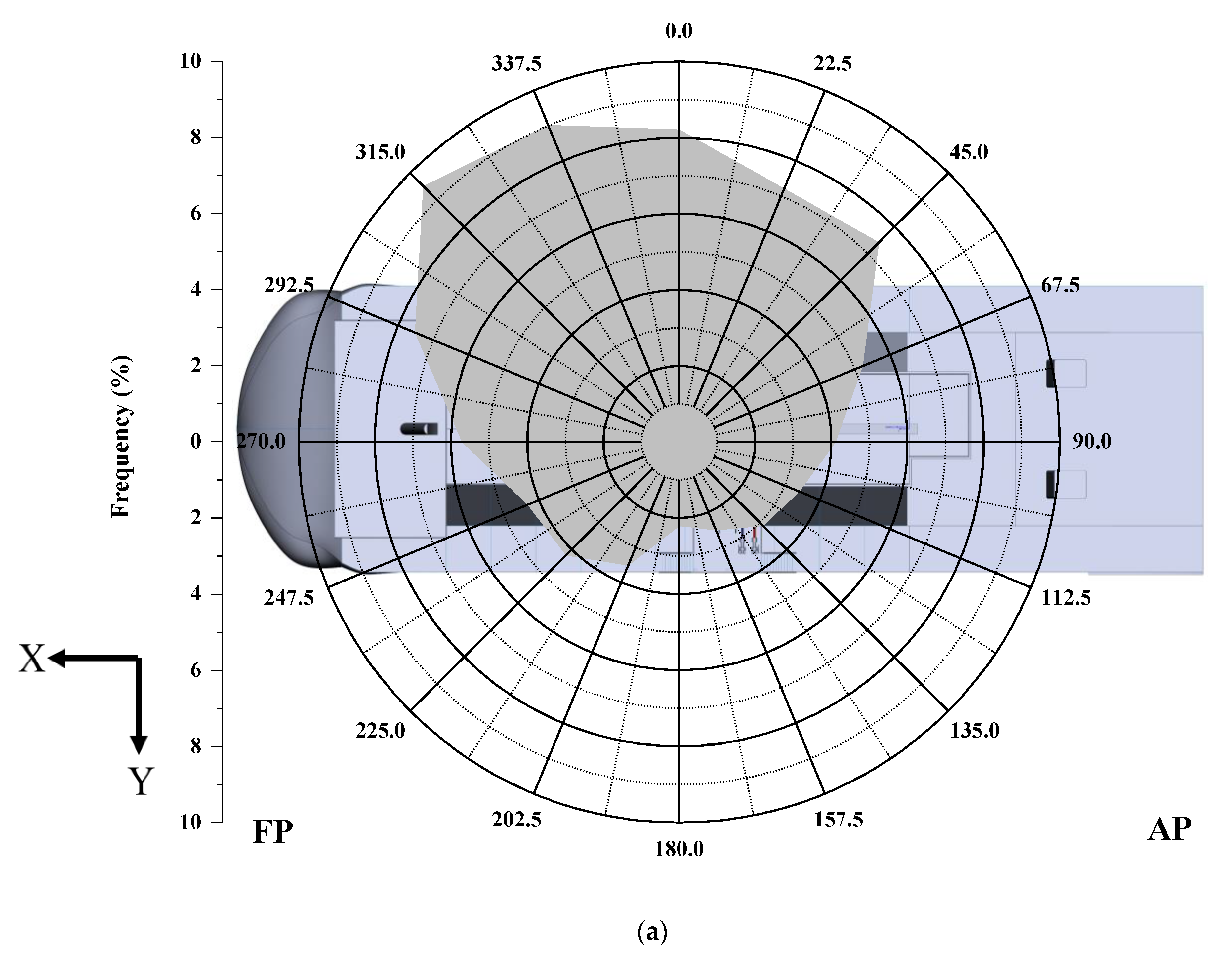
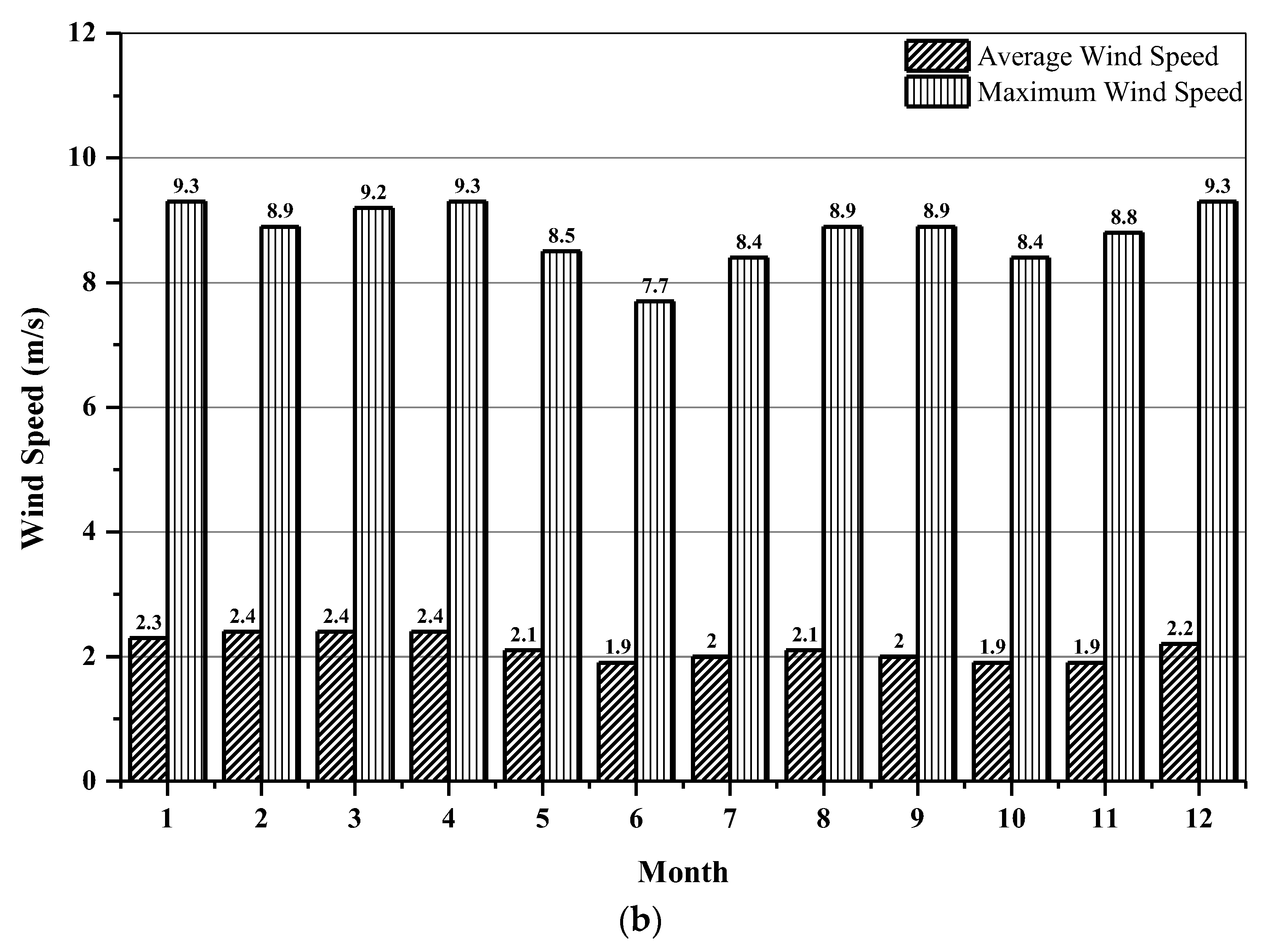
2.3. Environmental Parameters
2.4. LNG Leakage Scenario
3. Technical Reference of KFX
3.1. The Standard k-ε Turbulence Model
| Terrain Classification | z0 (m) |
|---|---|
| Open sea | 0.0002 |
| Mudflats, snow; no vegetation, no obstacles | 0.005 |
| Open flat terrain; grass, few isolated obstacles | 0.03 |
| Low crops; occasional large obstacles, x/H > 20 | 0.1 |
| High crops; scattered obstacles, 15 < x/H < 20 | 0.25 |
| Parkland, bushes; numerous obstacles, x/H= 10 | 0.5 |
| Regular large obstacle coverage (suburb, forest) | 1 |
| The city center with high- and low-rise buildings | >2 |
| x: typical upwind obstacle distance H: height of the corresponding major obstacle | |
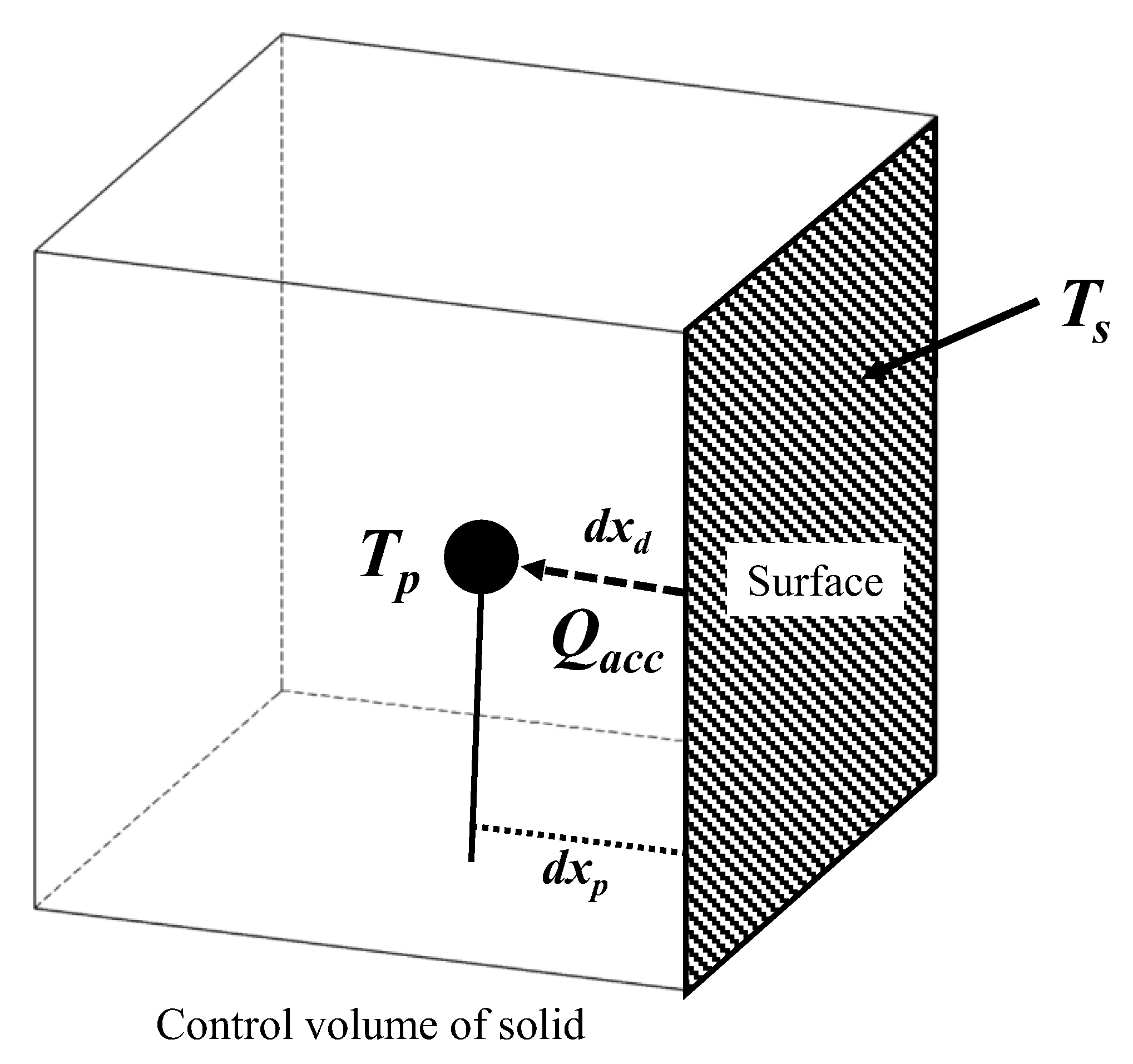
3.2. Heat Transfer
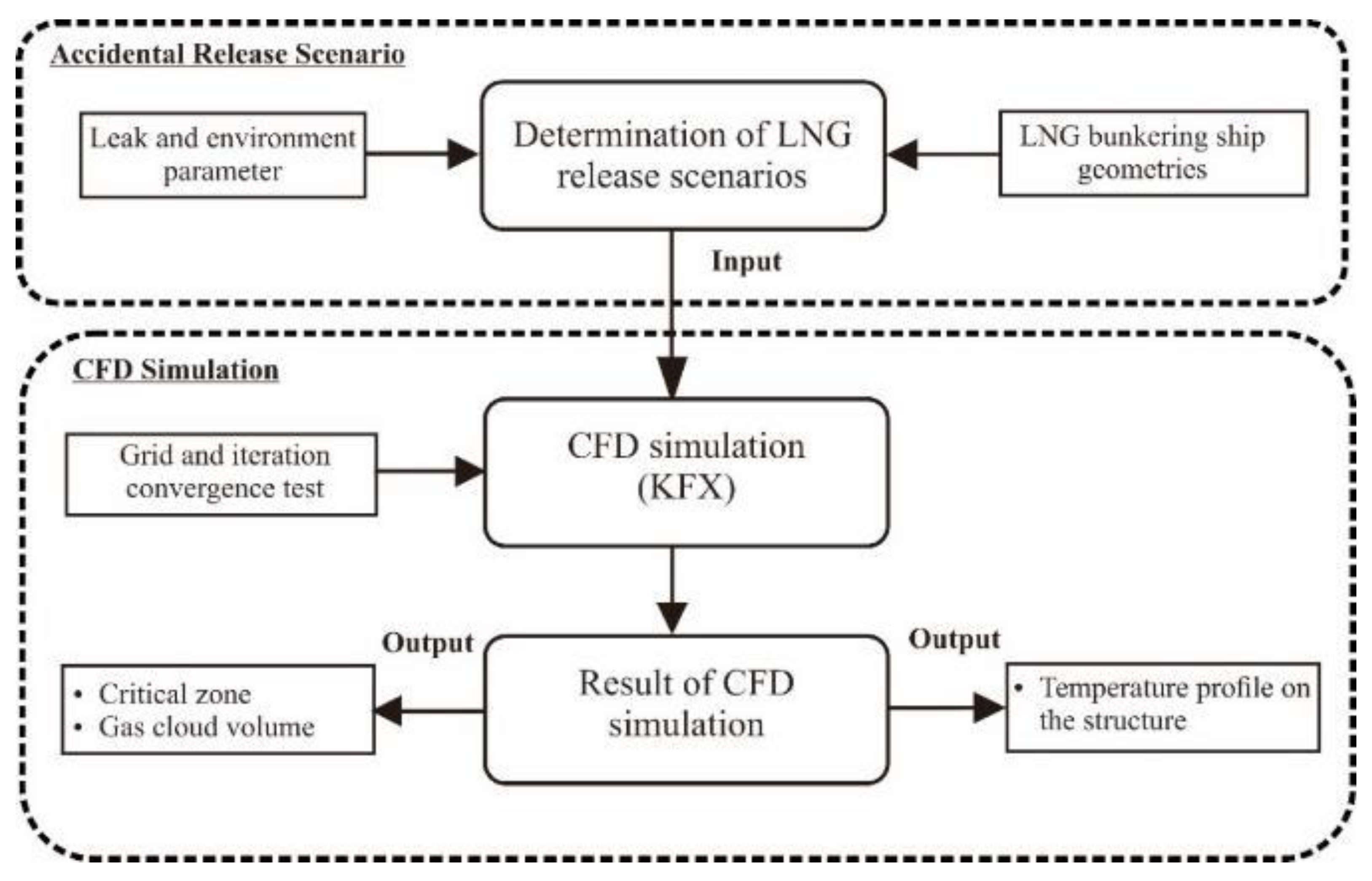
4. Procedure for CFD Analysis
4.1. KFX Validation
4.2. Grid and Iteration Convergence Tests
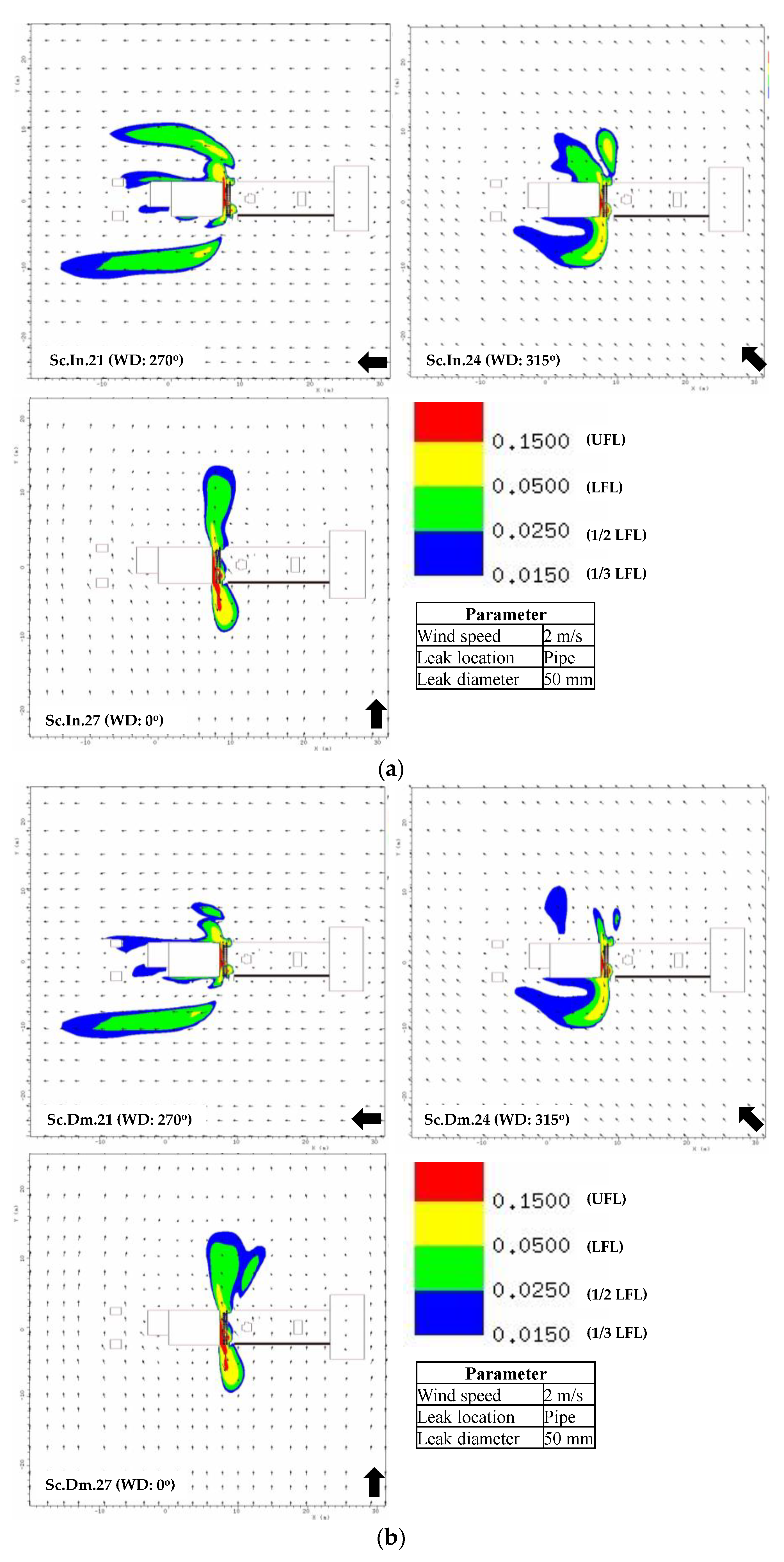
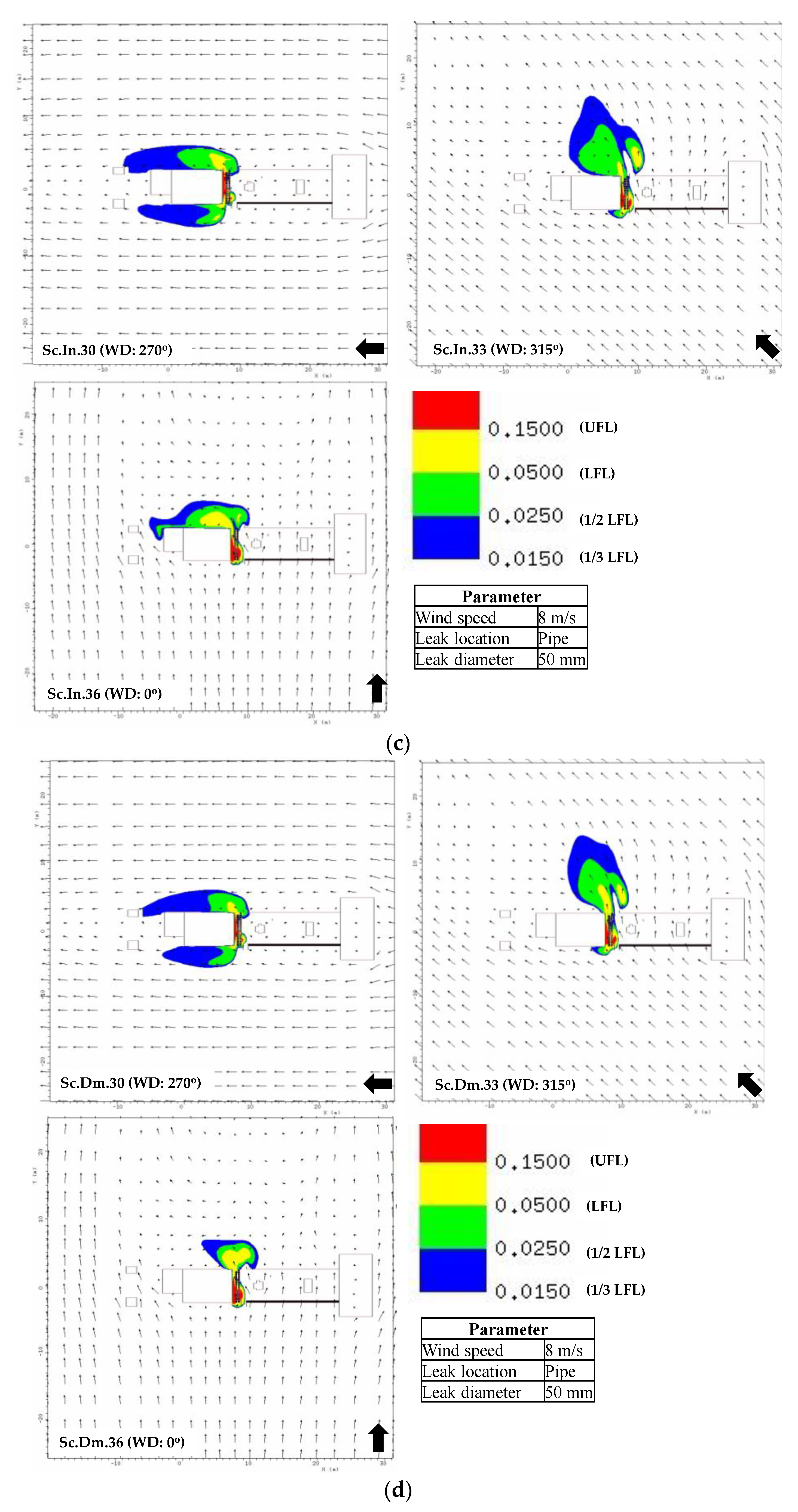
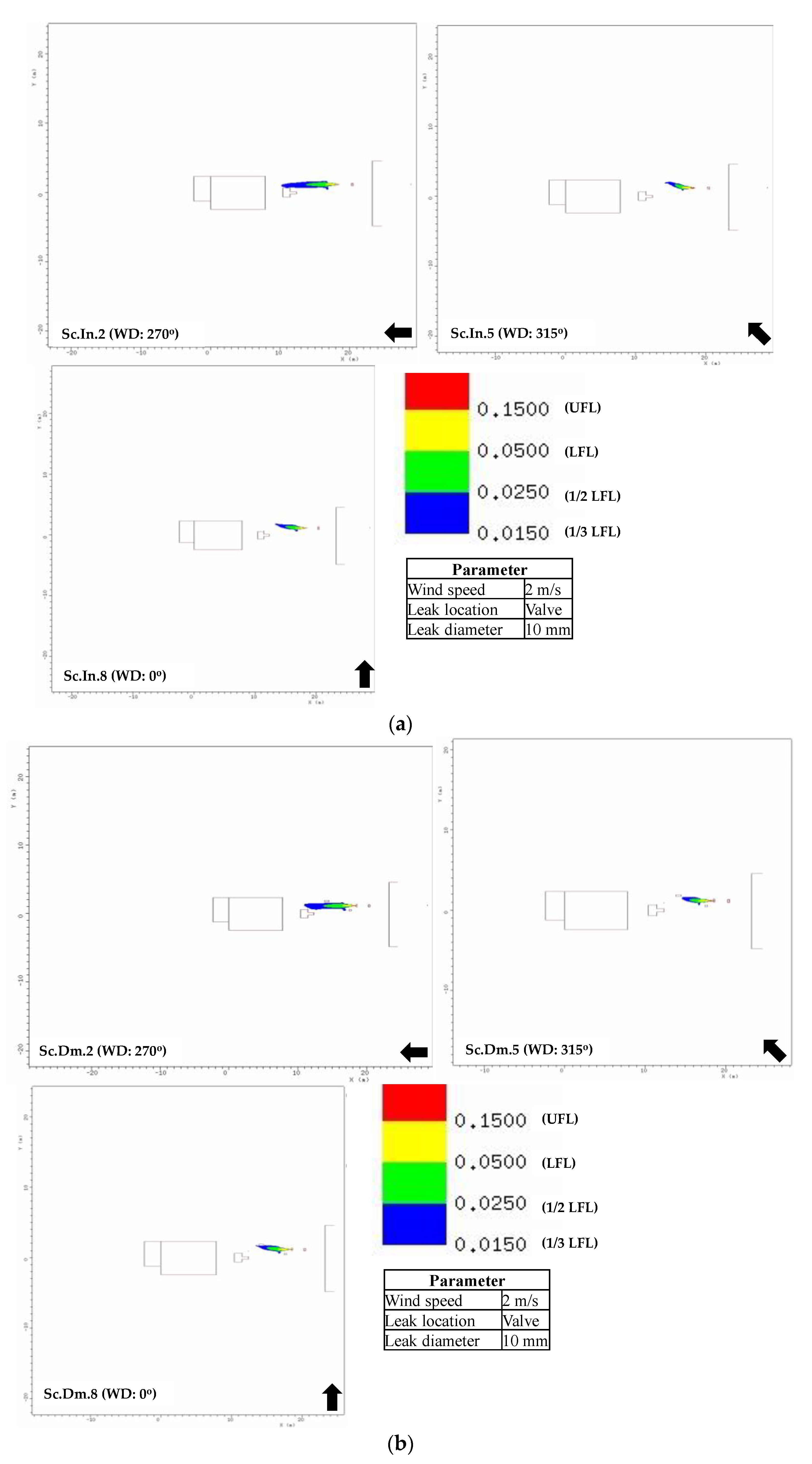
5. Parametric Study on Intact and Damaged Geometries
5.1. Gas Dispersion
5.2. Temperature Reduction
6. Conclusions
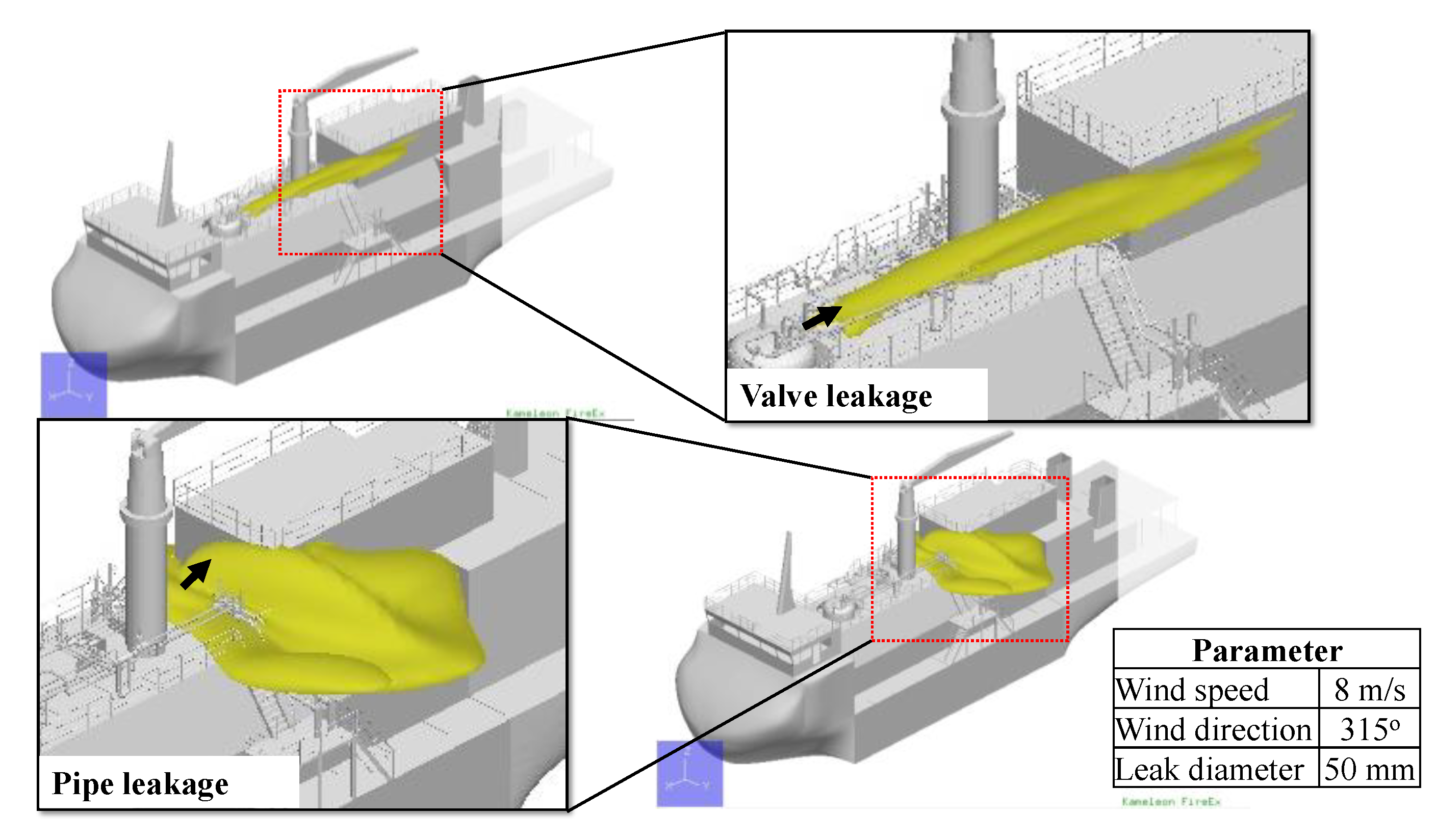
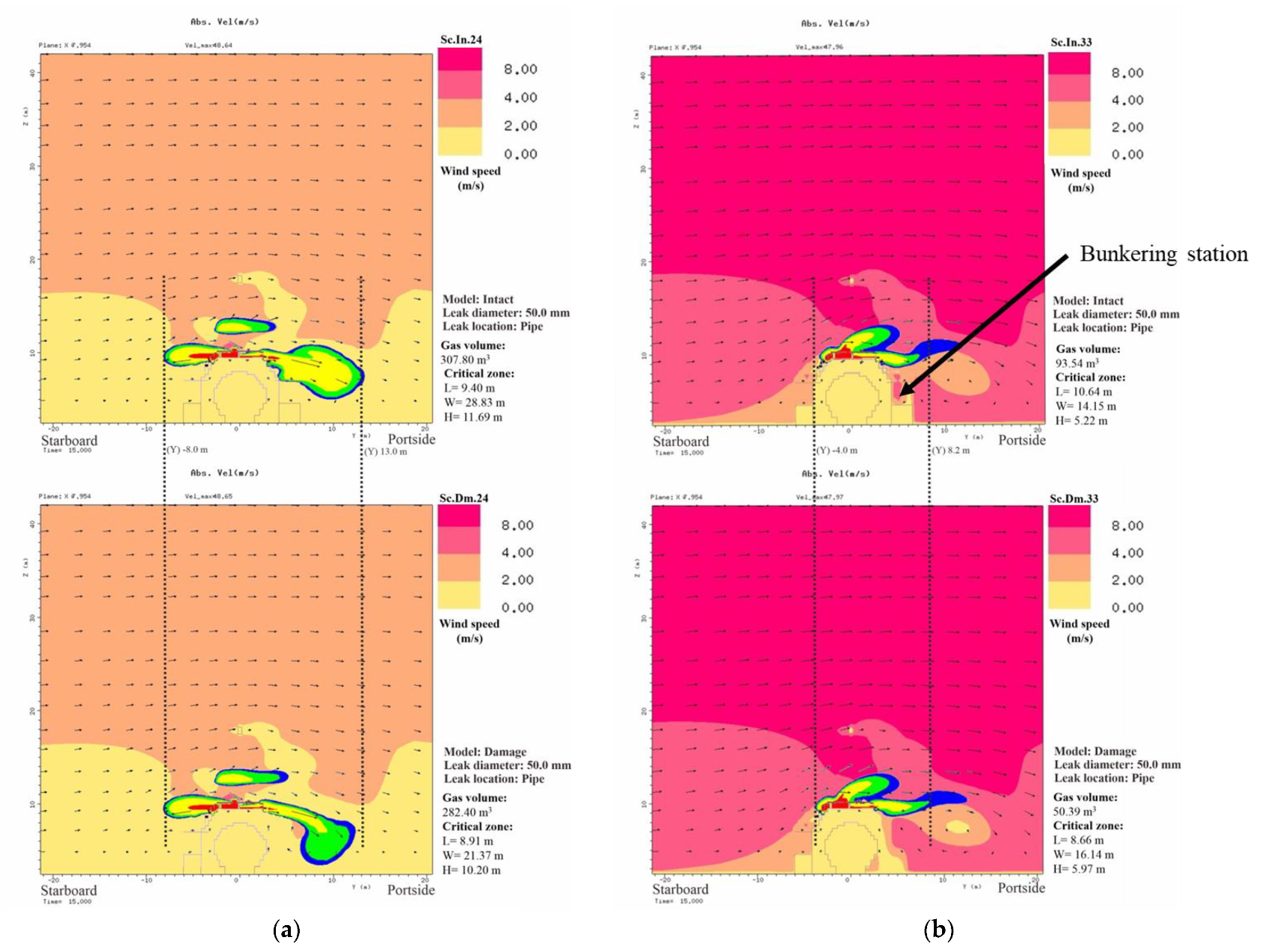
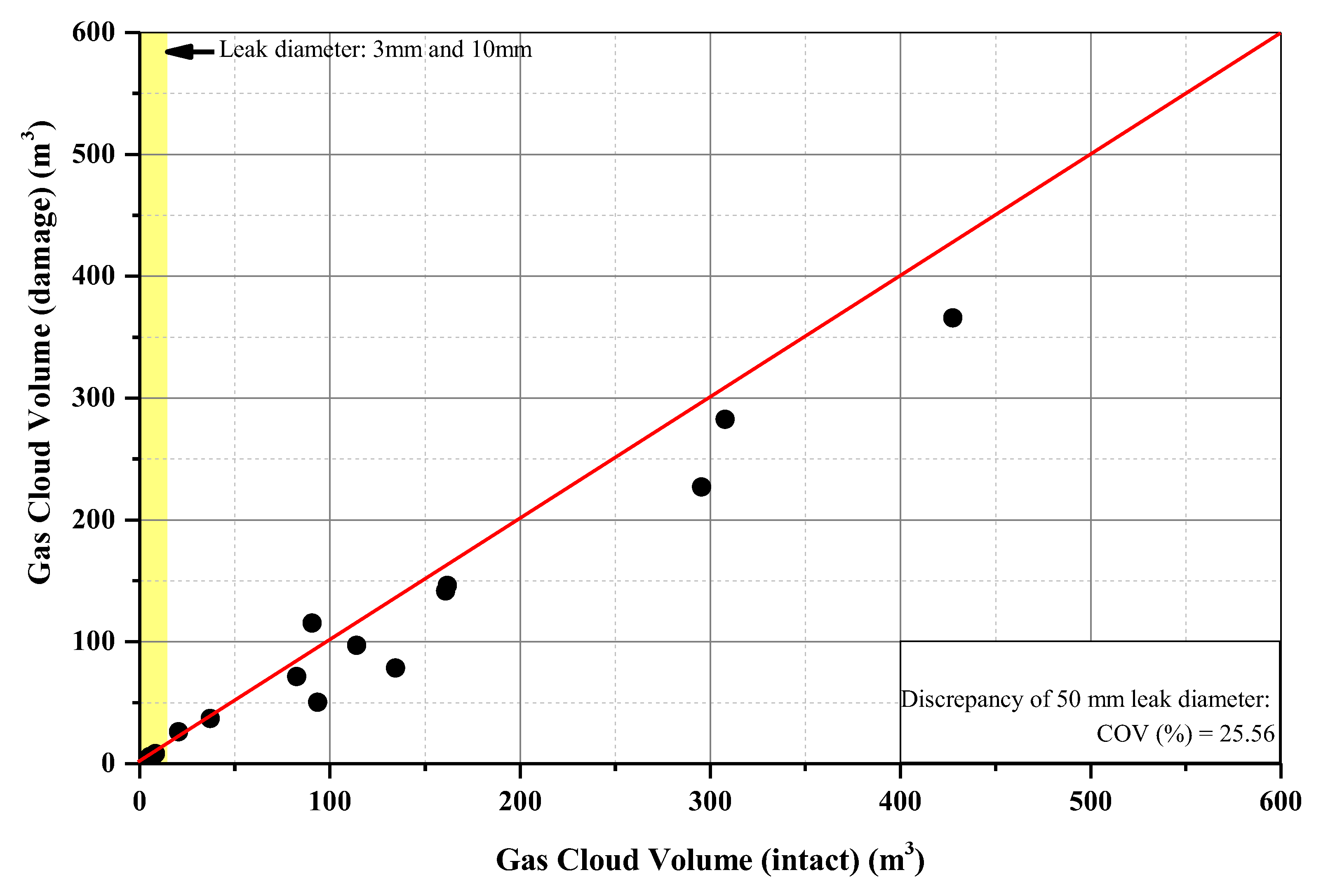
- The gas dispersion characteristics are inferred from the gas cloud volume and its shape. The wind and obstructions exert the main influence on the formation of the gas cloud. The CFD result shows that the leakage in the pipe involves a large accumulation of gas due to its position near an obstacle that causes the released gas to be re-entrained into the release path. For leakage in the valve, the gas cloud can be easily dissipated and mixed with the air since there is no significant obstacle to disturb its release path.
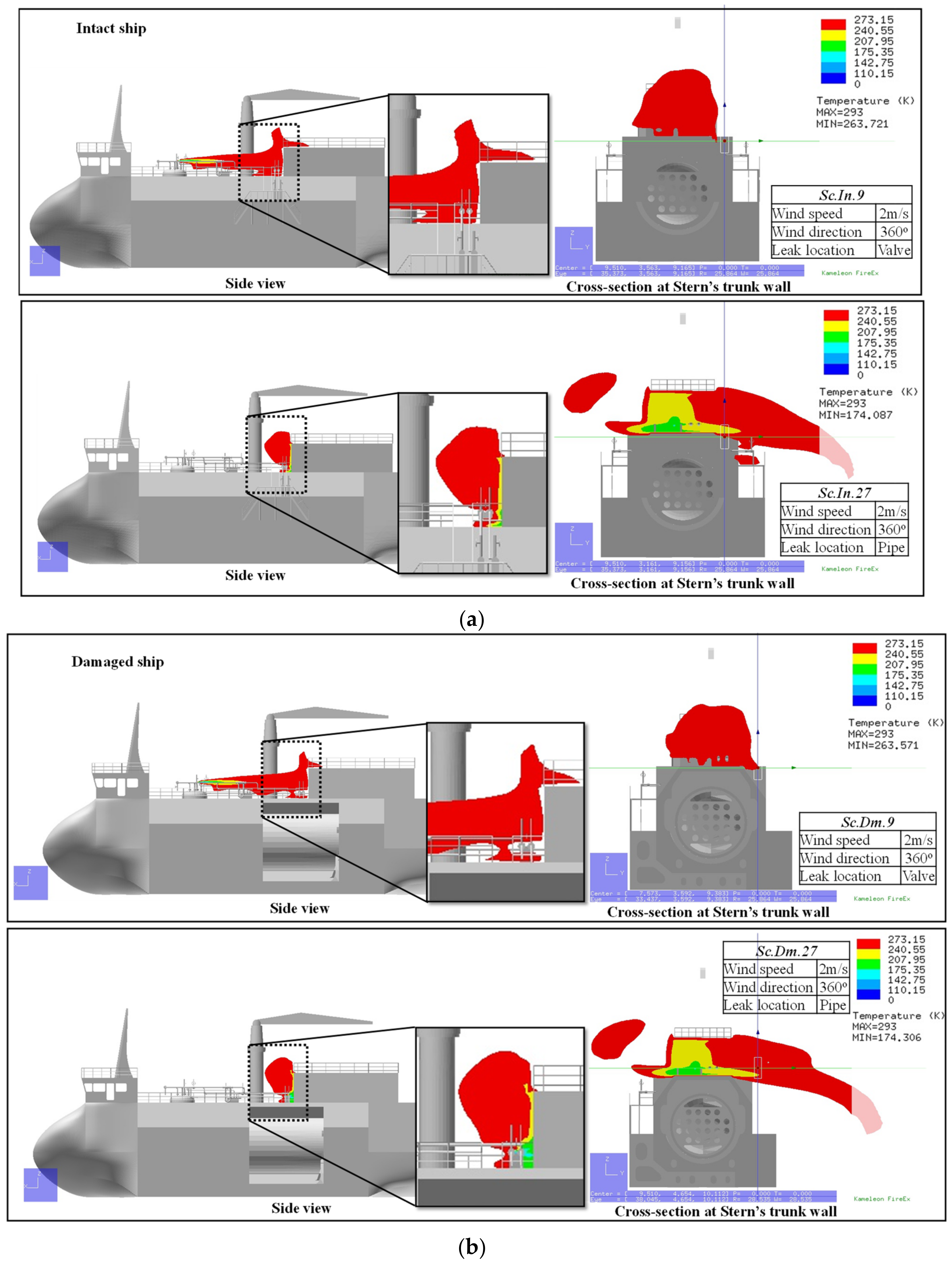
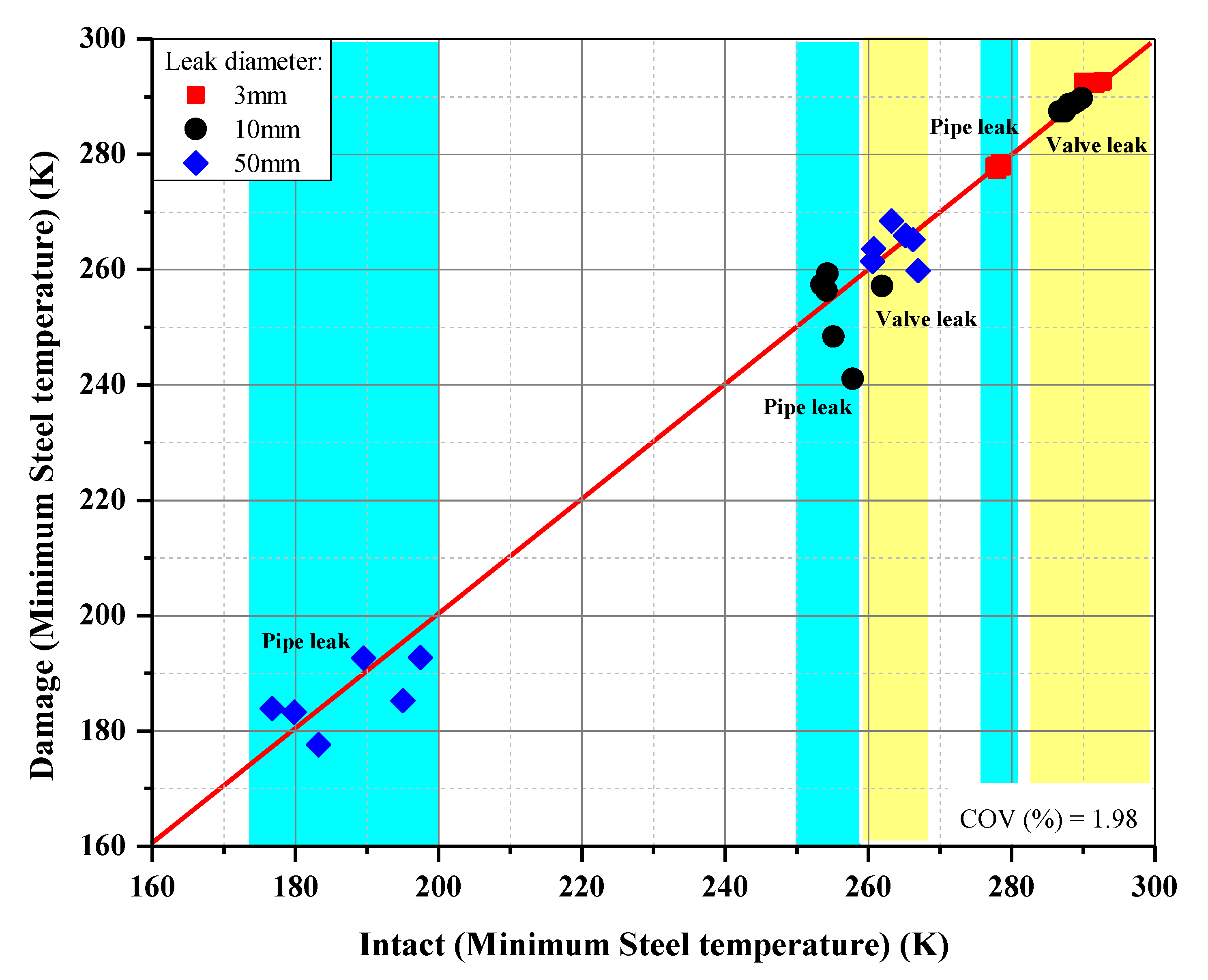
- The steel temperature reduces significantly in the stern trunk wall as a result of leakages from the pipe. The cold gas exposes this section due to the leak point adjacent to the stern trunk wall. For leakages from the valve, the cold gas was already expanded when it reached the stern trunk wall. Thus, the temperature reduction in this case was minor. Overall, the cold gas did not reach the broken part of the damaged ship, which was inside the cargo hold. As a result, there was no major difference in the cooling effect between the intact and damaged ships.
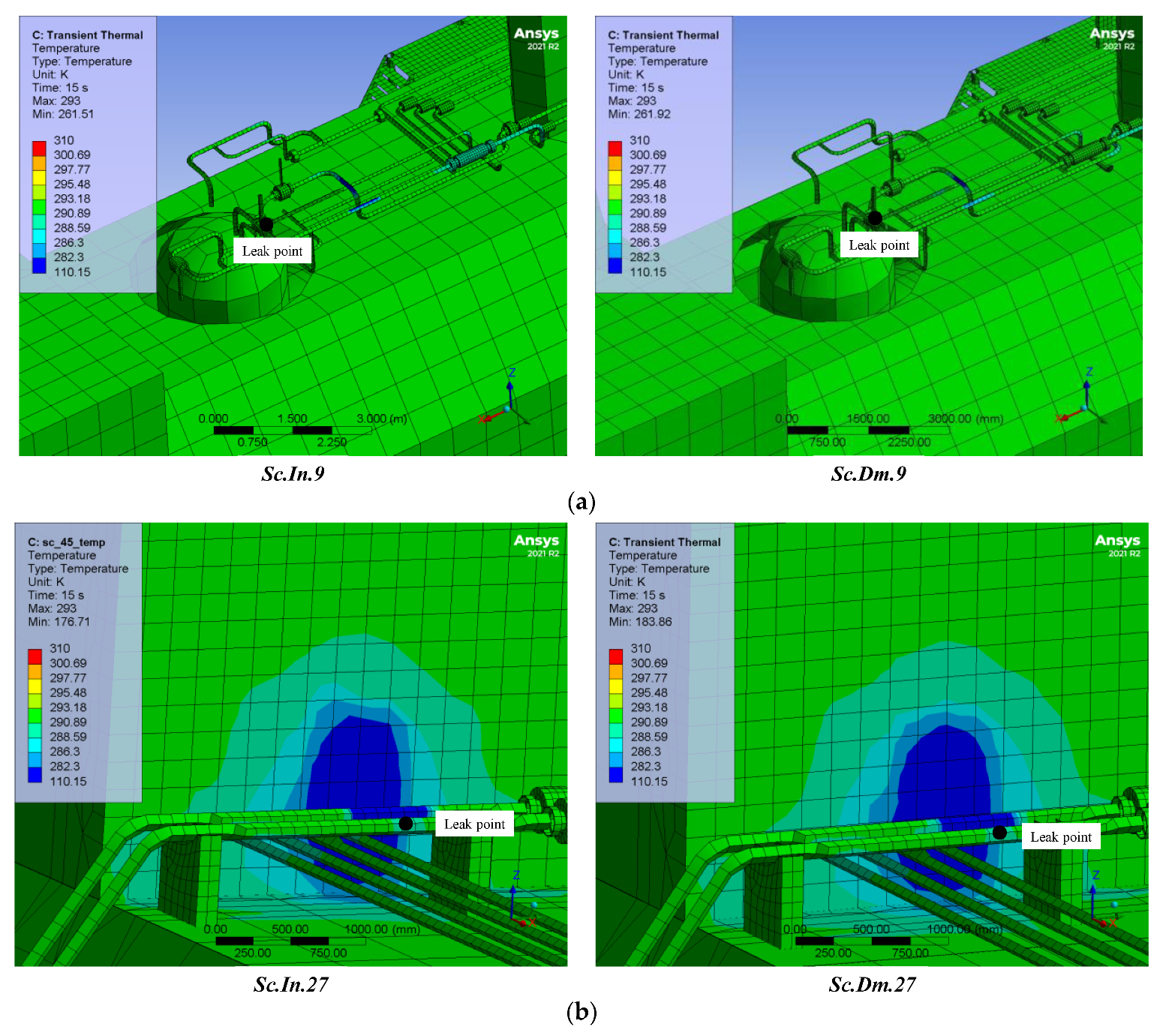
- A profile of steel temperature was retrieved from KFX to ANSYS/LS-DYNA. The temperature reduction was significant for the leakages from the pipe, and was typically below 200 K for a 50 mm leak diameter. Since the cold gas was built adjacent to the leak point, it had no noticeable impact on the ship’s structure for 3 and 10 mm leak diameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Maritime Organization. Resolution MEPC.203(62)—Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships, 1973, as Modified by the Protocol of 1978 Relating Thereto (Inclusion of Regulations on Energy Effi). 2011. Available online: https://wwwcdn.imo.org/localresources/en/OurWork/Environment/Documents/Technical%20and%20Operational%20Measures/Resolution%20MEPC.203%2862%29.pdf (accessed on 20 September 2022).
- Martinsen, K. Alternative Fuels Insight. Available online: https://www.dnv.com/services/alternative-fuels-insight-128171 (accessed on 20 September 2022).
- Le Fevre, C. A Review of Demand Prospects for LNG as a Marine Transport Fuel; The Oxford Institute for Energy Studies: Oxford, UK, 2018; ISBN 9781784671143. [Google Scholar]
- Park, N.K.; Park, S.K. A Study on the Estimation of Facilities in LNG Bunkering Terminal by Simulation—Busan Port Case. J. Mar. Sci. Eng. 2019, 7, 354. [Google Scholar] [CrossRef]
- Tam, J.H. Overview of Performing Shore-to-Ship and Ship-to-Ship Compatibility Studies for LNG Bunker Vessels. J. Mar. Eng. Technol. 2020, 21, 257–270. [Google Scholar] [CrossRef]
- Park, S.; Jeong, B.; Yoon, J.Y.; Paik, J.K. A Study on Factors Affecting the Safety Zone in Ship-to-Ship LNG Bunkering. Ships Offshore Struct. 2018, 13, 312–321. [Google Scholar] [CrossRef]
- Maritime Safety Agency (EMSA). Guidance on LNG Bunkering to Port Authorities and Administrations; EMSA: Lisbon, Portugal, 2018.
- Ahn, J.; Choi, Y.; Jo, C.; Cho, Y.; Chang, D.; Chung, H.; Bergan, P.G. Design of a Prismatic Pressure Vessel with Internal X-Beam Structures for Application in Ships. Ships Offshore Struct. 2017, 12, 781–792. [Google Scholar] [CrossRef]
- Kim, J.-W.; Jeong, J.; Chang, D.-J. Optimal Shape and Boil-Off Gas Generation of Fuel Tank for LNG Fueled Tugboat. J. Ocean. Eng. Technol. 2020, 34, 19–25. [Google Scholar] [CrossRef]
- Oh, S.; Jung, D.-W.; Kim, Y.-H.; Kwak, H.-U.; Jung, J.-H.; Jung, S.-J.; Park, B.; Cho, S.-K.; Jung, D.; Sung, H.G. Numerical Study on Characteristics and Control of Heading Angle of Floating LNG Bunkering Terminal for Improvement of Loading and Off-Loading Performance. J. Ocean. Eng. Technol. 2020, 34, 77–88. [Google Scholar] [CrossRef]
- Vanem, E.; Antão, P.; Østvik, I.; de Comas, F.D.C. Analysing the Risk of LNG Carrier Operations. Reliab. Eng. Syst. Saf. 2008, 93, 1328–1344. [Google Scholar] [CrossRef]
- European Commission. EMARS: Electronic Major Accident Report System. Available online: https://emars.jrc.ec.europa.eu/en/emars/content (accessed on 20 September 2022).
- Pujol, J.; Kleiveland, R.N.; Lileheie, N.I.; Holmas, T.; Amdahl, J. Advanced Cryogenic Structural Collapse Analysis CSCA—Part II: Cryogenic Flow and Structural Cooling. In Proceedings of the Offshore Technology Conference Asia, Kuala Lumpur, Malaysia, 22–25 March 2016; OnePetro: Richardson, TX, USA, 2016; pp. 108–115. [Google Scholar] [CrossRef]
- Paik, J.K.; Kim, B.J.; Jeong, J.S.; Kim, S.H.; Jang, Y.S.; Kim, G.S.; Woo, J.H.; Kim, Y.S.; Chun, M.J.; Shin, Y.S.; et al. CFD Simulations of Gas Explosion and Fire Actions. Ships Offshore Struct. 2010, 5, 3–12. [Google Scholar] [CrossRef]
- Jujuly, M.M.; Rahman, M.; Ahmed, S.; Khan, F. LNG Pool Fire Simulation for Domino Effect Analysis. Reliab. Eng. Syst. Saf. 2015, 143, 19–29. [Google Scholar] [CrossRef]
- Fu, S.; Yan, X.; Zhang, D.; Li, C.; Zio, E. Framework for the Quantitative Assessment of the Risk of Leakage from LNG-Fueled Vessels by an Event Tree-CFD. J. Loss Prev. Process Ind. 2016, 43, 42–52. [Google Scholar] [CrossRef]
- Baalisampang, T.; Abbassi, R.; Garaniya, V.; Khan, F.; Dadashzadeh, M. Accidental Release of Liquefied Natural Gas in a Processing Facility: Effect of Equipment Congestion Level on Dispersion Behaviour of the Flammable Vapour. J. Loss Prev. Process Ind. 2019, 61, 237–248. [Google Scholar] [CrossRef]
- Nubli, H.; Sohn, J.M. CFD-Based Simulation of Accidental Fuel Release from LNG-Fuelled Ships. Ships Offshore Struct. 2020, 17, 339–358. [Google Scholar] [CrossRef]
- Nubli, H.; Sohn, J.M. Procedure for Determining Design Accidental Loads in Liquified-Natural-Gas-Fuelled Ships under Explosion Using a Computational-Fluid-Dynamics-Based Simulation Approach. Ships Offshore Struct. 2021, 1–18. [Google Scholar] [CrossRef]
- Nubli, H.; Sohn, J.M.; Prabowo, A.R. Layout Optimization for Safety Evaluation on LNG-Fueled Ship under an Accidental Fuel Release Using Mixed-Integer Nonlinear Programming. Int. J. Nav. Arch. Ocean Eng. 2022, 14, 100443. [Google Scholar] [CrossRef]
- Magnussen, B.F. On the Structure of Turbulence and a Generalized Eddy Dissipation Concept for Chemical Reaction in Turbulent Flow. In Proceedings of the 19th Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1981. [Google Scholar]
- Rian, K.E.; Grimsmo, B.; Lakså, B.; Vembe, B.E.; Lilleheie, N.I.; Brox, E.; Evanger, T. Advanced CO2 Dispersion Simulation Technology for Improved CCS Safety. Energy Procedia 2014, 63, 2596–2609. [Google Scholar] [CrossRef]
- Hansen, O.R.; Gavelli, F.; Ichard, M.; Davis, S.G. Validation of FLACS against Experimental Data Sets from the Model Evaluation Database for LNG Vapor Dispersion. J. Loss Prev. Process Ind. 2010, 23, 857–877. [Google Scholar] [CrossRef]
- Society of Gas as a Marine Fuel. Gas as a Marine Fuel, Safety Guidelines; Bunkering: London, UK, 2017. [Google Scholar]
- Webber, D.M.; Ivings, M.J.; Santon, R.C. Ventilation Theory and Dispersion Modelling Applied to Hazardous Area Classification. J. Loss Prev. Process Ind. 2011, 24, 612–621. [Google Scholar] [CrossRef]
- Havens, J.; Spicer, T. LNG Vapor Cloud Exclusion Zones for Spills into Impoundments. Process Saf. Prog. 2005, 24, 181–186. [Google Scholar] [CrossRef]
- Cormier, B.R.; Qi, R.; Yun, G.W.; Zhang, Y.; Mannan, M.S. Application of Computational Fluid Dynamics for LNG Vapor Dispersion Modeling: A Study of Key Parameters. J. Loss Prev. Process Ind. 2009, 22, 332–352. [Google Scholar] [CrossRef]
- Nubli, H.; Prabowo, A.R.; Sohn, J.M. Gas Dispersion Analysis on the Open Deck Fuel Storage Configuration of the LNG-Fueled Ship. In Proceedings of the 6th International Conference and Exhibition on Sustainable Energy and Advanced Materials—Lecture Notes in Mechanical Engineering, Surakarta, Indonesia, 16–17 October 2019; pp. 109–118. [Google Scholar] [CrossRef]
- Park, S.I.; Paik, J.K. A Hybrid Method for the Safety Zone Design in Truck-to-Ship LNG Bunkering. Ocean Eng. 2022, 243, 110200. [Google Scholar] [CrossRef]
- International Organization for Standardization. Guidelines for Safety and Risk Assessment of LNG Fuel Bunkering Operations. Switzerland. 2021. Available online: https://www.iso.org/obp/ui/fr/#iso:std:iso:ts:18683:ed-2:v1:en (accessed on 20 September 2022).
- Lloyd’s Register. Guidance Notes for Risk Based Analyses; Cryogenic Spill: London, UK, 2015. [Google Scholar]
- Paik, J.K.; Lee, D.H.; Noh, S.H.; Park, D.K.; Ringsberg, J.W. Full-Scale Collapse Testing of a Steel Stiffened Plate Structure under Axial-Compressive Loading Triggered by Brittle Fracture at Cryogenic Condition. Ships Offshore Struct. 2020, 15, S29–S45. [Google Scholar] [CrossRef]
- Han, S.; Bae, J.; Joh, K.; Suh, Y.; Eom, J.K. Assessing Structural Safety of Inner Hull Structure under Cryogenic Temperature. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Rotterdam, The Netherlands, 19–24 June 2011; Volume 2, pp. 961–967. [Google Scholar]
- Petti, J.P.; Lopez, C.; Figueroa, V.; Kalan, R.J.; Wellman, G.; Dempsey, J.; Villa, D.; Hightower, M. LNG Vessel Cascading Damage Structural and Thermal Analyses. IGT Int. Liq. Nat. Gas Conf. Proc. 2013, 2, 899–922. [Google Scholar]
- Carvalho, E.D.; Marcer, R.; Audiffren, C.; Ciotat, L. Experimental Tests and Qualification of a CFD Simulation Tool for Cryogenic Release Modelling through the JIP “FLNG Cryogenic Spillage Protection. In Proceedings of the Gas Processors Association Europe—2017 Annual Conference, Budapest, Hungary, 13–16 September 2017. [Google Scholar]
- Xie, C.; Huang, L.; Wang, R.; Deng, J.; Shu, Y.; Jiang, D. Research on Quantitative Risk Assessment of Fuel Leak of LNG-Fuelled Ship during Lock Transition Process. Reliab. Eng. Syst. Saf. 2022, 221, 108368. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, X.; Zuo, T.; Wang, W.; Song, X. A Systematic Literature Review on Port LNG Bunkering Station. Transp. Res. Part D Transp. Environ. 2021, 91, 102704. [Google Scholar] [CrossRef]
- Sohn, J.M.; Jung, D. Structural Assessment of a 500-Cbm Liquefied Natural Gas Bunker Ship during Bunkering and Marine Operation under Collision Accidents. Ships Offshore Struct. 2021, 1–17. [Google Scholar] [CrossRef]
- Davies, P.A.; Fort, E. LNG as a Marine Fuel: Likelihood of LNG Releases. J. Mar. Eng. Technol. 2013, 12, 3–10. [Google Scholar] [CrossRef]
- IOGP. Risk Assessment Data Directory—Process Release Frequencies (IOGP Report 434-01); International Association of Oil and Gas Producers: London, UK, 2019. [Google Scholar]
- Vembe, B.E.; Rian, K.E.; Holen, J.; Lilleheie, N.I.; Grimsmo, B. Kameleon FireEx 2000 (Theory Manual); Computit: Brisbane, Australia, 2001. [Google Scholar]
- Fernández, I.A.; Gómez, M.R.; Gómez, J.R.; Insua, Á.B. Review of Propulsion Systems on LNG Carriers. Renew. Sustain. Energy Rev. 2017, 67, 1395–1411. [Google Scholar] [CrossRef]
- Woodward, J.L. Estimating the Flammable Mass of a Vapor Cloud; Wiley: New York, NY, USA, 1999; ISBN 978-0-816-90778-6. [Google Scholar]
- NOAA. Pasquill Stability Classes. Available online: https://www.ready.noaa.gov/READYpgclass.php (accessed on 15 July 2022).
- Luketa-Hanlin, A.; Koopman, R.P.; Ermak, D.L. On the Application of Computational Fluid Dynamics Codes for Liquefied Natural Gas Dispersion. J. Hazard. Mater. 2007, 140, 504–517. [Google Scholar] [CrossRef]
- Bærland, T. Release and Spreading of Dense Gases: Turbulence Modeling with Kameleon FireEx. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2011. [Google Scholar]
- Ro, K.S.; Hunt, P.G. Characteristic Wind Speed Distributions and Reliability of the Logarithmic Wind Profile. J. Environ. Eng. 2007, 133, 313–318. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: Abingdon-on-Thames, UK, 1987; Volume 7, ISBN 0203715454. [Google Scholar]
- Van Ulden, A.P.; Holtslag, A.A.M. Estimation of Atmospheric Boundary Layer Parameters for Diffusion Applications. J. Clim. Appl. Meteorol. 1985, 24, 1196–1207. [Google Scholar] [CrossRef]
- Huser, A.; Nilsen, P.J.; Skåtun, H. Application of K-ε Model to the Stable ABL: Pollution in Complex Terrain. J. Wind Eng. Ind. Aerodyn. 1997, 67–68, 425–436. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-74665-2. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007; ISBN 978031274983. [Google Scholar]
- Duynkerke, P.G. Application of the E-ϵ Turbulence Closure Model to the Neutral and Stable Atmospheric Boundary Layer. J. Atmos. Sci. 1988, 45, 865–880. [Google Scholar] [CrossRef]
- Thysenkrupp Material Data Sheet. Available online: https://ucpcdn.thyssenkrupp.com/_legacy/UCPthyssenkruppBAMXFrance/assets.files/product_pdf/carbon_flat_steel_/plates_and_slabs_carbon_steel/s235jr_1_0038_11_2016_engl.pdf (accessed on 8 August 2022).
- Rian, K.E.; Vembe, B.E.; Evanger, T. KFX™ Validation Handbook; ComputIT: Trondheim, Norway, 2016. [Google Scholar]
- Royle, M.; Willoughby, D.B. Release of Unignited Liquid Hydrogen; IGEM: Buxton, UK, 2014. [Google Scholar]
- Manchester CFD. All There Is to Know about Different Mesh Types in CFD! Available online: https://www.manchestercfd.co.uk/post/all-there-is-to-know-about-different-mesh-types-in-cfd (accessed on 10 July 2022).
- NASA. Examining Spatial (Grid) Convergence. Available online: www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 25 July 2022).
- Vembe, B.E.; Kleiveland, R.N.; Grimsmo, B.; Lilleheie, N.I.; Rian, K.E.; Olsen, R.; Lakså, B.; Nilsen, V.; Vembe, J.E.; Evanger, T. KFX—User’s Manual; Computit: Trondheim, Norway, 2017. [Google Scholar]
- Ennis, A. Development of Source Terms for Gas Dispersion and Vapour Cloud Explosion Modelling. In Institution of Chemical Engineers Symposium Series; Institution of Chemical Engineers: Rugby, UK, 2006; p. 108. [Google Scholar]
- Shao, H.; Duan, G. Risk Quantitative Calculation and ALOHA Simulation on the Leakage Accident of Natural Gas Power Plant. Procedia Eng. 2012, 45, 352–359. [Google Scholar] [CrossRef]
- Lim, B.H.; Ng, E.Y.K. Model for Cryogenic Flashing Lng Leak. Appl. Sci. 2021, 11, 9312. [Google Scholar] [CrossRef]



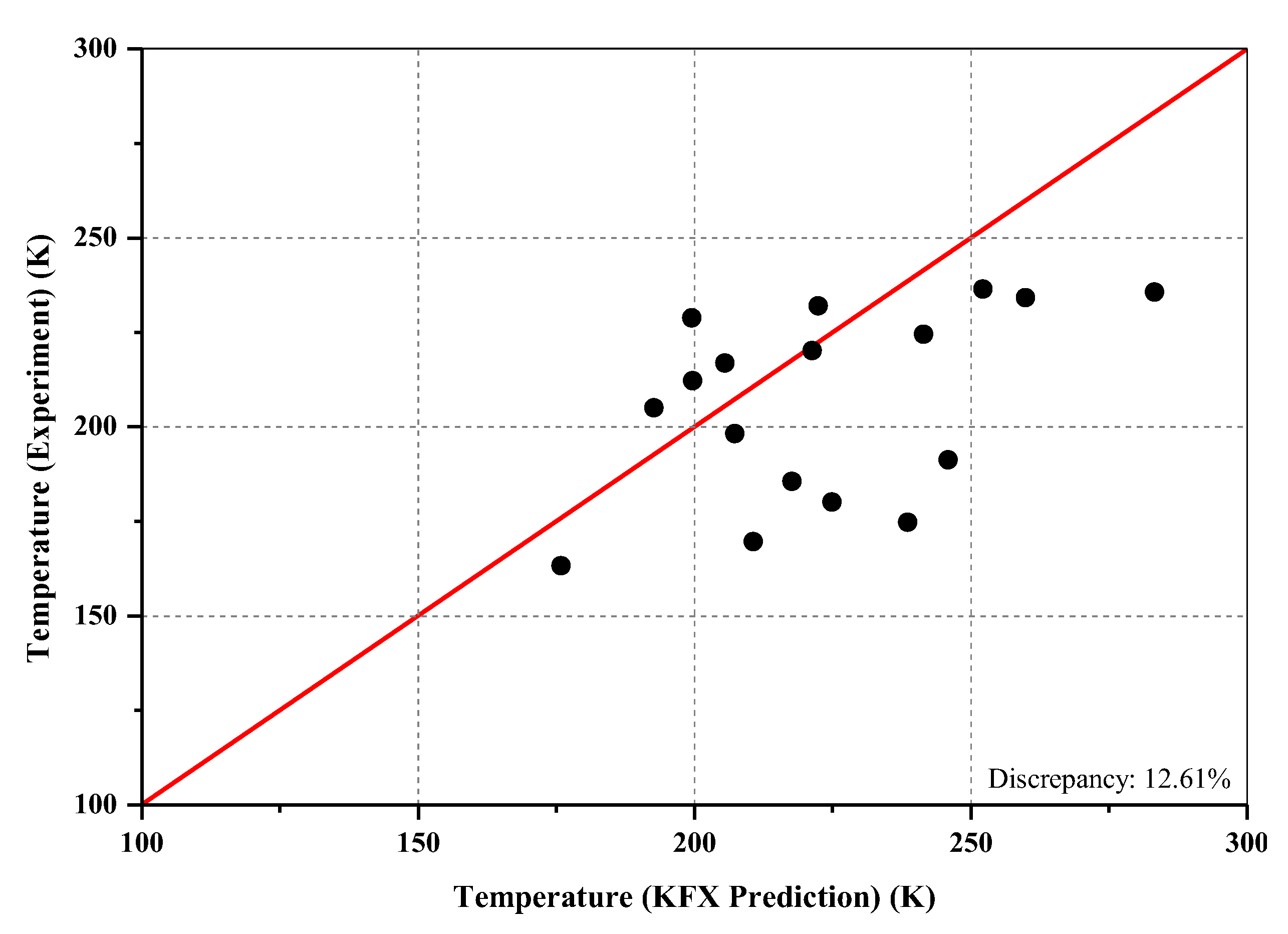



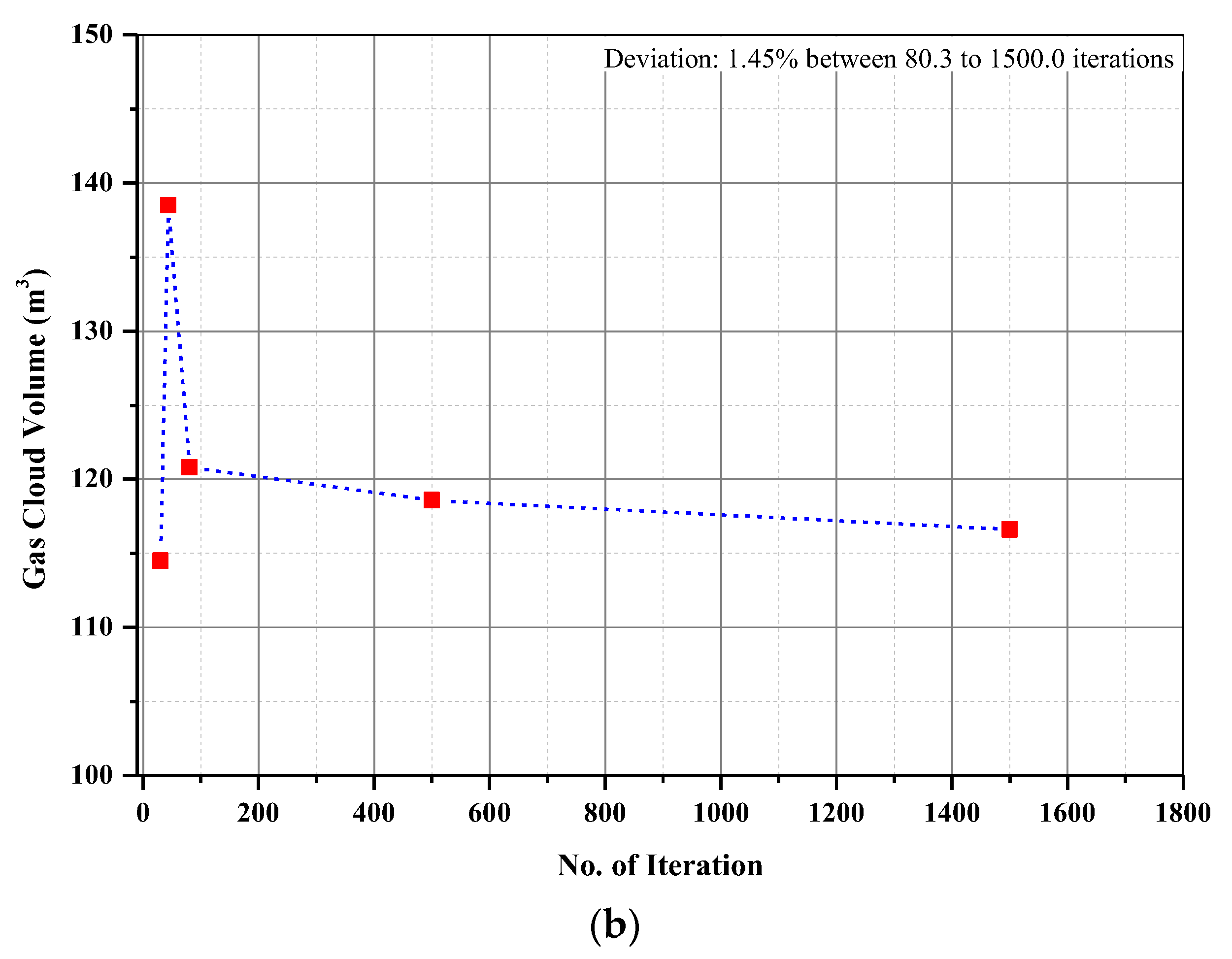
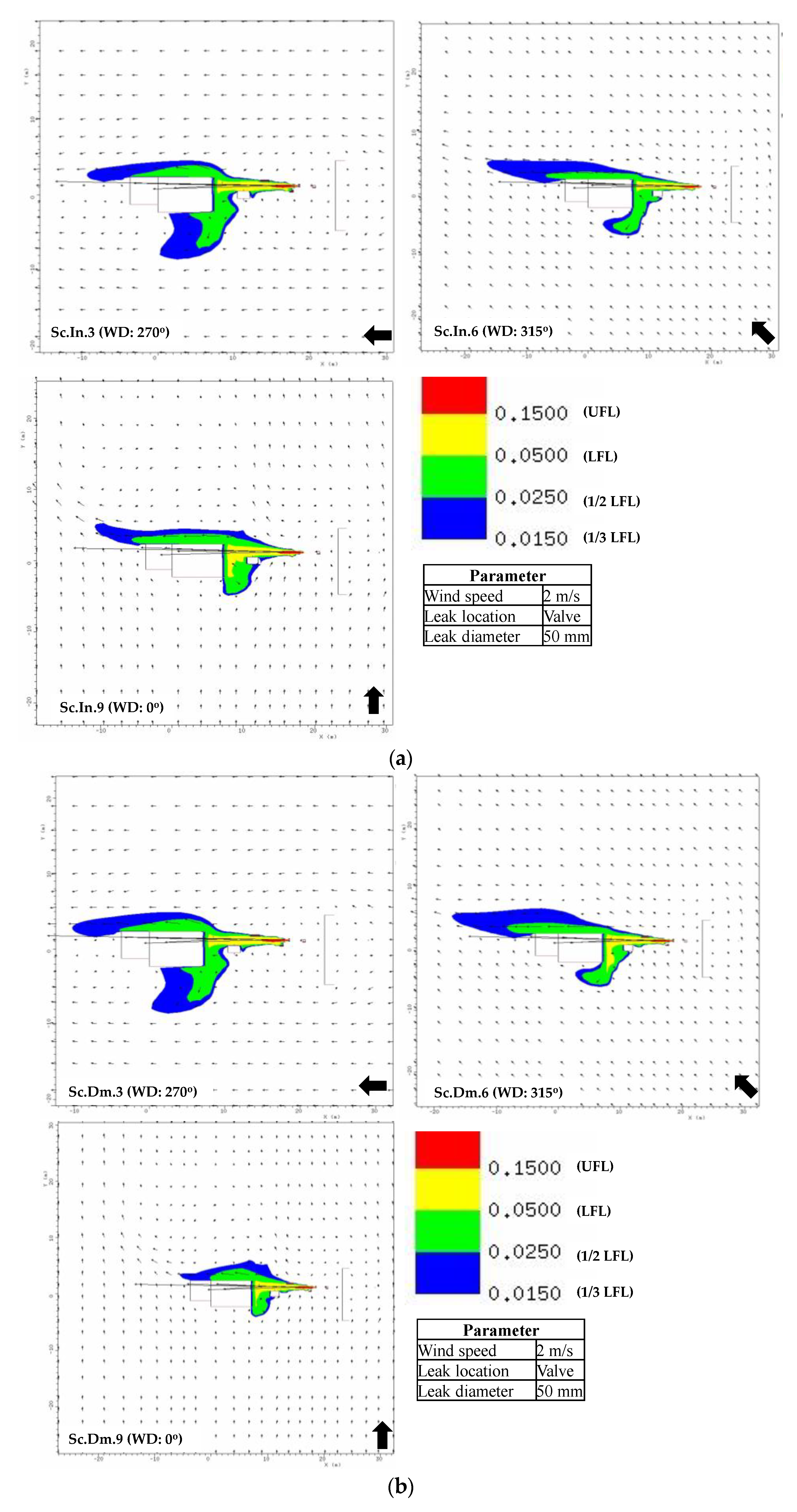
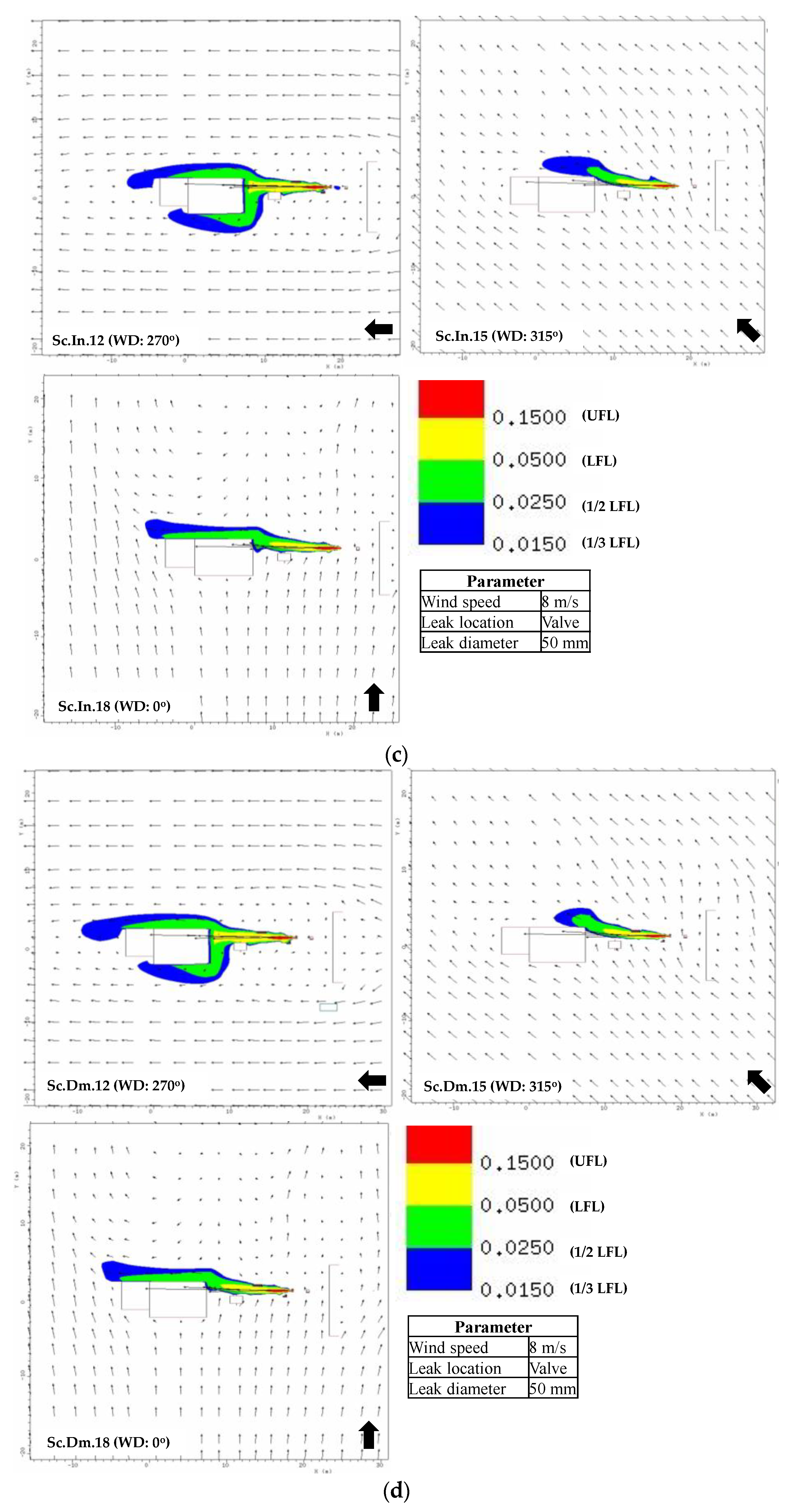


| Author (Year) | Object | Method | Description |
|---|---|---|---|
| Han et al., 2011 [33] | The cargo containment system of LNG carriers | Experiment (with a plate specimen) CFD analysis | Using a fixed leak rate with 1.02 bar of LNG pressure |
| Petti et al., 2013 [34] | The cargo containment system of LNG carriers | Experiment (with a plate specimen) CFD analysis (full ship model) |
|
| Pujol et al., 2016 [13] | Cryogenic release to a bearing of an offshore structure | CFD analysis (KFX) |
|
| Rivot et al., 2017 [35] | Cryogenic release to a steel plate | Experiment |
|
| Current study | Cryogenic release to the LNG bunkering ship | CFD analysis (KFX) |
|
| Parameter (Unit) | Value |
|---|---|
| Length (m) | 45.65 |
| Breadth (m) | 12.40 |
| Depth (m) | 4.50 |
| Draft (m) | 2.50 |
| Service speed (knot) | 8.00 |
| Hole Diameter (mm) | Mass Flow Rate (kg/s) | Severity | Frequency (/Year) | |
|---|---|---|---|---|
| Valve | Pipe | |||
| 3.00 | 0.01 | Minor | 1.30 × 10−5 | 6.70 × 10−6 |
| 10.00 | 0.13 | Medium | 6.20 × 10−6 | 2.70 × 10−6 |
| 50.00 | 3.32 | Major | 1.50 × 10−6 | 5.60 × 10−7 |
| Leak Parameter | Variable |
|---|---|
| Leak diameter (mm) | 3.00; 10.00; 50.00 |
| Leak rate (kg/s) | 0.01; 0.13; 3.32 |
| Reservoir pressure (bar) | 5.00 |
| Reservoir temperature (°C) | −163.00 |
| Leak direction (°) | 90 (to the ship’s stern) |
| Leak location | Valve and Pipe |
| Leak duration | 15.00 |
| Environment parameter | Variable |
| Wind direction (°) | 0; 270; 315 |
| Wind speed (m/s) | 2.00 and 8.00 |
| Ambient temperature (°C) | 14.95 |
| Roughness length (m) | 0.0002 |
| Mean Obukhov length (m) | 10,000.00 (neutral) |
| Stability Class | Mean Obukhov Length (L) (m) |
|---|---|
| D (neutral) | 10,000 |
| E (slightly stable) | 350 |
| F (moderately stable) | 130 |
| G (extremely stable) | 60 |
| Constant | Value | Remark |
|---|---|---|
| C1 | 1.44 | - |
| C2 | 1.92 | - |
| C3 | 1.00 (unstable) 2.00 (stable) | Depends on the local stability |
| CD | 0.09 | Discharge coefficient |
| σk | 1.00 | - |
| σε | 1.30 | - |
| f1 | 1.00 | The function of low Reynold numbers |
| f2 |
| Release Parameter | Variables |
|---|---|
| Mass flow rate (kg/s) | 4.71 |
| Reservoir temperature (°C) | −252.65 |
| Release duration (s) | 248.00 |
| Environment Parameter | Variables |
| Wind speed (m/s) | 2.70 |
| Wind direction (°) | 274.00 |
| Ambient temperature (°C) | 10.30 |
| Roughness length (m) | 0.001 (flat terrain) |
| Leak Parameter | Variable |
|---|---|
| Leak diameter (mm) | 50.00 |
| Mass flow rate (kg/s) | 3.33 |
| Leak position | at Valve |
| Leak direction (°) | 90 to the ship’s stern |
| Reservoir temperature (°C) | −163.00 |
| Environment Parameter | Variable |
| Wind speed (m/s) | 2.00 |
| Wind direction (°) | 270.00 |
| Ambient temperature (°C) | 14.95 |
| Roughness length (m) | 0.0002 |
| Scenario (Sc) | Leak Diameter (mm) | Wind Direction (°) | Wind Speed (m/s) | Leak Position | Intact (In) | Damage (Dm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gas Volume (m3) | Length (X) (m) | Width (Y) (m) | Height (Z) (m) | Area XY (m2) | Area YZ (m2) | Gas Volume (m3) | Length (X) (m) | Width (Y) (m) | Height (Z) (m) | Area XY (m2) | Area YZ (m2) | |||||
| 1 | 3 | 90 | 2 | Valve | 0.01 | 1.29 | 0.17 | 0.29 | 0.22 | 0.05 | 0.01 | 1.17 | 0.17 | 0.16 | 0.2 | 0.03 |
| 2 | 10 | 90 | 2 | Valve | 0.44 | 1.23 | 0.17 | 0.21 | 0.21 | 0.03 | 0.46 | 4.96 | 0.99 | 1.03 | 4.92 | 1.02 |
| 3 | 50 | 90 | 2 | Valve | 161 | 22.04 | 11.77 | 3.64 | 259.41 | 42.89 | 141.4 | 23.11 | 11.42 | 3.65 | 263.82 | 41.64 |
| 4 | 3 | 135 | 2 | Valve | 0.01 | 1.28 | 0.21 | 0.43 | 0.27 | 0.09 | 0.01 | 1.13 | 0.18 | 0.17 | 0.2 | 0.03 |
| 5 | 10 | 135 | 2 | Valve | 0.24 | 3.14 | 1.03 | 0.74 | 3.24 | 0.77 | 0.32 | 3.76 | 0.78 | 1.03 | 2.95 | 0.81 |
| 6 | 50 | 135 | 2 | Valve | 90.79 | 25.86 | 11.58 | 5.9 | 299.39 | 68.28 | 115.13 | 27.04 | 10.48 | 6.83 | 283.38 | 71.56 |
| 7 | 3 | 180 | 2 | Valve | 0.01 | 1.21 | 0.25 | 0.31 | 0.31 | 0.08 | 0.01 | 1.35 | 0.2 | 0.15 | 0.28 | 0.03 |
| 8 | 10 | 180 | 2 | Valve | 0.34 | 3.92 | 0.99 | 1.28 | 3.89 | 1.27 | 0.34 | 3.88 | 0.91 | 1.16 | 3.53 | 1.05 |
| 9 | 50 | 180 | 2 | Valve | 161.9 | 24.61 | 8.98 | 6.73 | 221.04 | 60.5 | 146 | 19.37 | 8.89 | 6.92 | 172.16 | 61.53 |
| 10 | 3 | 90 | 8 | Valve | 0.01 | 1.23 | 0.2 | 0.15 | 0.25 | 0.03 | 0.01 | 0.76 | 0.18 | 0.16 | 0.13 | 0.03 |
| 11 | 10 | 90 | 8 | Valve | 0.7 | 4.92 | 1.03 | 1.61 | 5.08 | 1.66 | 0.84 | 5.29 | 1.2 | 1.24 | 6.34 | 1.49 |
| 12 | 50 | 90 | 8 | Valve | 114 | 22.55 | 8.8 | 3.74 | 198.33 | 32.91 | 96.79 | 23.02 | 8.61 | 3.46 | 198.14 | 29.79 |
| 13 | 3 | 135 | 8 | Valve | 3.48 × 10−3 | 0.8 | 0.27 | 0.11 | 0.21 | 0.03 | 4.16 × 10−3 | 0.87 | 0.29 | 0.1 | 0.25 | 0.03 |
| 14 | 10 | 135 | 8 | Valve | 0.13 | 2.64 | 0.78 | 0.62 | 2.08 | 0.49 | 0.19 | 2.6 | 0.7 | 0.62 | 1.83 | 0.44 |
| 15 | 50 | 135 | 8 | Valve | 20.4 | 12.73 | 3.74 | 2.15 | 47.63 | 8.05 | 25.86 | 13.29 | 3.84 | 2.24 | 50.97 | 8.61 |
| 16 | 3 | 180 | 8 | Valve | 3.88 × 10−3 | 0.71 | 0.24 | 0.1 | 0.17 | 0.02 | 3.62 × 10−3 | 0.58 | 0.25 | 0.1 | 0.15 | 0.03 |
| 17 | 10 | 180 | 8 | Valve | 0.19 | 2.69 | 0.83 | 0.66 | 2.22 | 0.55 | 0.19 | 2.47 | 0.77 | 0.58 | 1.91 | 0.45 |
| 18 | 50 | 180 | 8 | Valve | 37.11 | 22.92 | 3.18 | 2.62 | 72.93 | 8.33 | 36.94 | 23.11 | 3.65 | 2.71 | 84.34 | 9.9 |
| 19 | 3 | 90 | 2 | Pipe | 0.04 | 0.77 | 0.82 | 0.11 | 0.63 | 0.09 | 0.15 | 0.78 | 0.64 | 0.14 | 0.5 | 0.09 |
| 20 | 10 | 90 | 2 | Pipe | 8.37 | 5.1 | 7.21 | 2.43 | 36.75 | 17.54 | 8.11 | 5.1 | 7.02 | 2.36 | 35.76 | 16.53 |
| 21 | 50 | 90 | 2 | Pipe | 295.4 | 19.08 | 22.02 | 7.64 | 420.17 | 168.14 | 226.8 | 18.07 | 20.28 | 7.64 | 366.44 | 154.83 |
| 22 | 3 | 135 | 2 | Pipe | 0.03 | 0.79 | 0.44 | 0.7 | 0.34 | 0.31 | 0.03 | 0.79 | 0.49 | 0.76 | 0.39 | 0.37 |
| 23 | 10 | 135 | 2 | Pipe | 5.48 | 4.79 | 5.68 | 2.83 | 27.17 | 16.06 | 5.45 | 4.4 | 6.47 | 2.6 | 28.5 | 16.82 |
| 24 | 50 | 135 | 2 | Pipe | 307.8 | 10.37 | 21.82 | 9.45 | 226.19 | 206.28 | 282.4 | 10.37 | 20.36 | 11.09 | 211.11 | 225.85 |
| 25 | 3 | 180 | 2 | Pipe | 0.07 | 0.8 | 1.38 | 0.57 | 1.1 | 0.78 | 0.03 | 0.79 | 0.5 | 0.76 | 0.39 | 0.38 |
| 26 | 10 | 180 | 2 | Pipe | 7.46 | 3.36 | 7.76 | 3.64 | 26.07 | 28.28 | 6.75 | 3.59 | 7.71 | 3.67 | 27.7 | 28.3 |
| 27 | 50 | 180 | 2 | Pipe | 427.7 | 4.63 | 25.2 | 12.26 | 116.77 | 308.94 | 365.6 | 7.1 | 29.67 | 12.38 | 210.71 | 367.4 |
| 28 | 3 | 90 | 8 | Pipe | 0.02 | 0.59 | 0.54 | 0.41 | 0.32 | 0.22 | 0.02 | 0.67 | 0.59 | 0.34 | 0.39 | 0.2 |
| 29 | 10 | 90 | 8 | Pipe | 4.9 | 5.98 | 6.33 | 1.78 | 37.89 | 11.25 | 4.94 | 5.79 | 6.25 | 1.89 | 36.22 | 11.83 |
| 30 | 50 | 90 | 8 | Pipe | 82.56 | 12.39 | 12.48 | 5.82 | 154.53 | 72.59 | 71.31 | 8.9 | 11.19 | 6.45 | 99.6 | 72.24 |
| 31 | 3 | 135 | 8 | Pipe | 0.01 | 0.42 | 0.21 | 0.29 | 0.09 | 0.06 | 0.01 | 0.45 | 0.26 | 0.29 | 0.12 | 0.08 |
| 32 | 10 | 135 | 8 | Pipe | 1.35 | 1.47 | 5.51 | 1.47 | 8.08 | 8.11 | 1.4 | 1.74 | 4.98 | 1.51 | 8.65 | 7.53 |
| 33 | 50 | 135 | 8 | Pipe | 93.54 | 9.63 | 13.85 | 4.91 | 133.45 | 68.01 | 50.39 | 8.26 | 15.14 | 4.45 | 124.99 | 67.43 |
| 34 | 3 | 180 | 8 | Pipe | 0.01 | 0.63 | 0.34 | 0.43 | 0.21 | 0.14 | 0.04 | 0.69 | 0.51 | 0.58 | 0.35 | 0.3 |
| 35 | 10 | 180 | 8 | Pipe | 1.97 | 1.51 | 3.94 | 2.44 | 5.93 | 9.62 | 2.17 | 1.58 | 4.32 | 2.47 | 6.85 | 10.69 |
| 36 | 50 | 180 | 8 | Pipe | 134.5 | 14.77 | 9.54 | 6.09 | 140.93 | 58.12 | 78.26 | 6.24 | 10.18 | 5.09 | 63.53 | 51.84 |
| Scenario | Steel Temperature (K) | Leak Position |
|---|---|---|
| Sc.In.9 | 261.51 | Valve |
| Sc.Dm.9 | 261.92 | |
| Sc.In.27 | 176.71 | Pipe |
| Sc.Dm.27 | 183.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nubli, H.; Sohn, J.-M.; Jung, D. Consequence Analysis of Accidental LNG Release on the Collided Structure of 500 cbm LNG Bunkering Ship. J. Mar. Sci. Eng. 2022, 10, 1378. https://doi.org/10.3390/jmse10101378
Nubli H, Sohn J-M, Jung D. Consequence Analysis of Accidental LNG Release on the Collided Structure of 500 cbm LNG Bunkering Ship. Journal of Marine Science and Engineering. 2022; 10(10):1378. https://doi.org/10.3390/jmse10101378
Chicago/Turabian StyleNubli, Haris, Jung-Min Sohn, and Dongho Jung. 2022. "Consequence Analysis of Accidental LNG Release on the Collided Structure of 500 cbm LNG Bunkering Ship" Journal of Marine Science and Engineering 10, no. 10: 1378. https://doi.org/10.3390/jmse10101378
APA StyleNubli, H., Sohn, J. -M., & Jung, D. (2022). Consequence Analysis of Accidental LNG Release on the Collided Structure of 500 cbm LNG Bunkering Ship. Journal of Marine Science and Engineering, 10(10), 1378. https://doi.org/10.3390/jmse10101378







