CFD-CNN Modeling of the Concentration Field of Multiport Buoyant Jets
Abstract
1. Introduction
2. Materials and Methods
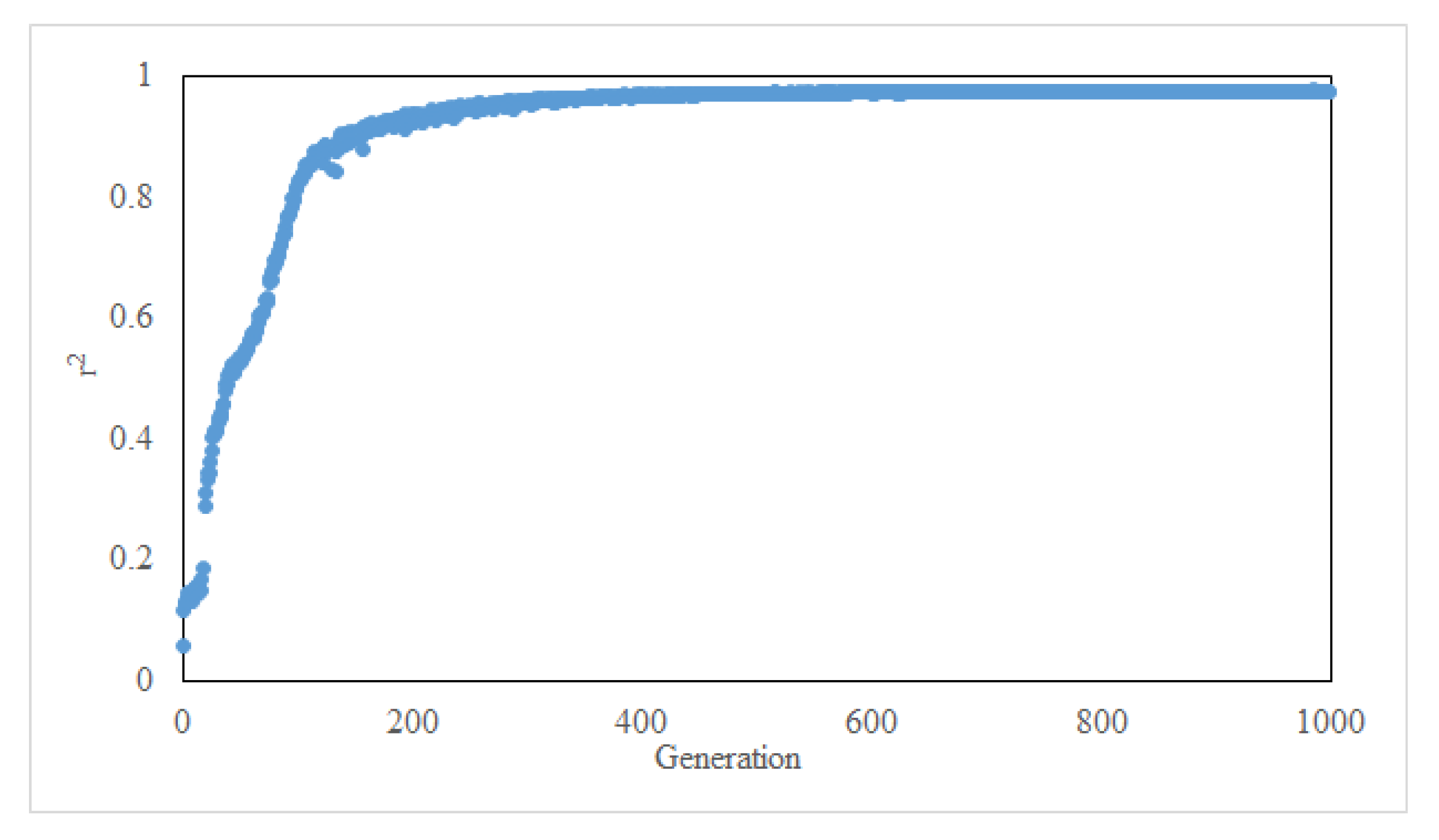
2.1. CNN Method
- (1)
- Select the training group and randomly set 60 percent of the samples as the training group, 20 percent as the verification group, and 20 percent as the test group from the sample set;
- (2)
- Set each weight and threshold value to a small random value close to 0 and initialize the precision control parameters and learning rate. Set the parameter epochs to 1000, batch size to 32, and verbose to 2;
- (3)
- Select Fr, x, and y as the input vectors, and normalize the concentration target output vector;
- (4)
- Calculate the output vector of the middle layer and calculate the actual output vector of the network;
- (5)
- The output error is calculated by comparing the elements in the output vector with the elements in the target vector. For the hidden elements of the middle layer, the error also needs to be calculated;
- (6)
- The adjustment amount of each weight and the adjustment amount of the threshold are calculated in turn;
- (7)
- Adjust weights and adjust thresholds;
- (8)
- When M is experienced, it is judged whether the indicator meets the accuracy requirements. If not, it returns (3) and continues to iterate. If satisfied, it proceeds to the next step;
- (9)
- At the end of training, the weights and thresholds in a document are saved. At this moment, it can be considered that the various weights have reached stability and the classifier has been formed. Training is performed again, exporting the weights and thresholds directly from the documents for training; no initialization is required.
2.2. The Joint Method of CFD-CNN
2.3. Comparison of Models
3. Results
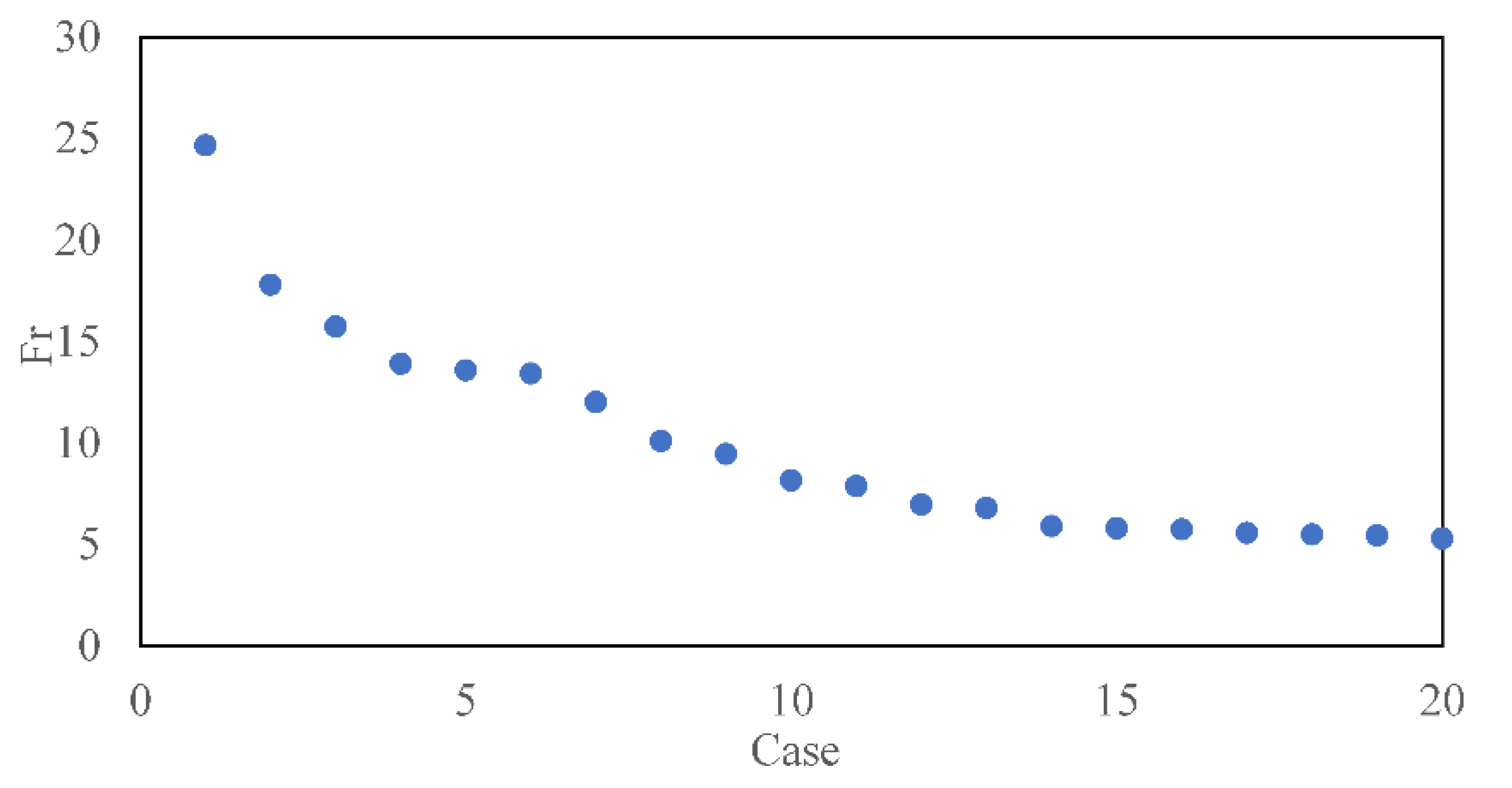
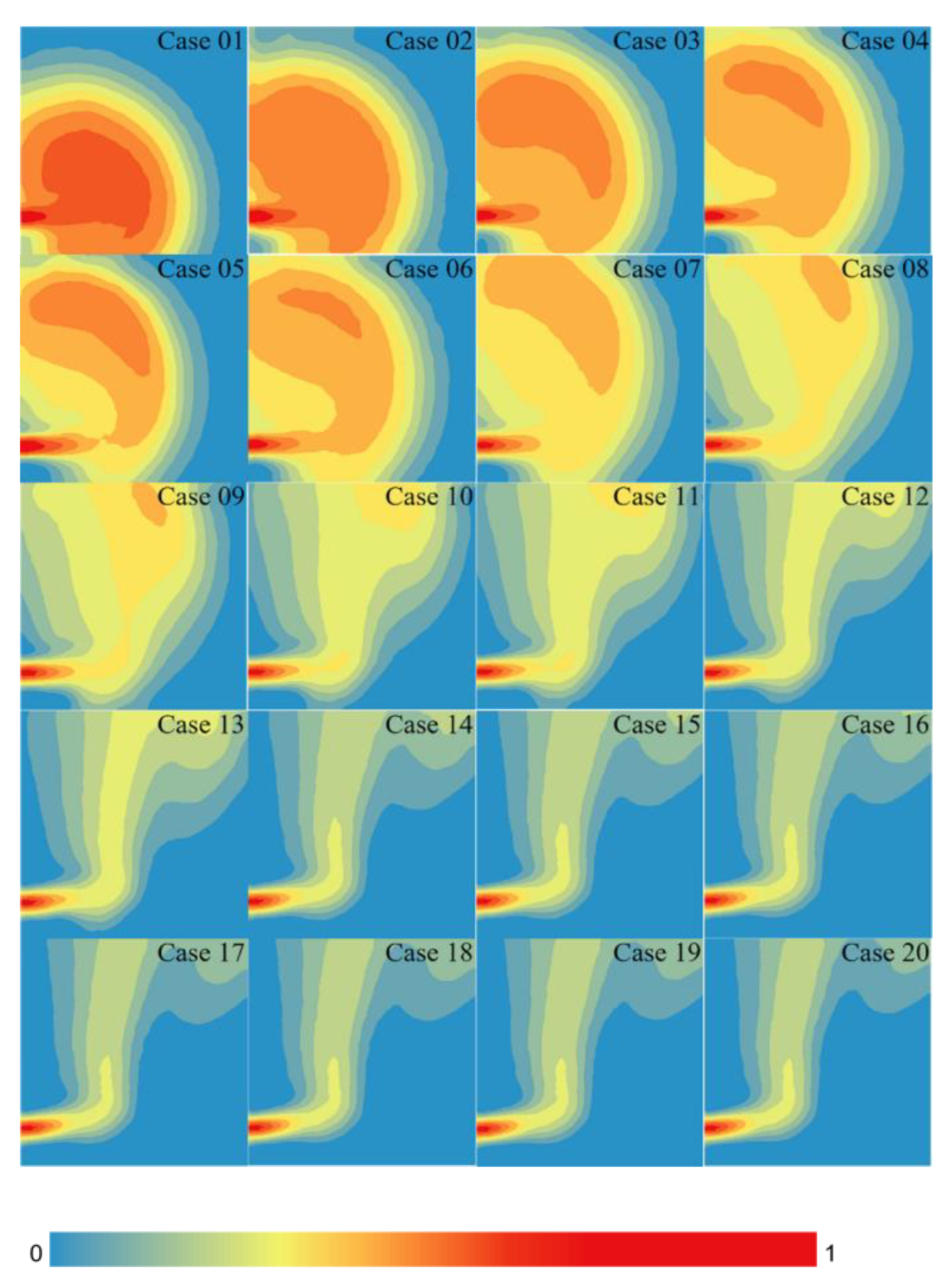
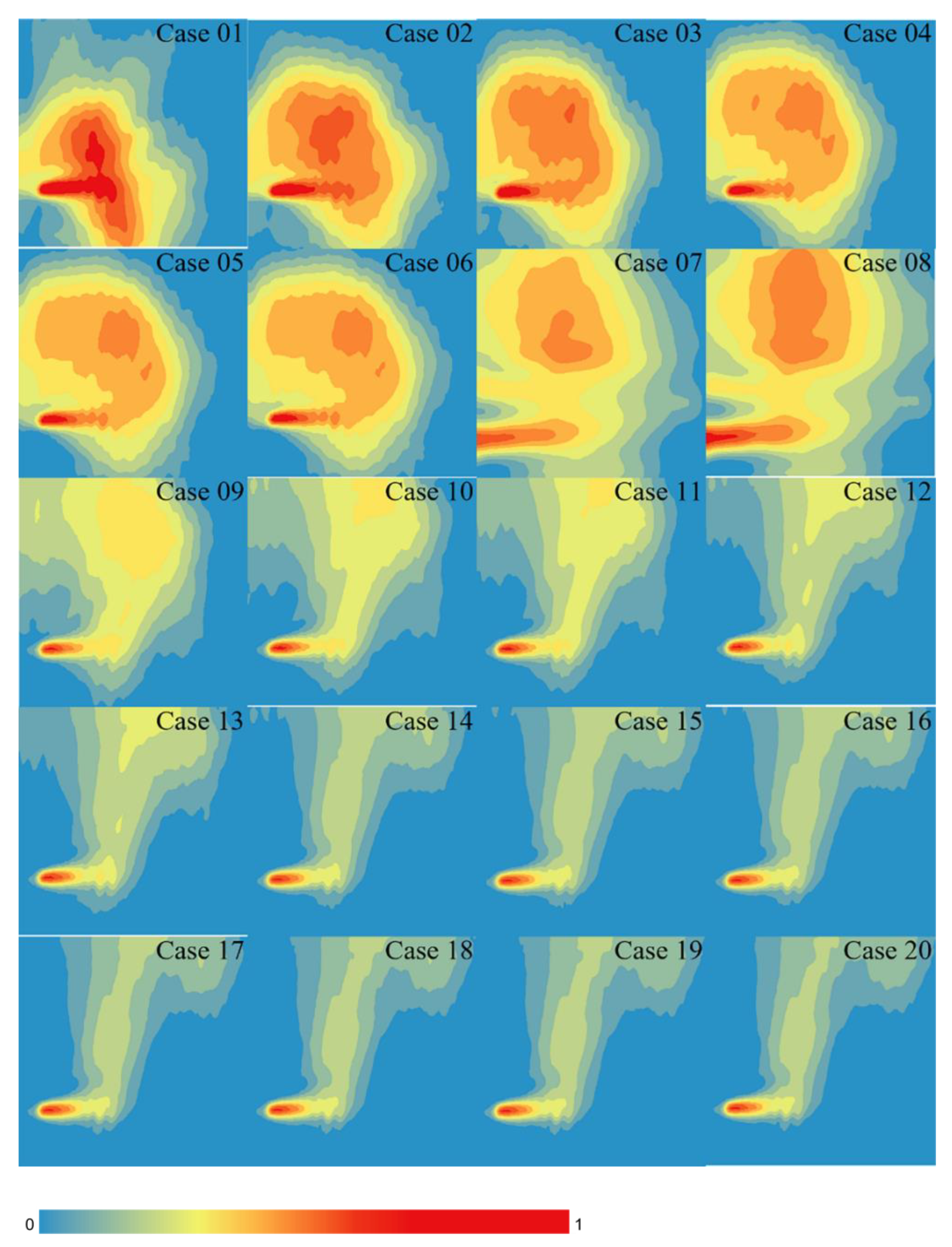
3.1. Results of CFD
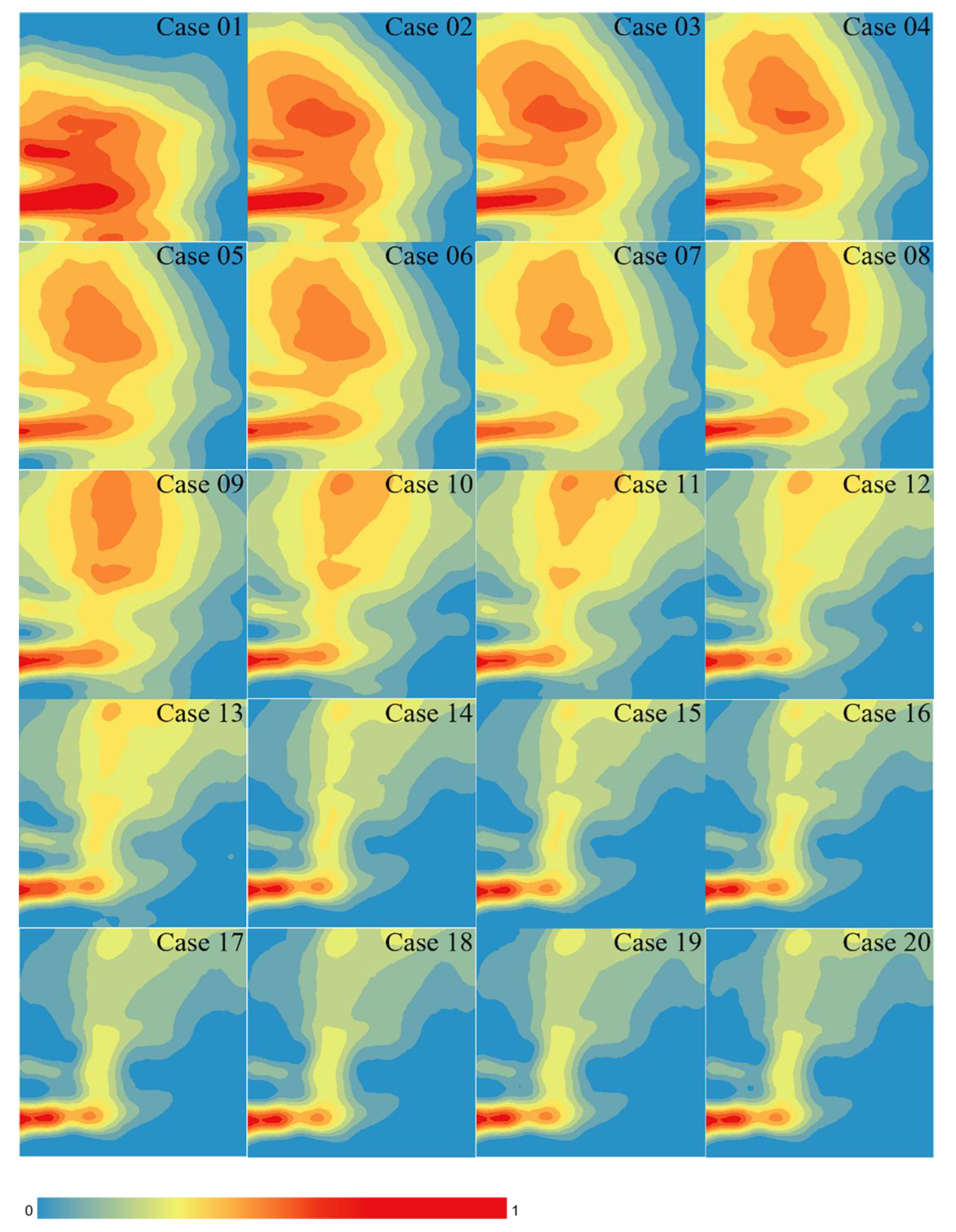
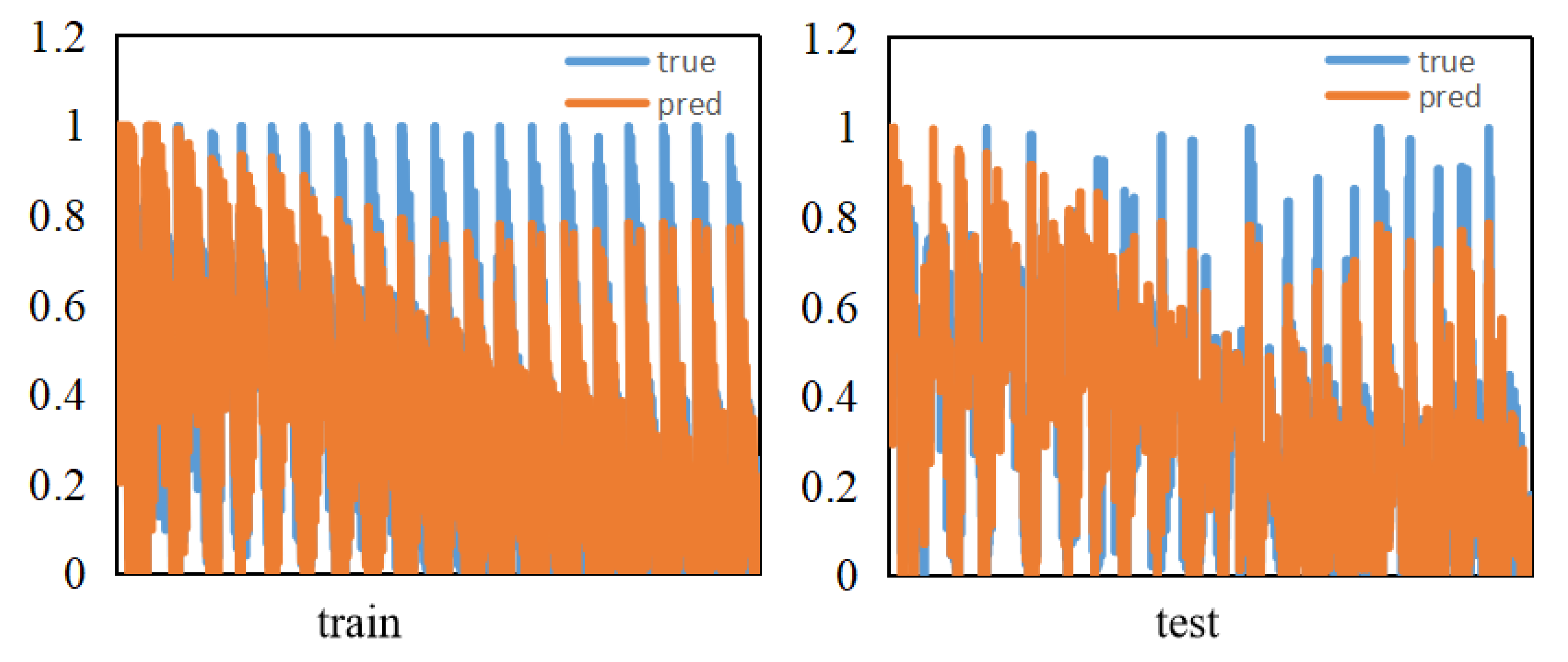
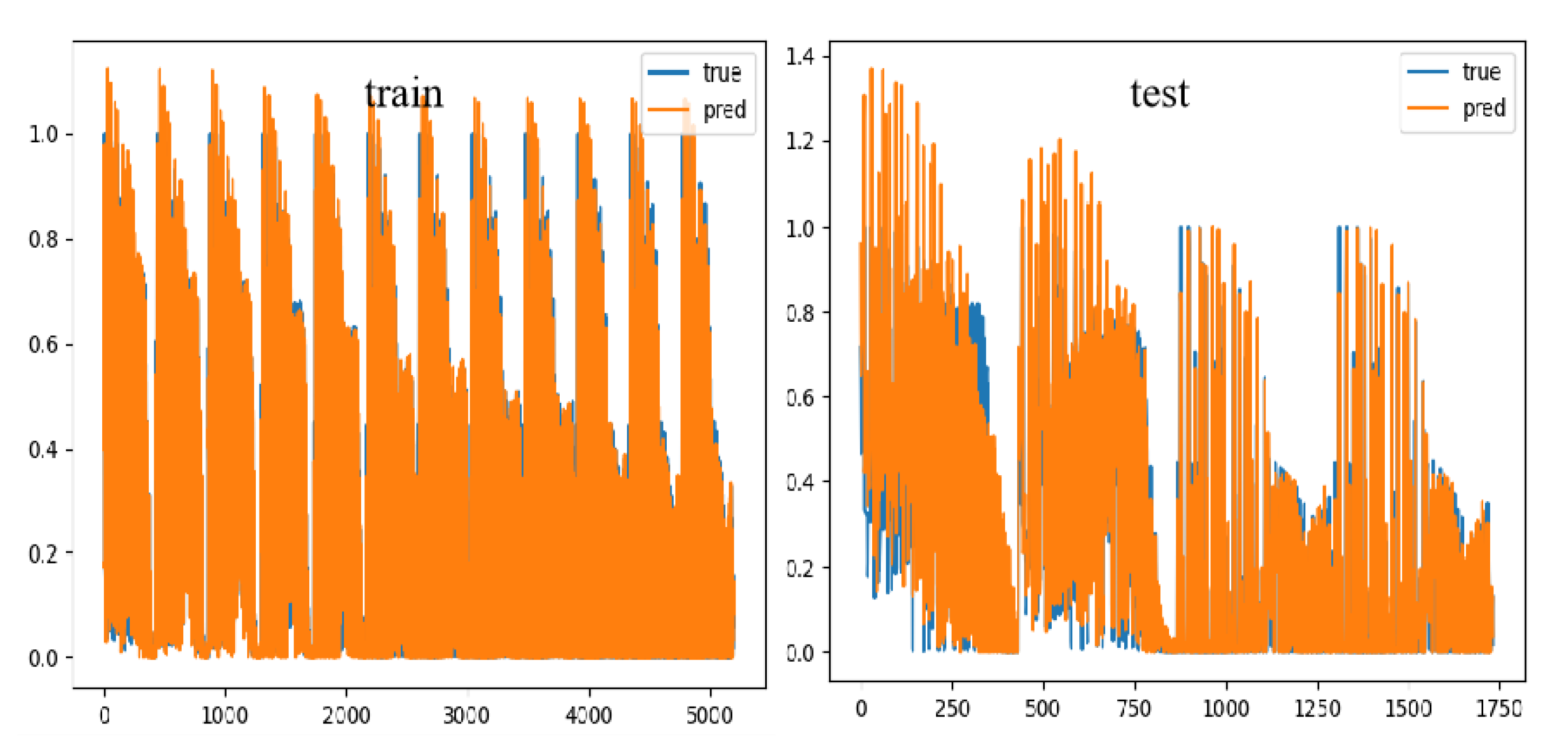
3.2. Results of CFD and CNN Joint Method
3.3. The Performance of the Proposed Approach
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, X.; Ghodoosipour, B.; Mohammadian, M. Three-dimensional numerical study of multiple vertical buoyant jets in stationary ambient water. J. Hydraul. Eng. 2020, 2020, 04020049. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A.; Chen, X. Three-dimensional numerical simulations of buoyant jets discharged from a rosette-type multiport diffuser. J. Mar. Sci. Eng. 2019, 7, 409. [Google Scholar] [CrossRef]
- Lai, A.C.; Lee, J.H. Dynamic interaction of multiple buoyant jets. J. Fluid Mech. 2012, 708, 539–575. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J. Rosette Diffusers for Dense Effluents in Flowing Currents. J. Hydraul. Eng. 2017, 144, m06017024. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.; Gandhi, V. Rosette diffusers for dense effluents. J. Hydraul. Eng. 2016, 143, 06016029. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical Modeling of Vertical Buoyant Jets Subjected to Lateral Confinement. J. Hydraul. Eng. 2017, 43, 04017016. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.K.; Jiang, M. Large eddy simulations of 45° and 60° inclined dense jets with bottom impact. J. Hydro-environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Glaze, D.J.; Frankel, S.H. Stochastic inlet conditions for large-eddy simulation of a fully turbulent jet. Aiaa J. 2015, 41, 1064–1073. [Google Scholar] [CrossRef]
- Knystautas, R. The turbulent jet from a series of holes in line. Aeronaut. Q. 2016, 15, 1–28. [Google Scholar] [CrossRef]
- Yannopoulos, P.C.; Noutsopoulos, G.C. Interaction of vertical round turbulent buoyant jets—Part I: Entrainment restriction approach. J. Hydraul. Res. 2006, 44, 218–232. [Google Scholar] [CrossRef]
- Wang, H.J.; Davidson, M.J. Jet interaction in a still ambient fluid. J. Hydraul. Eng. 2003, 129, 349–357. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Multigene Genetic-Programming-Based Models for Initial Dilution of Laterally Confined Vertical Buoyant Jets. J. Mar. Sci. Eng. 2019, 7, 246. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A.; Khelifa, A. Modeling spatial distribution of flow depth in fluvial systems using a hybrid two-dimensional hydraulic-multigene genetic programming approach. J. Hydrol. 2021, 600, 126517. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Peng, D.; Zuo, D. Urban flood susceptibility assessment based on convolutional neural networks. J. Hydrol. 2020, 590, 125235. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V. A pareto-optimal moving average-multigene genetic programming model for rainfall-runoff modelling. Environ. Model. Softw. 2017, 92, 239–251. [Google Scholar] [CrossRef]
- Bayazidi, A.M.; Wang, G.G.; Bolandi, H.; Alavi, A.H.; Gandomi, A.H. Multigene genetic programming for estimation of elastic modulus of concrete. Math. Probl. Eng. 2014, 2014, 474289. [Google Scholar]
- Paiva, G.M.D.; Pimentel, S.P.; Alvarenga, B.P.; Marra, E.G.; Leva, S. Multiple site intraday solar irradiance forecasting by machine learning algorithms: Mggp and mlp neural networks. Energies 2020, 13, 3005. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Mehr, A.D. Multigene genetic programming for sediment transport modeling in sewers for conditions of non-deposition with a bed deposit. Int. J. Sediment Res. 2018, 33, 46–54. [Google Scholar] [CrossRef]
- OpenFOAM User Guide; Version 4.0; The OpenCFD Foundation: London, UK, 2016.
- Yan, C.; Wang, C. Development and application of the convolutional neural network model. Comput. Sci. Explor. 2021, 15, 27–46. [Google Scholar]
- Wei, D.; Wang, B.; Zhang, M. Study on the Deep Learning Model of Concrete Dam Deformation Prediction Based on CNN. Water Conserv. Hydropower Technol. 2021, 52, 52–57. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/580/1/012042/pdf (accessed on 14 September 2022). [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2016. [Google Scholar]
- Eltner, A.; Bressan, P.O.; Akiyama, T.; Gonçalves, W.N.; Marcato Junior, J. Using deep learning for automatic water stage measurements. Water Resour. Res. 2021, 57, e2020WR027608. [Google Scholar] [CrossRef]
- Kreyenberg, P.J.; Bauser, H.H.; Roth, K. Velocity field estimation on density-driven solute transport with a convolutional neural network. Water Resour. Res. 2019, 55, 7275–7293. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Zuo, W. Image denoising using deep CNN with batch renormalization. Neural Netw. Off. J. Int. Neural Netw. Soc. 2020, 121, 461–473. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Hamila, R.; Gabbouj, M. Convolutional Neural Networks for patient-specific ECG classification. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 2608–2611. [Google Scholar] [CrossRef]
- Zihlmann, M.; Perekrestenko, D.; Tschannen, M. Convolutional Recurrent Neural Networks for Electrocardiogram Classification. 2017. Available online: http://arxiv.org/abs/1710.06122 (accessed on 1 January 2022).
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Sakhaei, Z.; Nikooee, E.; Riazi, M. A new formulation for non-equilibrium capillarity effect using multi-gene genetic programming (mggp): Accounting for fluid and porous media properties. Eng. Comput. 2022, 38, 1697–1709. [Google Scholar] [CrossRef]
- Searson, D.P. GPTIPS 2: An Open-Source Software Platform for Symbolic Data Mining. In Handbook of Genetic Programming Applications; Springer: Cham, Switzerland, 2015; pp. 551–573. [Google Scholar]
- Yan, X.; Wang, Y.; Mohammadian, A.; Liu, J. Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques. J. Mar. Sci. Eng. 2021, 9, 1311. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Hosseiny, H.; Nazari, F.; Smith, V.; Nataraj, C. A Framework for Modeling Flood Depth Using a Hybrid of Hydraulics and Machine Learning. Sci. Rep. 2020, 10, 8222. [Google Scholar] [CrossRef]
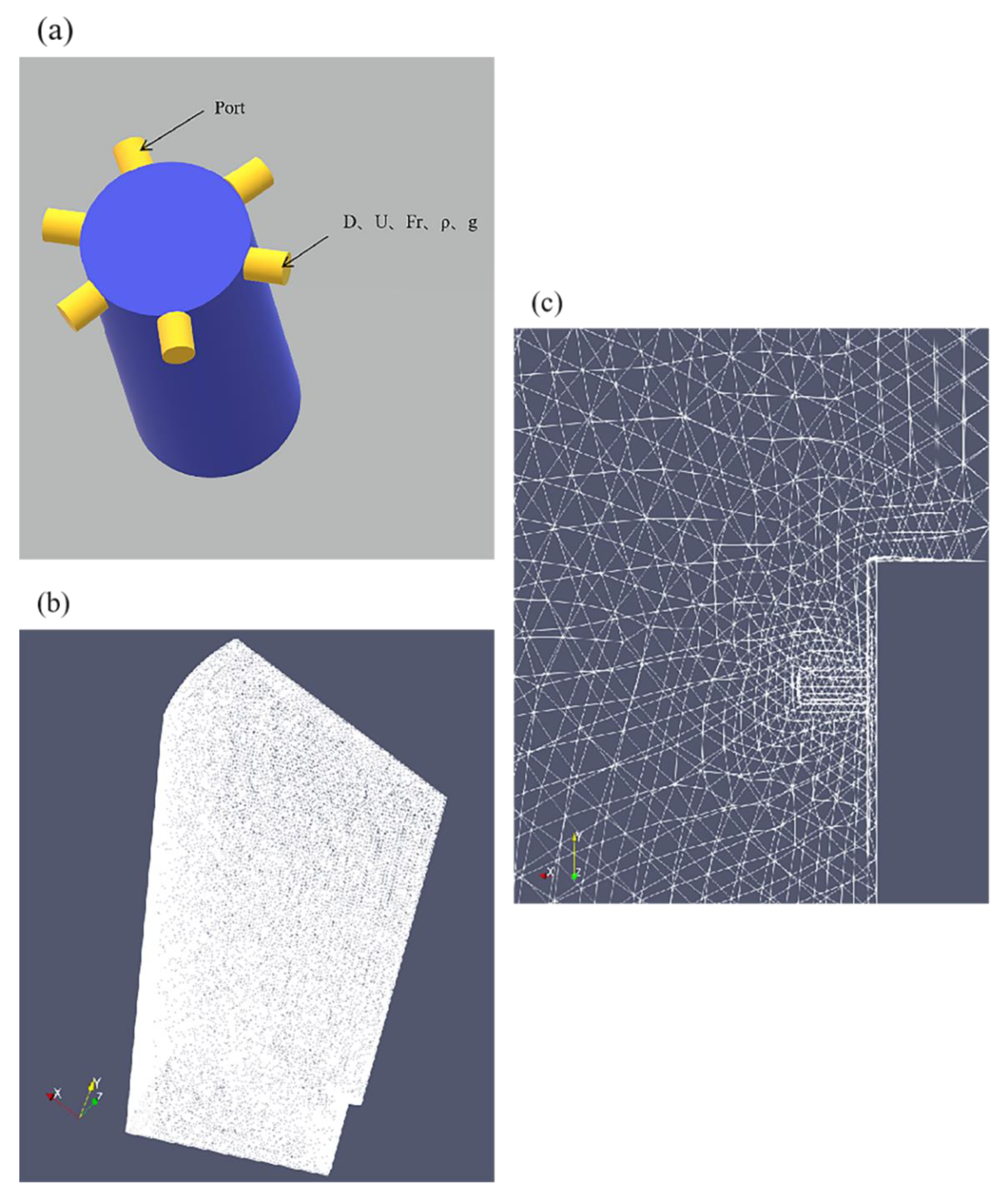
| D | U | Fr | ρ | g |
|---|---|---|---|---|
| 0.0044 m | 0.185 m/s | variable | 997 km/m3 | 9.8 |
| y/D | x/D (Exp) | x/D (Num) |
|---|---|---|
| 0.40 | 1.28 | 0.99 |
| 1.76 | 2.56 | 2.84 |
| 3.12 | 3.52 | 3.67 |
| 4.88 | 3.92 | 4.39 |
| 37.72 | 4.48 | 5.13 |
| 6.57 | 4.64 | 4.80 |
| 8.01 | 4.96 | 5.10 |
| 35.48 | 4.96 | 5.09 |
| 9.69 | 5.28 | 5.35 |
| 33.15 | 5.28 | 5.20 |
| 11.13 | 5.52 | 5.53 |
| 30.75 | 5.52 | 5.32 |
| 28.11 | 5.68 | 5.47 |
| 25.71 | 5.76 | 5.64 |
| 13.53 | 5.84 | 5.79 |
| 19.14 | 5.84 | 6.23 |
| 20.98 | 5.84 | 6.19 |
| 22.74 | 5.84 | 6.02 |
| 15.22 | 5.92 | 5.99 |
| 17.06 | 6 | 6.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Wang, Y.; Mohammadian, A.; Liu, J.; Chen, X. CFD-CNN Modeling of the Concentration Field of Multiport Buoyant Jets. J. Mar. Sci. Eng. 2022, 10, 1383. https://doi.org/10.3390/jmse10101383
Yan X, Wang Y, Mohammadian A, Liu J, Chen X. CFD-CNN Modeling of the Concentration Field of Multiport Buoyant Jets. Journal of Marine Science and Engineering. 2022; 10(10):1383. https://doi.org/10.3390/jmse10101383
Chicago/Turabian StyleYan, Xiaohui, Yan Wang, Abdolmajid Mohammadian, Jianwei Liu, and Xiaoqiang Chen. 2022. "CFD-CNN Modeling of the Concentration Field of Multiport Buoyant Jets" Journal of Marine Science and Engineering 10, no. 10: 1383. https://doi.org/10.3390/jmse10101383
APA StyleYan, X., Wang, Y., Mohammadian, A., Liu, J., & Chen, X. (2022). CFD-CNN Modeling of the Concentration Field of Multiport Buoyant Jets. Journal of Marine Science and Engineering, 10(10), 1383. https://doi.org/10.3390/jmse10101383








