Ballast Water Dynamic Allocation Optimization for Revolving Floating Cranes Based on a Hybrid Algorithm of Fuzzy-Particle Swarm Optimization with Domain Knowledge
Abstract
:1. Introduction
2. Multi-Stage Decision Optimization Model for Ballast Water Dynamic Allocation
2.1. Lifting Operation Process of the RFC
2.2. Ballast Water Allocation Optimization Model for the RFC
2.2.1. Objective Functions
2.2.2. Constraint Functions
- (1)
- Hull balance during the allocation process;
- (2)
- Unchanged total mass of ballast water during the allocation process;
- (3)
- The ballast tank height limitations.
2.2.3. Ballast Water Allocation Optimization Model
3. FPSO Algorithm Based on Domain Knowledge
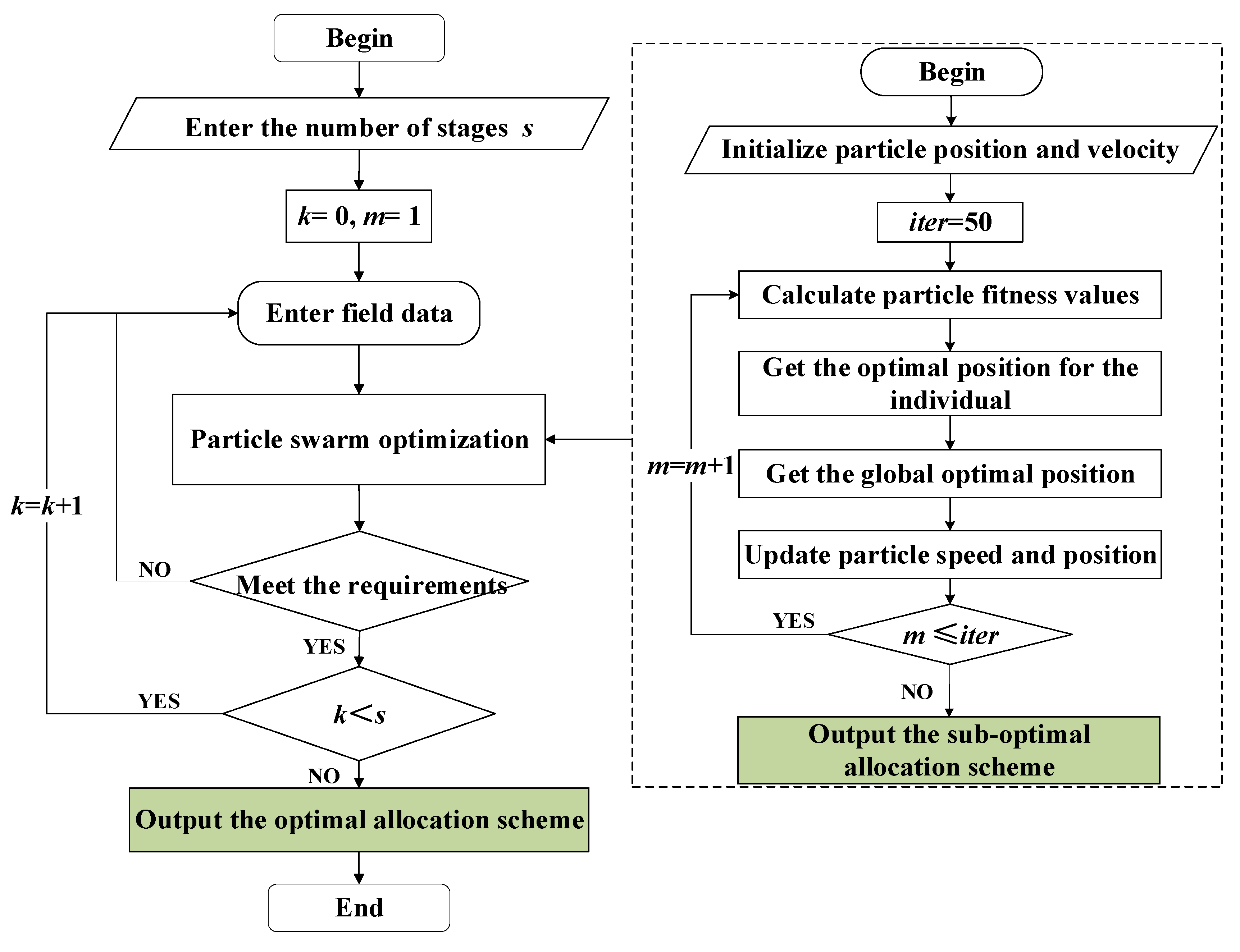
3.1. Standard Dynamic Programming Solving Strategy
3.2. Standard PSO Algorithm
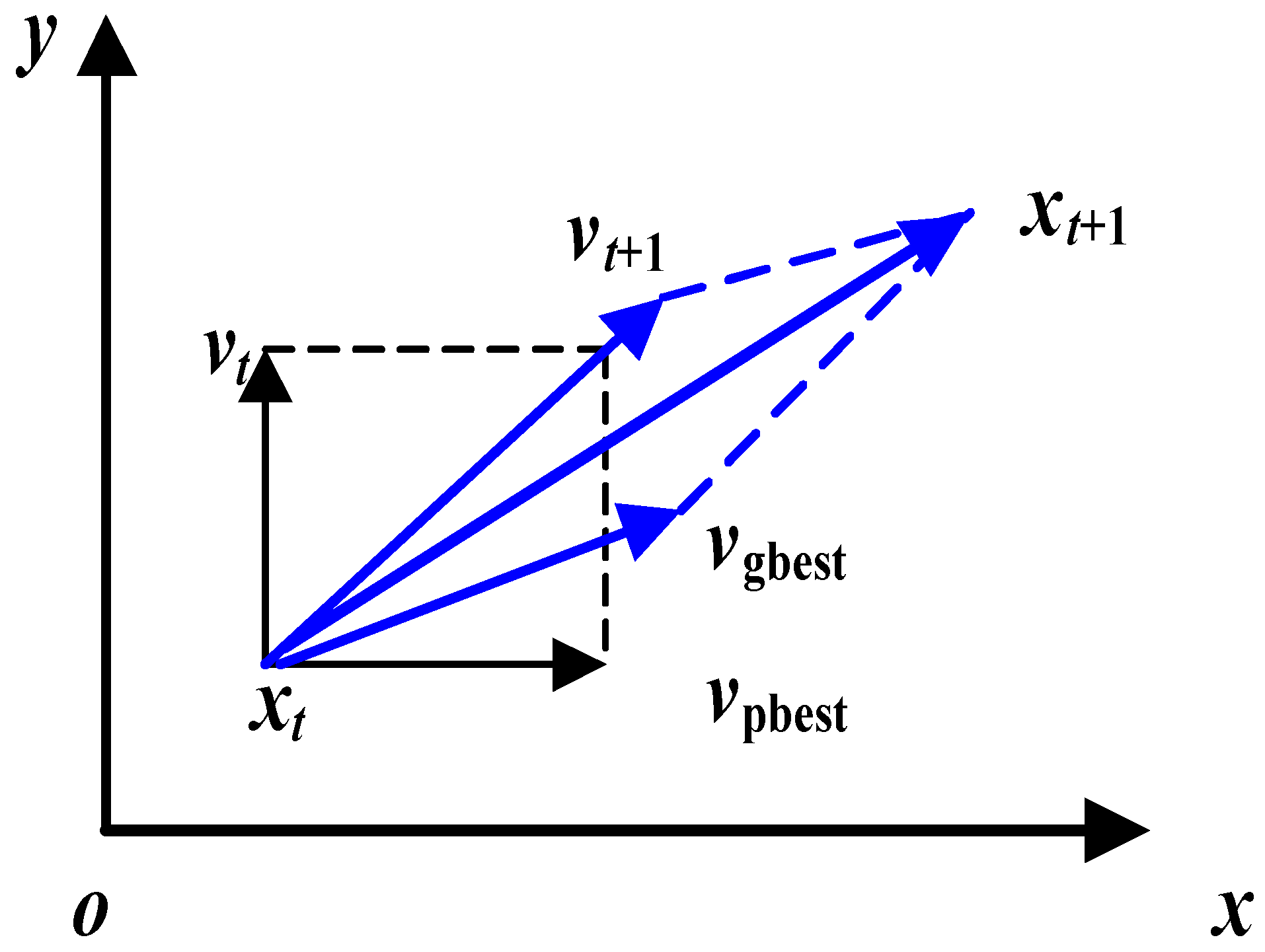
3.2.1. Optimization Strategy
3.2.2. Optimization Process
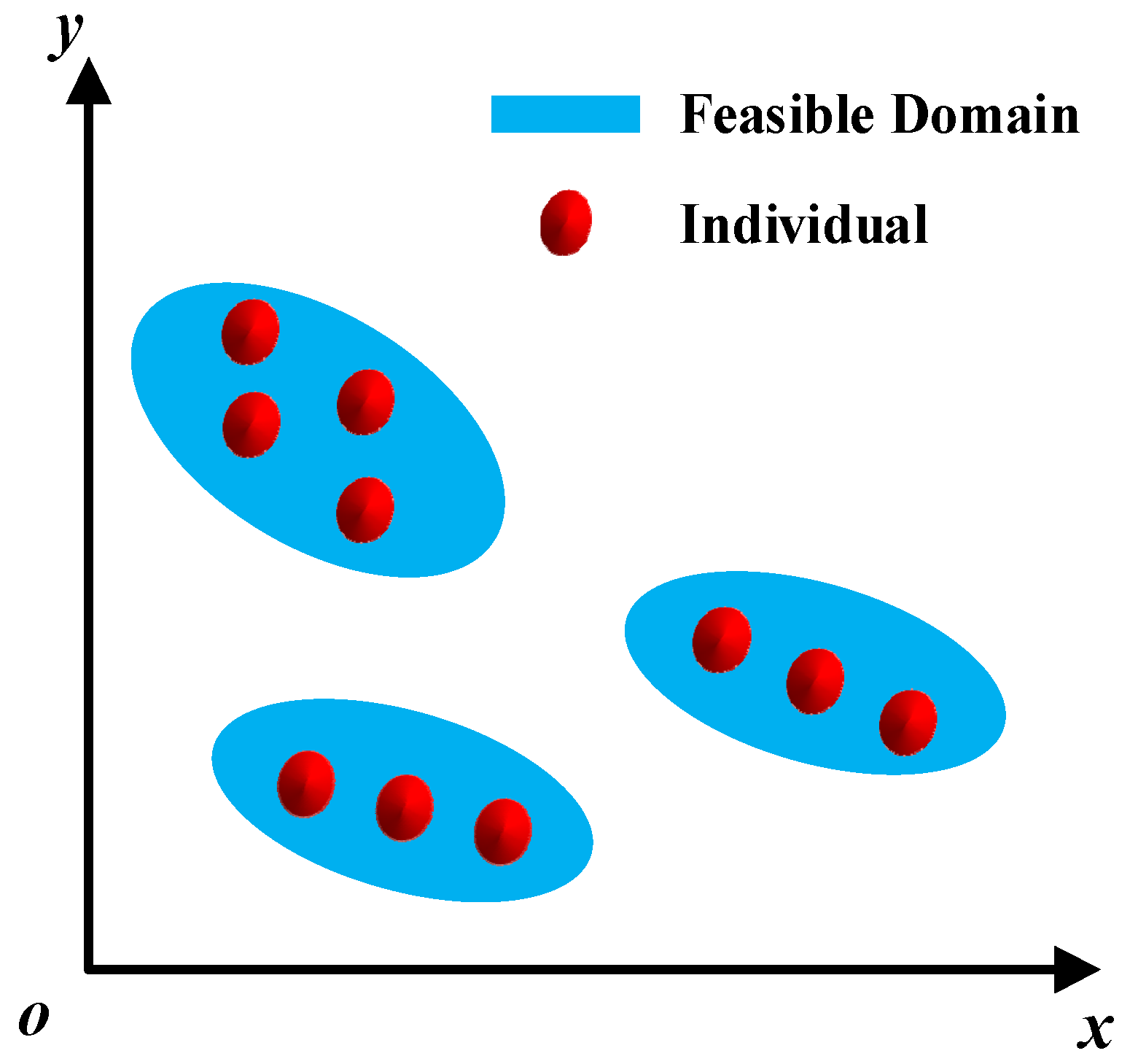
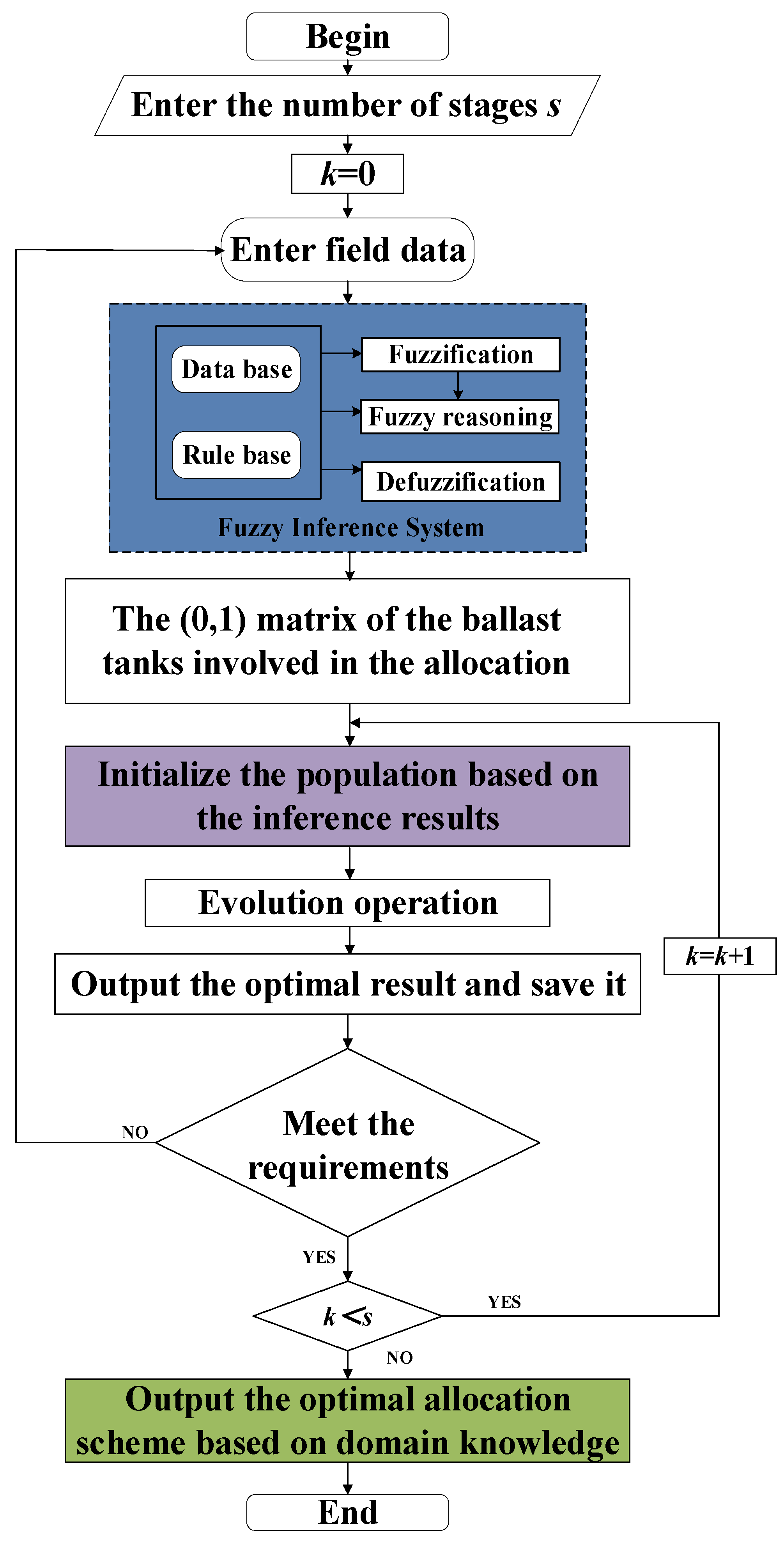
3.3. Fuzzy-Particle Swarm Optimization (FPSO)
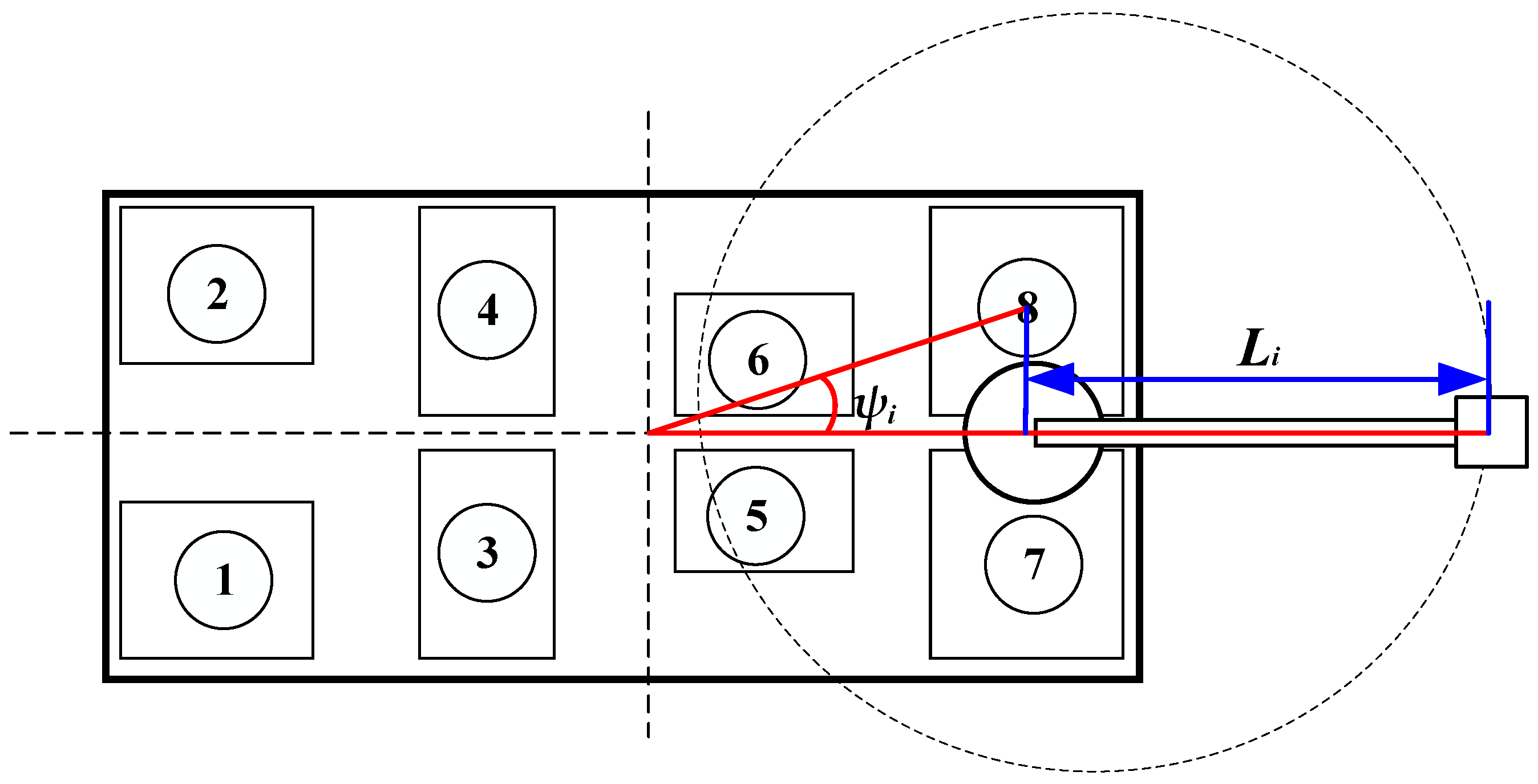
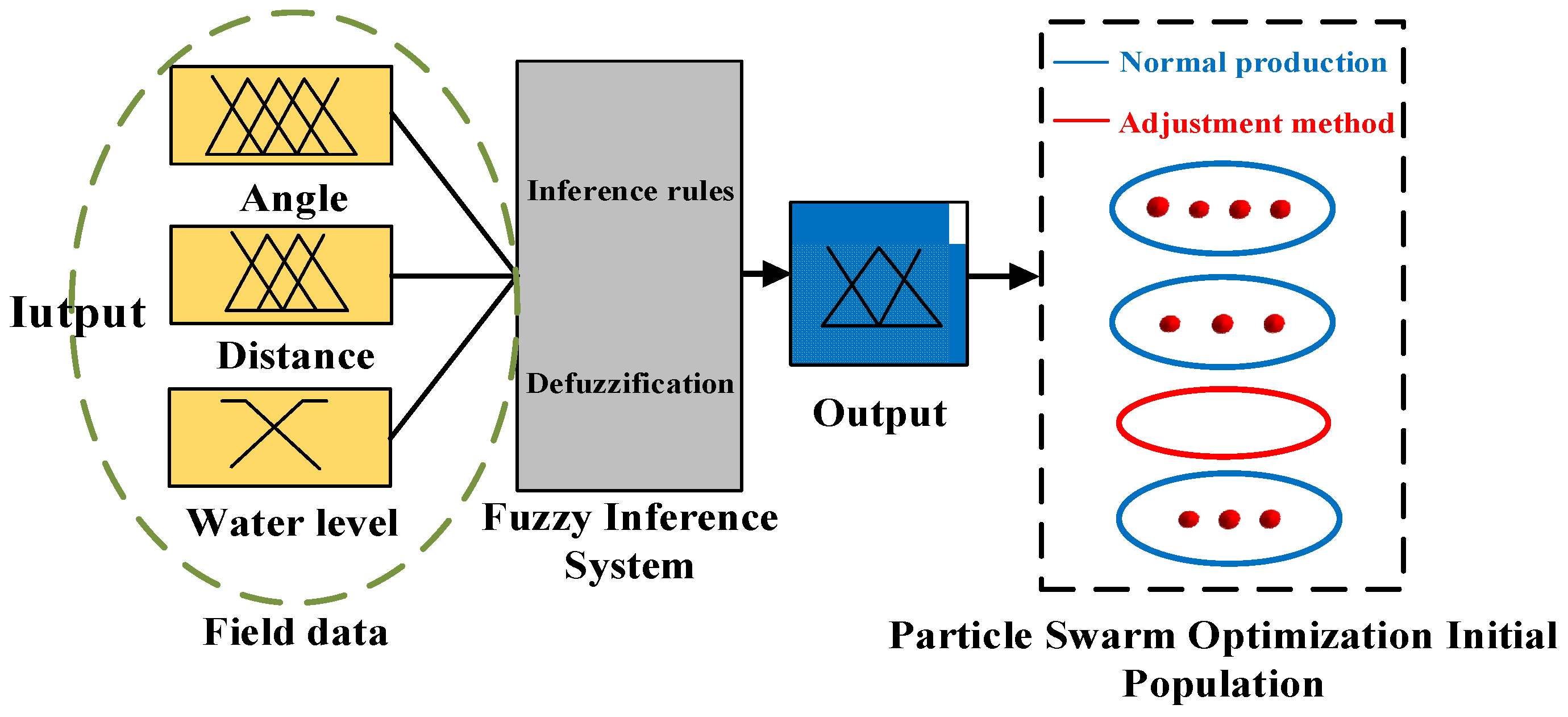
3.3.1. Ballast Tank Selection Method Based on Fuzzy Inference
- (1)
- Design variable selection and fuzzification
- (2)
- Establishment of fuzzy inference rules
- (3)
- Defuzzification
3.3.2. Combining Domain Knowledge with Evolutionary Algorithm
4. Case Analysis and Experimental Verification
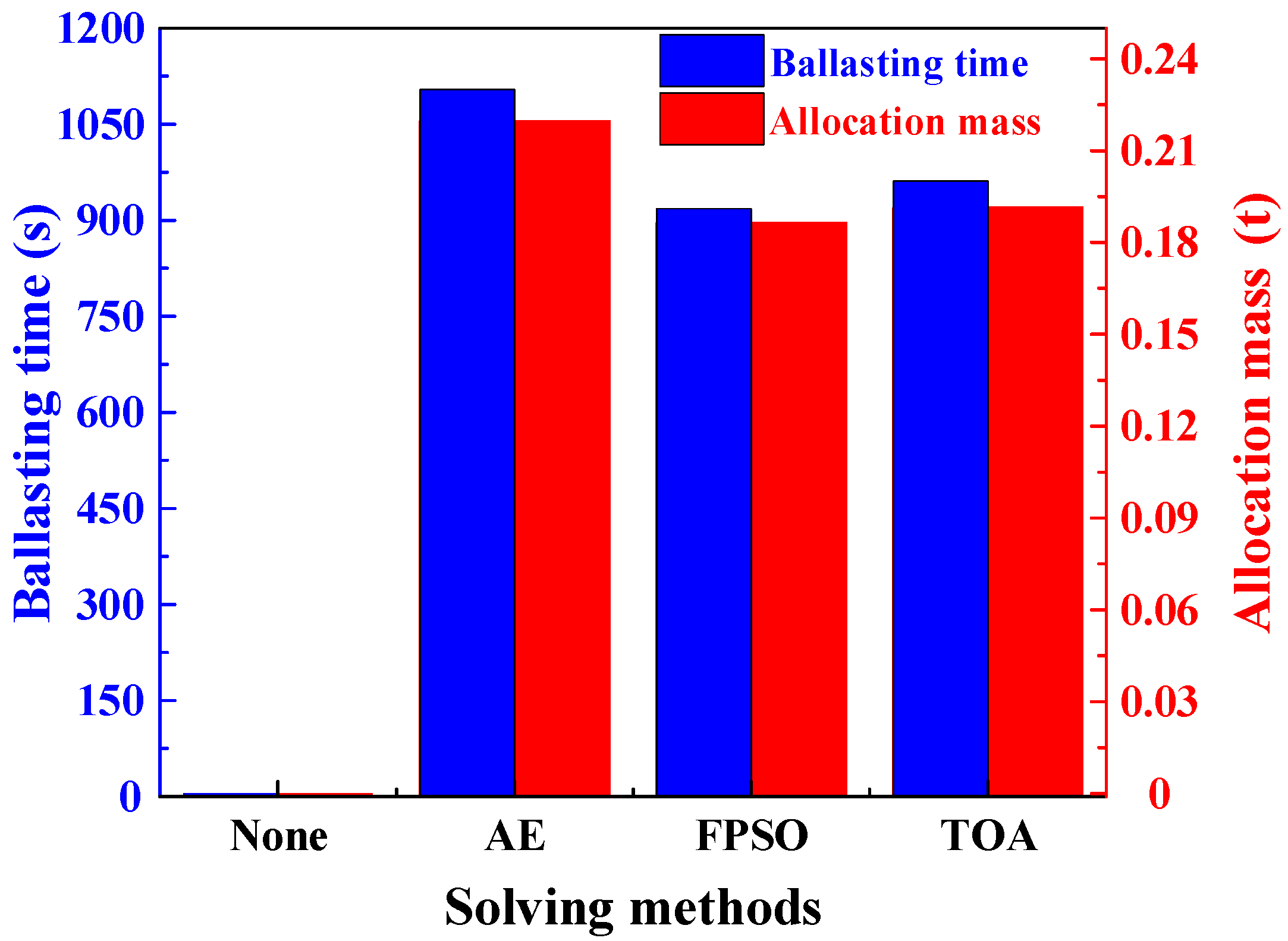
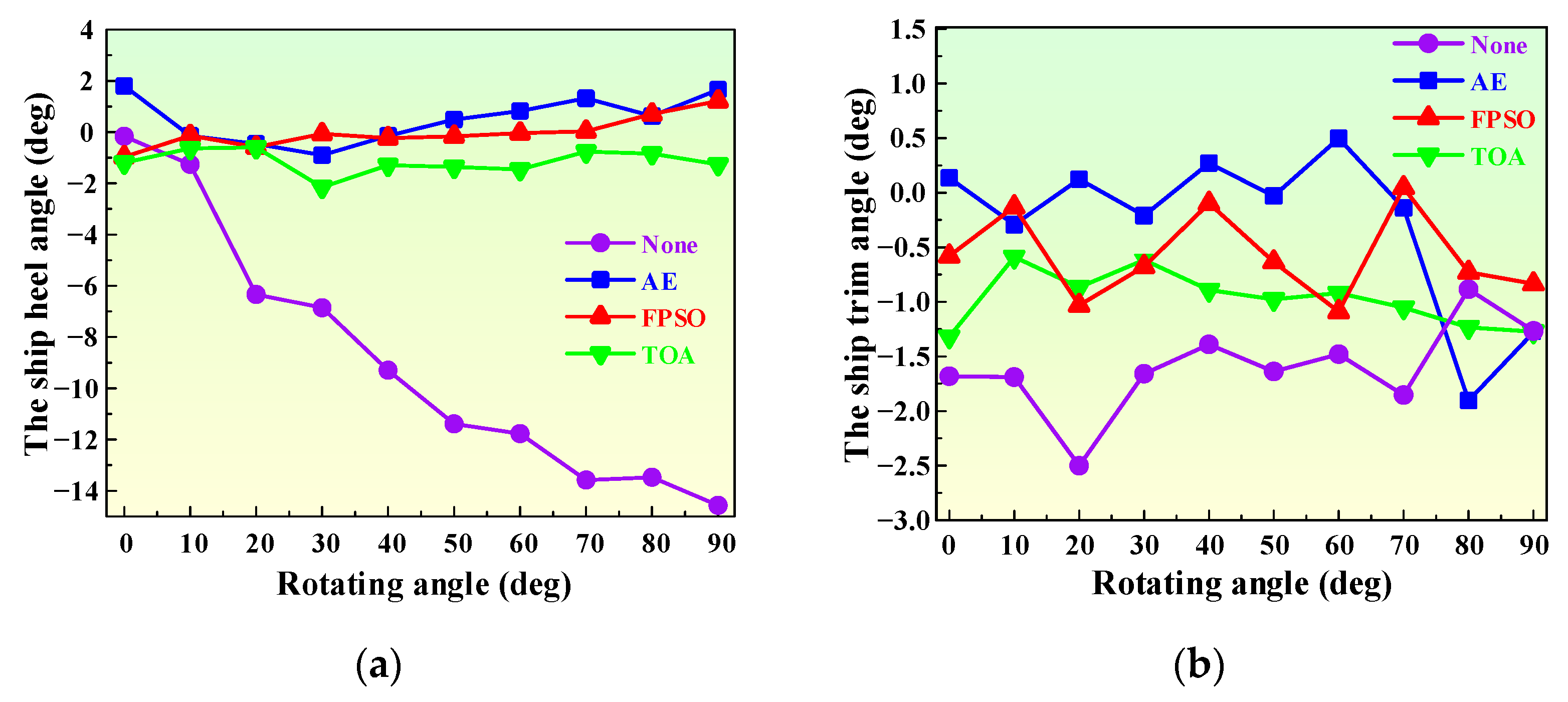
4.1. Feasibility Verification Based on the Experimental RFC
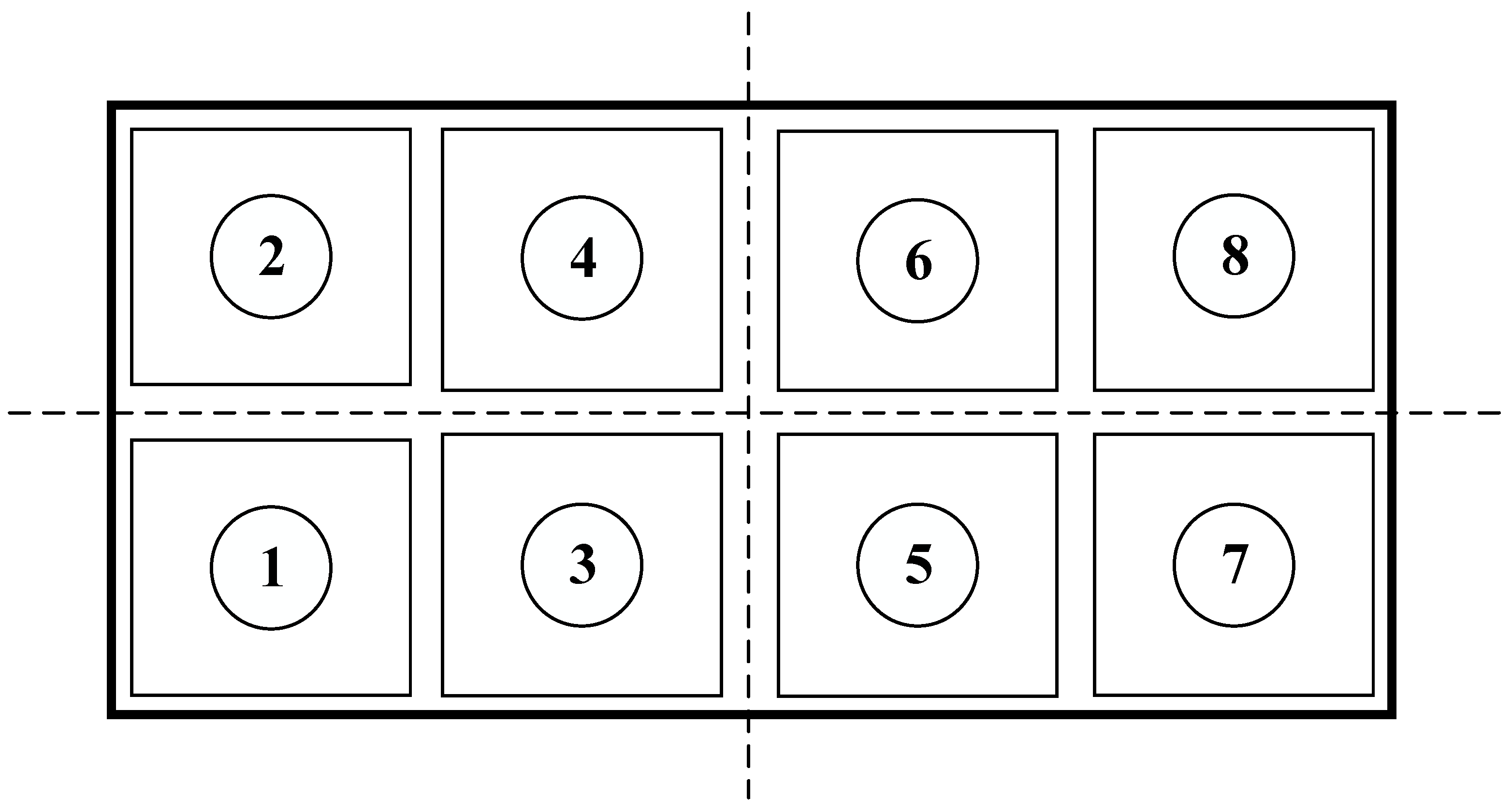
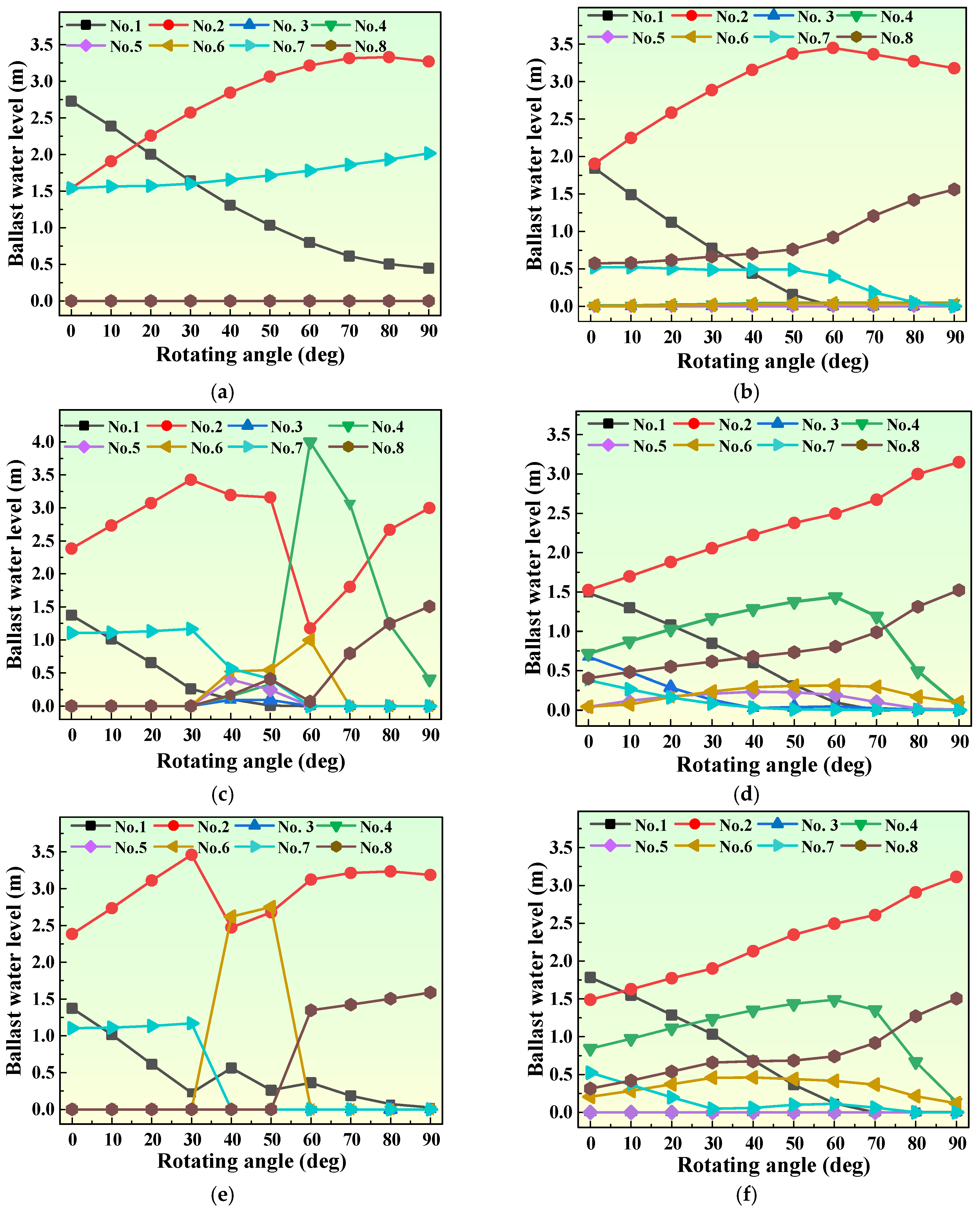
4.2. Ballast Water Allocation Optimization for the RFC with Eight Ballast Tanks
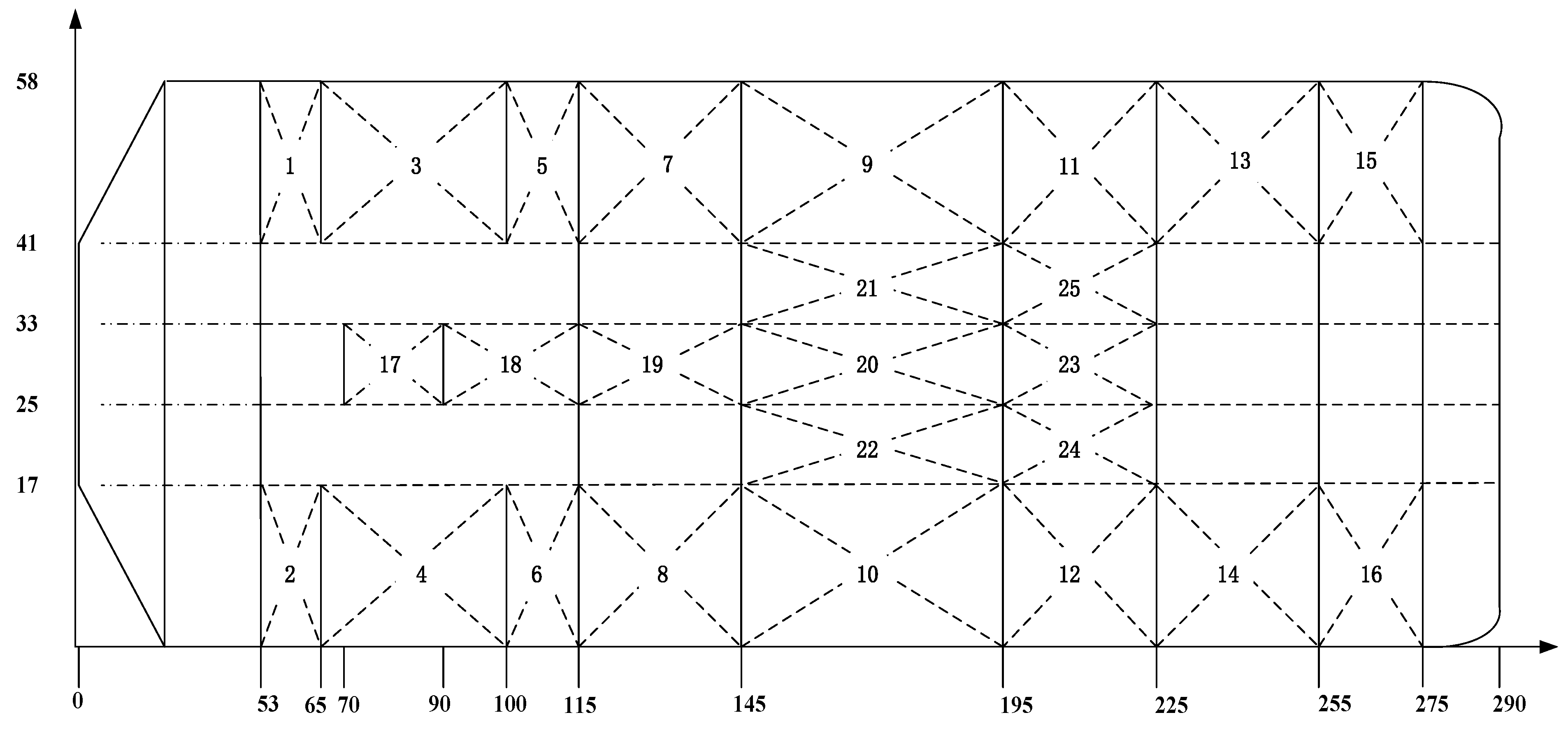
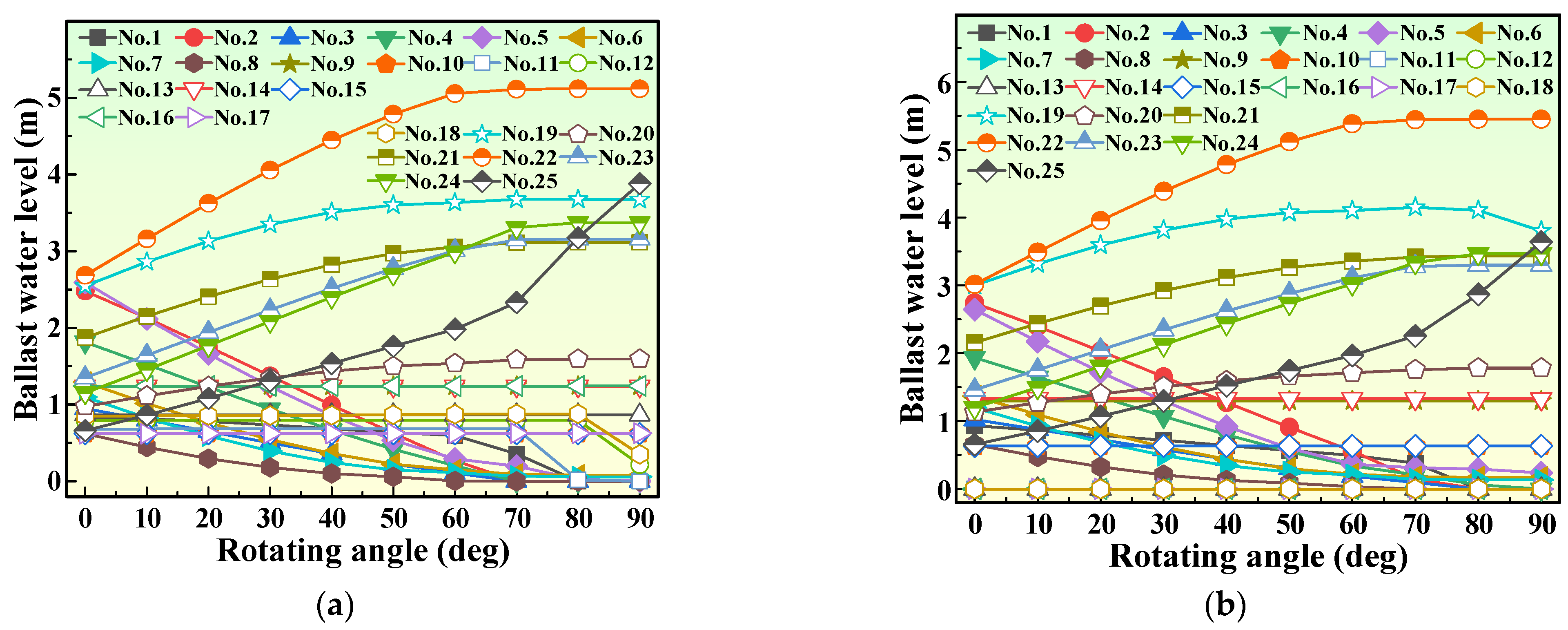
4.3. Ballast Water Allocation Optimization for the RFC with 25 Ballast Tanks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Wei, K.; Xu, H. On the development of my country’s offshore hoisting and salvage operations and basic equipment of large cranes. China Equip. Eng. 2020, 12, 219–220. [Google Scholar]
- Zhang, Q.; Zhang, J.J.; He, J.; Li, Y.F.; Qin, X.R. A method of dynamic modeling of a large floating crane and its external excitations. Adv. Mat. Res. 2010, 139–141, 2440–2445. [Google Scholar] [CrossRef]
- Pan, W.; Xie, X.L.; Bao, T.T.; Wei, Z.K. Research on optimization of ballast water regulation for azimuth crane operation. J. Harbin Eng. Univ. 2019, 40, 189–195. [Google Scholar]
- Samyn, L.M.; Paulo, J.; Cunha, V.S. Dynamic model of a semi-submersible platform for the development of ballast control systems. IFAC Proc. Vol. 2009, 42, 146–151. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, G.X.; Xu, G.H.; Zhang, W.; Wang, W.J. Hovering control of submarine based on L1 adaptive theory via ballast tanks. Int. J. Adv. Robot. Syst. 2017, 14, 172988141772419. [Google Scholar] [CrossRef]
- Meng, X.; Tang, P.; Li, D.J.; Sun, L.L. Optimization decision analysis of ballast allocation scheme for azimuth cranes. Coast. Eng. 2021, 40, 96–106. [Google Scholar]
- Zhou, J.; Song, L. Optimization of ballast water allocation for crane ships based on MOEA/D algorithm. Chin. Ship Res. 2021, 16, 155–163. [Google Scholar]
- Liu, Z.J.; Liu, X.Y.; Xiong, W.; Lin, C.X. Optimization model of ballast water allocation for crane ships. J. Traffic Transp. Eng. 2017, 17, 83–89. [Google Scholar]
- Liu, Z.J.; Jiang, J.Y.; Gan, Z.Q.; Lin, C.X. Ballast water dynamic allocation optimization model and analysis for safe and reliable operation of floating cranes. Ann. Oper. Res. 2022, 311, 279–294. [Google Scholar] [CrossRef]
- Liu, Z.J.; Jiang, J.Y.; Lin, C.X.; Sun, D.P. Ballast water high-efficiency allocation optimisation modelling with dynamic programming for revolving floating cranes. Ships Offshore Struc. 2018, 13, 857–867. [Google Scholar] [CrossRef]
- Zheng, Q.; Feng, B.W.; Liu, Z.Y.; Chang, H.C. Application of Improved Particle Swarm Optimisation Algorithm in Hull form Optimisation. J. Mar. Sci. Eng. 2021, 9, 955. [Google Scholar] [CrossRef]
- Xu, X.J.; Wang, L.Q.; Fang, X.M.; Li, Z. Interactive visual simulation and numerical simulation of offshore lifting operations. J. Harbin Inst. Technol. 2018, 50, 160–168. [Google Scholar]
- Wu, G.Q. Research on failure visualization of ship deck crane using PLC control. Ship Sci. Technol. 2022, 44, 161–164. [Google Scholar]
- Nam, J.H.; Kim, D.H. Construction of a preliminary simulation system for real-time prediction of ship ballasting process. J. Ship Prod. Des. 2010, 26, 163–172. [Google Scholar]
- Liu, Y.S.; Zhao, X.F.; Wu, D.F.; Li, D.L.; Li, X.H. Study on the control methods of a water hydraulic variable ballast system for submersible vehicles. Ocean Eng. 2015, 108, 648–661. [Google Scholar] [CrossRef]
- Zhao, X.F.; Liu, Y.S.; Han, M.X.; Wu, D.F.; Li, D.L. Improving the performance of an AUV hovering system by introducing low-cost flow rate control into water hydraulic variable ballast system. Ocean Eng. 2016, 125, 155–169. [Google Scholar] [CrossRef]
- Jesse, D.; Robert, B.; Mae, S. Coupled hydroplane and variable ballast control system for autonomous underwater vehicle altitude-keeping to variable seabed. IEEE J. Oceanic. Eng. 2018, 43, 837–887. [Google Scholar]
- Zhu, K.J.; Wang, L.P.; Shen, M.; Dong, J. An experience-based multi-lead decision model for electrocardiogram wave boundary detection. In Proceedings of the International Conference on Biomedical Engineering and Informatics, IEEE, Yantai, China, 16–18 October 2010; pp. 735–739. [Google Scholar]
- Mohammad, B. Development of an expert system for optimal design of the grinding process. Int. J. Adv. Manuf. Technol. 2021, 116, 2823–2833. [Google Scholar]
- Rogulj, K. Knowledge-based fuzzy expert system to the condition assessment of historic road bridges. Appl. Sci. 2021, 11, 1021. [Google Scholar] [CrossRef]
- Mahbub, M.S.; Wagner, M. Incorporating domain knowledge into the optimization of energy systems. Appl. Soft Comput. 2016, 47, 483–493. [Google Scholar] [CrossRef]
- Xiao, Y.J. Research on fault diagnosis method of rapier loom based on the fusion of expert system and fault tree. J. Intell. Fuzzy Syst. 2021, 41, 3429–3441. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Optimization of large-scale hydropower system peak operation with hybrid dynamic programming and domain knowledge. J. Clean. Prod. 2018, 171, 390–402. [Google Scholar] [CrossRef]
- Garcia, H.L.; Palomo, R.J.M.; Salas, M.L.; Arauzo, A.A.; Pierreval, H. A novel hybrid evolutionary approach for capturing decision maker knowledge into the unequal area facility layout problem. Expert Syst. Appl. 2015, 42, 4697–4708. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Nguyen, V.T.T.; Nguyen, Q.M.; Huynh, N.T.; Huynh, T.T. Optimal Design for Compliant Mechanism Flexure Hinges: Bridge-Type. Micromachines 2021, 12, 1304. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.V.T.; Huynh, N.T.; Vu, N.C.; Kieu, V.N.D.; Huang, S.C. Optimizing compliant gripper mechanism design by employing an effective bi-algorithm: Fuzzy logic and ANFIS. Microsyst. Technol. 2021, 27, 3389–3412. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Zhang, Z.; Wang, H. Multicriteria Ship Route Planning Method Based on Improved Particle Swarm Optimization–Genetic Algorithm. J. Mar. Sci. Eng. 2021, 9, 357. [Google Scholar] [CrossRef]
- Ji, C.M.; Jiang, Z.Q.; Sun, P.; Zhang, Y.K.; Wang, L.P. Research and application of multidimensional dynamic programming in cascade reservoirs based on multilayer nested structure. J. Water Res. Plan. Man. 2014, 141, 04014090. [Google Scholar] [CrossRef]
- Russell, E.; James, K. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, IEEE, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Syed, A.H.; Palani, K.K. Optimization of specific energy consumption in turning of GFRP composites using particle swarm optimization. Int. J. Innov. Technol. Explor. Eng. 2021, 10, 11–17. [Google Scholar]




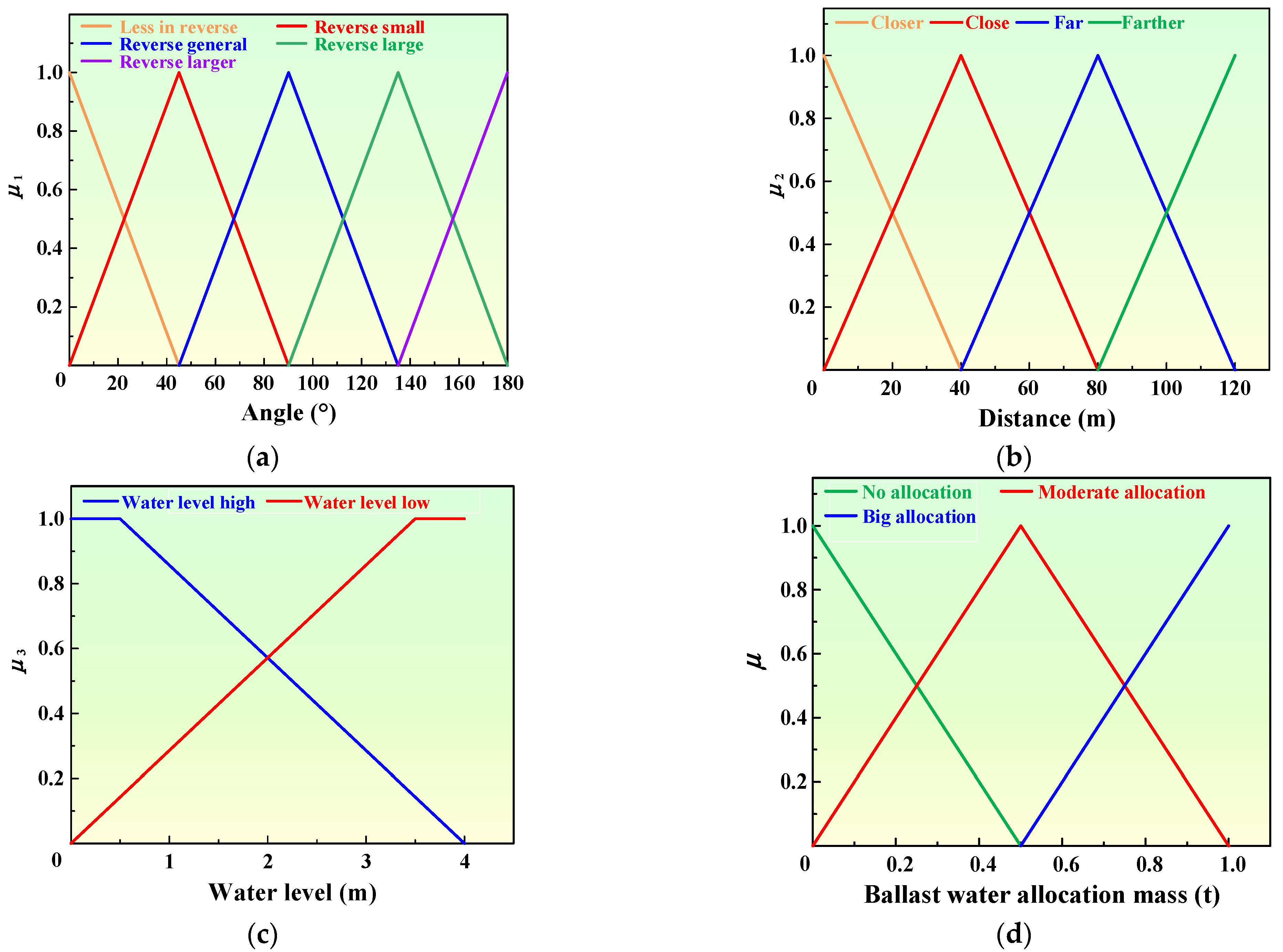





| Fuzzy Rule Antecedents | Reasoning Conclusion | |||
|---|---|---|---|---|
| Rule Number | Angle | Distance | Water Level | Ballast Water Allocation |
| 1 | Less in reverse | Closer | High | Big |
| 2 | Less in reverse | Closer | Low | No allocation |
| 3 | Reverse small | Closer | High | Moderate |
| 4 | Reverse general | Close | High | No allocation |
| 5 | Reverse large | Far | Low | Big |
| 6 | Reverse large | Far | High | No allocation |
| 7 | Reverse larger | Far | Low | Moderate |
| 8 | Reverse general | Farther | Low | No allocation |
| Parameters | Value |
|---|---|
| Total length (m) | 4.5 |
| Width (m) | 1.5 |
| Depth (m) | 0.7 |
| Ship mass (t) | 0.8 |
| Boom length (m) | 1.12 |
| Crane lifting capacity (t) | 0.1 |
| Ballast pump flow rate (m3·h−1) | 2 |
| Parameters | Value |
|---|---|
| Total length (m) | 100 |
| Width (m) | 30 |
| Depth (m) | 8 |
| Lifting capacity (t) | 2000 |
| Boom length (m) | 30 |
| Ballast pump flow rate (t·h−1) | 3000 |
| Solving Algorithm | AE | TOA | GA | PSO | FGA | FPSO |
|---|---|---|---|---|---|---|
| Number of ballast tanks involved in allocation | 3 | 8 | 8 | 6 | 6 | 6 |
| Calculation time (s) | ___ | 2193 | 1192 | 653 | 542 | 247 |
| Allocation mass (t) | 1300 | 2327 | 1921 | 1341 | 1510 | 1127 |
| Operation time (h) | 0.497 | 0.806 | 0.702 | 0.509 | 0.541 | 0.417 |
| Satisfaction | 6 | 4 | 5 | 6 | 6 | 8 |
| Parameters | Value |
|---|---|
| Total length (m) | 290 |
| Width (m) | 58 |
| Depth (m) | 28.8 |
| Lifting capacity (t) | 12,000 |
| Boom length (m) | 54 |
| Number of ballast tanks | 25 |
| Ballast pump flow rate (m3·h−1) | 6 × 4000 |
| Solving Algorithm | PSO | FPSO |
|---|---|---|
| Number of ballast tanks involved in allocation | 25 | 19 |
| Allocation mass (t) | 1201.6 | 1065 |
| Operation time (h) | 0.645 | 0.443 |
| Calculation time (s) | 2600 | 2105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Lu, Z.; Liu, Z.; Lin, P.; Wang, X. Ballast Water Dynamic Allocation Optimization for Revolving Floating Cranes Based on a Hybrid Algorithm of Fuzzy-Particle Swarm Optimization with Domain Knowledge. J. Mar. Sci. Eng. 2022, 10, 1454. https://doi.org/10.3390/jmse10101454
Liu Q, Lu Z, Liu Z, Lin P, Wang X. Ballast Water Dynamic Allocation Optimization for Revolving Floating Cranes Based on a Hybrid Algorithm of Fuzzy-Particle Swarm Optimization with Domain Knowledge. Journal of Marine Science and Engineering. 2022; 10(10):1454. https://doi.org/10.3390/jmse10101454
Chicago/Turabian StyleLiu, Qiao, Zhenxing Lu, Zhijie Liu, Peng Lin, and Xiaobang Wang. 2022. "Ballast Water Dynamic Allocation Optimization for Revolving Floating Cranes Based on a Hybrid Algorithm of Fuzzy-Particle Swarm Optimization with Domain Knowledge" Journal of Marine Science and Engineering 10, no. 10: 1454. https://doi.org/10.3390/jmse10101454
APA StyleLiu, Q., Lu, Z., Liu, Z., Lin, P., & Wang, X. (2022). Ballast Water Dynamic Allocation Optimization for Revolving Floating Cranes Based on a Hybrid Algorithm of Fuzzy-Particle Swarm Optimization with Domain Knowledge. Journal of Marine Science and Engineering, 10(10), 1454. https://doi.org/10.3390/jmse10101454





