Numerical and Experimental Study on the Bragg Reflection of Water Waves by Multiple Vertical Thin Plates
Abstract
1. Introduction
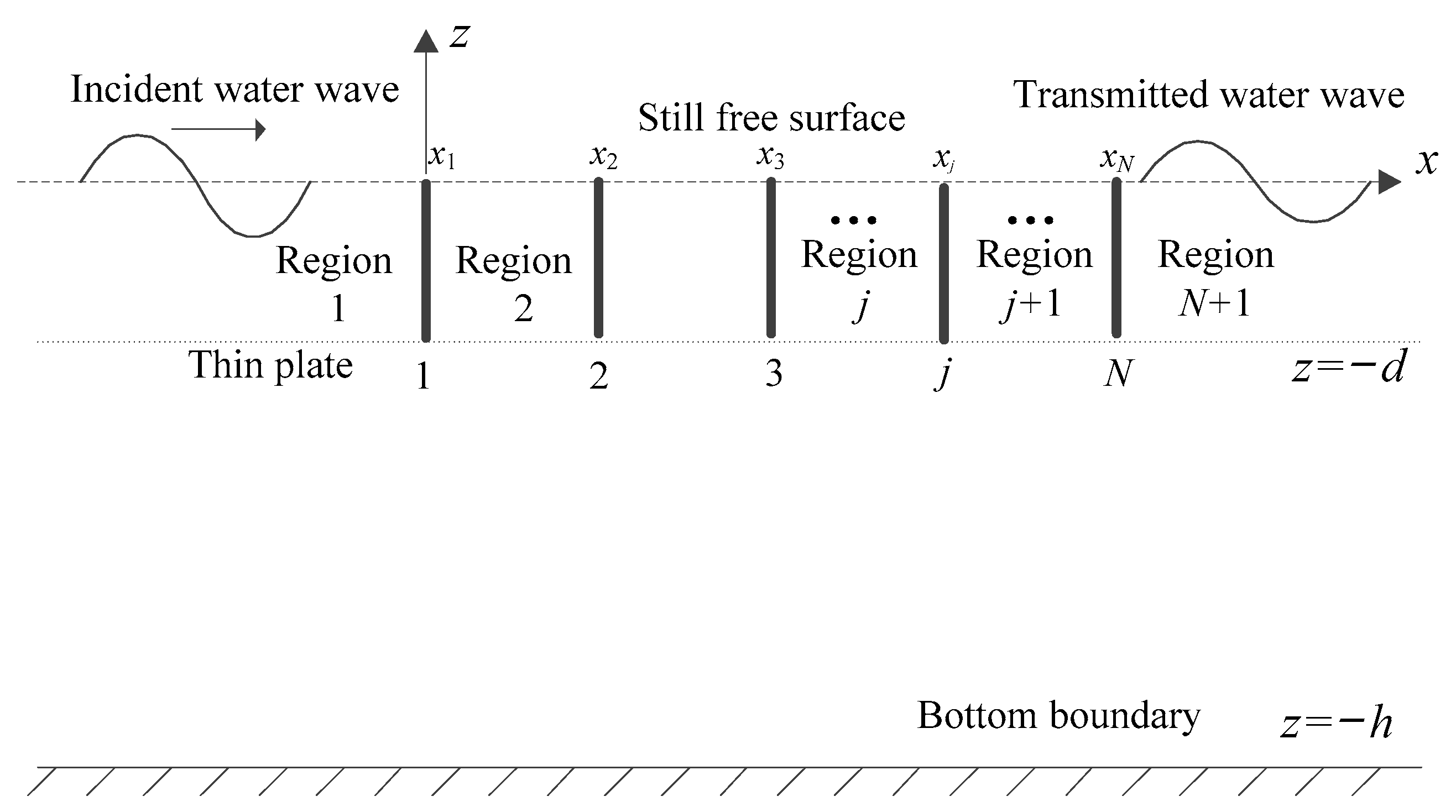
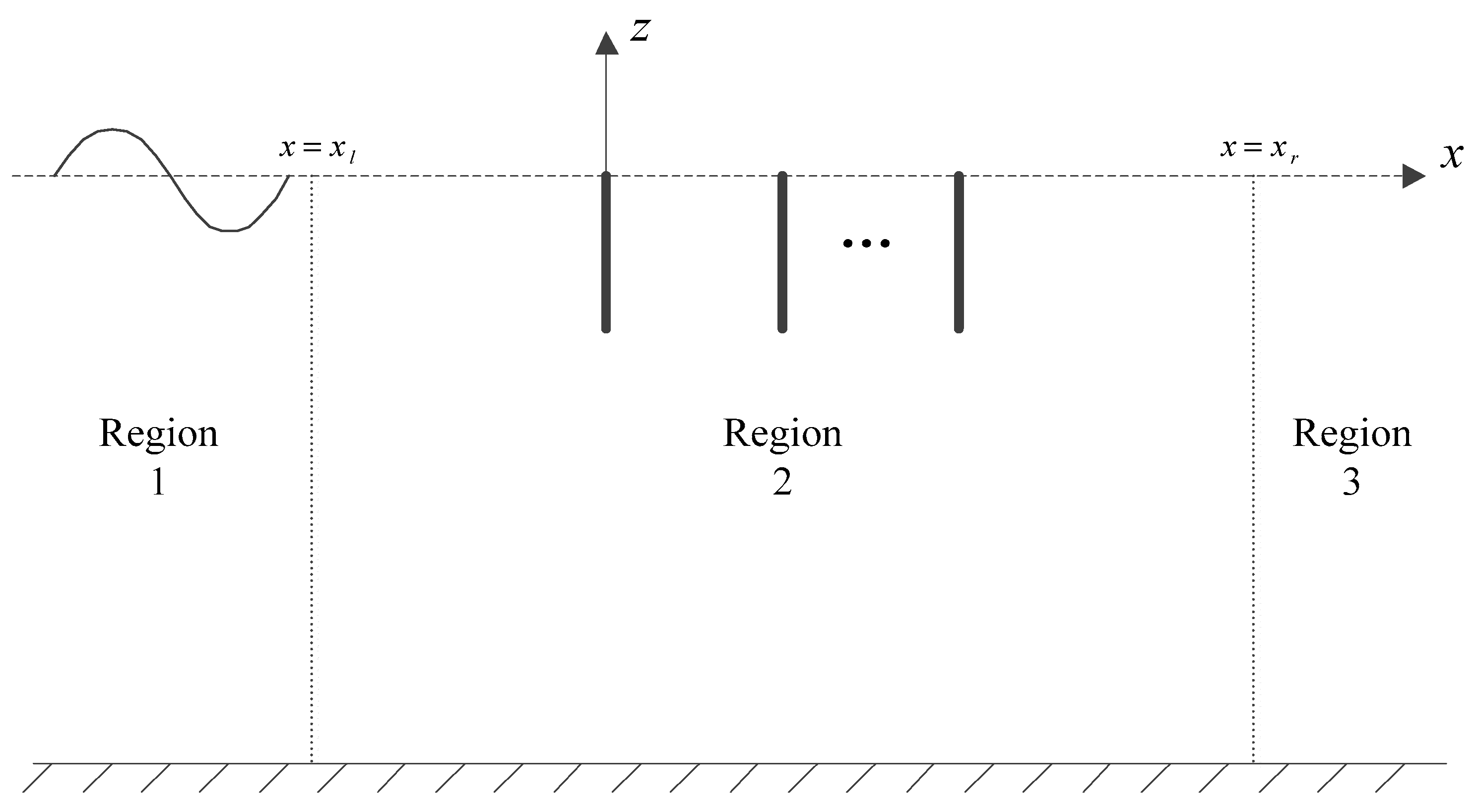
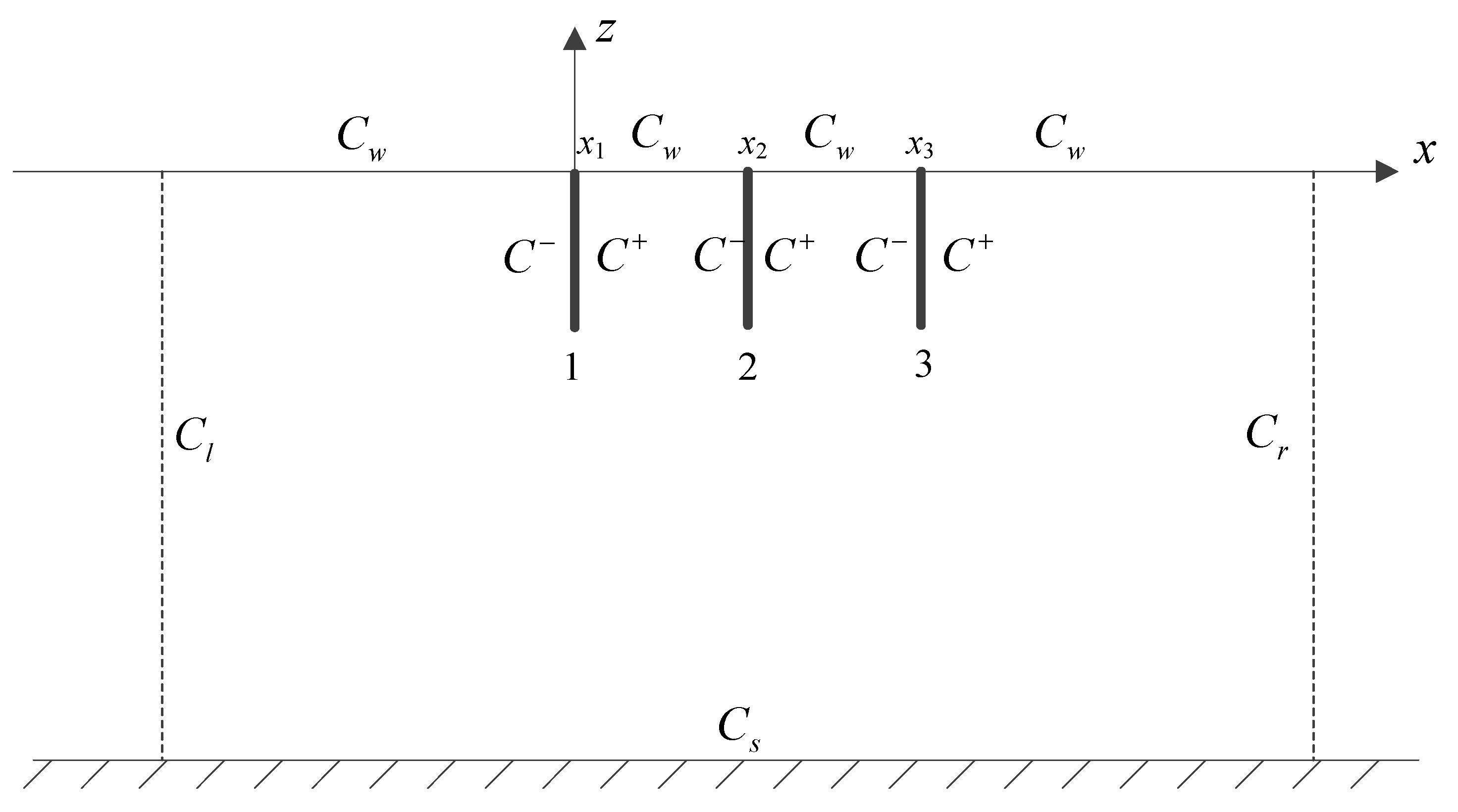
2. Mathematical Formulation
3. Numerical Solutions
4. Numerical Results and Discussion
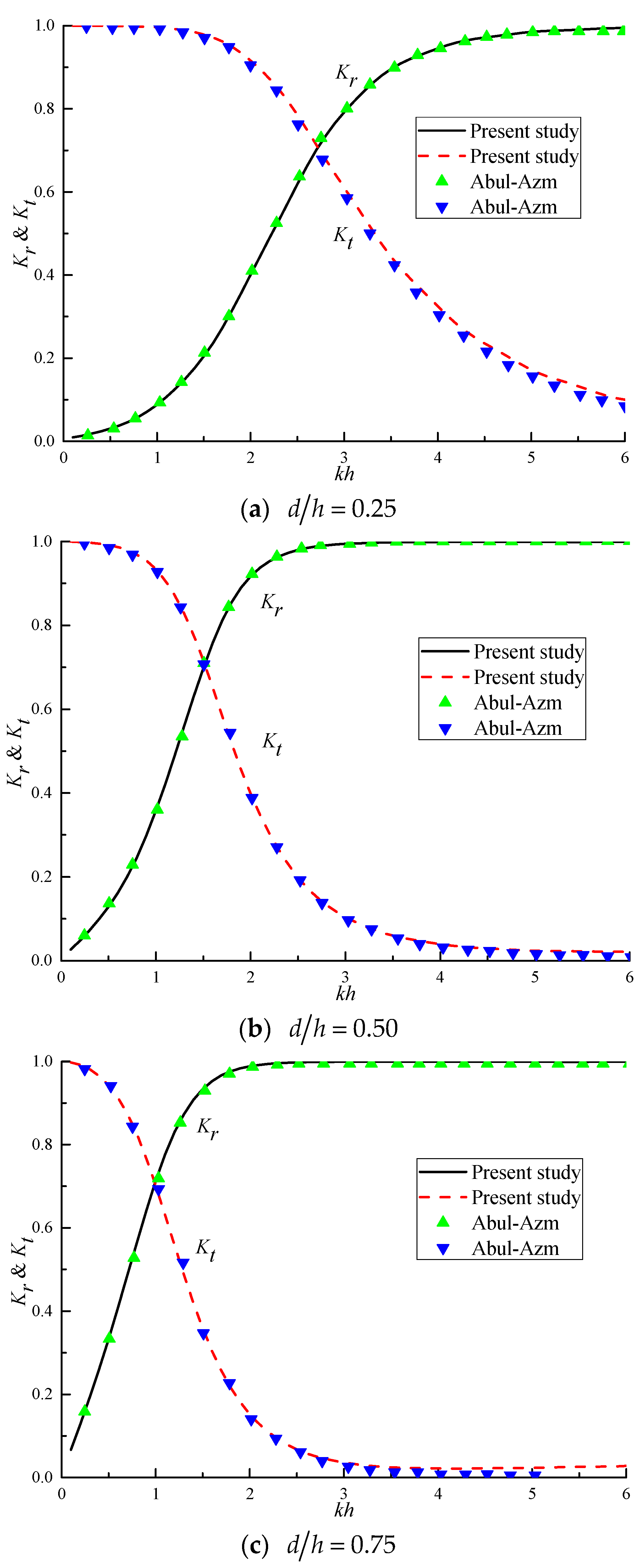
4.1. Validation of the Present Method
4.2. Definition of the Characteristics of Bragg Reflection
4.3. Effects of the Number of Plates
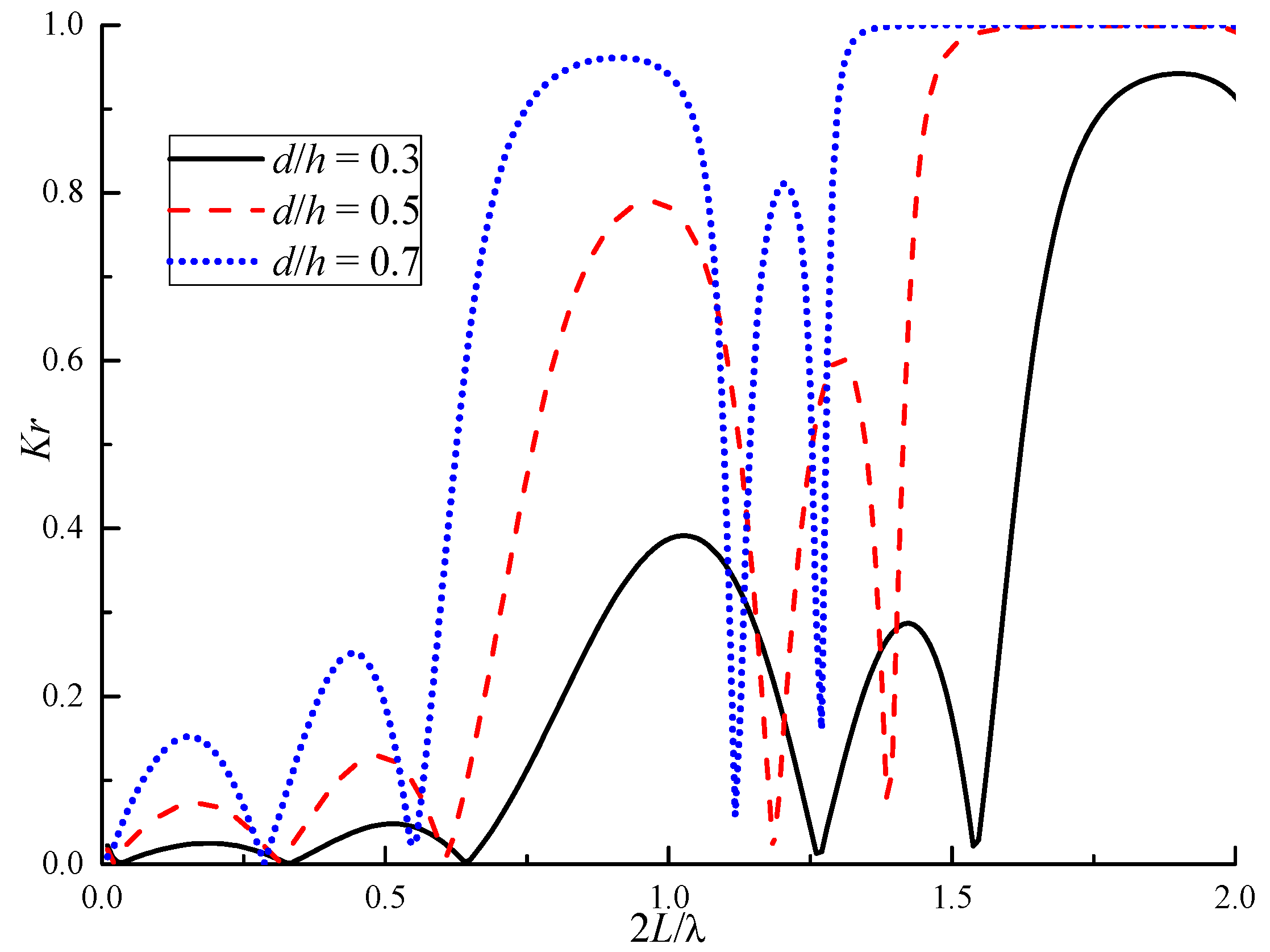
4.4. Effects of the Immerged Depth of Plates
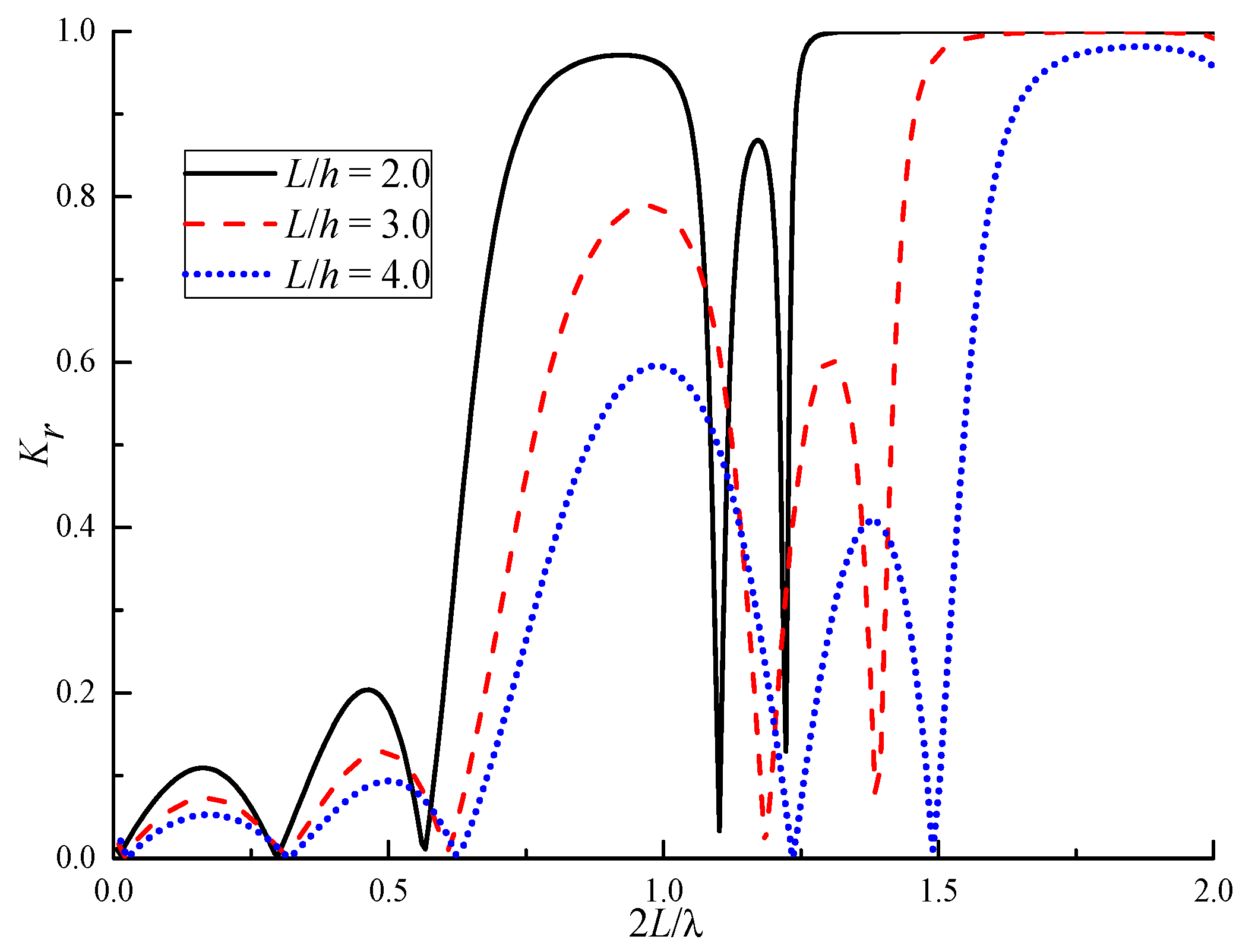
4.5. Effects of the Spacing of Plates
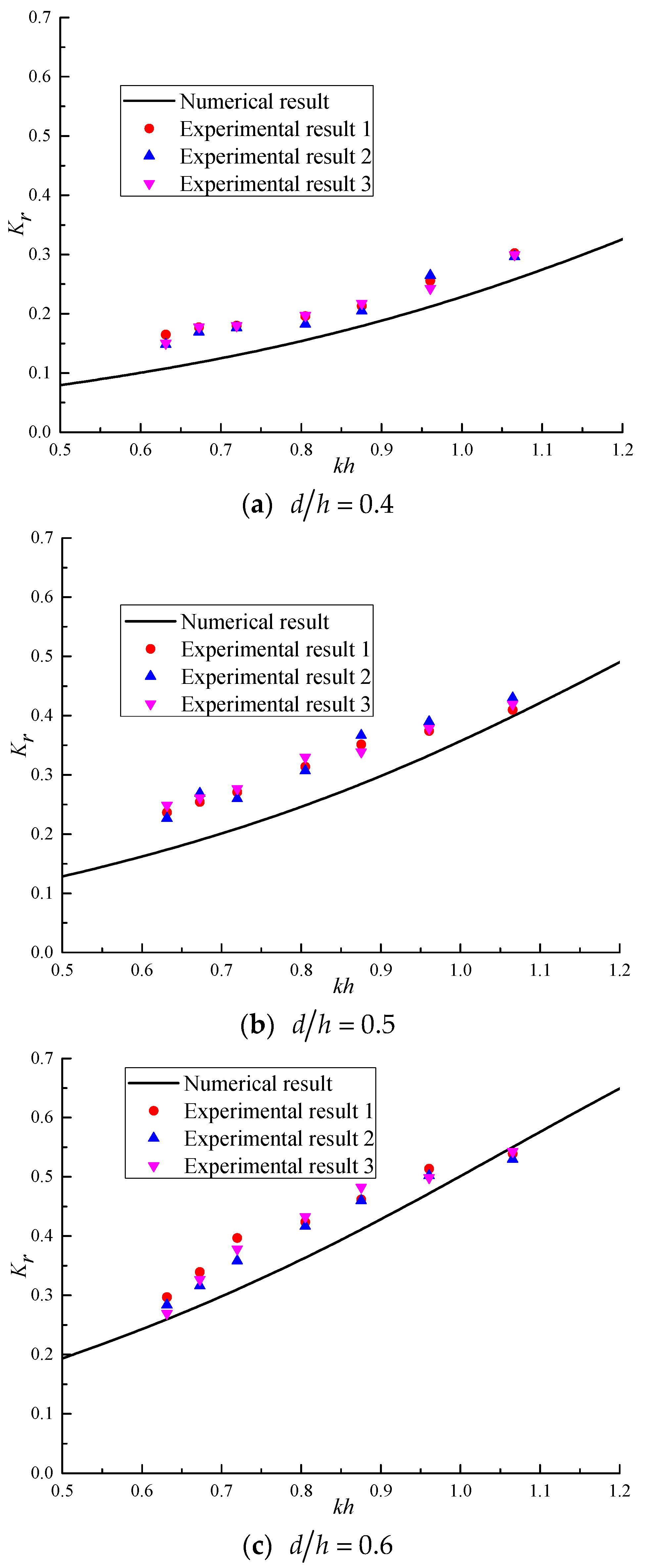
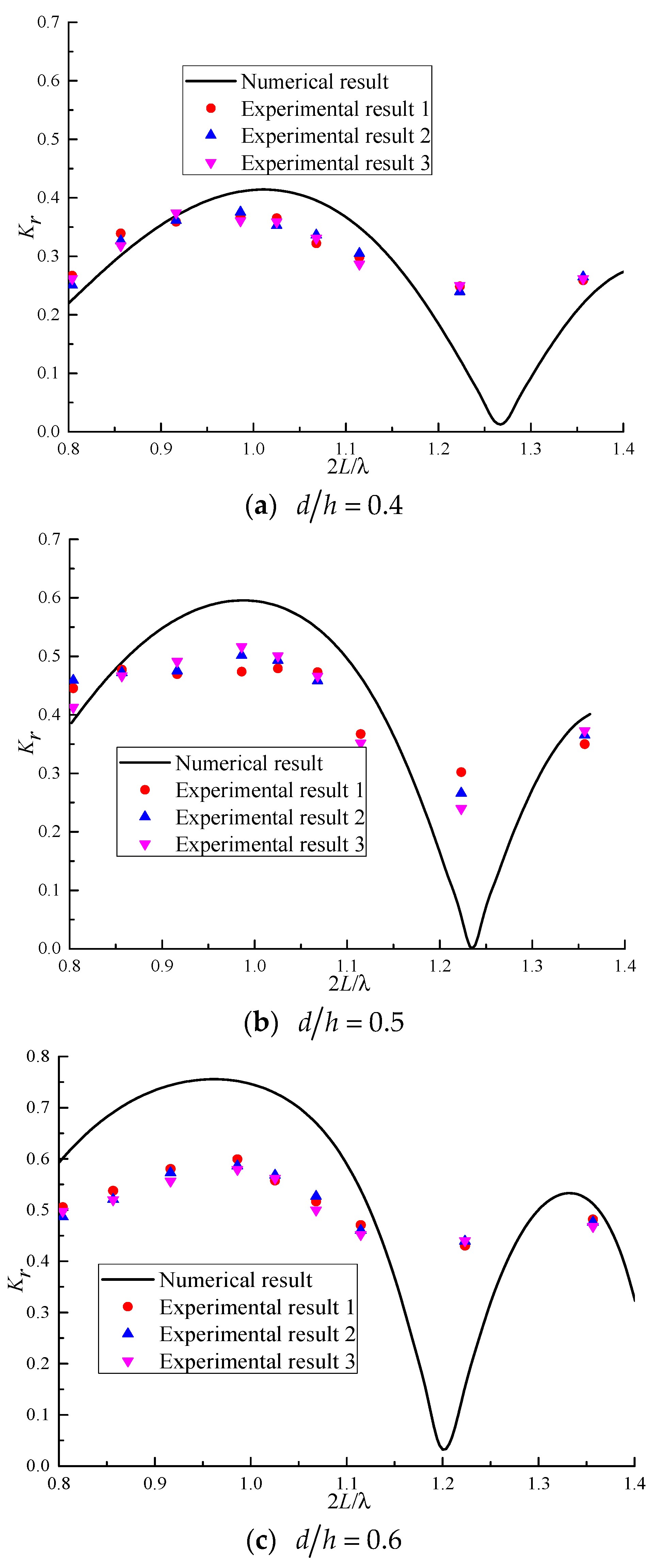
5. Model Experiments
5.1. Set-Up and Procedure
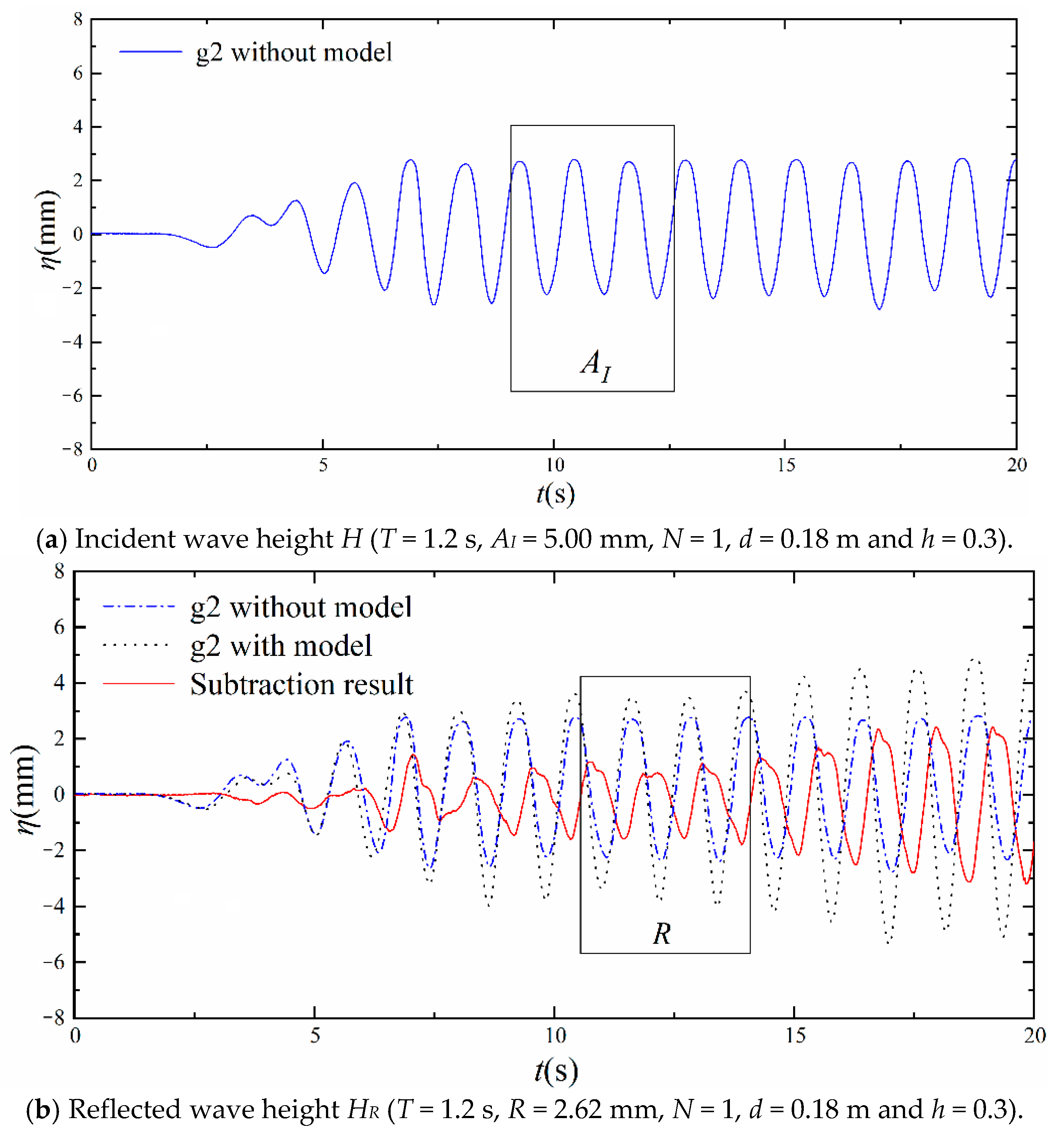
5.2. Comparison of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bragg, W.H.; Bragg, W.L. The reflection of X-rays by crystals. Proc. R. Soc. Lond. Ser. A-Math. Phys. Character 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Heathershaw, A.D. Seabed-wave resonance and sand bar growth. Nature 1982, 296, 343–345. [Google Scholar] [CrossRef]
- Mei, C.C.; Hara, T.; Naciri, M. Note on Bragg scattering of water waves by parallel bars on the seabed. J. Fluid Mech. 1988, 186, 147–162. [Google Scholar] [CrossRef]
- Bailard, J.A.; DeVries, J.W.; Kirby, J.T. Considerations in using Bragg reflection for storm erosion protection. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 62–74. [Google Scholar] [CrossRef]
- Tao, A.F.; Yan, J.; Wang, Y.; Zheng, J.H.; Fan, J.; Qin, C. Wave power focusing due to the Bragg resonance. China Ocean Eng. 2017, 31, 458–465. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zhang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Chang, J.Y.; Tsai, C.C. Wave forces on a partially reflecting wall by oblique Bragg scattering with porous breakwaters over uneven bottoms. J. Mar. Sci. Eng. 2022, 10, 409. [Google Scholar] [CrossRef]
- Zeng, H.; Qin, B.; Zhang, J. Optimal collocation of Bragg breakwaters with rectangular bars on sloping seabed for Bragg resonant reflection by long waves. Ocean Eng. 2017, 130, 156–165. [Google Scholar] [CrossRef]
- Ni, Y.L.; Teng, B. Bragg resonant reflection of water waves by a Bragg breakwater with porous rectangular bars on a sloping permeable seabed. Ocean Eng. 2021, 235, 109333. [Google Scholar] [CrossRef]
- Chang, H.K.; Liou, J.C. Long wave reflection from submerged trapezoidal breakwaters. Ocean Eng. 2007, 34, 185–191. [Google Scholar] [CrossRef]
- Liu, H.W.; Zeng, H.D.; Huang, H.D. Bragg resonant reflection of surface waves from deep water to shallow water by a finite array of trapezoidal bars. Appl. Ocean Res. 2020, 94, 101976. [Google Scholar] [CrossRef]
- Kar, P.; Koley, S.; Sahoo, T. Bragg scattering of long waves by an array of trenches. Ocean Eng. 2020, 198, 107004. [Google Scholar] [CrossRef]
- Guo, F.C.; Liu, H.W.; Pan, J.J. Phase downshift or upshift of Bragg resonance for water wave reflection by an array of cycloidal bars or trenches. Wave Motion 2021, 106, 102794. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Zhu, L. Bragg reflection of water waves by multiple submerged semi-circular breakwaters. Appl. Ocean Res. 2016, 56, 67–78. [Google Scholar] [CrossRef]
- Li, A.; Liu, Y.; Liu, X.; Zhao, Y. Analytical and experimental studies on Bragg scattering of water waves by multiple submerged perforated semi-circular breakwaters. Ocean Eng. 2020, 209, 107419. [Google Scholar] [CrossRef]
- Liu, H.W.; Shi, Y.P.; Cao, D.Q. Optimization of parabolic bars for maximum Bragg resonant reflection of long waves. J. Hydrodyn. 2015, 27, 373–382. [Google Scholar] [CrossRef]
- Hao, J.; Li, J.; Liu, S.; Wang, L. Wave amplification caused by Bragg resonance on parabolic-type topography. Ocean Eng. 2022, 244, 110442. [Google Scholar] [CrossRef]
- Liu, H.W. Band gaps for Bloch waves over an infinite array of trapezoidal bars and triangular bars in shallow water. Ocean Eng. 2017, 130, 72–82. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, A.; Tu, J.; Sun, J.W.; Xie, S.Y. The focusing waves induced by Bragg resonance with V-shaped undulating bottom. J. Mar. Sci. Eng. 2021, 9, 708. [Google Scholar] [CrossRef]
- Karmakar, D.; Bhattacharjee, J.; Guedes Soares, C. Scattering of gravity waves by multiple surface-piercing floating membrane. Appl. Ocean Res. 2013, 39, 40–52. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Chen, K.H.; Tsai, C.M. Investigation on Bragg reflection of surface water waves induced by a train of fixed floating pontoon breakwaters. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 951–963. [Google Scholar] [CrossRef]
- Ding, W.W.; Zou, Z.J.; Wu, J.P. Bragg reflection of water waves by multiple composite flexible membranes. Int. J. Offshore Polar Eng. 2018, 28, 135–142. [Google Scholar] [CrossRef]
- Ding, W.W.; Zou, Z.J.; Wu, J.P. Characteristics of Bragg reflection of water waves by multiple vertical flexible membranes. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Ding, W.W.; Zou, Z.J.; Wu, J.P.; Huang, B.G. Investigation of surface-piercing fixed structures with different shapes for Bragg reflection of water waves. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 819–827. [Google Scholar] [CrossRef]
- Ding, W.W.; Zou, Z.J.; Wu, J.P. Bragg reflection of water waves by multiple floating horizontal flexible membranes with submerged rectangular bars on the seabed. Appl. Ocean Res. 2019, 83, 103–111. [Google Scholar] [CrossRef]
- Tseng, I.F.; You, C.S.; Tsai, C.C. Bragg reflections of oblique water waves by periodic surface-piercing and submerged breakwaters. J. Mar. Sci. Eng. 2020, 8, 522. [Google Scholar] [CrossRef]
- Kar, P.; Sahoo, T.; Meylan, M.H. Bragg scattering of long waves by an array of floating flexible plates in the presence of multiple submerged trenches. Phys. Fluids 2020, 32, 096603. [Google Scholar] [CrossRef]
- Mohapatra, A.K.; Vijay, K.G.; Sahoo, T. Bragg scattering of surface gravity waves by a submerged wavy porous plate. Ocean Eng. 2021, 219, 108273. [Google Scholar] [CrossRef]
- Verduzco-Zapata, M.G.; García-Nava, H.; Ocampo-Torres, F.J.; Mendoza, E.; Ramírez-Serrano, E.I.; Torres-Orozco, E. Ocean surface waves propagating over a spatial arrangement of subsurface fixed horizontal plate breakwaters crowned with flexible medium. J. Fluids Struct. 2021, 100, 103188. [Google Scholar] [CrossRef]
- Zhao, X.; Xue, R.; Geng, J.; Göteman, M. Analytical investigation on the hydrodynamic performance of a multi-pontoon breakwater-WEC system. Ocean Eng. 2021, 220, 108394. [Google Scholar] [CrossRef]
- Abul-Azm, A.G. Wave diffraction through submerged breakwaters. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 587–605. [Google Scholar] [CrossRef]
- Losada, I.J.; Losada, M.A.; Roldán, A.J. Propagation of oblique incident waves past rigid vertical thin barriers. Appl. Ocean Res. 1992, 14, 191–199. [Google Scholar] [CrossRef]
- Cao, F.S.; Teng, B. Scaled boundary finite element analysis of wave passing a submerged breakwater. China Ocean Eng. 2008, 22, 241–251. [Google Scholar]
- Liu, Y.; Xie, L.; Zhang, Z. The wave motion over a submerged Jarlan-type perforated breakwater. Acta Oceanol. Sin. 2014, 33, 96–102. [Google Scholar] [CrossRef]
- Mandal, S.; Behera, H.; Sahoo, T. Oblique wave interaction with porous, flexible barriers in a two-layer fluid. J. Eng. Math. 2015, 100, 1–31. [Google Scholar] [CrossRef]
- Jaf, J.M.; Wang, K.H. Interaction of solitary waves with a submerged impermeable breakwater. J. Eng. Mech. 2015, 141, 04015030. [Google Scholar] [CrossRef]
- Wu, J.P.; Pan, J.; Ding, W.W.; Zou, Z.J.; Li, T.Q. Experimental studies on the transmission coefficients of multiple plates. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Miao, Y.; Wang, K.H. Approximate analytical solutions for a solitary wave interacting with a partially submerged porous wall. Ocean Eng. 2019, 181, 227–239. [Google Scholar] [CrossRef]
- Yueh, C.Y.; Tsaur, D.H. Wave scattering by submerged vertical plate-type breakwater using composite BEM. Coast Eng. J. 1999, 41, 65–83. [Google Scholar] [CrossRef]
- Chen, K.H.; Chen, J.T.; Chou, C.R.; Yueh, C.Y. Dual boundary element analysis of oblique incident wave passing a thin submerged breakwater. Eng. Anal. Bound. Elem. 2002, 26, 917–928. [Google Scholar] [CrossRef]
- Yueh, C.Y.; Chuang, S.H.; Wen, C.C. Wave scattering by submerged composite wavy plate breakwaters using a dual BEM. Ocean Eng. 2016, 124, 192–203. [Google Scholar] [CrossRef]
- Chen, J.T.; Yueh, C.Y.; Chang, Y.L.; Wen, C.C. Why dual boundary element method is necessary? Eng. Anal. Bound. Elem. 2017, 76, 59–68. [Google Scholar] [CrossRef]
- Yueh, C.Y.; Chuang, S.H.; Wen, C.C. Scattering of water waves by surface-piercing barriers using dual BEM. J. Hydro-Environ. Res. 2018, 21, 21–28. [Google Scholar] [CrossRef]
- Vijay, K.G.; Venkateswarlu, V.; Nishad, C.S. Wave scattering by inverted trapezoidal porous boxes using dual boundary element method. Ocean Eng. 2021, 219, 108149. [Google Scholar] [CrossRef]
- Nishad, C.S.; Vijay, K.G.; Neelamani, S.; Chen, J.T. Dual BEM for wave scattering by an H-type porous barrier with nonlinear pressure drop. Eng. Anal. Bound. Elem. 2021, 131, 280–294. [Google Scholar] [CrossRef]
- Vijay, K.G.; Nishad, C.S.; Neelamani, S.; Sahoo, T. Wave interaction with multiple wavy porous barriers using dual boundary element method. Eng. Anal. Bound. Elem. 2021, 122, 176–189. [Google Scholar] [CrossRef]
- Koley, S.; Vijay, K.G.; Nishad, C.S.; Sundaravadivelu, R. Performance of a submerged flexible membrane and a breakwater in the presence of a seawall. Appl. Ocean Res. 2022, 124, 103203. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Abbaspour, M. An integral equation method for the diffraction of oblique waves by an infinite cylinder. Int. J. Numer. Methods Eng. 1982, 18, 1497–1504. [Google Scholar] [CrossRef]
- Wu, J.P.; Bo, H.; Zhang, M.; Pan, J. A Reflection Wave Decomposition Method Based on the Linear Superposition Principle of Water Waves. CN201710605897.4, 24 July 2017. [Google Scholar]

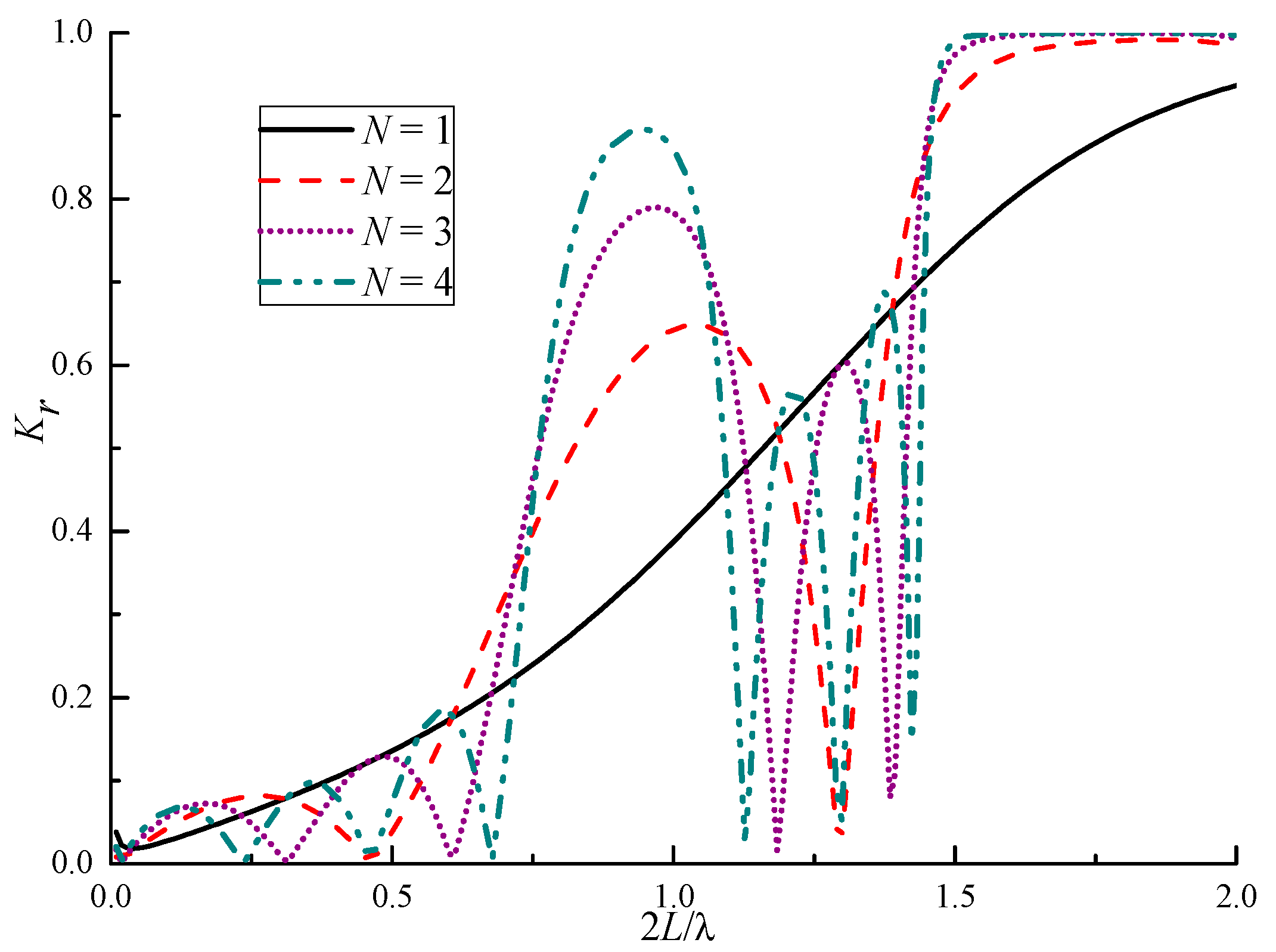


| N | 2L/λ 1 | ||
|---|---|---|---|
| 1 | -- | 0.42 | -- |
| 2 | 1.04 | 0.65 | 0.71~1.24 |
| 3 | 0.96 | 0.79 | 0.74~1.14 |
| 4 | 0.95 | 0.88 | 0.75~1.09 |
| d/h | 2L/λ | ||
|---|---|---|---|
| 0.3 | 1.03 | 0.39 | 0.81~1.19 |
| 0.5 | 0.96 | 0.79 | 0.74~1.14 |
| 0.7 | 0.91 | 0.96 | 0.63~1.10 |
| L/h | 2L/λ | ||
|---|---|---|---|
| 2.0 | 0.92 | 0.97 | 0.64~1.08 |
| 3.0 | 0.96 | 0.79 | 0.74~1.14 |
| 4.0 | 0.99 | 0.60 | 0.76~1.16 |
| Parameter | Unit | Value |
|---|---|---|
| Water depth h | m | 0.3 |
| Wavelength λ | m | 1.769~3.075 |
| Wave steepness ε | -- | 0.003 |
| Wave period T | s | 1.2~1.9 |
| Wave height H | mm | 5~9 |
| Number of plates N | -- | 1, 2, 3 |
| Immerged depth d | m | 0.12, 0.15, 0.18 |
| Spacing of plates L | m | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.-W.; Yue, W.-Z.; Sheng, S.-W.; Wu, J.-P.; Zou, Z.-J. Numerical and Experimental Study on the Bragg Reflection of Water Waves by Multiple Vertical Thin Plates. J. Mar. Sci. Eng. 2022, 10, 1464. https://doi.org/10.3390/jmse10101464
Ding W-W, Yue W-Z, Sheng S-W, Wu J-P, Zou Z-J. Numerical and Experimental Study on the Bragg Reflection of Water Waves by Multiple Vertical Thin Plates. Journal of Marine Science and Engineering. 2022; 10(10):1464. https://doi.org/10.3390/jmse10101464
Chicago/Turabian StyleDing, Wei-Wei, Wan-Zhen Yue, Song-Wei Sheng, Jing-Ping Wu, and Zao-Jian Zou. 2022. "Numerical and Experimental Study on the Bragg Reflection of Water Waves by Multiple Vertical Thin Plates" Journal of Marine Science and Engineering 10, no. 10: 1464. https://doi.org/10.3390/jmse10101464
APA StyleDing, W.-W., Yue, W.-Z., Sheng, S.-W., Wu, J.-P., & Zou, Z.-J. (2022). Numerical and Experimental Study on the Bragg Reflection of Water Waves by Multiple Vertical Thin Plates. Journal of Marine Science and Engineering, 10(10), 1464. https://doi.org/10.3390/jmse10101464





