A Review of Point Absorber Wave Energy Converters
Abstract
:1. Introduction
- Wave power is of a higher power intensity than solar and wind power. For instance, the intensities of solar, wind and wave power are 0.17 , 0.58 and 8.42 , respectively, at a latitude of 15° N within the Northeast Trades [12].
- Wave power has high availability, being available up to 90% of the time, while the availability of solar and wind power ranges from 20% to 30% [13].
- Harvesting wave energy is currently considered environmentally friendly, as several sea trails only showed little impact on the oceanic environment [22,23]. Currently, most WECs are designed and optimised for energetic sites, and the device size should be downscaled accordingly to perform well in low-energy seas [24].
2. Point Absorber Prototypes
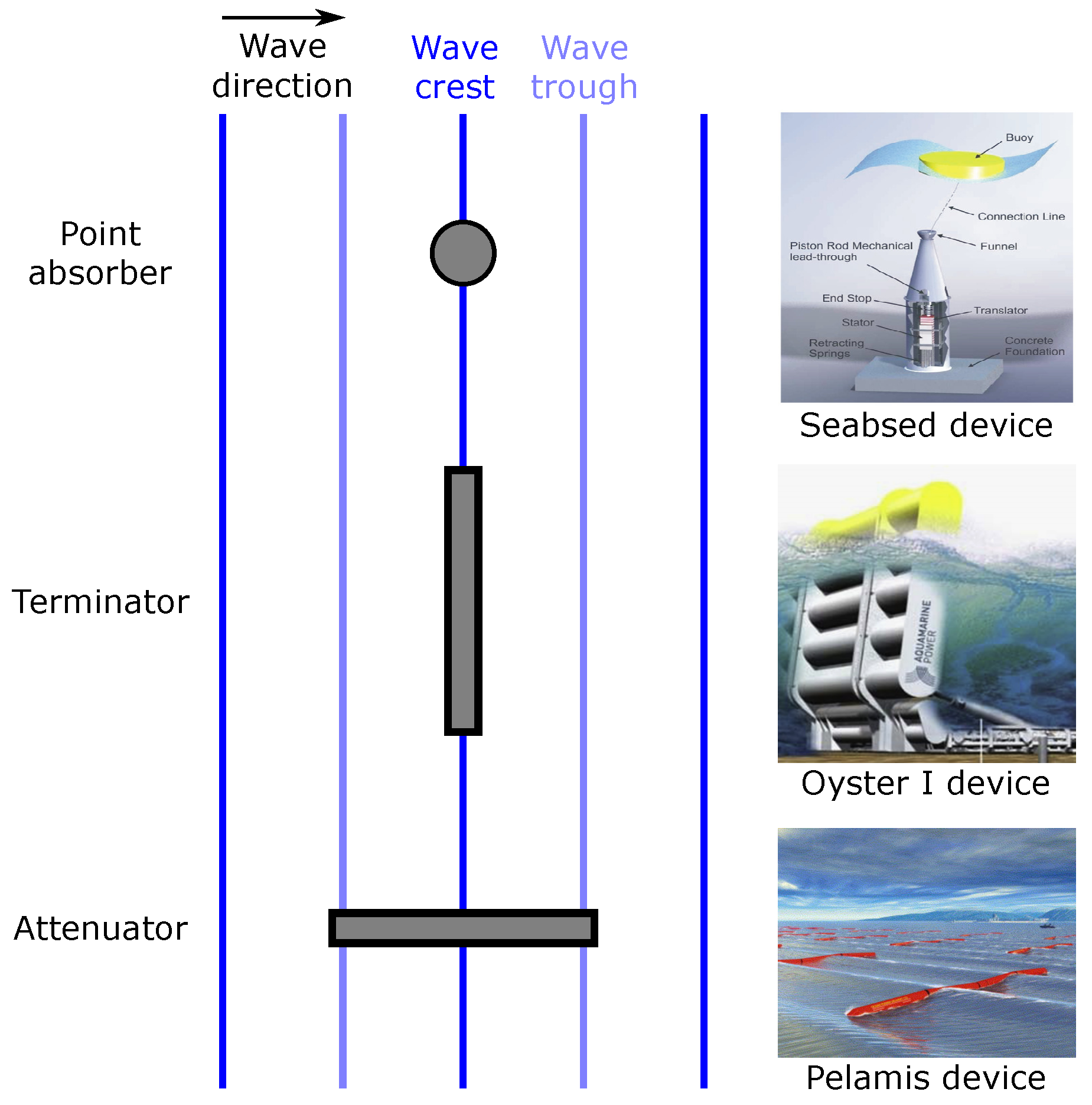
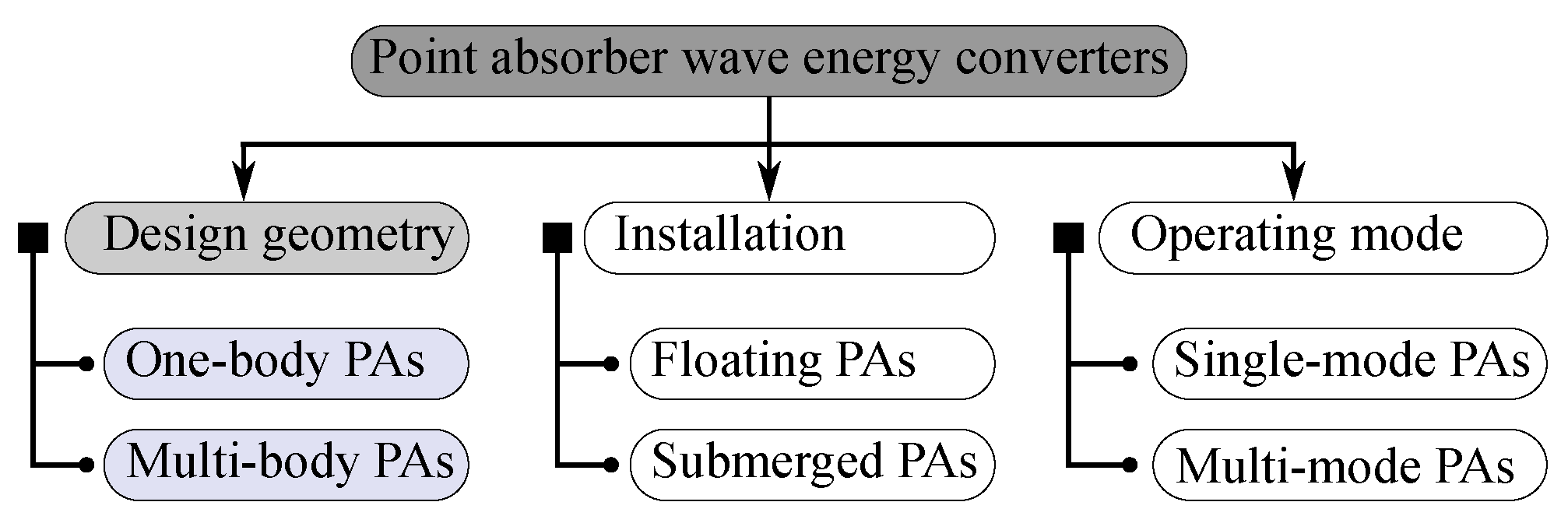
2.1. Classification of Point Absorbers
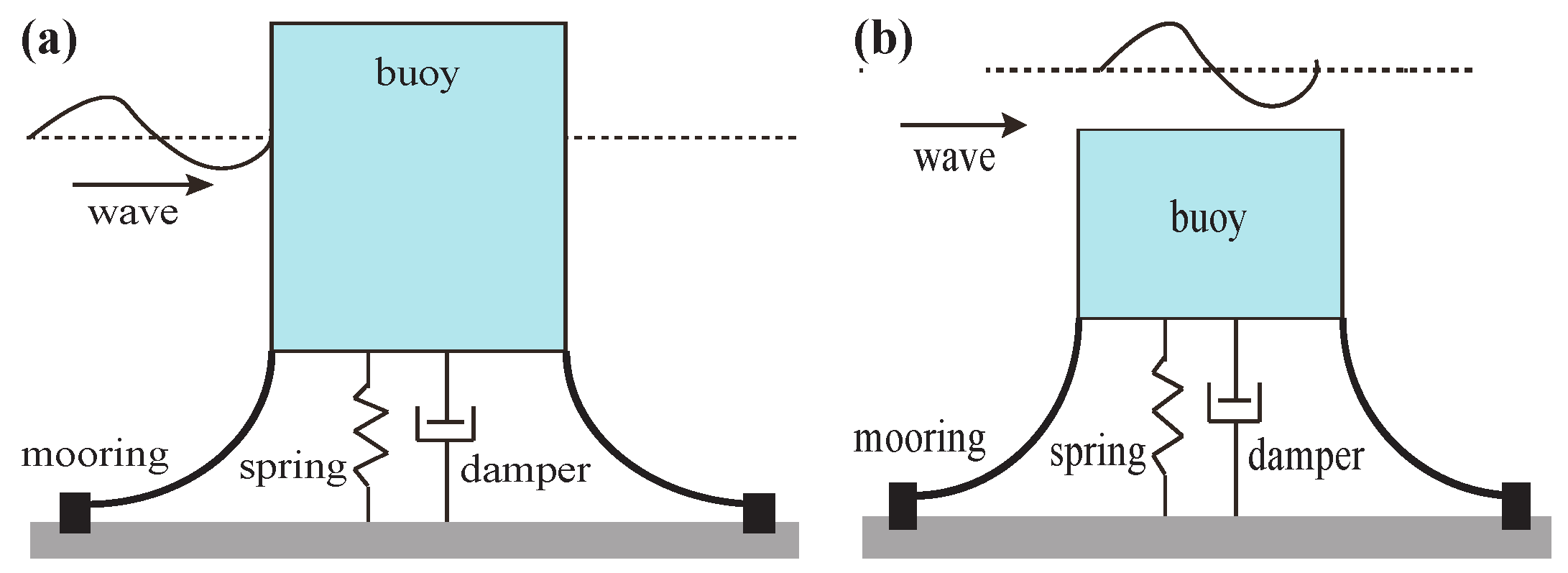
2.2. One-Body Point Absorbers
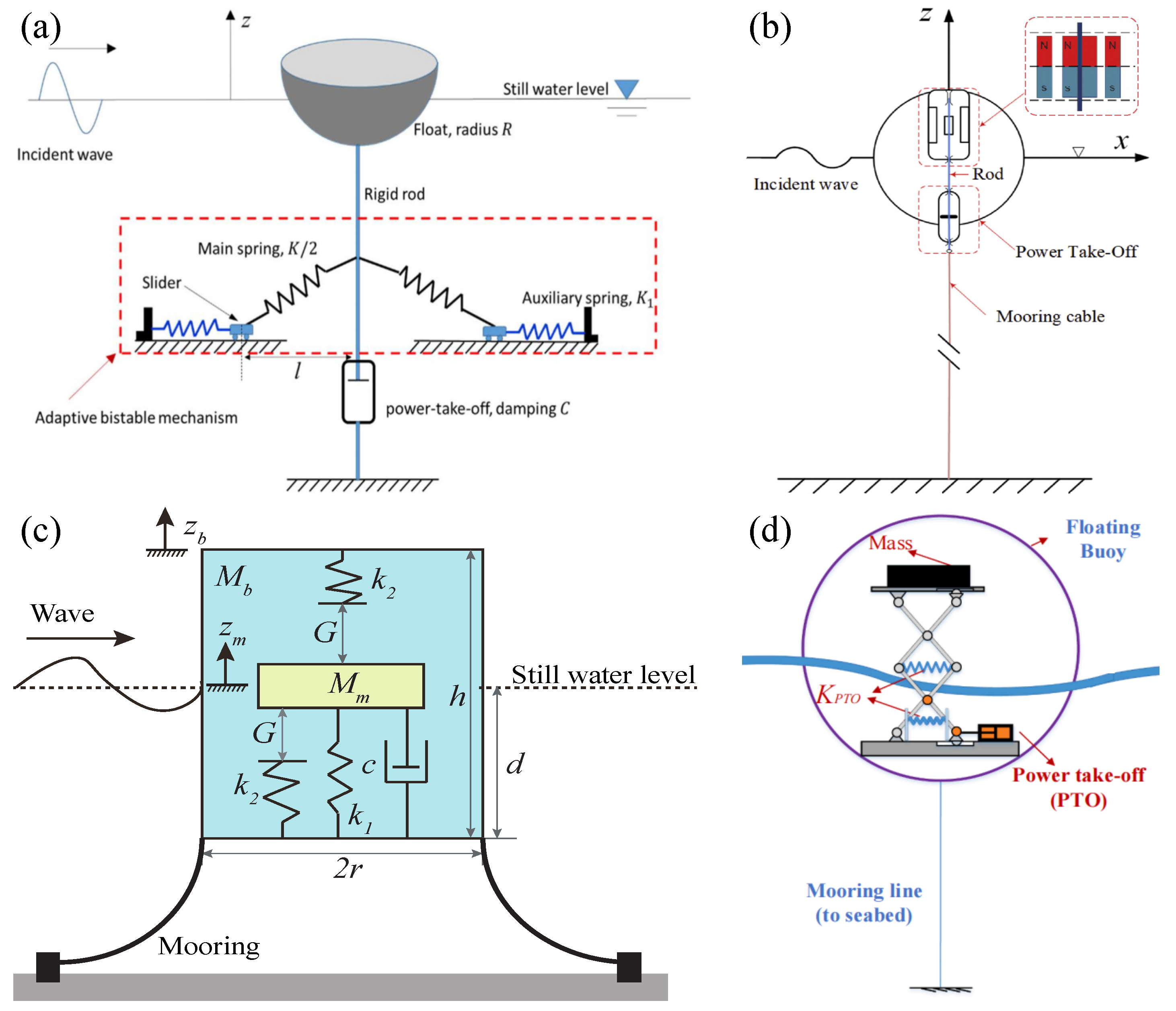
2.2.1. Floating One-Body Point Absorbers
2.2.2. Submerged One-Body Point Absorbers
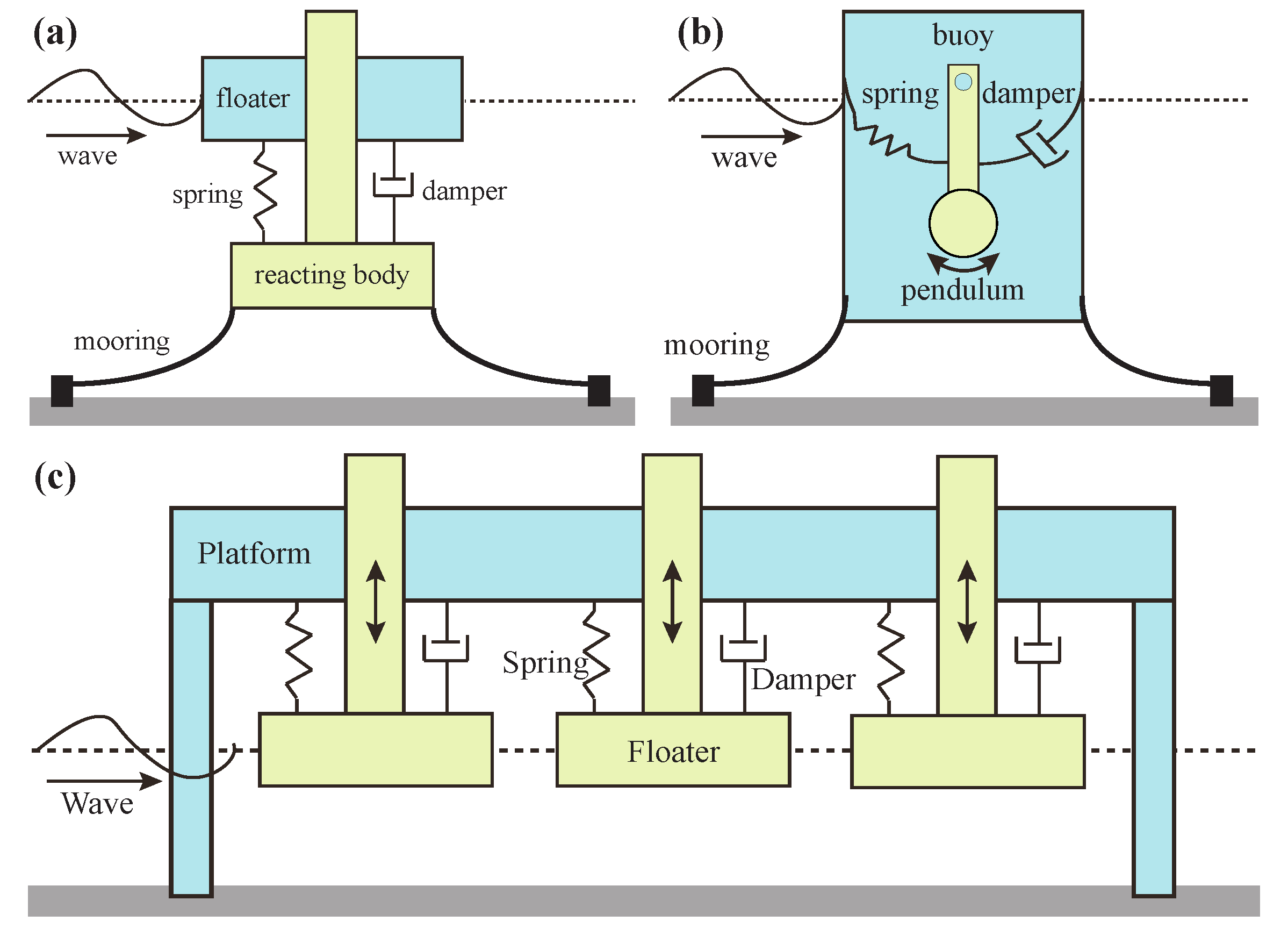
2.3. Multi-Body Point Absorbers
2.3.1. Self-Reacting Two-Body Point Absorbers
2.3.2. Self-Contained Two-Body Point Absorbers
2.3.3. Multi-Point Absorbers
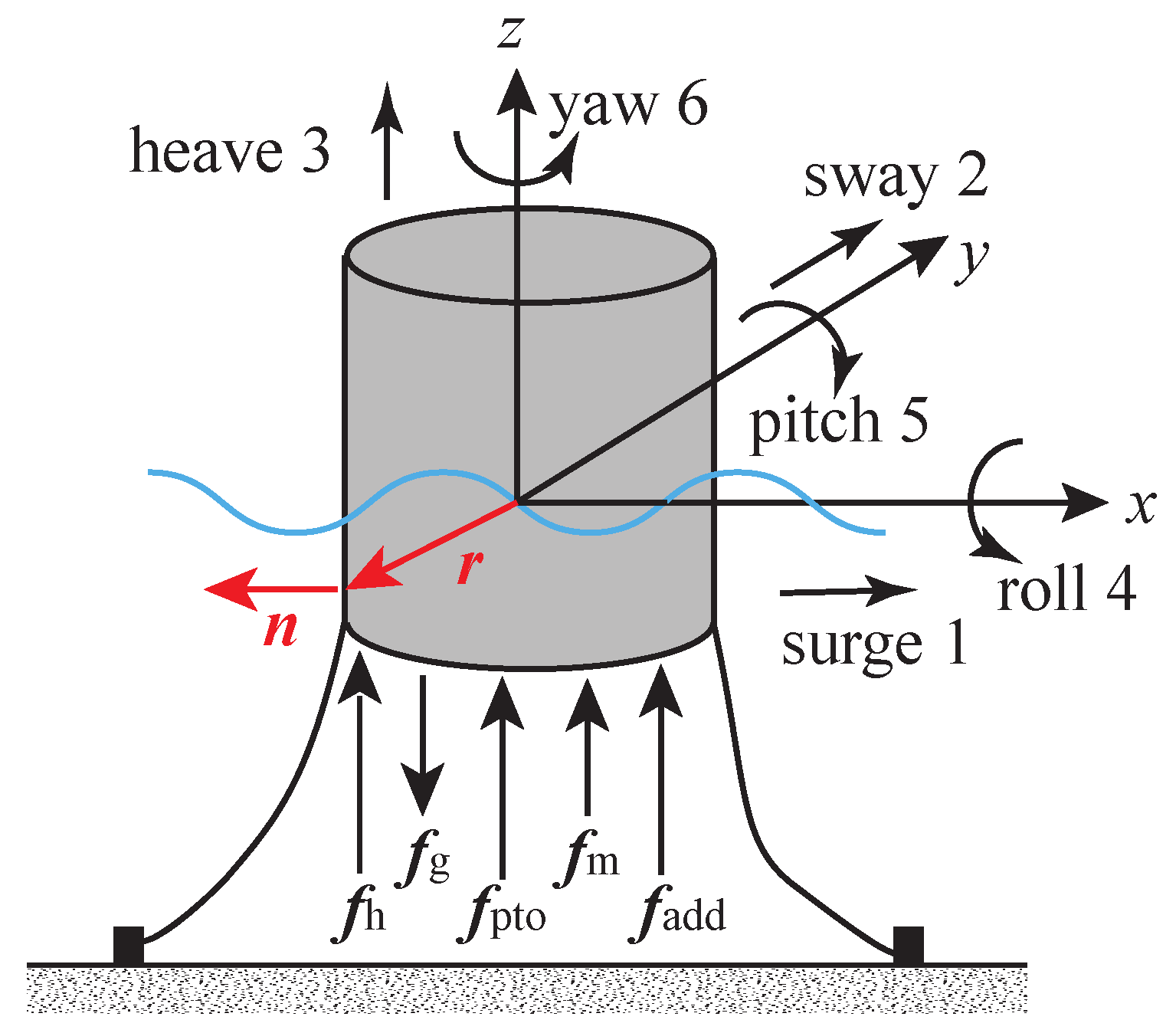
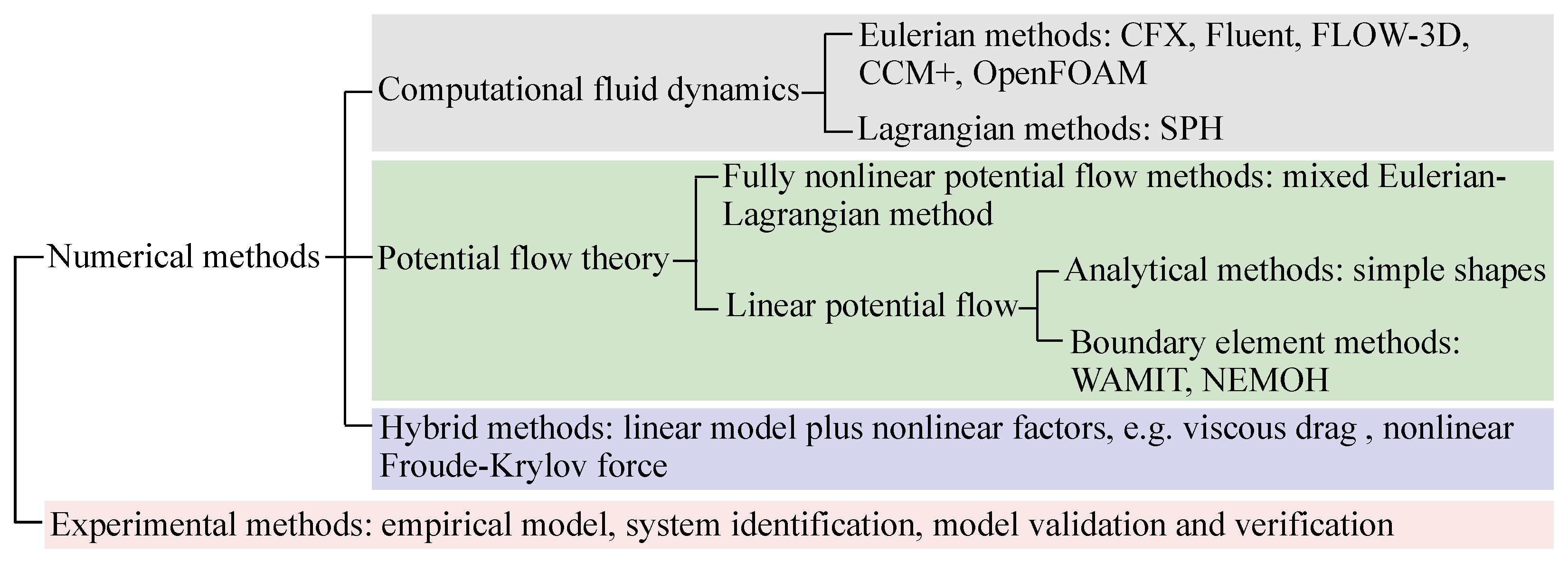
3. Hydrodynamic Modelling
3.1. Computational Fluid Dynamics Methods
3.2. Potential Flow Theory Methods
3.3. Hybrid Modelling Methods
- For the body-exact treatment method, the instantaneous body position is considered in computing the FK, diffraction, radiation and restoring forces in Equations (7)–(10), while the wave is still assumed to be small. When the body size is small, the nonlinearity in diffraction and radiation are neglectable. For a body with a varying horizontal cross-section, the nonlinearity in the hydrostatic force appears obvious. Considering the large body motion, the nonlinearity in the FK force is more critical than the other force and has a significant impact on PA hydrodynamics [146,149,150].
- For the weak scatterer treatment method, the instantaneous free surface is considered in computing the forces in Equations (7)–(10), while the wetted surface is linearised at the equilibrium point. This method linearises the free-surface boundary condition at . Thus, the second-order terms of and can be added to compute the diffraction and radiation forces in Equations (8) and (9). However, the importance of the nonlinear diffraction and radiation terms mainly depends on the body size. For a small body, these nonlinear forces can be neglected [151].
- For the viscosity treatment method, the viscosity is considered by adding a quadratic term to the Cummins’ equation, according to the Morison equation [152]. This method can significantly improve the modelling accuracy with little computing cost when the relative velocity between the body and fluid is large. The viscous coefficient can be determined analytically, numerically or experimentally [134,153,154]. However, a wide range of wave conditions should be tested to obtain a consistent value [155].
- The mixed treatment method has two subclasses: the body-exact viscosity treatment considering both large body motion and fluid viscosity and the weak-scatter viscosity treatment considering both a large wave height and fluid viscosity. In AQWA, the weak-scatter viscosity treatment is realised by computing the nonlinear FK and hydrostatic forces according to instantaneous wave elevation and adding the viscous force according to the Morison equation [156,157]. In general, PAs’ motion is significantly amplified by power maximisation control, and hence, the nonlinearity induced by large body motion is more critical than that induced by a large wave height. Therefore, the body-exact viscosity treatment is broadly used in PA modelling.
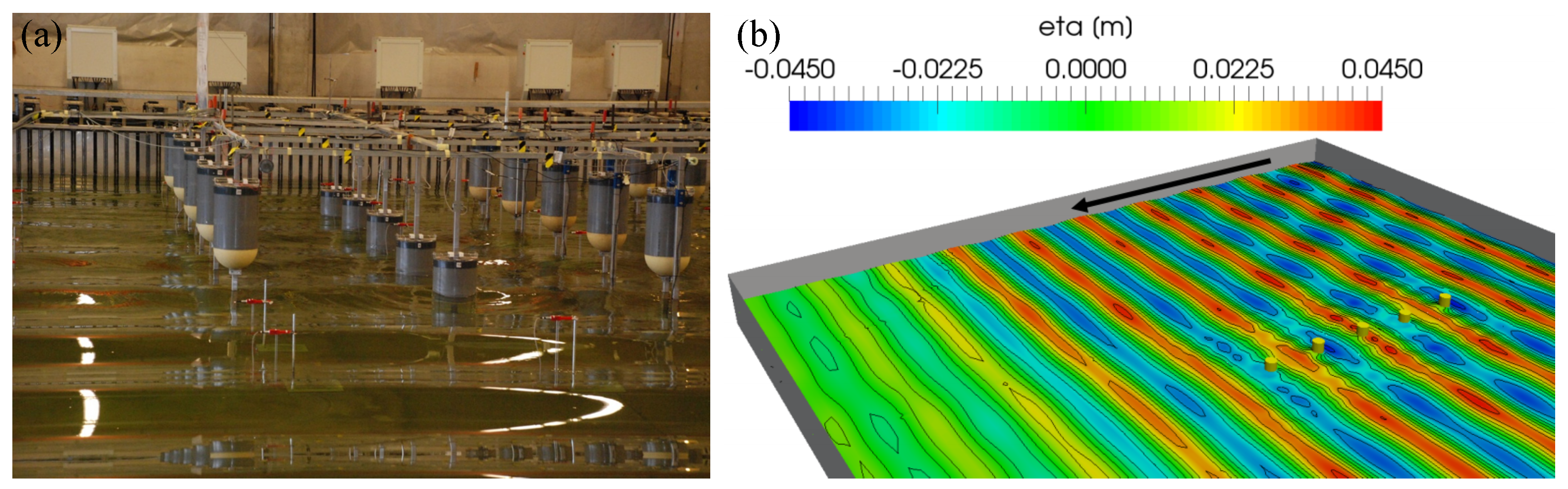
3.4. Experimental Modelling Methods
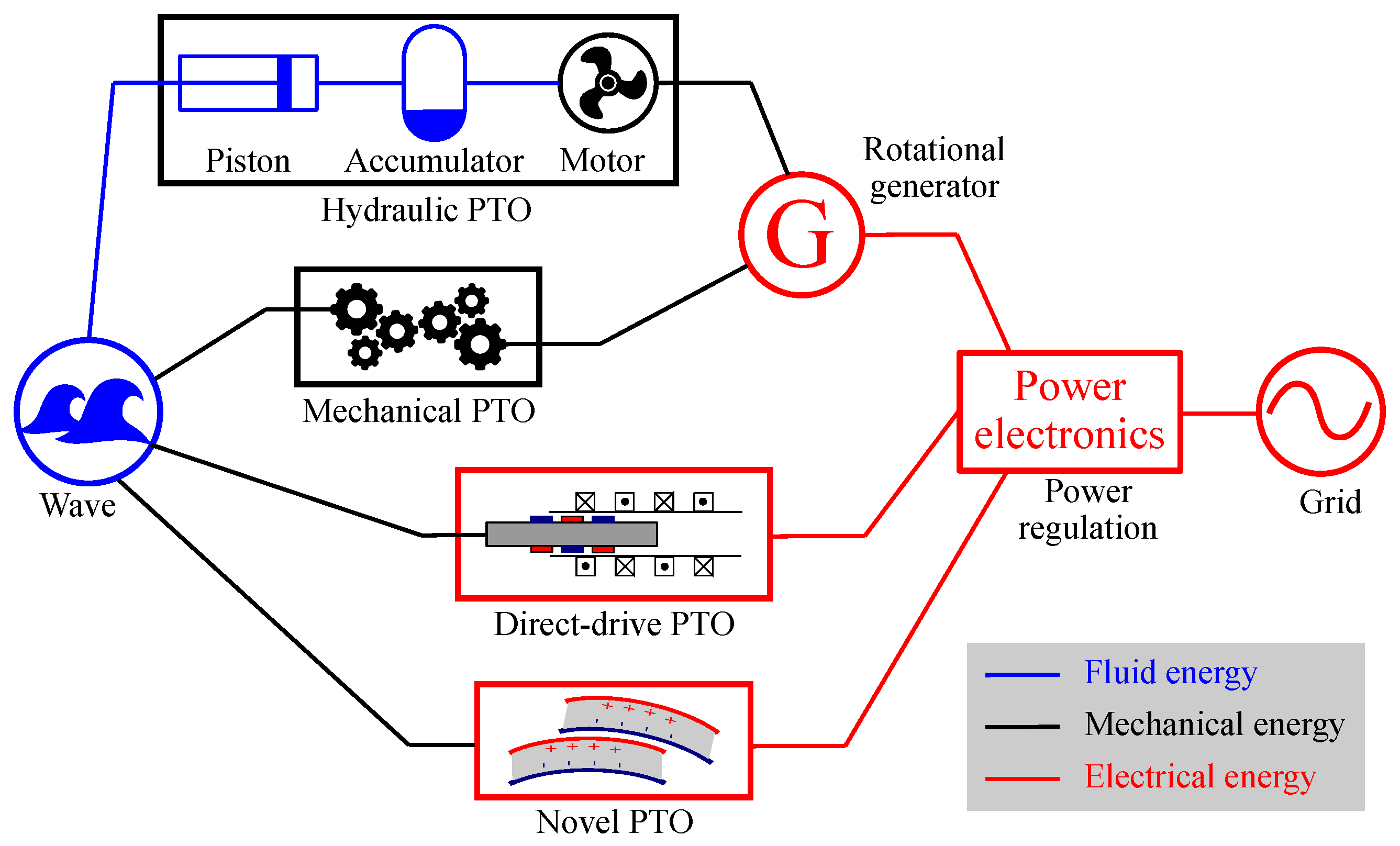
4. Power Take-Off Mechanisms
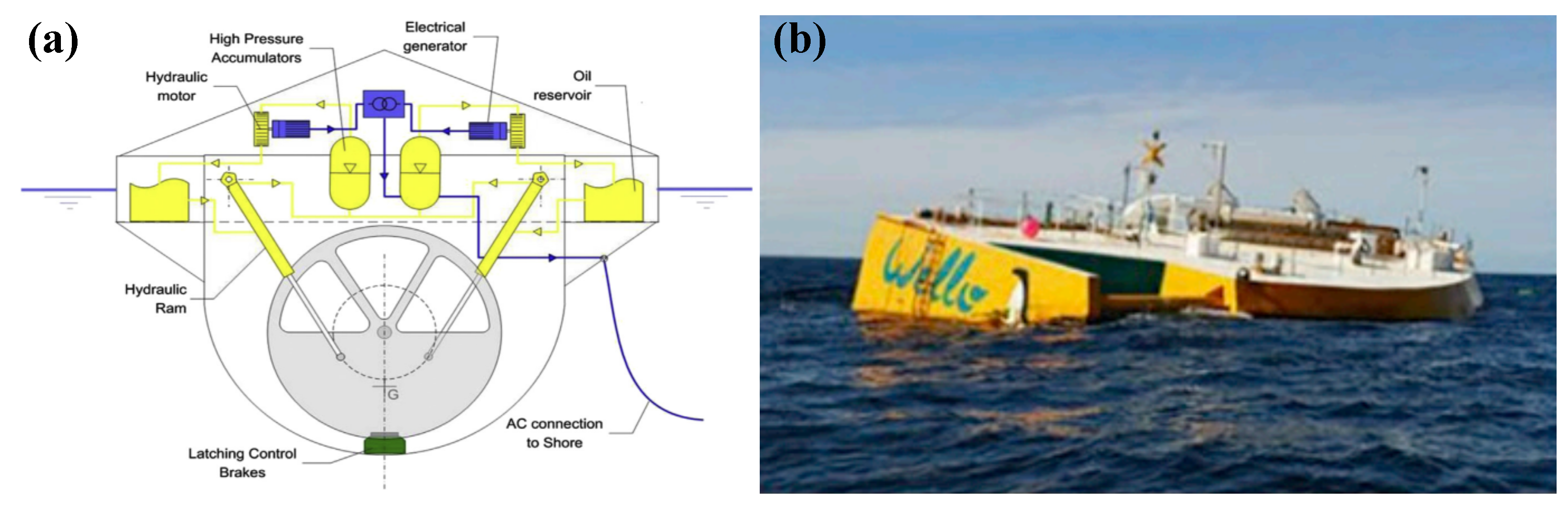
4.1. Hydraulic PTO Mechanisms
4.2. Mechanical PTO Mechanisms
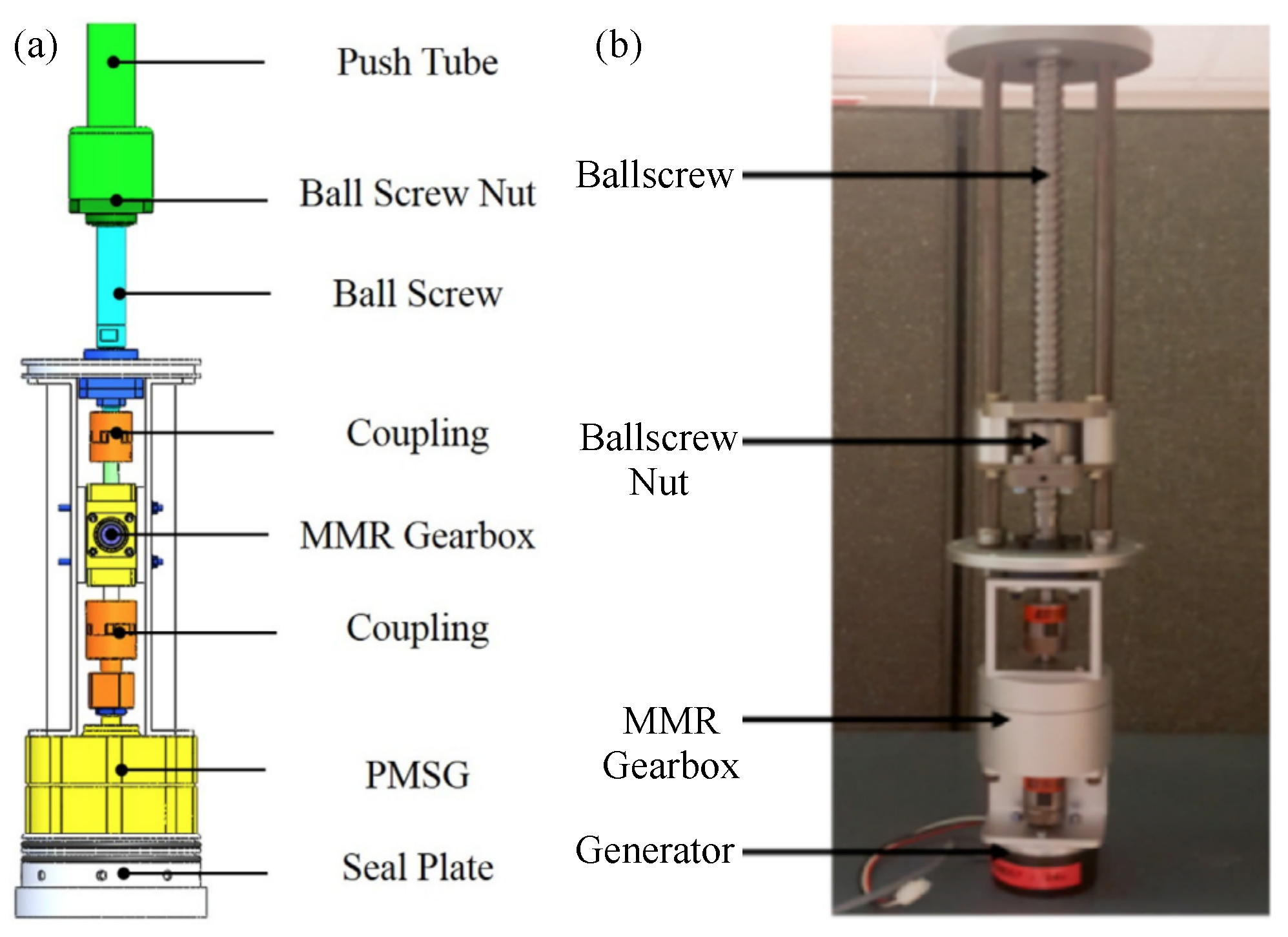
4.3. Direct-Drive PTO Mechanisms
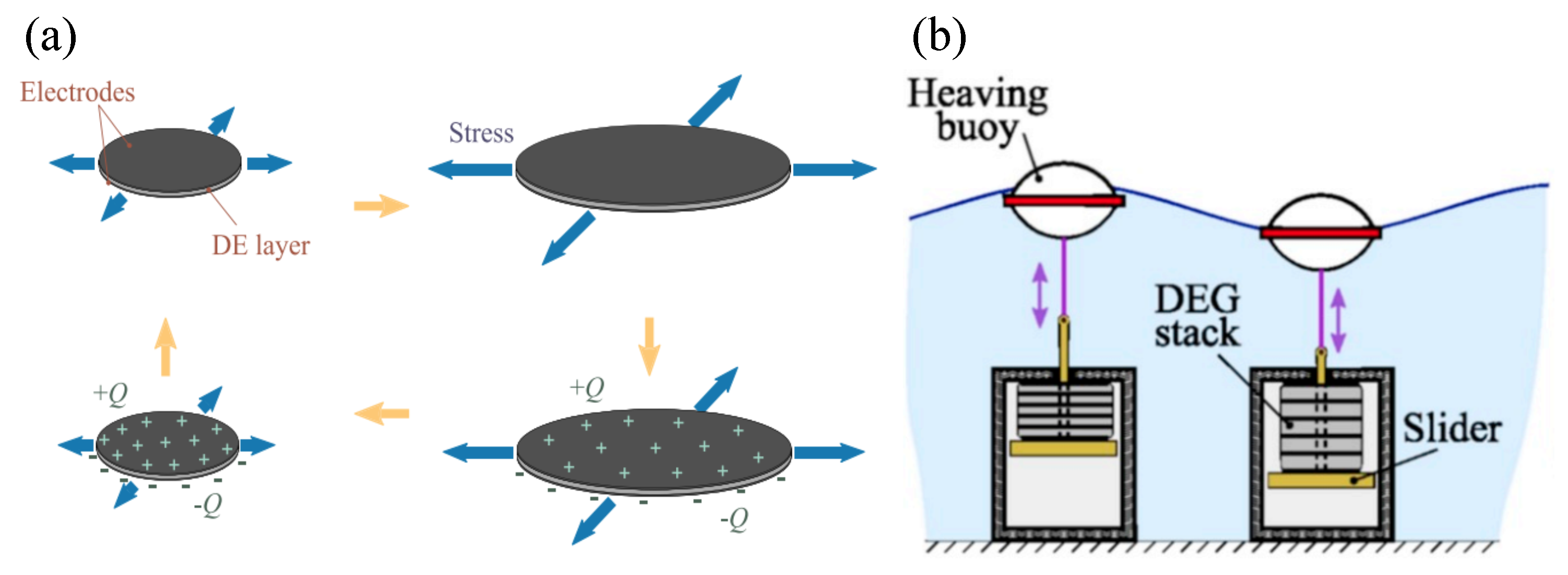
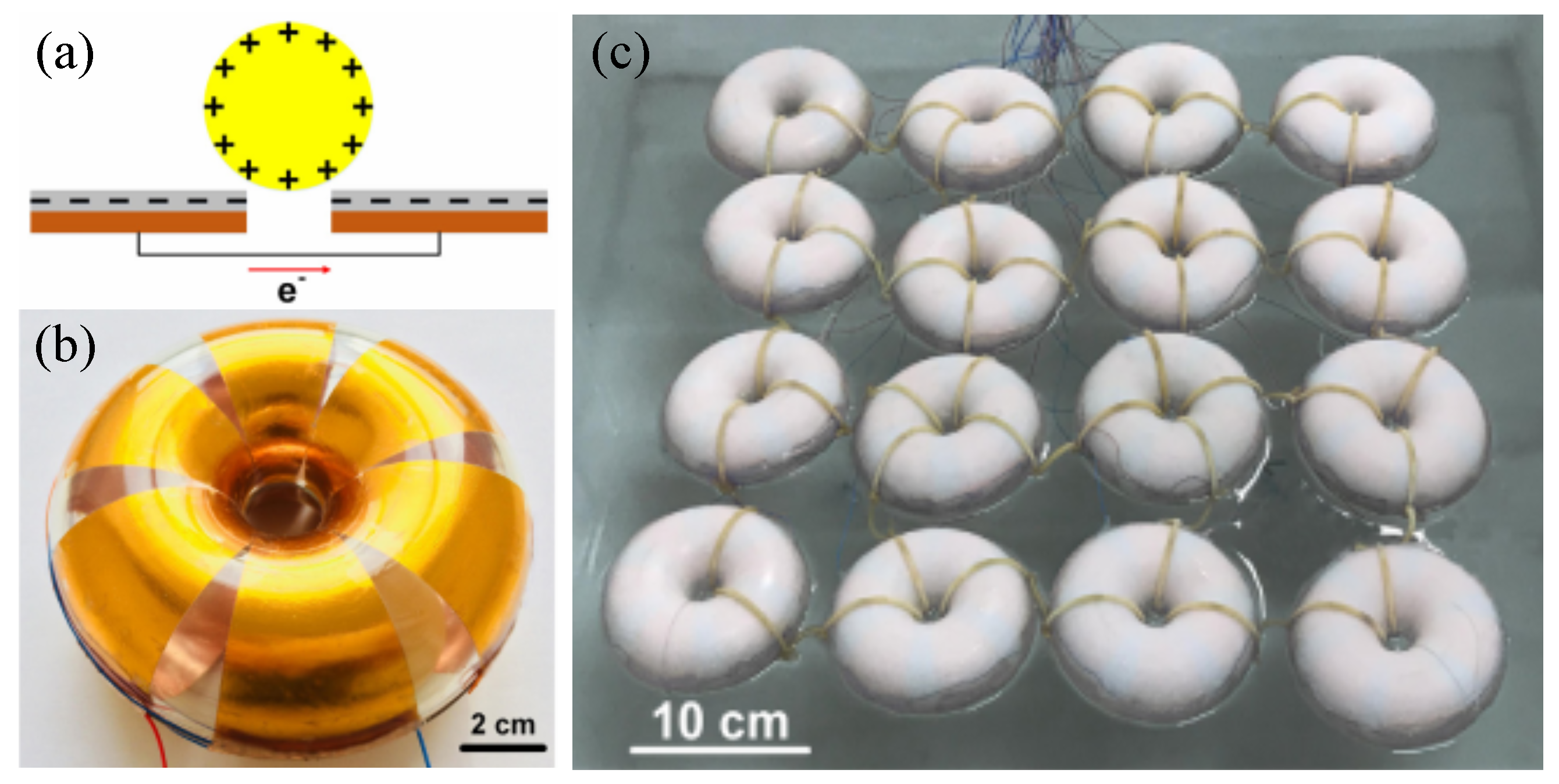
4.4. Novel PTO Mechanisms
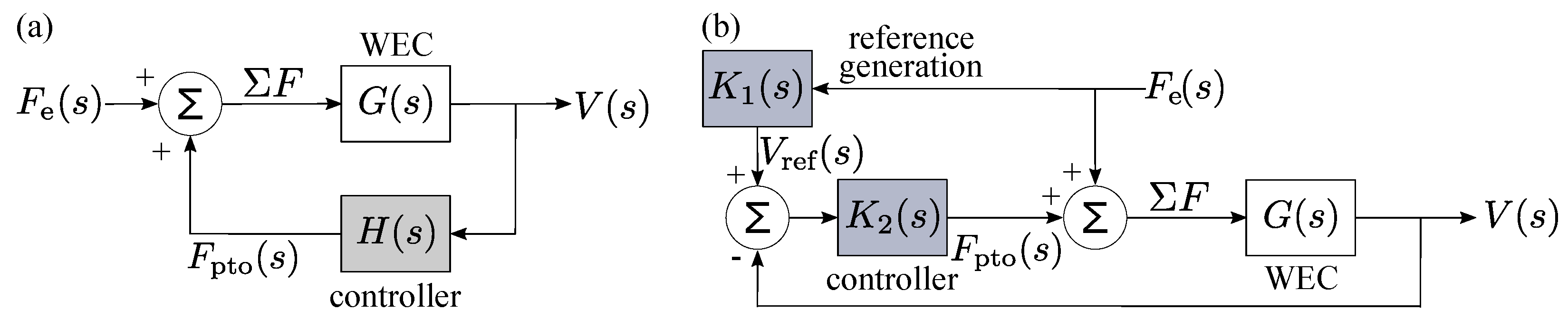
5. Control Strategies
5.1. Classical Control Strategy
5.2. Modern Control Strategies
6. Discussion
6.1. Perspectives on PA Concepts
6.2. Perspectives on PA Hydrodynamics
6.2.1. Nonlinear Hydrodynamics
6.2.2. Extreme Wave Loads
6.2.3. Array Operation
6.3. Perspectives on PA PTOs
6.4. Perspectives on PA Control
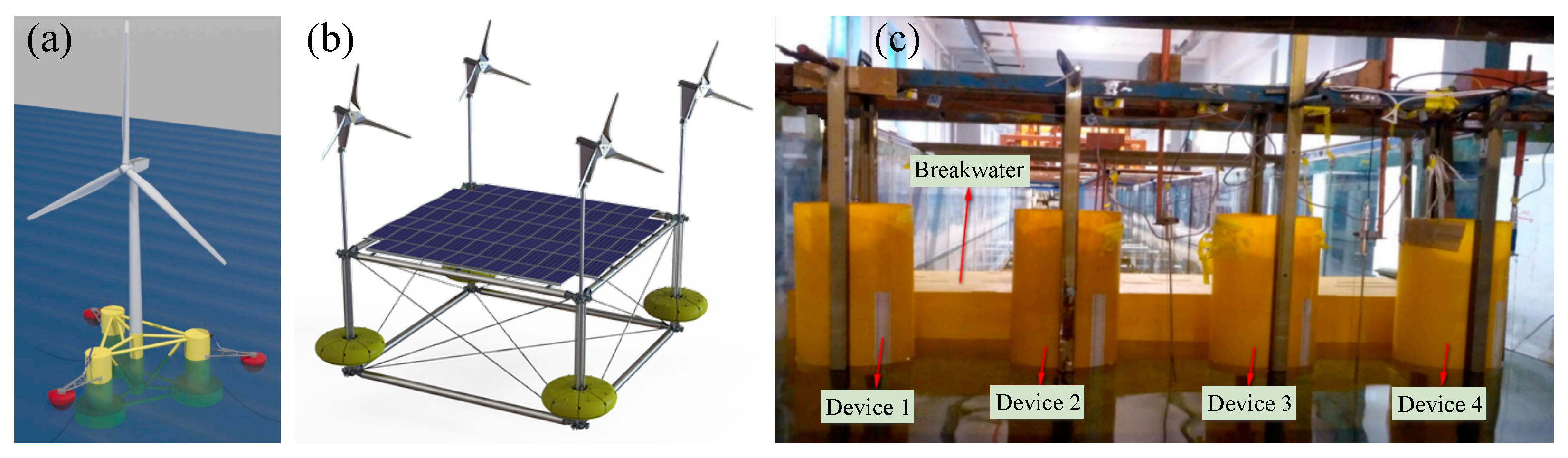
6.5. Perspectives on PA Application
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WEC | Wave energy converter |
| PAWEC | Point absorver wave energy converter |
| TRL | Technology readiness level |
| TPL | Technology performance level |
| LCoE | Levelised cost of energy |
| PTO | Power take-off |
| O&M | Operation and maintenance |
| PA | Point absorber |
| DoF | Degree of freedom |
| R&D | Research and development |
| RAO | Response amplitude operator |
| EMEC | European Marine Energy Centre |
| AWS | Archimedes wave swing |
| UPS | Uninterruptible power supply |
| FNT | Float-neck-tank |
| CFD | Computational fluid dynamics |
| PFT | Potential flow theory |
| FNPFT | Fully nonlinear potential flow theory |
| LPFT | Linear potential flow theory |
| FK | Froude–Krylov |
| PMLG | Permanent magnet linear generator |
| DEG | Dielectric elastomer generator |
| TENG | Triboelectric nanogenerator |
| RC | Reactive control |
| PC | Passive control |
| LC | Latching control |
| DC | Declutching control |
| ACC | Approximate complex conjugate |
| AVT | Approximate velocity tracking |
References
- Guterres, A. Carbon Neutrality by 2050: The World’s Most Urgent Mission. 2020. Available online: https://www.un.org/sg/en/content/sg/articles/2020-12-11/carbon-neutrality-2050-theworld%E2%80%99s-most-urgent-mission (accessed on 10 February 2021).
- EIA. International Energy Outlook 2019; Technical Report; EIA: Washington, DC, USA, 2019.
- UNEP. Emissions Gap Report 2020; Technical Report; UNEP: Nairobi, Kenya, 2020. [Google Scholar]
- IRENA. Global Renewalbes Outlook: Energy Transformation 2050; Technical Report; IRENA: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- EIA. International Energy Outlook 2021; Technical Report; EIA: Washington, DC, USA, 2021.
- Mork, G.; Barstow, S.; Kabuth, A.; Pontes, T. Assessing the global wave energy potential. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 49118, pp. 447–454. [Google Scholar]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A global wave power resource and its seasonal, interannual and long-term variability. Appl. Energy 2015, 148, 366–380. [Google Scholar] [CrossRef]
- OES. An International Vision for Ocean Energy; Technical Report; OES: Lisbon, Portugal, 2017. [Google Scholar]
- IRENA. Innovation Outlook: Ocean Energy Technologies; Technical Report; IRENA: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- IEA. Electricity Information Overview 2020 Edition. 2020. Available online: https://webstore.iea.org/electricity-information-overview-2020-edition (accessed on 10 February 2021).
- McCormick, M.E. Ocean Wave Energy Conversion; Courier Corporation: Chelmsford, MA, USA, 1981. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S.; De Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Fernandez-Chozas, J.; Soerensen, H.C.; Kofoed, J. Predictability and Variability of Wave and Wind: Wave and Wind Forecasting and Diversified Energy Systems in the Danish North Sea; Technical Report; Aalborg University: Aalborg, Denmark, 2013. [Google Scholar]
- Sasaki, W. Predictability of global offshore wind and wave power. Int. J. Mar. Energy 2017, 17, 98–109. [Google Scholar] [CrossRef]
- Fusco, F.; Nolan, G.; Ringwood, J.V. Variability reduction through optimal combination of wind/wave resources–An Irish case study. Energy 2010, 35, 314–325. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Gallagher, S.; Tiron, R.; Whelan, E.; Gleeson, E.; Dias, F.; McGrath, R. The nearshore wind and wave energy potential of Ireland: A high resolution assessment of availability and accessibility. Renew. Energy 2016, 88, 494–516. [Google Scholar] [CrossRef]
- Kalogeri, C.; Galanis, G.; Spyrou, C.; Diamantis, D.; Baladima, F.; Koukoula, M.; Kallos, G. Assessing the European offshore wind and wave energy resource for combined exploitation. Renew. Energy 2017, 101, 244–264. [Google Scholar] [CrossRef]
- Weiss, C.; Guanche, R.; Ondiviela, B.; Castellanos, O.F.; Juanes, J. Marine renewable energy potential: A global perspective for offshore wind and wave exploitation. Energy Convers. Manag. 2018, 177, 43–54. [Google Scholar] [CrossRef]
- Langhamer, O.; Haikonen, K.; Sundberg, J. Wave power–Sustainable energy or environmentally costly? A review with special emphasis on linear wave energy converters. Renew. Sustain. Energy Rev. 2010, 14, 1329–1335. [Google Scholar] [CrossRef]
- Copping, A.E.; Hemery, L.G.; Overhus, D.M.; Garavelli, L.; Freeman, M.C.; Whiting, J.M.; Gorton, A.M.; Farr, H.K.; Rose, D.J.; Tugade, L.G. Potential Environmental Effects of Marine Renewable Energy Development–The State of the Science. J. Mar. Sci. Eng. 2020, 8, 879. [Google Scholar] [CrossRef]
- Majidi, A.; Bingölbali, B.; Akpınar, A.; Iglesias, G.; Jafali, H. Downscaling wave energy converters for optimum performance in low-energy seas. Renew. Energy 2021, 168, 705–722. [Google Scholar] [CrossRef]
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave energy in Europe: Current status and perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Weber, J.; Costello, R.; Ringwood, J. WEC technology performance levels (TPLs)-metric for successful development of economic WEC technology. In Proceedings of the European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–6 September 2013; pp. 1–9. [Google Scholar]
- Folley, M.; Babarit, A.; Child, B.; Forehand, D.; Boyle, L.O.; Silverthorne, K.; Spinneken, J.; Stratigaki, V.; Troch, P.; Folley, M.; et al. A review of numerical modelling of wave energy converter arrays. In Proceedings of the International Conference on Ocean, Offshore and Artic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 535–545. [Google Scholar]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef] [Green Version]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Bard, J.; Kracht, P. Report on Linear Generator Systems for Wave Energy Converters; Technical Report; Aalborg University: Alborg, Denmark, 2013. [Google Scholar]
- Chiba, S.; Waki, M.; Wada, T.; Hirakawa, Y.; Masuda, K.; Ikoma, T. Consistent ocean wave energy harvesting using electroactive polymer (dielectric elastomer) artificial muscle generators. Appl. Energy 2013, 104, 497–502. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.; Gardner, F. Linear PM generator system for wave energy conversion in the AWS. IEEE Trans. Energy Convers. 2004, 19, 583–589. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Bao, J.; Liu, H.; Li, W.; Tu, L.; Zhang, D. Review of hydraulic transmission technologies for wave power generation. Renew. Sustain. Energy Rev. 2015, 50, 194–203. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Ahamed, R.; McKee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) systems: A review. Ocean Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-maximizing control of wave-energy converters: The development of control system technology to optimize their operation. IEEE Control Syst. Mag. 2014, 34, 30–55. [Google Scholar]
- Hong, Y.; Waters, R.; Boström, C.; Eriksson, M.; Engström, J.; Leijon, M. Review on electrical control strategies for wave energy converting systems. Renew. Sustain. Energy Rev. 2014, 31, 329–342. [Google Scholar] [CrossRef]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control 2017, 1, 37–56. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- Ringwood, J.V. Wave energy control: Status and perspectives 2020. In Proceedings of the IFAC World Congress, Berlin, Germany, 11–17 July 2020; pp. 1–12. [Google Scholar]
- Boake, C.B.; Whittaker, T.J.; Folley, M.; Ellen, H. Overview and initial operational experience of the LIMPET wave energy plant. In Proceedings of the International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; pp. 586–594. [Google Scholar]
- Falcão, A.F.; Sarmento, A.J.; Gato, L.M.; Brito-Melo, A. The Pico OWC wave power plant: Its lifetime from conception to closure 1986–2018. Appl. Ocean Res. 2020, 98, 102104. [Google Scholar]
- Ibarra-Berastegi, G.; Sáenz, J.; Ulazia, A.; Serras, P.; Esnaola, G.; Garcia-Soto, C. Electricity production, capacity factor, and plant efficiency index at the Mutriku wave farm (2014–2016). Ocean Eng. 2018, 147, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A 2012, 370, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Whittaker, T.; Folley, M. Nearshore oscillating wave surge converters and the development of Oyster. Philos. Trans. R. Soc. A 2012, 370, 345–364. [Google Scholar] [CrossRef] [Green Version]
- Kofoed, J.P.; Frigaard, P.; Friis-Madsen, E.; Sørensen, H.C. Prototype testing of the wave energy converter wave dragon. Renew. Energy 2006, 31, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Sjolte, J.; Bjerke, I.; Tjensvoll, G.; Molinas, M. Summary of performance after one year of operation with the lifesaver wave energy converter system. In Proceedings of the European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–6 September 2013; pp. 1–10. [Google Scholar]
- IRENA. Fostering a Blue Economy: Offshore Renewable Energy. 2020. Available online: https://www.irena.org/publications/2020/Dec/Fostering-a-blue-economy-Offshore-renewable-energy (accessed on 10 February 2021).
- Guo, B.; Ringwood, J.V. A review of wave energy technology from a research and commercial perspective. IET Renew. Power Gener. 2021, 15, 3065–3090. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. The economics of wave energy: A review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Koca, K.; Kortenhaus, A.; Oumeraci, H.; Zanuttigh, B.; Angelelli, E.; Cantu, M.; Suffredini, R.; Franceschi, G. Recent advances in the development of wave energy converters. In Proceedings of the European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Drew, B.; Plummer, A.; Sahinkaya, M. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, T.W. A Brief Review of Wave Energy: A Report Produced for UK Department of Trade and Industry; Technical Report, Report No ETSU-120; AEA Technology: Carlsbad, CA, USA, 1999. [Google Scholar]
- Falcão, A.F. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. Geometric optimisation of wave energy conversion devices: A survey. Appl. Energy 2021, 297, 117100. [Google Scholar] [CrossRef]
- Budar, K.; Falnes, J. A resonant point absorber of ocean-wave power. Nature 1975, 256, 478–479. [Google Scholar] [CrossRef]
- Chatzigiannakou, M.A.; Dolguntseva, I.; Leijon, M. Offshore deployments of wave energy converters by seabased industry AB. J. Mar. Sci. Eng. 2017, 5, 15. [Google Scholar] [CrossRef]
- Fadaeenejad, M.; Shamsipour, R.; Rokni, S.; Gomes, C. New approaches in harnessing wave energy: With special attention to small islands. Renew. Sustain. Energy Rev. 2014, 29, 345–354. [Google Scholar] [CrossRef]
- Retzler, C. Measurements of the slow drift dynamics of a model Pelamis wave energy converter. Renew. Energy 2006, 31, 257–269. [Google Scholar] [CrossRef]
- Penalba, M.; Ringwood, J.V. A review of wave-to-wire models for wave energy converters. Energies 2016, 9, 506. [Google Scholar] [CrossRef] [Green Version]
- Papillon, L.; Costello, R.; Ringwood, J.V. Boundary Element and Integral Methods in Potential Flow Theory: A Review with a Focus on Wave Energy Applications. J. Ocean Eng. Mar. Energy 2020, 6, 303–337. [Google Scholar] [CrossRef]
- Penalba Retes, M.; Giorgi, G.; Ringwood, J.V. A review of non-linear approaches for wave energy converter modelling. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–10. [Google Scholar]
- Ekström, R.; Ekergård, B.; Leijon, M. Electrical damping of linear generators for wave energy converters—A review. Renew. Sustain. Energy Rev. 2015, 42, 116–128. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; Forehand, D. A review of geometry optimisation of wave energy converters. Renew. Sustain. Energy Rev. 2021, 139, 110593. [Google Scholar] [CrossRef]
- Ricci, P.; Lopez, J.; Santos, M.; Villate, J.; Ruiz-Minguela, P.; Salcedo, F.; Falcao, A.d.O. Control strategies for a simple point-absorber connected to a hydraulic power take-off. In Proceedings of the European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–9 September 2009; pp. 746–755. [Google Scholar]
- Guo, B.; Patton, R.; Abdelrahman, M.; Lan, J. A continuous control approach to point absorber wave energy conversion. In Proceedings of the UKACC International Conference on Control, Belfast, UK, 31 August 2016–2 September 2016; pp. 1–6. [Google Scholar]
- Jin, S.; Greaves, D. Wave energy in the UK: Status review and future perspectives. Renew. Sustain. Energy Rev. 2021, 143, 110932. [Google Scholar] [CrossRef]
- Budal, K.; Falnes, J. Optimum operation of improved wave-power converter. Mar. Sci. Commun. 1977, 3, 133–150. [Google Scholar]
- Thomas, G.; Evans, D. Arrays of three-dimensional wave-energy absorbers. J. Fluid Mech. 1981, 108, 67–88. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Bozzi, S.; Archetti, R.; Passoni, G. Wave electricity production in Italian offshore: A preliminary investigation. Renew. Energy 2014, 62, 407–416. [Google Scholar] [CrossRef]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Salter, S.H. Power conversion systems for ducks. In Proceedings of the International Conference on Future Energy Concepts, London, UK, 30 January–1 February 1979; pp. 100–108. [Google Scholar]
- Naito, S.; Nakamura, S. Wave energy absorption in irregular waves by feedforward control system. In Hydrodynamics of Ocean Wave-Energy Utilization; Springer: Berlin/Heidelberg, Germany, 1986; pp. 269–280. [Google Scholar]
- Li, Y.; Yu, Y.H. A synthesis of numerical methods for modeling wave energy converter-point absorbers. Renew. Sustain. Energy Rev. 2012, 16, 4352–4364. [Google Scholar] [CrossRef]
- Al Shami, E.; Zhang, R.; Wang, X. Point absorber wave energy harvesters: A review of recent developments. Energies 2019, 12, 47. [Google Scholar] [CrossRef] [Green Version]
- Sjolte, J.; Sandvik, C.M.; Tedeschi, E.; Molinas, M. Exploring the potential for increased production from the wave energy converterLifesaver by reactive control. Energies 2013, 6, 3706–3733. [Google Scholar] [CrossRef]
- Sandberg, A.B.; Klementsen, E.; Muller, G.; De Andres, A.; Maillet, J. Critical factors influencing viability of wave energy converters in off-grid luxury resorts and small utilities. Sustainability 2016, 8, 1274. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, M. Modelling and Experimental Verification of Direct Drive Wave Energy Conversion: Buoy-Generator Dynamics. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2007. [Google Scholar]
- Rahm, M. Ocean Wave Energy: Underwater Substation System for Wave Energy Converters. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2010. [Google Scholar]
- Waters, R.; Stålberg, M.; Danielsson, O.; Svensson, O.; Gustafsson, S.; Strömstedt, E.; Eriksson, M.; Sundberg, J.; Leijon, M. Experimental results from sea trials of an offshore wave energy system. Appl. Phys. Lett. 2007, 90, 034105. [Google Scholar] [CrossRef]
- Lejerskog, E.; Boström, C.; Hai, L.; Waters, R.; Leijon, M. Experimental results on power absorption from a wave energy converter at the Lysekil wave energy research site. Renew. Energy 2015, 77, 9–14. [Google Scholar] [CrossRef]
- Boström, C.; Lejerskog, E.; Tyrberg, S.; Svensson, O.; Waters, R.; Savin, A.; Bolund, B.; Eriksson, M.; Leijon, M. Experimental results from an offshore wave energy converter. J. Offshore Mech. Arct. Eng. 2010, 132, 041103. [Google Scholar] [CrossRef]
- Leijon, M.; Boström, C.; Danielsson, O.; Gustafsson, S.; Haikonen, K.; Langhamer, O.; Strömstedt, E.; Stålberg, M.; Sundberg, J.; Svensson, O.; et al. Wave energy from the North Sea: Experiences from the Lysekil research site. Surv. Geophys. 2008, 29, 221–240. [Google Scholar] [CrossRef] [Green Version]
- Sjolte, J.; Tjensvoll, G.; Molinas, M. Power collection from wave energy farms. Appl. Sci. 2013, 3, 420–436. [Google Scholar] [CrossRef]
- Sjolte, J.; Tjensvoll, G.; Molinas, M. Self-sustained all-electric wave energy converter system. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 1705–1721. [Google Scholar] [CrossRef]
- Joslin, J.; Cotter, E.; Murphy, P.; Gibbs, P.; Cavagnaro, R.; Crisp, C.; Stewart, A.R.; Polagye, B.; Cross, P.S.; Hjetland, E.; et al. The wave-powered adaptable monitoring package: Hardware design, installation, and deployment. In Proceedings of the European Wave and Tidal Energy Conference, Naples, Italy, 1–6 September 2019; pp. 1–6. [Google Scholar]
- CorpowerOcean. Corpower Ocean. 2021. Available online: https://corpowerocean.com/ (accessed on 8 August 2021).
- Todalshaug, J.H.; Ásgeirsson, G.S.; Hjálmarsson, E.; Maillet, J.; Möller, P.; Pires, P.; Guérinel, M.; Lopes, M. Tank testing of an inherently phase-controlled wave energy converter. Int. J. Mar. Energy 2016, 15, 68–84. [Google Scholar] [CrossRef]
- Berenjkoob, M.N.; Ghiasi, M.; Soares, C.G. Influence of the shape of a buoy on the efficiency of its dual-motion wave energy conversion. Energy 2020, 214, 118998. [Google Scholar] [CrossRef]
- Jin, S.; Patton, R.J.; Guo, B. Enhancement of wave energy absorption efficiency via geometry and power take-off damping tuning. Energy 2019, 169, 819–832. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.E.; Gardner, F.; de Sousa Prado, M.G. Archimedes wave swing linear permanent-magnet generator system performance. In Proceedings of the European Wave and Tidal Energy Conference, Glasgow, UK, 29 August–2 September 2005; pp. 383–387. [Google Scholar]
- de Sousa Prado, M.G.; Gardner, F.; Damen, M.; Polinder, H. Modelling and test results of the Archimedes wave swing. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 855–868. [Google Scholar] [CrossRef]
- Rafiee, A.; Fiévez, J. Numerical prediction of extreme loads on the CETO wave energy converter. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–10. [Google Scholar]
- Valério, D.; Mendes, M.J.; Beirão, P.; da Costa, J.S. Identification and control of the AWS using neural network models. Appl. Ocean Res. 2008, 30, 178–188. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Guercio, A. Sea Wave Energy. A Review of the Current Technologies and Perspectives. Energies 2021, 14, 6604. [Google Scholar] [CrossRef]
- Prado, M.; Polinder, H. Direct drive in wave energy conversion–AWS full scale prototype case study. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Valerio, D.; Beirao, P.; Mendes, M.J.; da Costa, J.S. Comparison of control strategies performance for a wave energy converter. In Proceedings of the Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 773–778. [Google Scholar]
- Gaudin, C.; David, D.; Cai, Y.; Hansen, J.; Bransby, M.; Rijnsdorp, D.; Lowe, R.; O’Loughlin, C.; Lu, T.; Uzielli, M.; et al. From Single to Multiple Wave Energy Converters: Cost Reduction through Location and Configuration Optimisation; Technical Report; The University of Western Australia: Perth, Australia, 2021. [Google Scholar]
- ARENA. How a Perth Company Created the World’s Most Advanced Wave Energy Device. 2017. Available online: https://arena.gov.au/blog/ceto-6/ (accessed on 10 July 2022).
- Sergiienko, N.; Rafiee, A.; Cazzolato, B.; Ding, B.; Arjomandi, M. Feasibility study of the three-tether axisymmetric wave energy converter. Ocean Eng. 2018, 150, 221–233. [Google Scholar] [CrossRef]
- Sergiienko, N.Y.; Cazzolato, B.S.; Ding, B.; Hardy, P.; Arjomandi, M. Performance comparison of the floating and fully submerged quasi-point absorber wave energy converters. Renew. Energy 2017, 108, 425–437. [Google Scholar] [CrossRef] [Green Version]
- OPT. Ocean Power Technologies. 2021. Available online: https://oceanpowertechnologies.com/ (accessed on 8 August 2022).
- Tarrant, K.R. Numerical Modelling of Parametric Resonance of a Heaving Point Absorber Wave Energy Converter. Ph.D. Thesis, Trinity College Dublin, Dublin, Ireland, 2015. [Google Scholar]
- Liu, Y.; Li, Y.; He, F.; Wang, H. Comparison study of tidal stream and wave energy technology development between China and some Western Countries. Renew. Sustain. Energy Rev. 2017, 76, 701–716. [Google Scholar] [CrossRef]
- Tarrant, K.; Meskell, C. Investigation on parametrically excited motions of point absorbers in regular waves. Ocean Eng. 2016, 111, 67–81. [Google Scholar] [CrossRef]
- Edwards, K.; Mekhiche, M. Ocean power technologies Powerbuoy: System-level design, development and validation methodology. In Proceedings of the 2nd Marine Energy Technology Symposium (METS), Seattle, WA, USA, 15–18 April 2014; pp. 1–9. [Google Scholar]
- Mackay, E.; Cruz, J.; Retzler, C.; Arnold, P.; Bannon, E.; Pascal, R. Validation of a new wave energy converter design tool with large scale single machine experiments. In Proceedings of the 1st Asian Wave and Tidal Conference Series, Jeju Island, Korea, 27–30 November 2012; pp. 1–12. [Google Scholar]
- Mackay, E.; Cruz, J.; Livingstone, M.; Arnold, P. Validation of a Time-Domain Modelling Tool for Wave Energy Converter Arrays. In Proceedings of the European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–6 September 2013; pp. 1–8. [Google Scholar]
- Kazmierkowski, M.P.; Jasiński, M. Power electronics for renewable sea wave energy. In Proceedings of the 12th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010; pp. 4–9. [Google Scholar]
- Babarit, A.; Clément, A.; Ruer, J.; Tartivel, C. SEAREV: A fully integrated wave energy converter. In Proceedings of the Offshore Wind and other Marine Renewable Energies in Mediterranean and European Seas, Rome, Italy, 5–7 September 2006; pp. 1–11. [Google Scholar]
- Wello. The Future of Wave Energy. 2021. Available online: https://wello.eu/ (accessed on 8 August 2022).
- Cordonnier, J.; Gorintin, F.; De Cagny, A.; Clément, A.H.; Babarit, A. SEAREV: Case study of the development of a wave energy converter. Renew. Energy 2015, 80, 40–52. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Soares, C.G. Review of mooring design for floating wave energy converters. Renew. Sustain. Energy Rev. 2019, 111, 595–621. [Google Scholar] [CrossRef]
- Josset, C.; Babarit, A.; Clément, A. A wave-to-wire model of the SEAREV wave energy converter. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2007, 221, 81–93. [Google Scholar] [CrossRef]
- Babarit, A.; Clement, A.H. Shape optimisation of the SEAREV wave energy converter. In Proceedings of the World Renewable Energy Conference, Florence, Italy, 19–25 August 2006; pp. 1–6. [Google Scholar]
- Durand, M.; Babarit, A.; Pettinotti, B.; Quillard, O.; Toularastel, J.; Clément, A. Experimental validation of the performances of the SEAREV wave energy converter with real time latching control. In Proceedings of the 7th European Wave and Tidal Energy Conference (EWTEC), Porto, Portugal, 11–13 September 2007; Volume 1113. [Google Scholar]
- Beharie, R.; Side, J. Acoustic Environmental Monitoring:–Wello Penguin Cooling System Noise Study; A Report Commissioned by Aquatera Limited; Technical Report; International Centre for Island Technology: Orkney, UK, 2012.
- Mattiazzo, G. State of the art and perspectives of wave energy in the Mediterranean sea: Backstage of ISWEC. Front. Energy Res. 2019, 7, 114. [Google Scholar] [CrossRef] [Green Version]
- AMOG. AMOG Wave Energy Converter. 2021. Available online: https://amog.consulting/ (accessed on 8 September 2022).
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu, S.A.; Mattiazzo, G. PeWEC: Experimental validation of wave to PTO numerical model. Ocean Eng. 2018, 167, 114–129. [Google Scholar] [CrossRef]
- Crowley, S.; Porter, R.; Taunton, D.; Wilson, P.A. Modelling of the WITT wave energy converter. Renew. Energy 2018, 115, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Qian, C.; Zheng, S.; Chen, N.; Xia, D.; Göteman, M. Investigation on the wave energy converter that reacts against an internal inverted pendulum. Energy 2022, 247, 123493. [Google Scholar] [CrossRef]
- Ambühl, S.; Kramer, M.; Sørensen, J.D. Reliability-based structural optimization of wave energy converters. Energies 2014, 7, 8178–8200. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Moan, T. Mooring system analysis of multiple wave energy converters in a farm configuration. In Proceedings of the European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 509–518. [Google Scholar]
- Kramer, M.; Marquis, L.; Frigaard, P. Performance evaluation of the wavestar prototype. In Proceedings of the European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011; pp. 1–8. [Google Scholar]
- Ma, Y.; Zhang, A.; Yang, L.; Li, H.; Zhai, Z.; Zhou, H. Motion simulation and performance analysis of two-body floating point absorber wave energy converter. Renew. Energy 2020, 157, 353–367. [Google Scholar] [CrossRef]
- Marquis, L.; Kramer, M.; Frigaard, P. First power production figures from the Wave Star Roshage wave energy converter. In Proceedings of the 3rd International Conference on Ocean Energy (ICOE-2010), Bilbao, Spain, 6 October 2010; pp. 1–5. [Google Scholar]
- Leirbukt, A.; Tubass, P. A Wave of Renewable Energy. 2006. Available online: https://library.e.abb.com/public/1e2fadd298a58d14c12571d900412482/29-31%203M646_ENG72dpi.pdf (accessed on 10 July 2022).
- Wendt, F.; Nielsen, K.; Yu, Y.H.; Bingham, H.; Eskilsson, C.; Kramer, M.; Babarit, A.; Bunnik, T.; Costello, R.; Crowley, S.; et al. Ocean energy systems wave energy modelling task: Modelling, verification and validation of wave energy converters. J. Mar. Sci. Eng. 2019, 7, 379. [Google Scholar] [CrossRef] [Green Version]
- Sheng, W.; Alcorn, R.; Lewis, T. Physical modelling of wave energy converters. Ocean Eng. 2014, 84, 29–36. [Google Scholar] [CrossRef]
- Folley, M. Numerical Modelling of Wave Energy Converters: State-of-the-Art Techniques for Single Devices and Arrays; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Jin, S.; Patton, R.J.; Guo, B. Viscosity effect on a point absorber wave energy converter hydrodynamics validated by simulation and experiment. Renew. Energy 2018, 129, 500–512. [Google Scholar] [CrossRef]
- Tran, N.; Sergiienko, N.; Cazzolato, B.; Ghayesh, M.; Arjomandi, M. Design considerations for a three-tethered point absorber wave energy converter with nonlinear coupling between hydrodynamic modes. Ocean Eng. 2022, 254, 111351. [Google Scholar] [CrossRef]
- Dafnakis, P.; Bhalla, A.P.S.; Sirigu, S.A.; Bonfanti, M.; Bracco, G.; Mattiazzo, G. Comparison of wave–structure interaction dynamics of a submerged cylindrical point absorber with three degrees of freedom using potential flow and computational fluid dynamics models. Phys. Fluids 2020, 32, 093307. [Google Scholar] [CrossRef]
- Rusch, C.J.; Mundon, T.R.; Maurer, B.D.; Polagye, B.L. Hydrodynamics of an asymmetric heave plate for a point absorber wave energy converter. Ocean Eng. 2020, 215, 107915. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y.; Yu, Y.H.; Ding, B.; Jiang, Z.; Lin, Z.; Cazzolato, B. Experimental and numerical investigations of a two-body floating-point absorber wave energy converter in regular waves. J. Fluids Struct. 2019, 91, 102613. [Google Scholar] [CrossRef]
- Katsidoniotaki, E.; Göteman, M. Numerical modeling of extreme wave interaction with point-absorber using OpenFOAM. Ocean Eng. 2022, 245, 110268. [Google Scholar] [CrossRef]
- DualSPHysics. DualSPHysics. Available online: https://dual.sphysics.org/ (accessed on 10 September 2020).
- Ropero-Giralda, P.; Crespo, A.J.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Crespo, A.J.; Göteman, M.; Engström, J.; Gómez-Gesteira, M. A numerical study of a taut-moored point-absorber wave energy converter with a linear power take-off system under extreme wave conditions. Appl. Energy 2022, 311, 118629. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Li, A.; Liu, Y. New analytical solutions to water wave diffraction by vertical truncated cylinders. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 952–969. [Google Scholar] [CrossRef]
- Li, A.j.; Liu, Y.; Li, H.j. New analytical solutions to water wave radiation by vertical truncated cylinders through multi-term Galerkin method. Meccanica 2019, 54, 429–450. [Google Scholar] [CrossRef]
- Penalba Retes, M.; Mérigaud, A.; Gilloteaux, J.C.; Ringwood, J. Nonlinear Froude-Krylov force modelling for two heaving wave energy point absorbers. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–10. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Nonlinear Froude-Krylov and viscous drag representations for wave energy converters in the computation/fidelity continuum. Ocean Eng. 2017, 141, 164–175. [Google Scholar] [CrossRef] [Green Version]
- Cummins, W. The Impulse Response Function and Ship Motions; Technical Report; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Computationally efficient nonlinear Froude–Krylov force calculations for heaving axisymmetric wave energy point absorbers. J. Ocean Eng. Mar. Energy 2017, 3, 21–33. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Analytical representation of nonlinear Froude-Krylov forces for 3-DoF point absorbing wave energy devices. Ocean Eng. 2018, 164, 749–759. [Google Scholar] [CrossRef] [Green Version]
- Merigaud, A.; Gilloteaux, J.C.; Ringwood, J.V. A nonlinear extension for linear boundary element methods in wave energy device modelling. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 1–7. [Google Scholar]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.; Jin, S.; Gilbert, J.; Parsons, D. Nonlinear modeling and verification of a heaving point absorber for wave energy conversion. IEEE Trans. Sustain. Energy 2017, 9, 453–461. [Google Scholar] [CrossRef]
- Gudmestad, O.T.; Moe, G. Hydrodynamic coefficients for calculation of hydrodynamic loads on offshore truss structures. Mar. Struct. 1996, 9, 745–758. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J. Consistency of viscous drag identification tests for wave energy applications. In Proceedings of the European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–8. [Google Scholar]
- Wang, H.; Sitanggang, K.; Falzarano, J. Exploration of power take off in wave energy converters with two-body interaction. Ocean Syst. Eng. 2017, 7, 89–106. [Google Scholar]
- Ji, X.; Al Shami, E.; Monty, J.; Wang, X. Modelling of linear and non-linear two-body wave energy converters under regular and irregular wave conditions. Renew. Energ. 2020, 147, 487–501. [Google Scholar] [CrossRef]
- Flocard, F.; Finnigan, T.D. Increasing power capture of a wave energy device by inertia adjustment. Appl. Ocean Res. 2012, 34, 126–134. [Google Scholar] [CrossRef]
- Davidson, J.; Giorgi, S.; Ringwood, J.V. Identification of wave energy device models from numerical wave tank data—Part 1: Numerical wave tank identification tests. IEEE Trans. Sustain. Energy 2016, 7, 1012–1019. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, S.; Davidson, J.; Ringwood, J.V. Identification of wave energy device models from numerical wave tank data—Part 2: Data-based model determination. IEEE Trans. Sustain. Energy 2016, 7, 1020–1027. [Google Scholar] [CrossRef] [Green Version]
- Bacelli, G.; Coe, R.G.; Patterson, D.; Wilson, D. System identification of a heaving point absorber: Design of experiment and device modeling. Energies 2017, 10, 472. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, S.; Davidson, J.; Jakobsen, M.; Kramer, M.; Ringwood, J.V. Identification of dynamic models for a wave energy converter from experimental data. Ocean Eng. 2019, 183, 426–436. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, Y.H.; Zhang, W.C.; Zhao, Q.S. Hydrodynamic analysis and power conversion for point absorber WEC with two degrees of freedom using CFD. China Ocean Eng. 2018, 32, 718–729. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.J. Non-linear viscous and friction effects on a heaving point absorber dynamics and latching control performance. In Proceedings of the IFAC World Congress, Toulouse, France, 27 August–1 September 2017; pp. 15657–15662. [Google Scholar]
- Jin, S.; Guo, B.; Patton, R.; Gilbert, J.; Abdelrahman, M. Non-linear analysis of a point absorber wave energy converter. In Proceedings of the International Conference on Offshore Renewable Energy, Glasgow, Scotland, 12–14 September 2016; pp. 1–6. [Google Scholar]
- Jusoh, M.A.; Ibrahim, M.Z.; Daud, M.Z.; Albani, A.; Mohd Yusop, Z. Hydraulic power take-off concepts for wave energy conversion system: A review. Energies 2019, 12, 4510. [Google Scholar] [CrossRef] [Green Version]
- Têtu, A.; Ferri, F.; Kramer, M.B.; Hals Todalshaug, J. Physical and mathematical modeling of a wave energy converter equipped with a negative spring mechanism for phase control. Energies 2018, 11, 2362. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Li, W.; Lin, Y.; Bao, J. An overview of hydraulic systems in wave energy application in China. Renew. Sustain. Energy Rev. 2012, 16, 4522–4526. [Google Scholar] [CrossRef]
- Liu, C. Current Research Status and Challenge for Direct-Drive Wave Energy Conversions. IETE J. Res. 2021, 1, 1–13. [Google Scholar] [CrossRef]
- Penalba, M.; Sell, N.P.; Hillis, A.J.; Ringwood, J.V. Validating a wave-to-wire model for a wave energy converte–Part I: The Hydraulic Transmission System. Energies 2017, 10, 977. [Google Scholar] [CrossRef] [Green Version]
- Penalba, M.; Cortajarena, J.A.; Ringwood, J.V. Validating a wave-to-wire model for a wave energy converter–Part II: The electrical system. Energies 2017, 10, 1002. [Google Scholar] [CrossRef] [Green Version]
- Vantorre, M.; Banasiak, R.; Verhoeven, R. Modelling of hydraulic performance and wave energy extraction by a point absorber in heave. Appl. Ocean Res. 2004, 26, 61–72. [Google Scholar] [CrossRef]
- Kim, S.J.; Koo, W.; Shin, M.J. Numerical and experimental study on a hemispheric point-absorber-type wave energy converter with a hydraulic power take-off system. Renew. Energy 2019, 135, 1260–1269. [Google Scholar] [CrossRef]
- Li, X.; Chen, C.; Li, Q.; Xu, L.; Liang, C.; Ngo, K.; Parker, R.G.; Zuo, L. A compact mechanical power take-off for wave energy converters: Design, analysis, and test verification. Appl. Energy 2020, 278, 115459. [Google Scholar] [CrossRef]
- Liang, C.; Ai, J.; Zuo, L. Design, fabrication, simulation and testing of an ocean wave energy converter with mechanical motion rectifier. Ocean Eng. 2017, 136, 190–200. [Google Scholar] [CrossRef]
- Mueller, M.; Baker, N. Direct drive electrical power take-off for offshore marine energy converters. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 219, 223–234. [Google Scholar] [CrossRef]
- Rhinefrank, K.; Schacher, A.; Prudell, J.; Brekken, T.K.; Stillinger, C.; Yen, J.Z.; Ernst, S.G.; von Jouanne, A.; Amon, E.; Paasch, R.; et al. Comparison of direct-drive power takeoff systems for ocean wave energy applications. IEEE J. Ocean Eng. 2011, 37, 35–44. [Google Scholar] [CrossRef]
- Faiz, J.; Nematsaberi, A. Linear electrical generator topologies for direct-drive marine wave energy conversion-an overview. IET Renew. Power Gener. 2017, 11, 1163–1176. [Google Scholar] [CrossRef]
- Liu, W.; Xu, L.; Bu, T.; Yang, H.; Liu, G.; Li, W.; Pang, Y.; Hu, C.; Zhang, C.; Cheng, T. Torus structured triboelectric nanogenerator array for water wave energy harvesting. Nano Energy 2019, 58, 499–507. [Google Scholar] [CrossRef]
- Collins, I.; Hossain, M.; Dettmer, W.; Masters, I. Flexible membrane structures for wave energy harvesting: A review of the developments, materials and computational modelling approaches. Renew. Sustain. Energy Rev. 2021, 151, 111478. [Google Scholar] [CrossRef]
- Wu, S.; Liu, Y.; Qin, J. Experimental analyses of two-body wave energy converters with hydraulic power take-off damping in regular and irregular waves. IET Renew. Power Gener. 2021, 15, 3165–3175. [Google Scholar] [CrossRef]
- Polinder, H.; Mecrow, B.C.; Jack, A.G.; Dickinson, P.G.; Mueller, M.A. Conventional and TFPM linear generators for direct-drive wave energy conversion. IEEE Trans. Energy Convers. 2005, 20, 260–267. [Google Scholar] [CrossRef] [Green Version]
- Cargo, C.; Hillis, A.; Plummer, A. Strategies for active tuning of Wave Energy Converter hydraulic power take-off mechanisms. Renew. Energy 2016, 94, 32–47. [Google Scholar] [CrossRef] [Green Version]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- António, F.d.O. Phase control through load control of oscillating-body wave energy converters with hydraulic PTO system. Ocean Eng. 2008, 35, 358–366. [Google Scholar]
- Li, X.; Martin, D.; Liang, C.; Chen, C.; Parker, R.G.; Zuo, L. Characterization and verification of a two-body wave energy converter with a novel power take-off. Renew. Energy 2021, 163, 910–920. [Google Scholar] [CrossRef]
- Omholt, T. A wave activated electric generator. In Proceedings of the OCEANS, Washington, DC, USA, 6–8 September 1978; pp. 585–589. [Google Scholar]
- Mueller, M.; Baker, N.; Ran, L.; Chong, N.; Wei, H.; Tavner, P.; McKeever, P. Experimental tests of an air-cored PM tubular generator for direct drive wave energy converters. In Proceedings of the IET Conference on Power Electronics, Machines and Drives, York, UK, 2–4 April 2008; pp. 747–751. [Google Scholar]
- Hodgins, N.; Keysan, O.; McDonald, A.S.; Mueller, M.A. Design and testing of a linear generator for wave-energy applications. IEEE Trans. Ind. Electron. 2012, 59, 2094–2103. [Google Scholar] [CrossRef]
- Mueller, M.; Baker, N. A low speed reciprocating permanent magnet generator for direct drive wave energy converters. In Proceedings of the International Conference on Power Electronics Machines and Drives, Bath, UK, 16–18 April 2002; pp. 468–473. [Google Scholar]
- Mueller, M.; Polinder, H.; Baker, N. Current and novel electrical generator technology for wave energy converters. In Proceedings of the IEEE International Conference on Electric Machines and Drives (IEMDC), Antalya, Turkey, 3–5 May 2007; Volume 2, pp. 1401–1406. [Google Scholar]
- Khatri, P.; Wang, X. Comprehensive review of a linear electrical generator for ocean wave energy conversion. IET Renew. Power Gener. 2020, 14, 949–958. [Google Scholar] [CrossRef]
- Rhinefrank, K.; Prudell, J.; Schacher, A. Development and characterization of a novel direct drive rotary wave energy point absorber. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; pp. 1–5. [Google Scholar]
- Thorburn, K.; Leijon, M. Farm size comparison with analytical model of linear generator wave energy converters. Ocean Eng. 2007, 34, 908–916. [Google Scholar] [CrossRef]
- Leijon, M.; Danielsson, O.; Eriksson, M.; Thorburn, K.; Bernhoff, H.; Isberg, J.; Sundberg, J.; Ivanova, I.; Sjöstedt, E.; Ågren, O.; et al. An electrical approach to wave energy conversion. Renew. Energy 2006, 31, 1309–1319. [Google Scholar] [CrossRef]
- Genest, R.; Bonnefoy, F.; Clément, A.H.; Babarit, A. Effect of non-ideal power take-off on the energy absorption of a reactively controlled one degree of freedom wave energy converter. Appl. Ocean Res. 2014, 48, 236–243. [Google Scholar] [CrossRef] [Green Version]
- Sjolte, J.; Bjerke, I.; Crozier, A.; Tjensvoll, G.; Molinas, M. All-electric wave energy power take off system with improved power quality at the grid connection point. In Proceedings of the Transmission and Distribution Conference and Exposition (T&D), 2012 IEEE PES, Orlando, FL, USA, 7–10 May 2012; pp. 1–7. [Google Scholar]
- Moretti, G.; Herran, M.S.; Forehand, D.; Alves, M.; Jeffrey, H.; Vertechy, R.; Fontana, M. Advances in the development of dielectric elastomer generators for wave energy conversion. Renew. Sustain. Energy Rev. 2020, 117, 109430. [Google Scholar] [CrossRef]
- Di, K.; Bao, K.; Chen, H.; Xie, X.; Tan, J.; Shao, Y.; Li, Y.; Xia, W.; Xu, Z.; E, S. Dielectric elastomer generator for electromechanical energy conversion: A mini review. Sustainability 2021, 13, 9881. [Google Scholar] [CrossRef]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 2000, 287, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Chiba, S.; Waki, M.; Masuda, K.; Ikoma, T. Current status and future prospects of electric generators using electroactive polymer artificial muscle. In Proceedings of the OCEANS, Sydney, NSW, Australia, 24–27 May 2010; pp. 1–5. [Google Scholar]
- Papini, G.P.R.; Vertechy, R.; Fontana, M. Dynamic model of dielectric elastomer diaphragm generators for oscillating water column wave energy converters. In Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 16–18 September 2013; pp. 1–9. [Google Scholar]
- Vertechy, R.; Fontana, M.; Papini, G.R.; Bergamasco, M. Oscillating-water-column wave-energy-converter based on dielectric elastomer generator. In Proceedings of the SPIE Smart Structures and Materials+ Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 10–14 March 2013; p. 86870I. [Google Scholar]
- Fusco, F.; Ringwood, J.V. A simple and effective real-time controller for wave energy converters. IEEE Trans. Sustain. Energy 2012, 4, 21–30. [Google Scholar] [CrossRef]
- Davidson, J.; Genest, R.; Ringwood, J.V. Adaptive control of a wave energy converter. IEEE Trans. Sustain. Energy 2018, 9, 1588–1595. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A.; Guglielmi, M.; Clément, A.H. Declutching control of a wave energy converter. Ocean Eng. 2009, 36, 1015–1024. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Patton, R.J.; Jin, S.; Lan, J. Numerical and experimental studies of excitation force approximation for wave energy conversion. Renew. Energy 2018, 125, 877–889. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.; Jin, S. Identification and validation of excitation force for a heaving point absorber wave energy convertor. In Proceedings of the European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–9. [Google Scholar]
- Abdelrahman, M.; Patton, R.; Guo, B.; Lan, J. Estimation of wave excitation force for wave energy converters. In Proceedings of the 2016 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 7–9 September 2016; pp. 654–659. [Google Scholar]
- Garcia-Abril, M.; Paparella, F.; Ringwood, J.V. Excitation force estimation and forecasting for wave energy applications. In Proceedings of the IFAC World Congress, Toulouse, France, 9–14 July 2017; pp. 14692–14697. [Google Scholar]
- Peña-Sanchez, Y.; Windt, C.; Davidson, J.; Ringwood, J.V. A critical comparison of excitation force estimators for wave-energy devices. IEEE Trans. Control Syst. Technol. 2019, 28, 2263–2275. [Google Scholar] [CrossRef]
- French, M.J.; Bracewell, R. Ps Frog: A Point-Absorber Wave Energy Converter Working in a Pitch/Surge Mode. In Proceedings of the International Conference on Energy Options: The Role of Alternatives in the World Energy Scene, Reading, UK, 7–9 April 1987; pp. 198–200. [Google Scholar]
- Giassi, M.; Thomas, S.; Tosdevin, T.; Engström, J.; Hann, M.; Isberg, J.; Göteman, M. Capturing the experimental behaviour of a point-absorber WEC by simplified numerical models. J. Fluids Struct. 2020, 99, 103143. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J. On energy transfer of parametric resonance for wave energy conversion. In Proceedings of the European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021; pp. 1–10. [Google Scholar]
- Hollm, M.; Dostal, L.; Yurchenko, D.; Seifried, R. Performance increase of wave energy harvesting of a guided point absorber. Eur. Phys. J. Spec. Top. 2022, 231, 1465–1473. [Google Scholar] [CrossRef]
- López, M.; Taveira-Pinto, F.; Rosa-Santos, P. Numerical modelling of the CECO wave energy converter. Renew. Energy 2017, 113, 202–210. [Google Scholar] [CrossRef]
- López, M.; Ramos, V.; Rosa-Santos, P.; Taveira-Pinto, F. Effects of the PTO inclination on the performance of the CECO wave energy converter. Mar. Struct. 2018, 61, 452–466. [Google Scholar] [CrossRef]
- Rosa-Santos, P.; Taveira-Pinto, F.; Rodríguez, C.A.; Ramos, V.; López, M. The CECO wave energy converter: Recent developments. Renew. Energy 2019, 139, 368–384. [Google Scholar] [CrossRef]
- Ramos, V.; López, M.; Taveira-Pinto, F.; Rosa-Santos, P. Performance assessment of the CECO wave energy converter: Water depth influence. Renew. Energy 2018, 117, 341–356. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Hydrodynamic optimization of the geometry of a sloped-motion wave energy converter. Ocean Eng. 2020, 199, 107046. [Google Scholar] [CrossRef]
- Giannini, G.; López, M.; Ramos, V.; Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Geometry assessment of a sloped type wave energy converter. Renew. Energy 2021, 171, 672–686. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rosa-Santos, P.; Taveira-Pinto, F. Assessment of damping coefficients of power take-off systems of wave energy converters: A hybrid approach. Energy 2019, 169, 1022–1038. [Google Scholar] [CrossRef]
- Tay, Z.Y. Energy generation enhancement of arrays of point absorber wave energy converters via Moonpool’s resonance effect. Renew. Energy 2022, 188, 830–848. [Google Scholar] [CrossRef]
- Cong, D.; Shang, J.; Luo, Z.; Sun, C.; Wu, W. Energy efficiency analysis of multi-type floating bodies for a novel heaving point absorber with application to low-power unmanned ocean device. Energies 2018, 11, 3282. [Google Scholar] [CrossRef] [Green Version]
- Tay, Z.Y. Effect of resonance and wave reflection in semi-enclosed moonpool on performance enhancement of point absorber arrays. Ocean Eng. 2022, 243, 110182. [Google Scholar] [CrossRef]
- Guo, B.; Elmoosa, Q.; Windt, C.; Ringwood, J. Impact of nonlinear hydrodynamic modelling on geometric optimisation of a spherical heaving point absorber. In Proceedings of the European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021; pp. 1–10. [Google Scholar]
- Shahroozi, Z.; Göteman, M.; Engström, J. Experimental investigation of a point-absorber wave energy converter response in different wave-type representations of extreme sea states. Ocean Eng. 2022, 248, 110693. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Soares, C.G. Experimental study of the influence of the rope material on mooring fatigue damage and point absorber response. Ocean Eng. 2021, 232, 108667. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. Modelling of a vibro-impact power take-off mechanism for wave energy conversion. In Proceedings of the European Control Conference, St. Petersburg, Russia, 12–15 May 2020; pp. 1348–1353. [Google Scholar]
- Guo, B.; Ringwood, J.V. Non-Linear Modelling of a Vibro-Impact Wave Energy Converter. IEEE Trans. Sustain. Energy 2021, 12, 492–500. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. Parametric study of a vibro-impact wave energy converter. In Proceedings of the IFAC World Congress, Berlin, Germany, 11–17 July 2020; pp. 12283–12288. [Google Scholar]
- Chen, M.; Xiao, P.; Zhang, Z.; Sun, L.; Li, F. Effects of the end-stop mechanism on the nonlinear dynamics and power generation of a point absorber in regular waves. Ocean Eng. 2021, 242, 110123. [Google Scholar] [CrossRef]
- Zou, S.; Abdelkhalik, O.; Robinett, R.; Korde, U.; Bacelli, G.; Wilson, D.; Coe, R. Model Predictive Control of parametric excited pitch-surge modes in wave energy converters. Int. J. Mar. Energy 2017, 19, 32–46. [Google Scholar] [CrossRef] [Green Version]
- Davidson, J.; Kalmár-Nagy, T. A Real-Time Detection System for the Onset of Parametric Resonance in Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 819. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Bergdahl, L. Parametric Excitation of Moored Wave Energy Converters Using Viscous and Non-Viscous CFD Simulations; Taylor & Francis Group: Abingdon, UK, 2018. [Google Scholar]
- Kovacic, I.; Rand, R.; Mohamed Sah, S. Mathieu’s equation and its generalizations: Overview of stability charts and their features. Appl. Mech. Rev. 2018, 70, 020802. [Google Scholar] [CrossRef] [Green Version]
- Iseki, T.; Xu, P. Experimental Study on Coupled Motions of a Spar-Buoy Under Mathieu Instability. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; Volume 58899, p. V010T09A027. [Google Scholar]
- Giorgi, G.; Gomes, R.P.; Bracco, G.; Mattiazzo, G. Numerical investigation of parametric resonance due to hydrodynamic coupling in a realistic wave energy converter. Nonlinear Dyn. 2020, 101, 153–170. [Google Scholar] [CrossRef]
- Giorgi, G.; Gomes, R.P.; Bracco, G.; Mattiazzo, G. The effect of mooring line parameters in inducing parametric resonance on the spar-buoy oscillating water column wave energy converter. J. Mar. Sci. Eng. 2020, 8, 29. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Xu, P. Effect of hull geometry on parametric resonances of spar in irregular waves. Ocean Eng. 2015, 99, 14–22. [Google Scholar] [CrossRef]
- Haslum, H. Simplified Methods Applied to Nonlinear Motion of Spar Platforms. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2000. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Articulating parametric resonance for an OWC spar buoy in regular and irregular waves. J. Ocean. Eng. Mar. Energy 2018, 4, 311–322. [Google Scholar] [CrossRef]
- Rafiee, A.; Wolgamot, H.; Draper, S. Identifying the design wave group for the extreme response of a point absorber wave energy converter. In Proceedings of the Asian Wave and Tidal Energy Conference, Marina Bay Sands, Singapore, 24–28 October 2016; pp. 1–8. [Google Scholar]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Jakobsen, M.M.; Kramer, M. RANS-VOF modelling of the wavestar point absorber. Renew. Energy 2017, 109, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Dolguntseva, I.; Savin, A.; Zhang, Y.; Li, W.; Svensson, O.; Leijon, M. Numerical modelling of a point-absorbing wave energy converter in irregular and extreme waves. Appl. Ocean Res. 2017, 63, 90–105. [Google Scholar] [CrossRef]
- Bretl, J.; Parsa, K.; Edwards, K.; Montgomery, J.; Mekhiche, M. The deployment of the PB-3-50-A1 PowerBuoy: Power prediction and measurement comparison. In Proceedings of the Marine Energy Technology Symposium METS, Washington, DC, USA, 25–27 April 2016; pp. 1–4. [Google Scholar]
- Balitsky, P.; Bacelli, G.; Ringwood, J.V. Control-influenced layout optimization of arrays of wave energy converters. In Proceedings of the International Conference on Ocean, Offshore and Artic Engineering, San Francisco, CA, USA, 8–13 June 2014; pp. 1–10. [Google Scholar]
- Child, B.F.M. On the Configuration of Arrays of Floating Wave Energy Converters. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2011. [Google Scholar]
- Fang, H.W.; Feng, Y.Z.; Li, G.P. Optimization of wave energy converter arrays by an improved differential evolution algorithm. Energies 2018, 11, 3522. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Rosa, P.B.; Bacelli, G.; Ringwood, J.V. Control-informed optimal array layout for wave farms. IEEE Trans. Sustain. Energy 2015, 6, 575–582. [Google Scholar] [CrossRef] [Green Version]
- Giassi, M.; Göteman, M. Layout design of wave energy parks by a genetic algorithm. Ocean Eng. 2018, 154, 252–261. [Google Scholar] [CrossRef]
- Lyu, J.; Abdelkhalik, O.; Gauchia, L. Optimization of dimensions and layout of an array of wave energy converters. Ocean Eng. 2019, 192, 106543. [Google Scholar] [CrossRef]
- McGuinness, J.P.; Thomas, G. Hydrodynamic optimisation of small arrays of heaving point absorbers. J. Ocean Eng. Mar. Energy 2016, 2, 439–457. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, P.M.; Nava, V.; Topper, M.B.; Minguela, P.R.; Ferri, F.; Kofoed, J.P. Layout optimisation of wave energy converter arrays. Energies 2017, 10, 1262. [Google Scholar] [CrossRef] [Green Version]
- Penalba, M.; Touzón, I.; Lopez-Mendia, J.; Nava, V. A numerical study on the hydrodynamic impact of device slenderness and array size in wave energy farms in realistic wave climates. Ocean Eng. 2017, 142, 224–232. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, D.; Contal, E.; Vayatis, N.; Dias, F. Prediction and optimization of wave energy converter arrays using a machine learning approach. Renew. Energy 2016, 97, 504–517. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M. A hybrid cooperative co-evolution algorithm framework for optimising power take off and placements of wave energy converters. Inf. Sci. 2020, 534, 218–244. [Google Scholar] [CrossRef]
- Stratigaki, V.; Troch, P.; Stallard, T.; Forehand, D.; Folley, M.; Kofoed, J.P.; Benoit, M.; Babarit, A.; Vantorre, M.; Kirkegaard, J. Sea-state modification and heaving float interaction factors from physical modelling of arrays of wave energy converters. J. Renew. Sustain. Energy 2015, 7, 061705. [Google Scholar] [CrossRef]
- Devolder, B.; Stratigaki, V.; Troch, P.; Rauwoens, P. CFD simulations of floating point absorber wave energy converter arrays subjected to regular waves. Energies 2018, 11, 641. [Google Scholar] [CrossRef] [Green Version]
- Guo, B. Study of Scale Modelling, Verification and Control of a Heaving Point Absorber Wave Energy Converter. Ph.D. Thesis, University of Hull, Hull, UK, 2017. [Google Scholar]
- Falcão, A.F.; Henriques, J.C. Effect of non-ideal power take-off efficiency on performance of single-and two-body reactively controlled wave energy converters. J. Ocean Eng. Mar. Energy 2015, 1, 273–286. [Google Scholar] [CrossRef] [Green Version]
- de la Villa Jaén, A.; Santana, A.G. Considering linear generator copper losses on model predictive control for a point absorber wave energy converter. Energy Convers. Manag. 2014, 78, 173–183. [Google Scholar]
- Mueller, M. Electrical generators for direct drive wave energy converters. IEE Proc.—Gener. Transm. Distrib. 2002, 149, 446–456. [Google Scholar] [CrossRef]
- Bacelli, G.; Genest, R.; Ringwood, J.V. Nonlinear control of flap-type wave energy converter with a non-ideal power take-off system. Annu. Rev. Control 2015, 40, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yang, J. Power capture performance of an oscillating-body WEC with nonlinear snap through PTO systems in irregular waves. Appl. Ocean Res. 2015, 52, 261–273. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, X.; Xiao, L.; Li, X.; Chen, L. Application of an adaptive bistable power capture mechanism to a point absorber wave energy converter. Appl. Energy 2018, 228, 450–467. [Google Scholar] [CrossRef]
- Zhang, H.; Xi, R.; Xu, D.; Wang, K.; Shi, Q.; Zhao, H.; Wu, B. Efficiency enhancement of a point wave energy converter with a magnetic bistable mechanism. Energy 2019, 181, 1152–1165. [Google Scholar] [CrossRef]
- Li, M.; Jing, X. A bistable X-structured electromagnetic wave energy converter with a novel mechanical-motion-rectifier: Design, analysis, and experimental tests. Energy Convers. Manag. 2021, 244, 114466. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, X.; Xiao, L.; Wei, H.; Chen, W. Evaluation of long-term power capture performance of a bistable point absorber wave energy converter in South China Sea. Ocean Eng. 2021, 237, 109338. [Google Scholar] [CrossRef]
- Xi, R.; Zhang, H.; Xu, D.; Zhao, H.; Mondal, R. High-performance and robust bistable point absorber wave energy converter. Ocean Eng. 2021, 229, 108767. [Google Scholar] [CrossRef]
- Song, Y.; Guo, X.; Wang, H.; Tian, X.; Wei, H.; Zhang, X. Performance Analysis of an Adaptive Bistable Point Absorber Wave Energy Converter under White Noise Wave Excitation. IEEE Trans. Sustain. Energy 2021, 12, 1090–1099. [Google Scholar] [CrossRef]
- Younesian, D.; Alam, M.R. Multi-stable mechanisms for high-efficiency and broadband ocean wave energy harvesting. Appl. Energy 2017, 197, 292–302. [Google Scholar] [CrossRef]
- González-Esculpi, A.; Verde, C.; Maya-Ortiz, P. Fault-Tolerant Control for a Wave Energy Converter by Damping Injection. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), San Diego, CA, USA, 9–11 August 2021; pp. 673–678. [Google Scholar]
- Xu, N.; Chen, L.; Yang, R.; Zhu, Y. Multi-controller-based fault tolerant control for systems with actuator and sensor failures: Application to 2-body point absorber wave energy converter. J. Frankl. Inst. 2022, 359, 5919–5934. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, T.; Gao, Z. Fault Diagnosis and Fault-Tolerant Control of Energy Maximization for Wave Energy Converters. IEEE Trans. Sustain. Energy 2022, 13, 1771–1778. [Google Scholar] [CrossRef]
- Penalba, M.; Ringwood, J.V. A high-fidelity wave-to-wire model for wave energy converters. Renew. Energy 2019, 134, 367–378. [Google Scholar] [CrossRef]
- Fusco, F.; Ringwood, J.V. Robust control of wave energy converters. In Proceedings of the IEEE Conference on Control Applications, Juan Les Antibes, France, 8–10 October 2014; pp. 292–297. [Google Scholar]
- Na, J.; Li, G.; Wang, B.; Herrmann, G.; Zhan, S. Robust optimal control of wave energy converters based on adaptive dynamic programming. IEEE Trans. Sustain. Energy 2018, 10, 961–970. [Google Scholar] [CrossRef] [Green Version]
- García-Violini, D.; Ringwood, J.V. Robust Control of Wave Energy Converters Using Spectral and Pseudospectral Methods: A Case Study. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 4779–4784. [Google Scholar]
- Lao, Y.; Scruggs, J.T. Robust Control of Wave Energy Converters Using Unstructured Uncertainty. In Proceedings of the American Control Conference, Denver, CO, USA, 1–3 July 2020; pp. 4237–4244. [Google Scholar]
- Faedo, N.; García-Violini, D.; Scarciotti, G.; Astolfi, A.; Ringwood, J.V. Robust moment-based energy-maximising optimal control of wave energy converters. In Proceedings of the IEEE Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 4286–4291. [Google Scholar]
- Ringwood, J.V.; Mérigaud, A.; Faedo, N.; Fusco, F. An analytical and numerical sensitivity and robustness analysis of wave energy control systems. IEEE Trans. Control Syst. Technol. 2019, 28, 1337–1348. [Google Scholar] [CrossRef] [Green Version]
- Garrido, A.J.; Garrido, I.; Alberdi, M.; Amundarain, M.; Barambones, O.; Romero, J.A. Robust control of oscillating water column (OWC) devices: Power generation improvement. In Proceedings of the OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–4. [Google Scholar]
- Wahyudie, A.; Jama, M.; Saeed, O.; Noura, H.; Assi, A.; Harib, K. Robust and low computational cost controller for improving captured power in heaving wave energy converters. Renew. Energy 2015, 82, 114–124. [Google Scholar] [CrossRef]
- Zhan, S.; He, W.; Li, G. Robust feedback model predictive control of sea wave energy converters. In Proceedings of the IFAC World Congress, Toulouse, France, 9–14 July 2017; pp. 141–146. [Google Scholar]
- Fusco, F.; Ringwood, J. A model for the sensitivity of non-causal control of wave energy converters to wave excitation force prediction errors. In Proceedings of the Prod. European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011; pp. 1–10. [Google Scholar]
- Parrinello, L.; Dafnakis, P.; Pasta, E.; Bracco, G.; Naseradinmousavi, P.; Mattiazzo, G.; Bhalla, A.P.S. An adaptive and energy-maximizing control optimization of wave energy converters using an extremum-seeking approach. Phys. Fluids 2020, 32, 113307. [Google Scholar] [CrossRef]
- Thomas, S.; Giassi, M.; Eriksson, M.; Göteman, M.; Isberg, J.; Ransley, E.; Hann, M.; Engström, J. A model free control based on machine learning for energy converters in an array. Big Data Cogn. Comput. 2018, 2, 36. [Google Scholar] [CrossRef]
- Li, L.; Yuan, Z.; Gao, Y. Maximization of energy absorption for a wave energy converter using the deep machine learning. Energy 2018, 165, 340–349. [Google Scholar] [CrossRef] [Green Version]
- Anderlini, E.; Husain, S.; Parker, G.G.; Abusara, M.; Thomas, G. Towards real-time reinforcement learning control of a wave energy converter. J. Mar. Sci. Eng. 2020, 8, 845. [Google Scholar] [CrossRef]
- OES. International Levelised Cost of Energy for Ocean Energy Technologies; Technical Report; OES: Lisbon, Portugal, 2015. [Google Scholar]
- Tran, T.T.; Smith, A.D. Incorporating performance-based global sensitivity and uncertainty analysis into LCOE calculations for emerging renewable energy technologies. Appl. Energy 2018, 216, 157–171. [Google Scholar] [CrossRef]
- IEA-OES. Annual Report: An Overview of Ecean Energy Activities in 2019; Technical Report; OES: Lisbon, Portugal, 2019.
- Si, Y.; Chen, Z.; Zeng, W.; Sun, J.; Zhang, D.; Ma, X.; Qian, P. The influence of power-take-off control on the dynamic response and power output of combined semi-submersible floating wind turbine and point-absorber wave energy converters. Ocean Eng. 2021, 227, 108835. [Google Scholar] [CrossRef]
- Ghafari, H.R.; Neisi, A.; Ghassemi, H.; Iranmanesh, M. Power production of the hybrid Wavestar point absorber mounted around the Hywind spar platform and its dynamic response. J. Renew. Sustain. Energy 2021, 13, 033308. [Google Scholar] [CrossRef]
- SINNPOWER. Fostering a Blue Economy: Offshore Renewable Energy. 2022. Available online: https://www.sinnpower.com/socean (accessed on 10 July 2022).
- Zhao, X.; Ning, D.; Liang, D. Experimental investigation on hydrodynamic performance of a breakwater-integrated WEC system. Ocean Eng. 2019, 171, 25–32. [Google Scholar] [CrossRef]
- IEA. Blue Economy and Its Promising Markets for Ocean Energy; Technical Report; IEA: Paris, France, 2020. [Google Scholar]
- Dizon, C.; Cavagnaro, R.J.; Robertson, B.; Brekken, T.K. Modular horizontal pendulum wave energy converter: Exploring feasibility to power ocean observation applications in the US pacific northwest. IET Renew. Power Gener. 2021, 15, 3354–3367. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, D.; Zou, Q.; Qiao, D.; Cai, S. Hybrid floating breakwater-WEC system: A review. Ocean Eng. 2019, 186, 106126. [Google Scholar] [CrossRef]
- Leijon, J.; Boström, C. Freshwater production from the motion of ocean waves–A review. Desalination 2018, 435, 161–171. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, B.; Wang, T.; Jin, S.; Duan, S.; Yang, K.; Zhao, Y. A Review of Point Absorber Wave Energy Converters. J. Mar. Sci. Eng. 2022, 10, 1534. https://doi.org/10.3390/jmse10101534
Guo B, Wang T, Jin S, Duan S, Yang K, Zhao Y. A Review of Point Absorber Wave Energy Converters. Journal of Marine Science and Engineering. 2022; 10(10):1534. https://doi.org/10.3390/jmse10101534
Chicago/Turabian StyleGuo, Bingyong, Tianyao Wang, Siya Jin, Shunli Duan, Kunde Yang, and Yaming Zhao. 2022. "A Review of Point Absorber Wave Energy Converters" Journal of Marine Science and Engineering 10, no. 10: 1534. https://doi.org/10.3390/jmse10101534
APA StyleGuo, B., Wang, T., Jin, S., Duan, S., Yang, K., & Zhao, Y. (2022). A Review of Point Absorber Wave Energy Converters. Journal of Marine Science and Engineering, 10(10), 1534. https://doi.org/10.3390/jmse10101534