A Process-Based Model for Arctic Coastal Erosion Driven by Thermodenudation and Thermoabrasion Combined and including Nearshore Morphodynamics
Abstract
1. Introduction
2. Model Description
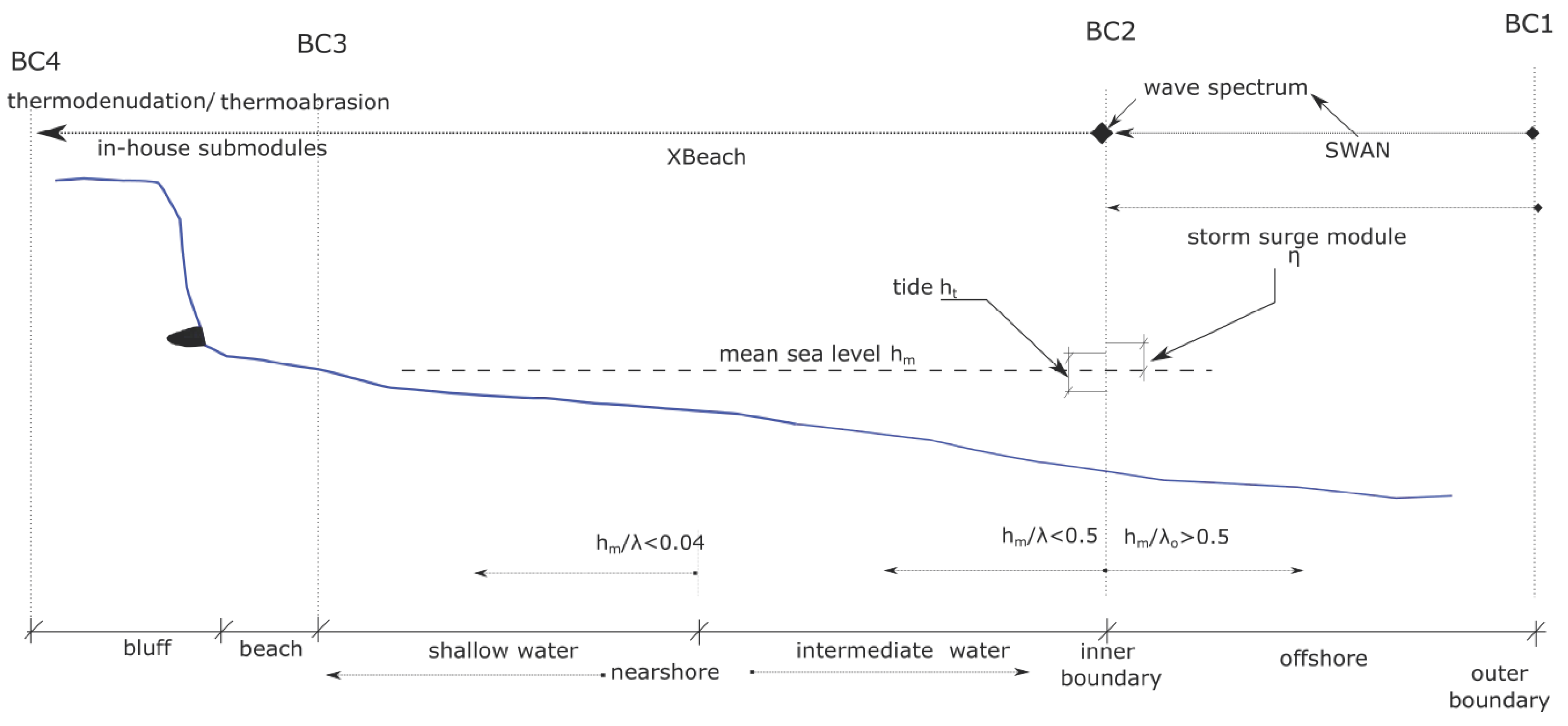
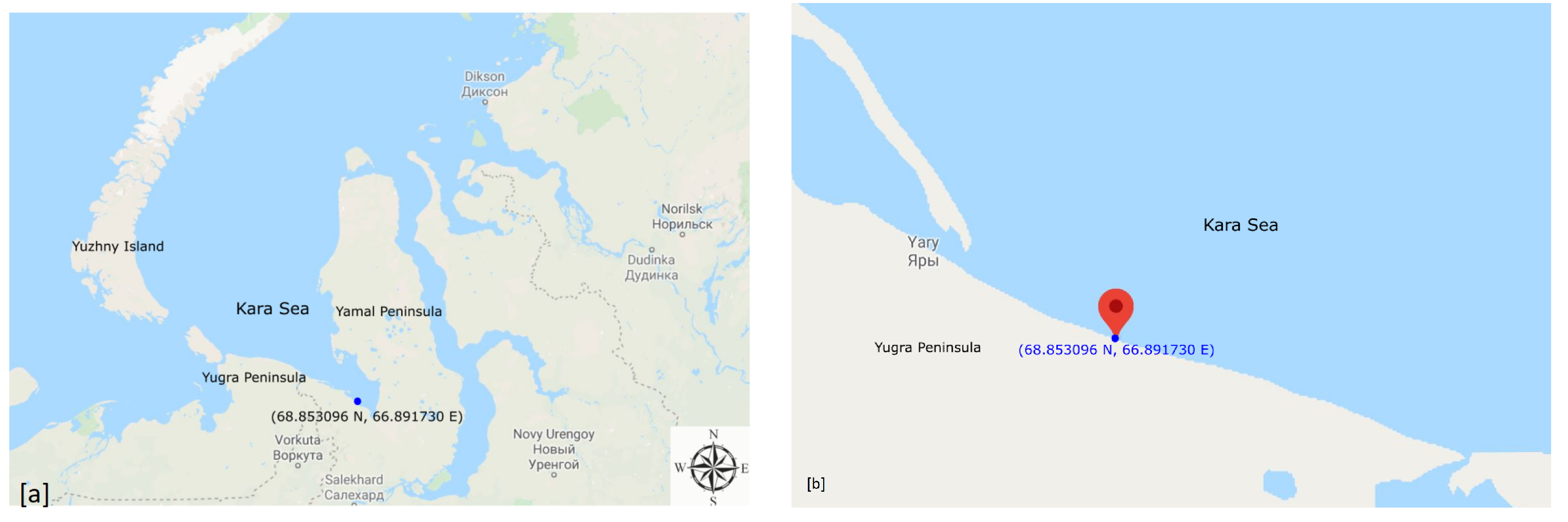
2.1. Model Domain and Input Data
2.2. Thermodenudation Module
2.2.1. Submodule: Permafrost Thaw
2.2.2. Submodule: Slumping
2.3. Thermoabrasion Module
2.3.1. Submodule: Niche Growth
2.3.2. Submodule: Bluff Collapse
2.3.3. Submodule: Degradation of Collapsed Bluffs
2.4. Numerical Implementation
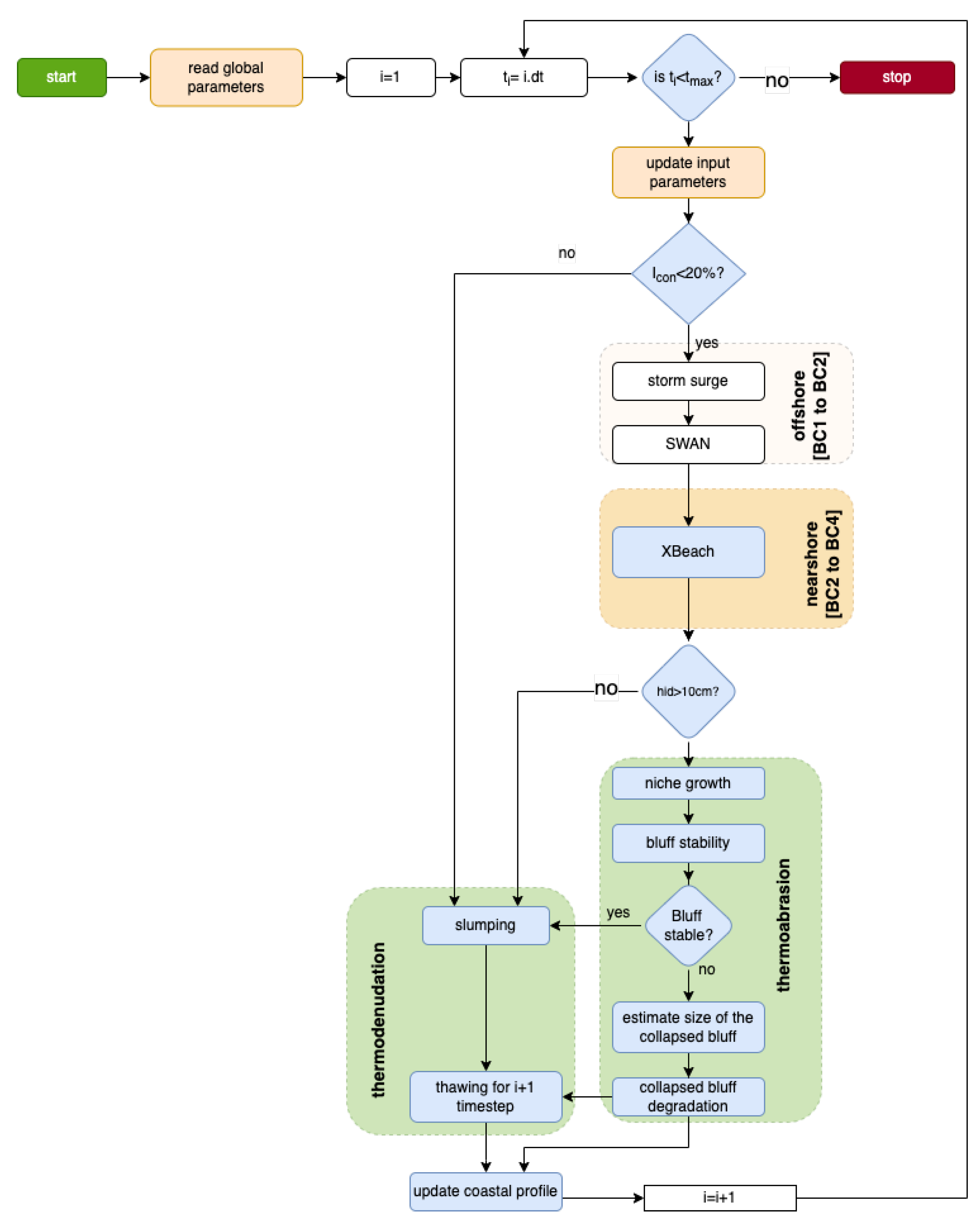
2.4.1. Hydrodynamics of the Offshore
2.4.2. Hydrodynamics of the Nearshore
2.4.3. Modelling Permafrost and Thawing Depth
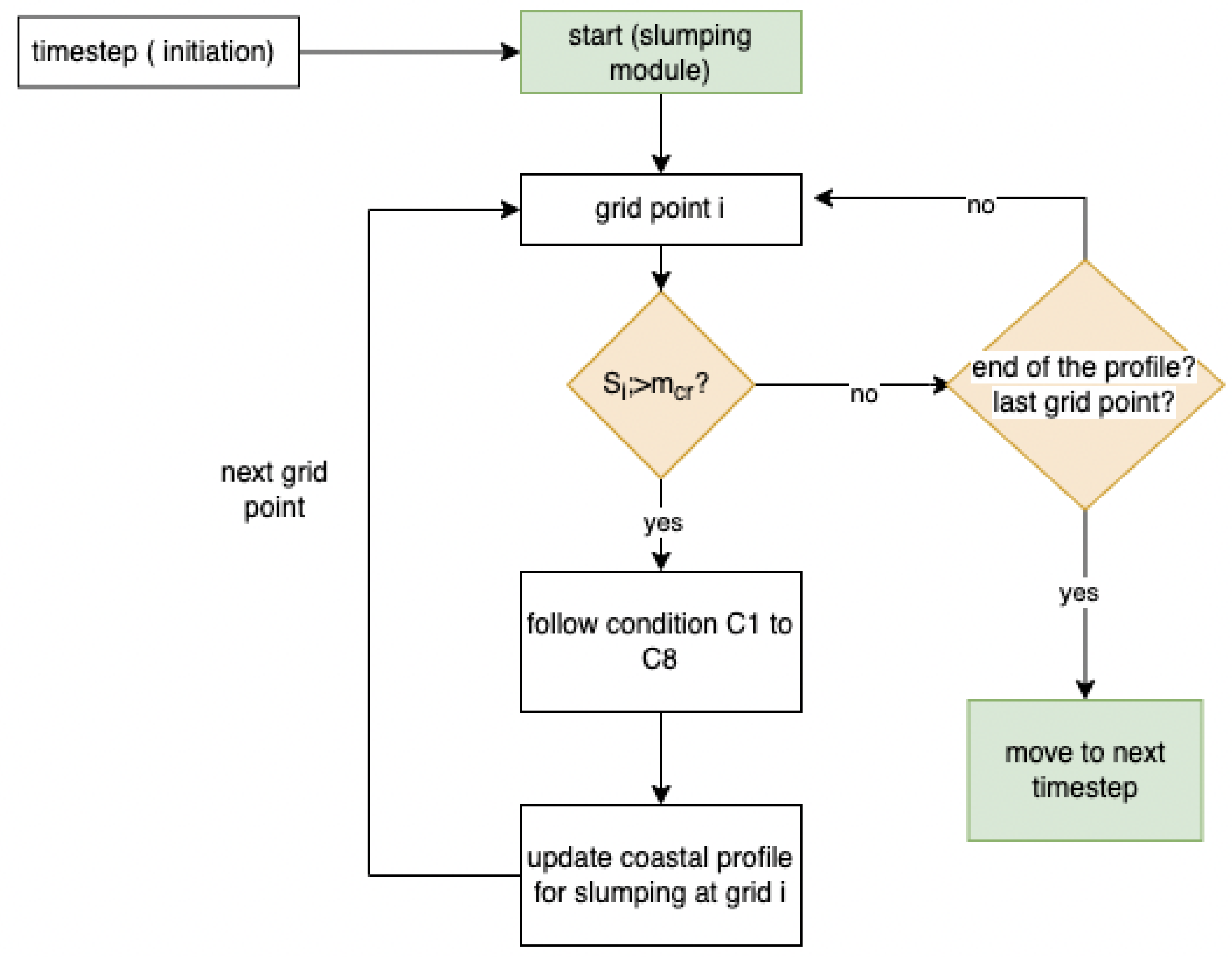
2.4.4. Workflow of the Numerical Model
3. Field Observations
3.1. Morphological Description
3.2. Data and Methods
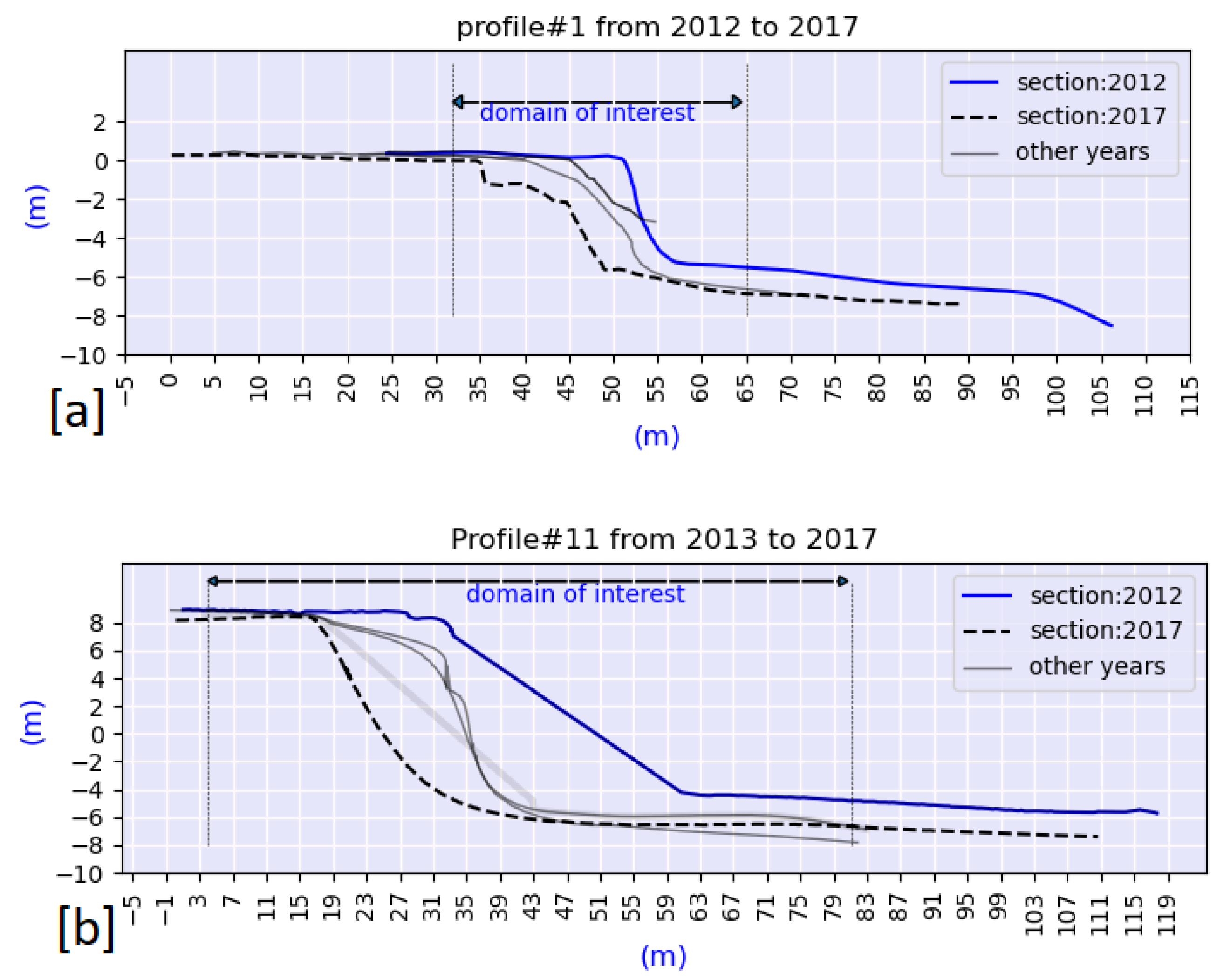
3.2.1. Coastal Profiles
3.2.2. Nearshore Marine Observations
3.2.3. Permafrost and Soil Temperature
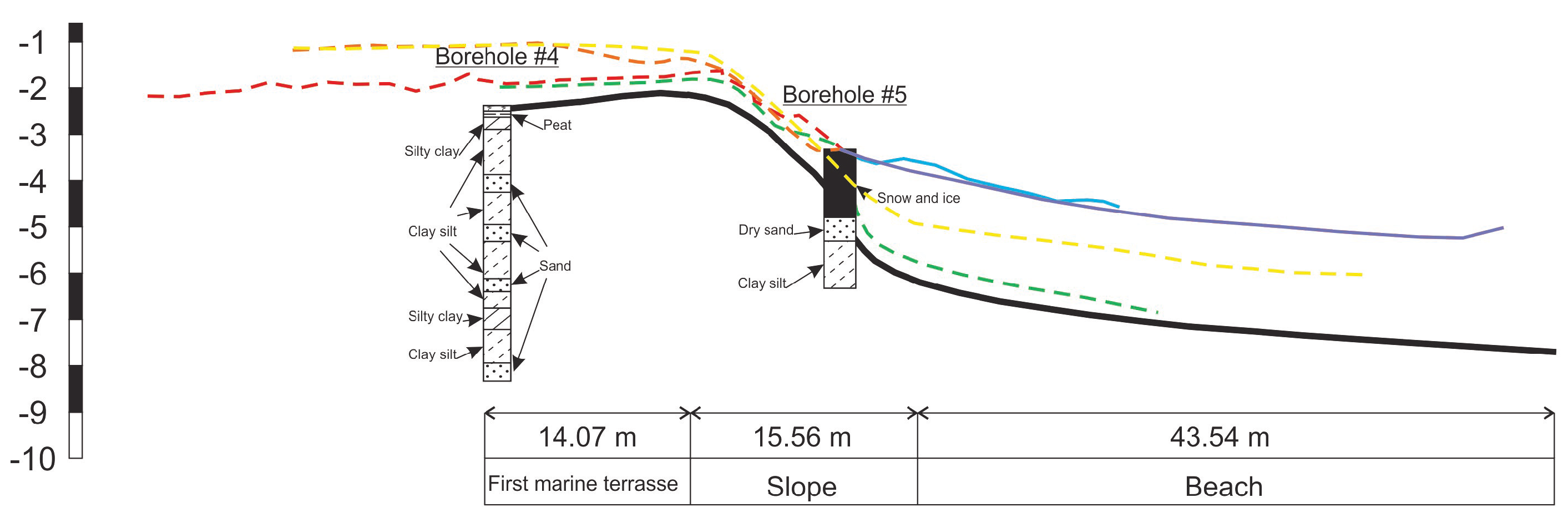
3.3. Permafrost and Soil Properties
3.4. Erosion Pattern in the Study Area
- Thermodenudation at the bluff face may be active, even when sea ice is present, and land-fast ice remains at the base of the bluffs. Unlike thermoabrasion, the open water season is not a prerequisite for thermodenudation.
- Thawed sediments from the bluffs fall under gravity and expose the permafrost underneath. The slumped materials are loose and accumulate on the beach.
- Wave-cut niches are developed at the base of the bluffs, while the bluffs may still be stable. Several storms may elongate the niche depth to a critical depth. Unless the niche depth reaches the critical length, the bluff remains stable.
- Thawed sediments accumulated at the base of the bluffs remain there until an extreme event creates a higher water level and return current.
4. Calibration of the Model
4.1. Methodology of Calibration
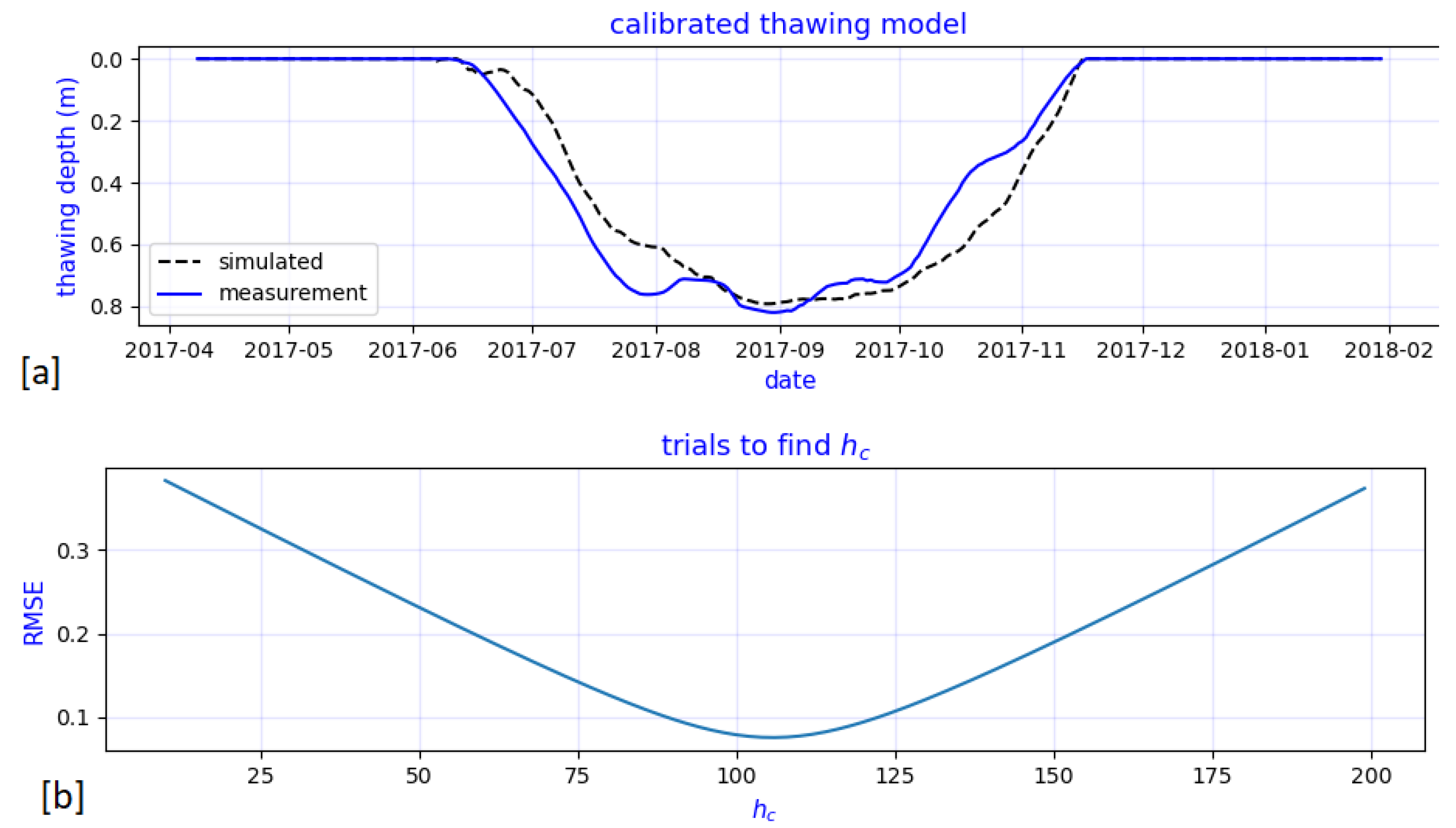
4.2. Calibration of the Convective Heat Transfer Coefficient for the Bluff Surface
4.3. Calibration of Remaining Parameters
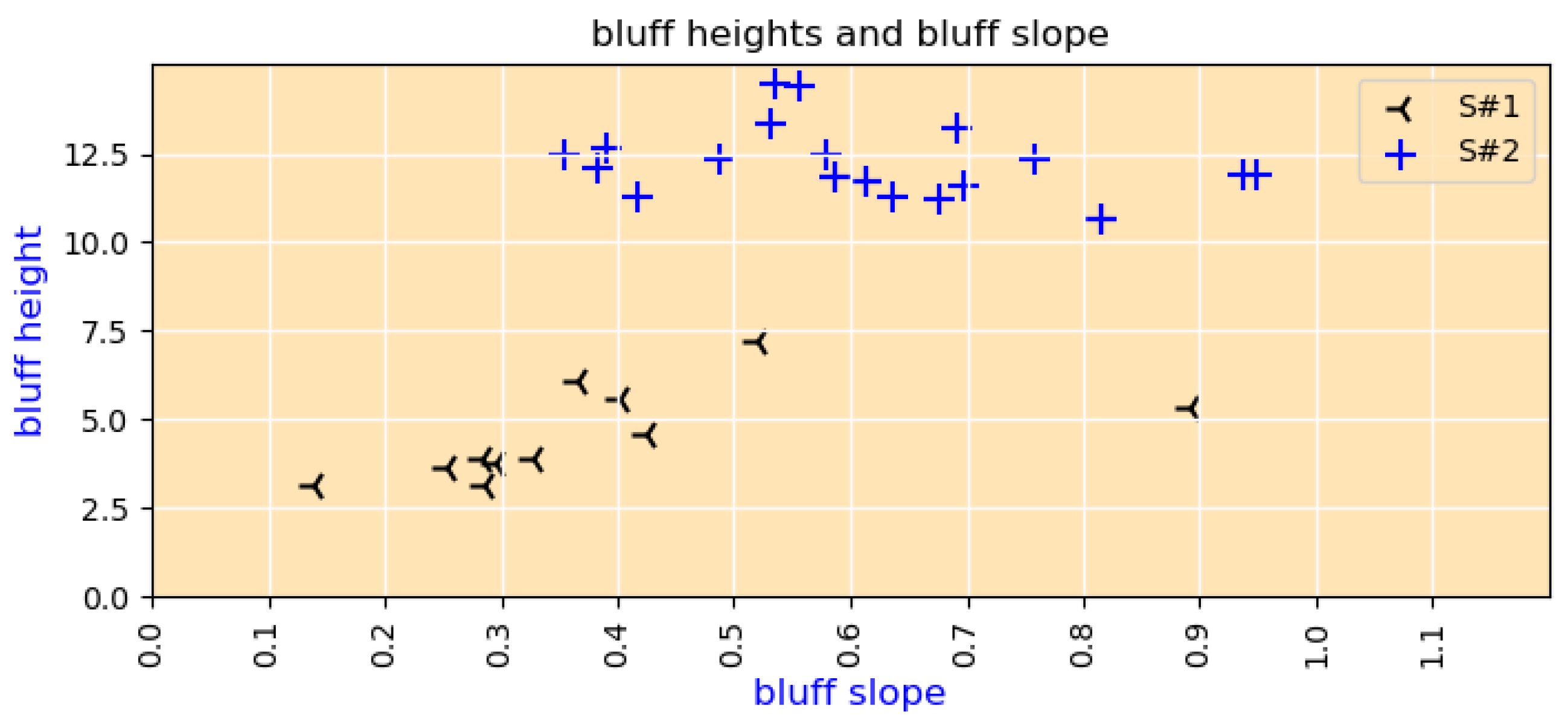
- 1.
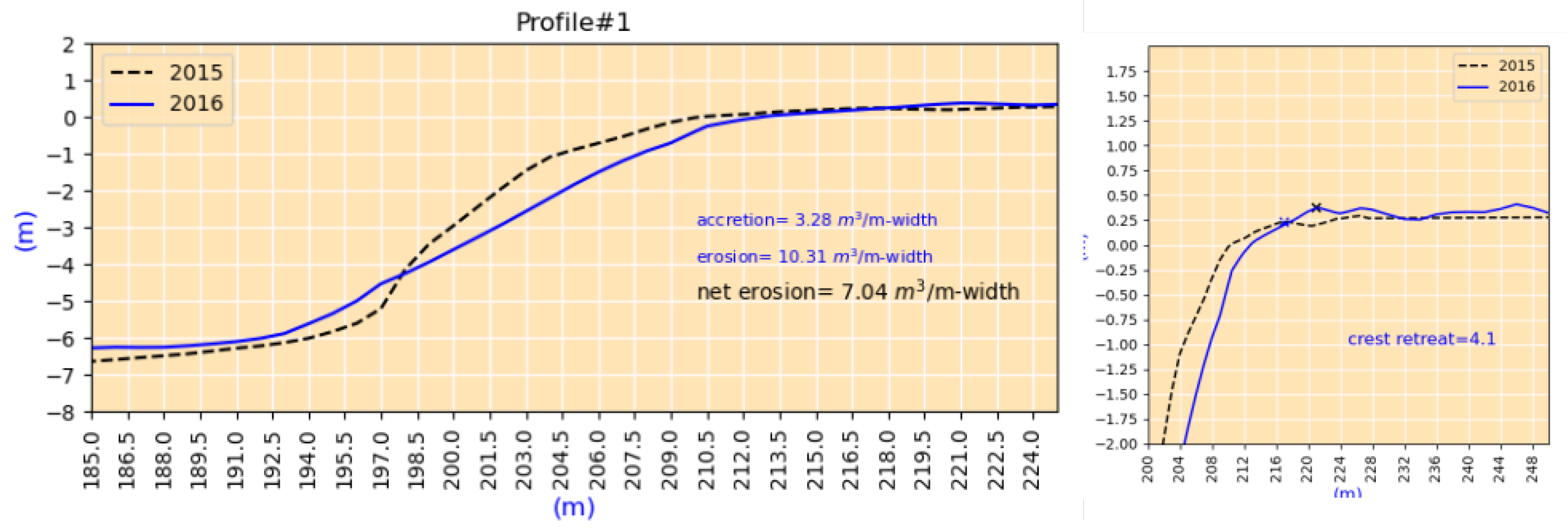
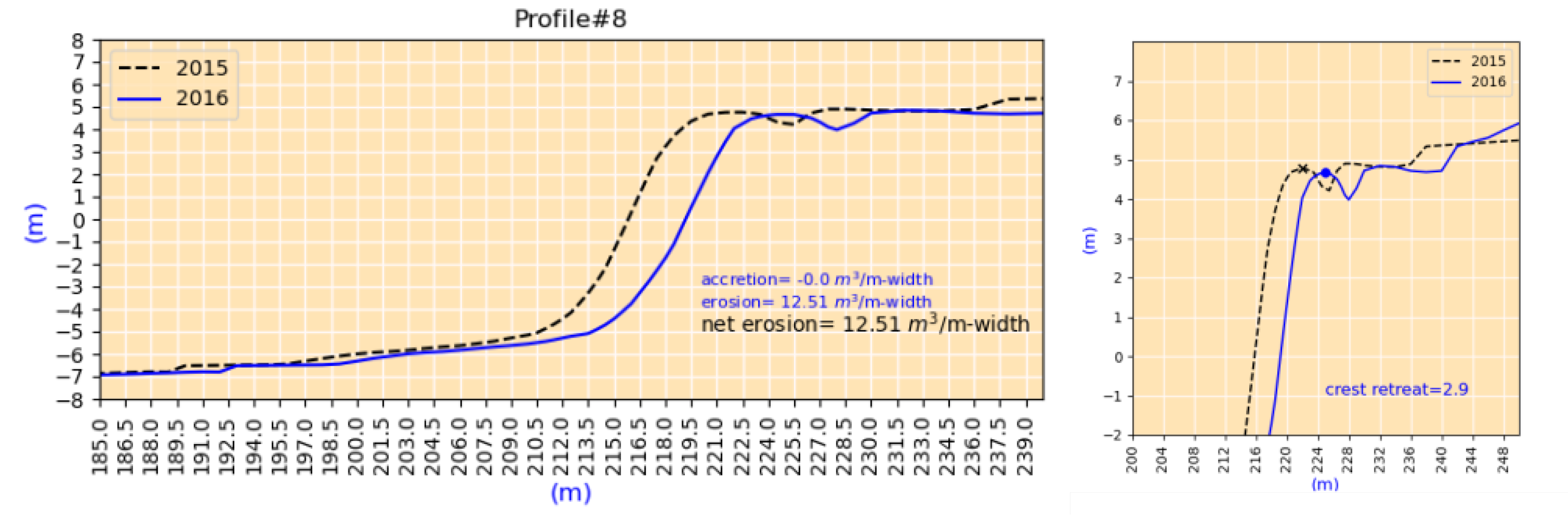
- The bluff height for case#1 is 6 m, and for case#2 is 13 m. The bluff slope of case#1 is approximately 0.4, which is lower than the bluff slope of case#2 (0.9).
- 2.
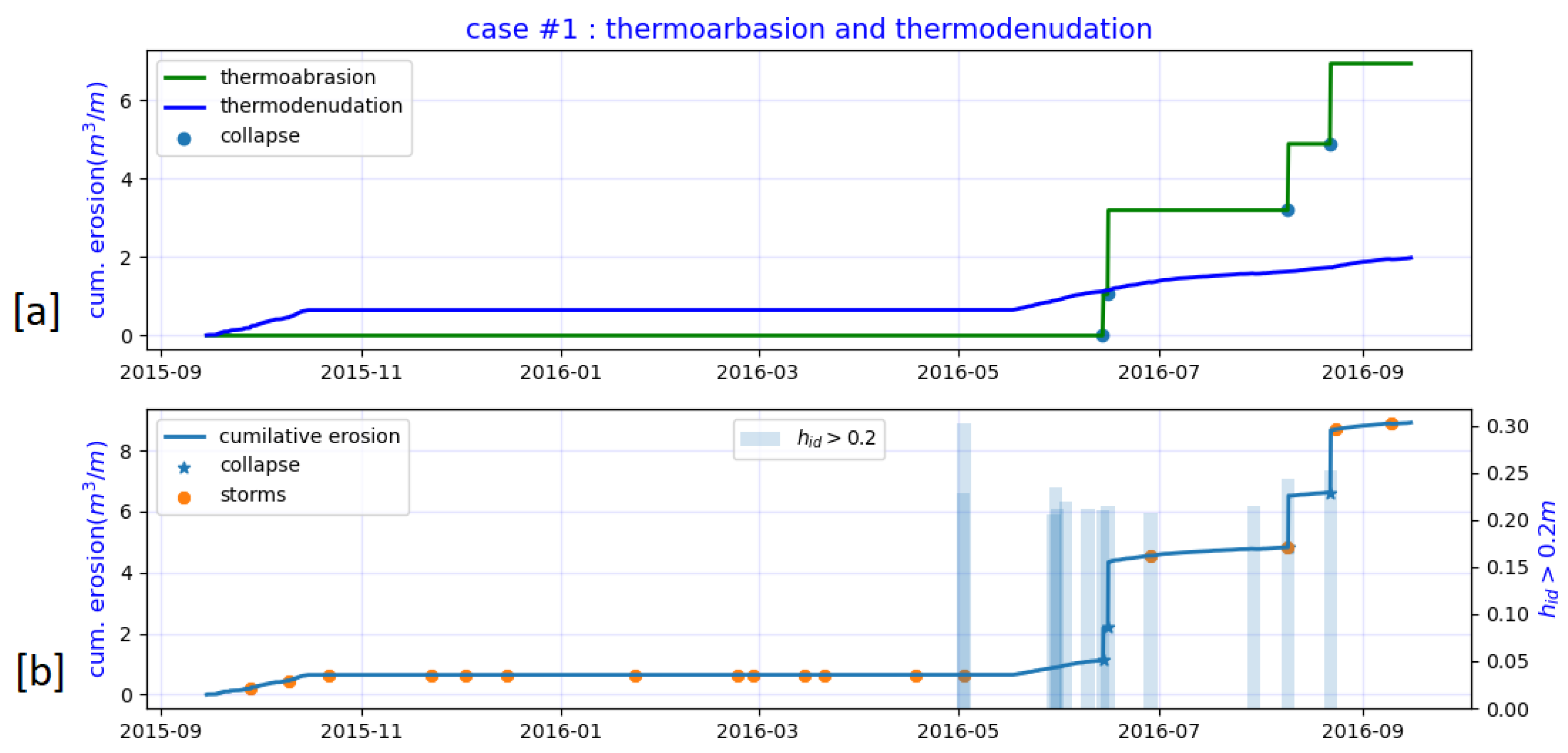
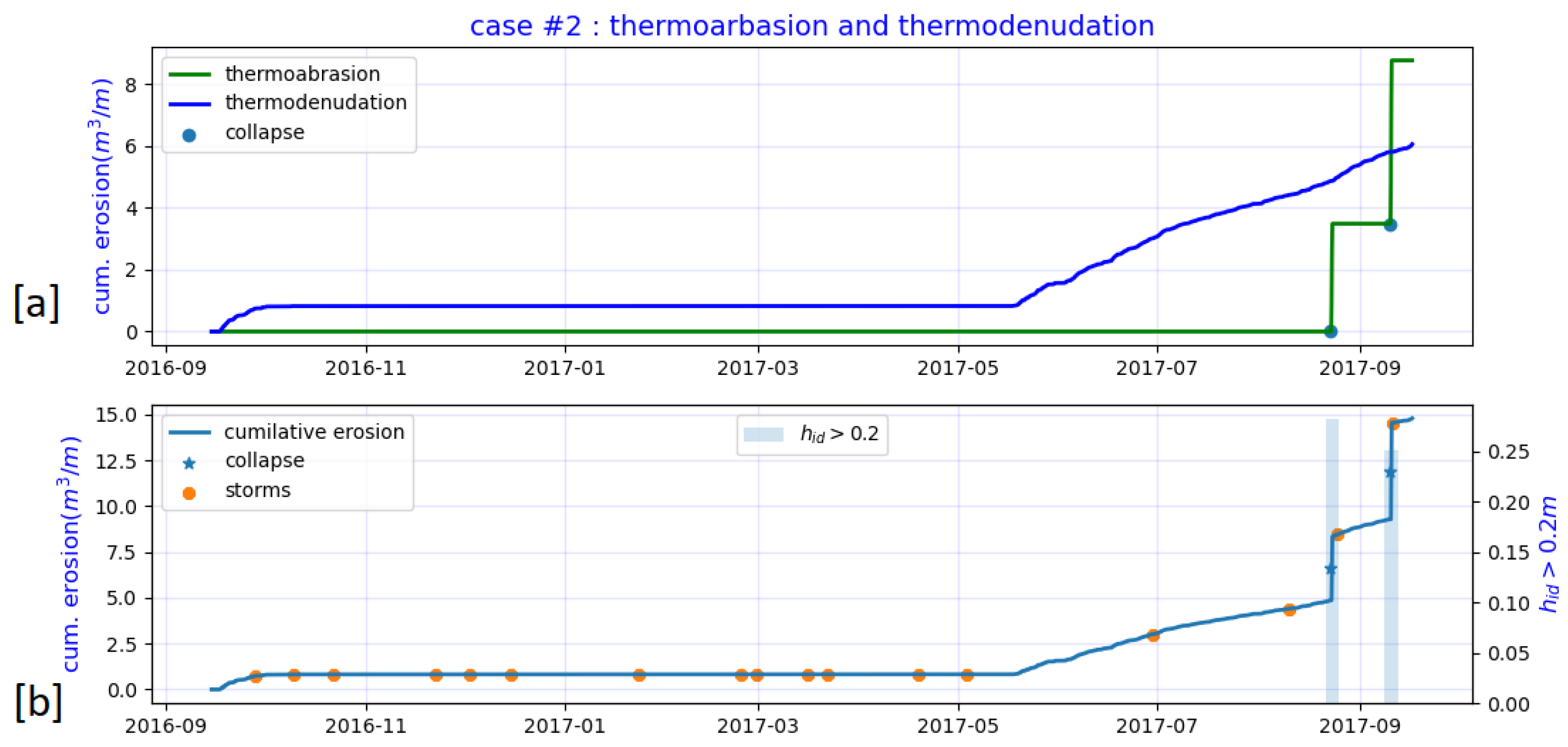
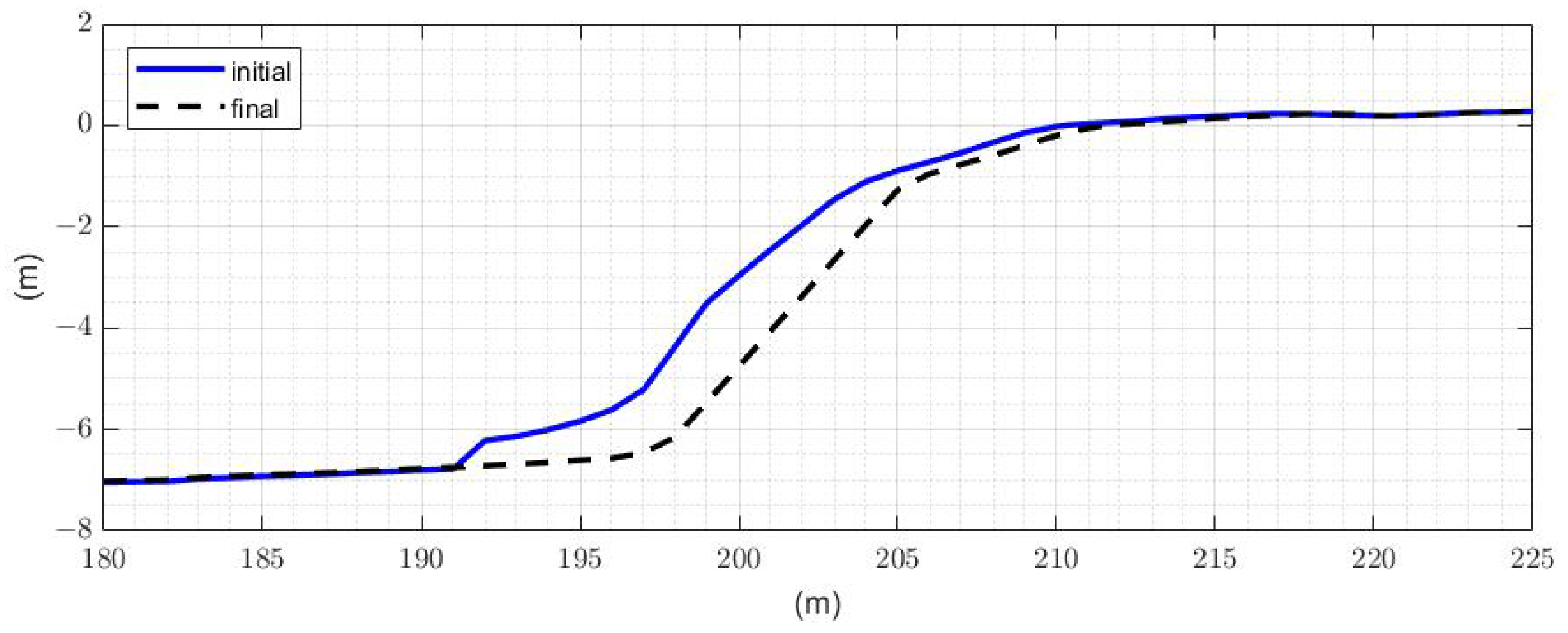
- The cases demonstrate different erosion patterns. For case#1, we note that the profile has undergone both erosion and accretion; the value of erosion is almost three times the accretion value (Figure 15). The accretion value indicates that the sediments accumulated in the lower part of the bluffs. No accretion is measured for cases#2 (Figure 16). For case#2, all the sediment from the erosion must have been washed away offshore.
- 3.
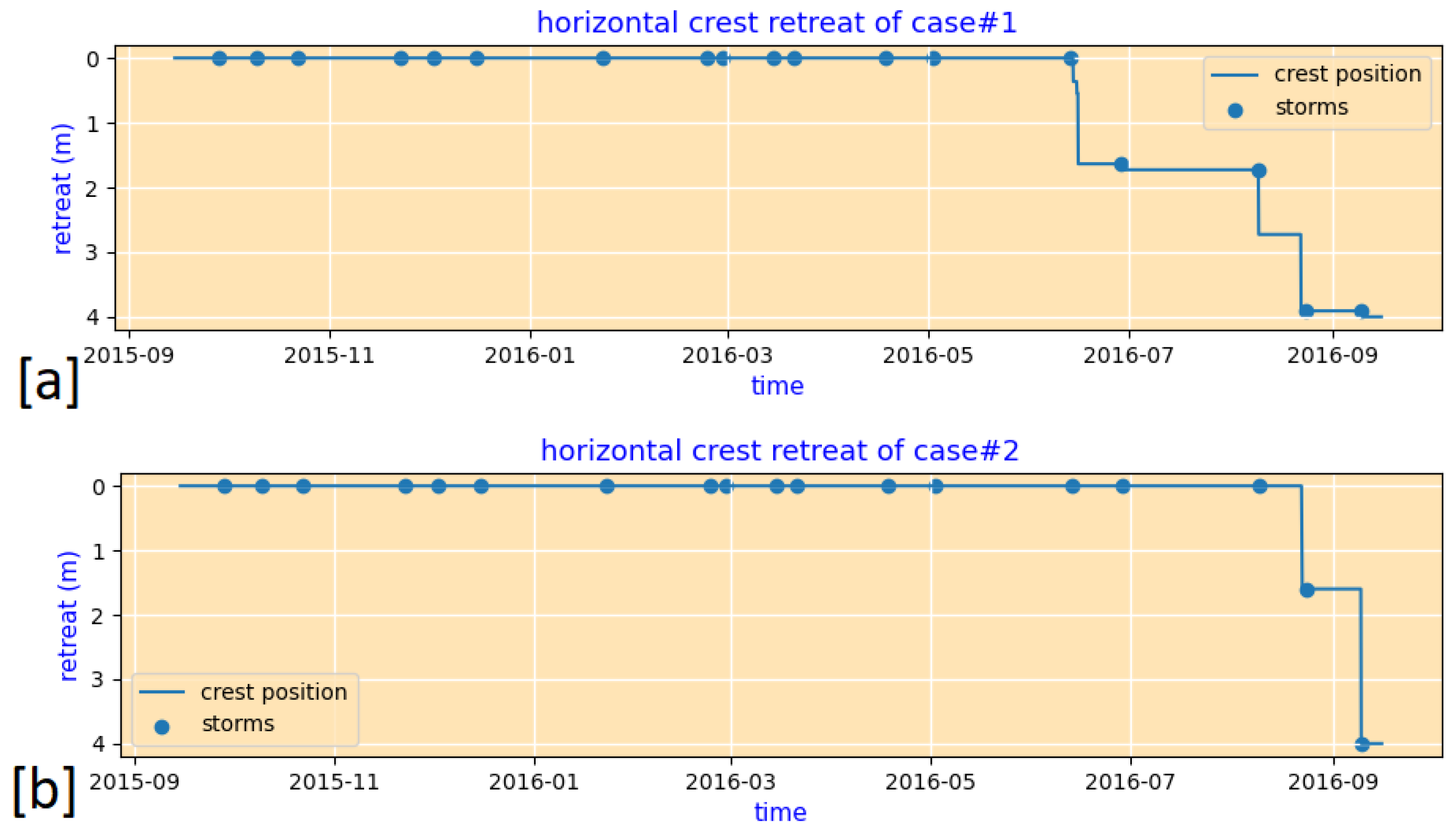
- The crest retreat for case#1 is 4.1, which is larger than that of case#2, even though the erosion volume of case#1 is lower. Because of the higher bluff heights (13 m vs. 6 m) for a similar crest retreat, case#2 had higher erosion volume.
- 4.
- The changes in the bluff slope are negligible for case#2 but significant for case#1. For case#1, the bluff base did not retreat; instead, the crest retreated, and the bluff slope was lowered as a result.
4.3.1. Upper and Lower Limit of the Mean Sea Level
4.3.2. Upper and Lower Limit of the Convective Heat Transfer Coefficient
4.3.3. Upper and Lower Limit of the Critical Slope ()
4.4. Calibration Result
4.4.1. Prediction of Erosion
4.4.2. Prediction of Crest Retreat
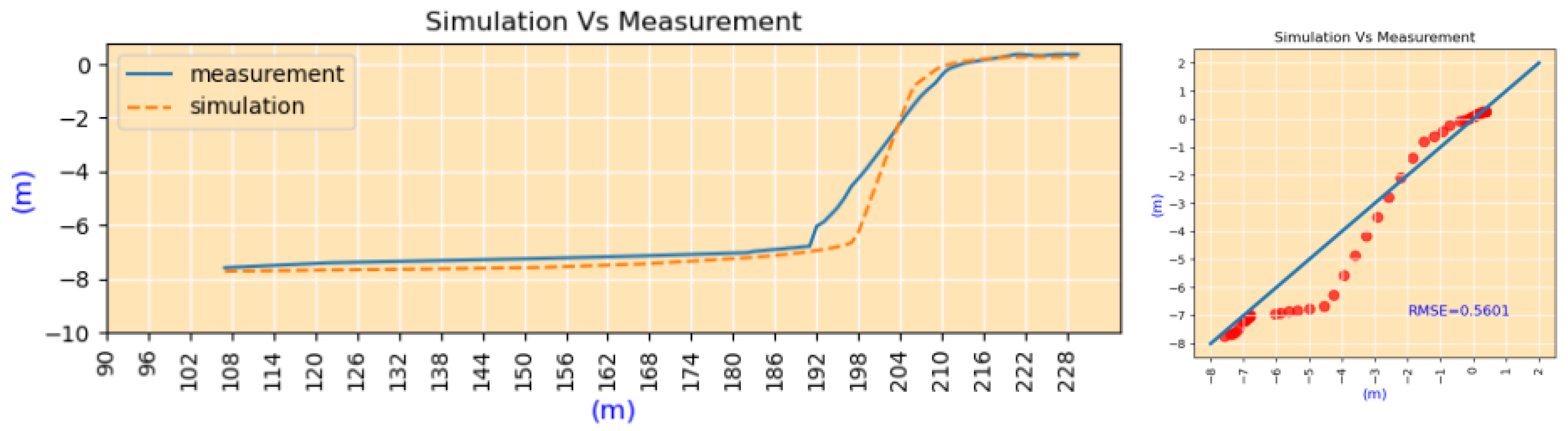
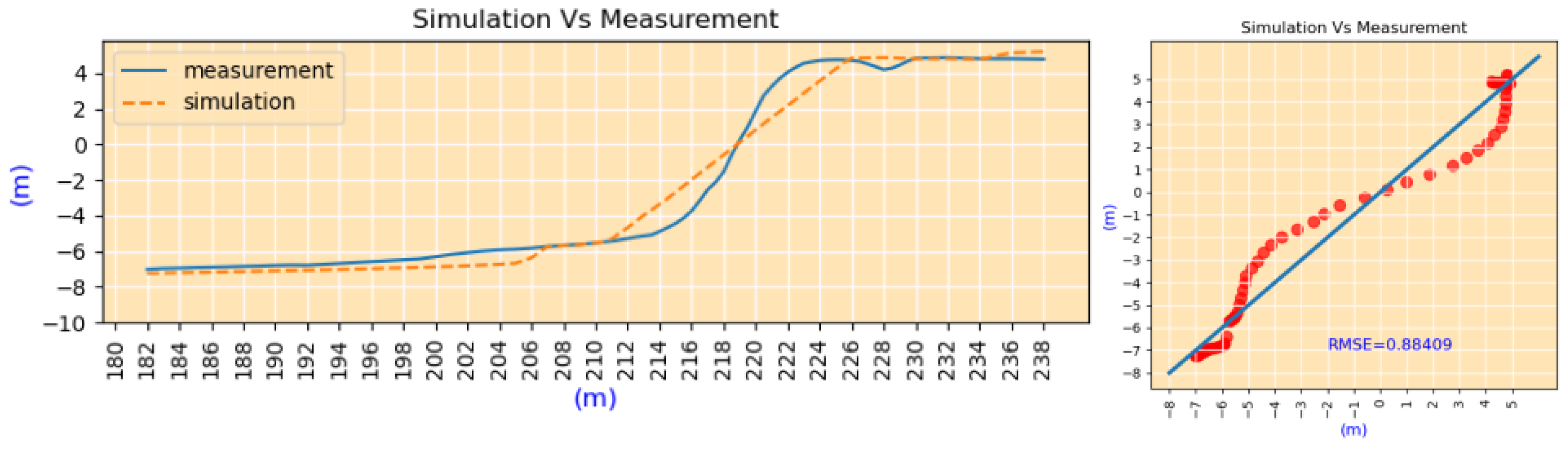
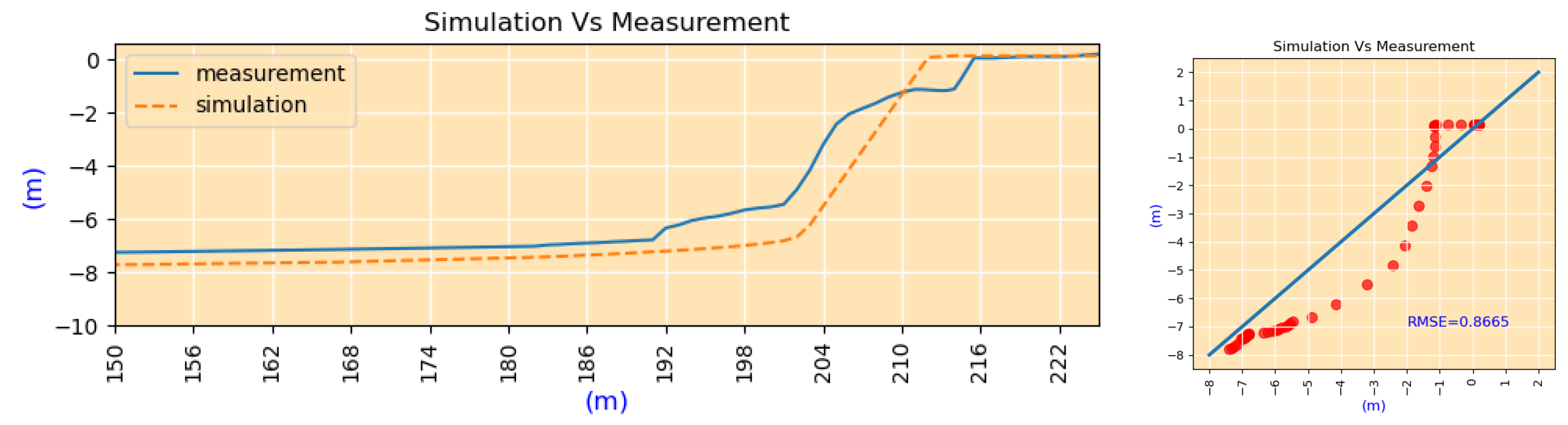
4.4.3. Prediction of the Shape of Coastal Profile
5. Validation
5.1. Methodology of the Validation
5.2. Validation Results
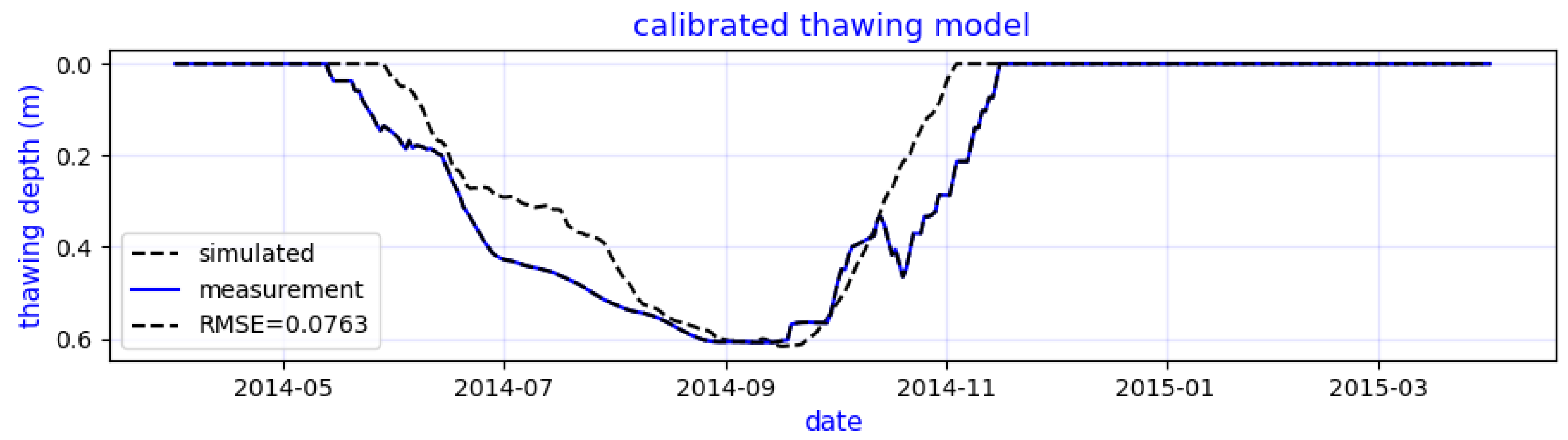
5.2.1. Validation of Permafrost Thawing Module
5.2.2. Validation of Case#3
5.2.3. Validation of Case#4
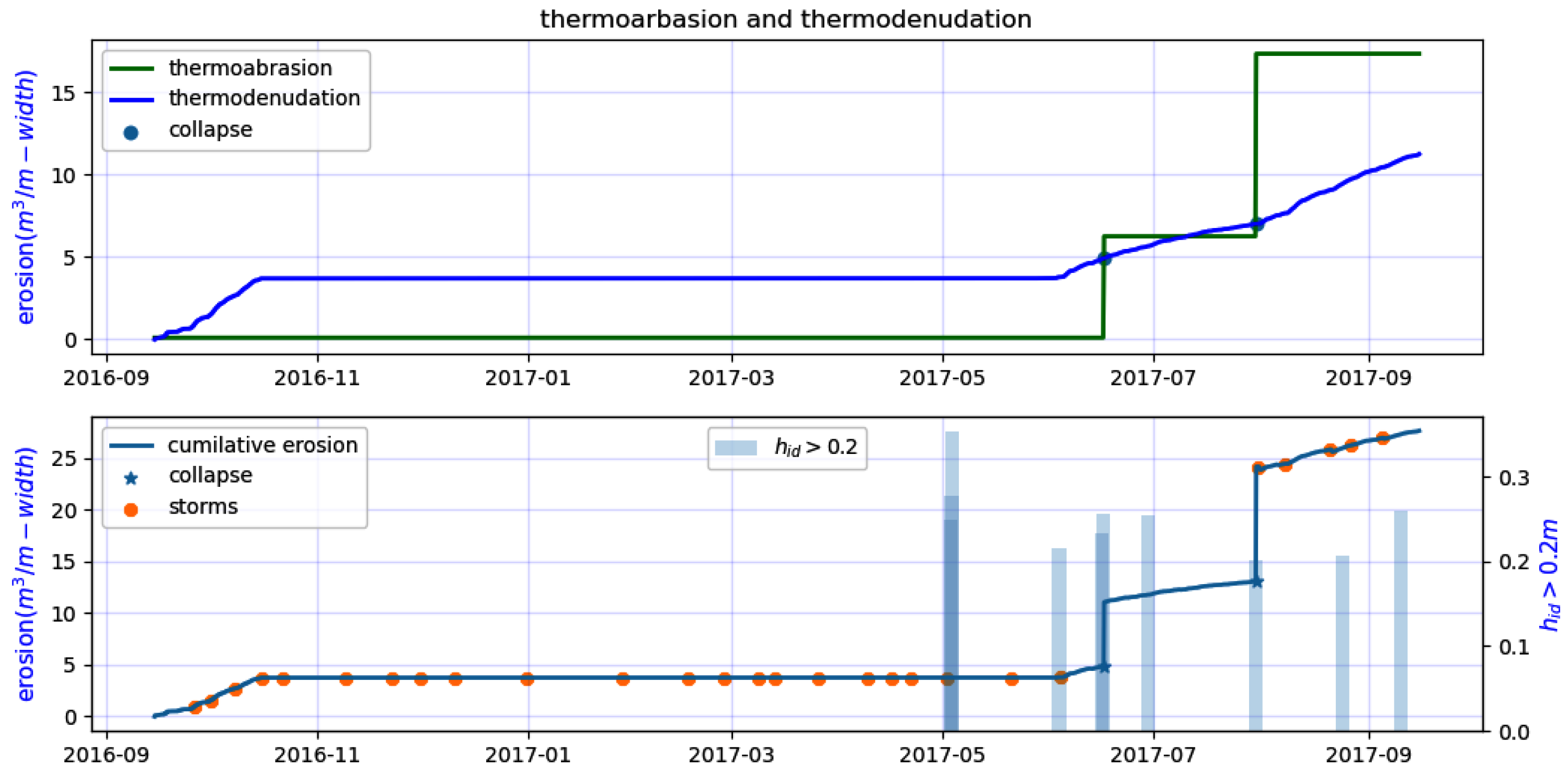
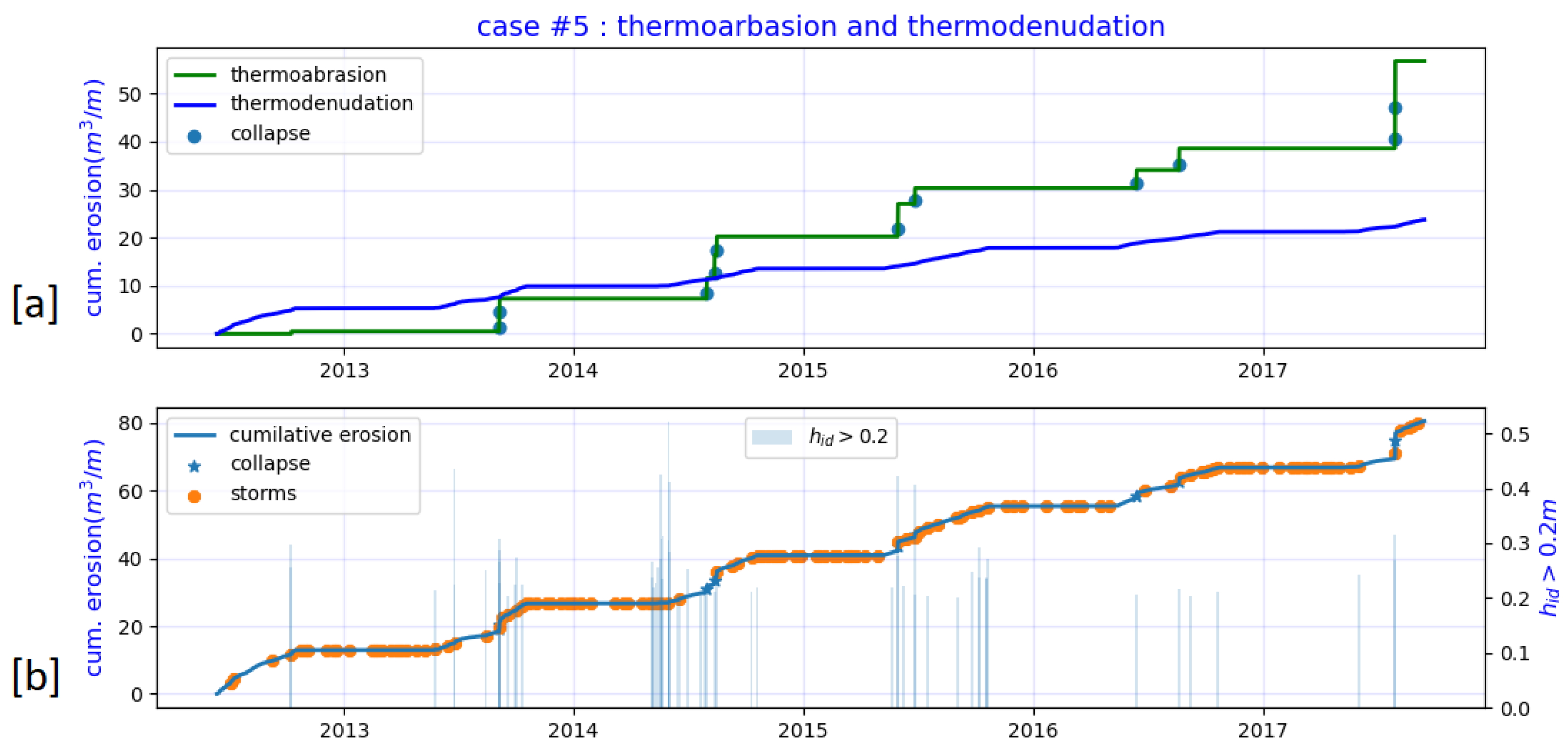
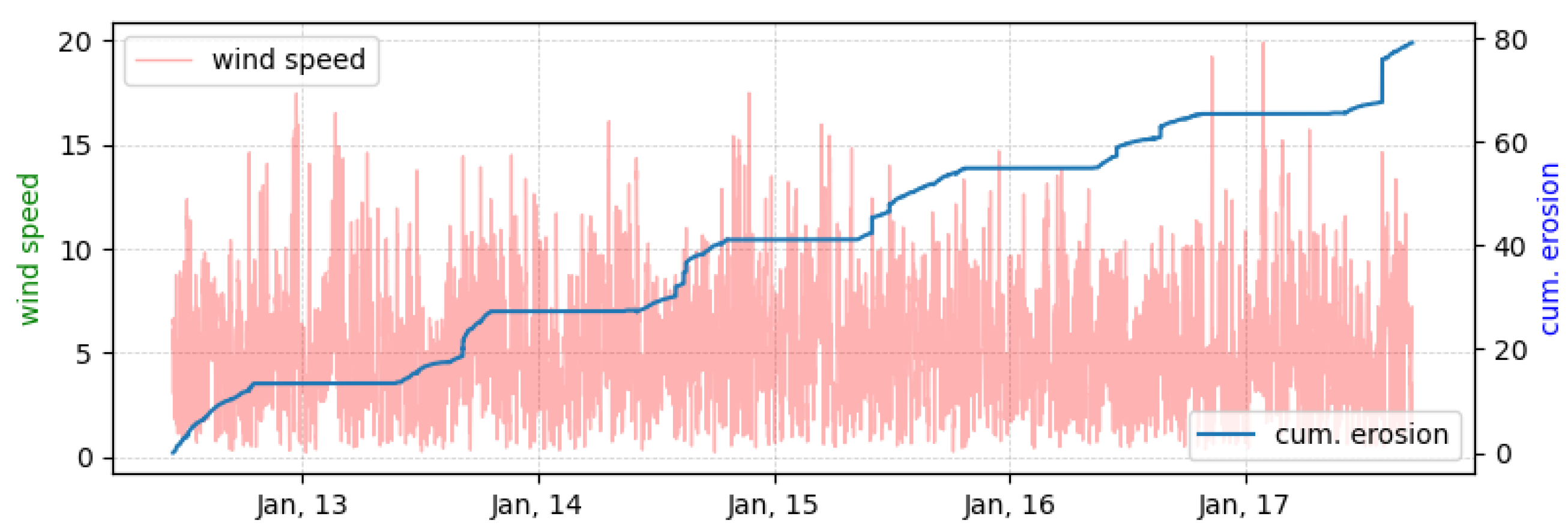
5.2.4. Case#5: Simulation of Long-Term Erosion
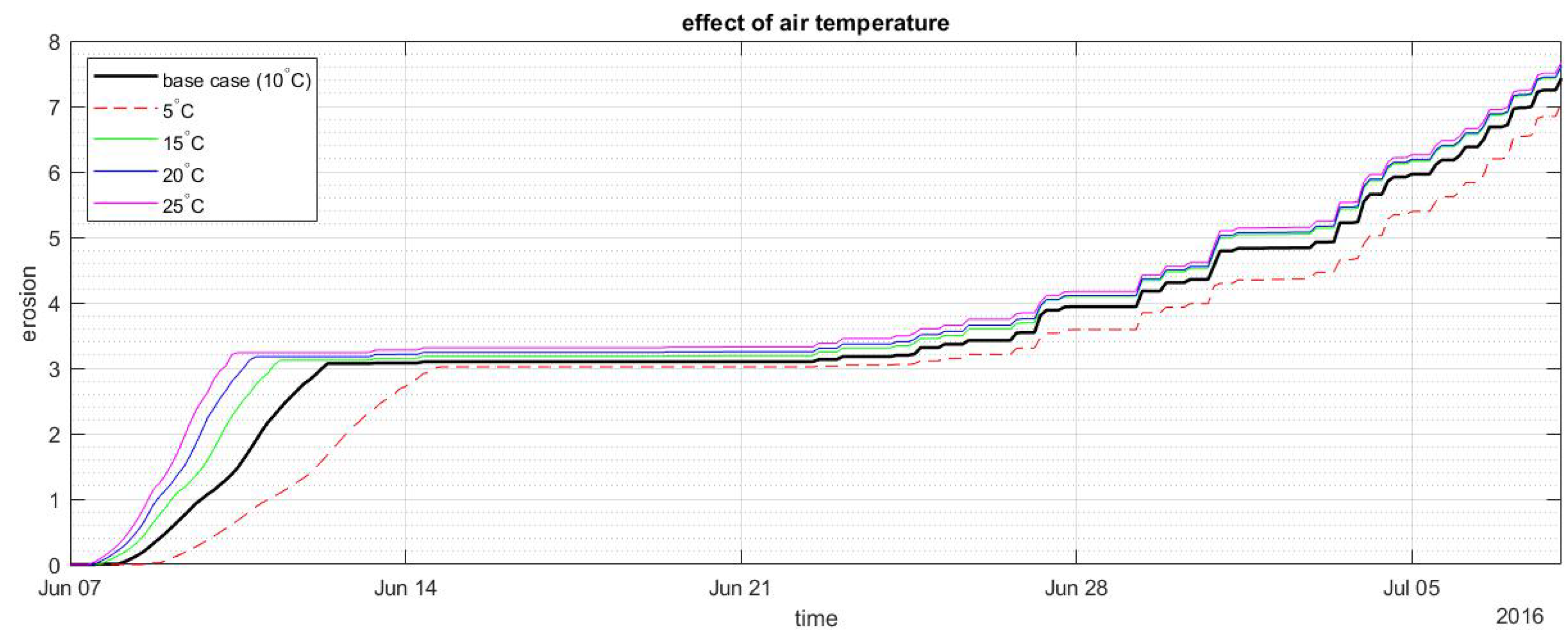
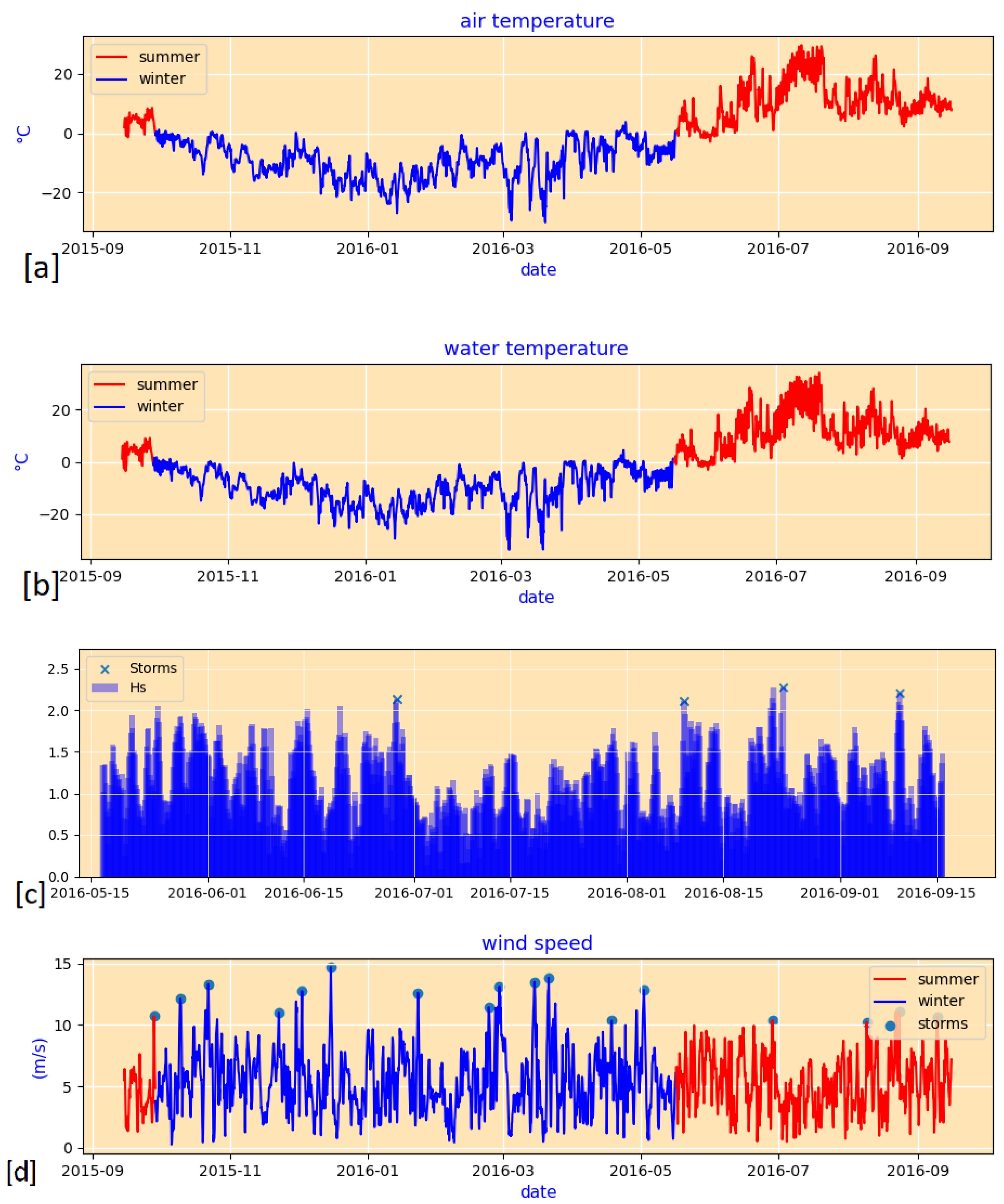
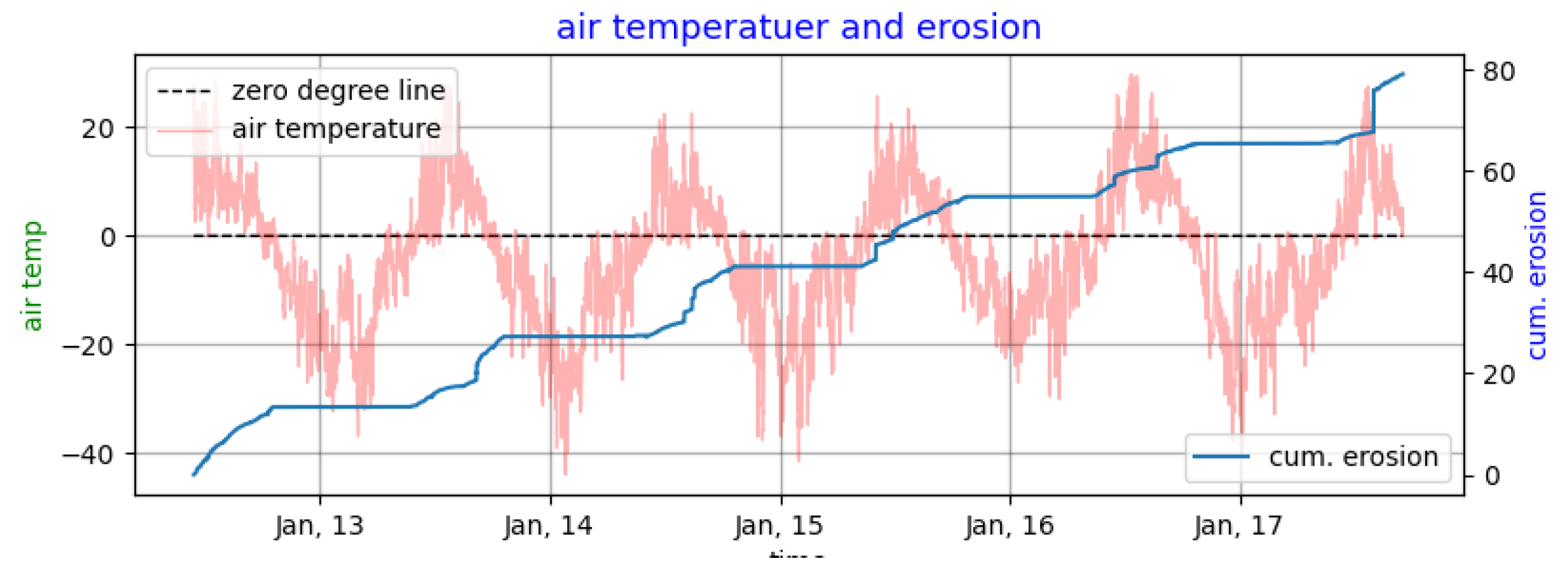
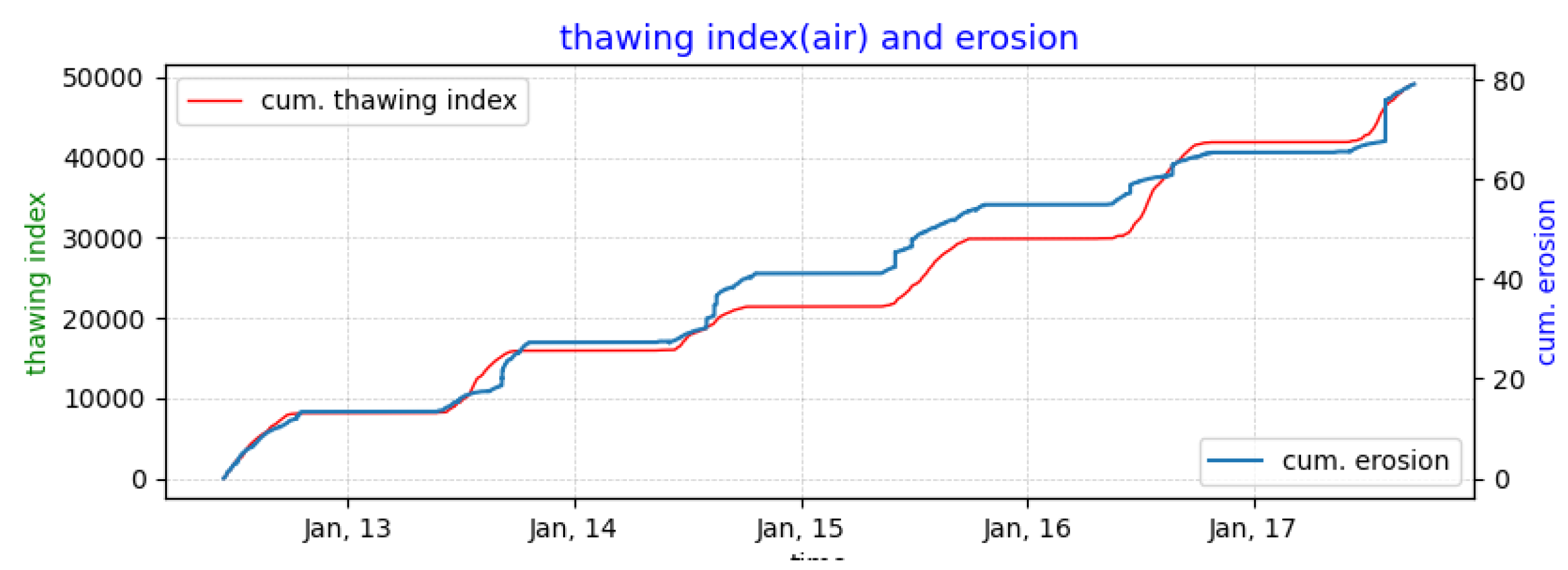
5.2.5. The Effect of Environmental Forcing on Erosion
6. Sensitivity Analysis of the Model
6.1. Base Case
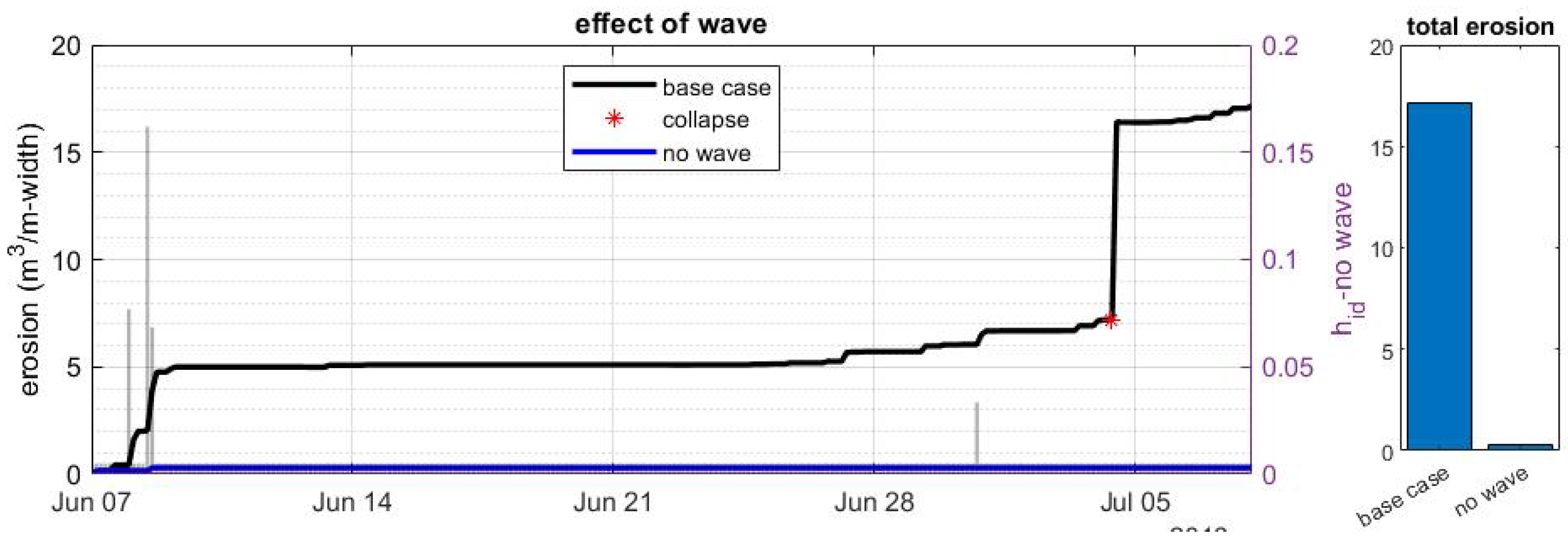
6.2. The Effect of Waves
- Thermoabrasion is controlled by both mechanical and thermal driving forces; the absence of one of the driving forces can withhold thermoabrasion.
- Mechanically driven forces do not control thermodenudation, i.e., they are not the limiting factor, but nearshore hydrodynamics can influence the rate of thermodenudation.
- Without the presence of waves, no bluff collapse occurs even when the model simulates positive values of ; indicating the importance of the combination of thermal and mechanical drivers.
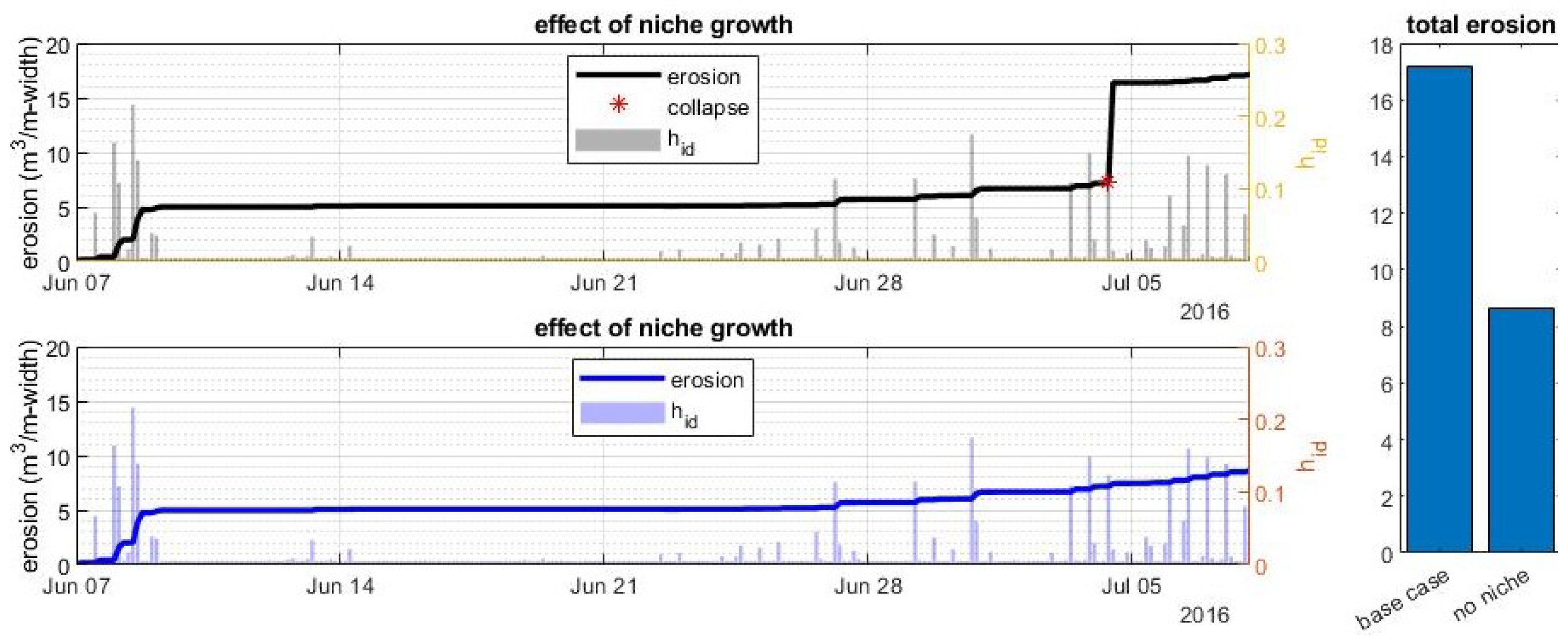
6.3. The Effect of Niche Growth
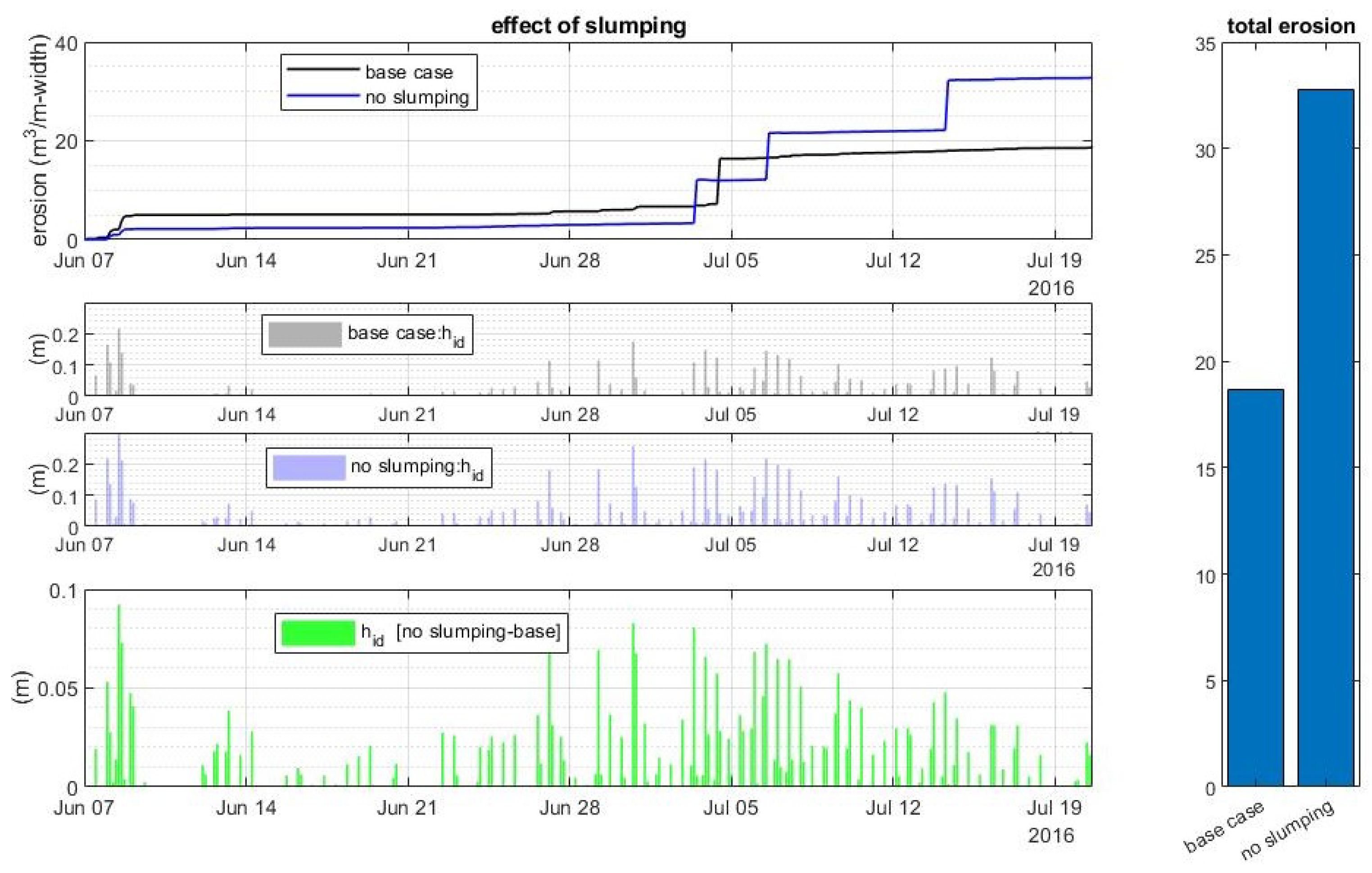
6.4. The Effect of Slumping Process
6.5. The Effect of Tide
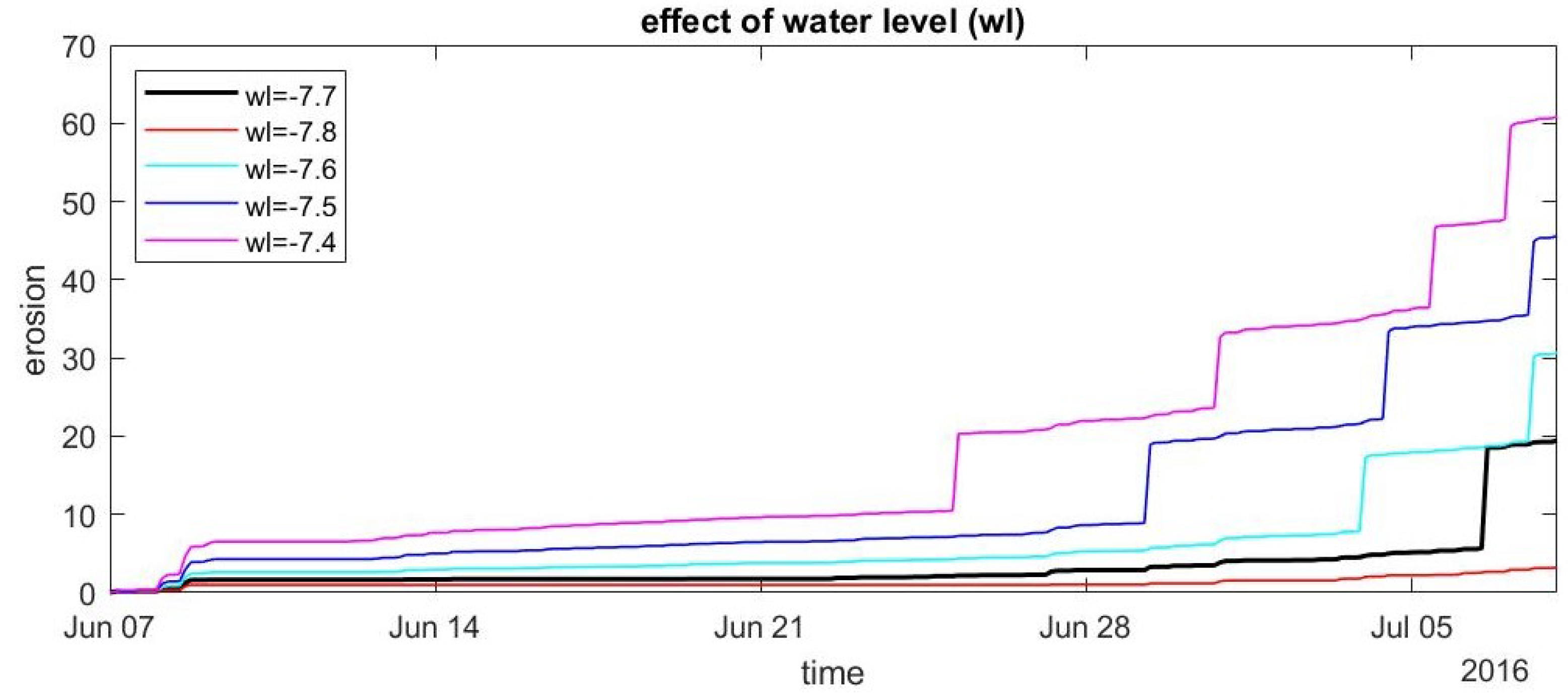
6.6. The Effect of Water Level
7. Conclusions
- 1.
- Erosion during the winter is negligible or absent. Barnhart et al. [30] concluded in their model that low erosion occurs at the end of summer and beginning of fall for the coast of Alaskan Beaufort Sea whereas our numerical model for Baydaratskya Bay in Kara sea simulates higher erosion at the middle and end of summer.
- 2.
- There is a slight phase lag between the commencement of summer (measured by air temperature) and the beginning of slumping. The air temperature had an upwards zero crossing at the end of May, but thawing began after June in both cases #1 and #2.
- 3.
- Smaller sudden spikes in air and water temperature at the beginning of summer do not contribute to thermodenudation. The model also does not show any immediate response to the spikes of temperature anomalies. This behaviour indicates that the limiting factor for thermal energy transfer and thawing of permafrost is the energy requirement for the latent heat of the transformation from ice to water.
- 4.
- Thermodenudation is continuous and of lower intensity, whereas thermoabrasion causes spikes in erosion volume. The limiting factors for thermodenudation and thermoabrasion are, respectively, the latent heat requirement and water depth at the base of the bluffs ().
- 1.
- The results of the numerical model suggest that thermoabrasion is a complex process and does not demonstrate a linear relation with the intensity of storms. In other words, the strongest storm does not necessarily lead to a collapse. A bluff collapse by a wave-cut niche results from a combination of the nearshore beach profile, storm surge duration, water temperature, and bluff geometry. A similar observation was made by Barnhart et al. [30] for the thermoabrasion numerical model of the Alaskan Beaufort coast.
- 2.
- The two consecutive bluff collapses routinely have an interval between them, and the time lapse between the two collapses is four to six weeks. The sediments released from the collapsed bluff alter the elevation near the swash zones, reducing the probability of inundating the beach with warm water and resulting in slow niche growth. The model by Ravens et al. [29] considered a numerical elevation of the beach by about 0.28 m to calibrate the model and achieve optimised calculation. In contrast, the model proposed herein assumes the sediment from the bluffs increases the elevation of the beach and the elevation is controlled by the morphodynamic module (XBeach).
- 3.
- The parameter inundation depth, , acts as an on–off switch for thermoabrasion; however, the numerical model does not show a clear relationship between the magnitude of and erosion. Our model agrees with the previous observation of Ravens et al. [29] that overall crest retreat is controlled by the niche erosion process.
- 4.
- The erosion rate of thermodenudation was found to be approximately 0.4 m/month for low bluff-height profiles in zone S#1. The erosion rate by thermodenudation for the zones with high bluff was estimated to be close to 1 m/month. The erosion rate of thermodenudation does not show a strong relationship with the thawing depth ().
- 1.
- The hydrodynamic forcing, especially wave condition, plays a vital role in the erosion mechanism; hence the inclusion of the nearshore hydrodynamics and morphological changes is important.
- 2.
- The limiting factor for the rate of thermodenudation is found to be the critical slope (). In the case of thermoabrasion, the limiting factor was .
- 3.
- Thermodenudation and thermoabrasion are intertwined; one mechanism can affect the other. For beaches where the two mechanisms are active, this feedback should be taken into consideration.
Future Development
- 1.
- The accumulation and melting of snow and related water flow are not exclusively modelled. Since there is no open water during the winter and coastal erosion is negligible, we did not model the effect of snow. A snow module will improve the accuracy of the model.
- 2.
- The presence of sea ice was considered in a binary mode, where we ignored sea ice when the ice concentration was less than 20%, and it was assumed to not affect the waves. The damping effect of the floating ice on the waves may also improve the model’s fidelity.
- 3.
- The critical slope () is taken as depth-averaged for the profiles. One depth-averaged value is estimated for each zone in the study area. A matrix of values at different depths and geometries will increase the model’s accuracy.
- 4.
- The collapse of the bluff is predetermined. A finite element model at the bluff face may better predict the irregular bluff slope.
- 5.
- The model is applicable to the unlithified Arctic coasts since gravel is not included in the XBeach explicitly.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
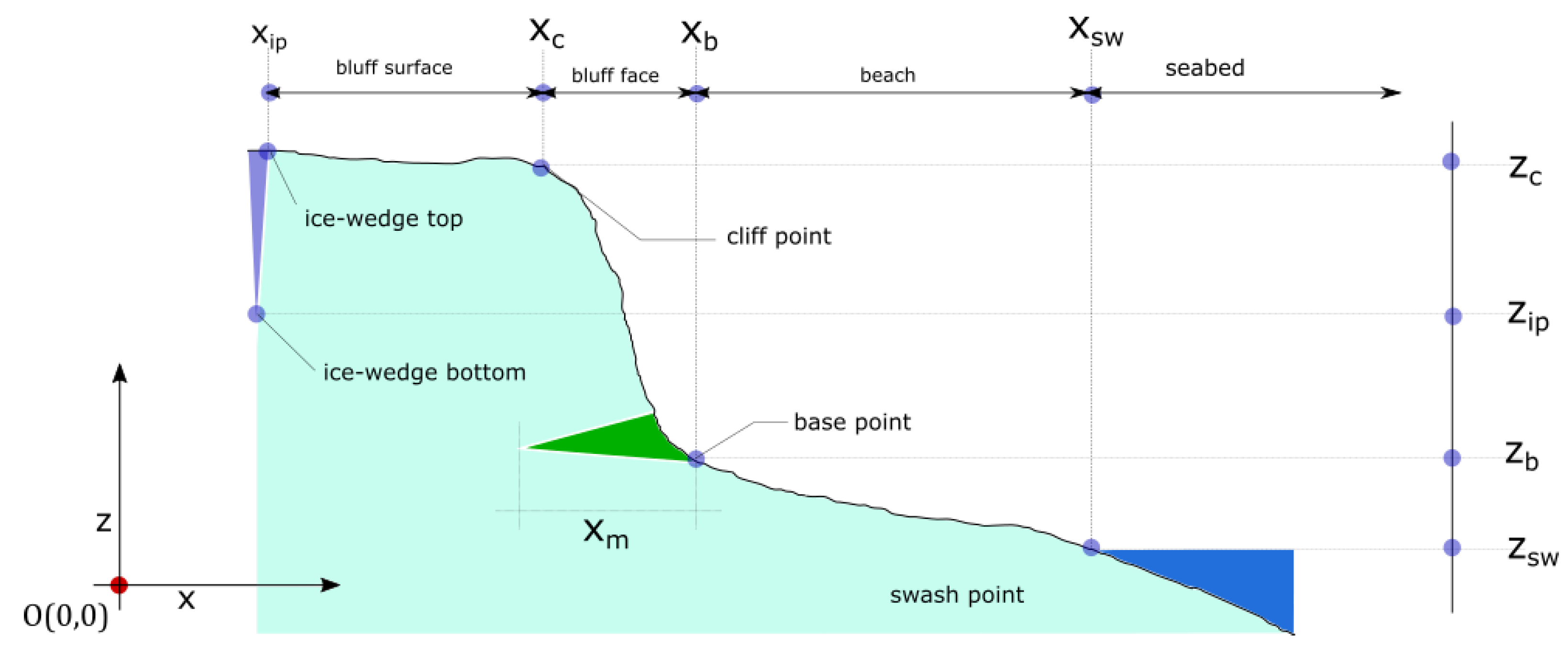
Appendix A. Definitions
- 1.
- profile line: the surface line of the beach profile not including the snow or ice sheets. During the summer, the profile line is exposed to environmental parameters.
- 2.
- permafrost table: the thawing face of the permafrost. During the winter, the line is assumed to collide with the profile line. The difference between the beach line and the permafrost table is the thawing depth.
- 3.
- base point: the point at the end of the beach where a sudden change in the slope occurs. Typically, it stands above the tidal range and in calm conditions, water level can not reach the base point.
- 4.
- cliff point: the end of the bluff-face and beginning of the bluff-surface; a sudden change in the slope.
- 5.
- ice-wedge top point: the point at the surface where the ice-wedge polygon is visible on the surface.
- 6.
- ice-wedge bottom point: not necessarily the bottom point of the ice-wedge. It is the point from which we can assume the continuity of the bluff is broken by the ice wedge.
- 7.
- swash point/line: Where the average water depth for a timestep is less than 5cm. The point(1D) or line(2D) is assumed to be constant for one timestep.
- 8.
- thawing depth: The difference between the permafrost line and profile line, calculated for the grid points on the profile line and normal to the tangent on the point at the profile line.
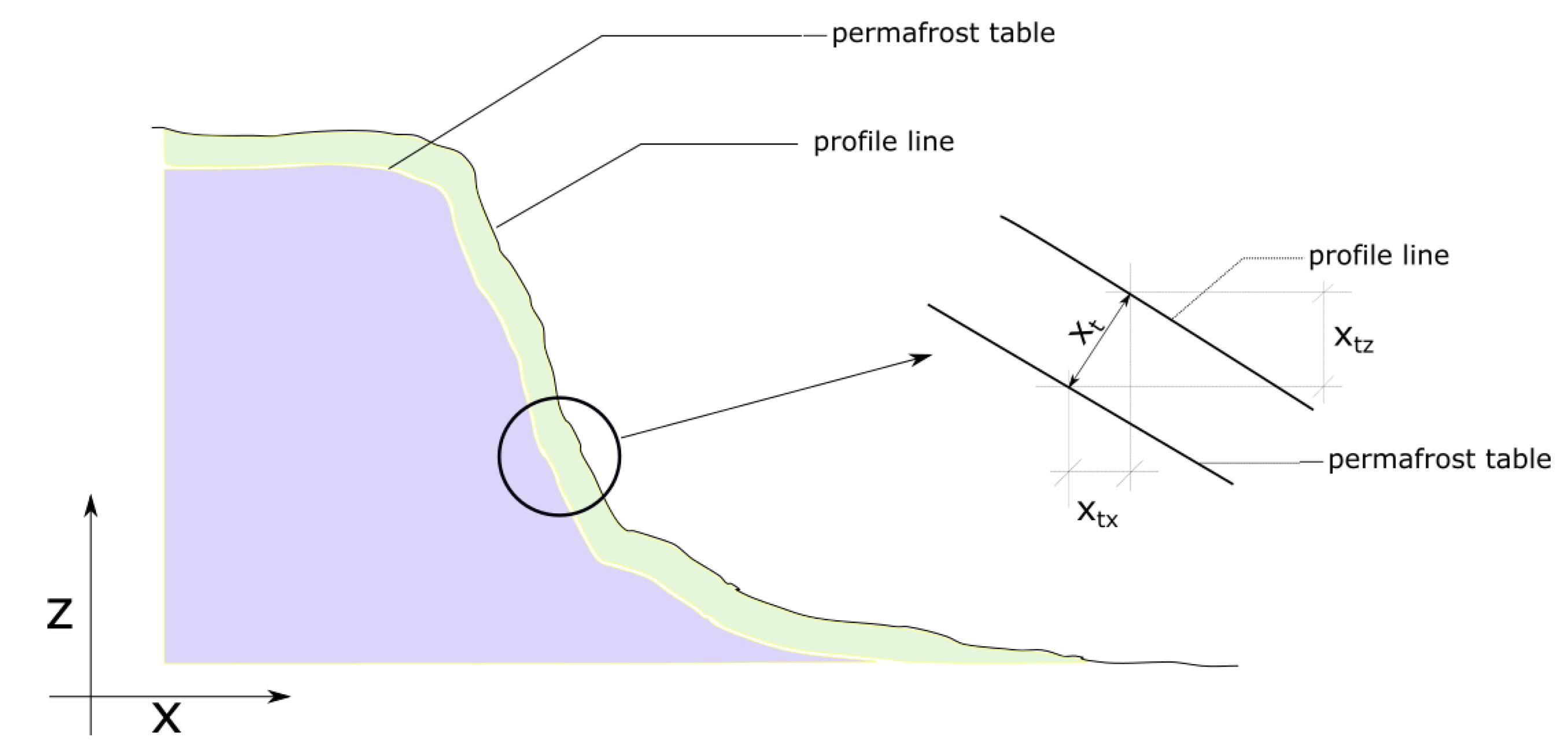
Appendix B. Four Zones of the Coastal Profile
- 1.
- bluff surface: it is the surface behind the cliff point . The slope in the zone is zero or close to zero. The surface is covered with vegetation during the summer. Subsidence due to the thawing of the permafrost is the major change in the profile. Thawing depth is dependent on the convection of air and solar radiation. We assume the erosion due to surface run-off is negligible (based on field observation). The bluffs are usually filled with ice-wedge polygons. The organic-active layer at the top of the surface has negligible shear strength but can contribute to the lower erodibility to surface run-offs.
- 2.
- bluff face: It is the steepest slope of the profile, in between the base point and cliff point and the most active part of the profile. The thawing process contributes directly to the mass loss by slumping and cliff retreat.
- 3.
- beach: The narrow beach in front of the bluff from the base point to the swash point . The thawed sediments accumulate on the beach. The collapsed bluffs fall on the beach. The beach is subject to inundation during the summer storms. The return currents created during the storms sort out the accumulated sediments and transport them offshore.
- 4.
- seabed: It is defined from the swash point to the offshore. The general direction of the sediment transport is offshore since there exist no restoration mechanisms at the Arctic beaches. The wave-induced particle movement is enough to transfer heat (convective heat transfer). The thawing depth is not the limiting factor, i.e., the permafrost lies quite deep. However, due to sea ice, sediment transport during the winter is negligible.
Appendix C. Numerical Schematisation of the Submodules
Appendix C.1. Modelling Storm Surge
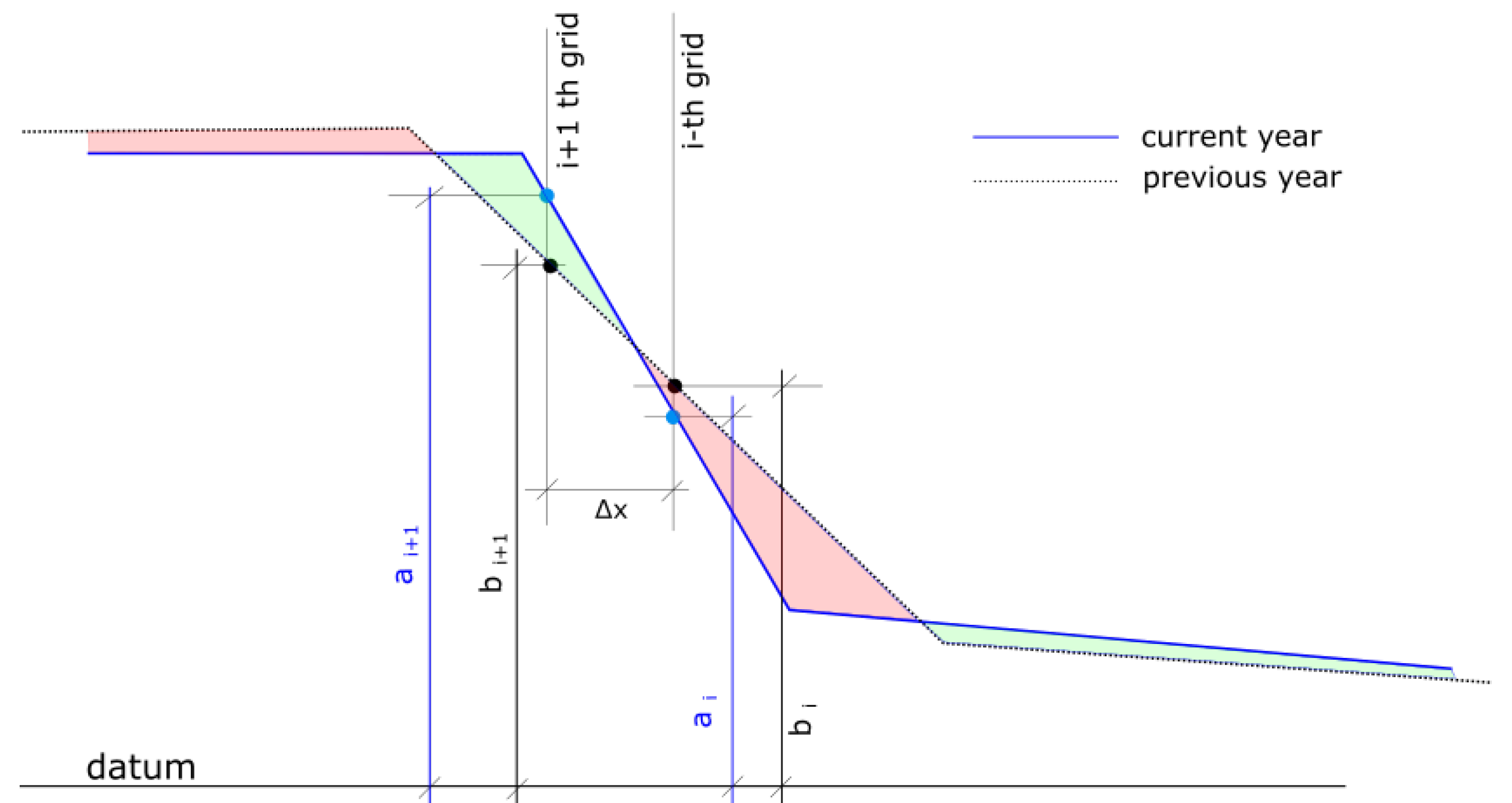
Appendix C.2. Modelling Slumping
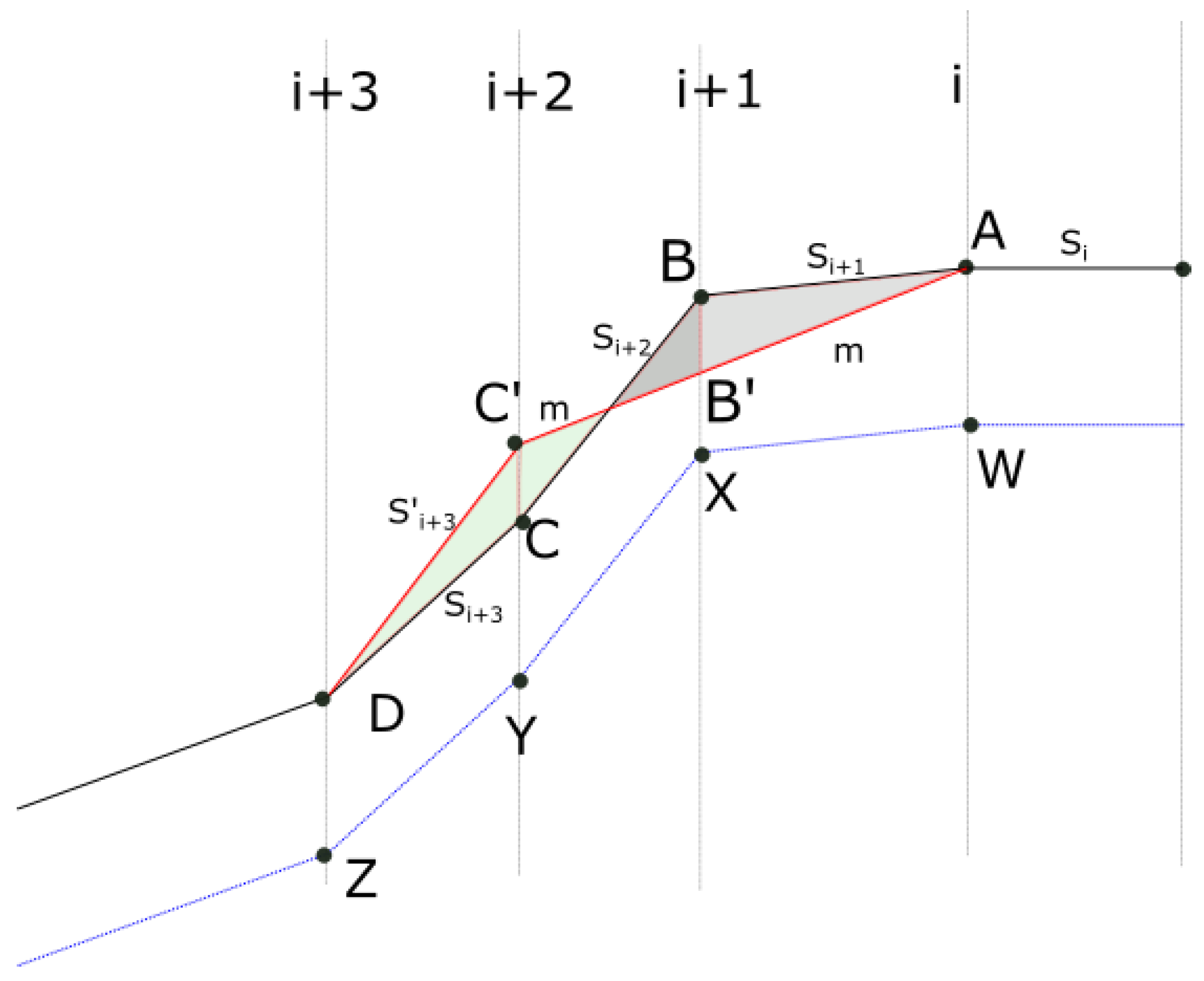
- C1. No slumping occurs at the permafrost table, the line WXYZ, irrespective of the slope. The failure within permafrost is considered in the bluff stability submodule. This submodule only simulates until thawing depth.
- C2. The slope at the grid point before the i th cell (point A) has a lower slope than critical .
- C3. The n-th timestep has j number of iterations where j is any number iteration until Equation (A3) is no more satisfied.
- C4. For slumping at i-th grid point at j th iteration, the mass transfer is limited to two adjacent grid cells; points B and C are moved to B′ and C′.
- C5. As a result of slumping, the grid point in consideration, point B, will be subsided to B′, increasing the elevation of point C to C′.
- C6. The subsidence of point B is such that the area under the curve ABCD will be equal to the area AB′C′D so that the conservation of mass is maintained.
- C7. Rule C6 is overridden when the subsidence of point B′ is limited by the permafrost line. Point B is not allowed to be lowered than point X. If C6 is overridden, then point C will move and still maintain mass balance. In this case, the movement of the mass will be lower.
- C8. The slumping process is always triggered in the downward direction. If for n th timestep, if two grid points have a slope more than the critical value , slumping will be initiated at the grid point in the higher vertical position.
- Figure A3a demonstrates the case when the is equal to the initial slope, i.e., no slumping can occur establishing the value acts as a triggering condition in the numerical model.
- Figure A3b demonstrate a case when we consider the = 0.4. The slumping occurred and part of the bluff surface was exposed (no thawing depth on the upper portion of the bluff surface).
- The effect of on the final profile is shown in Figure A3c. When we reduce the value to 0.3 from 0.4, keeping everything else the same, the exposed portion of the bluff surface got decreased. The slumped materials now moved further back on the beach.
- If we further decrease the value, the sediments are now distributed on almost 35 m along the beach (Figure A3d) and a large portion of the bluff surface is exposed.
- Figure A3e demonstrates a reduction in thawing depth on slumping. If the thawing depth is reduced to 0.5 m with a low value most of the bluff surface is exposed as a result.
- Figure A3f demonstrates the effect of very high thawing depth, the model behaviour is similar to active layer detachment, and a large portion of the thawed layer is moved.

Appendix C.3. Modelling Bluff Stability
- 1.
- Mode#1: The failure line is CE (from the cliff point to the base point E). The bluff face got steeper as a result.
- 2.
- Mode#2: The failure line is GE. Point G is determined using the same slope of the bluff.
- 3.
- Mode#3: The failure line is FE. F is the lowest point of the ice-wedge polygon. The shear failure line is the FE.
- 4.
- Mode#4: The failure line is PE and PF. This is the moment failure mode.

Appendix D. Physical Properties of Permafrost
| Particle Size (%-mm) | 1.0–0.5 | 0.5–0.25 | 0.25–0.1 | 0.1–0.05 | 0.05–0.01 | 0.01–0.005 | <0.005 | <0.002 | <0.001 | Moisture (%) | Density (gm/cm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 0.2 | 1.0 | 59.5 | 24.1 | 7.4 | 0.5 | 0.5 | 1.5 | 5.2 | 29 | 2.63 |
| Sample 2 | 0.1 | 0.9 | 58.4 | 26.6 | 5.2 | 1.6 | 0.5 | 1.0 | 5.7 | 29 | 2.64 |
| Sample 3 | 0.1 | 0.1 | 64.9 | 23.6 | 3.2 | 0.3 | 0.5 | 1.2 | 6.1 | 29 | 2.64 |
| Sample 4 | 0.1 | 0.8 | 62.1 | 24.6 | 3.8 | 0.8 | 0.5 | 1.2 | 6.0 | 29 | 2.63 |
Appendix E. Measurements of Thawing Depth
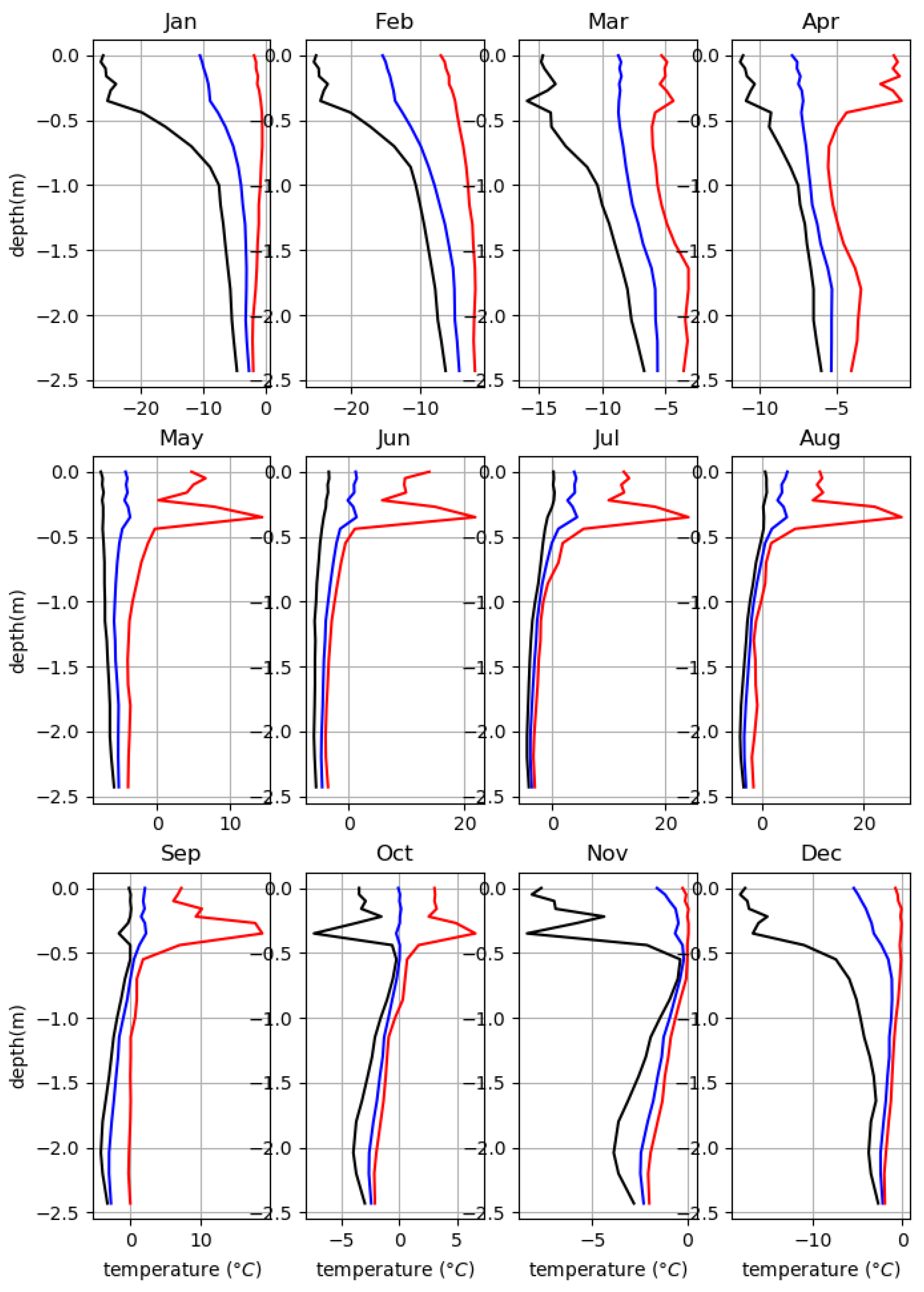
Appendix F. The Parameters of XBeach

Appendix G. Coastal Profiles for Validation Cases
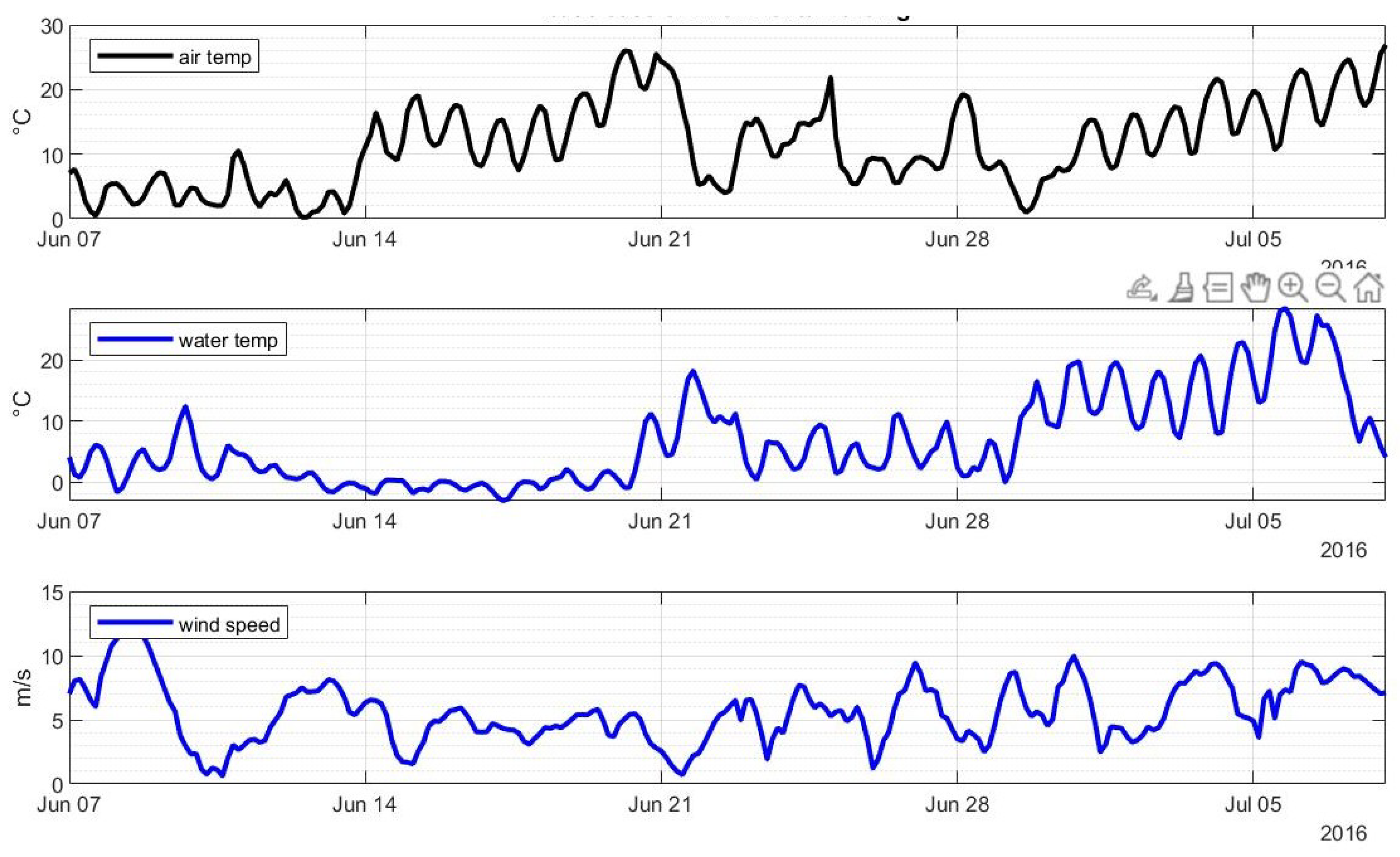
Appendix H. Base Case: Environmental Forcing
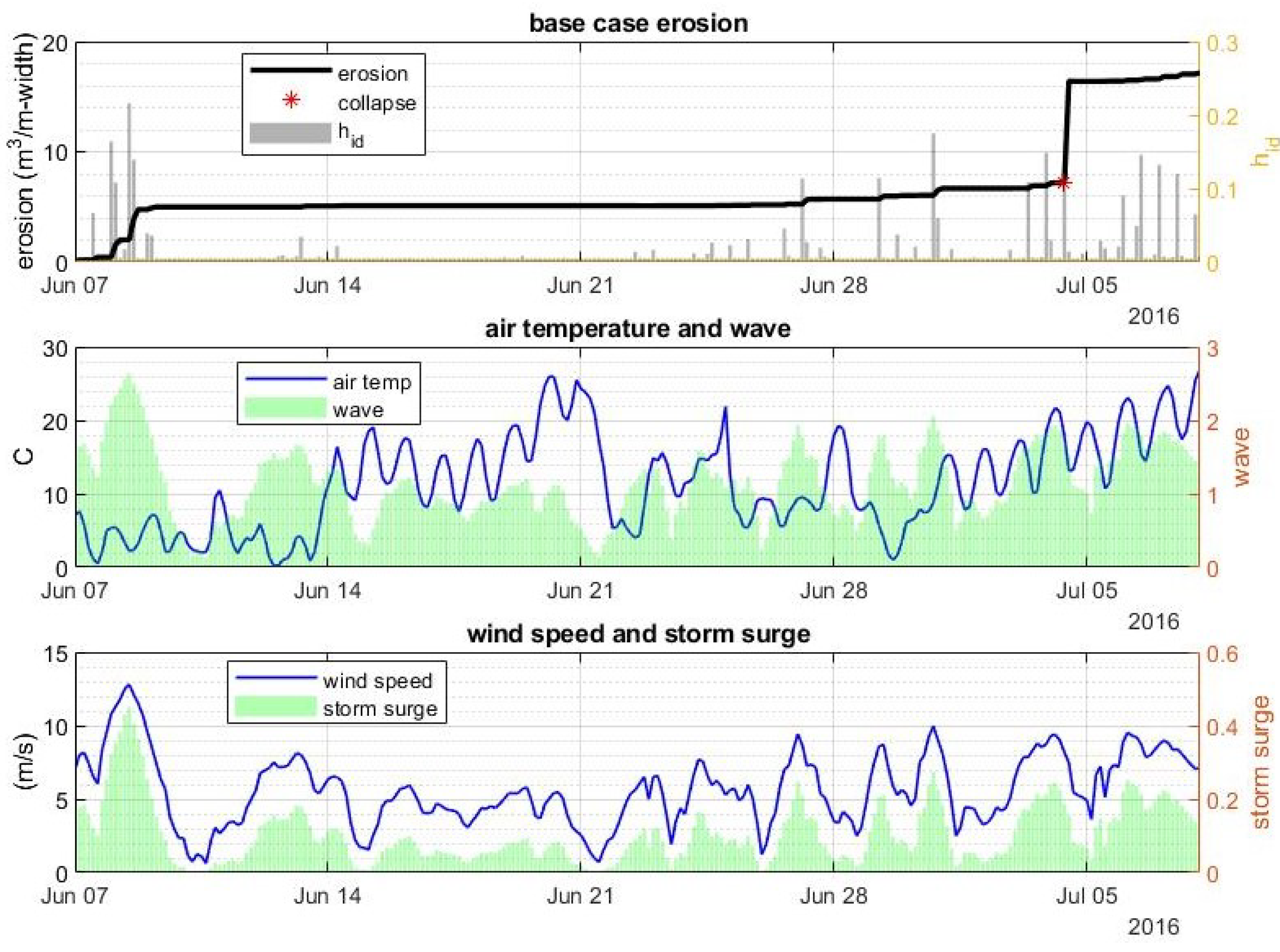
Appendix I. Effect of the Environmental Forcing
Appendix I.1. Effect of Seawater Temperature
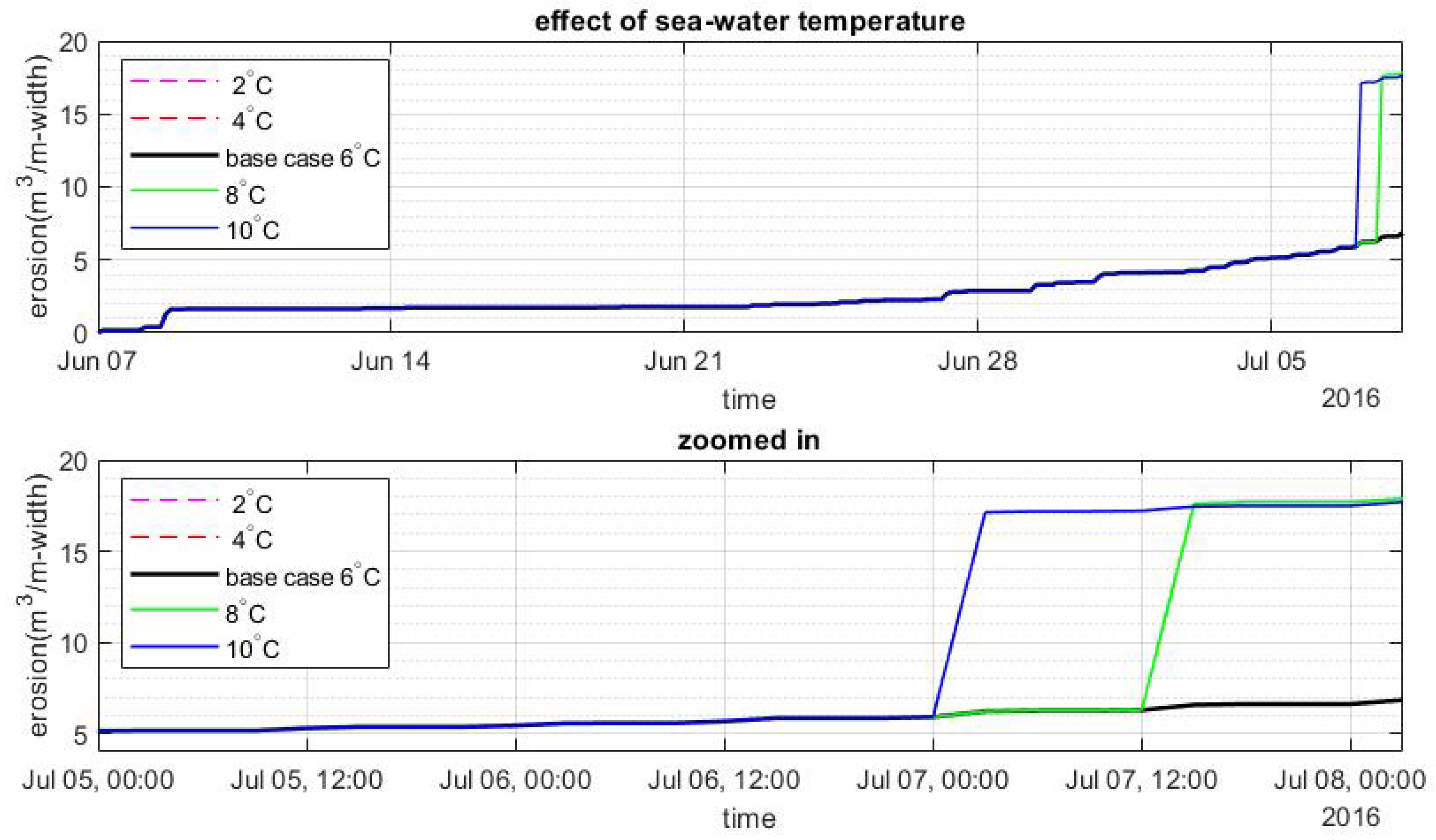
Appendix I.2. The Effect of Air Temperature
References
- Lantuit, H.; Overduin, P.P.; Couture, N.; Wetterich, S.; Aré, F.; Atkinson, D.; Brown, J.; Cherkashov, G.; Drozdov, D.; Forbes, D.L.; et al. The Arctic coastal dynamics database: A new classification scheme and statistics on Arctic permafrost coastlines. Estuaries Coasts 2012, 35, 383–400. [Google Scholar] [CrossRef]
- Gibbs, A.E.; Richmond, B.M. National Assessment of Shoreline Change: Historical Shoreline Change along the North Coast of Alaska, US-Canadian Border to Icy Cape; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2015.
- Isaev, V.; Koshurnikov, A.; Pogorelov, A.; Amangurov, R.; Podchasov, O.; Sergeev, D.; Buldovich, S.; Aleksyutina, D.; Grishakina, E.; Kioka, A. Cliff retreat of permafrost coast in south-west Baydaratskaya Bay, Kara Sea, during 2005–2016. Permafr. Periglac. Process. 2019, 30, 35–47. [Google Scholar] [CrossRef]
- Gibbs, A.; Richmond, B.; Erikson, L.; Jones, B. Long-term retreat of coastal permafrost bluffs, Barter Island, Alaska. In Proceedings of the 5th European Conference on permafrost, EUCOP5, Chamonix, France, 23 June–1 July 2018; Volume 1, pp. 1–2. [Google Scholar]
- Jones, B.M.; Arp, C.D.; Jorgenson, M.T.; Hinkel, K.M.; Schmutz, J.A.; Flint, P.L. Increase in the rate and uniformity of coastline erosion in Arctic Alaska. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Jones, B.; Bull, D.; Farquharson, L.; Buzard, R.; Arp, C.; Grosse, G.; Romanovsky, V. A decade of annual permafrost coastal observations indicate changes in the Arctic System. Environ. Res. Lett. 2018, 13, 1–13. [Google Scholar]
- Ogorodov, S.; Aleksyutina, D.; Baranskaya, A.; Shabanova, N.; Shilova, O. Coastal erosion of the Russian Arctic: An overview. J. Coast. Res. 2020, 95, 599–604. [Google Scholar] [CrossRef]
- Barnhart, K.; Overeem, I.; Anderson, R.S. The effect of changing sea ice on the physical vulnerability of Arctic coasts. Cryosphere 2014, 8, 1777–1799. [Google Scholar] [CrossRef]
- Stroeve, J.; Notz, D. Changing state of Arctic sea ice across all seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
- Serreze, M.; Barrett, A.; Stroeve, J.; Kindig, D.; Holland, M. The emergence of surface-based Arctic amplification. Cryosphere Discuss. 2008, 2, 601–622. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.C.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.; Dethloff, K.; Entekhabi, D.; Overland, J.; et al. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Nielsen, D.; Pieper, P.; Barkhordarian, A.; Overduin, P.; Ilyina, T.; Brovkin, V.; Baehr, J.; Dobrynin, M. Increase in Arctic coastal erosion and its sensitivity to warming in the twenty-first century. Nat. Clim. Chang. 2022, 12, 263–270. [Google Scholar] [CrossRef]
- Rowland, J.; Jones, C.; Altmann, G.; Bryan, R.; Crosby, B.; Hinzman, L.; Kane, D.; Lawrence, D.; Mancino, A.; Marsh, P.; et al. Arctic landscapes in transition: Responses to thawing permafrost. Eos Trans. Am. Geophys. Union 2010, 91, 229–230. [Google Scholar] [CrossRef]
- Overeem, I.; Anderson, R.S.; Wobus, C.W.; Clow, G.D.; Urban, F.E.; Matell, N. Sea ice loss enhances wave action at the Arctic coast. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Steele, M.; Ermold, W.; Zhang, J. Arctic Ocean surface warming trends over the past 100 years. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Holland-Bartels, L.; Pierce, B. An Evaluation of the Science Needs to Inform Decisions on Outer Continental Shelf Energy Development in the Chukchi and Beaufort Seas, Alaska; Technical Report; US Geological Survey: Reston, VI, USA, 2011.
- Günther, F.; Overduin, P.P.; Yakshina, I.A.; Opel, T.; Baranskaya, A.V.; Grigoriev, M.N. Observing Muostakh disappear: Permafrost thaw subsidence and erosion of a ground-ice-rich island in response to arctic summer warming and sea ice reduction. Cryosphere 2015, 9, 151–178. [Google Scholar] [CrossRef]
- Irrgang, A.M.; Lantuit, H.; Manson, G.K.; Günther, F.; Grosse, G.; Overduin, P.P. Variability in rates of coastal change along the Yukon coast, 1951 to 2015. J. Geophys. Res. Earth Surf. 2018, 123, 779–800. [Google Scholar] [CrossRef]
- Jones, B.M.; Irrgang, A.M.; Farquharson, L.M.; Lantuit, H.; Whalen, D.; Ogorodov, S.; Grigoriev, M.; Tweedie, C.; Gibbs, A.E.; Strzelecki, M.C.; et al. Coastal Permafrost Erosion. Arct. Rep. Card 2020, 15. [Google Scholar]
- Jones, B.M.; Hinkel, K.M.; Arp, C.D.; Eisner, W.R. Modern erosion rates and loss of coastal features and sites, Beaufort Sea coastline, Alaska. Arctic 2008, 61, 361–372. [Google Scholar] [CrossRef][Green Version]
- Landrum, L.; Holland, M.M. Extremes become routine in an emerging new Arctic. Nat. Clim. Chang. 2020, 10, 1108–1115. [Google Scholar] [CrossRef]
- Are F, E. Thermal abrasion of sea coast. Polar Geogr. Geol. 1988, 12, 1–157. [Google Scholar] [CrossRef]
- Squire, V.A.; Vaughan, G.L.; Bennetts, L.G. Ocean surface wave evolvement in the Arctic Basin. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Kobayashi, N. Formation of thermoerosional niches into frozen bluffs due to storm surges on the Beaufort Sea coast. J. Geophys. Res. Ocean. 1985, 90, 11983–11988. [Google Scholar] [CrossRef]
- Russell-Head, D. The melting of free-drifting icebergs. Ann. Glaciol. 1980, 1, 119–122. [Google Scholar] [CrossRef]
- White, F.M.; Spaulding, M.L.; Gominho, L. Theoretical Estimates of the Various Mechanisms Involved in Iceberg Deterioration in the Open Ocean Environment; Technical Report; Rhode Island Univ. Kingston: Kingston, RI, USA, 1980. [Google Scholar]
- Bull, D.L.; Bristol, E.M.; Brown, E.; Choens, R.C.; Connolly, C.T.; Flanary, C.; Frederick, J.M.; Jones, B.M.; Jones, C.A.; Ward Jones, M.; et al. Arctic Coastal Erosion: Modeling and Experimentation; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Hoque, M.A.; Pollard, W.H. Arctic coastal retreat through block failure. Can. Geotech. J. 2009, 46, 1103–1115. [Google Scholar] [CrossRef]
- Ravens, T.; Jones, B.; Zhang, J.; Arp, C.D.; Schmutz, J.A. Process-based coastal erosion modeling for drew point, North Slope, Alaska. J. Water. Port Coastal Ocean. Eng. 2012, 138, 122–130. [Google Scholar] [CrossRef]
- Barnhart, K.R.; Anderson, R.S.; Overeem, I.; Wobus, C.; Clow, G.D.; Urban, F.E. Modeling erosion of ice-rich permafrost bluffs along the Alaskan Beaufort Sea coast. J. Geophys. Res. Earth Surf. 2014, 119, 1155–1179. [Google Scholar] [CrossRef]
- Hoque, M.A.; Pollard, W. Thermal and mechanical erosion along ice-rich Arctic coasts. In Proceedings of the 9th Intl. Conf. on Permafrost, Fairbanks, Alaska, 29 June–3 July 2008; pp. 741–746. [Google Scholar]
- Ravens, T.; Ulmgren, M.; Wilber, M.; Hailu, G.; Peng, J. Arctic-capable coastal geomorphic change modeling with application to Barter Island, Alaska. In Proceedings of the OCEANS 2017-Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–4. [Google Scholar]
- Deltares. XBeach. 2022. Available online: https://oss.deltares.nl/web/xbeach/release-and-source (accessed on 10 October 2020).
- Frederick, J.; Mota, A.; Tezaur, I.; Bull, D. A thermo-mechanical terrestrial model of Arctic coastal erosion. J. Comput. Appl. Math. 2021, 397, 113533. [Google Scholar] [CrossRef]
- Rolph, R.; Overduin, P.P.; Ravens, T.; Lantuit, H.; Langer, M. ArcticBeach v1. 0: A physics-based parameterization of pan-Arctic coastline erosion. Geosci. Model Dev. Discuss. 2021, 1–26. [Google Scholar]
- Kobayashi, N.; Vidrine, J.; Nairn, R.; Soloman, S. Erosion of frozen cliffs due to storm surge on Beaufort Sea Coast. J. Coast. Res. 1999, 15, 332–344. [Google Scholar]
- Irrgang, A.M.; Bendixen, M.; Farquharson, L.M.; Baranskaya, A.V.; Erikson, L.H.; Gibbs, A.E.; Ogorodov, S.A.; Overduin, P.P.; Lantuit, H.; Grigoriev, M.N.; et al. Drivers, dynamics and impacts of changing Arctic coasts. Nat. Rev. Earth Environ. 2022, 3, 39–54. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; Volume 2. [Google Scholar]
- SWAN. Simulating Waves Nearshore. 2021. Available online: https://swanmodel.sourceforge.io/ (accessed on 13 January 2021).
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Guégan, E. Erosion of Permafrost Affected Coasts: Rates, Mechanisms and Modelling. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Longuet-Higgins, M.S. Longshore currents generated by obliquely incident sea waves: 1. J. Geophys. Res. 1970, 75, 6778–6789. [Google Scholar] [CrossRef]
- Ogorodov, S.; Arkhipov, V.; Kokin, O.; Marchenko, A.; Overduin, P.; Forbes, D. Ice effect on coast and seabed in Baydaratskaya Bay, Kara Sea. Geogr. Environ. Sustain. 2013, 6, 21–37. [Google Scholar] [CrossRef]
- Kamalov, A.; Ogorodov, S.; Birukov, V.Y.; Sovershaeva, G.; Tsvetsinsky, A.; Arkhipov, V.; Belova, N.; Noskov, A.; Solomatin, V. Coastal and seabed morpholithodynamics of the Baydaratskaya Bay at the route of gas pipeline crossing. Kriosf. Zemli (Earth Cryosphere) 2006, 10, 3–14. [Google Scholar]
- Bogorodskii, P.; Marchenko, A.; Pnyushkov, A.; Ogorodov, S. Formation of fast ice and its influence on the coastal zone of the Arctic seas. Oceanology 2010, 50, 317–326. [Google Scholar] [CrossRef]
- Rodrigues, J. The rapid decline of the sea ice in the Russian Arctic. Cold Reg. Sci. Technol. 2008, 54, 124–142. [Google Scholar] [CrossRef]
- Stein, R.; Fahl, K.; Fiitterer, D.; Galimov, E.; Stepanets, O. River run-off influence on the water mass formation in the Kara Sea. Siberian Rer Run-Off in the Kara Sea: Characterisation, Quantification, Variability and Environmental Significance; Elsevier: Amsterdam, The Netherlands, 2003; p. 9. [Google Scholar]
- Harms, I.; Karcher, M. Modeling the seasonal variability of hydrography and circulation in the Kara Sea. J. Geophys. Res. Ocean. 1999, 104, 13431–13448. [Google Scholar] [CrossRef]
- Isaev, V.; Pogorelov, A.; Amangurov, R.; Komarov, O.; Gorshkov, E.; Belova, N.; Aleksyutina, D.; Kokin, O. Field Investigation and Laboratory Analyses; Baydaratskaya bay 2017. Available online: https://www.researchgate.net/publication/322103499_Field_investigation_and_laboratory_analyses_Baydaratskaya_bay_2017 (accessed on 10 September 2022).
- Simpson, J.M.; Darrow, M.M.; Huang, S.L.; Daanen, R.P.; Hubbard, T.D. Investigating movement and characteristics of a frozen debris lobe, south-central Brooks Range, Alaska. J. Environ. Eng. Geosci. 2016, 22, 259–277. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Y. Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials. Materials 2022, 15, 1576. [Google Scholar] [CrossRef] [PubMed]









| Parameter | Definition | Typical Value | Units | References |
|---|---|---|---|---|
| thermal properties | ||||
| convective heat transfer coefficient of air | 100 | W/m2−k | [36] | |
| convective heat transfer coefficient of water | 700 | W/m2−k | [36] | |
| volumetric latent heat of permafrost | J/m3 | [36] | ||
| Temperature of air | varied | °C | NOAA [40] | |
| Temperature of water | varied | °C | NOAA, [40] | |
| Temperature of soil | varied | °C | field measurements | |
| geometry | ||||
| thawing depth | varied | m | ||
| water depth at the base | varied | m | ||
| mean sea level | varied | m | ||
| tide compared with MSL | varied | m | ||
| water level | varied | - | calculated by Equation (11) | |
| storm surge level compared with MSL | - | m | Equation (A1) | |
| niche opening parameter | 2 | - | Kobayashi [24] | |
| critical slope of slumping | 0.1–1 | - | field observations | |
| distance from niche to the ice-wedge polygon | 5–14 | m | field observations | |
| wind speed | - | m/s | NOAA reanalysis | |
| time steps | ||||
| timestep within XBeach | varied | s | XBeach Manual | |
| timestep within modules/global timestep | 10,800 | s | based on 3 h sea state | |
| timestep between two field measurements | 365 | days | Field report | |
| Cases | Zone | Profile | Time | Crest Retreat | Erosion | Accretion | Net Erosion | |
|---|---|---|---|---|---|---|---|---|
| From | To | (m) | (m/m−width) | (m/m−width) | (m/m−width) | |||
| case#1 | S#1 | P#1 | 15-09-2015 | 14-09-2016 | 4.1 | 10.31 | 3.28 | 7.04 |
| case#2 | S#2 | P#8 | 15-09-2015 | 15-09-2016 | 2.9 | 12.51 | 0.00 | 12.51 |
| Parameter | Zone | Symbol | Calibrated Value | Unit | Remarks |
|---|---|---|---|---|---|
| convective heat transfer coefficient | S#1 & S#2 | 106 | W/mk | for bluff-surface | |
| S#1 & S#2 | 98 | W/mk | for bluff-slope | ||
| S#1 & S#2 | 90 | W/mk | for beaches | ||
| convective heat transfer coefficient | S#1 & S#2 | 700 | W/mk | for sea beds | |
| tensile strength | S#1 & S#2 | N/m | |||
| critical slope (dry) | S#1 | 0.34 | - | ||
| S#2 | 0.52 | - | |||
| critical slope (wet) | S#1 | 0.2 | - | ||
| S#2 | 0.2 | - | |||
| mean sea level | S#1 & S#2 | −7.6 | m |
| Case | Criteria | Measured | Simulation | Error (%) | |||
|---|---|---|---|---|---|---|---|
| Volume | (%) | net | |||||
| case#1 | erosion volume (m/m−width) | 7.04 | td | 2.01 | 24.22% | 8.3 | 17.9% |
| ta | 6.29 | 75.78% | |||||
| crest retreat (m) | 4.1 | - | - | - | 3.9 | 4.8% | |
| case#2 | erosion volume (m/m−width) | 12.51 | td | 6.04 | 40.82% | 14.8 | 18.3% |
| ta | 8.75 | 59.18% | |||||
| crest retreat (m) | 2.9 | - | - | - | 4 | 37.9% | |
| Cases | Zone | Profile | Time | Crest Retreat | Erosion | Accretion | Net Erosion | |
|---|---|---|---|---|---|---|---|---|
| From | To | (m) (m/m−width) | (m/m−width) | (m/m−width) | (m/m−width) | |||
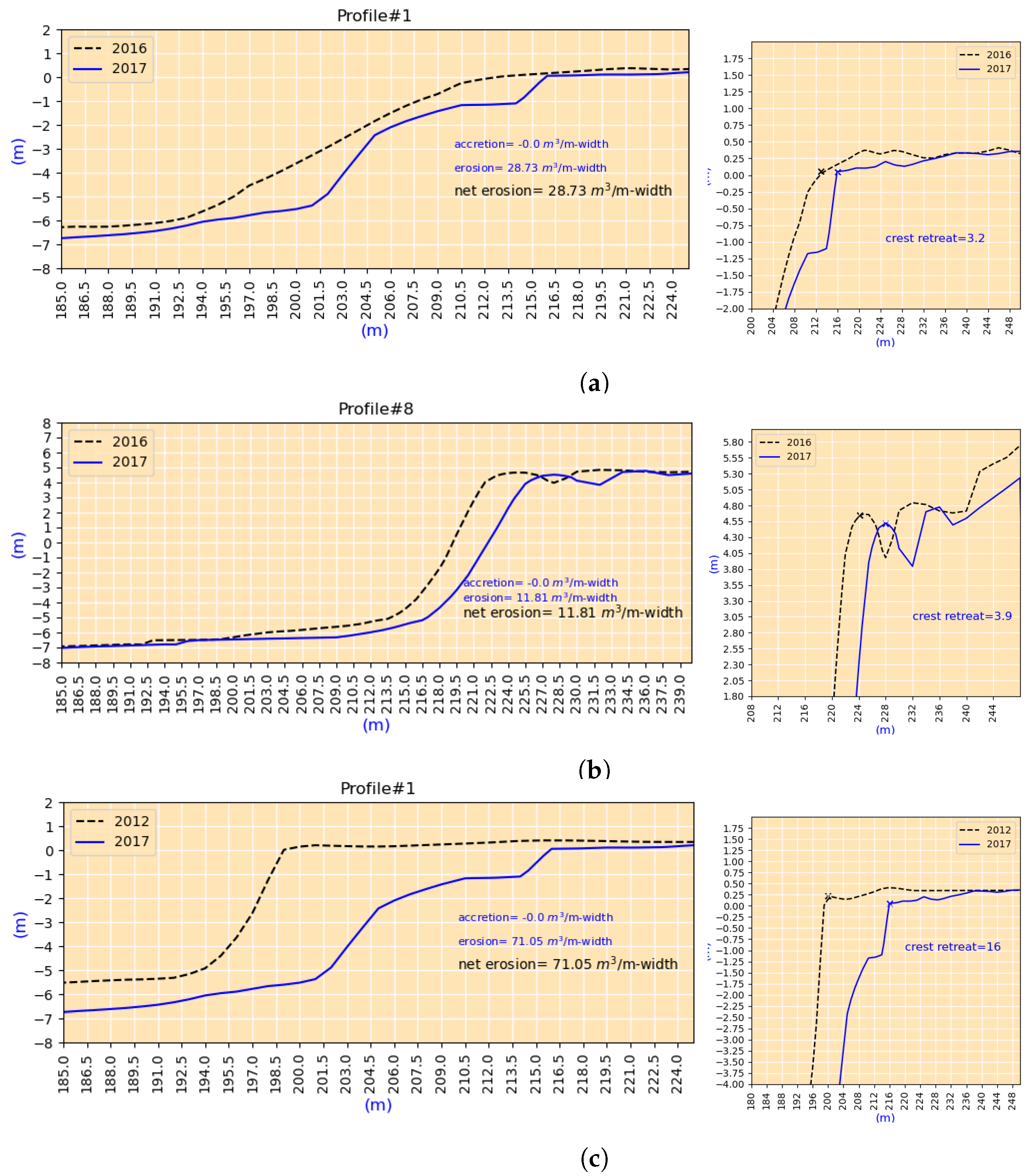
| case#3 | S#1 | P#1 | 15-09-2016 | 14-09-2017 | 3.2 | 28.73 | 0.00 | 28.73 |
| case#4 | S#2 | P#8 | 15-09-2016 | 15-09-2017 | 3.9 | 11.81 | 0.00 | 11.81 |
| case#5 | S#1 | P#1 | 13-06-2012 | 15-09-2017 | 16 | 71.05 | 0.00 | 71.05 |
| Case | Criteria | Measured | Simulation | Error (%) | |||
|---|---|---|---|---|---|---|---|
| Volume | (%) | net | |||||
| case#3 | erosion volume (m/m−width) | 28.73 | td | 10.18 | 39.46% | 25.8 | 10.2% |
| ta | 15.62 | 60.54% | |||||
| crest retreat (m) | 3.2 | - | - | - | 3.9 | 4.8% | |
| case#4 | erosion volume (m/m−width) | 11.81 | td | 3.75 | 24.83% | 15.1 | 27.8% |
| ta | 11.36 | 75.17% | |||||
| crest retreat (m) | 3.9 | - | - | - | - | 23.1% | |
| case#5 | erosion volume (m/m−width) | 71.05 | td | 23.6 | 29.32% | 80.5 | 13.3% |
| ta | 56.9 | 70.68% | |||||
| crest retreat (m) | 16 | 14.8 | 7.5% | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.A.; Lubbad, R. A Process-Based Model for Arctic Coastal Erosion Driven by Thermodenudation and Thermoabrasion Combined and including Nearshore Morphodynamics. J. Mar. Sci. Eng. 2022, 10, 1602. https://doi.org/10.3390/jmse10111602
Islam MA, Lubbad R. A Process-Based Model for Arctic Coastal Erosion Driven by Thermodenudation and Thermoabrasion Combined and including Nearshore Morphodynamics. Journal of Marine Science and Engineering. 2022; 10(11):1602. https://doi.org/10.3390/jmse10111602
Chicago/Turabian StyleIslam, Mohammad Akhsanul, and Raed Lubbad. 2022. "A Process-Based Model for Arctic Coastal Erosion Driven by Thermodenudation and Thermoabrasion Combined and including Nearshore Morphodynamics" Journal of Marine Science and Engineering 10, no. 11: 1602. https://doi.org/10.3390/jmse10111602
APA StyleIslam, M. A., & Lubbad, R. (2022). A Process-Based Model for Arctic Coastal Erosion Driven by Thermodenudation and Thermoabrasion Combined and including Nearshore Morphodynamics. Journal of Marine Science and Engineering, 10(11), 1602. https://doi.org/10.3390/jmse10111602







