Abstract
In crowded waters, the incidence of collision accidents of multiple vessels has increased significantly, most of which can be ascribed to human factors, particularly, human decision-making failures and inobservance with International Regulations for Preventing Collisions at Sea (COLREGS). On this basis, an automatic collision avoidance strategy for the encounter situations of multiple vessels is proposed herein. First of all, a COLREGS-complied evasive action decision-making mechanism is established, which can determine the evasive action from the give-way vessel and stand-on vessel separately. It is worth emphasizing that the situation of vessels against COLREGS is taken into consideration herein. Furthermore, a novel automatic collision avoidance controller of multiple vessels on account of model predictive control (MPC) is devised, which can carry out control action ahead of time and handle the problem of rudder saturation. Finally, the effectiveness of the proposed automatic collision avoidance strategy of multiple vessels is illustrated via extensive simulations.
1. Introduction
Over the years, the incidence of ship collision accidents has taken a large proportion in all kinds of marine accidents, causing environmental contamination, economic losses, and casualties. In the light of the exiting statistics, over 80% of ship collision accidents are ascribed to human factors, namely, human decision-making failures and inobservance with COLREGS [1,2,3,4]. Therefore, to eliminate or alleviate the influence of human factors on navigation safety, scholars have paid more attention into improving the automation level of autonomous surface vehicles (ASVs), which can solve the problem of poor human judgment and the inability to react quickly [5,6,7,8]. Meanwhile, under the premise of fully considering COLREGS, the automatic collision avoidance control of ASV will be realized, which can decrease the collision accident rate and guarantee navigation safety.
Although the automation level of ASV is improving, most of the existing research is limited to the automatic collision avoidance control between two vessels [9,10,11,12,13,14]. With the increasing congestion of marine traffic, the collision probability among multiple vessels is likely to increase drastically, which makes the decision-making for collision avoidance more complicated. Therefore, scholars have begun to concentrate on the studies of automatic collision avoidance control of multiple vessels and achieved a series of results [1,15,16,17,18]. Nevertheless, COLREGS were not considered in the above-mentioned studies, and in the actual marine navigation, vessels need to abide by COLREGS put forward by International Maritime Organization (IMO) in 1972. Firstly, it represents the underlying collision situations between encountering vessels and supplies a sequence of guidelines to guarantee navigation safety; secondly, owing to the complication of the actual marine environment, it is difficult to depict all probable situations in the form of guidelines [16]. It is worth noting that COLREGS are set out for the operators on board, and there are no detailed and specific rules about the decision-making of automatic collision avoidance, especially in the case of the encounter situations of multiple ships. After all, it is still a huge challenge to implement automatic collision avoidance of multiple vessels whether under the premise of considering or ignoring COLREGS, which needs further research.
For decades, most previous research about the automatic collision avoidance of multiple vessels have focused on the determination of evasive action, however, the influence of ship maneuverability on the automatic collision avoidance control is normally ignored [19,20,21,22,23]. In fact, owing to the large inertia and input constraints of ship motion, if ship maneuverability is not fully considered, it will lead to the failure of collision avoidance, which causes collision accidents and threatens navigation safety. MPC is increasingly used for ship motion control because of its advantages in forecasting ability and handling input constraints [24,25,26]. In particular, the forecasting ability of MPC can predict the future state of ships in advance, which can alleviate the influence of large inertia; and input constraints can be incorporated into the optimization process of MPC. Therefore, inspired by the above work, we will consider the ship maneuverability and use the advantages of MPC to achieve automatic collision avoidance control of multiple vessels herein.
Inspired by the aforementioned research, a COLREGS-complied automatic collision avoidance strategy for encounter situations of multiple vessels based on MPC is proposed herein. A COLREGS-complied real-time evasive action decision-making mechanism is firstly set up to determine the evasive action from the give-way vessel and stand-on vessel separately. Furthermore, it is worth emphasizing that the situation of ships against COLREGS is considered herein. Moreover, an automatic collision avoidance controller on account of MPC is devised, presenting the advantages of forecasting ability and solving input constraints, with the ability to carry out control action beforehand and solve the problem of rudder saturation.
The main contributions of this paper are summarized as follows:
- (1)
- A COLREGS-complied real-time evasive action decision-making mechanism is established to determine the evasive action from the give-way vessel and stand-on vessel separately, and the situation of vessels disregarding COLREGS is taken into account herein;
- (2)
- Taking the large inertia and input constraints into account, an automatic collision avoidance controller on the strength of MPC for multiple vessels is devised, which can carry out the control action beforehand and solve the problem of rudder saturation.
2. Preliminaries and Problem Formulation
2.1. The Ship Simulation Model
For the purpose of depicting the ship motion accurately, a sophisticated ship model is applied to simulate the ship motion in the collision avoidance of multiple vessels, and the specific form is depicted as in Ref. [27].
here denotes the numbers of ships in collision avoidance; , , and are the position and orientation; , , and represent velocities of 3-DoF; and are the length and velocity of ship; and are rudder angle and command rudder angle; and are constants; and are forces; is the moment; , , , , ; , , and et al. are the hydrodynamic parameters.
2.2. The COLREGS-Complied Evasive Action Decision-Making Mechanism
2.2.1. Estimate the Collision Risk of Multiple Vessels
The estimate of collision risk is the prerequisite to realize the automatic collision avoidance of multiple vessels. Most studies have poured more attention into the distance to the closest point of approach (DCPA) and the time to the closest point of approach (TCPA) to estimate the collision risk [28,29]. On this basis, the collision risk of multiple vessels is estimated via DCPA and TCPA. The and between and is calculated as follows.
According to the position and velocity of and , the velocity and course of relative to can be described as
where and indicate the velocity and course of relative to ; and are the velocity and course of ; and are the velocity and course of .
Then, the true bearing of relative to is calculated
here and denote the position of and ; the value range of function atan2 is , but the value range of and is , i.e., if the calculated value and are negative, and need to plus .
Furthermore, the and is obtained
On account of Equation (4), the collision risk can be estimated by the and . indicates the minimal distance of two vessels in approach, and denotes the time required for two vessels to reach the closest point. If is smaller than the threshold value, namely, the distance at the safety point of approach (DSPA) and is positive, it means two vessels are approaching and the minimal distance of two vessels in approach cannot ensure navigation safety, which cause the collision risk between and .
2.2.2. Distinguish the Collision Situation and Collision Avoidance Responsibility on Account of COLREGS
In the encounter situation of multiple vessels, there are no specific rules to regulate the evasive action of each vessel. However, the problem of the encounter situation of multiple vessels is separated into the multiple encounter situation of two vessels to handle. Therefore, the collision situation and collision avoidance responsibility of two vessels can be distinguished by rules 13–17 of COLREGS [21]. Among them, the encounter situation of two vessels is classified as three categories: head-on situation, crossing situation, and overtaking; and two ships in collision are distinguished as the give-way vessel and stand-on vessel [30,31]. The detailed distinguishing process is shown in Figure 1.
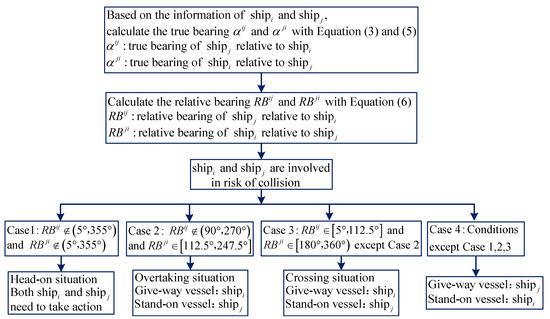
Figure 1.
The identification of collision situation and responsibility.
where is the true bearing of relative to
represents the bearing of relative to , and is contrary to . The specific form of and is depicted as
In accordance with COLREGS, the ships in collision are distinguished as the give-way vessel and stand-on vessel, and they require to take actions to avert collision respectively. The give-way vessel ought to take evasive action as early as possible to ensure that the stand-on vessel can understand its intention. In addition, the urgency of collision avoidance should be considered in the evasive action taken by the give-way vessel and stand-on vessel. According to the distance between two vessels, the area around the ship is divided into four concentric circles zones: safety zone, alerting zone, action zone, and emergency zone separately [11], as shown in Figure 2. Safety zone refers to the zone with a distance of more than 10 miles from own ship, and the collision risk between vessels is not considered. Alerting zone denotes the zone with a distance between 6 miles and 10 miles from own ship, where the collision risk between vessels may increase as ships get closer. Action zone means that the distance from own ship is less than 6 miles, and if there is the collision risk between two vessels, the give-way vessel demands to take evasive action. Emergency zone refers to the zone with a distance less than 4 miles from own ship, if the collision risk is existing, the stand-on vessel ought to take evasive action to ensure navigation safety. To sum up, combining the urgency of collision avoidance with DCPA and TCPA, the evasive action can be determined as the following two situations.
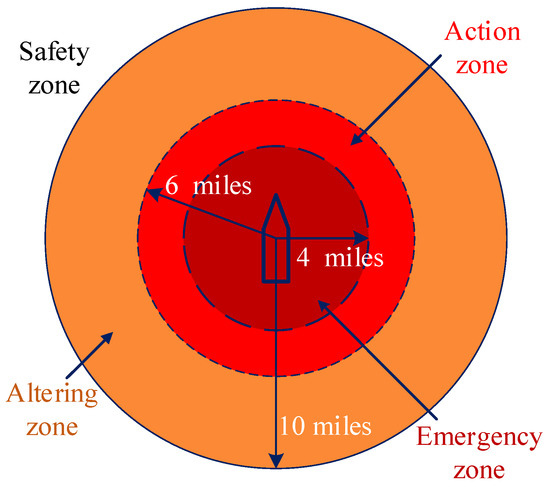
Figure 2.
The subdivision of area around the ship.
- (1)
- In the action zone, if , the give-way vessel requires to take evasive action;
- (2)
- In the emergency zone, if , the stand-on vessel demands to take evasive action to guarantee navigation safety.
2.2.3. The Evasive Action of the Give-Way Vessel
According to COLREGS, the evasive action taken by the give-way vessel requires to be timely and clearly to be detected by the stand-on vessel. If the give-way vessel alters course to avert collision, the course alteration ought to be dramatic. The evasive action of the give-way vessel is described in Figure 3. The OS and TS represent own ship and target ship; is the optional course alteration; is the number of the TS that OS requires to give way; is the course difference between the current ship course and the true bearing.
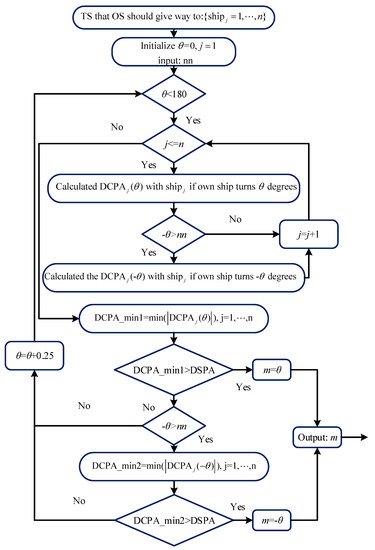
Figure 3.
The evasive action of the give-way vessel.
The evasive action of the give-way vessel is described as
- (1)
- Distinguish the give-way vessel and stand-on vessel. In the alerting zone and action zone, the OS is regarded as the give-way vessel, the TS which has collision risk with OS is deemed as the stand-on vessel;
- (2)
- Calculate and . After own ship turns degrees, the between OS and each TS is recalculated; if , the between OS and each TS after OS turns degrees is calculated;
- (3)
- Determine the safe course alteration based on DSPA. If , then is the safe course alteration; similarly, if , then is the safe course alteration; otherwise, the course alteration will increase 0.25 degrees, and back to step 2.
2.2.4. The Evasive Action of the Stand-On Vessel
Based on COLREGS, the stand-on vessel requires to maintain the velocity at the beginning of collision avoidance, however, if the give-way vessel breaches the rules, the stand-on vessel demands to take the appropriate evasive action. In this paper, if the give-way vessel enters the emergency zone of the stand-on vessel and the collision risk still exists, at the point, the stand-on vessel ought to take the evasive action. The detailed steps of the stand-on vessel to decide the evasive action is described in Figure 4. Similarly, the evasive action of the stand-on vessel is described as three steps as well as the give-way vessel, however, there is no limit of portside turning, because the ship can turn to portside or starboard side in the emergency zone.
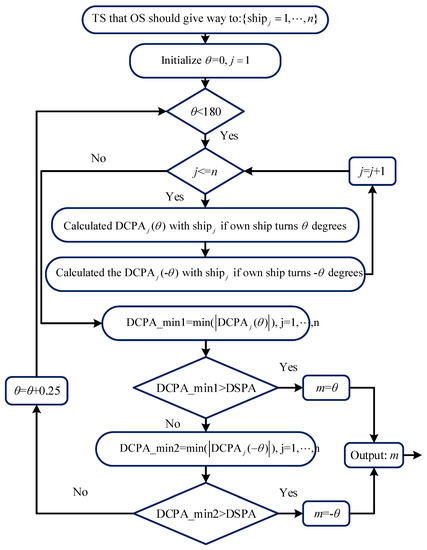
Figure 4.
The evasive action of the stand-on vessel.
2.3. Problem Formulation
A COLREGS-complied automatic collision avoidance strategy of multiple vessels is presented herein, and the design block diagram is shown in Figure 5. A COLREGS-complied real-time evasive action decision-making mechanism is firstly established. Specifically, the collision risk of multiple vessels is evaluated by the real-time DCPA and TCPA, and if there is collision risk, path-following of multiple vessels is achieved based on the LOS algorithm, which can calculate the desired course to make ship- follow the planned route before collision avoidance. Then, if there is collision risk, based on COLREGS, the evasive action can be determined from the give-way vessel and stand-on vessel. Meanwhile, on the strength of the current position and the desired position after collision avoidance, the desired course after collision avoidance is calculated by atan2 function. Furthermore, the situation which ships against COLREGS is taken into consideration herein. Finally, a novel automatic collision avoidance controller on account of MPC is devised, which can carry out control action beforehand and solve the problem of rudder saturation.
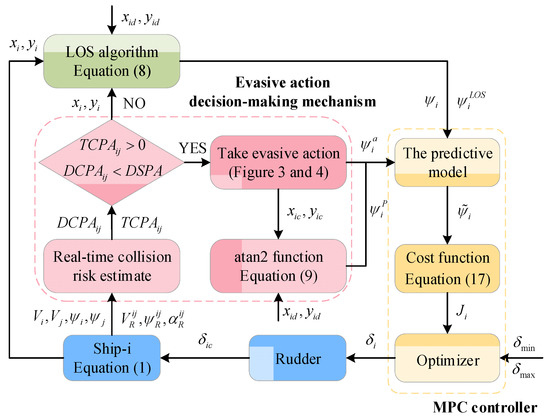
Figure 5.
The diagram of COLREGS-complied real-time automatic collision avoidance strategy.
3. Controller Design
The desired course is described as follows
here represents the desired course before collision avoidance, which can be calculated by the LOS algorithm [32,33,34].
where, denotes the position of LOS point; is the current position of before collision avoidance.
here, denotes the desired course after collision avoidance; represents the position of desired point; is the current position of after collision avoidance.
Generally, each ship should alter the course to the desired angle in the fastest way. Because the range of desired course and ship course is , Equation (7) is transformed as.
To alleviate the influence of large inertia and input constraints in collision avoidance, a novel automatic collision avoidance controller on the strength of MPC is devised, owing to its virtues of the forecasting ability and solving input constraints, which can carry out the control action beforehand and solve the input saturation [35,36].
By linearizing Equation (1), the model is transformed as
here , , before collision avoidance , and after collision avoidance, here, is the current course with the action of collision avoidance, and , here, is the course alteration of give-way and stand-on vessel determined by Figure 3 and Figure 4; , , , and are constants; is rudder input.
On account of a sampling time, Equation (11) is discretized as
Given as input horizon, as prediction horizon, and the future input . The future state sequence is expressed as
According to the future state sequence, the future output sequence is described as
The following vector is described as
For convenience, Equation (15) is expressed as
where , .
The cost function can be written as
here, , ; and are the weighting matrices.
It is worth noting that Equation (17) is subjected to the following condition.
4. Simulation Results
In this part, the simulations of four different scenarios in encounter situations of four ships are carried out to testify the effectiveness of the presented COLREGS-complied automatic collision avoidance strategy of multiple vessels. Specifically, the first simulation scenario is that all ships in the encounter situation follow the presented strategy; the second scenario is that all ships observe the presented strategy, except for ship-4; and the third simulation scenario is that only ship-1 abides by the presented strategy and the other ships keep the velocity and course; the last simulation is carried out in scenario 3 under environment disturbances. Note that a high-fidelity ship model is used in the simulations and the specific parameters are described in Ref. [27]. The parameters of the presented controller are set as , , , and .
4.1. The Effectiveness of the Presented Strategy in Scenario 1
In this part, the simulation in scenario 1 is conducted to validate the effectiveness of the presented strategy, in which all ships in the encounter situation are required to follow the presented strategy. The initial state of the four ships is described in Table 1 and the initial velocity of all ships is 15 knots.

Table 1.
The initial state of four ships in scenario 1.
Figure 6 denotes the initial situation of four ships in scenario 1; Figure 7, Figure 8, Figure 9 and Figure 10 show the situation of four ships in scenario 1 at 600 s, 1200 s, 2400 s, and 3200 s; and Figure 11 indicates the distance between two ships. As seen in Figure 6, the distance between any two ships is more than 6 miles, which means that no evasive action is required to be taken and four ships in scenario 1 sail on the planned route. However, with time going on, the distance is decreasing, which can raise the collision risk, and once the collision risk is higher than the threshold value, the evasive action ought to be taken. According to the rule 15 of COLREGS, ship-1 and ship-3 are in a crossing situation and ship-1 should give way to ship-3; similarly, ship-3 demands to keep away from ship-2, ship-2 requires to remove from ship-4, and ship-4 should stand off ship-1. It is shown in the simulation results that each ship in scenario 1 takes evasive action based on COLREGS, and in Figure 11, the minimal distance between any two ships is not less than 1 mile, which means that the navigation safety of each ship can be guaranteed. Furthermore, whether before or after collision avoidance, four ships can navigate to the next waypoint ().
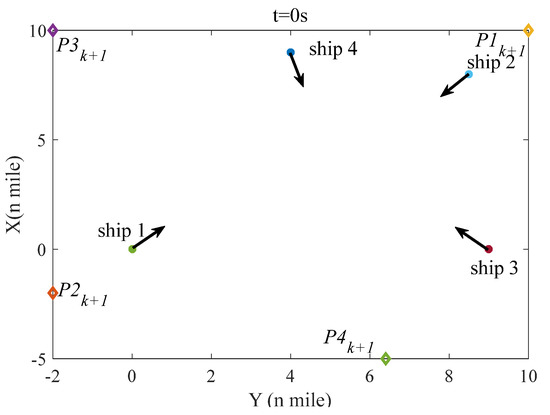
Figure 6.
The initial situation of four ships in scenario 1.
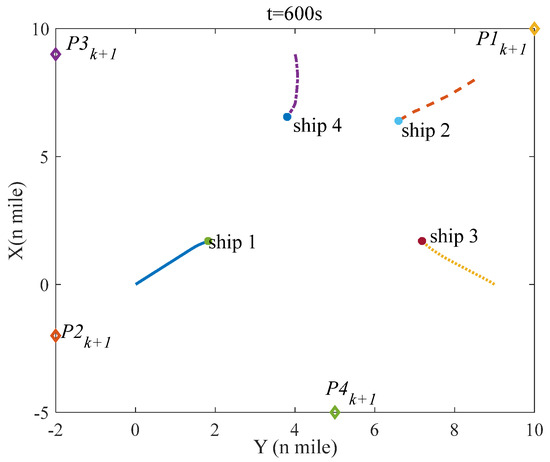
Figure 7.
The situation of four ships at t = 600 s in scenario 1.
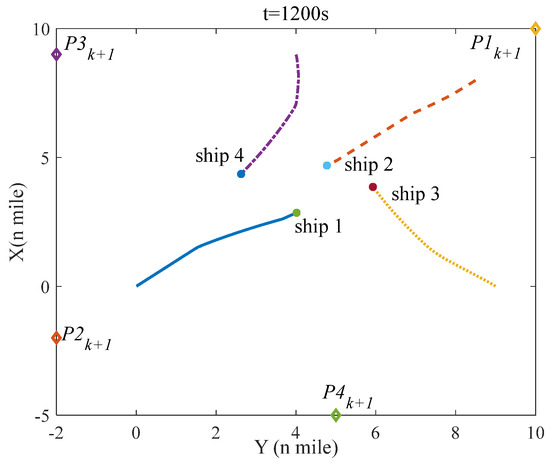
Figure 8.
The situation of four ships at t = 1200 s in scenario 1.
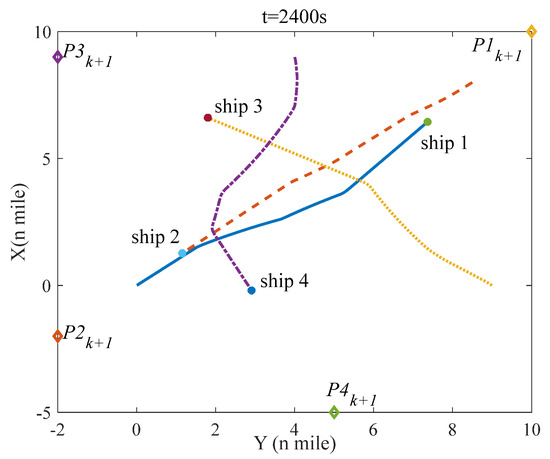
Figure 9.
The situation of four ships at t = 2400 s in scenario 1.
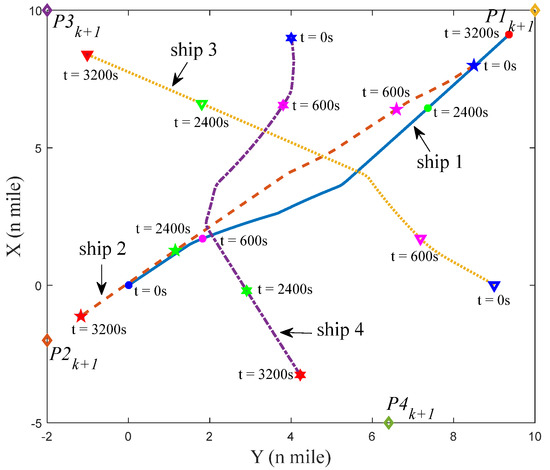
Figure 10.
The situation of four ships at t = 3200 s in scenario 1.
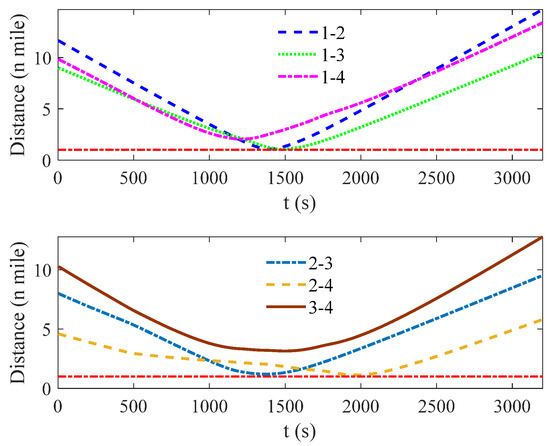
Figure 11.
The distance between two ships in scenario 1.
4.2. The Effectiveness of the Presented Strategy in Scenario 2
In scenario 2, all ships in the encounter situation comply with the presented strategy, except for ship–4. The initial state of the four ships is described in Table 2 and the initial velocity of all ships is 15 knots.

Table 2.
The initial state of four ships in scenarios 2 and 3.
Figure 12 shows the initial situation of four ships in scenario 2; Figure 13, Figure 14, Figure 15 and Figure 16 indicate the situation of four ships at 600 s, 1200 s, 2400 s, and 3200 s; and Figure 17 denotes the distance between two ships in scenario 2. The initial situation is the same as scenario 1, thus, the responsibility for collision avoidance of each ship is also the same. However, unlike scenario 1, ship–4 breaches COLREGS in scenario 2, and ship–4 is a give–way vessel but does not take evasive action and sails on the current velocity and course. Owing to the violations of ship–4, ship–1 as a stand–on vessel in a crossing situation ought to take evasive action based on rule 17 of COLREGS. As shown in the simulation results, ship–1 has taken the appropriate evasive action to keep away from ship–2 and ship–4, and Figure 17 shows that the minimal distance of any two ships is more than 1 mile, which ensures the navigation safety of each ship, and each ship can sail to the next waypoint ().
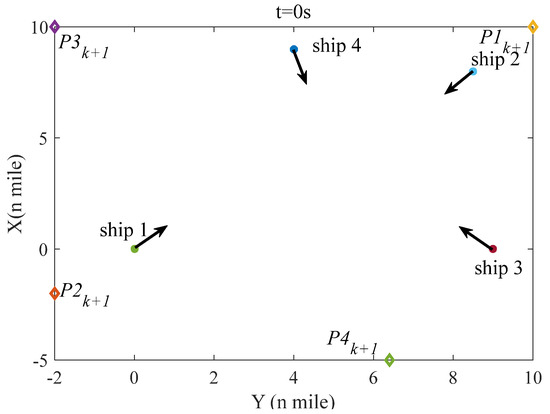
Figure 12.
The initial situation of four ships in scenario 2.
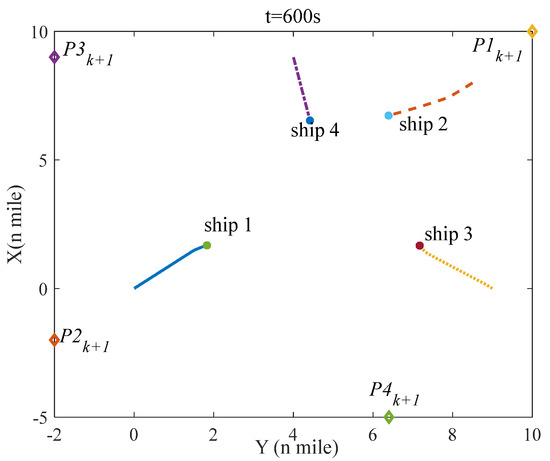
Figure 13.
The situation of four ships at t = 600 s in scenario 2.
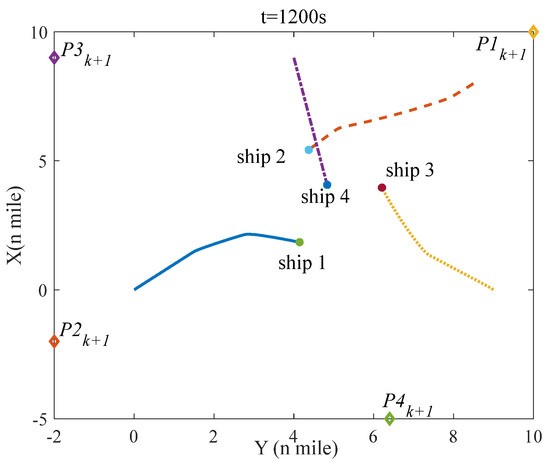
Figure 14.
The situation of four ships at t = 1200 s in scenario 2.
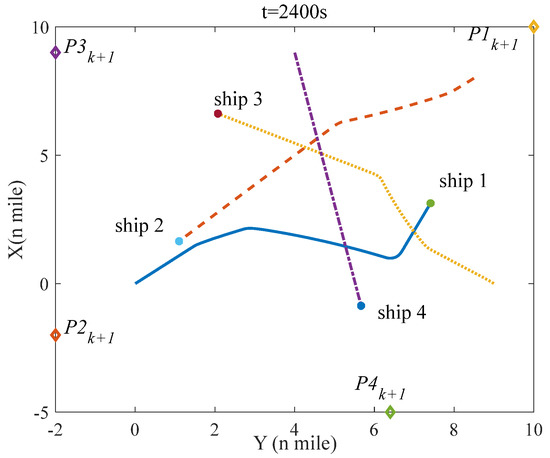
Figure 15.
The situation of four ships at t = 2400 s in scenario 2.
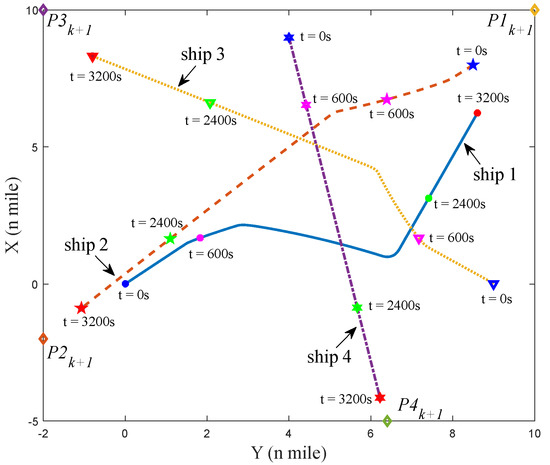
Figure 16.
The situation of four ships at t = 3200 s in scenario 2.
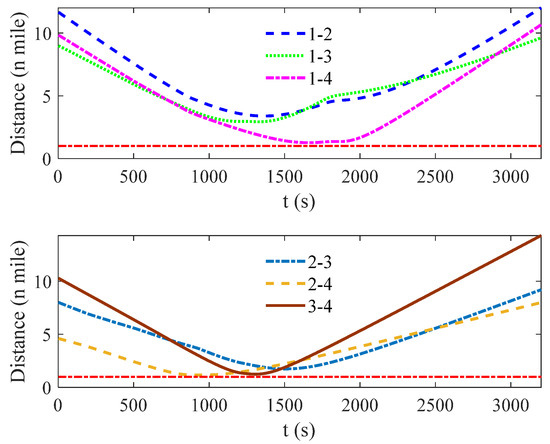
Figure 17.
The distance between any two ships in scenario 2.
4.3. The Effectiveness of the Presented Strategy in Scenario 3
The simulation in scenario 3 is carried out to validate the effectiveness of the presented COLREGS–complied automatic collision avoidance strategy in case some ships disregard the rules, in which only ship–1 complies with the presented strategy. The initial state of the four ships is described in Table 2, and the initial velocity of all ships is 15 knots.
Figure 18 indicates the initial situation of four ships in scenario 3; Figure 19, Figure 20 and Figure 21 denote the situation of the four ships in scenario 3 at 600 s, 2400 s, and 3200 s separately; Figure 22 denotes the distance between ship–1 and other ships; and Figure 23 indicates the course and rudder angle of ship–1. As we can see in Figure 19, Figure 20, Figure 21 and Figure 22, the distance between ship–1 and other ships is more than 1 mile, which means that the collision avoidance between ship–1 and other ships can be achieved, and after collision avoidance, ship–1 can navigate to the destination. From Figure 23, it can be concluded that the rudder angle of ship–1 is within the limitation.
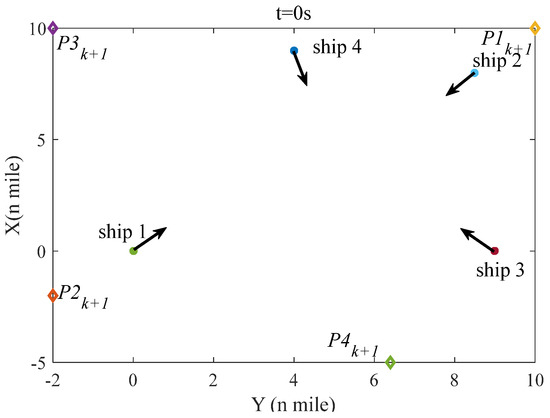
Figure 18.
The initial situation of four ships in scenario 3.
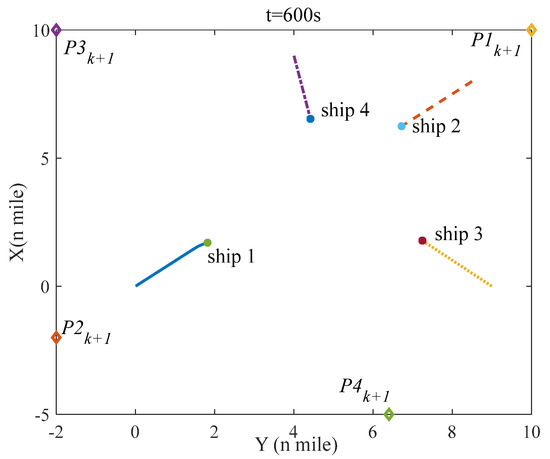
Figure 19.
The situation of four ships at t = 600 s in scenario 3.
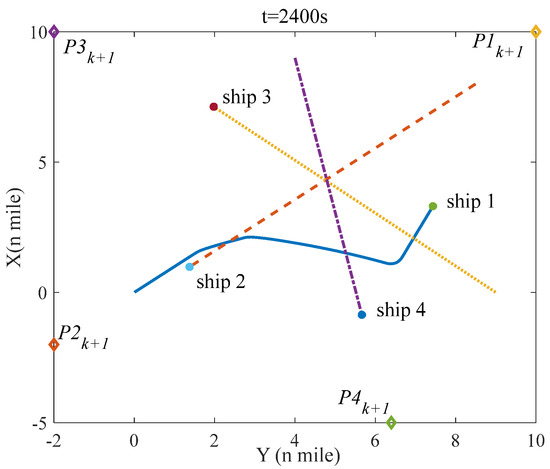
Figure 20.
The situation of four ships at t = 2400 s in scenario 3.
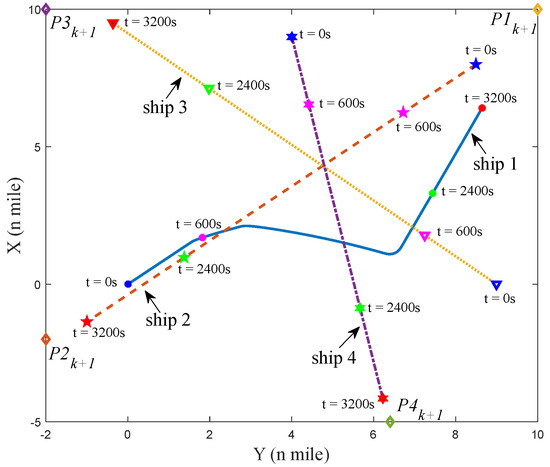
Figure 21.
The situation of four ships at t = 3200 s in scenario 3.
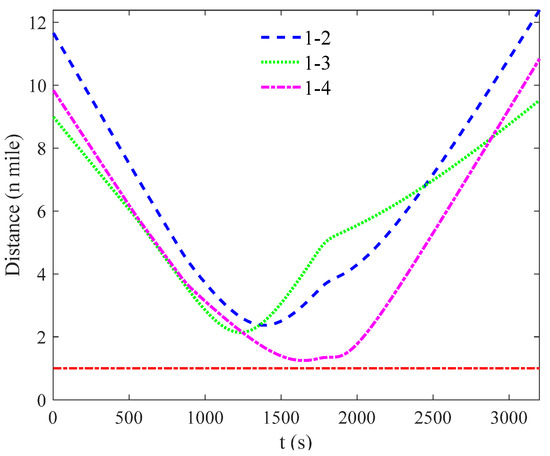
Figure 22.
The distance between ship–1 and other ships in scenario 3.

Figure 23.
The course and rudder angle of ship–1 in scenario 3.
In summary, the effectiveness of the presented COLREGS–complied automatic collision avoidance strategy for the encounter situations of multiple vessels has been illustrated in the above simulations.
4.4. The Effectiveness of the Presented Strategy in Scenario 3 under Environment Disturbance
Taking the environment disturbances into account [37,38], the simulation based on scenario 3 is carried out to validate the effectiveness of the presented strategy under environment disturbance. The disturbance is set as .
Figure 24 indicates the initial situation of four ships in scenario 3; Figure 25, Figure 26 and Figure 27 denote the situation of four ships in scenario 3 at 600 s, 2400 s, and 3200 s separately; Figure 28 denotes the distance between ship–1 and other ships; and Figure 29 indicates the course and rudder angle of ship–1. As we can see in Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28, the distance between ship–1 and other ships is more than 1 mile, which means that the collision avoidance between ship–1 and other ships can be achieved, and after collision avoidance, ship–1 can navigate to the destination. From Figure 29, it can be concluded that the rudder angle of ship–1 is within the limitation.
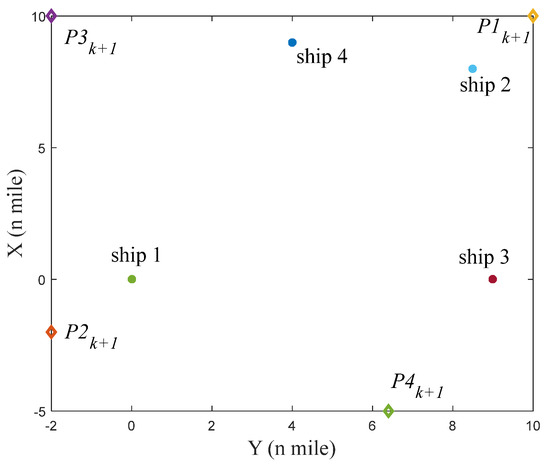
Figure 24.
The initial situation of four ships in scenario 3 under environment disturbance.
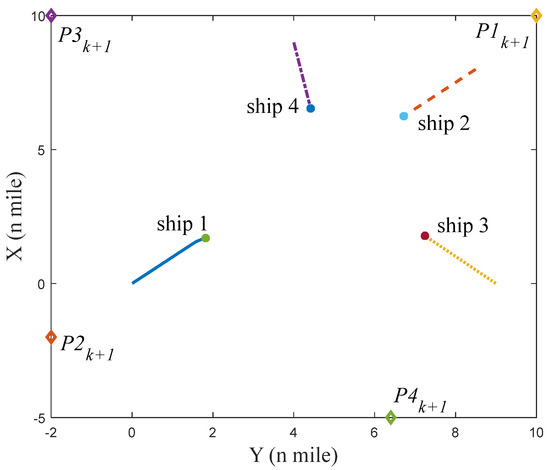
Figure 25.
The situation of four ships at t = 600 s in scenario 3 under environment disturbance.
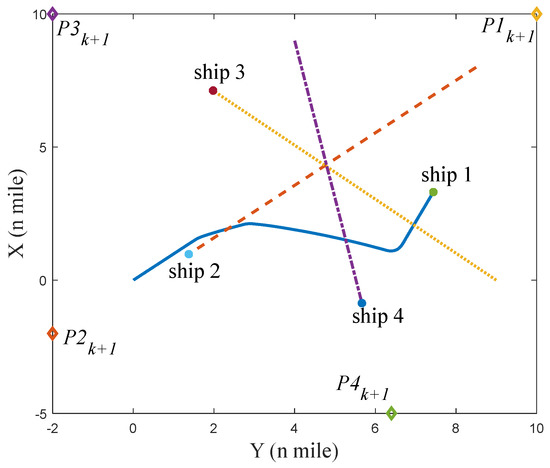
Figure 26.
The situation of four ships at t = 2400 s in scenario 3 under environment disturbance.
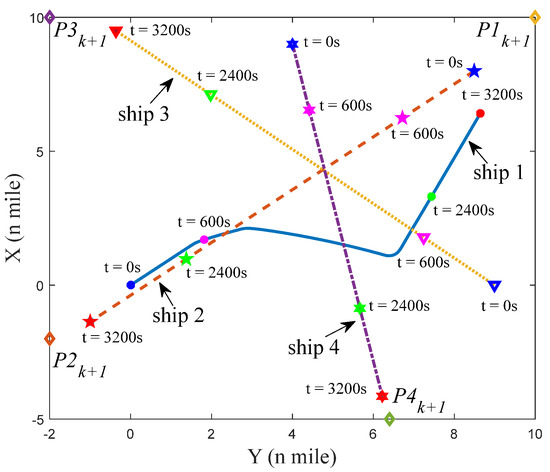
Figure 27.
The situation of four ships at t = 3200 s in scenario 3 under environment disturbance.
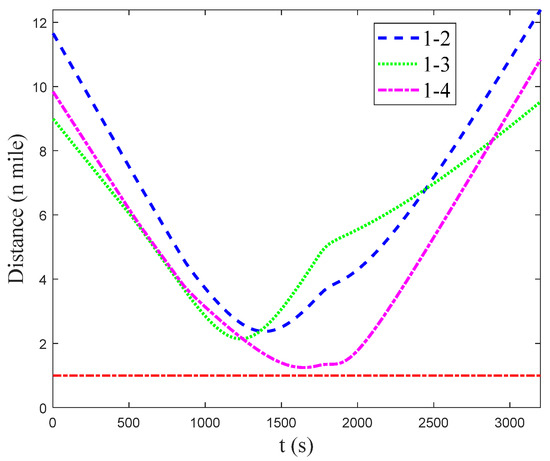
Figure 28.
The distance between ship–1 and other ships in scenario 3 under environment disturbance.
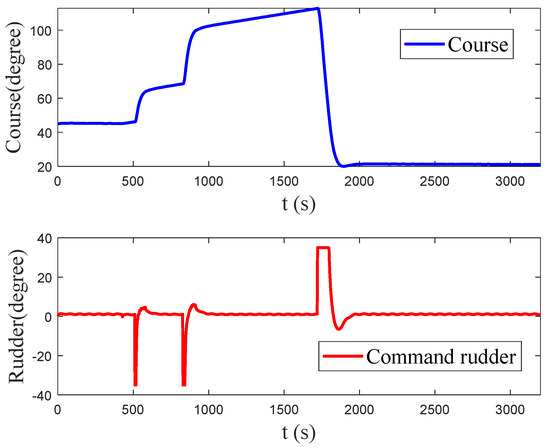
Figure 29.
The course and rudder angle of ship–1 in scenario 3 under environment disturbance.
In summary, the effectiveness of the presented COLREGS–complied automatic collision avoidance strategy for the encounter situations of multiple vessels has been illustrated in scenario 3 under environment disturbance.
5. Conclusions
In this paper, a COLREGS–complied automatic collision avoidance strategy for encounter situations of multiple vessels is presented. Firstly, a COLREGS–complied evasive action real–time decision–making mechanism is established, which can determine the evasive action from the give–way vessel and stand–on vessel separately. Furthermore, it is worth noting that the situation of ships against COLREGS is considered herein. Moreover, a novel automatic collision avoidance controller of multiple vessels on account of MPC is devised, presenting the advantages of forecasting ability and solving input constraints, with the ability to carry out control action beforehand and solve the problem of rudder saturation. Finally, the multiple simulations have validated the effectiveness of the presented COLREGS–complied automatic collision avoidance strategy.
Author Contributions
Conceptualization, C.L. (Cheng Liu), T.S., Q.H., S.X., and C.L. (Cheng Li); methodology, C.L. (Cheng Liu), T.S., C.L. (Cheng Li), and Q.H.; software, C.L. (Cheng Liu), Q.H., and C.L. (Cheng Li); validation, C.L. (Cheng Liu), T.S., and Q.H.; formal analysis, T.S., Q.H., and C.L. (Cheng Li); investigation, C.L. (Cheng Liu); resources, C.L. (Cheng Liu); data curation, T.S., Q.H., S.X., and C.L. (Cheng Li); writing—original draft preparation, T.S. and C.L. (Cheng Liu); writing—review and editing, T.S., C.L. (Cheng Liu) and S.X.; visualization, C.L. (Cheng Liu), T.S. and Q.H.; supervision, C.L. (Cheng Liu); project administration, C.L. (Cheng Liu); funding acquisition, C.L. (Cheng Liu) All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52101397, U1813203, U1801262, and 51879024; Funds for Dalian Distinguished Young Scholar, grant number 2020RQ014; Natural Science Foundation of Liaoning, grant number 20180520034; National Postdoctoral Program for Innovative Talent, grant number BX201700041 and Fundamental Research Funds of Central Universities, grant number 3132022127 and 3132021139.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.X.; Wang, H.B.; Guan, Z.Y.; Chong, P. Distributed Multi-Objective Algorithm for Preventing Multi-Ship Collisions at Sea. J. Navig. 2020, 73, 971–990. [Google Scholar] [CrossRef]
- Zhao, L.M.; Roh, M.L.; Lee, S.J. Control mothed for path following and collision avoidance of autonomous ship based on deep reinforcement learning. J. Mar. Sci. Technol. 2019, 27, 293–310. [Google Scholar]
- Tu, E.M.; Zhang, G.H.; Rachmawati, L.; Rajabally, E.; Huang, G.B. Exploiting AIS Data for Intelligent Maritime Navigation: A Comprehensive Survey. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1559–1582. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.F.; Chen, X.Q.; Chu, X.M.; Yan, X.P. A spatial-temporal forensic analysis for inland-water ship collisions using AIS data. Saf. Sci. 2013, 57, 187–202. [Google Scholar] [CrossRef]
- Pietrzykowski, Z.; Wołejsza, P.; Nozdrzykowski, Ł.; Borkowski, P. The autonomous navigation system of a sea-going vessel. Ocean Eng. 2022, 261, 112104. [Google Scholar] [CrossRef]
- Ramos, M.A.; Utne, I.B.; Mosleh, A. Collision avoidance on maritime autonomous surface ships: Operators’ tasks and human failure events. Saf. Sci. 2019, 116, 33–44. [Google Scholar] [CrossRef]
- Campbell, S.; Naeem, W.; Irwin, G.W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres. Annu. Rev. Control 2012, 36, 267–283. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, J. Real-time collision avoidance planning for unmanned surface vessels based on field theory. ISA Trans. 2020, 106, 233–242. [Google Scholar] [CrossRef]
- Woo, J.H.; Kim, N.K. Collision avoidance for an unmanned surface vehicle using deep reinforcement learning. Ocean Eng. 2020, 199, 107001. [Google Scholar] [CrossRef]
- Huang, Y.M.; Chen, L.Y.; Chen, P.F.; Negenborn, R.R.; van Gelder, P.H.A.J.M. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Lyu, H.G.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2018, 72, 588–608. [Google Scholar] [CrossRef]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Obstacle Avoidance Approaches for Autonomous Navigation of Unmanned Surface Vehicles. J. Navig. 2018, 71, 241–256. [Google Scholar] [CrossRef]
- Liu, Z.X.; Zhang, Y.M.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Zhang, R.B.; Tang, P.P.; Su, Y.M.; Li, X.Y.; Yang, G.; Shi, C.T. An Adaptive Obstacle Avoidance Algorithm for Unmanned Surface Vehicle in Complicated Marine Environments. IEEE/CAA J. Autom. Sin. 2014, 1, 385–396. [Google Scholar]
- Li, S.J.; Liu, J.L.; Negenborn, R.R. Distributed coordination for collision avoidance of multiple ships considering ship maneuverability. Ocean Eng. 2019, 181, 212–226. [Google Scholar] [CrossRef]
- Kim, D.; Hirayama, K.; Okimoto, T. Distributed Stochastic Search Algorithm for Multi-ship Encounter Situations. J. Navig. 2017, 70, 699–718. [Google Scholar] [CrossRef]
- Praczyk, T. Neural anti-collision system for Autonomous Surface Vehicle. Neurocomputing 2015, 149, 559–572. [Google Scholar] [CrossRef]
- Lisowski, J. Synthesis of a Path-Planning Algorithm for Autonomous Robots Moving in a Game Environment during Collision Avoidance. Electronics 2021, 10, 675. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, W. Concise deep reinforcement learning obstacle avoidance for underactuated unmanned marine vessels. Neurocomputing 2018, 272, 63–73. [Google Scholar] [CrossRef]
- Fang, M.C.; Tsai, K.Y.; Fang, C.C. A simplified simulation model of ship navigation for safety and collision avoidance in heavy traffic areas. J. Navig. 2018, 71, 837–860. [Google Scholar] [CrossRef]
- Song, L.; Su, B.Y.; Dong, C.Z.P.; Shen, D.W.; Xiang, E.Z.Q.; Mao, F.P.X. A two-level dynamic obstacle avoidance algorithm for unmanned surface vehicles. Ocean Eng. 2018, 170, 351–360. [Google Scholar] [CrossRef]
- Tsou, M.C. Multi-target collision avoidance route planning under an ECDIS framework. Ocean Eng. 2016, 121, 268–278. [Google Scholar] [CrossRef]
- Zhai, P.Y.; Zhang, Y.J.; Wang, S.B. Intelligent Ship Collision Avoidance Algorithm Based on DDQN with Prioritized Experience Replay under COLREGs. J. Mar. Sci. Eng. 2022, 10, 585. [Google Scholar] [CrossRef]
- Wang, W.X.; Liu, C. An efficient ship autopilot design using observer-based model predictive control. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2020, 235, 203–212. [Google Scholar] [CrossRef]
- Liu, C.; Li, C.; Li, W.H. Computationally efficient MPC for path following of underactuated marine vessels using projection neural network. Neural Comput. Appl. 2019, 32, 7455–7464. [Google Scholar] [CrossRef]
- Skorohod, B.A. Obstacles avoidance for autonomous marine vehicles based on the model predictive control. J. Phys. Conf. Ser. 2019, 1333, 042030. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
- Tsou, M.C.; Kao, S.L.; Su, C.M. Decision Support from Genetic Algorithms for Ship Collision Avoidance Route Planning and Alerts. J. Navig. 2010, 63, 167–182. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.J.; Cai, Y. The ship maneuverability based collision avoidance dynamic support system in close-quarters situation. Ocean Eng. 2017, 146, 486–497. [Google Scholar] [CrossRef]
- Naeem, W.; Irwin, G.W.; Yang, A. COLREGs-based collision avoidance strategies for unmanned surface vehicles. Mechatronics 2012, 22, 669–678. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.L. COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean Eng. 2019, 191, 106436. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Sun, L. Path following control for marine surface vessel with uncertainties and input saturation. Neurocomputing 2015, 177, 158–167. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.H. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles With Exact Sideslip Compensation. Ocean Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Oh, S.R.; Sun, J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Eng. 2010, 37, 289–295. [Google Scholar] [CrossRef]
- Wang, L.P. Model Predictive Control System Design and Implementation Using MATLAB; Springer: Berlin, Germany, 2009. [Google Scholar]
- Liu, C.; Sun, J.; Zou, Z.J. Integrated line of sight and model predictive control for path following and roll motion control using rudder. J. Ship Res. 2015, 59, 99–112. [Google Scholar] [CrossRef]
- Gao, Q.; Song, L.; Yao, J. RANS Prediction of Wave-Induced Ship Motions, and Steady Wave Forces and Moments in Regular Waves. J. Mar. Sci. Eng. 2021, 9, 1459. [Google Scholar] [CrossRef]
- Borkowski, P. Numerical Modeling of Wave Disturbances in the Process of Ship Movement Control. Algorithms 2018, 11, 130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).