A Study on the Vortex Induced Vibration of a Cylindrical Structure with Surface Bulges
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. SSTk-ω. Turbulence Model
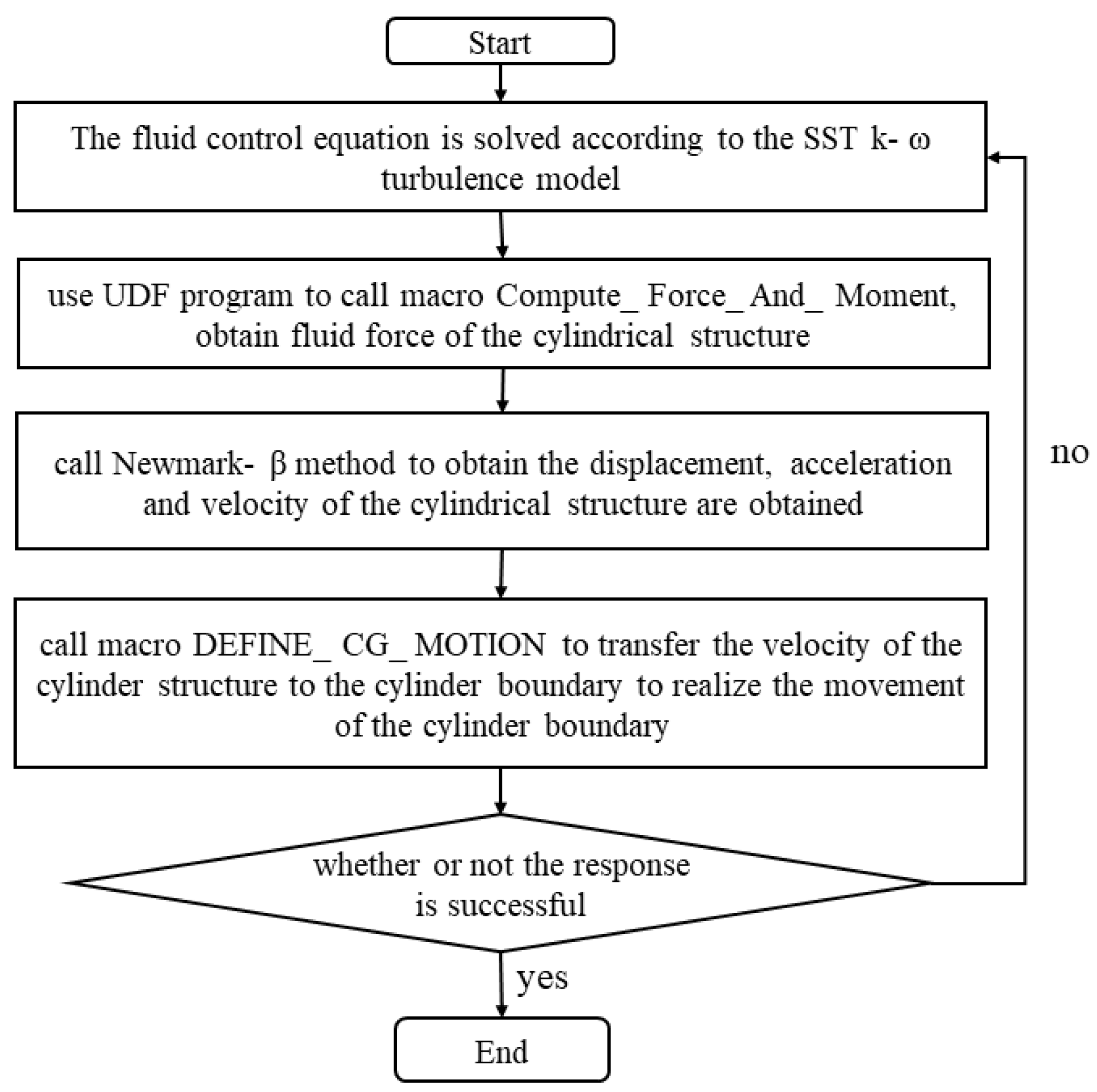
2.3. Kinematic Equations
- Step 1:
- Extract the forces in both streamwise and transverse direction by the macro Compute_Force_And_Moment;
- Step 2:
- Substitute the force in the right hand of Equation (16);
- Step 3:
- Calculate the displacement, acceleration, and velocity of the cylinder by Equations (18)–(20);
- Step 4:
- Assign the displacement and velocity to the centroid of the cylinder by the macro DEFINE_CG_MOTION.
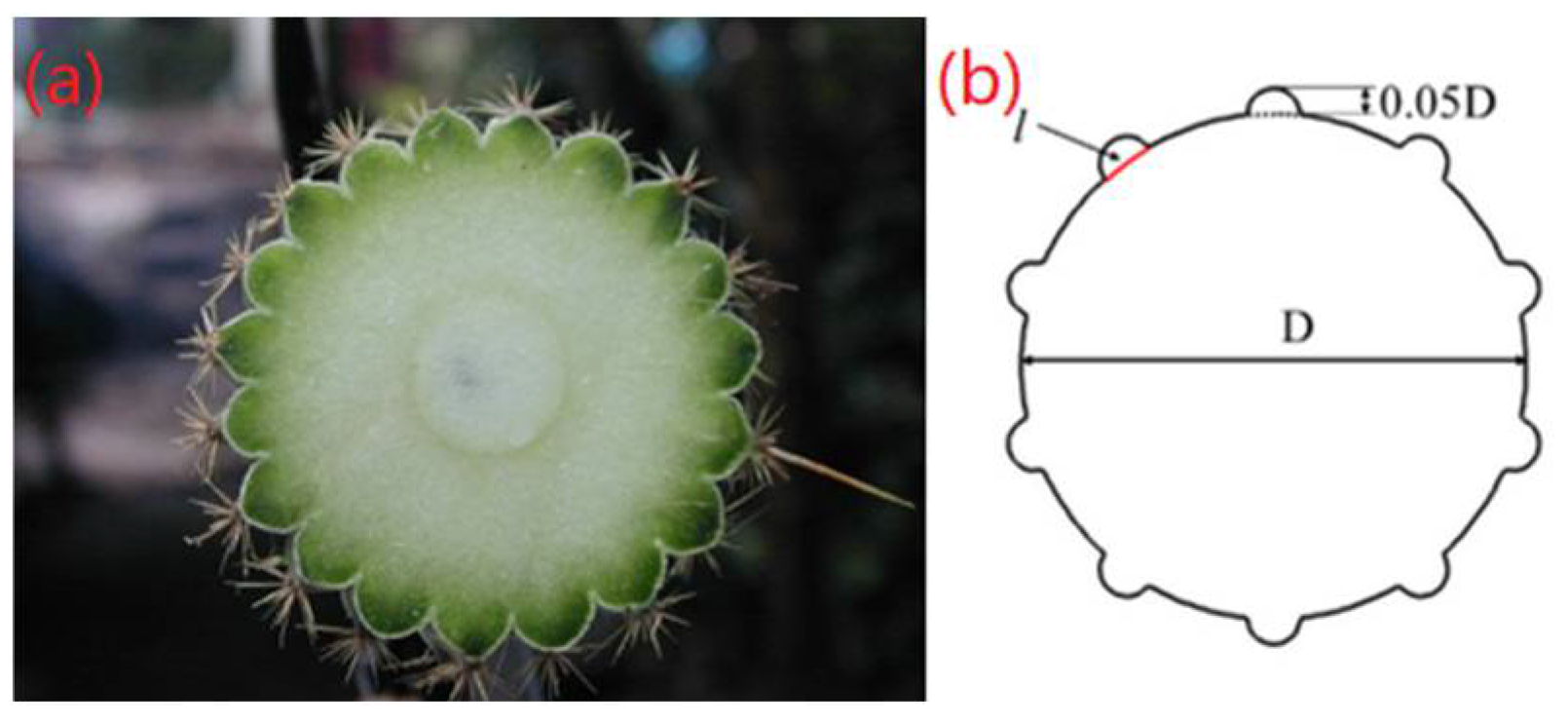
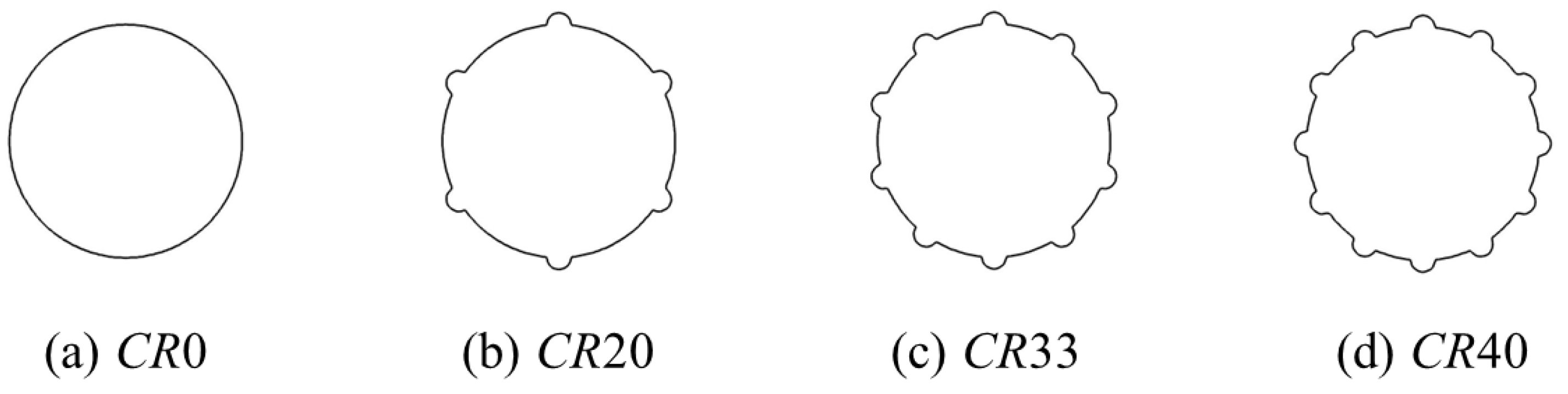
3. Computational Model
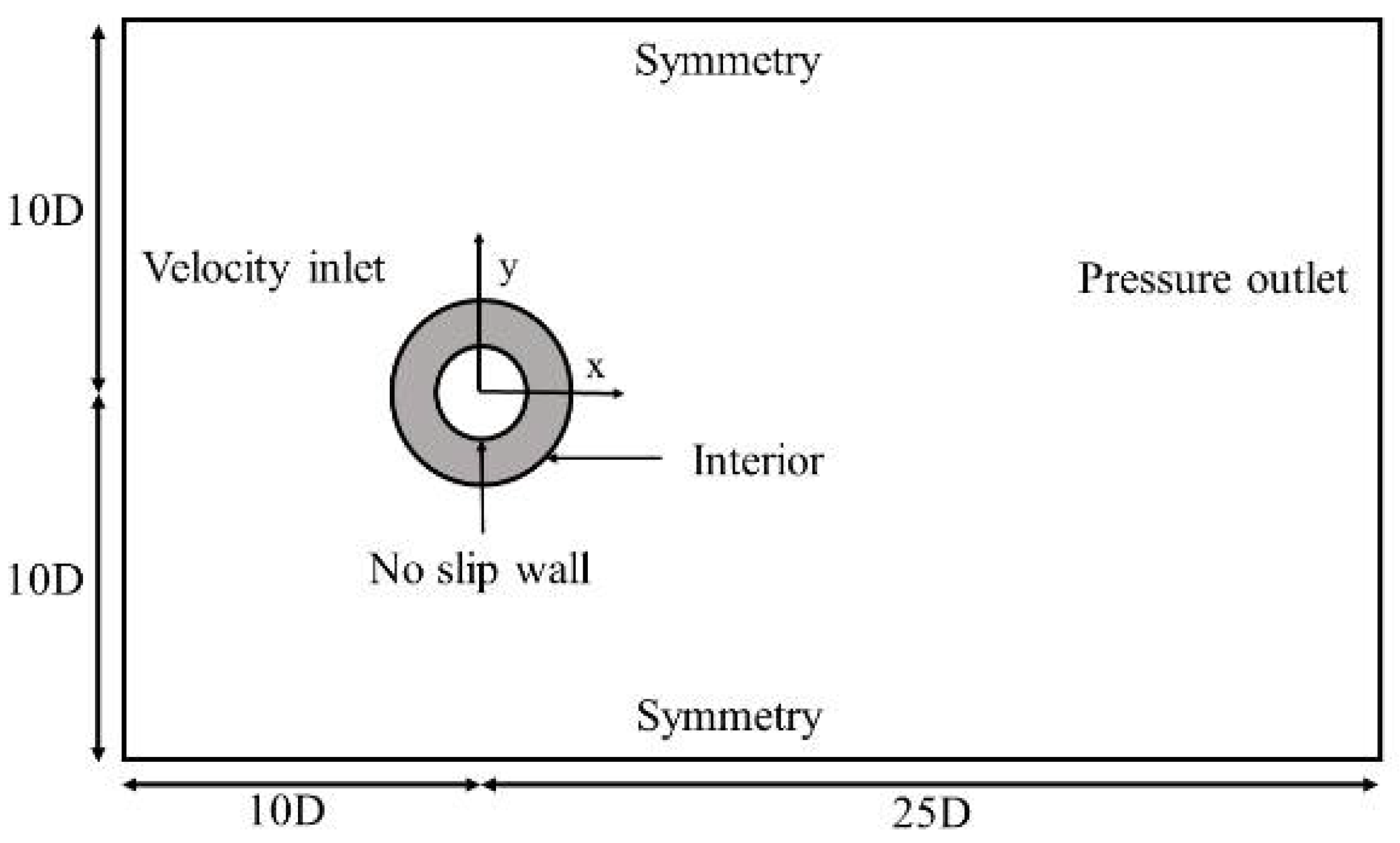
3.1. Computational Domain
3.2. Boundary Conditions
3.3. Mesh Setup
3.4. Mesh Independence Study
3.5. Numerical Method Validation
4. Results and Discussion
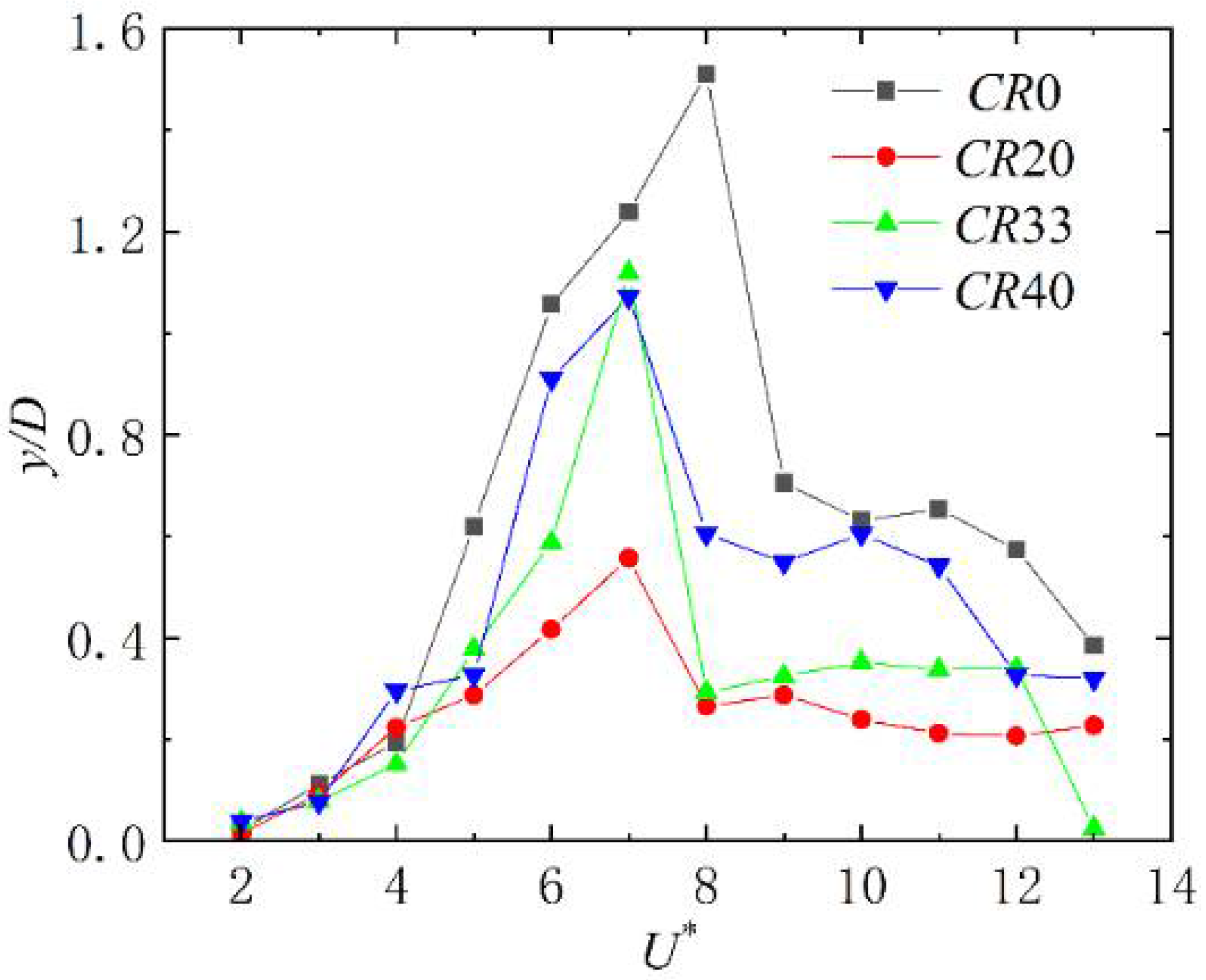
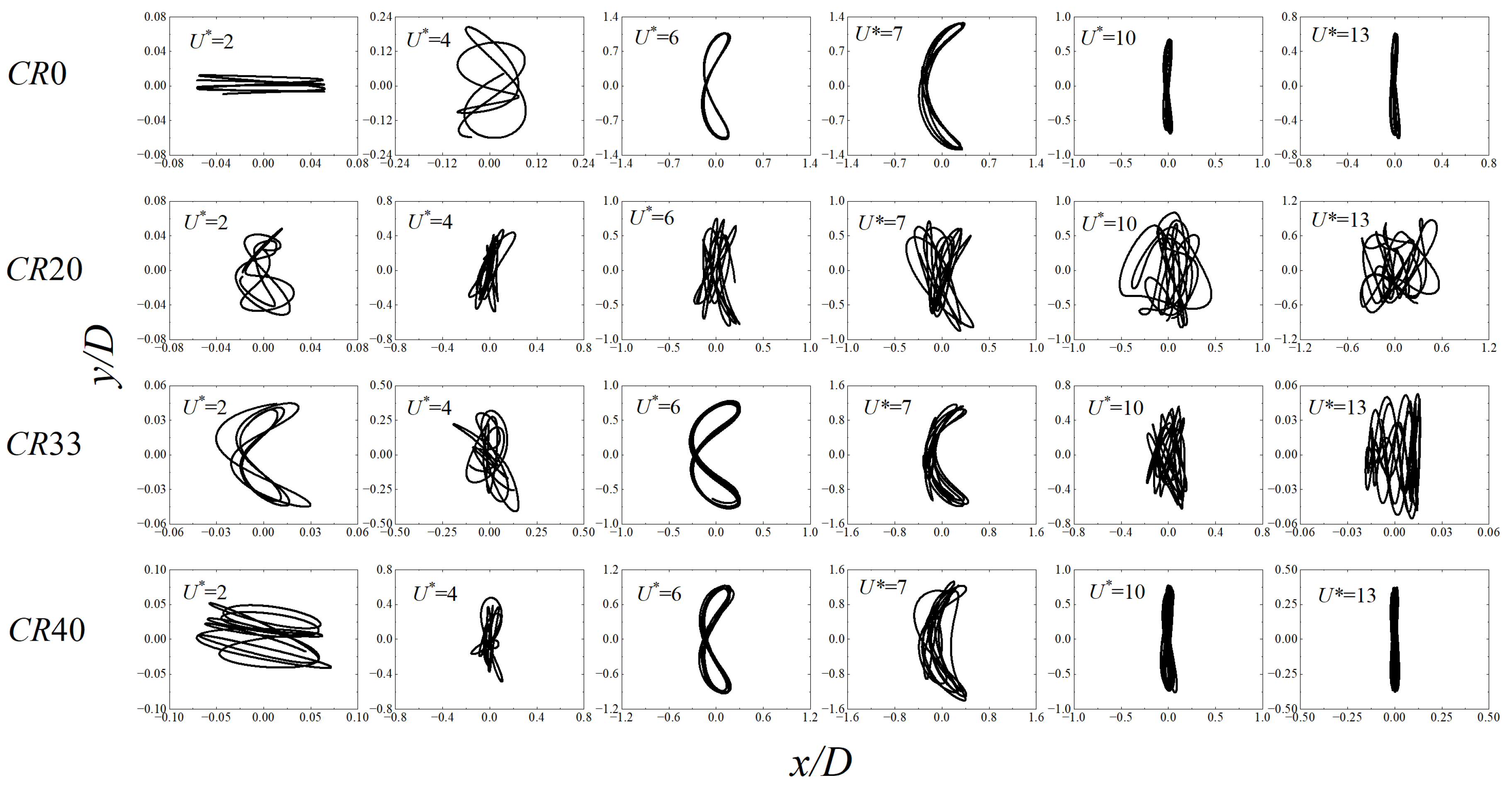
4.1. Vibration Amplitude
4.2. Motion Trajectory
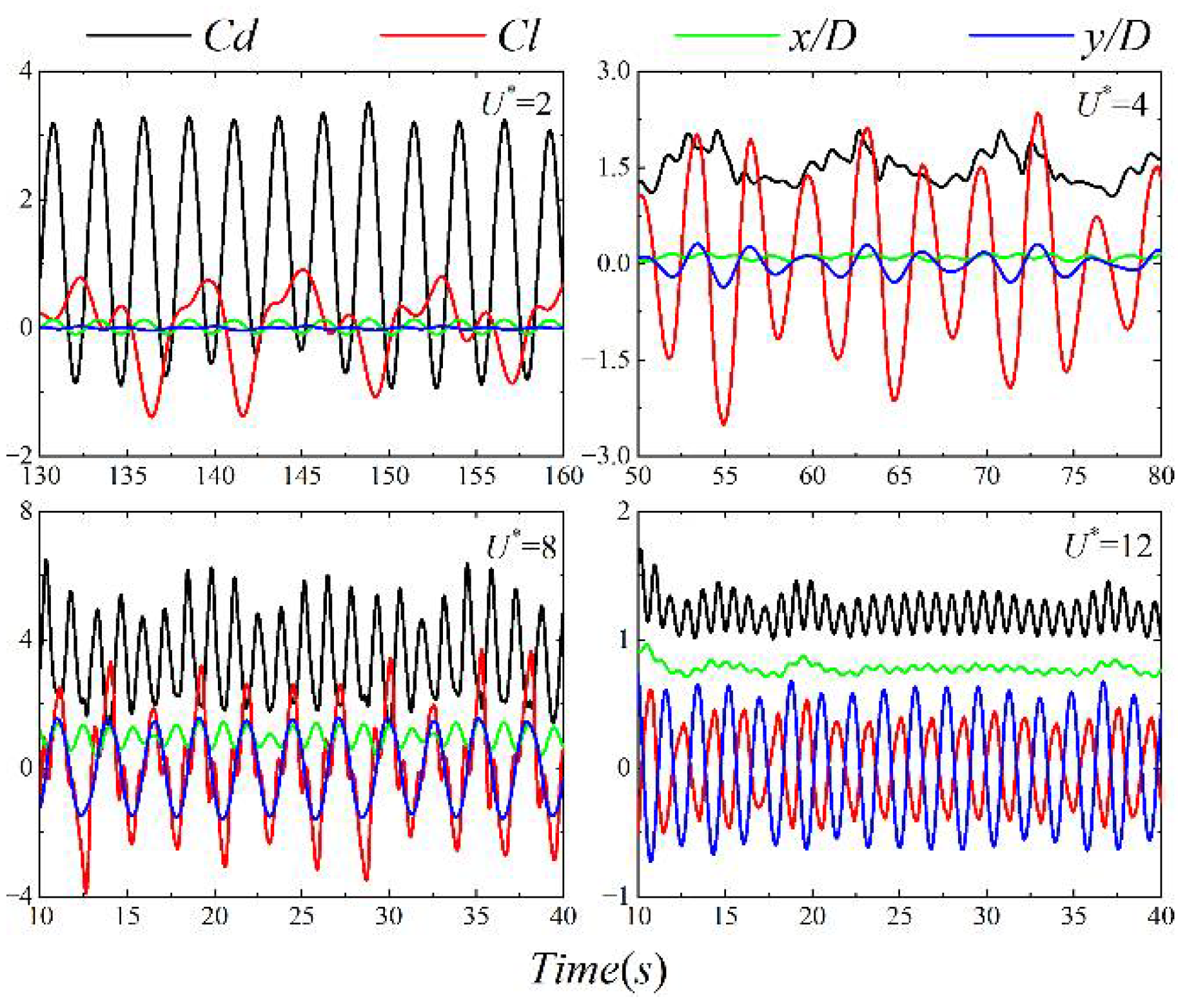
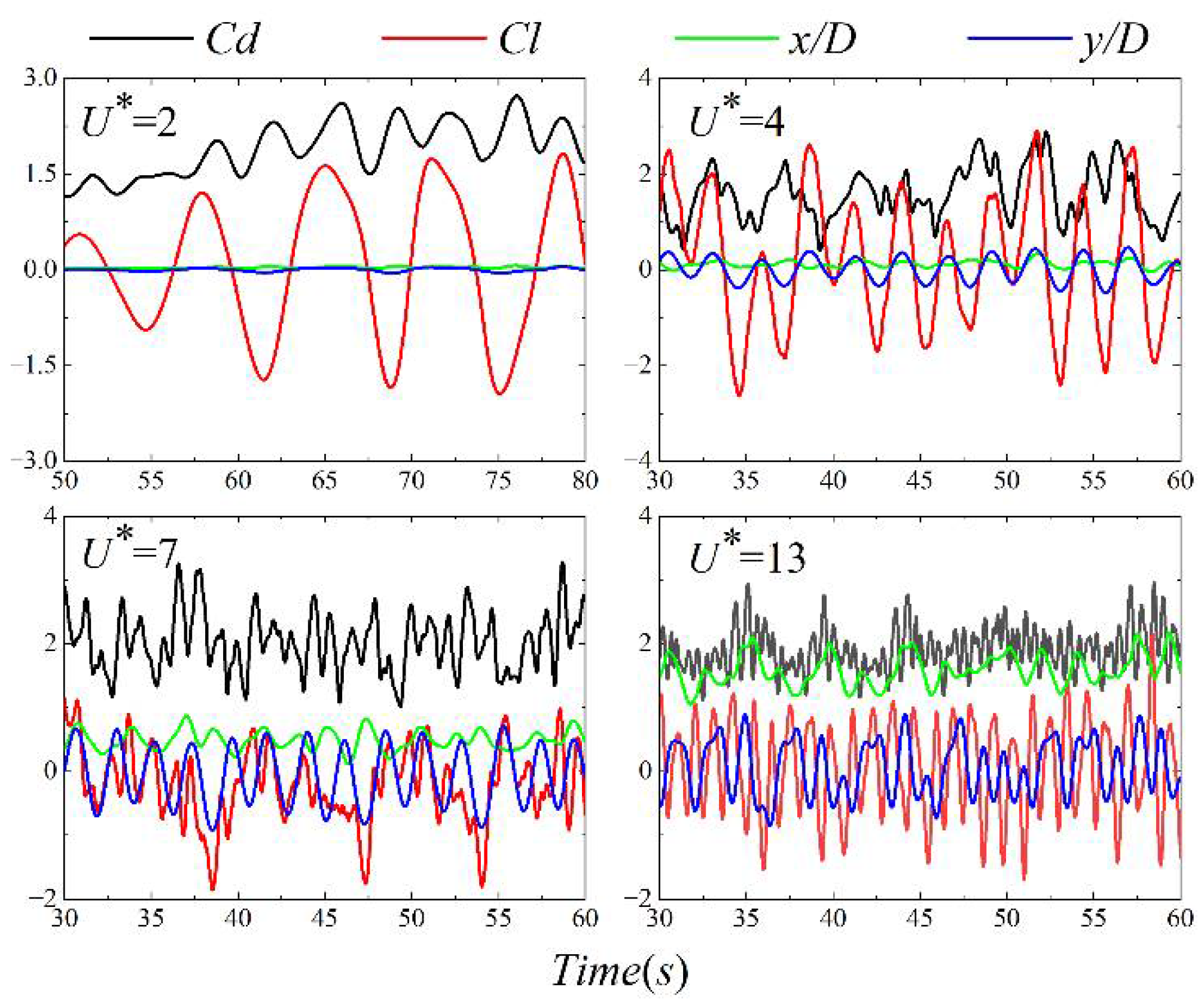
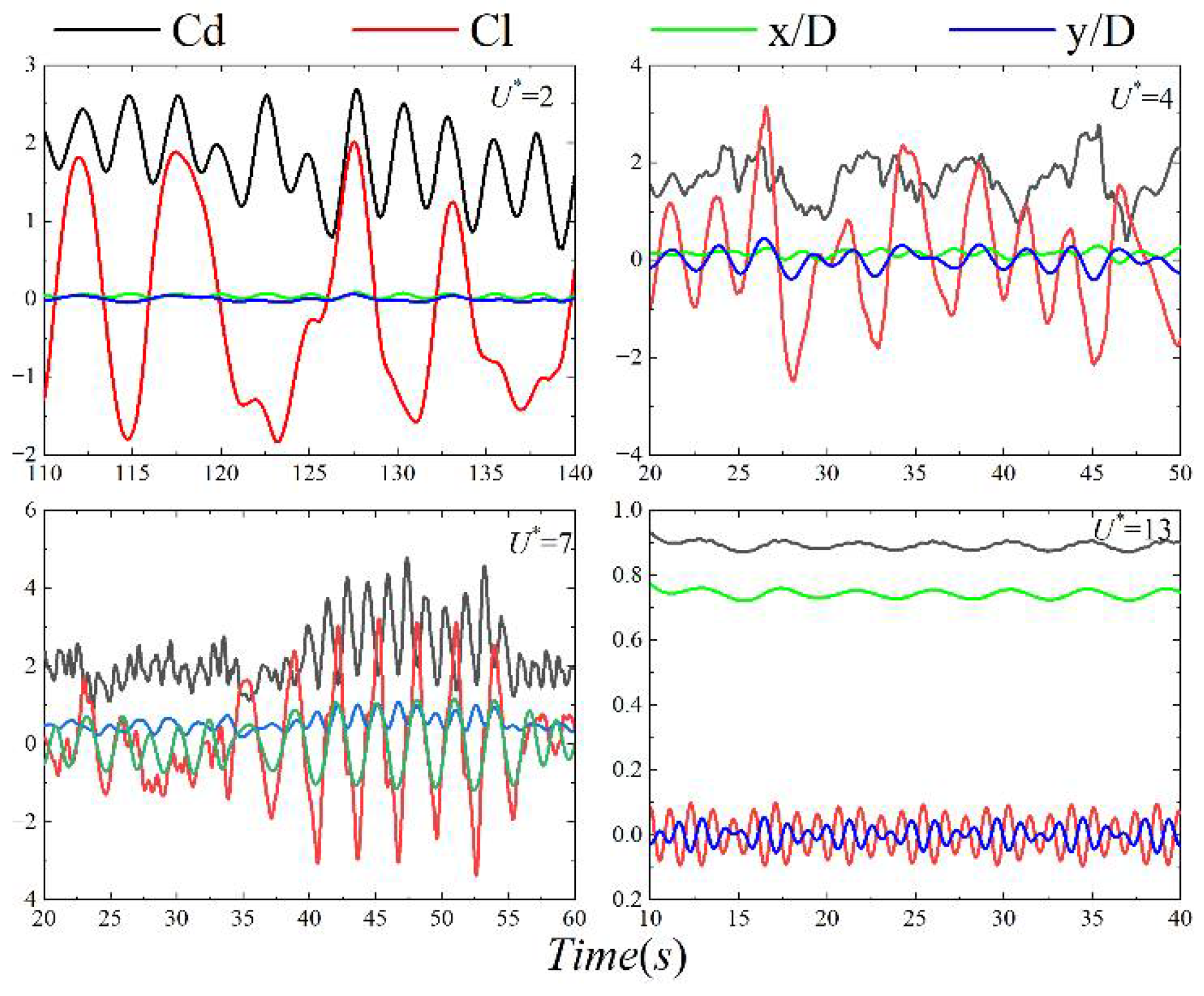
4.3. Force and Displacement of Structure
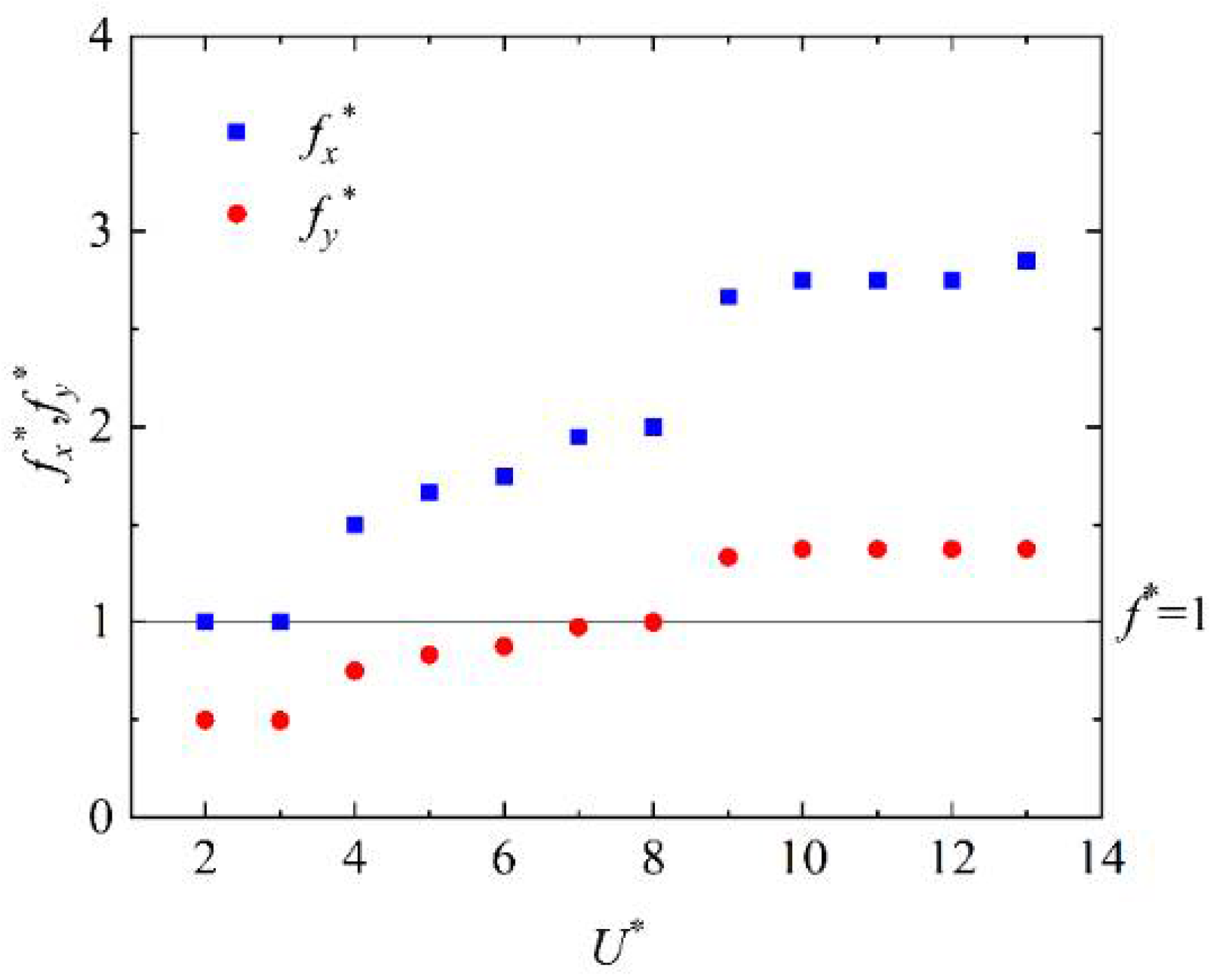
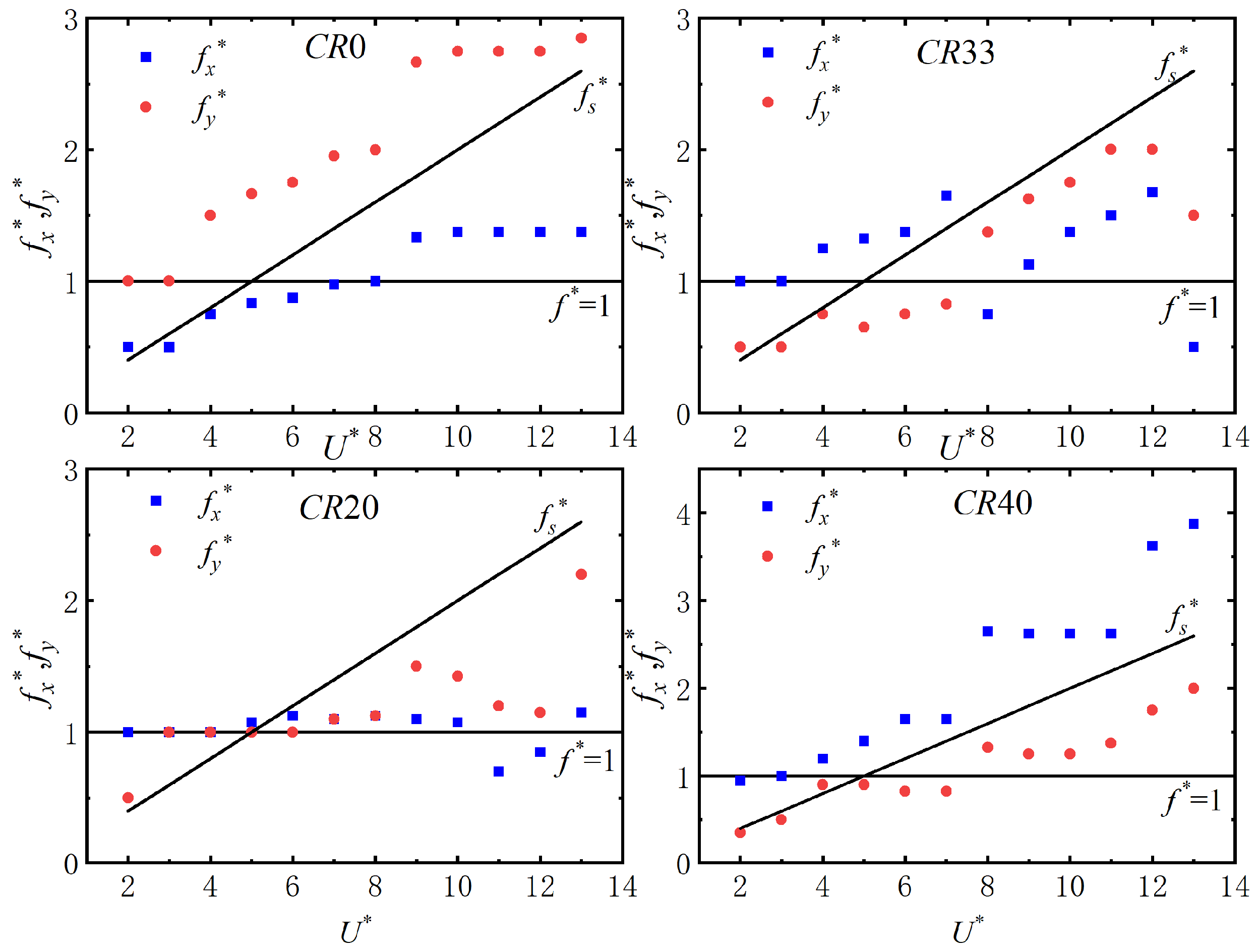
4.4. Vibration Frequency
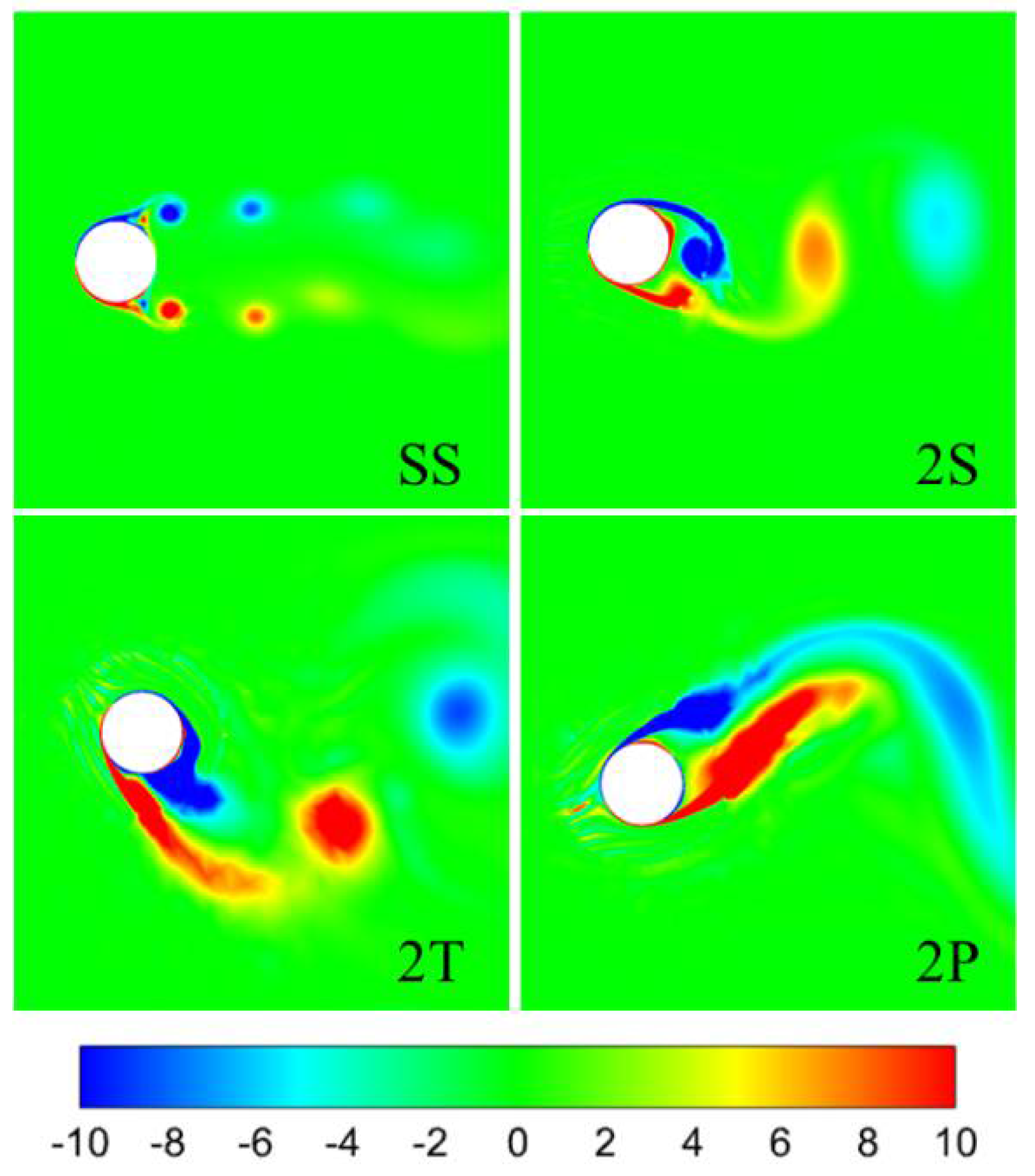
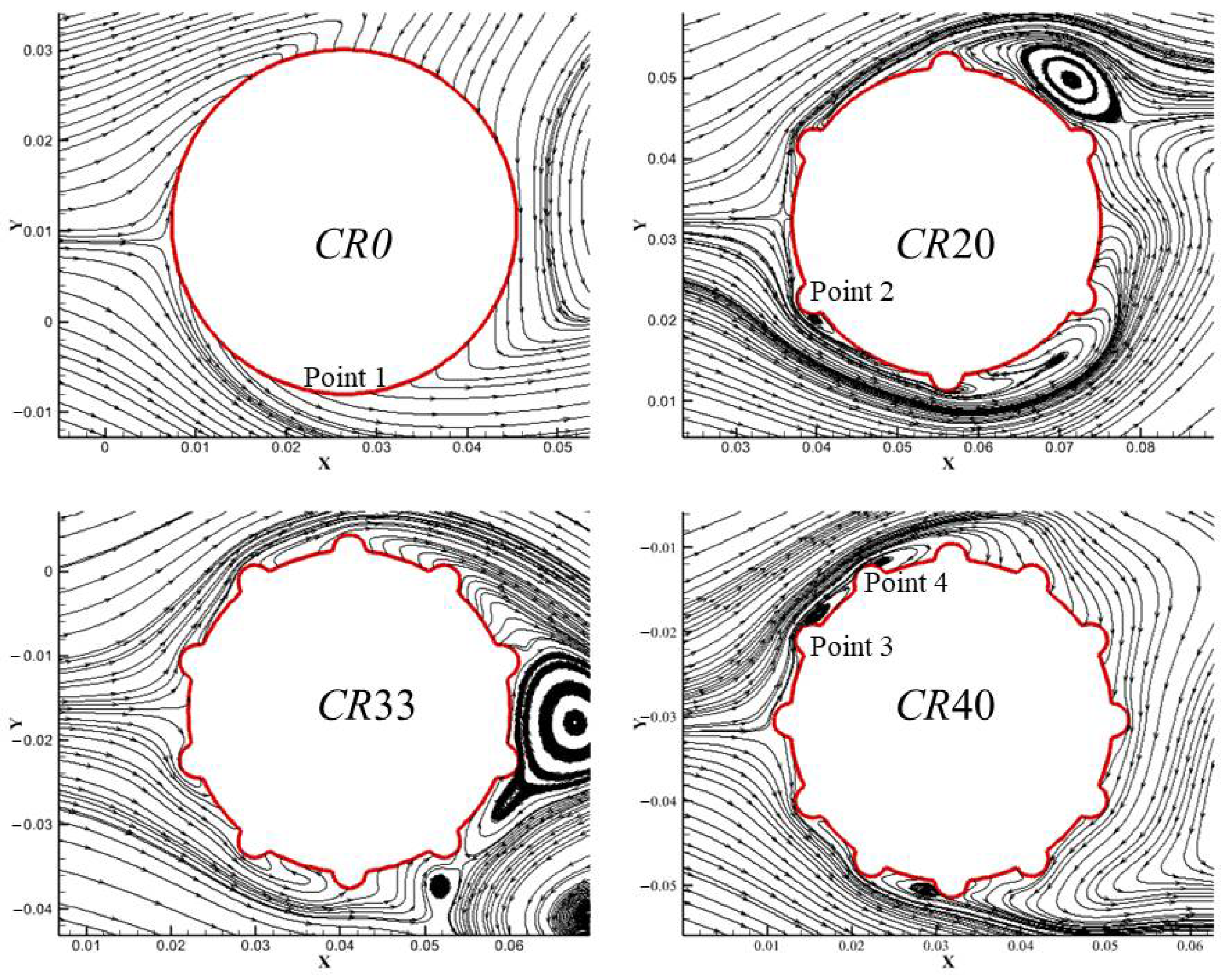
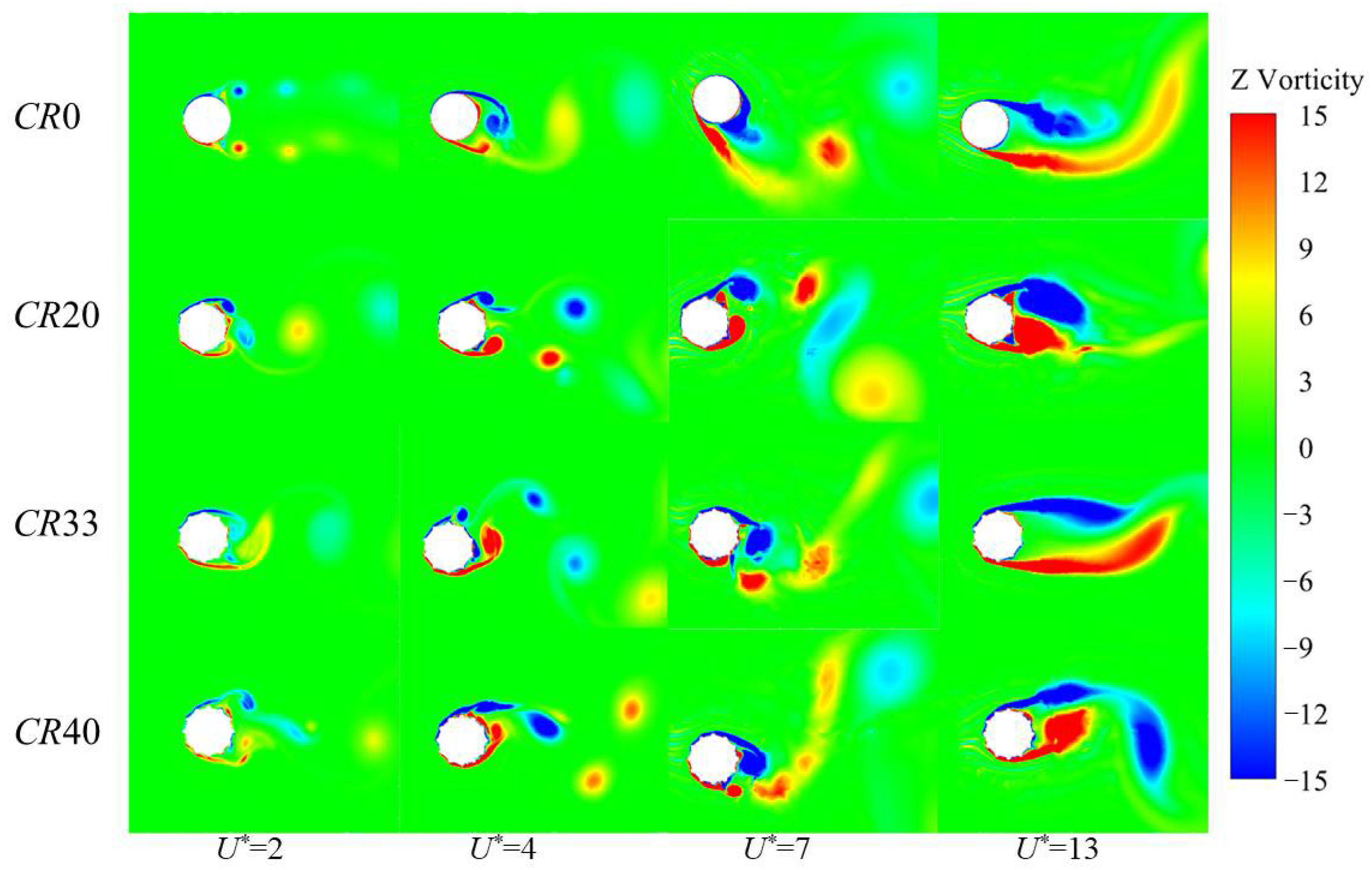
4.5. Streamline and Vorticity
5. Conclusions
- (1)
- The in-house code successfully captures the hydrodynamic characteristics of a cylinder with low mass ratio experiencing 2DOF VIV, including all response branches, i.e., the SS and SA branches in the streamwise direction and I, SU and L branch in the transverse direction, well-defined lock-in regime, wake modes, i.e., SS, 2S, 2T, 2P. The maximum transverse vibration amplitude reaches y/D = 1.51, which is consistent with the experimental results;
- (2)
- The VIV of a cylinder attached with surface bulges can be effectively suppressed. CR20 performs the best in VIV suppression and the suppression efficiency in streamwise and transverse direction are 44.6% and 63.1%, respectively. Moreover, the variation trend of CR40 is analogous to that of a smooth cylinder, which indicates that the VIV suppression capacity of surface bulges reaches its limitation, and a further increase in the coverage ratio will not achieve a better performance in VIV suppression;
- (3)
- The mechanism of a surface bulge on the VIV suppression is the shift of the separation point of the shear layer and vortices form between the surface bulges. For a cylinder with a low coverage ratio, the distance between the adjacent vortex is relatively small and a medium-size vortex forms between the surface bulges. The vibration of the structure is greatly affected by the near wall vortex. With the increase of coverage ratio, the separation point of the shear layer moves forward and the size of the vortex forms between the surface bulges decreases, which minimizes its influence on the vortex shedding. When the coverage ratio reaches 40%, the surface bulges are dense enough and the bulged cylinder can be simplified as a smooth circular cylinder with a diameter of 1.1 D, thus the hydrodynamic characteristics is similar to those of a smooth cylinder.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. A brief review of recent results in vortex-induced vibrations. J. Wind Eng. Ind. Aerodyn. 2008, 96, 713–735. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, W.; Zhang, X. An Overview on VIV of Slender Marine Structures. J. Ship Mech. 2005, 6, 135–154. [Google Scholar]
- Gabbai, R.D.; Benaroya, H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 2005, 282, 575–616. [Google Scholar] [CrossRef]
- Gad-el-Hak, M. Flow Control: Passive, Active, and Reactive Flow Management, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zhou, T.; Razali, S.F.M.; Hao, Z.; Cheng, L. On the study of vortex-induced vibration of a cylinder with helical strakes. J. Fluid Struct. 2011, 27, 903–917. [Google Scholar] [CrossRef]
- Shih, W.C.L.; Wang, C.; Coles, D.; Roshko, A. Experiments on Flow Past Rough Circular-Cylinders at Large Reynolds-Numbers. J. Wind Eng. Ind. Aerodyn. 1993, 49, 351–368. [Google Scholar] [CrossRef]
- Bianchi, V.; Silva, L.S.P.; Cenci, F.; Hirabayashi, S.; Suzuki, H.; Goncalves, R.T. Spoiler plate effects on the suppression of vortex-induced motions of a single circular cylinder. Ocean Eng. 2020, 210, 107569. [Google Scholar] [CrossRef]
- Xu, F.; Chen, W.L.; Xiao, Y.Q.; Li, H.; Ou, J.P. Numerical study on the suppression of the vortex-induced vibration of an elastically mounted cylinder by a traveling wave wall. J. Fluid Struct. 2014, 44, 145–165. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, J.; Yao, Z.; Liu, H.; Han, X. Vortex-induced vibration characteristics of a cylinder with additional rectifier. J. Vib. Shock 2022, 41, 121–127. [Google Scholar]
- Hwang, J.Y.; Yang, K.S.; Sun, S.H. Reduction of flow-induced forces on a circular cylinder using a detached splitter plate. Phys. Fluids 2003, 15, 2433–2436. [Google Scholar] [CrossRef]
- Díaz-Ojeda, H.R.; González, L.M.; Huera-Huarte, F.J. On the influence of the free surface on a stationary circular cylinder with a flexible splitter plate in laminar regime. J. Fluid Struct. 2019, 87, 102–123. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Teng, B.; Liang, D.F. Numerical simulation of viscous flow past two circular cylinders of different diameters. Appl. Ocean Res. 2005, 27, 39–55. [Google Scholar] [CrossRef]
- Assi, G.R.S.; Orselli, R.M.; Silva-Ortega, M. Control of vortex shedding from a circular cylinder surrounded by eight rotating wake-control cylinders at Re = 100. J. Fluid Struct. 2019, 89, 13–24. [Google Scholar] [CrossRef]
- Marcollo, H.; Potts, A.E.; Johnstone, D.R.; Pezet, P.; Kurts, P. Drag Reduction and Vortex-Induced Vibration Suppression Behavior of Longitudinally Grooved Suppression Technology Integral to Drilling Riser Buoyancy Units. J. Offshore Mech. Arct. 2018, 140, 061802. [Google Scholar] [CrossRef]
- Talley, S.; Mungal, G. Flow around cactus-shaped cylinders. Annu. Res. Briefs. Stanford University. Calif. 2002, 363–375. [Google Scholar]
- Wang, J.; Shi, C.; Liu, Y.; Bao, X. Simulations on Hydrodynamic Coefficients of Stationary Cactus-Shaped Cylinders at a Low Reynolds Number. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; ASME: Little Falls, NJ, USA, 2018. [Google Scholar]
- Qian, Q.; Wang, G. Numerical Simulation of Drag Reduction of V-Grooved Circular Cylinder at Subcritical Reynolds Number. Adv. Mar. Sci. 2019, 37, 150–160. [Google Scholar]
- Zhou, B.; Wang, X.; Guo, W.; Gho, W.M.; Tan, S.K. Experimental study on flow past a circular cylinder with rough surface. Ocean Eng. 2015, 109, 7–13. [Google Scholar] [CrossRef]
- Wang, W.; Song, B.; Mao, Z.; Tian, W.; Zhang, T. Numerical investigation on VIV suppression of the cylinder with the bionic surface inspired by giant cactus. Ocean Eng. 2020, 214, 107775. [Google Scholar] [CrossRef]
- Wang, W.; Mao, Z.; Song, B.; Han, P. Numerical investigation on vortex-induced vibration suppression of the cactus-inspired cylinder with some ribs. Phys. Fluids 2021, 33, 037127. [Google Scholar] [CrossRef]
- Jauvtis, N.; Williamson, C.H.K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar] [CrossRef]
- Pasetto, M.; Waisman, H.; Chen, J.S. A waveform relaxation Newmark method for structural dynamics problems. Comput. Mech. 2019, 63, 1223–1242. [Google Scholar] [CrossRef]
- Han, X. Numerical Simulation of Vortex Induced Vibration Mechanism of Marine Riser Considering Surface Roughness. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Gsell, S.; Bourguet, R.; Braza, M. Two-degree-of-freedom vortex-induced vibrations of a circular cylinder at Re = 3900. J. Fluid Struct. 2016, 67, 156–172. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, J.; Yao, Z.; Zhang, G.; Han, X.; Wang, X. Vortex-induced vibration of a cylinder downstream of an elliptical cylinder with different aspect ratios. J. Mar. Sci. Tech. Jpn 2020, 25, 1044–1062. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| Diameter of the cylinder D | 0.0381 | m |
| Mass ratio | 2.6 | - |
| Spring stiffness K | 25.86 | N/m |
| Damping ratio | 0.00381 | - |
| Natural frequency in water | 0.4 | Hz |
| Fluid density | 995.3 | kg/m3 |
| Kinematic viscosity | 7.877 × 10−6 | m2/s |
| Mesh | Node on the Circumference | y/D | 𝜺 |
|---|---|---|---|
| Mesh 1 | 160 | 0.542 | 26.5% |
| Mesh 2 | 240 | 0.595 | 19.3% |
| Mesh 3 | 320 | 0.698 | 5.3% |
| Mesh 4 | 320 | 0.706 | 4.2% |
| Mesh 5 | 400 | 0.672 | 8.8% |
| Exp. [20] | - | 0.737 | - |
| CR | xmax/D | ymax/D |
|---|---|---|
| 0 | 0.287 | 1.511 |
| 20 | 0.159 (44.6%) | 0.557 (63.1%) |
| 33 | 0.254 (11.5%) | 1.120 (25.9%) |
| 40 | 0.189 (34.1%) | 1.072 (29.1%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Wang, J.; Li, Z.; Liu, K.; Yu, J.; Zhou, B. A Study on the Vortex Induced Vibration of a Cylindrical Structure with Surface Bulges. J. Mar. Sci. Eng. 2022, 10, 1785. https://doi.org/10.3390/jmse10111785
Xu H, Wang J, Li Z, Liu K, Yu J, Zhou B. A Study on the Vortex Induced Vibration of a Cylindrical Structure with Surface Bulges. Journal of Marine Science and Engineering. 2022; 10(11):1785. https://doi.org/10.3390/jmse10111785
Chicago/Turabian StyleXu, Haoyuan, Jie Wang, Zhiqing Li, Kaihua Liu, Jiawei Yu, and Bo Zhou. 2022. "A Study on the Vortex Induced Vibration of a Cylindrical Structure with Surface Bulges" Journal of Marine Science and Engineering 10, no. 11: 1785. https://doi.org/10.3390/jmse10111785
APA StyleXu, H., Wang, J., Li, Z., Liu, K., Yu, J., & Zhou, B. (2022). A Study on the Vortex Induced Vibration of a Cylindrical Structure with Surface Bulges. Journal of Marine Science and Engineering, 10(11), 1785. https://doi.org/10.3390/jmse10111785











