Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials and Instruments
2.2. Test Method
3. Results and Analyses
3.1. Development Law of Axial Cumulative Strain
3.2. Development Law of Elastic Modulus
3.2.1. Influence of Confining Pressure
3.2.2. Influence of Cyclic Load Amplitude
3.2.3. Influence of Consolidation Stress Ratio
3.2.4. Influence of Cyclic Load Frequency
3.2.5. Influence of Compaction Degree
3.2.6. Influence of Water Content
3.3. Development Law of Damping Ratio
3.3.1. Influence of Confining Pressure
3.3.2. Influence of Cyclic Load Amplitude
3.3.3. Influence of Consolidation Stress Ratio
3.3.4. Influence of Cyclic Load Frequency
3.3.5. Influence of Compaction Degree
3.3.6. Influence of Water Content
4. Evolution Model
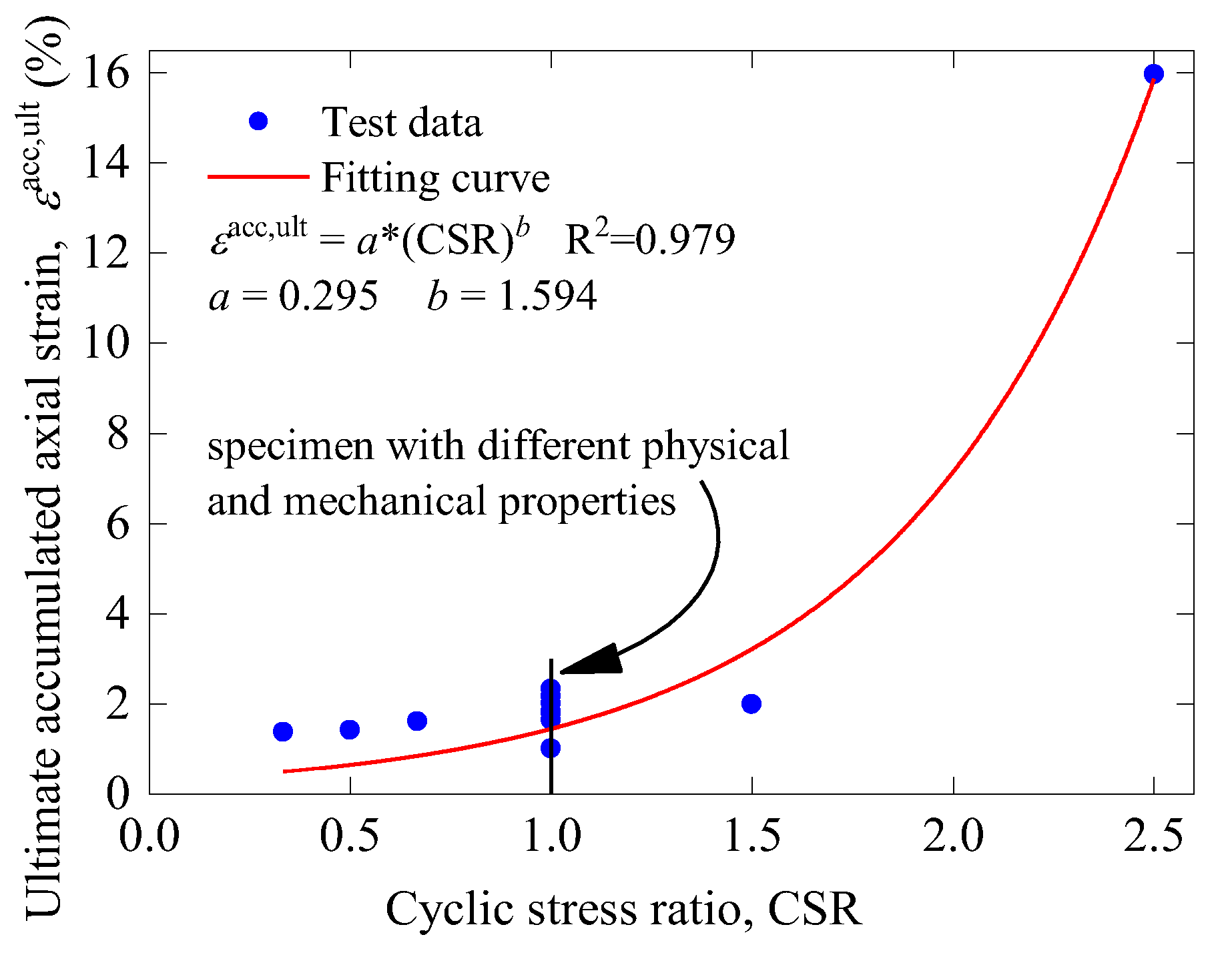
4.1. Normalized Model of Permanent Deformation
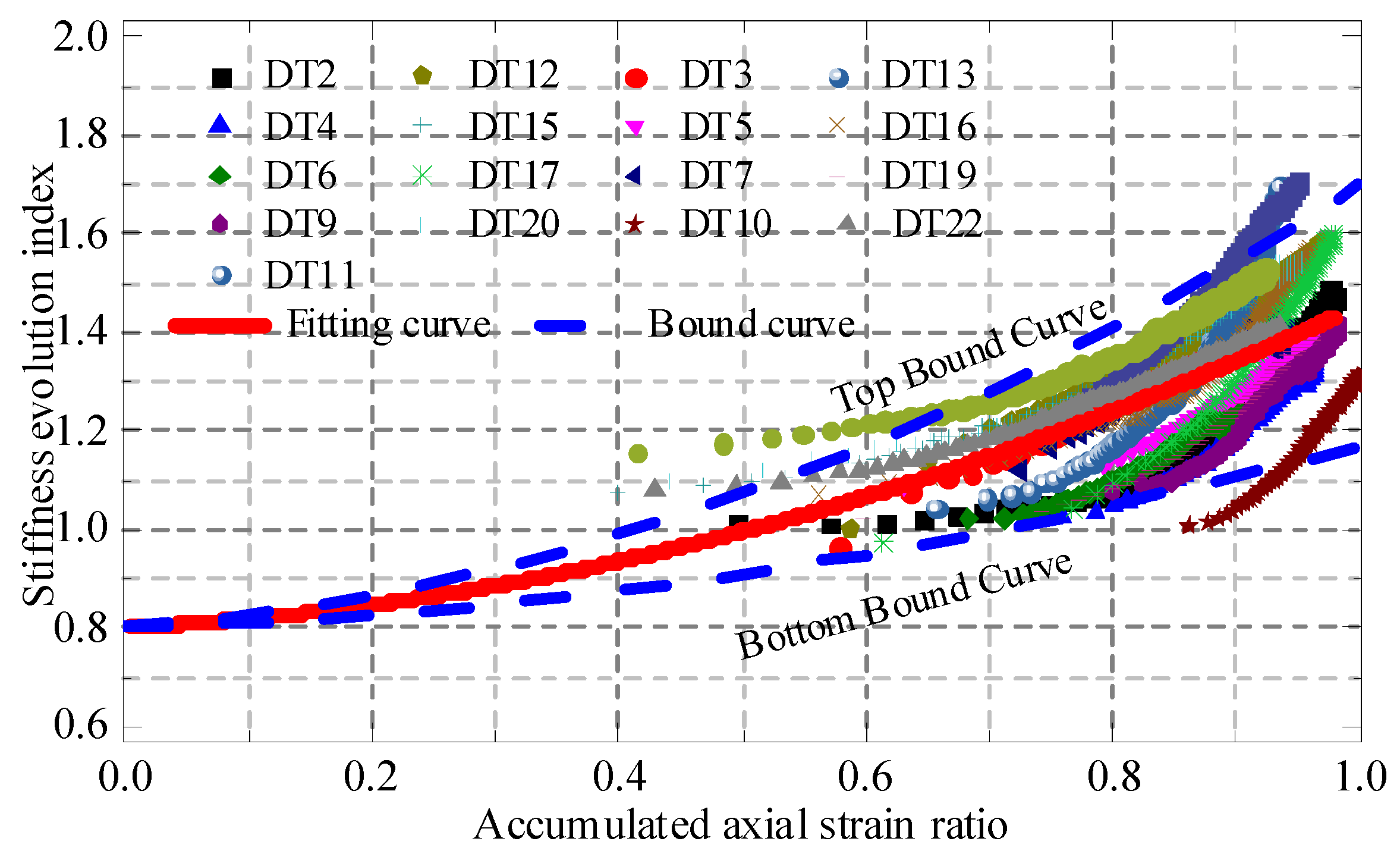
4.2. Elastic Modulus Normalization Model
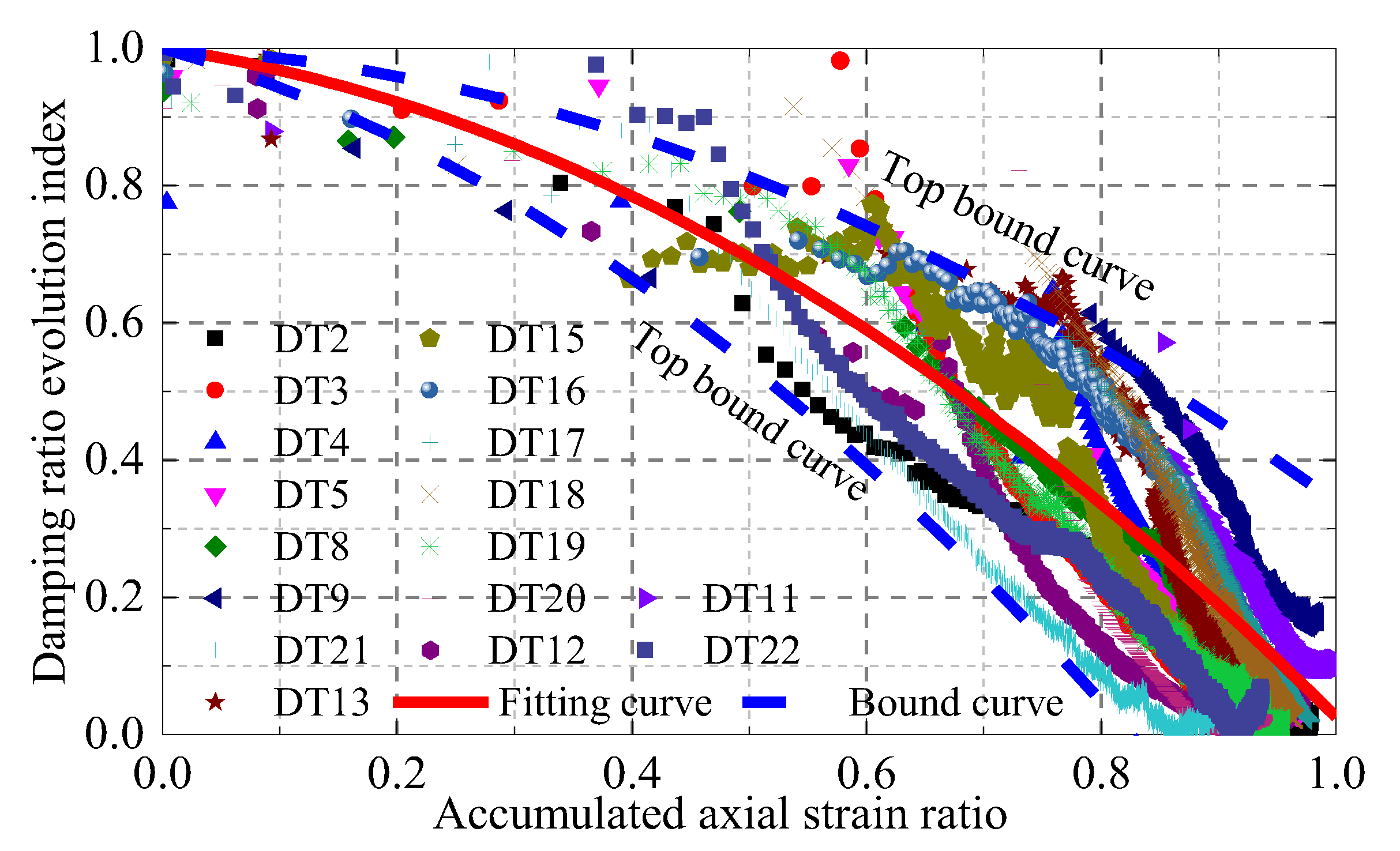
4.3. Damping Ratio Normalization Model
5. Conclusions
- (1)
- The dynamic triaxial test shows that the stiffness of calcareous sand increases with increased cyclic loading, whereas the damping ratio decreases with increased cyclic loading. When cyclic loading approaches infinity, the stiffness of the sample tends to be stable, and the damping ratio becomes less than 0.05.
- (2)
- The initial value and rate of change of stiffness and damping ratio vary under different parameters. When the vibration number of the cyclic load is kept constant, the dynamic stress amplitude is larger, the confining pressure is lower, water and salt contents are higher, and the change of stiffness and damping ratio from the initial to the given cycle increases.
- (3)
- At higher dynamic stress amplitudes, the frequency is higher, the confining pressure, consolidation stress, and compactness are lower, and the moisture content is closer to its optimal value. Furthermore, the axial cumulative strain is higher, the elastic modulus is lower, and the damping ratio is higher.
- (4)
- The permanent deformation of the calcareous sand subgrade can be calculated by inputting the cyclic load stress. Moreover, according to the field settlement deformation monitoring data, the dynamic elastic modulus and damping ratio evolution of the subgrade can be calculated, and then the long-term service performance of the subgrade can be reasonably predicted.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shahnazari, H.; Rezvani, R. Effective parameters for the particle breakage of calcareous sands: An experimental study. Eng. Geol. 2013, 159, 98–105. [Google Scholar] [CrossRef]
- Wang, X.Z.; Jiao, Y.-Y.; Wang, R.; Hu, M.; Meng, Q.; Tan, F. Engineering characteristics of the calcareous sand in Nansha Islands, South China Sea. Eng. Geol. 2011, 120, 40–47. [Google Scholar] [CrossRef]
- Shahnazari, H.; Rezvani, R.; Tutunchian, M.A. Post-cyclic volumetric strain of calcareous sand using hollow cylindrical torsional shear tests. Soil Dyn. Earthq. Eng. 2019, 124, 162–171. [Google Scholar] [CrossRef]
- Wang, X.; Weng, Y.; Wei, H.; Meng, Q.; Hu, M. Particle obstruction and crushing of dredged calcareous soil in the Nansha Islands, South China Sea. Eng. Geol. 2019, 261, 105274. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, C.-Q.; Wang, X.Z. Experimental study on the coefficient of lateral pressure at rest for calcareous soils. Mar. Georesour. Geotechnol. 2020, 38, 989–1001. [Google Scholar] [CrossRef]
- Chen, W.; Jeng, D.; Chen, W.; Chen, G.; Zhao, H. Seismic-induced dynamic responses in a poro-elastic seabed: Solutions of different formulations. Soil Dyn. Earthq. Eng. 2020, 131, 106021. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, Y.; Yao, W.; Liu, X.; Ren, C.; Cai, Y.; Tang, X. Stress relaxation behaviour of marble under cyclic weak disturbance and confining pressures. Measurement 2021, 182, 109777. [Google Scholar] [CrossRef]
- Datta, M.; Rao, G.V.; Gulhati, S. Development of pore water in a dense calcareous sand under repeated compressive stress cydes. In Proceedings of the International Symposium on Soils under Cyclic and Transient Loading, Suansea, Wales, UK, 7–11 January 1980; pp. 33–47. [Google Scholar]
- Knight, K. Contribution to the performance of calcareous sands under cyclic loading. In Proceedings of the International Conference on Calcareous Sediments, Perth, WA, Australia, 15–18 March 1988; pp. 877–880. [Google Scholar]
- Kaggwa, W.S.; Poulos, H.G.; Carter, J.P. Response of carbonate sediments under cyclic triaxial test conditions. In Proceeding of the 1st International Conference on Calcareous Sediments, Perth, WA, Australia, 15–18 March 1988; Volume 1, pp. 97–107. [Google Scholar]
- Haizhen, Y.; Ren, W. The cyclic strength test research on calcareous sand. Rock Soil Mech. 1999, 4, 3–5. (In Chinese) [Google Scholar]
- Jianguo, L.; Ren, W.; Haizhen, Y. Experimental research on effect of initial principal stress orientation on dynamic properties of calcareous sand. Rock Soil Mech. 2005, 5, 723–727. (In Chinese) [Google Scholar]
- Jianguo, L. Experimental Research on Dynamic Behavior of Saturated Calcareous Sand under Wave Loading; Institute of Rock and Soil Mechanics, Chinese Academy of Sciences: Wuhan, China, 2005. (In Chinese) [Google Scholar]
- Coop, M.R.; Sorensen, K.K.; Bodas Freitas, T.M.; Georgoutsos, G. Particle breakage during shearing of a carbonate sand. Géotechnique 2004, 54, 157–163. [Google Scholar] [CrossRef]
- Donohue, S.; O’sullivan, C.; Long, M. Particle breakage during cyclic triaxial loading of a carbonate sand. Géotechnique 2009, 59, 477–482. [Google Scholar] [CrossRef]
- Li, X.; Liu, J. One-dimensional compression feature and particle crushability behavior of dry calcareous sand considering fine-grained soil content and relative compaction. Bull. Eng. Geol. Environ. 2021, 80, 4049–4065. [Google Scholar] [CrossRef]
- Gang, W.; Jingjing, Z.; Xing, W. Evolution of particle crushing of carbonate sands under cyclic triaxial stress path. Chin. J. Geotech. Eng. 2019, 41, 755–760. (In Chinese) [Google Scholar]
- Shaoheng, H.; Zhi, D.; Tangdai, X. Long-term behaviour and degradation of calcareous sand under cyclic loading. Eng. Geol. 2020, 276, 105756. [Google Scholar] [CrossRef]
- Sizhen, Z. Dynamic Analysis of Mining Tunnel and Airport Runway under Aircraft Moving Loads. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2012. (In Chinese). [Google Scholar]
- Lei, Q. Study on Deformation of Airport Pavement Foundation under the Action of Airport Loads and Groundwater. Ph.D. Thesis, Zhengzhou University, Zhengzhou, China, 2017. (In Chinese). [Google Scholar]
- Sujie, Z. Study on Dynamic Response and Deformation of Airport Pavement Foundation under the Action of Aircraft Loads. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Feng, Z. Heavy Track Induced Dynamic Response and Permanent Deformation of Subgrade in Deep Seasonally Frozen Region. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2012. (In Chinese). [Google Scholar]
- Idriss, I.M.; Dobry, R.; Singh, R.D. Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div. ASCE 1978, 104, 1427–1447. [Google Scholar] [CrossRef]
- Ling, X.; Li, Q.; Wang, L.; Zhang, F.; An, L.; Xu, P. Stiffness and damping ratio evolution of frozen clays under long-term low-level repeated cyclic loading: Experimental evidence and evolution model. Cold Reg. Sci. Technol. 2013, 86, 45–54. [Google Scholar] [CrossRef]
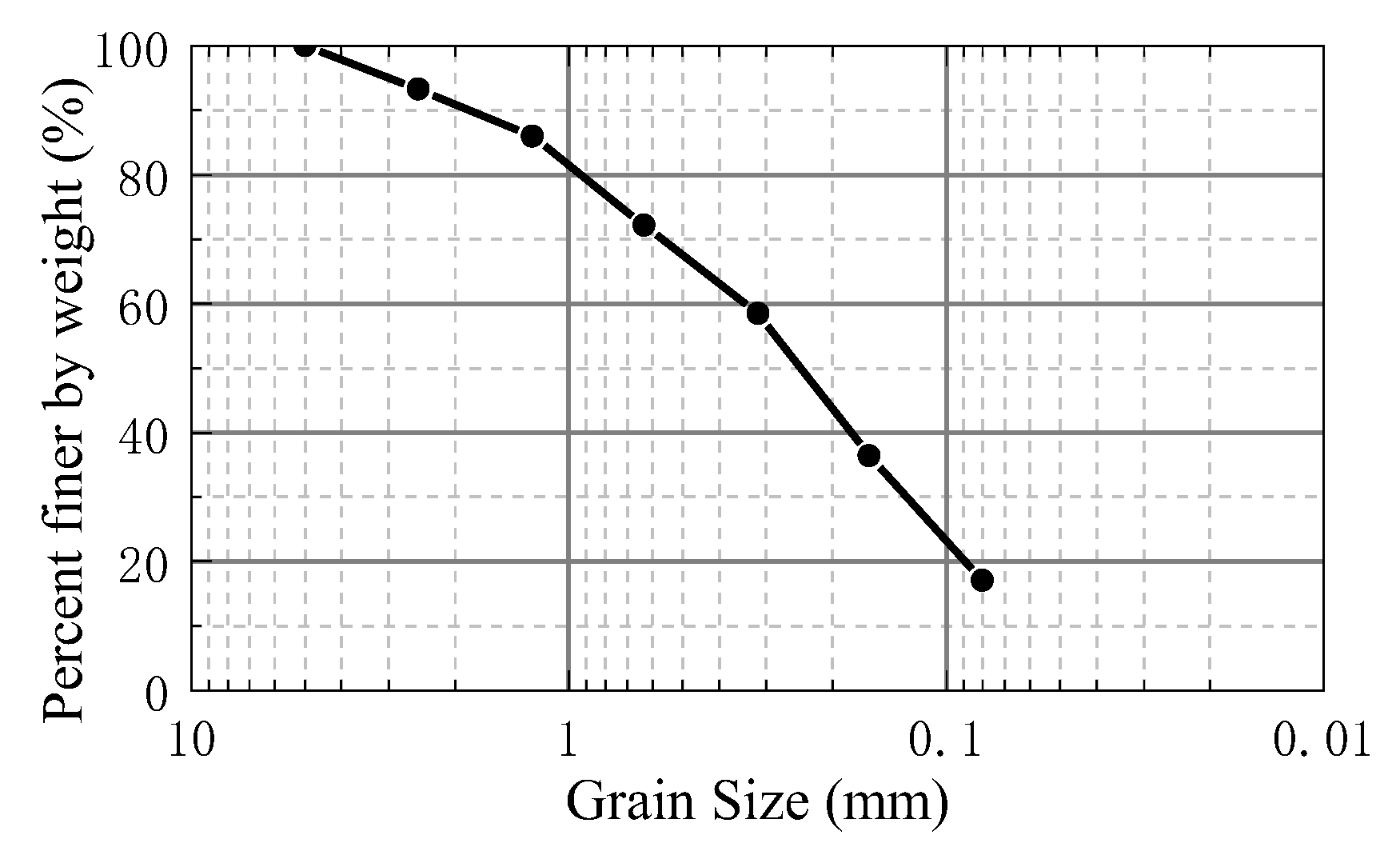
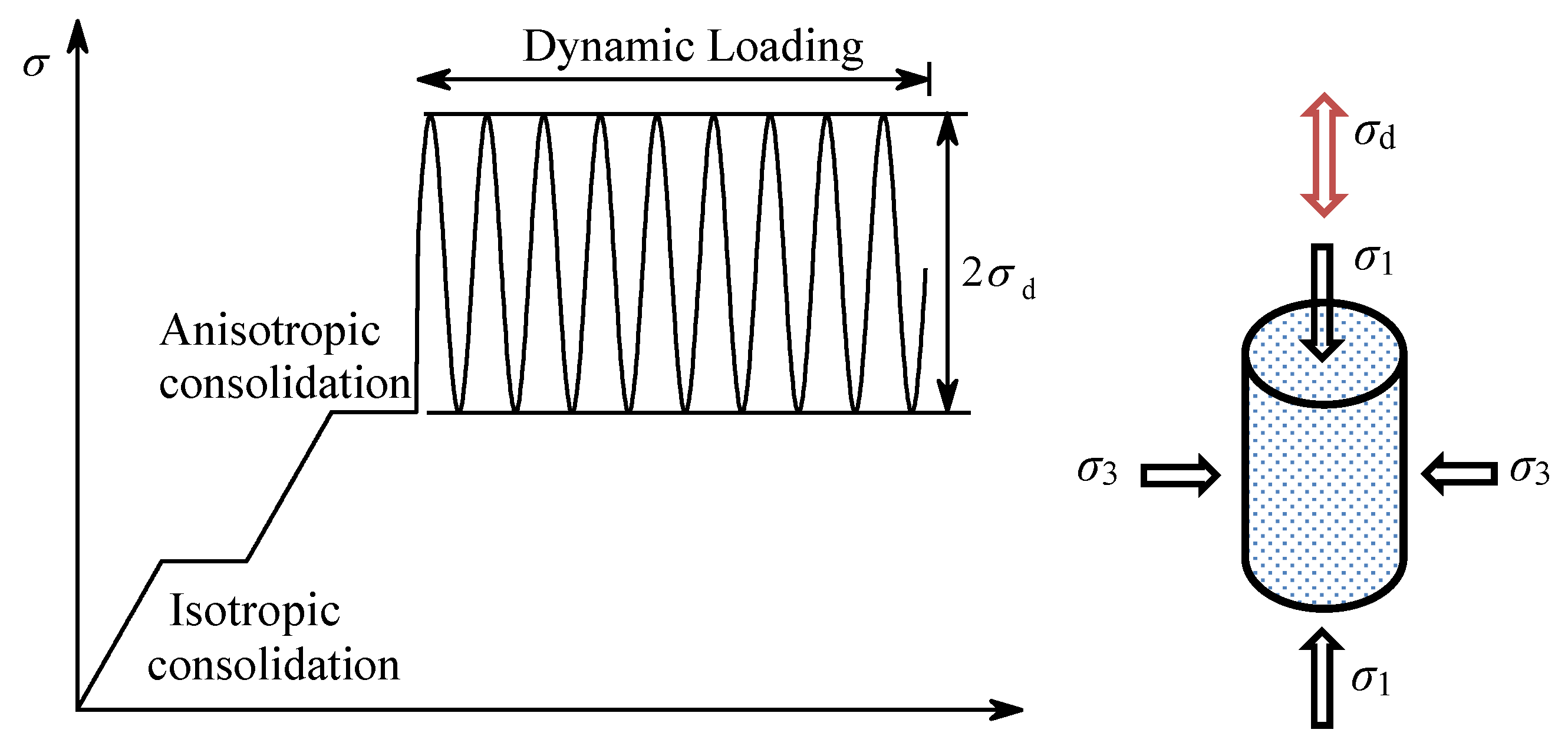

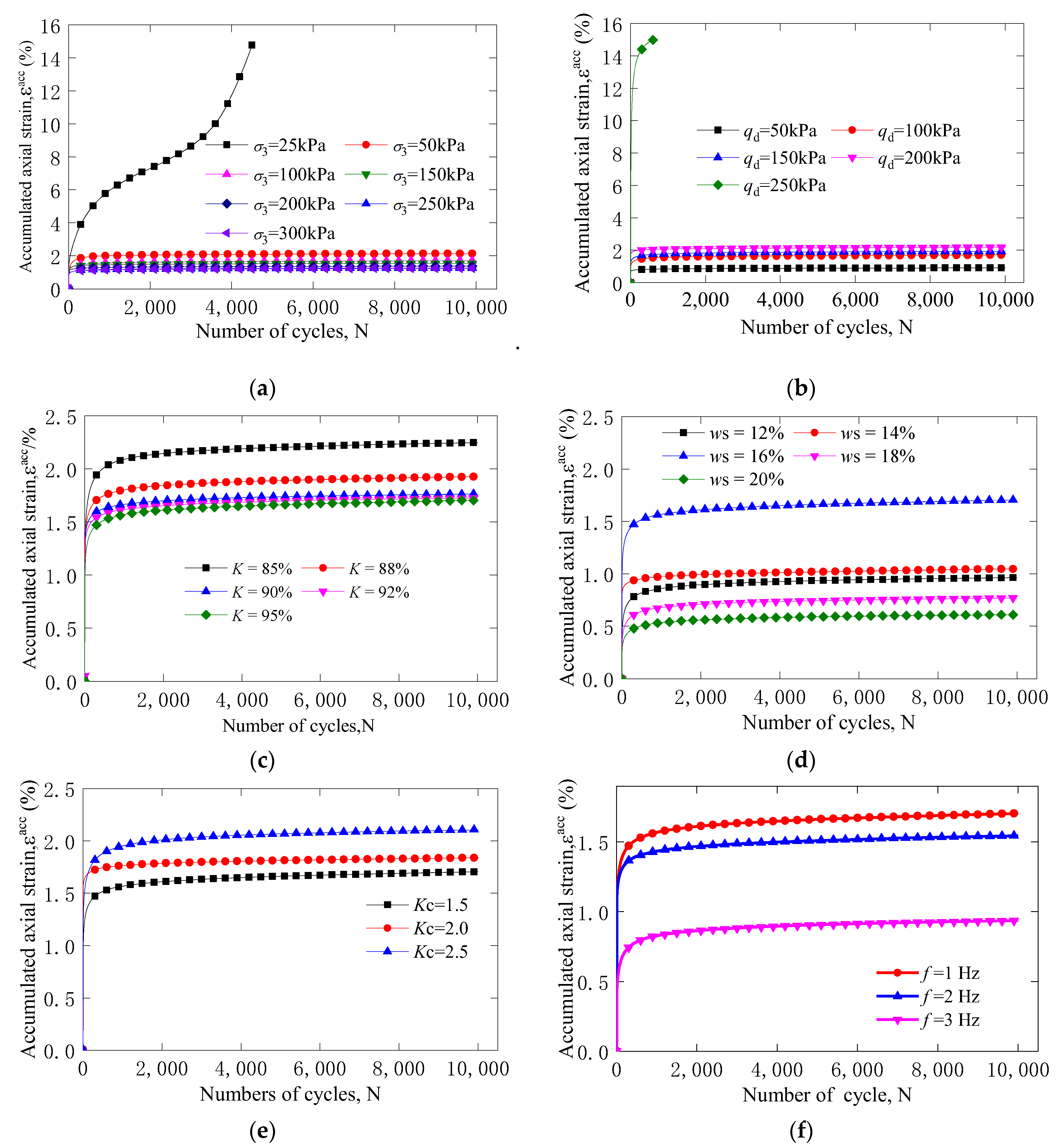

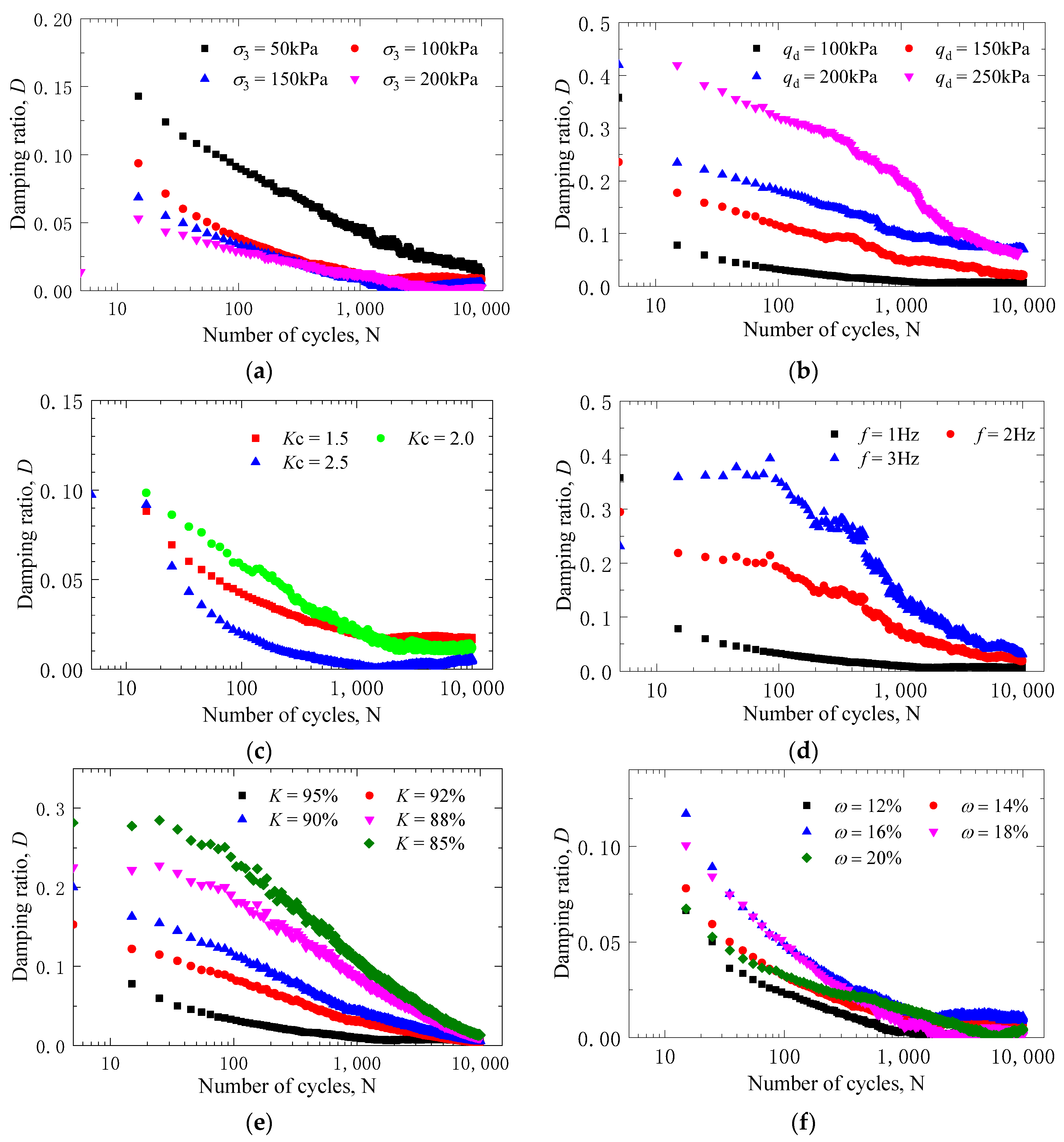
| Sample Number | Confining Pressure | Cyclic Loading | Consolidation Stress Ratio | Relative Density | Loading Frequency | Moisture Content |
|---|---|---|---|---|---|---|
| F/Hz | Ws/% | |||||
| DT-1 | 25 | 100 | 1.5 | 95 | 1 | 16 |
| DT-2 | 50 | 100 | 1.5 | 95 | 1 | 16 |
| DT-3 | 100 | 100 | 1.5 | 95 | 1 | 16 |
| DT-4 | 150 | 100 | 1.5 | 95 | 1 | 16 |
| DT-5 | 200 | 100 | 1.5 | 95 | 1 | 16 |
| DT-6 | 300 | 100 | 1.5 | 95 | 1 | 16 |
| DT-7 | 100 | 50 | 1.5 | 95 | 1 | 16 |
| DT-8 | 100 | 150 | 1.5 | 95 | 1 | 16 |
| DT-9 | 100 | 200 | 1.5 | 95 | 1 | 16 |
| DT-10 | 100 | 250 | 1.5 | 95 | 1 | 16 |
| DT-11 | 100 | 100 | 2 | 95 | 1 | 16 |
| DT-12 | 100 | 100 | 2.5 | 95 | 1 | 16 |
| DT-13 | 100 | 100 | 1.5 | 85 | 1 | 16 |
| DT-14 | 100 | 100 | 1.5 | 88 | 1 | 16 |
| DT-15 | 100 | 100 | 1.5 | 90 | 1 | 16 |
| DT-16 | 100 | 100 | 1.5 | 92 | 1 | 16 |
| DT-17 | 100 | 100 | 1.5 | 95 | 2 | 16 |
| DT-18 | 100 | 100 | 1.5 | 95 | 3 | 16 |
| DT-19 | 100 | 100 | 1.5 | 95 | 1 | 12 |
| DT-20 | 100 | 100 | 1.5 | 95 | 1 | 14 |
| DT-21 | 100 | 100 | 1.5 | 95 | 1 | 18 |
| DT-22 | 100 | 100 | 1.5 | 95 | 1 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, L. Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading. J. Mar. Sci. Eng. 2022, 10, 1806. https://doi.org/10.3390/jmse10121806
Wang Z, Zhang L. Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading. Journal of Marine Science and Engineering. 2022; 10(12):1806. https://doi.org/10.3390/jmse10121806
Chicago/Turabian StyleWang, Ziyu, and Lei Zhang. 2022. "Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading" Journal of Marine Science and Engineering 10, no. 12: 1806. https://doi.org/10.3390/jmse10121806
APA StyleWang, Z., & Zhang, L. (2022). Experimental Study on Dynamic Parameters of Calcareous Sand Subgrade under Long-Term Cyclic Loading. Journal of Marine Science and Engineering, 10(12), 1806. https://doi.org/10.3390/jmse10121806






