Branch-And-Price Algorithm for the Tramp Ship Routing and Scheduling Problem Considering Ship Speed and Payload
Abstract
:1. Introduction
2. Mathematical Model
2.1. A Nonlinear Programming Model
- set of ports, 0, represent the virtual origin and destination depots respectively
- set of pickup ports
- set of delivery ports
- set of arcs
- a directed graph
- set of ships (note: a ship carries only one type of cargo)
- ship capacity
- weight of ballast ship
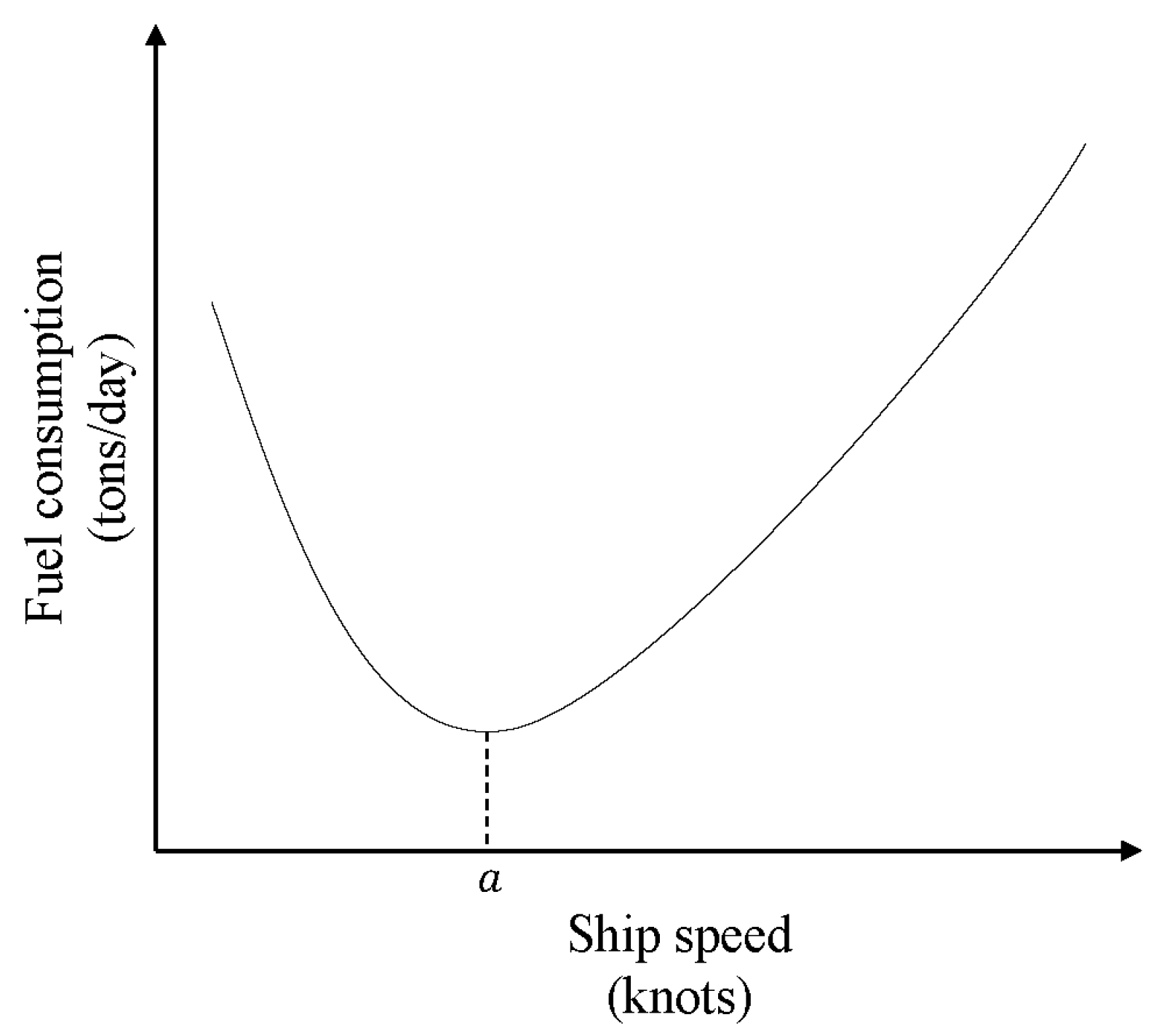
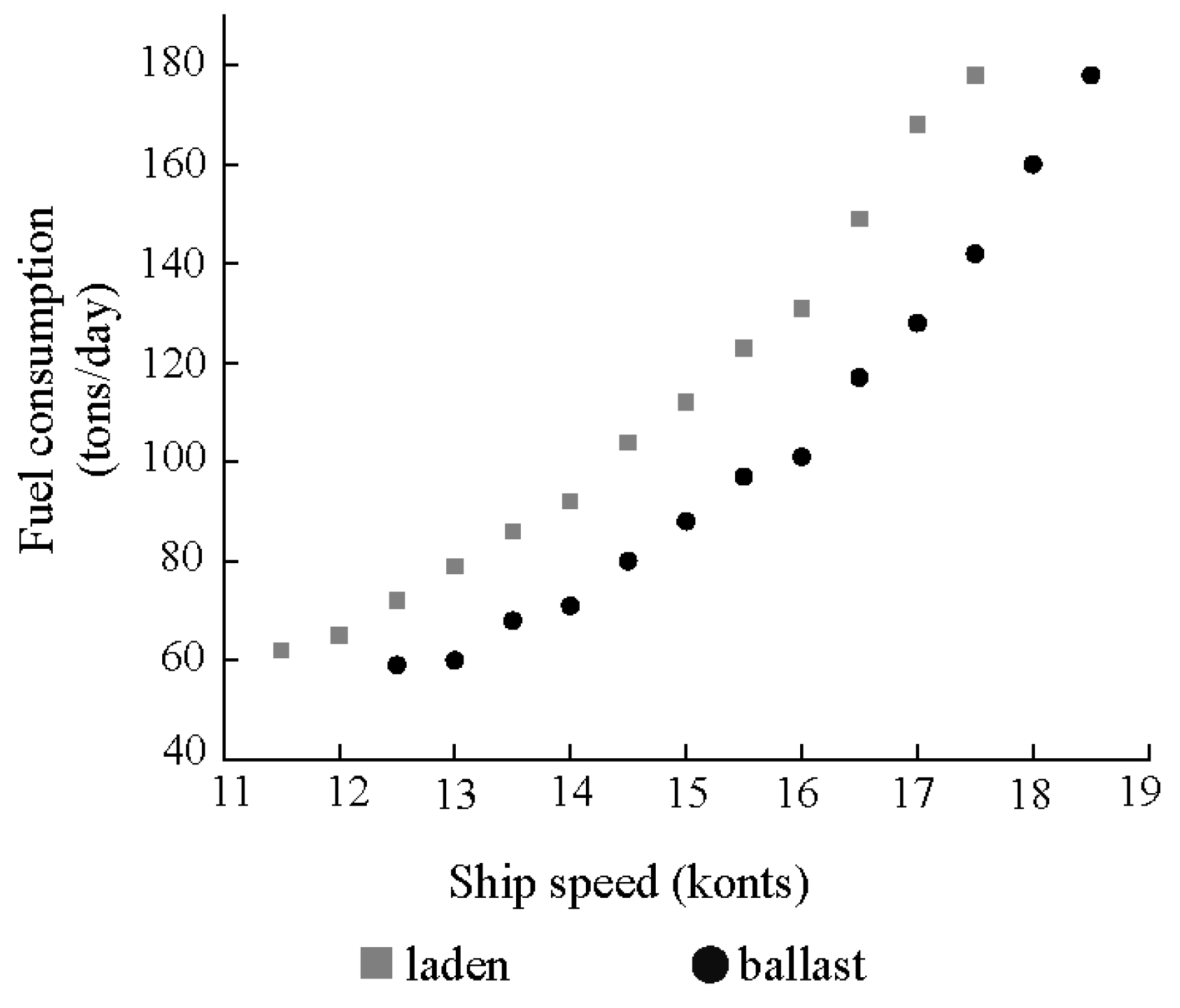
- set of ship optional speed, assuming that the speed set on each arc is the same, the number of speed discretization points is , then the speed set , for any corresponds to the same speed range
- index of cargo, each cargo is associated with a pickup port and a delivery port
- distance between port and
- demand of port , ,
- time window of port , , represent the earliest departure time at origin depot and the latest arrival time at destination depots respectively
- service time at port
- equals to 1 if ship k travel from port to port , and 0 otherwise
- equals to 1 if ship k travel from port to port with speed , and 0 otherwise
- payload of ship when leaving port
- the time for start of service for ship k at port
- 1.
- Changing objective function (2), obtain model for tramp ship routing and scheduling problem considering ship speed.s.tconstraints (3)–(17).
- 2.
- Changing objective function (2) and related constraints, obtain model for distance minimizing tramp ship routing and scheduling problem.
2.2. Set Partitioning Formulation
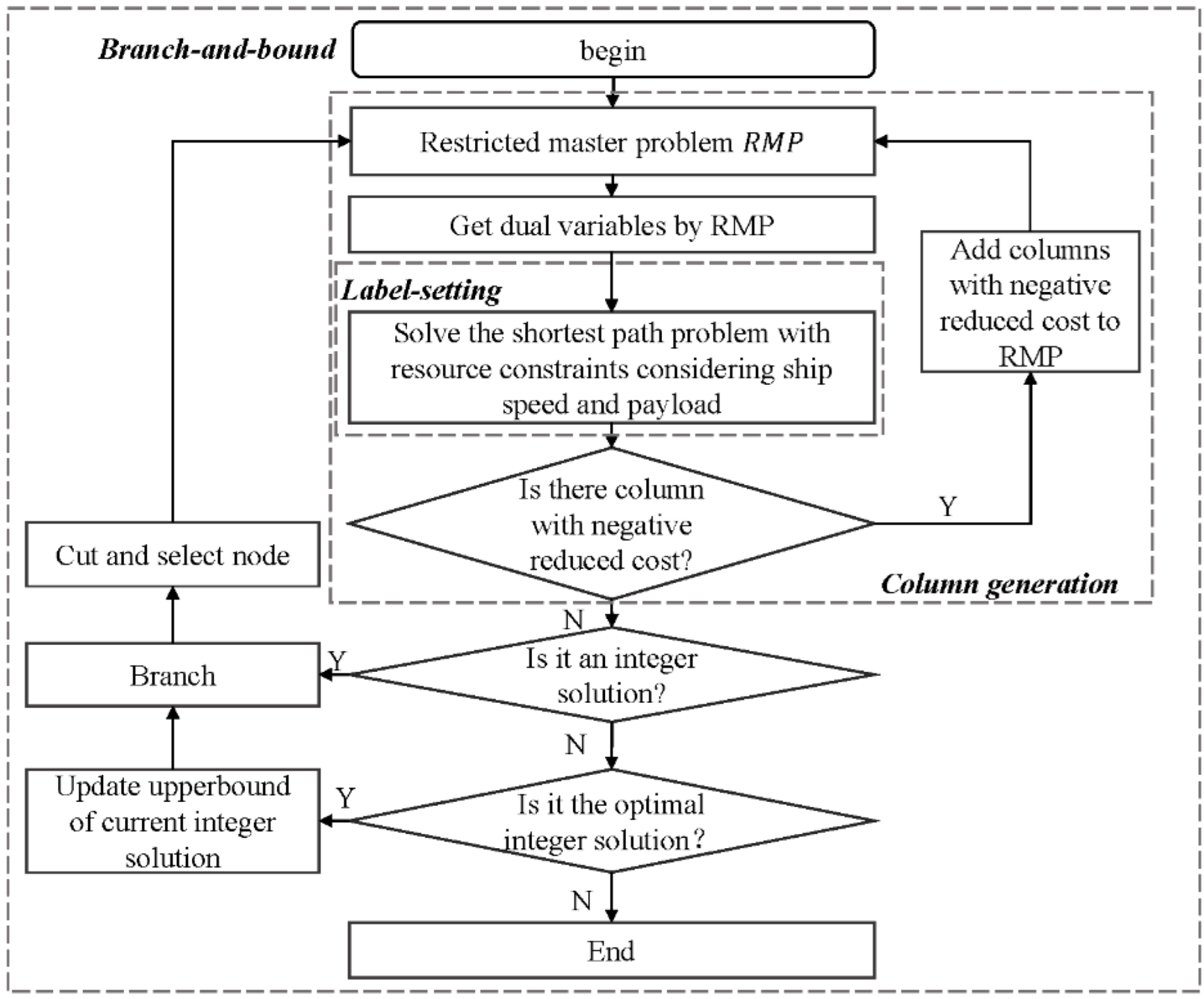
3. Solution Approach
3.1. Label Setting Algorithm
3.1.1. Labels
- : the node of the label
- : the accumulated reduced cost of the route
- : the payload of the ship after visiting node
- : the arrival time at node
- : the speed travel between the predecessor node and node
- : the set of pickup nodes which has been visited, but corresponding delivery node has not been visited
- : the set of unreachable nodes
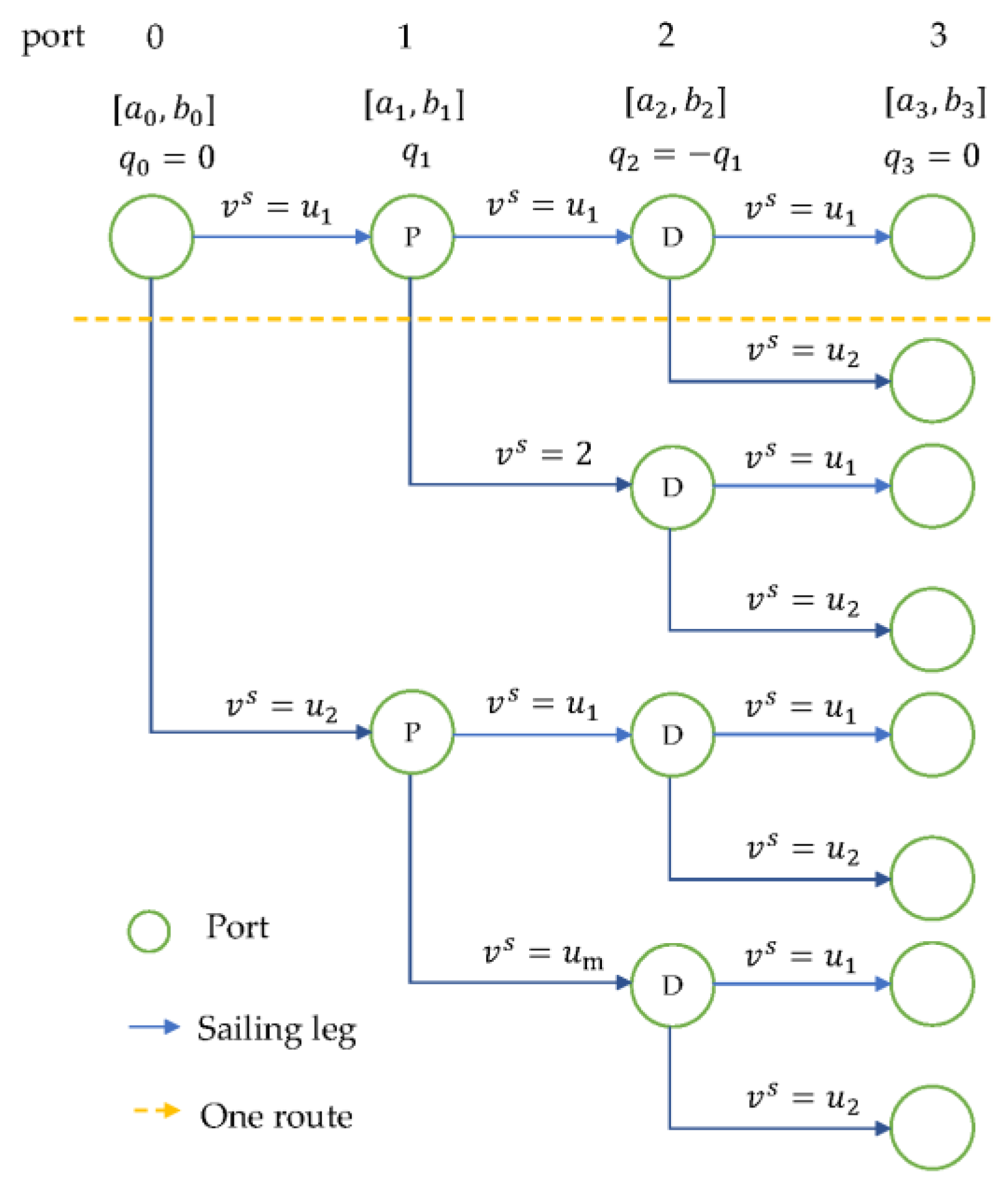
3.1.2. Label Extension
3.1.3. Dominance Criterion
3.1.4. Acceleration Strategies
- 1.
- acceleration strategies S1: set a threshold to control the number of feasible columns generated by subproblem, speeding up the convergence, and stop the search when the number of feasible columns equal to the threshold. Generally, set the threshold to twice the number of nodes. When this strategy is adopted, the number of iterations of the master problem usually increases, but the time to solve the subproblems will be greatly reduced, which can reduce the overall solution time of the branch-and-price algorithm without destroying the optimal solution of the approach.
- 2.
- acceleration strategies S2: Feillet et al. [22] introduced the successor node set of the current label, includes nodes that satisfy resource constraints but have not been visited. If a delivery node is included in , it is necessary to ensure that its corresponding pickup node has been visited. In addition, since the subproblem considers speed optimization, there will be at least one arc connection between two nodes due to different speeds, and it is only necessary to ensure that sailing at any speed in the optional speed set does not violate the time window constraints.
3.1.5. Label Setting Algorithm for the Subproblem
- Step 1: generate initial label and store it in the label set .
- Step 2: traversal set , if , generate a new label according to the label extension rules; otherwise, go to step4.
- Step 3: based on the dominance criterion, delete dominated labels, update set , go to step 2.
- Step 4: detect the feasibility of the routes corresponding to the label with a negative reduced cost in the label set and add the feasible routes to the restricted master problem.
| Algorithm 1 Pseudo-Code of Label Setting Algorithm | |
| : | |
| Output: | |
| Initialization: | |
| . stores unprocessed labels | |
| . stores the label corresponding to node 2n + 1 with negative reduced cost | |
| 1: | |
| 2: | while & nbsol < 4n do |
| 3: | |
| 4: | ), |
| 5: | if & do |
| 6: | |
| 7: | else |
| 8: | for each feasible extension of do |
| 9: | j = ) |
| 10: | if no label in dominates then |
| 11: | |
| 12: | |
| 13: | end if |
| 14: | end for |
| 15: | end while |
| 16: | return |
3.2. Branching Strategies
4. Computational Experiments
4.1. Test Instances
4.2. Result of Solving by BP and CPLEX
4.3. Analysis of the Influence of Speed and Payload
4.4. Analysis of Acceleration Strategies Performance
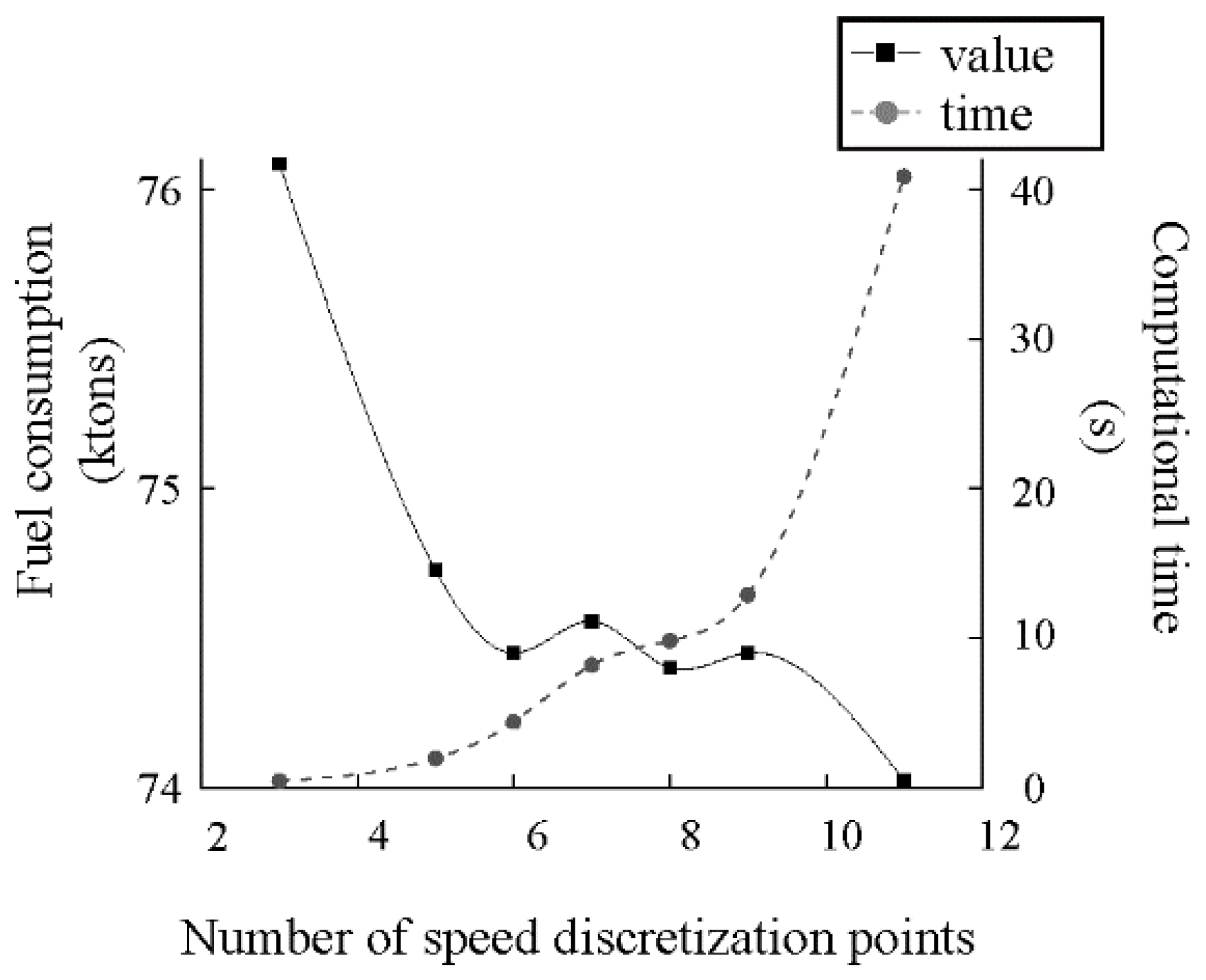
4.5. Analysis of the Number of Speed Discretization Points
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, M.; Ji, B.; Fang, X.; Yu, S.S. Discretization-Strategy-Based Solution for Berth Allocation and Quay Crane Assignment Problem. J. Mar. Sci. Eng. 2022, 10, 495. [Google Scholar] [CrossRef]
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Ship routing and scheduling in the new millennium. Eur. J. Oper. Res. 2013, 228, 467–483. [Google Scholar] [CrossRef]
- Fan, H.; Yu, J.; Liu, X. Tramp Ship Routing and Scheduling with Speed Optimization Considering Carbon Emissions. Sustainability 2019, 11, 6367. [Google Scholar] [CrossRef] [Green Version]
- IMO. Fourth IMO GHG Study 2020; International Maritime Organization (IMO): London, UK, 2020. [Google Scholar]
- Psaraftis, H.N.; Kontovas, C.A. Speed models for energy-efficient maritime transportation: A taxonomy and survey. Transp. Res. Part C Emerg. Technol. 2013, 26, 331–351. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Kontovas, C.A. Ship speed optimization: Concepts, models and combined speed-routing scenarios. Transp. Res. Part C Emerg. Technol. 2014, 44, 52–69. [Google Scholar] [CrossRef] [Green Version]
- Wen, M.; Røpke, S.; Petersen, H.L.; Larsen, R.; Madsen, O.B.G. Full-shipload tramp ship routing and scheduling with variable speeds. Comput. Oper. Res. 2016, 70, 1–8. [Google Scholar] [CrossRef] [Green Version]
- De, A.; Choudhary, A.; Tiwari, M.K. Multi objective Approach for Sustainable Ship Routing and Scheduling with Draft Restrictions. IEEE Trans. Eng. Manag. 2019, 66, 35–51. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Ma, D.; Ma, Y.; Zhang, J.; Wang, D. Green maritime: A routing and speed multi-objective optimization strategy. J. Clean. Prod. 2021, 305, 127179. [Google Scholar] [CrossRef]
- Fagerholt, K.; Laporte, G.; Norstad, I. Reducing fuel emissions by optimizing speed on shipping routes. J. Oper. Res. Soc. 2017, 61, 523–529. [Google Scholar] [CrossRef]
- Norstad, I.; Fagerholt, K.; Laporte, G. Tramp ship routing and scheduling with speed optimization. Transp. Res. Part C Emerg. Technol. 2011, 19, 853–865. [Google Scholar] [CrossRef]
- De, A.; Mamanduru, V.K.R.; Gunasekaran, A.; Subramanian, N. Composite particle algorithm for sustainable integrated dynamic ship routing and scheduling optimization. Comput. Ind. Eng. 2016, 96, 201–215. [Google Scholar] [CrossRef]
- Duan, G.; Fan, T.; Chen, L.; Ma, J. Floating marine debris mitigation by vessel routing modeling and optimization considering carbon emission and travel time. Transp. Res. Part C Emerg. Technol. 2021, 133, 103449. [Google Scholar] [CrossRef]
- Gkonis, K.G.; Psaraftis, H.A. Modeling Tankers’ Optimal Speed and Emissions. In Proceedings of the SNAME Maritime Convention, F, 2012, Providence, RI, USA, 24 October 2012. [Google Scholar]
- Wen, M.; Pacino, D.; Kontovas, C.A.; Psaraftis, H.N. A multiple ship routing and speed optimization problem under time, cost and environmental objectives. Transp. Res. Part D Transp. Environ. 2017, 52, 303–321. [Google Scholar] [CrossRef]
- Barrass, B. Ship Design and Performance for Masters and Mates; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The Pollution-Routing Problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Desaulniers, G.; Desrosiers, J.; Solomon, M.M. Column Generation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Lübbecke, M.E.; Desrosiers, J. Selected topics in column generation. Oper. Res. 2005, 53, 1007–1023. [Google Scholar] [CrossRef] [Green Version]
- Desrosiers, J.; Soumis, F.; Desrochers, M. Routing with time windows by column generation. Networks 1984, 14, 545–565. [Google Scholar] [CrossRef]
- Ropke, S.; Cordeau, J.F. Branch and cut and price for the pickup and delivery problem with time windows. Transp. Sci. 2009, 43, 267–286. [Google Scholar] [CrossRef] [Green Version]
- Feillet, D.; Dejax, P.; Gendreau, M.; Gueguen, C. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Networks 2004, 44, 216–229. [Google Scholar] [CrossRef]
- Hemmati, A.; Hvattum, L.M.; Fagerholt, K.; Norstad, I. Benchmark Suite for Industrial and Tramp Ship Routing and Scheduling Problems. Inf. Syst. Oper. Res. 2016, 52, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Brouer, B.D.; Alvarez, J.F.; Plum, C.E.M.; Pisinger, D.; Sigurd, M.M. A Base Integer Programming Model and Benchmark Suite for Liner-Shipping Network Design. Transp. Sci. 2014, 48, 281–312. [Google Scholar] [CrossRef] [Green Version]
- Lamb, T. Ship Design and Construction; Lamb, T., Ed.; SNAME: Alexandria, VA, USA, 2003; ISBN: 0-939773-40-6. [Google Scholar]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
| Instances | CPLEX | BP | Instances | CPLEX | BP | ||||
|---|---|---|---|---|---|---|---|---|---|
| f (ktons) | t (s) | f (ktons) | t (s) | f (ktons) | t (s) | f (ktons) | t (s) | ||
| 0801 | 12,060 | 7 | 12,060 | 0.11 | 1206 | 14,060 | 7 | 14,060 | 0.05 |
| 0802 | 11,190 | 39 | 11,190 | 0.03 | 1207 | 10,720 | 3 | 10,720 | 0.20 |
| 0803 | 9540 | 5 | 9540 | 0.02 | 1208 | 14,320 | 4 | 14,320 | 0.06 |
| 0804 | 10,620 | 10 | 10,620 | 0.03 | 1209 | 13,500 | 3 | 13,500 | 0.18 |
| 0805 | 9590 | 4 | 9590 | 0.01 | 1601 | 15,540 | 2721 | 15,540 | 0.97 |
| 0806 | 10,880 | 7 | 10,880 | 0.02 | 1602 | 19,190 | 5658 | 19,190 | 0.97 |
| 0807 | 11,380 | 11 | 11,380 | 0.02 | 1603 | 22,910 | 1975 | 22,910 | 0.96 |
| 0808 | 12,300 | 4 | 12,300 | 0.01 | 1604 | 22,550 | 4208 | 22,550 | 0.47 |
| 0809 | 14,230 | 8 | 14,230 | 0.01 | 1605 | 26,940 | 7343 | 26,940 | 0.28 |
| 1201 | 14,250 | 768 | 14,250 | 0.39 | 1606 | 25,140 | 776 | 25,140 | 3.98 |
| 1202 | 16,980 | 22 | 16,980 | 0.12 | 1607 | 18,770 | 15,011 | 18,770 | 12.52 |
| 1203 | 20,210 | 204 | 20,210 | 0.09 | 1608 | 13,270 | 8555 | 13,270 | 0.64 |
| 1204 | 15,210 | 129 | 15,210 | 0.11 | 1609 | 13,710 | 16,276 | 13,710 | 0.49 |
| 1205 | 16,390 | 4836 | 16,390 | 0.09 | |||||
| BP | CPLEX | BP | CPLEX | BP | CPLEX | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Instances | F (ktons) | T (s) | F (ktons) | Instances | F (ktons) | t (s) | F (ktons) | Instances | F (ktons) | T (s) | F (ktons) |
| 2001 | 29,860 | 7 | 29,860 | 2801 | 28,431 | 37 | 33,173 | 3601 | 38,320 | 2032 | 49,337 |
| 2002 | 29,770 | 10 | 29,770 | 2802 | 28,430 | 5 | 29,076 | 3602 | 28,680 | 125 | 42,452 |
| 2003 | 35,099 | 22 | 35,099 | 2803 | 43,880 | 11 | 43,880 | 3603 | 39,040 | 16 | 46,897 |
| 2004 | 32,490 | 54 | 32,490 | 2804 | 39,930 | 414 | 40,899 | 3604 | 38,320 | 2009 | 53,403 |
| 2005 | 23,350 | 8 | 23,352 | 2805 | 36,020 | 24 | 36,027 | 3605 | 40,510 | 205 | 53,590 |
| 2006 | 18,648 | 15 | 18,648 | 2806 | 30,960 | 44 | 31,482 | 3606 | 34,950 | 237 | 39,842 |
| 2007 | 23,646 | 53 | 23,646 | 2807 | 34,620 | 328 | 35,216 | 3607 | 36,820 | 4 | 40,260 |
| 2008 | 23,890 | 578 | 23,890 | 2808 | 30,990 | 104 | 31,517 | 3608 | 38,960 | 323 | 86,679 |
| 2009 | 29,200 | 10 | 29,202 | 2809 | 36,160 | 38 | 38,913 | 3609 | 54,550 | 82 | 82,466 |
| 2401 | 23,270 | 678 | 23,731 | 3201 | 39,460 | 7 | 41,177 | 4001 | 44,860 | 607 | 74,231 |
| 2402 | 25,700 | 123 | 25,753 | 3202 | 41,090 | 26 | 46,832 | 4002 | 42,540 | 102 | 101,334 |
| 2403 | 31,990 | 27 | 31,992 | 3203 | 39,250 | 704 | 42,055 | 4003 | 42,190 | 2937 | 91,918 |
| 2404 | 20,940 | 116 | 20,943 | 3204 | 32,830 | 23 | 65,834 | 4004 | 47,220 | 2357 | 105,974 |
| 2405 | 29,080 | 311 | 29,429 | 3205 | 41,170 | 227 | 45,537 | 4005 | 33,960 | 883 | 65,315 |
| 2406 | 24,030 | 5 | 24,282 | 3206 | 41,120 | 36 | 44,440 | 4006 | 38,250 | 690 | 86,150 |
| 2407 | 23,620 | 24 | 23,736 | 3207 | 36,600 | 55 | 38,600 | 4007 | 50,230 | 311 | 76,224 |
| 2408 | 23,870 | 31 | 24,126 | 3208 | 33,990 | 42 | 36,584 | 4008 | 48,960 | 110 | 88,521 |
| 2409 | 25,590 | 41 | 25,805 | 3209 | 38,870 | 17 | 46,588 | 4009 | 38,250 | 691 | 86,150 |
| 16 | FU | 1.92 | 39.80 | 4.58 | 81.66 |
| TT | −9.50% | −11.66% | −1.47% | −25.09% | |
| DI | −1.69% | 1.03% | 4.84% | −7.42% | |
| LO | 21.94% | 12.86% | −6.15% | 45.44% | |
| VE | −11.11% | −9.07% | 0.00% | −27.04% | |
| 20 | FU | 3.96% | 46.41% | 12.29% | 91.20% |
| TT | −11.05% | −15.49% | 46.86% | −23.58% | |
| DI | −0.94% | −0.56% | 39.93% | −6.72% | |
| LO | 22.74% | 28.54% | −43.02% | 41.10% | |
| VE | −11.67% | −16.67% | 50.00% | −24.44% | |
| 24 | FU | 2.34% | 43.61% | 4.11% | 92.99% |
| TT | −11.05% | −10.61% | −20.68% | −19.80% | |
| DI | −3.53% | −3.17% | −1.78% | −6.12% | |
| LO | 28.19% | 23.04% | 34.18% | 38.60% | |
| VE | −12.22% | −9.44% | −20.00% | −16.67% | |
| 28 | FU | 2.16% | 39.11% | 3.83% | 84.71% |
| TT | −12.54% | −17.28% | −4.83% | −25.74% | |
| DI | −12.64% | −12.22% | −90.27% | −16.77% | |
| LO | 23.68% | 29.82% | 15.38% | 50.31% | |
| VE | −12.33% | −13.07% | 0.00% | −24.92% | |
| 32 | FU | 1.07% | 33.40% | 3.69% | 70.66% |
| TT | −9.20% | −4.26% | 16.19% | −13.74% | |
| DI | −3.74% | 1.16% | 18.47% | −6.98% | |
| LO | 14.56% | 9.33% | −17.46% | 23.42% | |
| VE | −10.69% | 1.01% | 50.00% | −15.45% | |
| 36 | FU | 2.91% | 38.85% | −0.35% | 80.55% |
| TT | −10.57% | −16.76% | 26.38% | −25.37% | |
| DI | −3.06% | −3.28% | 18.43% | −9.03% | |
| LO | 23.12% | 14.78% | −11.29% | 42.20% | |
| VE | −10.12% | −14.75% | 37.50% | −26.06% | |
| 40 | FU | 2.58% | 36.31% | 11.39% | 76.59% |
| TT | −10.65% | −4.72% | 0.29% | −22.04% | |
| DI | −3.59% | −0.59% | 14.98% | −8.45% | |
| LO | 20.96% | −0.32% | −5.56% | 26.81% | |
| VE | −9.52% | 3.44% | 28.57% | −19.58% | |
| Ave | FU | 2.42% | 39.64% | 5.65% | 82.62% |
| TT | −10.65% | −11.54% | 8.96% | −22.20% | |
| DI | −4.17% | −2.52% | 0.66% | −8.78% | |
| LO | 22.17% | 16.87% | −4.85% | 38.27% | |
| VE | −11.09% | −8.37% | 20.87% | −22.02% |
| Computational Time (ms) | Number of Instances with Optimal Solution | Ratio (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 30 | 99 | 44 | 166 | 9 | 9 | 9 | 9 | 18.20 | 59.83 | 26.56 | 30.41 | 68.50 |
| 12 | 121 | 1510 | 252 | 4527 | 9 | 9 | 9 | 9 | 2.67 | 33.36 | 5.57 | 8.01 | 47.99 |
| 16 | 2365 | 3075 | 3913 | 13,282 | 9 | 9 | 9 | 9 | 17.80 | 23.15 | 29.46 | 76.90 | 60.43 |
| 20 | 24,005 | 54,945 | 53,828 | 822,034 | 9 | 9 | 9 | 9 | 2.92 | 6.68 | 6.55 | 43.69 | 44.60 |
| 24 | 445,151 | 1,021,615 | 832,471 | 6,910,953 | 9 | 9 | 9 | 5 | 6.44 | 14.78 | 12.05 | 43.57 | 53.47 |
| 28 | 201,202 | 851,233 | 848,163 | 2,164,770 | 9 | 8 | 9 | 5 | 9.29 | 39.32 | 39.32 | 23.64 | 23.72 |
| 32 | 399,739 | 7,110,375 | 1,035,148 | - | 9 | 8 | 9 | 1 | - | 5.62 | 38.62 | ||
| 36 | 341,667 | 8,615,200 | 2,555,752 | - | 9 | 5 | 9 | 0 | - | - | - | 3.97 | 13.37 |
| 40 | 985,862 | 9,327,397 | 5,771,614 | - | 9 | 2 | 8 | 0 | - | - | - | 10.57 | 17.08 |
| Ave | 266,682 | 2,998,383 | 1,233,465 | - | - | - | - | - | 9.55 | 29.52 | 19.89 | 27.38 | 40.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Ji, B.; Yu, S.S.; Zhou, S.; Fang, X. Branch-And-Price Algorithm for the Tramp Ship Routing and Scheduling Problem Considering Ship Speed and Payload. J. Mar. Sci. Eng. 2022, 10, 1811. https://doi.org/10.3390/jmse10121811
Li L, Ji B, Yu SS, Zhou S, Fang X. Branch-And-Price Algorithm for the Tramp Ship Routing and Scheduling Problem Considering Ship Speed and Payload. Journal of Marine Science and Engineering. 2022; 10(12):1811. https://doi.org/10.3390/jmse10121811
Chicago/Turabian StyleLi, Lingzi, Bin Ji, Samson S. Yu, Saiqi Zhou, and Xiaoping Fang. 2022. "Branch-And-Price Algorithm for the Tramp Ship Routing and Scheduling Problem Considering Ship Speed and Payload" Journal of Marine Science and Engineering 10, no. 12: 1811. https://doi.org/10.3390/jmse10121811
APA StyleLi, L., Ji, B., Yu, S. S., Zhou, S., & Fang, X. (2022). Branch-And-Price Algorithm for the Tramp Ship Routing and Scheduling Problem Considering Ship Speed and Payload. Journal of Marine Science and Engineering, 10(12), 1811. https://doi.org/10.3390/jmse10121811








