Potential Influence of Offshore Wind Farms on the Marine Stratification in the Waters Adjacent to China
Abstract
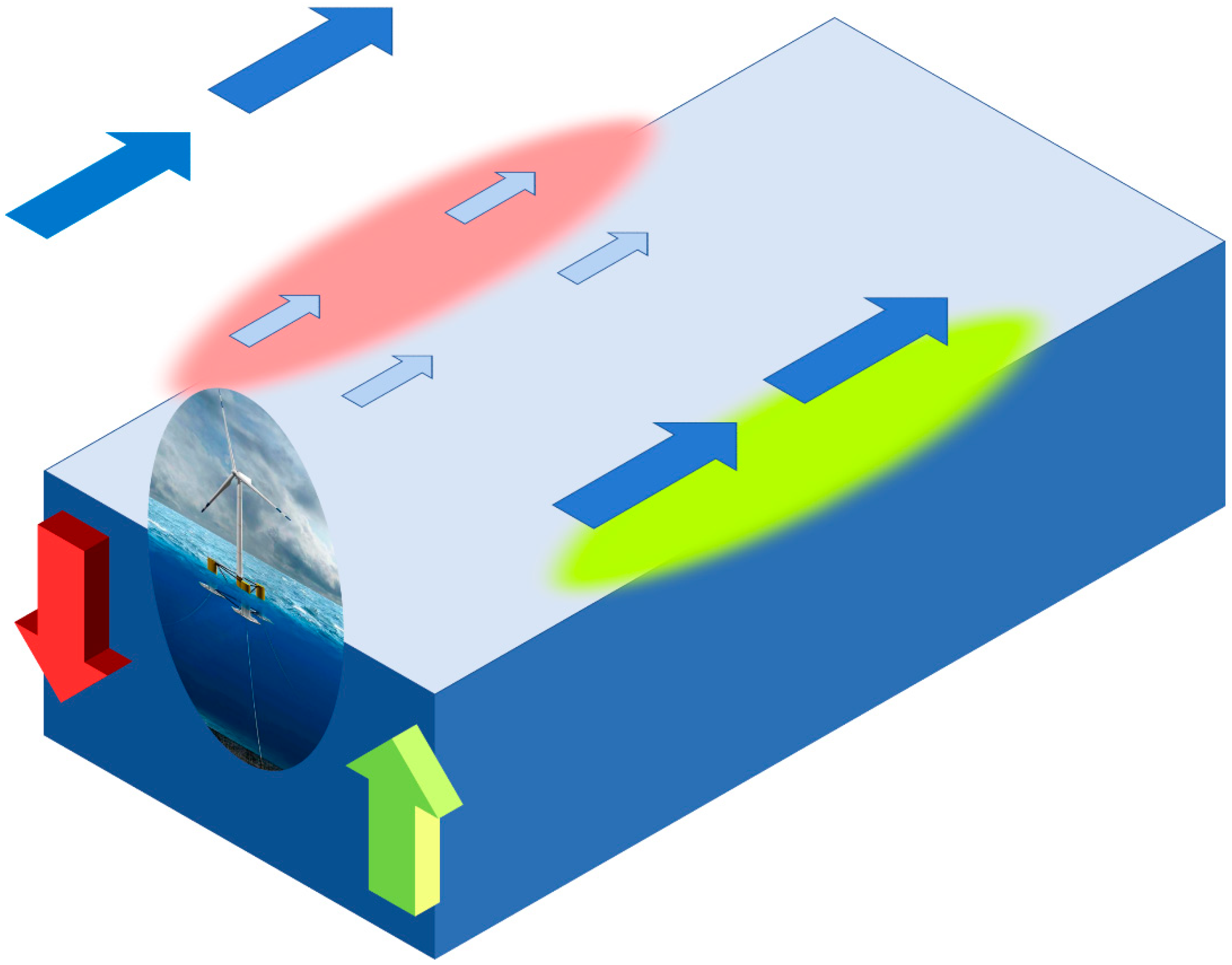
1. Introduction
2. Methodology
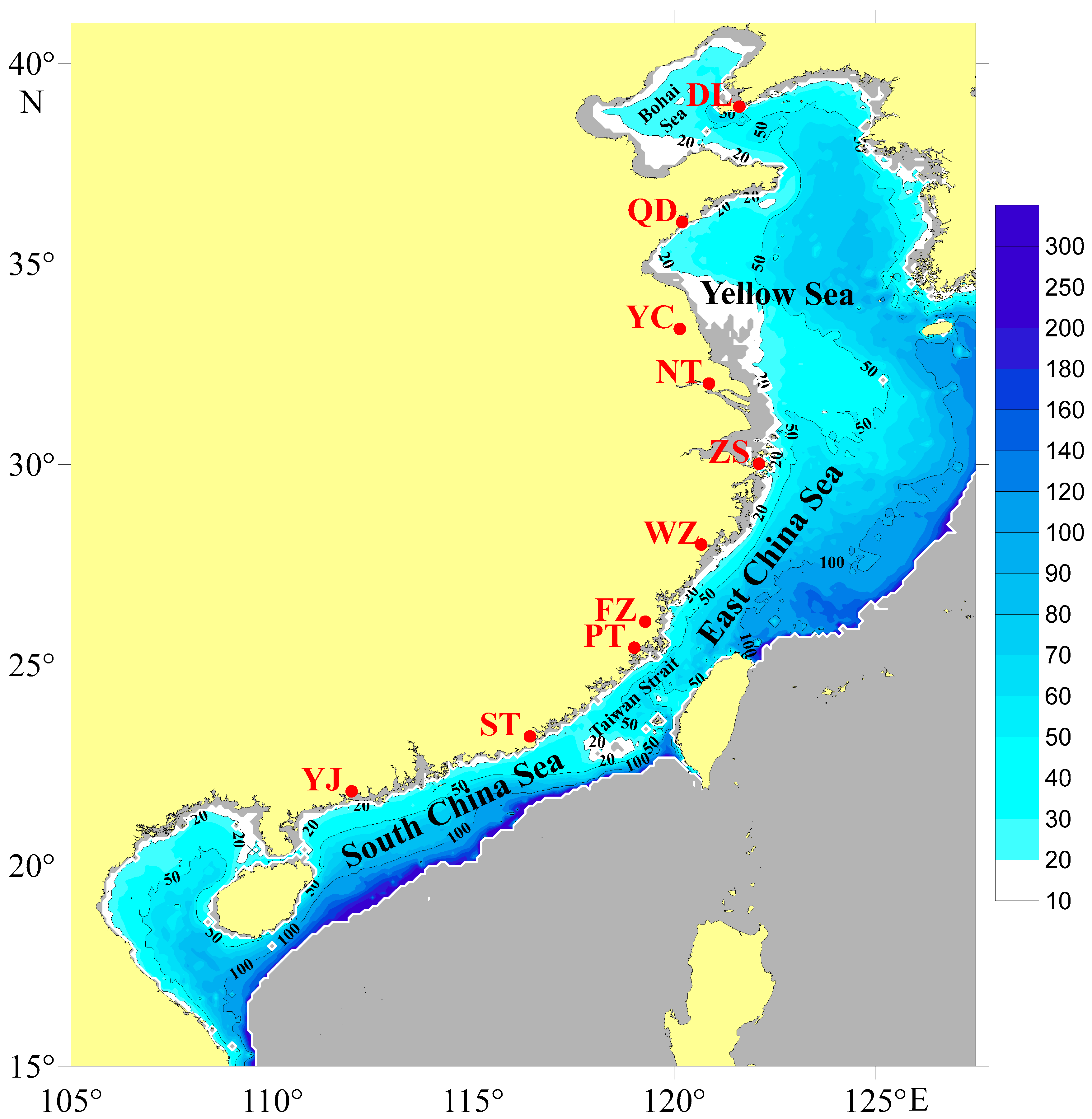
2.1. Study Region
2.2. Basic Equations
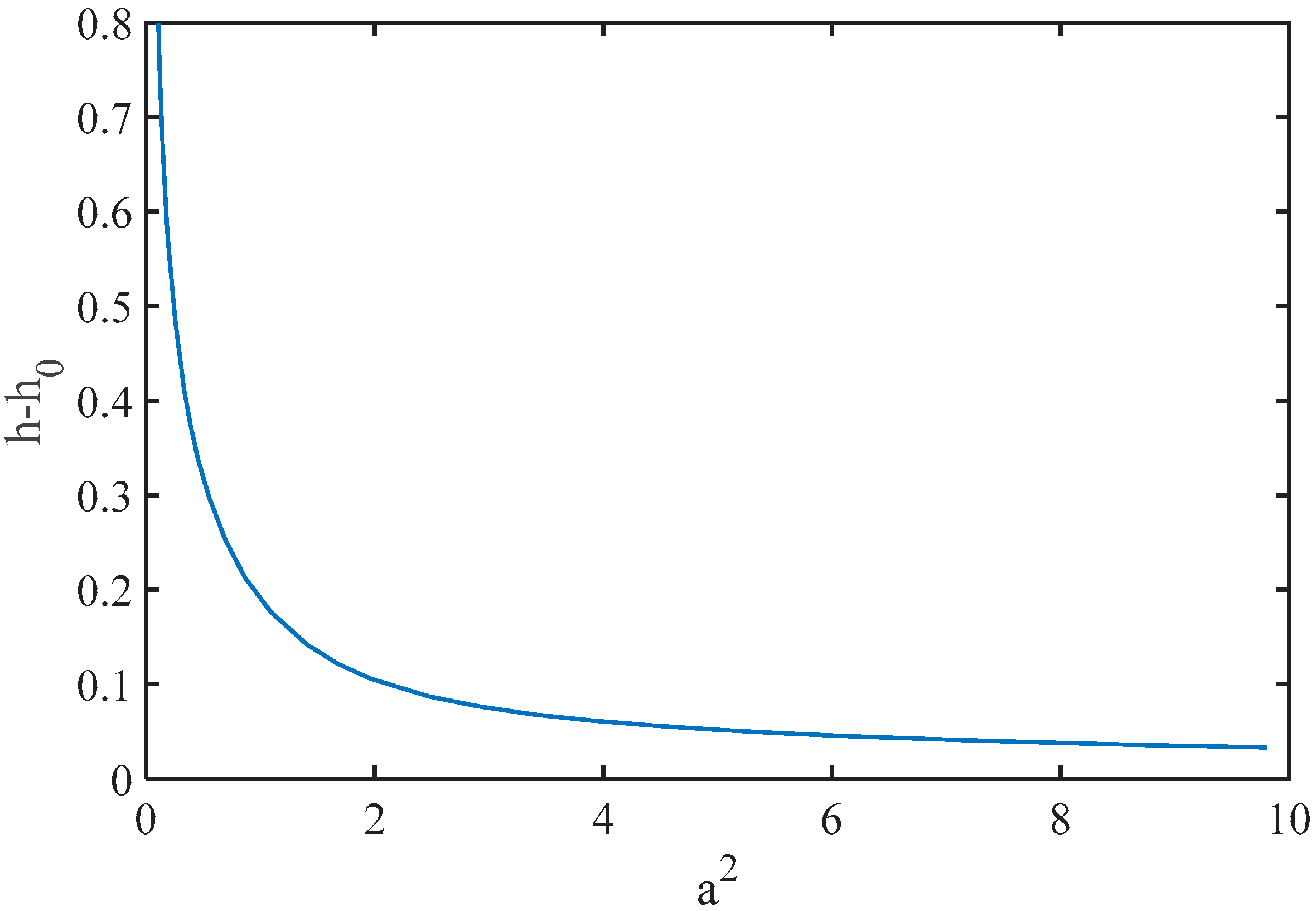
2.3. Definition of the Upper Layer Depth (ULD)
2.4. Data
3. Results
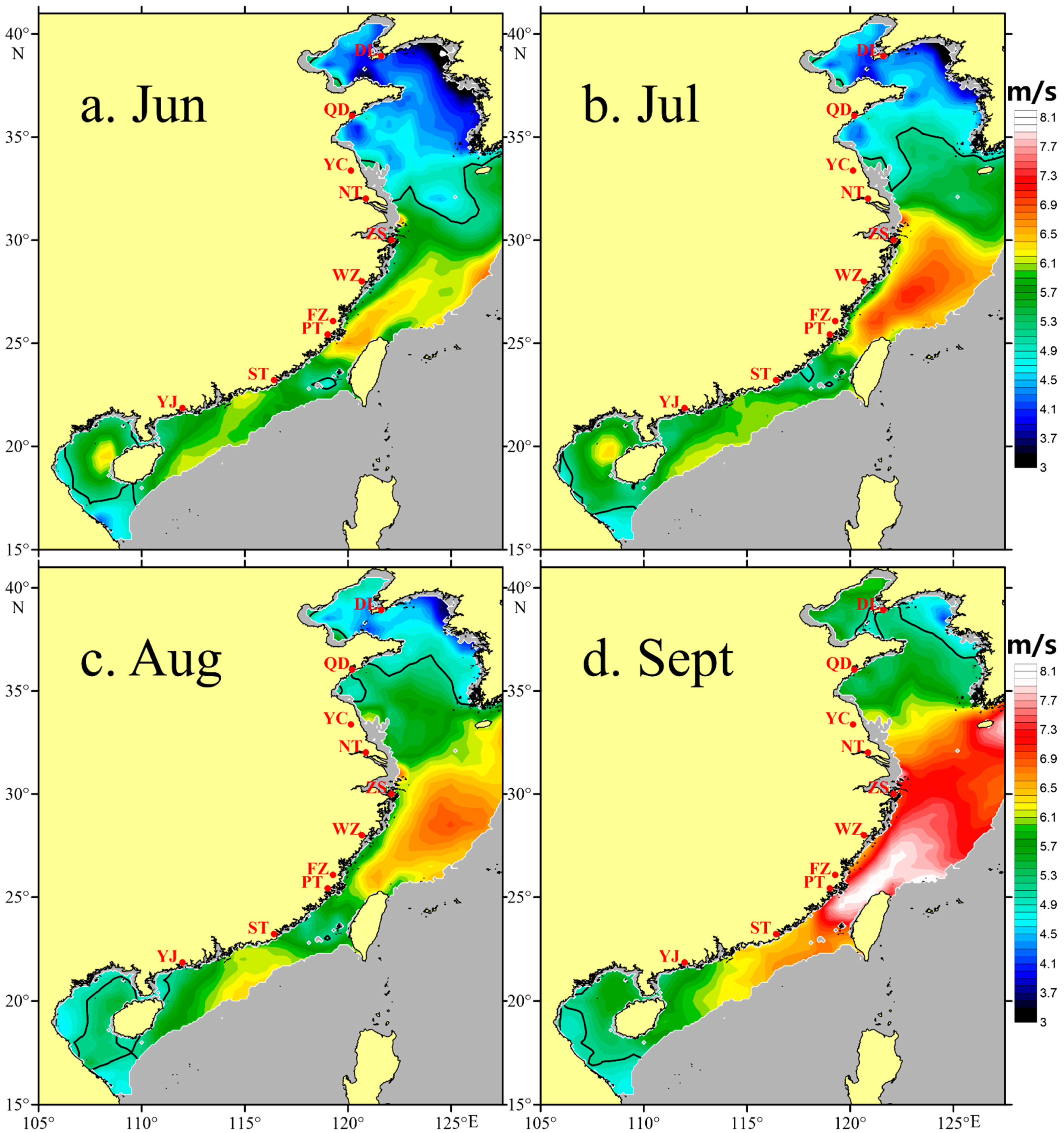
3.1. Climatological Mean of Dynamic Marine and Atmosphere Factors
3.2. Impact of OWFs Layout on Marine Stratification
4. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Esteban, M.D.; Diez, J.J.; López, J.S.; Negro, V. Why offshore wind energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Díaz, H.; Guedes Soares, C. Review of the current status, technology and future trends of offshore wind farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, X.; Yuan, J.; Liu, X.; Hu, H.; Lin, P. A Review of the Development of Key Technologies for Offshore Wind Power in China. J. Mar. Sci. Eng. 2022, 10, 929. [Google Scholar] [CrossRef]
- Hall, R.; Topham, E.; João, E. Environmental Impact Assessment for the decommissioning of offshore wind farms. Renew. Sustain. Energy Rev. 2022, 165, 112580. [Google Scholar] [CrossRef]
- Ivanov, E.; Capet, A.; De Borger, E.; Degraer, S.; Delhez, E.J.M.; Soetaert, K.; Vanaverbeke, J.; Grégoire, M. Offshore Wind Farm Footprint on Organic and Mineral Particle Flux to the Bottom. Front. Mar. Sci. 2021, 8, 631799. [Google Scholar] [CrossRef]
- Slavik, K.; Lemmen, C.; Zhang, W.; Kerimoglu, O.; Klingbeil, K.; Wirtz, K.W. The large-scale impact of offshore wind farm structures on pelagic primary productivity in the southern North Sea. Hydrobiologia 2019, 845, 35–53. [Google Scholar] [CrossRef]
- Jiao, N.; Liu, J.; Jiao, F.; Chen, Q.; Wang, X. Microbes mediated comprehensive carbon sequestration for negative emission in the ocean. Natl. Sci. Rev. 2020, 7, 1858–1860. [Google Scholar] [CrossRef]
- Jiao, N.; Cai, R.; Zheng, Q.; Tang, K.; Liu, J.; Jiao, F.; Wallace, D.; Chen, F.; Li, C.; Amann, R.; et al. Unveiling the enigma of refractory carbon in the ocean. Natl. Sci. Rev. 2018, 5, 459–463. [Google Scholar] [CrossRef]
- Worden, A.Z.; Follows, M.J.; Giovannoni, S.J.; Wilken, S.; Zimmerman, A.E.; Keeling, P.J. Rethinking the marine carbon cycle: Factoring in the multifarious lifestyles of microbes. Science 2015, 347, 1257594. [Google Scholar] [CrossRef]
- Cazenave, P.W.; Torres, R.; Allen, J.I. Unstructured grid modelling of offshore wind farm impacts on seasonally stratified shelf seas. Prog. Oceanogr. 2016, 145, 25–41. [Google Scholar] [CrossRef]
- Frandsen, S. On the wind speed reduction in the center of large clusters of wind turbines. J. Wind Eng. Ind. Aerodyn. 1992, 39, 251–265. [Google Scholar] [CrossRef]
- Christiansen, M.B.; Hasager, C.B. Wake effects of large offshore wind farms identified from satellite SAR. Remote Sens. Environ. 2005, 98, 251–268. [Google Scholar] [CrossRef]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Zhao, L.; Xue, L.; Li, Z.; Wang, J.; Yang, Z.; Xue, Y. Progress on Offshore Wind Farm Dynamic Wake Management for Energy. J. Mar. Sci. Eng. 2022, 10, 1395. [Google Scholar] [CrossRef]
- Broström, G. On the influence of large wind farms on the upper ocean circulation. J. Mar. Syst. 2008, 74, 585–591. [Google Scholar] [CrossRef]
- Ahsbahs, T.; Badger, M.; Volker, P.; Hansen, K.S.; Hasager, C.B. Applications of satellite winds for the offshore wind farm site Anholt. Wind Energy Sci. 2018, 3, 573–588. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Newcombe, A.C. Wake behind an offshore wind farm observed with dual-Doppler radars. J. Phys. Conf. Ser. 2018, 1037, 072008. [Google Scholar] [CrossRef]
- Cañadillas, B.; Foreman, R.; Barth, V.; Siedersleben, S.; Lampert, A.; Platis, A.; Djath, B.; Schulz-Stellenfleth, J.; Bange, J.; Emeis, S.; et al. Offshore wind farm wake recovery: Airborne measurements and its representation in engineering models. Wind Energy 2020, 23, 1249–1265. [Google Scholar] [CrossRef]
- Van der Hoven, I. Power sprecturm of horizontal wind speed in the frequency range from 0.0007 to 900 cycles per hour. J. Atmos. Sci. 1957, 14, 160–164. [Google Scholar] [CrossRef]
- Ludewig, E. On the Effect of Offshore Wind Farms on the Atmosphere and Ocean Dynamics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Platis, A.; Siedersleben, S.K.; Bange, J.; Lampert, A.; Bärfuss, K.; Hankers, R.; Cañadillas, B.; Foreman, R.; Schulz-Stellenfleth, J.; Djath, B. First in situ evidence of wakes in the far field behind offshore wind farms. Sci. Rep. 2018, 8, 2163. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1987; Volume 710. [Google Scholar]
- Lange, M.; Burkhard, B.; Garthe, S.; Gee, K.; Kannen, A.; Lenhart, H.; Windhorst, W. Analyzing Coastal and Marine Changes: Offshore Wind Farming as a Case Study, 1383–4304; GKSS Research Center: Geesthacht, Germany, 2010; p. 212. [Google Scholar]
- Paskyabi, M.B.; Fer, I. Upper Ocean Response to Large Wind Farm Effect in the Presence of Surface Gravity Waves. Energy Procedia 2012, 24, 245–254. [Google Scholar] [CrossRef]
- Afsharian, S.; Taylor, P.A. On the Potential Impact of Lake Erie Wind Farms on Water Temperatures and Mixed-Layer Depths: Some Preliminary 1-D Modeling Using COHERENS. J. Geophys. Res. Ocean. 2019, 124, 1736–1749. [Google Scholar] [CrossRef]
- Floeter, J.; van Beusekom, J.E.E.; Auch, D.; Callies, U.; Carpenter, J.; Dudeck, T.; Eberle, S.; Eckhardt, A.; Gloe, D.; Hänselmann, K.; et al. Pelagic effects of offshore wind farm foundations in the stratified North Sea. Prog. Oceanogr. 2017, 156, 154–173. [Google Scholar] [CrossRef]
- Floeter, J.; Pohlmann, T.; Harmer, A.; Möllmann, C. Chasing the offshore wind farm wind-wake-induced upwelling/downwelling dipole. Front. Mar. Sci. 2022, 9, 1390. [Google Scholar] [CrossRef]
- Fennel, W.; Lass, H.U. On the impact of wind curls on coastal currents. J. Mar. Syst. 2007, 68, 128–142. [Google Scholar] [CrossRef]
- Albert, A.; Echevin, V.; Lévy, M.; Aumont, O. Impact of nearshore wind stress curl on coastal circulation and primary productivity in the Peru upwelling system. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Farr, H.; Ruttenberg, B.; Walter, R.K.; Wang, Y.-H.; White, C. Potential environmental effects of deepwater floating offshore wind energy facilities. Ocean Coast. Manag. 2021, 207, 105611. [Google Scholar] [CrossRef]
- Okkonen, S.; Niebauer, H. Ocean circulation in the Bering Sea marginal ice edge zone from Acoustic Doppler Current Profiler observations. Cont. Shelf Res. 1995, 15, 1879–1902. [Google Scholar] [CrossRef]
- Foreman, R.; Cañadillas, B.; Neumann, T.; Emeis, S. Measurements of heat and humidity fluxes in the wake of offshore wind turbines. J. Renew. Sustain. Energy 2017, 9, 053304. [Google Scholar] [CrossRef]
- Paskyabi, M.B. Offshore Wind Farm Wake Effect on Stratification and Coastal Upwelling. Energy Procedia 2015, 80, 131–140. [Google Scholar] [CrossRef][Green Version]
- Carpenter, J.R.; Merckelbach, L.; Callies, U.; Clark, S.; Gaslikova, L.; Baschek, B. Potential impacts of offshore wind farms on North Sea stratification. PLoS ONE 2016, 11, e0160830. [Google Scholar] [CrossRef] [PubMed]
- Siedersleben, S.K.; Lundquist, J.K.; Platis, A.; Bange, J.; Bärfuss, K.; Lampert, A.; Cañadillas, B.; Neumann, T.; Emeis, S. Micrometeorological impacts of offshore wind farms as seen in observations and simulations. Environ. Res. Lett. 2018, 13, 124012. [Google Scholar] [CrossRef]
- Mallapaty, S. How China could be carbon neutral by mid-century. Nature 2020, 586, 482–483. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, J.; Chen, X.; Zhao, Y. China in global wind power development: Role, status and impact. Renew. Sustain. Energy Rev. 2020, 127, 109881. [Google Scholar] [CrossRef]
- Global Wind Energy Council. GWEC Global Wind Report 2019; Global Wind Energy Council: Brussels, Belgium, 2019. [Google Scholar]
- Notice on the Development Strategy of Offshore Wind Farms in Guangdong Issued by Guangdong Provincial on Development and Reform Commission. Available online: http://drc.gd.gov.cn/gkmlpt/content/1/1060/post_1060661.html#876 (accessed on 26 October 2022).
- Yang, Q.; Chen, G.Q.; Liao, S.; Zhao, Y.H.; Peng, H.W.; Chen, H.P. Environmental sustainability of wind power: An emergy analysis of a Chinese wind farm. Renew. Sustain. Energy Rev. 2013, 25, 229–239. [Google Scholar] [CrossRef]
- Leung, D.Y.C.; Yang, Y. Wind energy development and its environmental impact: A review. Renew. Sustain. Energy Rev. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Chang, K.-T.; Jeng, D.-S. Numerical study for wave-induced seabed response around offshore wind turbine foundation in Donghai offshore wind farm, Shanghai, China. Ocean Eng. 2014, 85, 32–43. [Google Scholar] [CrossRef]
- Wang, T.; Ru, X.; Deng, B.; Zhang, C.; Wang, X.; Yang, B.; Zhang, L. Evidence that offshore wind farms might affect marine sediment quality and microbial communities. Sci. Total Environ. 2023, 856, 158782. [Google Scholar] [CrossRef]
- Wang, T.; Yu, W.; Zou, X.; Zhang, D.; Li, B.; Wang, J.; Zhang, H. Zooplankton Community Responses and the Relation to Environmental Factors from Established Offshore Wind Farms within the Rudong Coastal Area of China. J. Coast. Res. 2017, 34, 843–855. [Google Scholar] [CrossRef]
- Wang, T.; Zou, X.; Li, B.; Yao, Y.; Li, J.; Hui, H.; Yu, W.; Wang, C. Microplastics in a wind farm area: A case study at the Rudong Offshore Wind Farm, Yellow Sea, China. Mar. Pollut. Bull. 2018, 128, 466–474. [Google Scholar] [CrossRef]
- Huang, C.-T.; Afero, F.; Hung, C.-W.; Chen, B.-Y.; Nan, F.-H.; Chiang, W.-S.; Tang, H.-J.; Kang, C.-K. Economic feasibility assessment of cage aquaculture in offshore wind power generation areas in Changhua County, Taiwan. Aquaculture 2022, 548, 737611. [Google Scholar] [CrossRef]
- Wang, J.; Zou, X.; Yu, W.; Zhang, D.; Wang, T. Effects of established offshore wind farms on energy flow of coastal ecosystems: A case study of the Rudong offshore wind farms in China. Ocean Coast. Manag. 2019, 171, 111–118. [Google Scholar] [CrossRef]
- Yang, J.; Chang, Y.; Zhang, L.; Hao, Y.; Yan, Q.; Wang, C. The life-cycle energy and environmental emissions of a typical offshore wind farm in China. J. Clean. Prod. 2018, 180, 316–324. [Google Scholar] [CrossRef]
- Li, H.; Jiang, H.-D.; Dong, K.-Y.; Wei, Y.-M.; Liao, H. A comparative analysis of the life cycle environmental emissions from wind and coal power: Evidence from China. J. Clean. Prod. 2020, 248, 119192. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, R.; Wang, Y.; Yan, H.; Liu, Q.; Guo, Y.; Ren, Y. A New Framework for Assessment of Offshore Wind Farm Location. J. Mar. Sci. Eng. 2022, 15, 6758. [Google Scholar] [CrossRef]
- Make, M.; Vaz, G. Analyzing scaling effects on offshore wind turbines using CFD. Renew. Energy 2015, 83, 1326–1340. [Google Scholar] [CrossRef]
- Yang, D.; Meneveau, C.; Shen, L. Large-eddy simulation of offshore wind farm. Phys. Fluids 2014, 26, 025101. [Google Scholar] [CrossRef]
- Hao, J.; Chen, Y.; Wang, F.; Lin, P. Seasonal thermocline in the China Seas and northwestern Pacific Ocean. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Locarnini, R.A.; Mishonov, A.V.; Antonov, J.I.; Boyer, T.P.; Garcia, H.E.; Baranova, O.K.; Zweng, M.M.; Paver, C.R.; Reagan, J.R.; Johnson, D.R.; et al. World Ocean Atlas 2013, Volume 1: Temperature; NOAA Atlas NESDIS 73; Ocean Climate Laboratory, National Oceanographic Data Center: Washington, DC, USA, 2013; p. 40. [Google Scholar]
- Colorado Research Associates/Northwest Research Associates/Inc. N.R. QSCAT/NCEP Blended Ocean Winds from Colorado Research Associates (Version 5.0), Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory: Boulder, CO, USA, 1999–2009. Available online: http://rda.ucar.edu/datasets/ds744.4/ (accessed on 4 October 2021).
- Yelland, M.; Taylor, P.K. Wind Stress Measurements from the Open Ocean. J. Phys. Oceanogr. 1996, 26, 541–558. [Google Scholar] [CrossRef]
- Zheng, C.W.; Pan, J. Assessment of the global ocean wind energy resource. Renew. Sustain. Energy Rev. 2014, 33, 382–391. [Google Scholar] [CrossRef]
- Larsén, X.G.; Fischereit, J. A case study of wind farm effects using two wake parameterizations in the Weather Research and Forecasting (WRF) model (V3.7.1) in the presence of low-level jets. Geosci. Model. Dev. 2021, 14, 3141–3158. [Google Scholar] [CrossRef]
- Zhang, T.; Tian, B.; Sengupta, D.; Zhang, L.; Si, Y. Global offshore wind turbine dataset. Sci. Data 2021, 8, 191. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Z.; Liu, K.; Yang, T. Potential Influence of Offshore Wind Farms on the Marine Stratification in the Waters Adjacent to China. J. Mar. Sci. Eng. 2022, 10, 1872. https://doi.org/10.3390/jmse10121872
Lian Z, Liu K, Yang T. Potential Influence of Offshore Wind Farms on the Marine Stratification in the Waters Adjacent to China. Journal of Marine Science and Engineering. 2022; 10(12):1872. https://doi.org/10.3390/jmse10121872
Chicago/Turabian StyleLian, Zhan, Kun Liu, and Tong Yang. 2022. "Potential Influence of Offshore Wind Farms on the Marine Stratification in the Waters Adjacent to China" Journal of Marine Science and Engineering 10, no. 12: 1872. https://doi.org/10.3390/jmse10121872
APA StyleLian, Z., Liu, K., & Yang, T. (2022). Potential Influence of Offshore Wind Farms on the Marine Stratification in the Waters Adjacent to China. Journal of Marine Science and Engineering, 10(12), 1872. https://doi.org/10.3390/jmse10121872





