Accumulation and Dispersion of Microplastics near A Submerged Structure: Basic Study Using A Numerical Wave Tank
Abstract
:1. Introduction
2. Materials and Methods
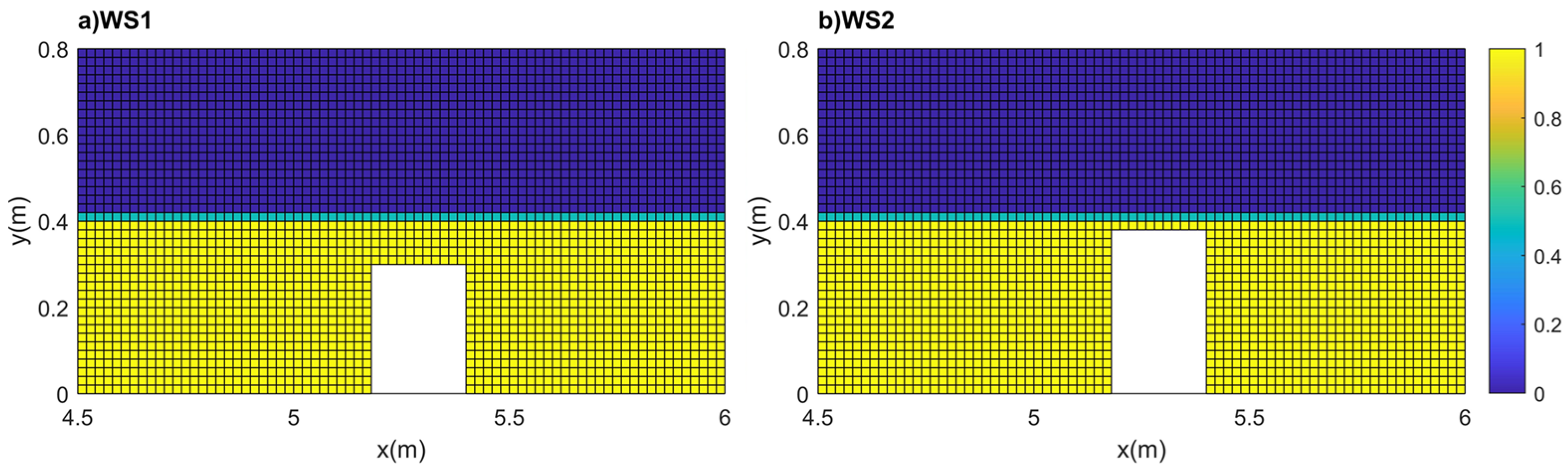
2.1. Basic Model Setups
2.2. Volume of Fluid and Wave Generation
2.3. Microplastic Simulation by Discrete Phase Model
2.4. Numerical Simulation Case Study
3. Results
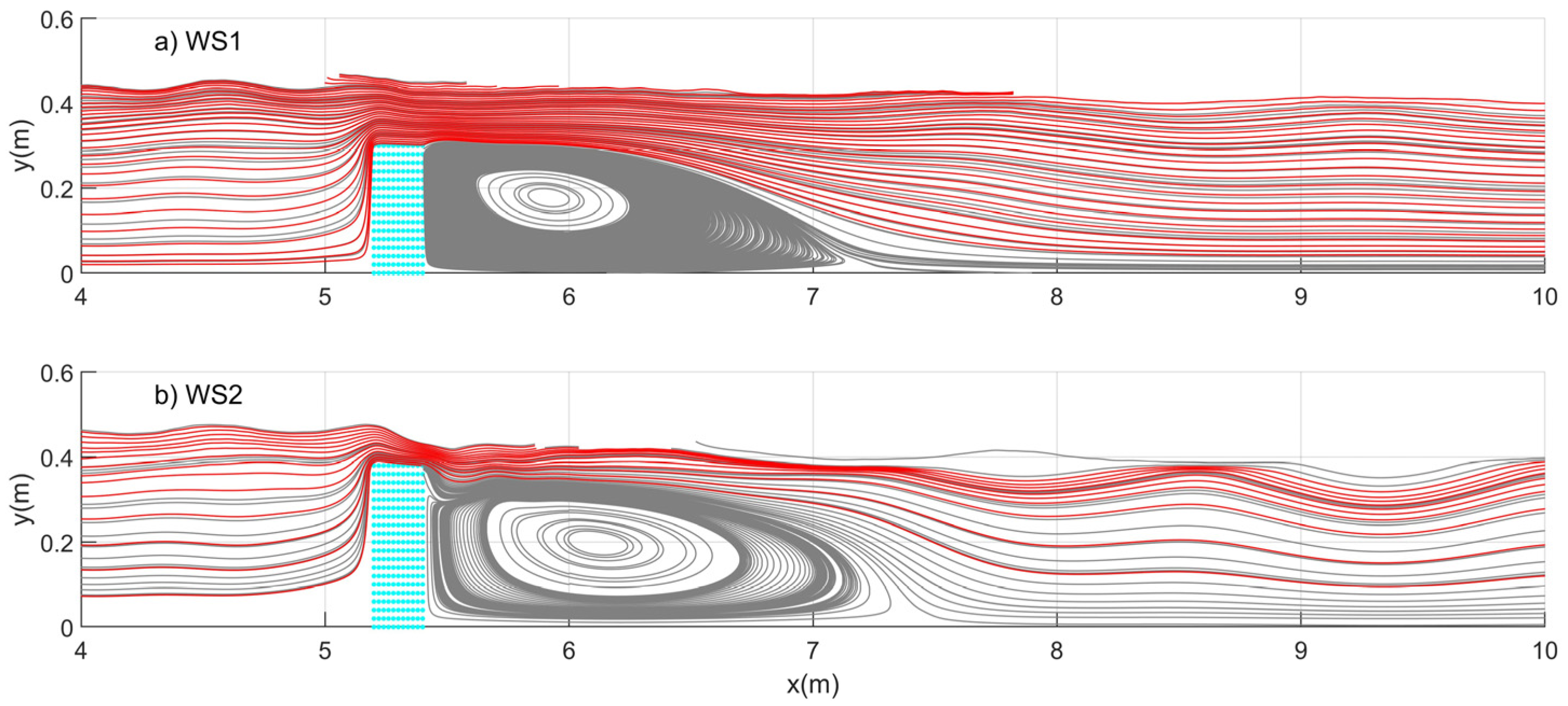
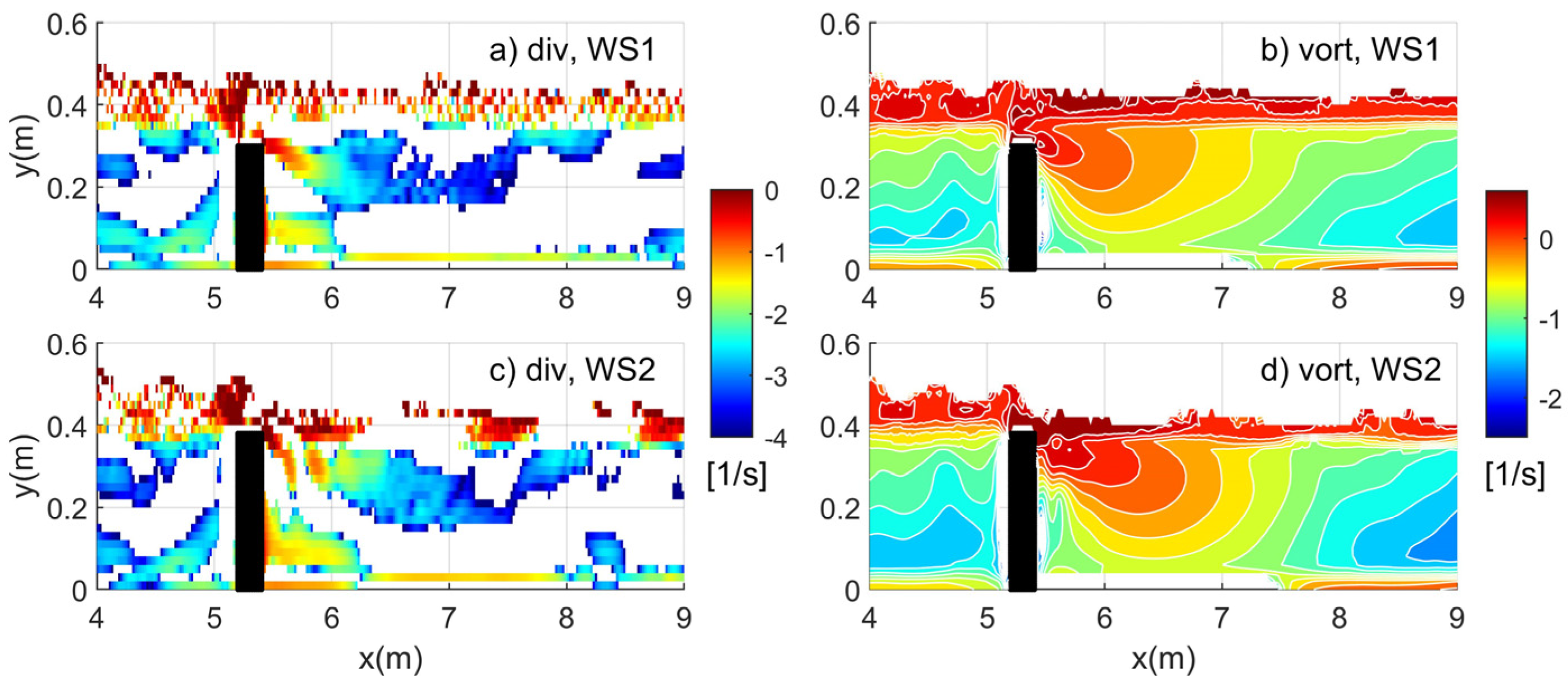
3.1. Eulerian Observations
3.2. General Particle Behaviors
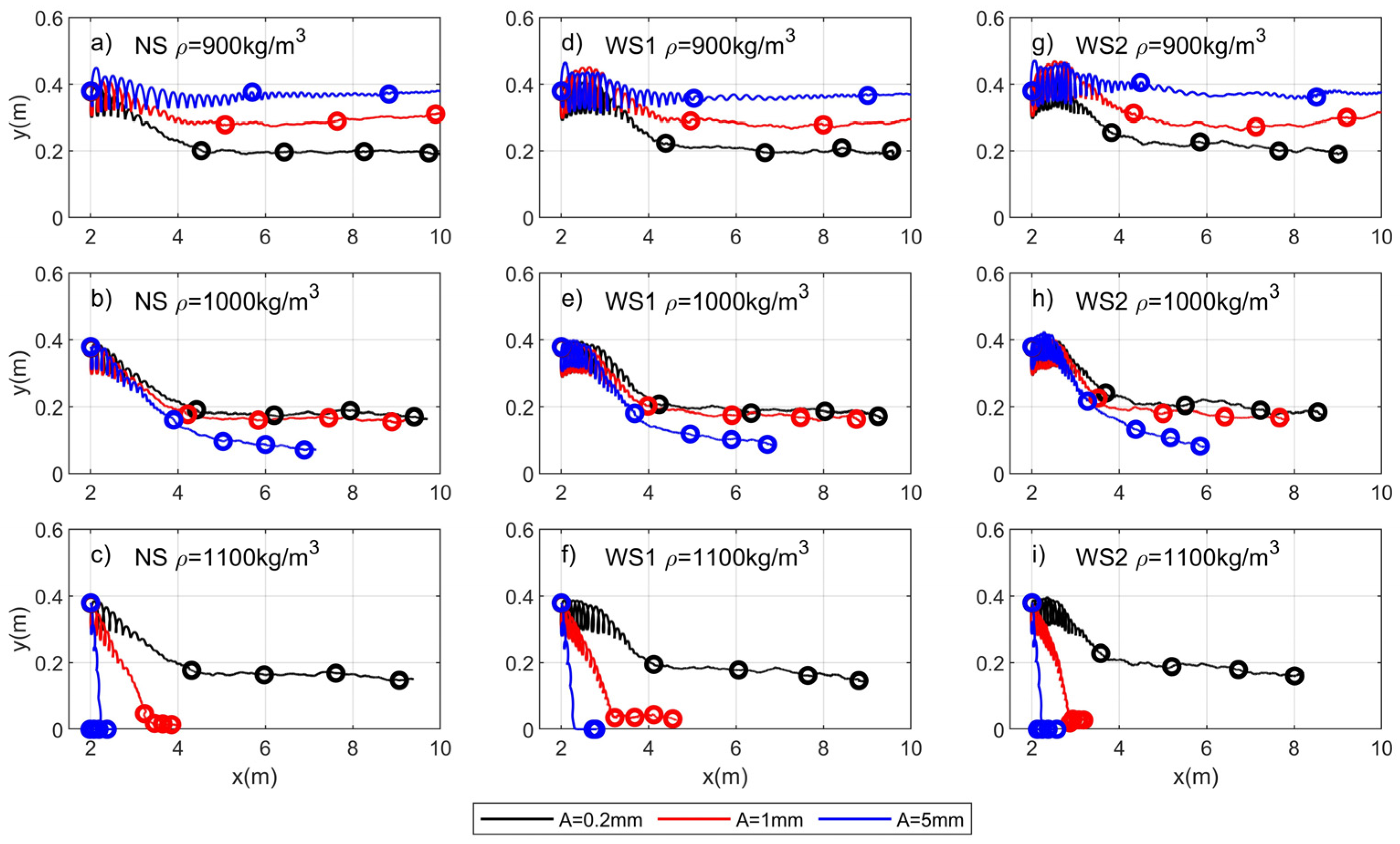
3.3. Mean Particle Trajectories
4. Discussion
4.1. Microplastic Accumulation
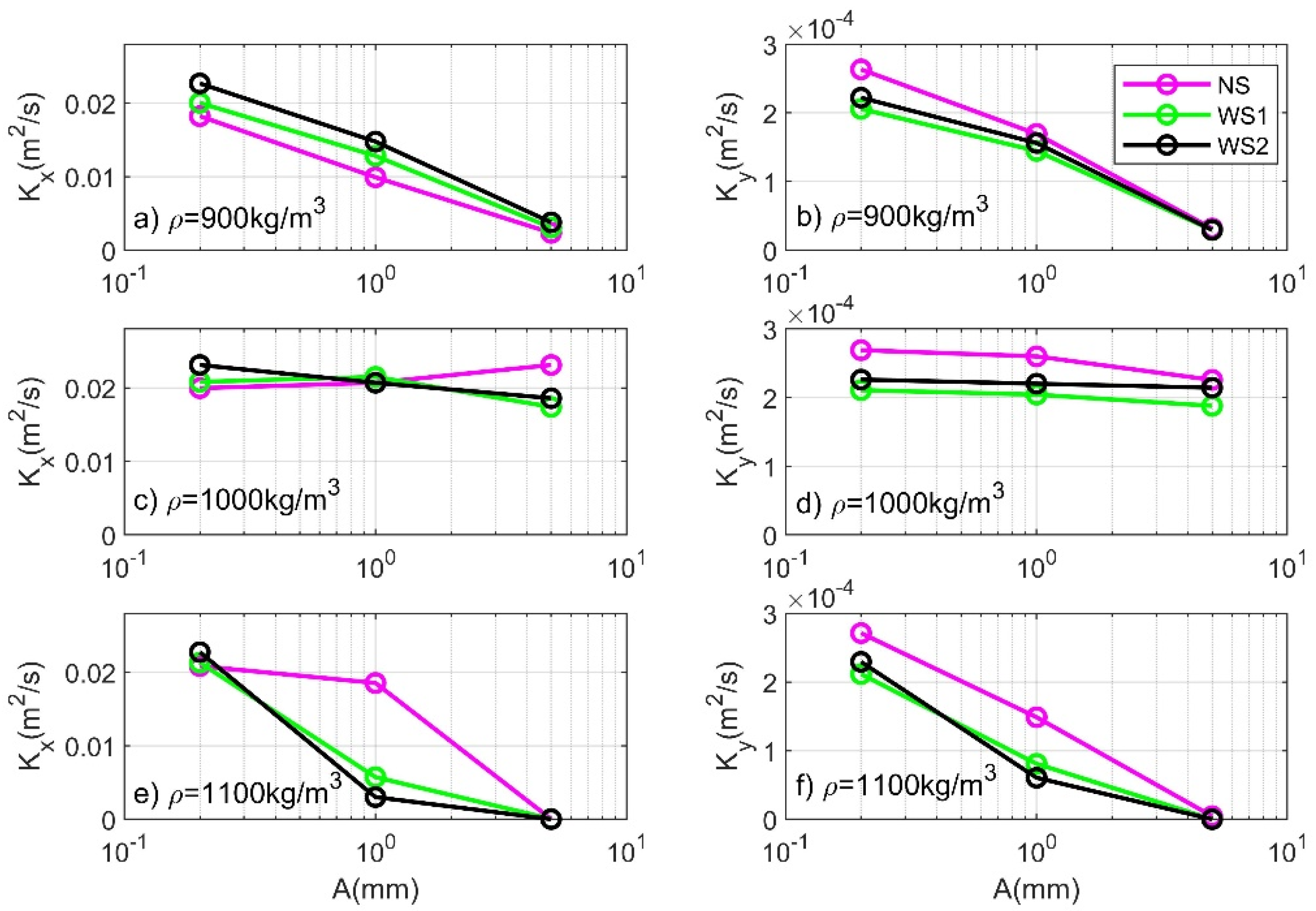
4.2. Microplastic Dispersion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koelmans Albert, A.; Redondo-Hasselerharm, P.E.; Nor, N.H.; de Ruijter, V.N.; Mintenig, S.M.; Kooi, M. Risk assessment of microplastic particles. Nat. Rev. Mater. 2022, 7, 138–152. [Google Scholar] [CrossRef]
- Li, C.; Zhu, L.; Wang, X.; Liu, K.; Li, D. Cross-oceanic distribution and origin of microplastics in the subsurface water of the South China Sea and Eastern Indian Ocean. Sci. Total Environ. 2022, 805, 150243. [Google Scholar] [CrossRef] [PubMed]
- Tien, C.-J.; Wang, Z.-X.; Colin, S.C. Microplastics in water, sediment and fish from the Fengshan River system: Relationship to aquatic factors and accumulation of polycyclic aromatic hydrocarbons by fish. Environ. Pollut. 2020, 265, 114962. [Google Scholar] [CrossRef]
- Abeynayaka, A.; Kojima, F.; Miwa, Y.; Ito, N.; Nihei, Y.; Fukunaga, Y.; Yashima, Y.; Itsubo, N. Rapid sampling of suspended and floating microplastics in challenging riverine and coastal water environments in Japan. Water 2020, 12, 1903. [Google Scholar] [CrossRef]
- Crawford, C.B.; Quinn, B. 5-Microplastics, standardisation and spatial distribution. In Microplastic Pollutants; Elsevier: Amsterdam, The Netherlands, 2017; pp. 101–130. [Google Scholar]
- Law, K.L. Plastics in the marine environment. Annu. Rev. Mar. Sci. 2017, 9, 205–229. [Google Scholar] [CrossRef] [Green Version]
- McAfee, D.; Connell, S.D. The global fall and rise of oyster reefs. Front. Ecol. Environ. 2021, 19, 118–125. [Google Scholar] [CrossRef]
- Caputo, F.; Vogel, R.; Savage, J.; Vella, G.; Law, A.; Della Camera, G.; Hannon, G.; Peacock, B.; Mehn, D.; Ponti, J.; et al. Measuring particle size distribution and mass concentration of nanoplastics and microplastics: Addressing some analytical challenges in the sub-micron size range. J. Colloid Interface Sci. 2021, 588, 401–417. [Google Scholar] [CrossRef] [PubMed]
- de Paiva JN, S.; Walles, B.; Ysebaert, T.; Bouma, T.J. Understanding the conditionality of ecosystem services: The effect of tidal flat morphology and oyster reef characteristics on sediment stabilization by oyster reefs. Ecol. Eng. 2018, 112, 89–95. [Google Scholar] [CrossRef]
- Shnada, A.H.; Emenike, C.U.; Fauziah, S.H. Distribution and importance of microplastics in the marine environment: A review of the sources, fate, effects, and potential solutions. Environ. Int. 2017, 102, 165–176. [Google Scholar]
- Chubarenko, I.; Esiukova, E.; Bagaev, A.; Isachenko, I.; Demchenko, N.; Zobkov, M.; Efimova, I.; Bagaeva, M.; Khatmullina, L. Behavior of microplastics in coastal zones. In Microplastic Contamination in Aquatic Environments; Elsevier: Amsterdam, The Netherlands, 2018; pp. 175–223. [Google Scholar]
- Rezania, S.; Park, J.; Din, M.F.; Taib, S.M.; Talaiekhozani, A.; Yadav, K.K.; Kamyab, H. Microplastics pollution in different aquatic environments and biota: A review of recent studies. Mar. Pollut. Bull. 2018, 133, 191–208. [Google Scholar] [CrossRef]
- Savoca, S.; Bottari, T.; Fazio, E.; Bonsignore, M.; Mancuso, M.; Luna, G.M.; Romeo, T.; D’Urso, L.; Capillo, G.; Panarello, G.; et al. Plastics occurrence in juveniles of Engraulis encrasicolus and Sardina pilchardus in the Southern Tyrrhenian Sea. Sci. Total Environ. 2020, 718, 137457. [Google Scholar] [CrossRef] [PubMed]
- Savoca, M.S.; McInturf, A.G.; Hazen, E.L. Plastic ingestion by marine fish is widespread and increasing. Glob. Chang. Biol. 2021, 27, 2188–2199. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Nag, R.; Cummins, E. Human health concerns regarding microplastics in the aquatic environment-From marine to food systems. Sci. Total Environ. 2022, 823, 153730. [Google Scholar] [CrossRef]
- Han, Z.; Jiang, T.; Xie, L.; Zhang, R. Microplastics impact shell and pearl biomineralization of the pearl oyster Pinctada fucata. Environ. Pollut. 2022, 293, 118522. [Google Scholar] [CrossRef] [PubMed]
- Heemink, A.W. Stochastic modelling of dispersion in shallow water. Stoch. Hydrol. Hydraul. 1990, 4, 161–174. [Google Scholar] [CrossRef] [Green Version]
- Spagnol, S.; Wolanski, E.; Deleersnijder, E.; Brinkman, R.; McAllister, F.; Cushman-Roisin, B.; Hanert, E. An error frequently made in the evaluation of advective transport in two-dimensional Lagrangian models of advection-diffusion in coral reef waters. Mar. Ecol. Prog. Ser. 2002, 235, 299–302. [Google Scholar] [CrossRef] [Green Version]
- Deleersnijder, E. A Depth-Integrated Diffusion Problem in a Depth-Varying, Unbounded Domain for Assessing Lagrangian Schemes. In Technical Report; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2015. [Google Scholar]
- Critchell, K.; Lambrechts, J. Modelling accumulation of marine plastics in the coastal zone; what are the dominant physical processes? Estuar. Coast. Shelf Sci. 2016, 171, 111–122. [Google Scholar] [CrossRef]
- van Bergeijk, V.; Warmink, J.; Frankena, M.; Hulscher, S. Modelling dike cover erosion by overtopping waves: The effects of transitions. Coast. Struct. 2019, 2019, 1097–1106. [Google Scholar]
- Camins, E.; de Haan, W.P.; Salvo, V.S.; Canals, M.; Raffard, A.; Sanchez-Vidal, A. Paddle surfing for science on microplastic pollution. Sci. Total Environ. 2020, 709, 136178. [Google Scholar] [CrossRef]
- Barrientos, E.E.; Paris, A.; Rohindra, D.; Rico, C. Presence and abundance of microplastics in edible freshwater mussel (Batissa violacea) on Fiji’s main island of Viti Levu. Mar. Freshw. Res. 2022, 73, 528–539. [Google Scholar] [CrossRef]
- Wu, Z.; Tweedley, J.R.; Loneragan, N.R.; Zhang, X. Artificial reefs can mimic natural habitats for fish and macroinvertebrates in temperate coastal waters of the Yellow Sea. Ecol. Eng. 2019, 139, 105579. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H.; Yu, D.; Song, J.; Duan, G. The migration of viscous fish eggs in artificial reefs. Ecol. Model. 2022, 469, 109985. [Google Scholar] [CrossRef]
- Zheng, Y.; Kuang, C.; Zhang, J.; Gu, J.; Chen, K.; Liu, X. Current and turbulence characteristics of perforated box-type artificial reefs in a constant water depth. Ocean Eng. 2022, 244, 110359. [Google Scholar] [CrossRef]
- Walles, B.; Troost, K.; van den Ende, D.; Nieuwhof, S.; Smaal, A.C.; Ysebaert, T. From artificial structures to self-sustaining oyster reefs. J. Sea Res. 2016, 108, 1–9. [Google Scholar] [CrossRef]
- Allan, R.P.; Hawkins, E.; Bellouin, N.; Collins, B. Summary for Policymakers. IPCC 2021, 2021, 3–32. [Google Scholar]
- Tebaldi, C.; Ranasinghe, R.; Vousdoukas, M.; Rasmussen, D.J.; Vega-Westhoff, B.; Kirezci, E.; Kopp, R.E.; Sriver, R.; Mentaschi, L. Extreme sea levels at different global warming levels. Nat. Clim. Chang. 2021, 11, 746–751. [Google Scholar] [CrossRef]
- Chowdhury, M.S.N. Ecological Engineering with Oysters for Coastal Resilience: Habitat Suitability, Bioenergetics, and Ecosystem Services. Ph.D. Thesis, Wageningen University and Research, Wageningen, The Netherlands, 2019. [Google Scholar]
- Wang, X.; Feng, J.; Lin, C.; Liu, H.; Chen, M.; Zhang, Y. Structural and Functional Improvements of Coastal Ecosystem Based on Artificial Oyster Reef Construction in the Bohai Sea, China. Front. Mar. Sci. 2022, 9, 829557. [Google Scholar] [CrossRef]
- Fodrie, F.J.; Rodriguez, A.B.; Gittman, R.K.; Grabowski, J.H.; Lindquist, N.L.; Peterson, C.H.; Piehler, M.F.; Ridge, J.T. Oyster reefs as carbon sources and sinks. Proc. R. Soc. B Biol. Sci. 2017, 284, 20170891. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Woo, J.; Yoon, H.S.; Na, W.B. Wake lengths and structural responses of Korean general artificial reefs. Ocean Eng. 2014, 92, 83–91. [Google Scholar] [CrossRef]
- Van Sebille, E.; Wilcox, C.; Lebreton, L.; Maximenko, N.; Hardesty, B.D.; Van Franeker, J.A.; Eriksen, M.; Siegel, D.; Galgani, F.; Law, K.L. A global inventory of small floating plastic debris. Environ. Res. Lett. 2015, 10, 124006. [Google Scholar] [CrossRef]
- Morteza, A.; Passandideh-Fard, M.; Moghiman, M. Fully nonlinear viscous wave generation in numerical wave tanks. Ocean Eng. 2013, 59, 73–85. [Google Scholar]
- Alsina, J.M.; Jongedijk, C.E.; van Sebille, E. Laboratory Measurements of the Wave-Induced Motion of Plastic Particles: Influence of Wave Period, Plastic Size and Plastic Density. J. Geophys. Res. Ocean. 2020, 125, e2020JC016294. [Google Scholar] [CrossRef]
- Eldeen AS, S.; El-Baz, A.M.; Elmarhomy, A.M. CFD Modeling of Regular and Irregular Waves Generated by Flap Type WaveMaker. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 85, 128–144. [Google Scholar] [CrossRef]
- Ma, Y.; Yuan, C.; Ai, C.; Dong, G. Comparison between a non-hydrostatic model and OpenFOAM for 2D wave-structure interactions. Ocean Eng. 2019, 183, 419–425. [Google Scholar] [CrossRef]
- Miquel, A.M.; Kamath, A.; Alagan Chella, M.; Archetti, R.; Bihs, H. Analysis of different methods for wave generation and absorption in a CFD-based numerical wave tank. J. Mar. Sci. Eng. 2018, 6, 73. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.Z.; Greaves, D.; Raby, A. Numerical wave tank study of extreme waves and wave-structure interaction using OpenFoam®. Ocean Eng. 2016, 126, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Oakley, O.H., Jr. CFD modeling of fully nonlinear water wave tank. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; ASME: New York, NY, USA, 2019; Volume 43451, pp. 815–823. [Google Scholar]
- Fatahi, M.; Akdogan, G.; Dorfling, C.; Van Wyk, P. Numerical Study of Microplastic Dispersal in Simulated Coastal Waters Using CFD Approach. Water 2021, 13, 3432. [Google Scholar] [CrossRef]
- Ahmadi, P.; Elagami, H.; Dichgans, F.; Schmidt, C.; Gilfedder, B.S.; Frei, S.; Peiffer, S.; Fleckenstein, J.H. Systematic Evaluation of Physical Parameters affecting the Terminal Settling Velocity of Microplastic Particles in Lakes using CFD. Front. Environ. Sci. 2022, 10, 389. [Google Scholar] [CrossRef]
- Morsi, S.A.J.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Okubo, A. Oceanic diffusion diagrams. In Deep Sea Research and Oceanographic Abstracts; Elsevier: Amsterdam, The Netherlands, 1971; Volume 18, pp. 789–802. [Google Scholar]
- Choi, J.; Troy, C.; Hawley, N.; McCormick, M.; Wells, M. Lateral dispersion of dye and drifters in the center of a very large lake. Limnol. Oceanogr. 2020, 65, 336–348. [Google Scholar] [CrossRef]
- Sundermeyer, M.A.; Ledwell, J.R. Lateral dispersion over the continental shelf: Analysis of dye release experiments. J. Geophys. Res. Ocean. 2001, 106, 9603–9621. [Google Scholar] [CrossRef]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1922, 2, 196–212. [Google Scholar] [CrossRef]


| Properties Meshing | |||||||
|---|---|---|---|---|---|---|---|
| Type Structure | Type Meshing/Method | Nodes | Elements | Average Surface Area | Minimum Edge Length (m) | Element Order | Grid Size (m) |
| NS | Rectangular/ Quadrilaterals | 24,641 | 24,000 | 9.6 | 0.8 | Linear | 0.02 |
| WS1 | Rectangular/ Quadrilaterals | 24,506 | 23,850 | 9.54 | 0.2 | Linear | 0.02 |
| WS2 | Rectangular/ Quadrilaterals | 24,470 | 23,810 | 9.52 | 0.2 | Linear | 0.02 |
| A (mm) | NS | WS1 | WS2 | |
|---|---|---|---|---|
| 900 | 0.2 | 1.64 | 1.49 (0.91) | 1.00 (0.61) |
| 900 | 1 | 2.33 | 2.02 (0.87) | 1.60 (0.69) |
| 900 | 5 | 2.62 | 1.89 (0.72) | 1.81 (0.69) |
| 1000 | 0.2 | 1.47 | 1.32 (0.90) | 0.85 (0.58) |
| 1000 | 1 | 1.21 | 1.05 (0.87) | 0.62 (0.51) |
| 1000 | 5 | 0.62 | 0.49 (0.78) | 0.30 (0.49) |
| 1100 | 0.2 | 1.32 | 1.18 (0.89) | 0.69 (0.52) |
| 1100 | 1 | 0.13 | 0.07 (0.61) | 0.01 (0.12) |
| 1100 | 5 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quyen, L.D.; Choi, J.M. Accumulation and Dispersion of Microplastics near A Submerged Structure: Basic Study Using A Numerical Wave Tank. J. Mar. Sci. Eng. 2022, 10, 1934. https://doi.org/10.3390/jmse10121934
Quyen LD, Choi JM. Accumulation and Dispersion of Microplastics near A Submerged Structure: Basic Study Using A Numerical Wave Tank. Journal of Marine Science and Engineering. 2022; 10(12):1934. https://doi.org/10.3390/jmse10121934
Chicago/Turabian StyleQuyen, Le Duc, and Jun Myoung Choi. 2022. "Accumulation and Dispersion of Microplastics near A Submerged Structure: Basic Study Using A Numerical Wave Tank" Journal of Marine Science and Engineering 10, no. 12: 1934. https://doi.org/10.3390/jmse10121934





