Examining the Ability of CMIP6 Models to Reproduce the Upwelling SST Imprint in the Eastern Boundary Upwelling Systems
Abstract
1. Introduction
2. Methods
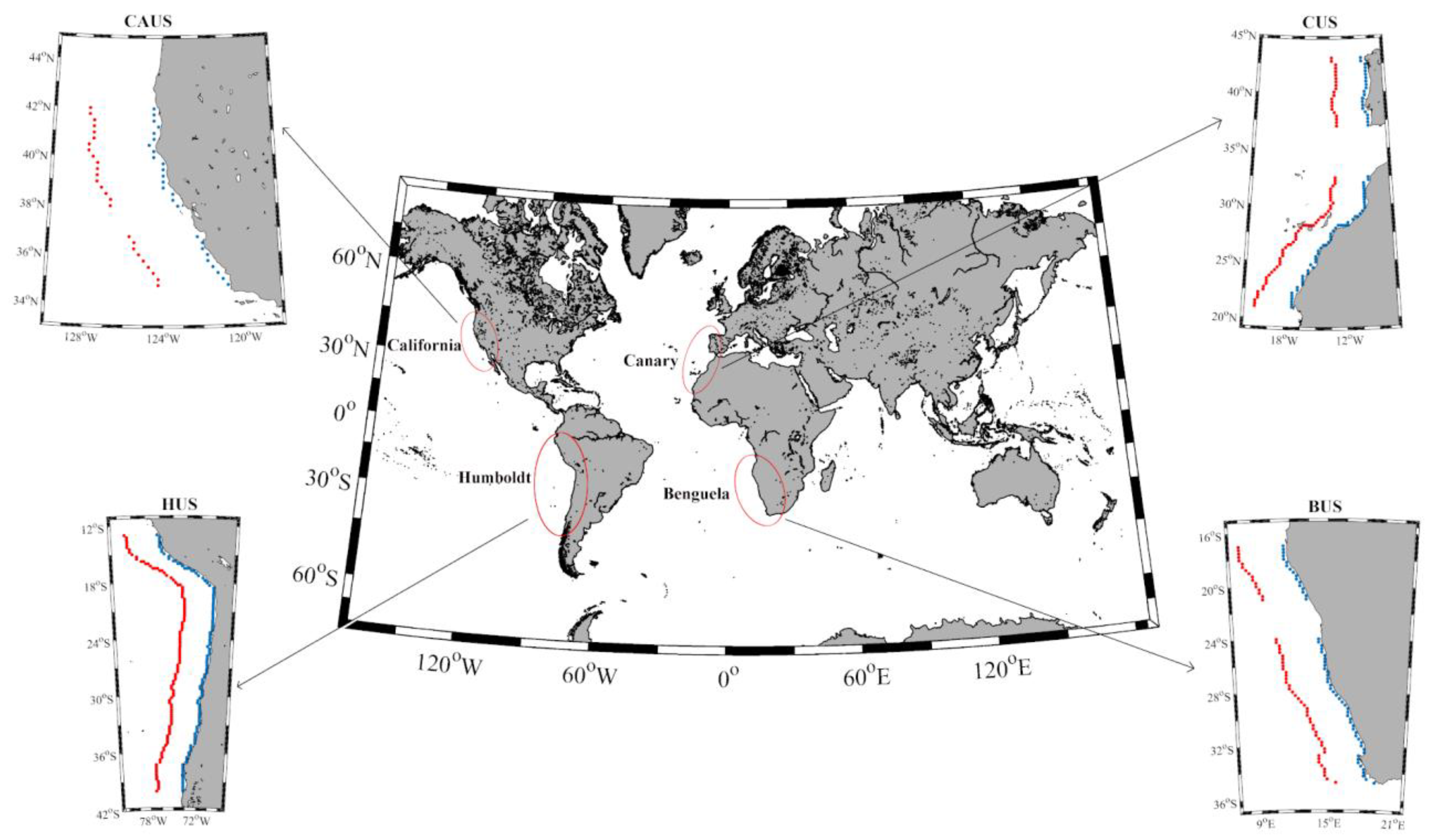
2.1. SST Data
2.2. Analysis of Coastal and Oceanic SST
2.3. Validation
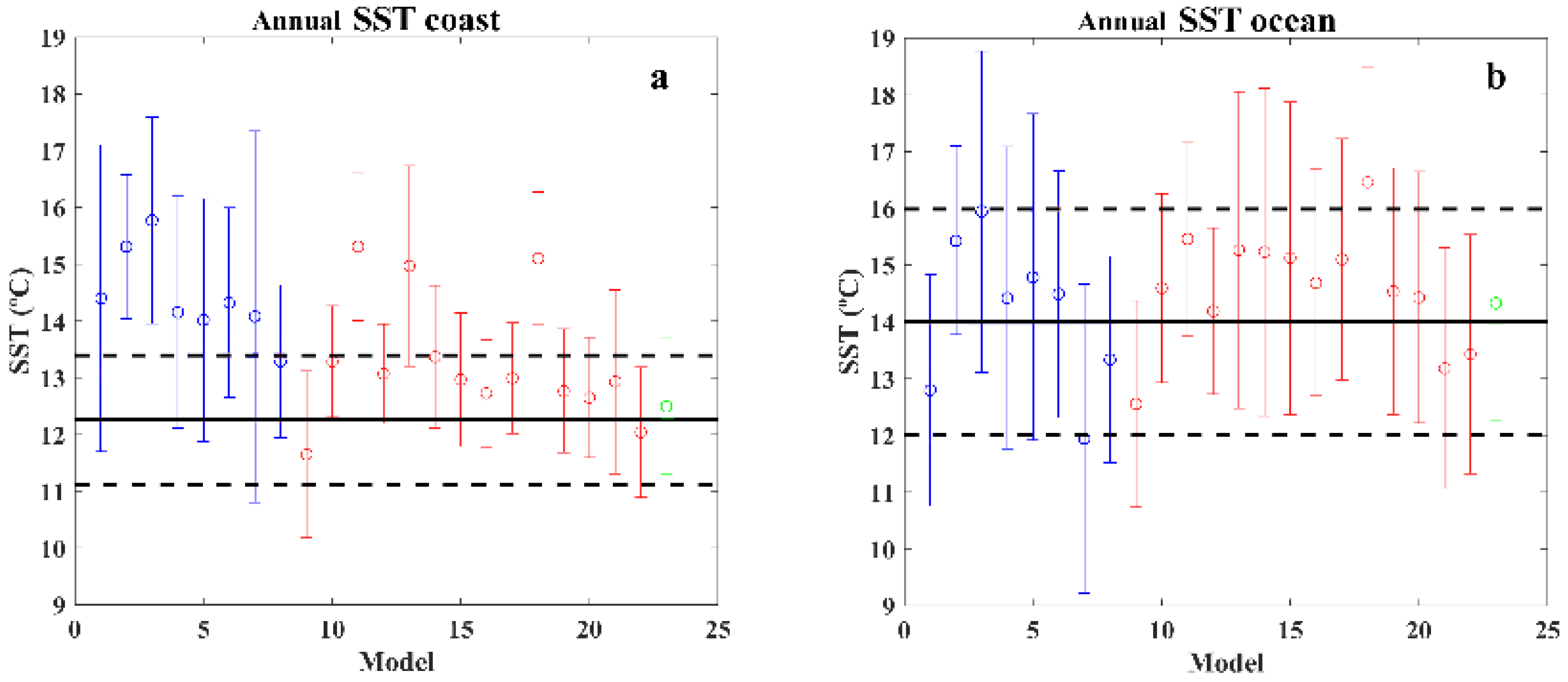
3. Results and Discussion
4. Conclusions
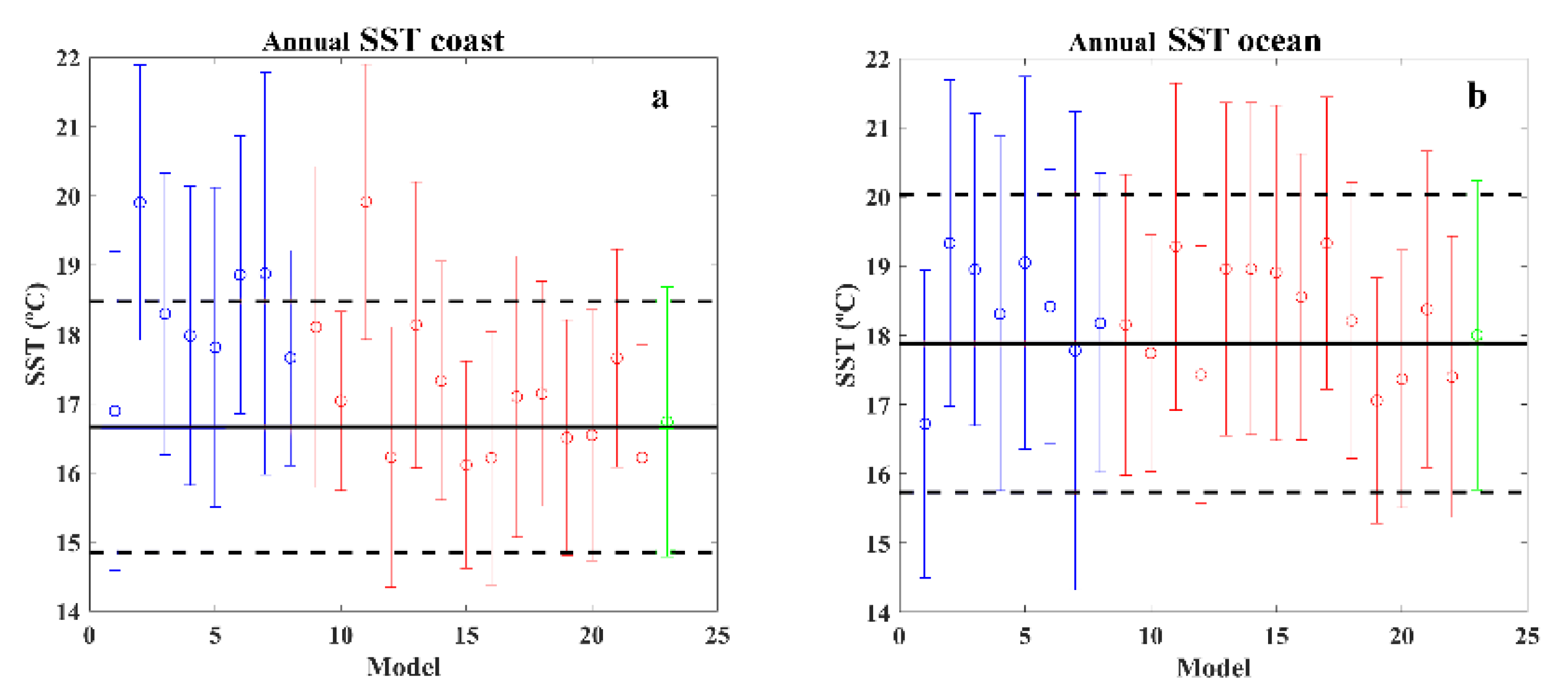
- Benguela: No model adequately reproduces the SST imprint under the conditions established in the present study.
- Canary: CNRM-HR (historical and hist-1950) (3 and 13), GFDL-CM4 (4), HadGEM-MM (6), CMCC-VHR4 (12), and EC-Earth3P (14).
- Humboldt: CESM1-HR (10), CMCC-VHR4 (12), ECMWF-HR (16), and HadGEM-HM (20).
- California: HadGEM-HH and HadGEM-HM (19 and 20).
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brewin, R.J.; Smale, D.A.; Moore, P.J.; Dall’Olmo, G.; Miller, P.I.; Taylor, B.H.; Smyth, T.J.; Fishwick, J.R.; Yang, M. Evaluating operational AVHRR sea surface temperature data at the coastline using benthic temperature loggers. Remote Sens. 2018, 10, 925. [Google Scholar] [CrossRef]
- Thakur, K.K.; Vanderstichel, R.; Barrell, J.; Stryhn, H.; Patanasatienkul, T.; Revie, C.W. Comparison of remotely-sensed sea surface temperature and salinity products with in situ measurements from British Columbia, Canada. Front. Mar. Sci. 2018, 5, 121. [Google Scholar] [CrossRef]
- Demarcq, H. Trends in primary production, sea surface temperature and wind in upwelling systems (1998–2007). Prog. Oceanogr. 2009, 83, 376–385. [Google Scholar] [CrossRef]
- Lima, F.P.; Wethey, D.S. Three decades of high-resolution coastal sea surface temperatures reveal more than warming. Nat. Commun. 2012, 3, 704. [Google Scholar] [CrossRef]
- Benazzouz, A.; Mordane, S.; Orbi, A.; Chagdali, M.; Hilmi, K.; Atillah, A.; Pelegrí, J.L.; Hervé, D. An improved coastal upwelling index from sea surface temperature using satellite-based approach—The case of the Canary Current upwelling system. Cont. Shelf Res. 2014, 81, 38–54. [Google Scholar] [CrossRef]
- Tim, N.; Zorita, E.; Hünicke, B. Decadal variability and trends of the Benguela upwelling system as simulated in a high-resolution ocean simulation. Ocean Sci. 2015, 11, 483–502. [Google Scholar] [CrossRef]
- Varela, R.; Lima, F.P.; Seabra, R.; Meneghesso, C.; Gómez-Gesteira, M. Coastal warming and wind-driven upwelling: A global analysis. Sci. Total. Environ. 2018, 639, 1501–1511. [Google Scholar] [CrossRef]
- Seabra, R.; Varela, R.; Santos, A.M.; Gómez-Gesteira, M.; Meneghesso, C.; Wethey, D.S.; Lima, F.P. Reduced Nearshore Warming Associated With Eastern Boundary Upwelling Systems. Front. Mar. Sci. 2019, 6, 104. [Google Scholar] [CrossRef]
- Meneghesso, C.; Seabra, R.; Broitman, B.R.; Wethey, D.S.; Burrows, M.T.; Chan, B.K.; Guy-Haim, T.; Ribeiro, P.A.; Rilov, G.; Santos, A.M.; et al. Remotely-sensed L4 SST underestimates the thermal fingerprint of coastal upwelling. Remote. Sens. Environ. 2020, 237, 111588. [Google Scholar] [CrossRef]
- Dufois, F.; Penven, P.; Whittle, C.P.; Veitch, J. On the warm nearshore bias in Pathfinder monthly SST products over Eastern Boundary Upwelling Systems. Ocean Model. 2012, 47, 113–118. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Fischer, E.M.; Gruber, N. Marine heatwaves under global warming. Nature 2018, 560, 360–364. [Google Scholar] [CrossRef] [PubMed]
- Darmaraki, S.; Somot, S.; Sevault, F.; Nabat, P.; Narvaez, W.D.C.; Cavicchia, L.; Djurdjevic, V.; Li, L.; Sannino, G.; Sein, D.V. Future evolution of Marine Heatwaves in the Mediterranean Sea. Clim. Dyn. 2019, 53, 1371–1392. [Google Scholar] [CrossRef]
- Alexander, M.A.; Scott, J.D.; Friedland, K.D.; Mills, K.E.; Nye, J.A.; Pershing, A.J.; Thomas, A.C. Projected sea surface temperatures over the 21st century: Changes in the mean, variability and extremes for large marine ecosystem regions of Northern Oceans. Elementa Sci. Anthr. 2018, 6, 9. [Google Scholar] [CrossRef]
- Sousa, M.C.; Alvarez, I.; Decastro, M.; Gomez-Gesteira, M.; Dias, J.M. Seasonality of coastal upwelling trends under future warming scenarios along the southern limit of the canary upwelling system. Prog. Oceanogr. 2017, 153, 16–23. [Google Scholar] [CrossRef]
- Varela, R.; Rodríguez-Díaz, L.; de Castro, M.; Gómez-Gesteira, M. Influence of Canary upwelling system on coastal SST warming along the 21st century using CMIP6 GCMs. Glob. Planet. Chang. 2021, 208, 103692. [Google Scholar] [CrossRef]
- Oyarzún, D.; Brierley, C.M. The future of coastal upwelling in the Humboldt current from model projections. Clim. Dyn. 2018, 52, 599–615. [Google Scholar] [CrossRef]
- Sylla, A.; Mignot, J.; Capet, X.; Gaye, A.T. Weakening of the Senegalo–Mauritanian upwelling system under climate change. Clim. Dyn. 2019, 53, 4447–4473. [Google Scholar] [CrossRef]
- Sousa, M.C.; Ribeiro, A.; Des, M.; Gomez-Gesteira, M.; Decastro, M.; Dias, J.M. NW Iberian Peninsula coastal upwelling future weakening: Competition between wind intensification and surface heating. Sci. Total. Environ. 2019, 703, 134808. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Artal, O.; Sepúlveda, H.H.; Mery, D.; Pieringer, C. Detecting and characterizing upwelling filaments in a numerical ocean model. Comput. Geosci. 2018, 122, 25–34. [Google Scholar] [CrossRef]
- Santana-Falcón, Y.; Mason, E.; Arístegui, J. Offshore transport of organic carbon by upwelling filaments in the Canary Current System. Prog. Oceanogr. 2020, 186, 102322. [Google Scholar] [CrossRef]
- Hauschildt, J.; Thomsen, S.; Echevin, V.; Oschlies, A.; José, Y.S.; Krahmann, G.; Bristow, L.A.; Lavik, G. The fate of upwelled nitrate off Peru shaped by submesoscale filaments and fronts. Biogeosciences 2021, 18, 3605–3629. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, L.; Lee, S.-K.; Wu, L.; Mechoso, C.R. A global perspective on CMIP5 climate model biases. Nat. Clim. Chang. 2014, 4, 201–205. [Google Scholar] [CrossRef]
- Richter, I. Climate model biases in the eastern tropical oceans: Causes, impacts and ways forward. WIREs Clim. Chang. 2015, 6, 345–358. [Google Scholar] [CrossRef]
- Ma, J.; Xu, S.; Wang, B. Warm bias of sea surface temperature in Eastern boundary current regions—A study of effects of horizontal resolution in CESM. Ocean Dyn. 2019, 69, 939–954. [Google Scholar] [CrossRef]
- Gent, P.R.; Yeager, S.G.; Neale, R.B.; Levis, S.; Bailey, D.A. Improvements in a half degree atmosphere/land version of the CCSM. Clim. Dyn. 2009, 34, 819–833. [Google Scholar] [CrossRef]
- Small, R.J.; Curchitser, E.; Hedstrom, K.; Kauffman, B.; Large, W.G. The Benguela Upwelling System: Quantifying the Sensitivity to Resolution and Coastal Wind Representation in a Global Climate Model*. J. Clim. 2015, 28, 9409–9432. [Google Scholar] [CrossRef]
- Des, M.; Martínez, B.; Decastro, M.; Viejo, R.; Sousa, M.; Gómez-Gesteira, M. The impact of climate change on the geographical distribution of habitat-forming macroalgae in the Rías Baixas. Mar. Environ. Res. 2020, 161, 105074. [Google Scholar] [CrossRef]
- Castro-Olivares, A.; Des, M.; Olabarria, C.; de Castro, M.; Vázquez, E.; Sousa, M.C.; Gómez-Gesteira, M. Does global warming threaten small-scale bivalve fisheries in NW Spain? Mar. Environ. Res. 2022, 180, 105707. [Google Scholar] [CrossRef]
- Des, M.; Gómez-Gesteira, J.; Decastro, M.; Iglesias, D.; Sousa, M.; ElSerafy, G.; Gómez-Gesteira, M. Historical and future naturalization of Magallana gigas in the Galician coast in a context of climate change. Sci. Total Environ. 2022, 838, 156437. [Google Scholar] [CrossRef]
- Haarsma, R.J.; Roberts, M.J.; Vidale, P.L.; Senior, C.A.; Bellucci, A.; Bao, Q.; Chang, P.; Corti, S.; Fučkar, N.S.; Guemas, V.; et al. High Resolution Model Intercomparison Project (HighResMIP v1.0) for CMIP6. Geosci. Model Dev. 2016, 9, 4185–4208. [Google Scholar] [CrossRef]
- Richter, I.; Tokinaga, H. An overview of the performance of CMIP6 models in the tropical Atlantic: Mean state, variability, and remote impacts. Clim. Dyn. 2020, 55, 2579–2601. [Google Scholar] [CrossRef]
- Li, J.F.; Xu, K.; Jiang, J.H.; Lee, W.; Wang, L.; Yu, J.; Stephens, G.; Fetzer, E.; Wang, Y. An Overview of CMIP5 and CMIP6 Simulated Cloud Ice, Radiation Fields, Surface Wind Stress, Sea Surface Temperatures, and Precipitation Over Tropical and Subtropical Oceans. J. Geophys. Res. Atmos. 2020, 125, e2020JD032848. [Google Scholar] [CrossRef]
- Halder, S.; Parekh, A.; Chowdary, J.S.; Gnanaseelan, C.; Kulkarni, A. Assessment of CMIP6 models’ skill for tropical Indian Ocean sea surface temperature variability. Int. J. Clim. 2020, 41, 2568–2588. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Kodama, C.; Ohno, T.; Seiki, T.; Yashiro, H.; Noda, A.T.; Nakano, M.; Sugi, M. The non-hydrostatic global atmospheric model for CMIP6 HighResMIP simulations (NICAM16-S): Experimental design, model description, and sensitivity experiments. Geosci. Model Dev. Discuss. 2020, 2020, 1–50. [Google Scholar]
- Costoya, X.; Rocha, A.; Carvalho, D. Using bias-correction to improve future projections of offshore wind energy resource: A case study on the Iberian Peninsula. Appl. Energy 2020, 262, 114562. [Google Scholar] [CrossRef]
- Arguilé-Pérez, B.; Ribeiro, A.S.; Costoya, X.; Decastro, M.; Carracedo, P.; Dias, J.M.; Rusu, L.; Gómez-Gesteira, M. Harnessing of Different WECs to Harvest Wave Energy along the Galician Coast (NW Spain). J. Mar. Sci. Eng. 2022, 10, 719. [Google Scholar] [CrossRef]
- Santos, F.; Gómez-Gesteira, M.; deCastro, M.; Álvarez, I. Differences in coastal and oceanic SST trends due to the strengthening of coastal upwelling along the Benguela current system. Cont. Shelf Res. 2012, 34, 79–86. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, X.-H.; Jo, Y.-H.; Jiang, L.; Jiang, Y. A study of Benguela upwelling system using different upwelling indices derived from remotely sensed data. Cont. Shelf Res. 2012, 45, 27–33. [Google Scholar] [CrossRef]
- Santos, F.; Decastro, M.; Gómez-Gesteira, M.; Álvarez, I. Differences in coastal and oceanic SST warming rates along the Canary upwelling ecosystem from 1982 to 2010. Cont. Shelf Res. 2012, 47, 1–6. [Google Scholar] [CrossRef]
- Barton, E.D.; Field, D.B.; Roy, C. Canary current upwelling: More or less? Prog. Oceanogr. 2013, 116, 167–178. [Google Scholar] [CrossRef]
- Cropper, T.E.; Hanna, E.; Bigg, G.R. Spatial and temporal seasonal trends in coastal upwelling off Northwest Africa, 1981–2012. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2014, 86, 94–111. [Google Scholar] [CrossRef]
- Wang, Y.; Castelao, R.M.; Yuan, Y. Seasonal variability of alongshore winds and sea surface temperature fronts in Eastern Boundary Current Systems. J. Geophys. Res. Oceans 2015, 120, 2385–2400. [Google Scholar] [CrossRef]
- Gutiérrez, D.; Bouloubassi, I.; Sifeddine, A.; Purca, S.; Goubanova, K.; Graco, M.; Field, D.; Méjanelle, L.; Velazco, F.; Lorre, A.; et al. Coastal cooling and increased productivity in the main upwelling zone off Peru since the mid-twentieth century. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Pardo, P.C.; Padín, X.; Gil Coto, M.; Fariña-Busto, L.; Perez, F.F. Evolution of upwelling systems coupled to the long-term variability in sea surface temperature and Ekman transport. Clim. Res. 2011, 48, 231–246. [Google Scholar] [CrossRef]
- Echevin, V.; Goubanova, K.; Belmadani, A.; Dewitte, B. Sensitivity of the Humboldt Current system to global warming: A downscaling experiment of the IPSL-CM4 model. Clim. Dyn. 2011, 38, 761–774. [Google Scholar] [CrossRef]
- Gutiérrez, D.; Akester, M.; Naranjo, L. Productivity and Sustainable Management of the Humboldt Current Large Marine Ecosystem under climate change. Environ. Dev. 2016, 17, 126–144. [Google Scholar] [CrossRef]
- Hernandez, O.; Jouanno, J.; Echevin, V.; Aumont, O. Modification of sea surface temperature by chlorophyll concentration in the Atlantic upwelling systems. J. Geophys. Res. Ocean. 2017, 122, 5367–5389. [Google Scholar] [CrossRef]
- Iitembu, J.A.; Dalu, T. Patterns of trophic resource use among deep-sea shrimps in the Northern Benguela current ecosystem, Namibia. Food Webs 2018, 16, e00089. [Google Scholar] [CrossRef]
- Siemer, J.P.; Machín, F.; González-Vega, A.; Arrieta, J.M.; Gutiérrez-Guerra, M.A.; Pérez-Hernández, M.D.; Vélez-Belchí, P.; Hernández-Guerra, A.; Fraile-Nuez, E. Recent Trends in SST, Chl-a, Productivity and Wind Stress in Upwelling and Open Ocean Areas in the Upper Eastern North Atlantic Subtropical Gyre. J. Geophys. Res. Oceans 2021, 126, e2021JC017268. [Google Scholar] [CrossRef]
- García-Reyes, M.; Largier, J.L. Seasonality of coastal upwelling off central and northern California: New insights, including temporal and spatial variability. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Sylla, A.; Gomez, E.S.; Mignot, J.; López-Parages, J. Impact of increased resolution on the representation of the Canary upwelling system in climate models. Geosci. Model Dev. 2022, 15, 8245–8267. [Google Scholar] [CrossRef]
- Farneti, R.; Stiz, A.; Ssebandeke, J.B. Improvements and persistent biases in the southeast tropical Atlantic in CMIP models. NPJ Clim. Atmos. Sci. 2022, 5, 42. [Google Scholar] [CrossRef]
- Balaguru, K.; Van Roekel, L.P.; Leung, L.R.; Veneziani, M. Subtropical Eastern North Pacific SST Bias in Earth System Models. J. Geophys. Res. Oceans 2021, 126, e2021JC017359. [Google Scholar] [CrossRef]
- Liu, H.; Song, Z.; Wang, X.; Misra, V. An ocean perspective on CMIP6 climate model evaluations. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2022, 201, 105120. [Google Scholar] [CrossRef]
- Wang, Y.; Heywood, K.J.; Stevens, D.P.; Damerell, G.M. Seasonal extrema of sea surface temperature in CMIP6 models. Ocean Sci. 2022, 18, 839–855. [Google Scholar] [CrossRef]
- Richter, I.; Xie, S.-P. On the origin of equatorial Atlantic biases in coupled general circulation models. Clim. Dyn. 2008, 31, 587–598. [Google Scholar] [CrossRef]
- Xu, Z.; Li, M.; Patricola, C.; Chang, P. Oceanic origin of southeast tropical Atlantic biases. Clim. Dyn. 2013, 43, 2915–2930. [Google Scholar] [CrossRef]
- Patricola, C.M.; Chang, P. Structure and dynamics of the Benguela low-level coastal jet. Clim. Dyn. 2016, 49, 2765–2788. [Google Scholar] [CrossRef]
- Kurian, J.; Li, P.; Chang, P.; Patricola, C.M.; Small, J. Impact of the Benguela coastal low-level jet on the southeast tropical Atlantic SST bias in a regional ocean model. Clim. Dyn. 2021, 56, 2773–2800. [Google Scholar] [CrossRef]
- Oettli, P.; Yuan, C.; Richter, I. The Other Coastal Niño/Niña—The Benguela, California and Dakar Niños/Niñas. In Tropical and Extra-Tropical Air-Sea Interactions; Behera, S.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128181560. [Google Scholar]
- Song, Z.; Liu, H.; Chen, X. Eastern equatorial Pacific SST seasonal cycle in global climate models: From CMIP5 to CMIP6. Acta Oceanol. Sin. 2020, 39, 50–60. [Google Scholar] [CrossRef]
- Burrows, M.T.; Schoeman, D.S.; Richardson, A.J.; Molinos, J.G.; Hoffmann, A.; Buckley, L.B.; Moore, P.J.; Brown, C.J.; Bruno, J.F.; Duarte, C.M.; et al. Geographical limits to species-range shifts are suggested by climate velocity. Nature 2014, 507, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, C.R.; Zardi, G.I.; McQuaid, C.D.; Serrão, E.A.; Pearson, G.A.; Jacinto, R.; Nicastro, K.R. Upwelling areas as climate change refugia for the distribution and genetic diversity of a marine macroalga. J. Biogeogr. 2016, 43, 1595–1607. [Google Scholar] [CrossRef]
- Renault, L.; Deutsch, C.; McWilliams, L.R.J.C.; Frenzel, C.D.H.; Liang, J.-H.; Colas, F. Partial decoupling of primary productivity from upwelling in the California Current system. Nat. Geosci. 2016, 9, 505–508. [Google Scholar] [CrossRef]





| Model Number | Name | Experiment ID | Oceanic Resolution (°) | Atmospheric Resolution (°) | Variant Label |
|---|---|---|---|---|---|
| 1 | AWI-CM-1-1-MR | Historical | 0.25 | 1 | r1i1p1f1 |
| 2 | CMCC-CM2-HR4 | Historical | 0.25 | 1 | r1i1p1f1 |
| 3 | CNRM-CM6-1-HR | Historical | 0.25 | 1 | r1i1p1f2 |
| 4 | GFDL-CM4 | Historical | 0.25 | 1 | r1i1p1f1 |
| 5 | GFDL-ESM4 | Historical | 0.5 | 1 | r1i1p1f1 |
| 6 | HadGEM3-GC31-MM | Historical | 0.25 | 1 | r1i1p1f3 |
| 7 | ICON-ESM-LR | Historical | 0.5 | 2.5 | r1i1p1f1 |
| 8 | MPI-ESM1-2-HR | Historical | 0.5 | 1 | r1i1p1f1 |
| 9 | BCC-CSM2-HR | Hist-1950 | 0.5 | 0.5 | r1i1p1f1 |
| 10 | CESM1-CAM5-SE-HR | Hist-1950 | 0.1 | 0.25 | r1i1p1f1 |
| 11 | CMCC-CM2-HR4 | Hist-1950 | 0.25 | 1 | r1i1p1f1 |
| 12 | CMCC-CM2-VHR4 | Hist-1950 | 0.25 | 0.25 | r1i1p1f1 |
| 13 | CNRM-CM6-1-HR | Hist-1950 | 0.25 | 1 | r1i1p1f2 |
| 14 | EC-Earth3P | Hist-1950 | 1 | 0.8 | r3i1p2f1 |
| 15 | EC-Earth3P-HR | Hist-1950 | 0.25 | 0.5 | r1i1p2f1 |
| 16 | ECMWF-IFS-HR | Hist-1950 | 0.25 | 0.25 | r1i1p1f1 |
| 17 | ECMWF-IFS-MR | Hist-1950 | 0.25 | 0.5 | r1i1p1f1 |
| 18 | FGOALS-f3-H | Hist-1950 | 0.1 | 0.25 | r1i1p1f1 |
| 19 | HadGEM3-GC31-HH | Hist-1950 | 0.1 | 0.5 | r1i1p1f1 |
| 20 | HadGEM3-GC31-HM | Hist-1950 | 0.25 | 0.5 | r1i1p1f1 |
| 21 | MPI-ESM1-2-HR | Hist-1950 | 0.5 | 1 | r1i1p1f1 |
| 22 | MPI-ESM1-2-XR | Hist-1950 | 0.5 | 0.5 | r1i1p1f1 |
| 23 | NICAM16-8S | HighresSST-present | None | 0.5 | r1i1p1f1 |
| Benguela | Canary | Humboldt | California | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | NBias (%) | NRMSE (%) | NBias (%) | NRMSE (%) | NBias (%) | NRMSE (%) | NBias (%) | |||||||||
| Model | Coast | Ocean | Coast | Ocean | Coast | Ocean | Coast | Ocean | Coast | Ocean | Coast | Ocean | Coast | Ocean | Coast | Ocean |
| 1 | 23.93 | 7.15 | 22.28 | 2.28 | 7.01 | 3.46 | −4.67 | −2.04 | 6.49 | 7.81 | 1.38 | −6.74 | 19.03 | 9.07 | 16.04 | −8.91 |
| 2 | 32.43 | 11.70 | 29.21 | 10.52 | 5.75 | 5.53 | −0.92 | −1.77 | 18.79 | 8.40 | 17.95 | 7.76 | 22.35 | 9.81 | 22.12 | 9.74 |
| 3 | 29.05 | 7.98 | 27.02 | 5.43 | 4.97 | 3.10 | −3.86 | −2.89 | 10.32 | 6.78 | 9.59 | 5.77 | 25.16 | 13.02 | 25.08 | 12.99 |
| 4 | 23.17 | 6.01 | 21.43 | −0.45 | 3.96 | 1.93 | 0.69 | 0.33 | 9.03 | 3.94 | 7.57 | 2.36 | 14.69 | 3.35 | 14.09 | 3.02 |
| 5 | 29.48 | 8.89 | 28.36 | 7.35 | 8.45 | 3.29 | 5.60 | 2.34 | 10.34 | 7.21 | 9.37 | 6.29 | 13.06 | 5.73 | 12.51 | 5.50 |
| 6 | 25.92 | 4.99 | 24.86 | 2.60 | 4.14 | 1.89 | −0.86 | −0.15 | 14.40 | 5.30 | 12.61 | 2.89 | 15.77 | 3.65 | 15.51 | 3.46 |
| 7 | 43.89 | 14.75 | 39.17 | 12.12 | 7.74 | 3.38 | 3.42 | −0.24 | 15.48 | 8.08 | 11.34 | −0.59 | 19.55 | 17.10 | 14.60 | −15.82 |
| 8 | 28.96 | 7.37 | 27.62 | 6.52 | 4.33 | 5.24 | −2.97 | −4.69 | 6.89 | 6.39 | 5.80 | 1.62 | 9.96 | 5.28 | 8.06 | −4.82 |
| 9 | 30.13 | 8.55 | 21.64 | 7.45 | 11.00 | 3.51 | 7.34 | 0.74 | 12.68 | 8.83 | 8.11 | 1.47 | 7.87 | 11.47 | −5.09 | −10.85 |
| 10 | 16.96 | 4.38 | 9.81 | 2.17 | 6.01 | 3.99 | 4.98 | 3.38 | 4.04 | 1.52 | 2.22 | −0.81 | 8.21 | 4.31 | 8.03 | 4.17 |
| 11 | 31.58 | 11.23 | 28.30 | 9.99 | 5.90 | 5.61 | −0.18 | −0.65 | 18.85 | 8.21 | 18.00 | 7.51 | 22.37 | 10.00 | 22.17 | 9.93 |
| 12 | 16.91 | 7.08 | 11.69 | 6.02 | 3.09 | 4.31 | −1.36 | −2.85 | 3.27 | 3.65 | −2.41 | −2.57 | 6.75 | 2.04 | 6.41 | 1.38 |
| 13 | 19.64 | 7.54 | 16.42 | 3.54 | 4.59 | 3.43 | −3.24 | −3.23 | 9.72 | 6.82 | 8.69 | 5.80 | 20.08 | 8.70 | 19.91 | 8.66 |
| 14 | 24.19 | 12.73 | 23.67 | 11.95 | 2.48 | 3.57 | −1.31 | −2.97 | 5.93 | 8.02 | 1.62 | 5.84 | 10.71 | 8.63 | 10.36 | 8.45 |
| 15 | 13.09 | 10.51 | 11.67 | 9.85 | 6.43 | 1.85 | −5.69 | −1.03 | 4.70 | 6.92 | −3.10 | 5.54 | 5.77 | 7.97 | 5.61 | 7.72 |
| 16 | 5.71 | 5.44 | 0.91 | 4.10 | 9.48 | 4.90 | −8.97 | −4.63 | 4.20 | 4.94 | −2.50 | 3.69 | 4.55 | 5.11 | 3.75 | 4.83 |
| 17 | 8.56 | 6.97 | 4.78 | 5.34 | 8.85 | 4.38 | −8.31 | −4.10 | 5.15 | 9.31 | 2.83 | 7.76 | 6.34 | 7.63 | 5.80 | 7.57 |
| 18 | 6.61 | 6.40 | 4.64 | −2.55 | 11.91 | 5.68 | 11.54 | 5.62 | 5.59 | 3.56 | 2.64 | 1.83 | 20.81 | 16.23 | 20.77 | 16.17 |
| 19 | 8.58 | 4.69 | −5.87 | −4.13 | 5.96 | 2.49 | −4.55 | −1.72 | 4.10 | 5.48 | −0.93 | −4.74 | 4.24 | 3.98 | 4.08 | 3.79 |
| 20 | 8.84 | 4.22 | −4.01 | −3.28 | 8.27 | 4.16 | −7.55 | −3.48 | 4.32 | 4.14 | −0.48 | −2.93 | 3.58 | 3.66 | 3.16 | 3.08 |
| 21 | 16.92 | 5.81 | 12.85 | 4.15 | 6.22 | 4.60 | −4.80 | −3.99 | 7.28 | 7.62 | 5.78 | 2.71 | 8.90 | 6.42 | 5.31 | −5.98 |
| 22 | 8.88 | 2.94 | 3.55 | 0.46 | 6.72 | 4.77 | −5.94 | −4.37 | 7.80 | 5.68 | −2.71 | −2.74 | 3.95 | 5.79 | −1.79 | −4.15 |
| 23 | 2.27 | 0.94 | 0.16 | 0.83 | 1.64 | 0.79 | 0.41 | 0.59 | 1.65 | 1.33 | −0.70 | 0.65 | 2.85 | 2.42 | 2.36 | 2.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varela, R.; DeCastro, M.; Rodriguez-Diaz, L.; Dias, J.M.; Gómez-Gesteira, M. Examining the Ability of CMIP6 Models to Reproduce the Upwelling SST Imprint in the Eastern Boundary Upwelling Systems. J. Mar. Sci. Eng. 2022, 10, 1970. https://doi.org/10.3390/jmse10121970
Varela R, DeCastro M, Rodriguez-Diaz L, Dias JM, Gómez-Gesteira M. Examining the Ability of CMIP6 Models to Reproduce the Upwelling SST Imprint in the Eastern Boundary Upwelling Systems. Journal of Marine Science and Engineering. 2022; 10(12):1970. https://doi.org/10.3390/jmse10121970
Chicago/Turabian StyleVarela, Rubén, Maite DeCastro, Laura Rodriguez-Diaz, João Miguel Dias, and Moncho Gómez-Gesteira. 2022. "Examining the Ability of CMIP6 Models to Reproduce the Upwelling SST Imprint in the Eastern Boundary Upwelling Systems" Journal of Marine Science and Engineering 10, no. 12: 1970. https://doi.org/10.3390/jmse10121970
APA StyleVarela, R., DeCastro, M., Rodriguez-Diaz, L., Dias, J. M., & Gómez-Gesteira, M. (2022). Examining the Ability of CMIP6 Models to Reproduce the Upwelling SST Imprint in the Eastern Boundary Upwelling Systems. Journal of Marine Science and Engineering, 10(12), 1970. https://doi.org/10.3390/jmse10121970









